Abstract
We report the simultaneous operation and two-qubit-coupling measurement of a pair of two-electron spin qubits, actively decoupled from quasi-static nuclear noise in a GaAs quadruple quantum dot array. Coherent Rabi oscillations of both qubits (decay time ≈2 μs; frequency few MHz) are achieved by continuously tuning their drive frequency using rapidly converging real-time Hamiltonian estimators. We observe strong two-qubit capacitive interaction (>190 MHz), combined with detuning pulses, inducing a state-conditional frequency shift. The two-qubit capacitive interaction is beyond the bilinear regime, consistent with recent theoretical predictions. We observe a high ratio (>16) between coherence and conditional phase-flip time, which supports the possibility of generating high-fidelity and fast quantum entanglement between encoded spin qubits using a simple capacitive interaction.
Similar content being viewed by others
Introduction
Spins in semiconductor quantum dot (QD) nanostructures offer a promising platform for realizing scalable quantum information-processing units with high-fidelity universal quantum control1,2,3. Recent progress in III–V and IV semiconducting materials demonstrated several achievements including the demonstration of single- and two-qubit gate fidelities exceeding 99% in NatSi and 28Si (ref. 2,3), simultaneous qubit operations in GaAs with a coherence time over 2 µs (refs. 4,5), a few qubit entanglements in Ge and 28Si (refs. 6,7,8), high-temperature operations of spin qubits9,10,11, and long-range coupling of spin qubits using superconducting cavity structures12,13. The field is currently moving towards the high-fidelity control of multiple qubits and the generation of controlled entanglement.
However, low-frequency noise, including quasi-static nuclear fluctuation and slow charge noise, is one of the main factors reducing coherence times below the intrinsic limit of a given host material14,15,16,17,18,19,20. For example, the spin coherence time is often affected by charge noise coupled through the inhomogeneous magnetic field generated by micromagnets18,19. In addition, exchange- or capacitive-coupling-based two-qubit control is inherently susceptible to charge noise14,16,20,21,22. Thus, eliminating or mitigating slow magnetic and electric noises is an important task in semiconductor QD platforms.
Real-time Hamiltonian parameter estimation and measurement-based feedback4,23,24 are two complementary techniques to coherent quantum feedback25 capable of error mitigation, which is compatible —albeit sequentially—with general qubit controls. Previously, the Hamiltonian parameter estimation applied to GaAs has shown that the effect of quasi-static nuclear spin fluctuations can be strongly suppressed for single-spin23 and singlet–triplet (ST0) qubits4. Nevertheless, extending the technique to a multiqubit system is desirable. While this has not been demonstrated to date, the simultaneous Hamiltonian estimation is also crucial for the accurate measurement of inter-qubit coupling strength. This is particularly important in the case of GaAs, for which the application of real-time calibrated single-qubit rotations on each qubit is a prerequisite.
In this study, we demonstrate the simultaneous drive of a pair of ST0 qubits in GaAs. The quasi-static nuclear noise for each qubit is actively decoupled using a Bayesian inference-based real-time Hamiltonian estimation circuit. We show high-quality Rabi oscillations for both qubits with an oscillation quality factor above 10. We further exploit this result to demonstrate the measurement of the electrostatic coupling of two ST0 qubits, which grows beyond an empirically assumed bilinear form26,27 for large intra-qubit exchange energies. Combining this with the spin-echo sequence, we assess the potential to generate a high-fidelity and fast conditional phase gate using capacitive interactions in a linear QD array.
Results
Simultaneous Hamiltonian parameter estimation
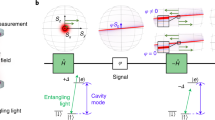
Figure 1a shows a quadruple QD device on top of a GaAs/AlGaAs heterostructure, hosting a pair of ST0 qubits with singlet \(\left| S \right\rangle\) and triplet-zero \(\left| {T_0} \right\rangle\) basis states (See methods section and ref. 28 for details of the material structure and device fabrication). High-frequency and synchronous voltage pulses, combined with DC voltages through bias-tees, were input to gates V1–V6. Fast dual RF reflectometry was performed by injecting a carrier signal having a frequency \(\approx\)125 MHz (153 MHz) and power of –100 dBm at the Ohmic contacts of the left (right) RF single-electron transistors (see Fig. 1a). The reflected power was monitored through a frequency-multiplexed homodyne detection. The device was operated in a dilution refrigerator with a base temperature\(\approx \,7{{{\mathrm{ }}}}mK\), where an external magnetic field (0.7 T) was applied in the direction shown in Fig. 1a. The measured electron temperature is \(\approx\)72 mK (ref. 28).
a A schematic of the experimental setup. Yellow circles indicate the RF single-electron transistors for dual RF reflectometry. Orange (green) circles indicate QDs for the left (right) ST0 qubit (QL and QR). The plunger and barrier gates are connected to the arbitrary waveform generator for the application of detuning and RF pulses. The white scale bar corresponds to 500 nm. b Schematic diagram of the dual Hamiltonian estimation of the field gradient ΔBL and ΔBR. See main text for the estimation procedure. The green box shows the energy selective tunneling-based single-shot readout method. c The example traces of the simultaneously estimated field gradient ΔB of each qubit as a function of time.
The Hamiltonian of the two-qubit system is given (up to a constant term) by26
where \(J_{{{\mathrm{L}}}}\left( {\varepsilon _{{{\mathrm{L}}}}} \right)\left( {J_{{{\mathrm{R}}}}\left( {\varepsilon _{{{\mathrm{R}}}}} \right)} \right)\) is the exchange splitting between states \(\left| S \right\rangle\) and \(\left| {T_0} \right\rangle\), controlled by potential detuning \(\varepsilon _{{{\mathrm{L}}}}\)\(\left( {\varepsilon _{{{\mathrm{R}}}}} \right)\) of the left (right) qubit (QL and QR). \(\sigma _{i = {{{\mathrm{xL}}}},z{{{\mathrm{L}}}}}\)\(\left( {\sigma _{i = {{{\mathrm{xR}}}},z{{{\mathrm{R}}}}}} \right)\) is the Pauli matrix for QL (QR), I is the identity matrix, and ΔBzL (ΔBzR) is the magnetic field difference between the constituent QDs of each qubit, set by the local hyperfine interaction with the host Ga and As nuclei. Here, we adopted \(g^\ast \mu _B/h\) = 1 for units, where g* ≈ −0.44 is the effective gyromagnetic ratio in GaAs, \(\mu _B\) is the Bohr magneton, and h is Planck’s constant.
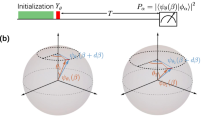
For the real-time Hamiltonian estimation of the quasi-static fluctuations of ΔBzL and ΔBzR, owing to statistical fluctuations of the nuclei, we extended the methodology developed in refs. 4,23,28 for two-qubit systems. Briefly, we initialized and measured the (2,0)L ((0,4)R) charge configuration for QL (QR), respectively, via fast energy selective tunneling (EST)-based single-shot readout and adaptive initialization29,30,31 (see also Supplementary Note 1). In contrast to previous studies, in which sequential measurements were performed using the Pauli spin blockade (PSB)-based readout26,32, here we simultaneously measured both qubits to minimize the estimation latency. During the estimation sequence, when qubits are in the evolution step, \(J_{{{\mathrm{L}}}}\left( {\varepsilon _{{{\mathrm{L}}}}} \right)\), \(J_{{{\mathrm{R}}}}\left( {\varepsilon _{{{\mathrm{R}}}}} \right)\), and \(J_{{{{\mathrm{RL}}}}}\left( {\varepsilon _{{{\mathrm{L}}}},\varepsilon _{{{\mathrm{R}}}}} \right)\) are abruptly turned off. Each qubit evolves around the x axis of the respective Bloch sphere during the evolution time tk = 1.67 k ns at the kth estimation trial (Fig. 1b). For each simultaneous single-shot measurement, the Bayesian inference is simultaneously performed according to the following rule (up to a normalization constant)4
where N is the number of single-shot measurements per Hamiltonian estimation, \(P_0\left( {{\Delta}B_{{{{\mathrm{z}}}}i}} \right)\) is the uniform initial distribution, \(r_{ki}\) = 1(−1) for \(m_{ki} = \left| S \right\rangle \left( {\left| {T_0} \right\rangle } \right)\), and \(\alpha = 0.1\left( {\beta = 0.8} \right)\) is the parameter determined by the axis of rotation on the Bloch sphere (oscillation visibility). After the Nth round, the value of ΔBzi is estimated, where the posterior distribution \(P\left( {{\Delta}B_{{{{\mathrm{z}}}}i}\left| {m_{{{{\mathrm{N}}}}i},} \right.m_{({{{\mathrm{N}}}} - 1)i}, \ldots m_{1i}} \right)\)reaches its maximum. The Bayesian circuit was implemented using a commercial field-programmable gate array (FPGA)4 (see Supplementary Note 2).
Figure 1c shows a typical time trace of the estimated ΔBzL and ΔBzR. The time resolution of these estimations is ~1.8 ms, which consists of (N = 70) × 26 μs, where a single Bayesian update takes 16 μs and 10 μs for a single-shot measurement and calculation according to Eq. (2), respectively. We found that both ΔBzs exhibit nonzero average values, likely arising from unintentional nuclear polarization, as reported previously for similarly prepared GaAs devices17,33. When ensemble-averaged, this fluctuation leads to a nuclear fluctuation-limited coherence time T2* of the order of 20 ns. Moreover, the difference between the mean values of ΔBzL and ΔBzR is at least twice the standard deviation. While the microscopic origin of this phenomenon is not well known yet, we used this difference to set the range of qubit frequencies to 25 < ΔBzL < 50 (100 < ΔBzR < 160) MHz for simultaneous qubit drive and active frequency feedback.
As shown in the inset of Fig. 2a, we concatenate the Bayesian estimators, acting as probe and operation steps, to control the two qubits in the frequency feedback mode. The controller triggers the operation step when the estimated ΔBz in the probe step is in the range described above; otherwise, the cases are discarded. However, the preset range of allowed ΔBz covers almost the entire distribution (Fig. 1c), so heralding does not significantly increase the total experimental time. When triggered, each qubit is first adiabatically initialized near the x axis on the Bloch sphere. The controller also adjusts the RF drive frequency using the probed ΔBz for each qubit. Then, an RF pulse, with a varied pulse length, is applied to gate V2 (V5) to resonantly modulate JL (JR) and induce Rabi oscillation. In all experiments, ~50 shots of operations were performed after one probe step.
a Individually driven Rabi oscillation of the triplet return probability PT of QL and QR as a function of controlled detuning δf and RF pulse duration tRF. b The representative PT oscillation of each qubit as a function of RF pulse duration for an individual and simultaneous operation. Solid curves are a fit to sinusoidal functions with a Gaussian envelope. c Ramsey fringe of PT as a function of controlled detuning δf and Ramsey delay tW, showing a typical Ramsey interference pattern. Inset: the line cut at the resonance condition. The solid curve is a fit to a Gaussian decay function \(P_T(t_W) = A\exp ( { - (t_W/T_2^\ast )^2} ) + B\) with the best fit parameter T2* \(\approx\) 151 (183) ns for QL (QR).
The main panel of Fig. 2a shows the coherent Rabi oscillation for each qubit measured as a function of the RF pulse duration tRF and the controlled detuning δf with respect to the actively adjusted resonant frequency. The chevron pattern of QR shows a resonance frequency shift, most likely caused by the AC stark effect34. Figure 2b compares the Rabi oscillations for individual and simultaneous qubit operations under resonant conditions. For the former (latter), both the probe and RF pulses were applied to only one qubit (simultaneously on both qubits). For individual operations, QL (QR) shows a Rabi decay time TRabi = 1.75 μs (1.88 μs) at the Rabi frequency fRabi = 3.09 MHz (5.69 MHz) and oscillation visibility of 90.8% (93.6%), yielding the oscillation quality factor \(Q = f_{{{{\mathrm{Rabi}}}}}T_{{{{\mathrm{Rabi}}}}} \approx 5\;\left( {11} \right)\). For simultaneous operations, corresponding results are 1.68 μs (1.59 μs), 3.12 MHz (5.68 MHz), and 88.4% (88.9%).
The comparison reveals that the Rabi frequency remains virtually unchanged regardless of the operation scheme, indicating a negligible RF crosstalk between the two qubits. This is expected from the Rabi chevron pattern for each qubit (Fig. 2a) because the separation between the set target frequency range (50 MHz) is larger than the width of each chevron pattern (~10 MHz). In contrast, simultaneous qubit operation generally reduces TRabi and oscillation visibility. The time required for the Bayesian calculation depends on the type of operation mode. It takes 10 μs for the single-qubit probe-feedback mode and two-qubit probe-only mode. However, it takes 50 μs for the two-qubit probe-feedback mode, leading to ~70 shots × 65 μs = 4.6 ms of latency per Hamiltonian estimation. This is because of the limited resources available on the FPGA setup for parallel computations. Thus, we ascribe the reduced TRabi to the increased latency for simultaneous Bayesian estimation and frequency feedback, during which the uncertainty of the estimation increases owing to the diffusion of ΔBz. In addition, reduced oscillation visibility is induced by the finite readout crosstalk between two qubits (see Supplementary Note 3).
Furthermore, we performed a simultaneous Ramsey interference of two qubits by applying calibrated π/2 pulses separated by tW and by varying δf, as shown in Fig. 2c. We then extract \(T_2^\ast \approx 151\left( {183} \right){{{\mathrm{ns}}}}\) for QL (QR) (inset of Fig. 3c), by fitting the Ramsey amplitude decay to a Gaussian function at each resonant frequency20. There is room for further improvements in T2* by increasing computational resources of the FPGA setup and removing the readout crosstalk, using newly developed machine learning techniques35, for example. Nevertheless, we keep these tasks for future work.
a A pulse sequence to produce the control qubit (QC) state-dependent exchange oscillation of the target qubit (QT). A schematic illustration of the state of both qubits in each step is depicted in the upper panel. b, c The exchange oscillations of QL (QR) depending on the state of the other qubit as control. The lower and upper traces are measured when the state of QT is \(\left| S \right\rangle\) and \(\left| {T_0} \right\rangle\), respectively.
Capacitive coupling between two ST0 qubits
We now discuss the two-qubit capacitive-coupling measurements using the dual Hamiltonian estimation circuit discussed in the previous section. Specifically, throughout the experiment, a resonant RF pulse is applied to the control qubit to observe the state-dependent frequency shift of the target qubit, whose frequency is estimated by the Hamiltonian estimator. In addition, using the simultaneous Hamiltonian estimation circuit, the control qubit is operated when the separation between the qubit frequency is larger than 50 MHz to prevent the unwanted flip of the target qubit by the RF crosstalk.
The capacitive coupling between singlet–triplet qubits originates from the different electric dipole moments of states \(\left| S \right\rangle\) and \(\left| {T_0} \right\rangle\) (ref. 36). It has been considered to be a simple method to generate leakage-free two-qubit gates22,26,27,37 unlike the inter-qubit exchange coupling-based method, in which the inter-qubit magnetic field difference should be sizable to prevent leakage of the qubits outside the computational space22. Nevertheless, the weak coupling dependent on the intra-qubit exchange energies constitutes the main disadvantage of the capacitive-coupling method. For example, the pioneering demonstration of entanglement in GaAs26 used a coupling strength on the order of a few MHz, whereas individual exchange energies were approximately 300 MHz. Moreover, it has been assumed that capacitive coupling follows a bilinear form JRL ∝ JLJR. In this bilinear form, the entanglement fidelity is expected to remain constant since the fidelity is limited by the dephasing of an individual qubit in \(J_{{{{\mathrm{RL}}}}} < < J_{{{{\mathrm{L}}}}({{{\mathrm{R}}}})}\), giving a constant quality factor for \(T_{2{{{\mathrm{L}}}}\left( {{{\mathrm{R}}}} \right)}^\ast \propto \left( {J_{{{{\mathrm{L}}}}\left( {{{\mathrm{R}}}} \right)}} \right)^{ - 1}\) (ref. 26). This constant entanglement fidelity is experimentally confirmed in previous research, indicating that the bilinear form seems to hold, at least for the experiment in which the inter-qubit distance is larger than the distance between dots within a qubit26,36.
The validity of the previously assumed scaling of JRL was experimentally tested in a regularly and compactly spaced linear QD array. Motivated by theoretical works showing that JRL can actually be a stronger function of JL and JR (ref. 37), we measured JRL by performing state-dependent exchange oscillation in combination with the dual Hamiltonian estimator. Figure 3a shows the pulse sequence for the target and control qubits. After the probe step, the control qubit is initialized to the x axis of a Bloch sphere, followed by an optional π pulse. JRL is then adiabatically switched on by slowly adjusting the detuning of the control qubit while the target qubit is initialized to the x axis of a Bloch sphere. The exchange oscillation of the target qubit is then performed by diabatically changing the detuning of the target qubit for a time texch to induce exchange oscillations, whose frequency depends on the control qubit state as \(\scriptstyle f^{{{\mathrm{T}}}} = \sqrt {(J^{{{\mathrm{T}}}} - J_{{{{\mathrm{RL}}}}}r_{{{\mathrm{C}}}})^2 + {\Delta}B_{{{\mathrm{z}}}}^2}\) according to Eq. (1), where \(J^{{{\mathrm{T}}}}\) is the intra-qubit exchange energy of the target qubit and rC = 0 (1) when the state of the control qubit is \(\left| S \right\rangle \left( {\left| {T_0} \right\rangle } \right)\).
Figure 3b (Fig. 3c) shows the resultant state-conditional frequency shift of QL (QR) as a function of texch, with JR(L) ~3.61 (4.13) GHz. The precession frequency of the qubit is lower when the control qubit is in the \(\left| S \right\rangle\) state for both cases, which is consistent with the charge configuration of the QD array38. The observed frequency shifts of 34.9 (40.6) MHz for QL (QR) is a direct measure of JRL, which is significantly larger than the value reported in (ref. 38). As predicted in recent theoretical works, we hypothesize that the different relative orientations and the shorter distance between the qubits are related to this enhancement39. In addition, we observe the beating of the target qubit oscillation when the control qubit is prepared as a superposition of \(\left| S \right\rangle\) and \(\left| {T_0} \right\rangle\) (see Supplementary Note 4).
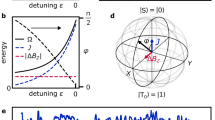
We also measured T2* and spin-echo coherence time, Techo, for each qubit to quantify the quality factor of the conditional phase-flip operation. Figure 4a, b shows T2* and Techo for each qubit, where T2* is extracted from the exponentially decaying exchange oscillation and Techo is measured by fitting the data to the echo envelope using calibrated π/2 and π pulses. Along with the form \(J \propto \exp \left( { - \varepsilon } \right)\) (inset of Fig. 4a, b), we observe charge noise-limited coherence time, where T2* and Techo are close to the form (dJ/dε)−1 (ref. 20). This essentially explains why previously demonstrated entanglement quality showed no improvement when increasing JL and JR if JRL \(\propto\) JLJR (ref. 26).
a, b T2* and Techo of QL(QR). The solid curves are fit to the forms \(\left( {dJ/d\varepsilon } \right)^{ - b}\) with best fit parameter b \(\approx\) 1.0. Inset: the intra-qubit exchange energy of each qubit as a function of detuning amplitude ε. The solid line denotes an exponential fit of a form \(J\left( \varepsilon \right) = J_0 + J_1\exp \left( {\left( {\varepsilon _0 - \varepsilon } \right) /\alpha } \right)\). c JRL (black circle) and JRL/JLJR (red square) as a function of JL and JR. The black solid line is a fit to \(J_{{{{\mathrm{RL}}}}} = a\left( {J_{{{\mathrm{L}}}}J_{{{\mathrm{R}}}}} \right)^\alpha\) with the best fit parameter α = 2.14 indicating super-linear behavior. The error bars are estimated from the fitting uncertainty. d The conditional phase-flip quality factors \(Q_{T_2^\ast }\) and Qecho of QL (orange circle) and QR (green circle).
Next, we perform the experiment in Fig. 3 with varying JL and JR near \(J_R = J_L\) to investigate the super-linearity of JRL when both qubits show reasonable coherence. Figure 4c shows the nonlinear behavior of JRL as JL and JR increase, manifesting the deviation from the bilinear proportionality26,27 in our device. Here, the error bar of the estimated JRL is determined by the fitting uncertainty limited by the sampling rate of the arbitrary waveform generator (see Supplementary Note 5). By fitting the measured JRL to (JLJR)a, the agreement with experimental data is found for \(a = 2.14\), which is close to the theoretically expected form JRL~(JLJR)2 using the effective Hamiltonian obtained from a Hund–Mulliken model independent of the details of the confinement potential in the regime where intra-qubit tunnel coupling overwhelms the intra-qubit exchange energy37 (see Supplementary Note 6). Moreover, we estimated the dipolar energy D ≈ 46 GHz, the order of which is consistent with the recent experimental work using a similar interdot spacing40. With this super-linear proportionality, we observe JRL > 190 MHz when JL and JR \(\approx\) 900 MHz, showing that more than 20% of the state-conditional qubit frequency shift can be obtained in a closely spaced QD array.
Discussion
The nonlinear JRL(JL, JR) form implies that the two-qubit gate quality should increase at larger JL and JR. We calculated \(Q_{T_2 \ast \left( {{{{\mathrm{echo}}}}} \right)} \equiv 2JT_{{{\mathrm{2}}}} \ast \left( {T_{{{{\mathrm{echo}}}}}} \right)\), which quantifies the number of conditional phase flips within T2*(Techo), as shown in Fig. 4d. We observed Qecho as high as ~16 (~7) for QL (QR), predicting that the fidelity of a conditional phase-flip operation of QL (QR) with QR (QL) in the σz eigenstate reaches as high as \(e^{ - 1/Q_{{{{\mathrm{echo}}}}}} = 94.0{{{\mathrm{ }}}}(86.7){{{\mathrm{ \% }}}}\) and also monotonically increases as a function of JL and JR. In addition, the simulation based on the measured values predicts that the maximum attainable Bell state fidelity FBell reaches \(\approx\)95% and increases at larger JL and JR, where the Bell state is prepared by the echo-like pulse implemented in ref. 26 in which FBell maximizes at \(\approx\)72% with \(J_{{{{\mathrm{RL}}}}} \approx 1\;{{{\mathrm{MHz}}}}\)(see Supplementary Note 7).
Previously, a Bell state fidelity with a capacitive coupling has enhanced to \(\approx\)93% with simultaneous rotary echo and rapid dynamic nuclear polarization (DNP), which enabled an approximately tenfold increase of a coherence time with ΔBz = 900 MHz, but JRL on the order of a few MHz was rather exploited27. Thus we expect that FBell could be enhanced more by applying simultaneous rotary echo to the closely spaced QD array at a large JRL, although the application is not currently viable in our device due to the insufficient DNP rate. In addition, the minimum time step and pulse rise times are currently limited by the sample rate of the waveform generator (2.4 Gsa/s), which also prevents performing full two-qubit gate operations and entanglement demonstration. Therefore further optimization with a faster signal source is still required. Note also that the pulse sequence in Fig. 3a is proper only for a two-qubit interaction measurement since the control qubit is likely to decohere while adiabatically turning on the interaction. Thus, a different qubit driving strategy (for example, using a non-adiabatic pulse) should be devised for entanglement demonstration, which will be considered in future work. Nonetheless, as our Hamiltonian estimation technique and readout method are compatible with large ΔBz, we anticipate that performing a full two-qubit experiment in a regularly and closely spaced linear QD array, with increased ΔBz by micromagnets or dynamic nuclear polarization, may show an even higher two-qubit gate fidelity that is also fast, exploiting large JRL.
In conclusion, we demonstrated the simultaneous Hamiltonian parameter estimation and active suppression of the quasi-static noise of two ST0 qubits in a GaAs quadruple QD array. Using fast qubit calibration routines, we also showed that both the magnitude and scaling of the capacitive coupling in a closely spaced QD array can be stronger than the previously measured bilinear form, leading to a state-conditional frequency shift of over 20 % and a quality factor of conditional phase flip of over 16. Our measurement confirms recent theoretical calculations and supports the possibility of realizing a high-fidelity and fast entanglement of encoded spin qubits in both GaAs and Si using a simple capacitive interaction.
Methods
Device fabrication
The quadruple QD device shown in Fig. 1a was fabricated on a GaAs/AlGaAs heterostructure where two-dimensional electronic gas (2DEG) is located 70 nm below the surface. Mesa was defined by a wet etching technique to eliminate 2DEG outside the region of interest to suppress unwanted leakage. Five ohmic contacts were formed by metal diffusion with thermal annealing. Nano-gates were fabricated by e-beam lithography and metal evaporation.
Measurement
The device was placed on the 7 mK plate in a commercial dilution refrigerator (Oxford Instruments, Triton-500). The battery-operated voltage sources (Stanford Research Systems, SIM928) supplied by stable DC voltages rapid voltage pulses generated by the arbitrary waveform generator with the maximum sampling rate of 2.4 Gsa/s (Zurich Instruments, HDAWG) were applied to metallic gates through on-board bias-tees. A detailed description of the experimental setup and FPGA implementation can be found in Supplementary Note 2.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120 (1998).
Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotechnol. 13, 102–106 (2018).
Mills, A. R. et al. Two-qubit silicon quantum processor with operation fidelity exceeding 99%. Sci. Adv. 8, eabn5130 (2022).
Shulman, M. D. et al. Suppressing qubit dephasing using real-time Hamiltonian estimation. Nat. Commun. 5, 1–6 (2014).
Fedele, F. et al. Simultaneous operations in a two-dimensional array of singlet-triplet qubits. PRX Quantum 2, 040306 (2021).
Hendrickx, N. W. et al. A four-qubit germanium quantum processor. Nature 591, 580–585 (2021).
Takeda, K. et al. Quantum tomography of an entangled three-qubit state in silicon. Nat. Nanotechnol. 16, 965–969 (2021).
Philips, S. G. et al. Universal control of a six-qubit quantum processor in silicon. Nature 609, 919–924 (2022).
Petit, L. et al. Universal quantum logic in hot silicon qubits. Nature 580, 355–359 (2020).
Yang, C. H. et al. Operation of a silicon quantum processor unit cell above one kelvin. Nature 580, 350–354 (2020).
Camenzind, L. C. et al. A hole spin qubit in a fin field-effect transistor above 4 kelvin. Nat. Electron. 5, 178–183 (2022).
Harvey-Collard, P. et al. Coherent spin-spin coupling mediated by virtual microwave photons. Phys. Rev. X 12, 021026 (2022).
Mi, X. et al. A coherent spin–photon interface in silicon. Nature 555, 599–603 (2018).
Taylor, J. M. et al. Relaxation, dephasing, and quantum control of electron spins in double quantum dots. Phys. Rev. B 76, 035315 (2007).
Coish, W. A. & Loss, D. Singlet-triplet decoherence due to nuclear spins in a double quantum dot. Phys. Rev. B 72, 125337 (2005).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Malinowski, F. K. et al. Spectrum of the nuclear environment for GaAs spin qubits. Phys. Rev. Lett. 118, 177702 (2017).
Kha, A., Joynt, R. & Culcer, D. Do micromagnets expose spin qubits to charge and Johnson noise? Appl. Phys. Lett. 107, 172101 (2015).
Kawakami, E. et al. Gate fidelity and coherence of an electron spin in an Si/SiGe quantum dot with micromagnet. Proc. Natl Acad. Sci. USA 113, 11738–11743 (2016).
Dial, O. E. et al. Charge noise spectroscopy using coherent exchange oscillations in a singlet-triplet qubit. Phys. Rev. Lett. 110, 146804 (2013).
Meunier, T., Calado, V. E. & Vandersypen, L. M. K. Efficient controlled-phase gate for single-spin qubits in quantum dots. Phys. Rev. B 83, 121403 (2011).
Srinivasa, V. & Taylor, J. M. Capacitively coupled singlet-triplet qubits in the double charge resonant regime. Phys. Rev. B 92, 235301 (2015).
Nakajima, T. et al. Coherence of a driven electron spin qubit actively decoupled from quasistatic noise. Phys. Rev. X 10, 011060 (2020).
Sergeevich, A., Chandran, A., Combes, J., Bartlett, S. D. & Wiseman, H. M. Characterization of a qubit Hamiltonian using adaptive measurements in a fixed basis. Phys. Rev. A 84, 052315 (2011).
Hirose, M. & Cappellaro, P. Coherent feedback control of a single qubit in diamond. Nature 532, 77–80 (2016).
Shulman, M. D. et al. Demonstration of entanglement of electrostatically coupled singlet-triplet qubits. Science 336, 202–205 (2012).
Nichol, J. M. et al. High-fidelity entangling gate for double-quantum-dot spin qubits. NPJ Quantum Inf. 3, 1–5 (2017).
Kim, J. et al. Approaching ideal visibility in singlet-triplet qubit operations using energy-selective tunneling-based Hamiltonian estimation. Phys. Rev. Lett. 129, 040501 (2022).
Jang, W. et al. Robust energy-selective tunneling readout of singlet-triplet qubits under large magnetic field gradient. NPJ Quantum Inf. 6, 1–7 (2020).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).
Dehollain, J. P. et al. Bell’s inequality violation with spins in silicon. Nat. Nanotechnol. 11, 242–246 (2016).
Kandel, Y. P. et al. Coherent spin-state transfer via Heisenberg exchange. Nature 573, 553–557 (2019).
Qiao, H. et al. Coherent multispin exchange coupling in a quantum-dot spin chain. Phys. Rev. X 10, 031006 (2020).
Takeda, K. et al. Optimized electrical control of a Si/SiGe spin qubit in the presence of an induced frequency shift. NPJ Quantum Inf. 4, 1–6 (2018).
Duan, P. et al. Mitigating crosstalk-induced qubit readout error with shallow-neural-network discrimination. Phys. Rev. Appl. 16, 024063 (2021).
Taylor, J. M. et al. Fault-tolerant architecture for quantum computation using electrically controlled semiconductor spins. Nat. Phys. 1, 177–183 (2005).
Buterakos, D., Throckmorton, R. E. & Sarma, S. D. Simulation of the coupling strength of capacitively coupled singlet-triplet qubits. Phys. Rev. B 100, 075411 (2019).
Van Weperen, I. et al. Charge-state conditional operation of a spin qubit. Phys. Rev. Lett. 107, 030506 (2011).
Hiltunen, T. & Harju, A. Capacitative coupling of singlet-triplet qubits in different interqubit geometries. Phys. Rev. B 90, 125303 (2014).
Neyens, S. F. et al. Measurements of capacitive coupling within a quadruple-quantum-dot array. Phys. Rev. Appl. 12, 064049 (2019).
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (MSIT) (No. 2018R1A2A3075438, No. 2019M3E4A1080144, No. 2019M3E4A1080145, and No. 2019R1A5A1027055), Korea Basic Science Institute (National Research Facilities and Equipment Center) grant funded by the Ministry of Education (No. 2021R1A6C101B418), and Creative-Pioneering Researchers Program through Seoul National University (SNU). The cryogenic measurement used equipment supported by the Samsung Science and Technology Foundation under Project Number SSTF-BA1502–03.
Author information
Authors and Affiliations
Contributions
D.K. and J.Y. conceived the project. J.Y. performed the measurements and analyzed the data. J.K. and H.J. fabricated the device. J.P., H.J., W.J., Y.S., M.C., and H.S. built the experimental setup and configured the measurement software. V.U. synthesized and provided the GaAs heterostructure. All the authors contributed to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yun, J., Park, J., Jang, H. et al. Probing two-qubit capacitive interactions beyond bilinear regime using dual Hamiltonian parameter estimations. npj Quantum Inf 9, 30 (2023). https://doi.org/10.1038/s41534-023-00699-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-023-00699-4
This article is cited by
-
Real-time two-axis control of a spin qubit
Nature Communications (2024)
-
Limitations on the maximal level of entanglement of two singlet–triplet qubits in GaAs quantum dots
Quantum Information Processing (2024)