Abstract
Adopting quantum resources for parameter estimation discloses the possibility to realize quantum sensors operating at a sensitivity beyond the standard quantum limit. Such an approach promises to reach the fundamental Heisenberg scaling as a function of the employed resources N in the estimation process. Although previous experiments demonstrated precision scaling approaching Heisenberg-limited performances, reaching such a regime for a wide range of N remains hard to accomplish. Here, we show a method that suitably allocates the available resources permitting them to reach the same power law of Heisenberg scaling without any prior information on the parameter. We demonstrate experimentally such an advantage in measuring a rotation angle. We quantitatively verify sub-standard quantum limit performances for a considerable range of N (O(30,000)) by using single-photon states with high-order orbital angular momentum, achieving an error reduction, in terms of the obtained variance, >10 dB below the standard quantum limit. Such results can be applied to different scenarios, opening the way to the optimization of resources in quantum sensing.
Similar content being viewed by others
Introduction
The measurement process permits gaining information about a physical parameter at the expense of a dedicated amount of resources N. Intuitively, the amount of information that can be extracted will depend on the number of employed resources, thus affecting the measurement precision of the parameter. By limiting the process to using only classical resources, the best achievable sensitivity is bounded by the standard quantum limit (SQL) and it scales as \(1/\sqrt{N}\). Such a limit can be surpassed by employing N quantum resources, defining the ultimate precision bound π/N, known as the Heisenberg limit (HL)1,2. To achieve such fundamental limit3,4,5, a crucial requirement is a capability of allocating them efficiently, in particular for ab-initio parameter estimation where no initial knowledge in the whole periodicity of the system is assumed6. Indeed, the independent use of each resource results in an uncertainty that scales as the SQL, while the optimal sensitivity can be achieved by exploiting quantum correlations in the probe preparation stage7,8.
An example of quantum resource enabling Heisenberg-limit performances in parameter estimation is the class of two-mode maximally entangled states, also called N00N states. Such kind of states has been widely exploited in quantum metrology experiments performed on photonic platforms9. In particular, one of the most investigated scenarios is the study of the phase sensitivity resulting from interferometric measurements, thanks to their broad range of applications ranging from imaging10 to biological sensing11,12. In this context, the optimal sensitivity can be achieved through the super-resolving interference obtained with N photons N00N states9,13. However, current experiments relying on N00N states are limited to regimes with a small number of N14,15,16,17,18. Indeed, scaling the number of entangled particles for this kind of state is particularly demanding due to the high complexity required for their generation, which cannot be realized deterministically with linear optics for N > 2. Experiments with up to 10-photon states have been realized19,20,21, but going beyond such order of magnitude requires a significant technological leap. Furthermore, this class of states results to be very sensitive to losses, which quickly cancels the quantum advantage as a function of the number of resources N. For this reason, the unconditional demonstration of a sub-SQL estimation precision, taking into account all the effective resources, has been reported only recently in ref. 22 with two-photon states.
Alternative approaches have been implemented for ab-initio phase estimations, sampling multiple times the investigated phase shift23 through adaptive and non-adaptive multi-pass strategies6, achieving Heisenberg scaling performances in an entanglement-free fashion. The estimation of one or multiple parameters with several approaches in different contexts has been studied in the last years24,25,26,27,28,29,30,31,32. However, one of the main challenges is to maintain the Heisenberg scaling when increasing the number of dedicated resources. Beyond the experimental difficulties encountered when increasing the number of times the probe state propagates through the sample, such protocols become exponentially sensitive to losses. Therefore, the demonstration of sub-SQL estimation precision with such an approach still remains confined to small N.
All the previous approaches present a fundamental sensitivity to losses, which prevent the observation of Heisenberg-limited performances in the asymptotic limit of very large N, where the advantage substantially reduces to a constant factor33: using multi-pass or multiparticle N00N states, the overall efficiency in these scenarios will indeed scale as ηoverall ~ ηN. In particular, in lossy scenarios, the employed states can be optimized to maintain such constant factor improvement as demonstrated in refs. 34,35. Thus, it becomes crucial to focus the investigation of quantum-enhanced parameter estimation in the non-asymptotic regime, with the aim of progressively extending the range of observation of Heisenberg scaling sensitivity (in N). Furthermore, such a non-asymptotic regime is the relevant scenario when dealing with any implementation of quantum sensors, which operate with limited values of N. In this respect, appropriate strategies must be developed to reach a sensitivity that follows the same power law (N−1) of the Heisenberg scaling for finite values of N, which here we call the non-asymptotic Heisenberg limit. To this end, it is necessary to properly allocate the use of resources in the estimation process, as previously done in ref. 36.
In this Article, using N00N-like quantum states encoded in the total angular momentum of every single photon, more robust to losses than the aforementioned approaches (using these states the efficiency impacts the estimation only with a factor η37), we implement a method able to identify and perform optimal allocation of the available resources. In particular, the protocol not only requires the generation of high-dimensional N00N-like superposition states but also the capability of tuning their dimensionality, allocating individually the resources at the single-photon level in order to achieve a sub-SQL estimation precision showing considerable regions following the same power law of Heisenberg scaling. Notably, the approach does not require an expensive online calculation for adapting the measurements, but only offline pre-calculated procedures. We test the developed protocol for an ab-initio measurement of an unknown rotation angle defined in the system’s overall periodicity interval [0, π). By this approach, we demonstrate the capability of resolving the ambiguity among the possible equivalent angle values. We perform a detailed study on the precision scaling as a function of the dedicated resources, demonstrating sub-SQL performances for a wide range of the overall amount of resources N. This task has direct applications to spatial synchronization of communication stations with relatively rotating reference frames.
Results
Estimation protocol
In the considered scenario, we are interested in recovering the value of an unknown parameter θ ∈ [0, π) represented by an optical phase shift or, as in the case discussed in this work, by a rotation angle between two different platforms. The idea is then to prepare a certain number of copies n of the input state \((\left\vert 0\right\rangle +\left\vert 1\right\rangle )/\sqrt{2}\), let transform each one of them into the associated output configuration \(\left\vert {\Psi }_{s}(\theta )\right\rangle =(\left\vert 0\right\rangle +{e}^{-i2s\theta }\left\vert 1\right\rangle )/\sqrt{2}\) by a proper imprinting process, and then measure (see Fig. 1). In these expressions, \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) stand for proper orthogonal states of the electromagnetic field. The integer quantity s describes instead the number of quantum resources devoted in the production of each individual copy of \(\left\vert {\Psi }_{s}(\theta )\right\rangle\), i.e., adopting the language of ref. 5, the number of black-box operations needed to imprint θ on a single copy of \((\left\vert 0\right\rangle +\left\vert 1\right\rangle )/\sqrt{2}\). Therefore, in the case of n copies, the total number of operations corresponds to ns. Considering our implementation and the mentioned resource counting, our approach employs non-entangled resources that are in a coherent superposition of different total angular momentum si states. For instance, in the scenario where one has access to a joint collection of s correlated modes which get independently imprinted by θ, \(\left\vert 0\right\rangle\) can be identified with the joint vacuum state of the radiation and \(\left\vert 1\right\rangle\) with a tensor product Fock state where all the modes of the model contain exactly one excitation (in this case s can also be seen as the size of the GHZ state \(({\left\vert 0\right\rangle }^{\otimes s}+{\left\vert 1\right\rangle }^{\otimes s})/\sqrt{2}\)). On the contrary, in a multi-round scenario where a single mode undergoes s subsequent imprintings of θ, \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) represents instead the zero and one photon states of such mode.
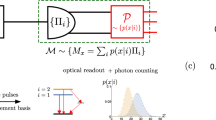
At stage i, ni copies of the state \(\left\vert {\Psi }_{{s}_{i}}(\theta )\right\rangle\) characterized by a resource number si are employed. In our experiment, the encoded parameter is the rotation angle θ between two reference systems, associated, respectively, with two platforms corresponding to the photon generation stage and to the measurement apparatus. The quantum resource is related to the total angular momentum of the photons. Each stage is successful if and only if it could identify the correct interval for the angle θ among the possible ones, using the information on the previously selected interval. This allows the last stage (with maximal sensitivity) to produce an unambiguous estimator \(\hat{\theta }\). In the figure, the plausible intervals for the phase, computed from the outcomes of the independent and non-adaptive measurements are colored, and the selected one is highlighted.
The problem of determining the optimal allocation of resources that ensures the best estimation of θ is that, while states \(\left\vert {\Psi }_{s}(\theta )\right\rangle\) with larger s have greater sensitivity to changes in θ, an experiment that uses just such output signals will only be able to distinguish θ within a period of size π/s, being totally blind to the information on where exactly locate such interval into the full domain \(\left[0,\pi \right)\). The problem can be solved by using a sequence of experiments with growing values s of the allocated quantum resources. We devised therefore a multistage procedure that works with an arbitrarily growing sequence of K quantum resources s1; s2; s3; …; sK, aiming at passing down the information stage by stage in order to disambiguate θ as the quantum resource (i.e. the sensitivity) grows, see Fig. 1 for a conceptual scheme of the protocol. Note that these s values are not chosen adaptively, but are precalculated according to the heuristic prescription reported in the “Methods” section.
At the ith stage ni copies of \(\left\vert {\Psi }_{{s}_{i}}(\theta )\right\rangle\) are measured, individually and non-adaptively, and a multivalued ambiguous estimator is constructed. Then si plausible intervals for the phase are identified, centered around the many values of the ambiguous multivalued estimator. Finally, one and only one value is deterministically chosen according to the position of the selected interval in the previous step, removing the estimator ambiguity. In this step, it is crucial to identify the suitable number of employed copies ni in order to avoid fringe ambiguity when changing si. At each stage, the algorithm might incur an error, providing an incorrect range selection for θ. When this happens, the subsequent stages of estimation are also unreliable. The probability of an error occurring at the ith stage decreases as increasing the number ni of probes used in such a stage. The precision of the final estimator, \(\hat{\theta }\), resulting from the multistage procedure, is optimized in the number of probes n1, n2, …, nK. The overall number of consumed resources, \(N=\mathop{\sum }\nolimits_{i = 1}^{K}{n}_{i}{s}_{i}\), is kept constant. We thus obtain the optimal number of probes ni to be used at each stage. The details of the algorithm and the optimization are reported in the “Methods” section. Remarkably, it can be analytically proved that protocols with si = 2i−1 work at the Heisenberg scaling23,38,39,40,41, provided that the right probe distribution is chosen. Due to the limited amount of available quantum resources, when growing the total number N of resources, the scaling of the error \(\Delta \hat{\theta }\) eventually approaches the SQL. In the non-asymptotic region, however, a sub-SQL scaling is reasonably expected. An important feature of such a protocol is that being non-adaptive, the measurement stage decouples completely from the algorithmic processing of the measurement record. This means that the algorithm producing the estimator \(\hat{\theta }\) can be considered post-processing of the measured data. Non-unitary visibility can be easily accounted for in the optimization of resource distribution. We emphasize that this phase estimation algorithm has been adapted to work for an arbitrary sequence of quantum resources, which in our case corresponds to the experimentally accessible si values, in contrast with previous formulations23,40,42.
Experimental setup
The total angular momentum of light is given by the sum of the spin angular momentum, that is, the polarization with eigenbasis given by the two circular polarization states of the photon, and its orbital angular momentum (OAM). The latter is associated with modes with spiral wavefronts or, more generally, with modes having non-cylindrically symmetric wavefronts43,44. The OAM space is infinite-dimensional and states with arbitrarily high OAM values are in principle possible. This enables to exploit of OAM states for multiple applications such as quantum simulation45,46,47, quantum computation48,49,50,51, and quantum communication52,53,54,55,56,57,58,59. Recently, photon states with more than 10,000 quanta of orbital angular momentum have been experimentally generated60. Importantly, states with high angular momentum values can be also exploited to improve the sensitivity of the rotation measurements37,61,62,63,64, thanks to the obtained super-resolving interference. The single-photon superposition of opposite angular momenta, indeed, represents a state with N00N-like features when dealing with rotation angles. Furthermore, the use of OAM in this context is more robust against losses compared to approaches relying on entangled states or multi-pass protocols. The N00N-like behavior of such states emerges when considering the OAM as a resource at the same level of the number of photons, in the same spirit as multipass protocols42. The mentioned resources counting together with the use of coherent superposition of OAM states allow in principle to reach a sensitivity following the same power law of Heisenberg scaling, avoiding all the problems related to noise fragility typical of multiparticle N00N entangled states.
In the present experiment, we employ the total angular momentum of single photons as a tool to measure the rotation angle θ between two reference frames associated with two physical platforms37. The full apparatus is shown in Fig. 2. The key elements for the generation and measurement of OAM states are provided by q-plates (QPs) devices, able to modify the photons’ OAM conditionally to the value of their polarization. A q-plate is a topologically charged half-wave plate that imparts an OAM 2ℏq to an impinging photon and flips its handedness65.
Single photon pairs are generated by a degenerate type-II SPDC process inside a ppKTP pumped by a 404 nm cw laser. The idler photon is measured by a single photon avalanche photodiode (APD) and acts as a trigger for the signal that enters the apparatus. This consists of an encoding stage which is composed of a first polarizing beam splitter (PBS) and three q-plates with different topological charges q = 1/2, 5, 25, respectively, followed by a motorized half-waveplate (HWP). The decoding stage is composed of the same elements of the preparation mounted, in the reverse order, in a compact and motorized cage that can be freely rotated around the light propagation axis of an angle θ. After the final PBS, the photons are measured through a set of two APDs. Coincidences with the trigger photon are measured, analyzed via a time-tagger, and sent to a computing unit. The latter, according to the pre-calculated optimal strategy, controls all the voltages applied to the q-plates and the angle of rotation of the measurement stage.
In the preparation stage, single photon pairs at 808 nm are generated by a 20 mm-long periodically poled titanyl phosphate (ppKTP) crystal pumped by a continuous laser with a wavelength equal to 404 nm. One of the two photons, the signal, is sent along the apparatus, while the other is measured by a single photon detector and acts as a trigger for the experiment. The probe state is prepared by initializing the single-photon polarization in the linear horizontal state \(\left\vert H\right\rangle\), through a polarizing beam splitter (PBS). After the PBS, the photon passes through a QP with a topological charge q and a half-wave plate (HWP) which inverts its polarization, generating the following superposition:
where m = 2q is the value, in modulus, of the OAM carried by the photon. In this way, considering also the spin angular momentum carried by the polarization, the total angular momenta of the two components of the superposition are ±∣m + 1∣.
After the probe preparation, the generated state propagates and reaches the receiving station, where it enters a measurement apparatus rotated by an angle θ. Such a rotation is encoded in the photon state by means of a relative phase shift with a value 2∣m + 1∣θ between the two components of the superposition:
To measure and retrieve efficiently the information on θ, such a vector vortex state is then reconverted into a polarization state with zero OAM. This is achieved by means of a second HWP and a QP with the same topological charge as the first one, oriented as the rotated measurement station:
where the zero OAM state factorizes and is thus omitted for ease of notation.
In this way, the relative rotation between the two apparatuses is embedded in the polarization of the photon in a state which, for s = m + 1, exactly mimics the output vector \(\left\vert {\Psi }_{s}(\theta )\right\rangle\) of the previous section and that is finally measured with a PBS (concordant with the rotated station) followed by single photon detectors. Note that an HWP is inserted just after the preparation of PBS and before the first three QPs. Such an HWP is rotated by 0° and 22.5° during the measurements to obtain the projections in the \(\left\vert H\right\rangle\), \(\left\vert V\right\rangle\) basis and in the diagonal one (\(\left\vert D\right\rangle\), \(\left\vert A\right\rangle\)). In each stage, half of the photons are measured on the former basis and half on the latter. The entire measurement station is mounted on a single motorized rotation cage. The interference fringes at the output of such a setup oscillate with an output transmission probability \(P={\cos }^{2}[(m+1)\theta ]\) with a periodicity that is π/(m + 1). Hence, the maximum periodicity is π at m = 0 and, consequently, one can unambiguously estimate at most all the rotations in the range [0, π).
The limit of the error on the estimation \(\hat{\theta }\) of the rotation θ is
where n is the number of employed single photons carrying a total angular momentum (m + 1) times the number of repetitions of the measurement. Such a scaling is Heisenberg-like in the angular momentum resource m + 1 and can be associated with the Heisenberg scaling achievable by multi-pass protocols for phase estimation, using non-entangled states42. This kind of protocol can overcome the SQL scaling, that in our case reads \(1/(2\,\sqrt{n})\), corresponding to the limit calculated considering single-photon probes with zero OAM. However, such a limit can be achieved only in the asymptotic limit of n → ∞, where the scaling of the precision in the total number of resources used is again the classical one \(\Delta \hat{\theta }\propto 1/\sqrt{n}\), if the angular momentum is not increased. This is the case of the three-step adaptive algorithm proposed in ref. 37, which is conversely tailored to remove phase-ambiguities due to the periodicity of the measurement probabilities. Here, we investigate both the non-asymptotic and near-asymptotic regimes using non-adaptive protocols. Our apparatus is an all-automatized toolbox generalizing the photonic gear presented in ref. 37. In our case, six QPs are simultaneously aligned in a cascaded configuration and actively participate in the estimation process. The first three QPs, each with a different topological charge q, lie in the preparation stage, while the other three, each having, respectively, the same q as the first three, are in the measurement stage. All the QPs are mounted inside the same robust and compact rotation stage, able to rotate around the photon propagation direction. Notably, the whole apparatus is completely motorized and automated. Indeed, both the rotation stage and the voltages applied to the q-plates are driven by a computing unit that fully controls the measurement process.
During the estimation protocol of a rotation angle, only one pair of QPs with the same charge, one in the preparation and the other in the measurement stage, is simultaneously turned on. For a fixed value of the rotation angle, representing the parameter to measure, pairs of QPs with the same charge are turned on, while keeping the other pairs turned off. Data are then collected for each of the four possible configurations, namely all the q-plates turned off, i.e. s = 1, and the three settings producing s = 2, 11, 51, respectively. Finally, the measured events are divided among different estimation strategies and exploited for post-processing analysis.
Analysis of the measured precision
The optimization of the uncertainty on the estimated rotation angle is obtained by employing the protocol described above. In particular, such an approach determines the use of the resources of each estimation stage. In this experiment, we have access to two different kinds of resources, namely the number of photon-pairs n employed in the measurement and the value of their total angular momentum s. Therefore, the total number of employed resources is \(N=\mathop{\sum }\nolimits_{i = 1}^{K}{n}_{i}{s}_{i}\), where ni is the number of photons with momentum si, and K = 4. According to the above procedure, for every N we determine the sequence of the multiplicative factors si and ni associated with the optimal resource distribution. Note that, in the same spirit of multi-pass protocols, where the resources invested for the estimation are given by the number of interactions of the probe with the sample, it is natural to consider the total angular momentum as a resource in the estimation protocol. Indeed, generating, propagating, and measuring higher-order OAM states of light require more effort, due to the necessity of using higher topological charge q-plates, of facing their divergence and challenging measurements, respectively.
The distance between the true value, θ, and the one obtained with the estimation protocol, \(\hat{\theta }\), in the system periodicity [0, π), is obtained by computing the circular error as follows:
Repeating the procedure for r = 1, …, R different runs of the protocol with R = 200, we retrieve, for each estimation strategy, the corresponding root-mean-square error (RMSE):
We remark that R in Eq. (6) and n in Eq. (4) do not have the same interpretation. Indeed R is not a part of the protocol but is merely the number of times we repeat it in order to get a reliable estimate of its precision. We then averaged such quantity over 17 different rotations with values between 0 and π (see Supplementary Note 1 for more details), leading to \(\overline{\Delta \hat{\theta }}\). In such a way, we investigate the uncertainty independently on the particular rotation angle inspected.
In the following, we report the results of our investigation on how the measurement sensitivity is improved by exploiting strategies that have access to states with an increasing value of the total angular momentum, obtained by tuning QPs with higher topological charge. We first consider the scenario where only photon states with s = 1 are generated. In this case, the RMSE follows as expected, the SQL scaling as a function of the number of total resources. The obtained estimation error for the strategies constrained by the such condition is represented by the blue points in Fig. 3a. Running the estimation protocol and exploiting also states with s > 1, it is possible to surpass the SQL and progressively approach performances following the same power law of Heisenberg scaling, for high values of s. In particular, we demonstrate such improvement by progressively adding to the estimation process a new step with a higher OAM value. We run the protocol limiting first the estimation strategy to states with s = 1; 2 (green points), then to s = 1; 2; 11 (cyan points), and finally to s = 1; 2; 11; 51 (magenta points). For each scenario, the number of photons n per step is optimized accordingly. Performing the estimation with all 4 available orders of OAM allows us to achieve an error reduction, in terms of the obtained variance, up to 10.7 dB below the SQL. Note that the achievement of the Heisenberg scaling is obtained by progressively increasing the order of the OAM states employed in the probing process, mimicking the increase of N when using N00N-like states in multi-pass protocols. This is highlighted by a further analysis performed in Fig. 3b, c. More specifically, if beyond a certain value of N the OAM value is kept fixed, the estimation process will soon return to scale as the SQL.
a Averaged measurement uncertainty over R = 200 repetitions of the algorithm and over 17 different angle measurements, in the interval [0, π), as a function of the total amount of resources N. The adoption of single-photon states with progressively higher-order total angular momentum allows to reach sub-SQL performance, progressively approaching the same power law of Heisenberg scaling. The red dashed line is the standard quantum limit for this system \(1/(2\sqrt{N})\), while the green dashed line is the HL π/(2N). b Value of the coefficient α and its standard deviation obtained by fitting the points from N = 2 to the value reported on the x-axis with the curve C/Nα. c Value of the coefficient α and its standard deviation obtained by fitting the points from N = N0 to the value reported on the x-axis with the curve C/Nα. Purple points: estimation process with the full strategy. Blue points: estimation process by using only s = 1. Green points: estimation process by using only s = 1; 2. Cyan points: estimation by using only s = 1; 2; 11.
To certify the quantum-inspired enhancement of the sensitivity scaling, we performed a first global analysis on the uncertainty scaling, considering the full range of N. This is performed by fitting the obtained experimental results with the function C/Nα. In particular, such a fitting procedure is performed considering batches of increasing size of the overall data. This choice permits to investigate how the overall scaling of the measurement uncertainty, quantified by the coefficient α, changes as a function of N. Starting from the point N = 2, we performed the fit considering each time the subsequent 10 experimental averaged angle estimations (reported in Fig. 3a) and evaluated the scaling coefficient α with its corresponding confidence interval for each data batch. The results of this analysis are reported in Fig. 3b. As shown in the plot, α is compatible with the SQL, i.e. α = 0.5, when the protocol employs only states with s = 1. Sub-SQL performance is conversely achieved when states with s > 1 are introduced in the estimation protocol. The scaling coefficient of the best fit on the experimental data collected when exploiting all the available QPs (magenta points) achieves a maximum value of α = 0.7910 ± 0.0002, corresponding to the use of 6460 resources. The enhancement is still verified when the fit is performed considering the full set of 30,000 resources. Indeed, the scaling coefficient value in this scenario still remains well above the SQL, reaching a value of α = 0.6786 ± 0.0001. Given that the data sets corresponding to s = 1 inherently follow the SQL, we now focus on those protocols with s > 1, thus taking into account only points starting from N0 = 62. This value coincides with the first strategy exploiting states with s = 2. Fitting only such region, the maximum value of the obtained coefficient increases to α = 0.8301 ± 0.0003 for N = 4764. Note that, as higher resource values s are introduced, the overall scaling coefficient of the estimation process, taking into account the full data set, progressively approaches the same power law of Heisenberg scaling.
Then, we focus on the protocols which have access to the full set of states with s = 1; 2; 11; 51, and we perform a local analysis of the scaling, studying individually the regions defined by the order of OAM used, and characterized by different colors of the data points in the top panel of Fig. 4. This is performed by fitting the scaling coefficient with a batch procedure (as described previously) within each region. We first report in the top panel of Fig. 4 the obtained uncertainty \(\overline{\Delta \hat{\theta }}\). Then, we study the overall uncertainty scaling, which shows a different trend depending on the maximum s value we have access to. To certify locally the achieved scaling, we study the obtained coefficient for the four different regions sharing strategies requiring states with the same maximum value of s. In the first region (2 ≤ N ≤ 60), since s = 1 no advantage can be obtained with respect to the SQL. This can be quantitatively demonstrated by studying the compatibility, in 3σ, of the best-fit coefficient α with 0.5. Each of the blue points in the lower panel of Fig. 4 is indeed compatible with the red dashed line. In the second region (62 ≤ N ≤ 264), since states with s = 2 are also introduced, it is possible to achieve a sub-SQL scaling. When states with up to s = 11 and s = 51 are also employed (N > 264) we observe that the scaling coefficient α > 0.75 is well above the value obtained for the SQL. Finally, we can identify two regions (266 ≤ N ≤ 554 and 1772 ≤ N ≤ 2996) where the scaling coefficient α obtained from a local fit is compatible, within 3σ, with the value α = 1 corresponding to the same power law of the Heisenberg scaling. This holds for extended resource regions of size ~300 and ~1000, respectively, and provides a quantitative certification of the achievement of Heisenberg scaling performances (see Supplementary Note 2 for more details). Notably, such performances are achieved for values of si which are different from the optimal ones according to the method of ref. 41, i.e. si = 2i−1, showing the versatility of the approach that can be effectively adapted depending on the employed resources.
Upper panel: measurement uncertainty averaged over 17 different angle values in the interval [0, π) as a function of the number of resources N. We highlight the points with the color code associated with the maximum value of s exploited in each strategy. Blue points: strategies with s = 1. Green points: strategies relative to s = 1; 2. Cyan points: strategies relative to s = 1; 2; 11. Purple points: strategies for s = 1; 2; 11; 51. Error bars are smaller than the size of each point. Lower panel: the value of the coefficient α and the relative confidence interval for the four inspected regions. Such a confidence interval consists of a 3σ region, obtained for the best fit with function C/Nα. The fit is done on batches of data as described in the main text. The continuous lines show the average value of α in the respective region, while the shaded area is its standard deviation. The last reported point of α corresponds to the maximum batch of data which we can fit all together with the function C/Nα, without taking into account other sources of noise. In both the plots the salmon, yellow, and green colored areas represent, respectively, regions with SQL scaling (α = 0.5), sub-SQL scaling (0.5 < α ≤ 0.75), and a scaling approaching the same power law of Heisenberg scaling (0.75 < α≤1). The red dotted line represents the SQL \(=1/(2\sqrt{N})\) (α = 0.5) while the green one is the limit = C/(2N) (obtained fixing α = 1 and C = 6 which has been arbitrarily chosen in order to have the Heisenberg scaling comparison close to the experimental data in the regions of interest). The gray dotted line is the threshold α = 0.75.
Discussion
The achievement of Heisenberg precision for a large range of resources N is one of the most investigated problems in quantum metrology. Recent progress has been made demonstrating a sub-SQL measurement precision approaching the Heisenberg limit when employing a restricted number of physical resources. However, beyond the fundamental purpose of demonstrating the effective realization of a Heisenberg limited estimation precision, it becomes crucial for practical applications to maintain such enhanced scaling for a sufficiently large range of resources.
We have experimentally implemented a protocol that allows to estimate a physical parameter in the non-asymptotic regime, demonstrating sub-SQL performances for the whole experiment. In order to accomplish such a task, we employ single-photon states carrying high total angular momentum generated and measured in a fully automatized toolbox using a non-adaptive estimation protocol. Overall, we have demonstrated a sub-SQL scaling for a large resource interval O(30, 000), and we have validated our results with a detailed global analysis of the achieved scaling as a function of the employed resources. Furthermore, thanks to the extension of the investigated resource region and to the abundant number of data points, we can also perform a local analysis which quantitatively proves to follow the same power law of Heisenberg scaling in a considerable range of resources O(1, 300). This represents a substantial improvement over the state of the art of protocols allowing sub-SQL estimation precision for a large resource range. Notably, this goal is reached using only a limited number of N00N-like states with momenta up to 50.
These results provide an experimental demonstration of a solid and versatile protocol to optimize the use of resources for the achievement of quantum advantage in ab-initio parameter estimation protocols. Indeed, we have performed enhanced estimation in a resource range where previous photonic experiments are missing, opening new perspectives for the implementation of recently developed theoretical protocols41. For instance, the demonstrated approach and platform have direct application for robust enhanced estimation of angular rotations in quantum communication systems. Given that its use can be adapted to different platforms, this approach can represent a significant tool in several scenarios. Direct near-term applications of the methods can be foreseen in different fields including sensing, quantum communication, and information processing.
Methods
Experimental details
Generation and measurement of the OAM states are obtained through the q-plate devices. A q-plate is a tunable liquid crystal birefringent element that couples the polarization and the orbital angular momentum of the incoming light. Given an incoming photon carrying an OAM value l, the action of a tuned QP in the circular polarization basis \(\left\vert R\right\rangle ,\left\vert L\right\rangle\) is the following transformations:
where \({\left\vert X\right\rangle }_{\pi }\) indicates the polarization X, while \({\left\vert l\pm 2q\right\rangle }_{{\rm {oam}}}\) indicates the OAM value ±2q, being q is the topological charge characterizing the QP. Tuning of the q-plate is performed by changing the applied voltage.
The two sources of error are photon loss and the non-unitary conversion efficiency of the QPs. Each stage of the protocol is characterized by a certain photon loss η, which reduces the amount of detected signal. In general, each stage will have its own noise level ηj. Conversely, the non-unitary efficiency of the QPs translates to a non-unitary visibility v, which changes the probability outcomes for the two measurement projections as follows:
The limit of the error on the estimation of the rotation θ in this setting is
However, if the actual experiment is performed in post-selection, then η = 1, and the only source of noise is the reduced visibility.
Data processing algorithm and optimization
In this section, we present extensively the phase estimation algorithm which we used to process the measured data and its optimization. As it naturally applies to the phase in \(\left[0,2\pi \right)\) we present it for \(\varphi =2\theta \in \left[0,2\pi \right)\). At each stage of the procedure, the estimator \(\hat{\varphi }\) and its error \(\Delta \hat{\varphi }\) can be easily converted into an estimator and error for the rotation angle: \(\hat{\theta }=\hat{\varphi }/2\) and \(\Delta \hat{\theta }=\Delta \hat{\varphi }/2\). In the ith stage of the procedure, we are given the result of ni/2 photon polarization measurements on the basis of HV and ni/2 measurements on the basis DA. We define \({\hat{f}}_{{\rm {HV}}}\) and \({\hat{f}}_{{\rm {DA}}}\) the observed frequencies of the outcomes H and D, respectively, and introduce the estimator \(\widehat{{s}_{i}\theta }=\,{{\mbox{atan}}}\,2(2{\hat{f}}_{{\rm {HV}}}-1,2{\hat{f}}_{{\rm {DA}}}-1)\in [0,2\pi )\). From the probabilities in Eq. (8) it is easy to conclude that \(\widehat{{s}_{i}\varphi }\) is a consistent estimator of \({s}_{i}\varphi \,{{\mathrm{mod}}}\,\,2\pi\). This does not identify an unambiguous φ alone though, but instead a set of si possible values \(\widehat{{s}_{i}\varphi }/{s}_{i}+2\pi m/{s}_{i}\) with m = 0, 1, 2, ⋯ , si − 1. Centered around these points we build intervals of size 2π/(siγi), where
The algorithm then chooses among these intervals the only one that overlaps with the previously selected interval. The choice of γi, computed recursively with the formula in Eq. (10), is fundamental in order to have one and only one overlap. The starting point γ1 of the recursive formula can be chosen freely inside an interval of values that guarantees γi ≥ 1 ∀ i, therefore it will be subject to optimization. By convention, we set γ0 = 1. Algorithm 1 reports in pseudocode the processing of the measurement outcomes required to get the estimator \(\hat{\varphi }\) working at Heisenberg scaling.
Algorithm 1
Phase estimation
1: \(\hat{\varphi }\leftarrow 0\)
2: for i = 1 → K do
3: \(\left[0,2\pi \right)\ni \widehat{{s}_{i}\varphi }\leftarrow\) Estimated from measurements.
4: \(\left[0,\frac{2\pi }{{s}_{i}}\right)\ni \hat{\xi }\leftarrow \frac{\widehat{{s}_{i}\varphi }}{{s}_{i}}\)
5: \(m\leftarrow \left\lfloor \frac{{s}_{i}\hat{\varphi }}{2\pi }-\frac{1}{2}\frac{{s}_{i}}{{s}_{i-1}{\gamma }_{i-1}}\right\rfloor\)
6: \(\hat{\xi }\leftarrow \hat{\xi }+\frac{2\pi m}{{s}_{i}}\)
7: if \(\hat{\varphi }+\frac{\pi (2{\gamma }_{i}-1)}{{s}_{i}{\gamma }_{i}}-\frac{\pi }{{s}_{i-1}{\gamma }_{i-1}} < \hat{\xi } < \hat{\varphi }+\frac{\pi (2{\gamma }_{i}+1)}{{s}_{i}{\gamma }_{i}}+\frac{\pi }{{s}_{i-1}{\gamma }_{i-1}}\) then
8: \(\hat{\varphi }\leftarrow \hat{\xi }-\frac{2\pi }{{s}_{i}}\)
9: else if \(\hat{\varphi }-\frac{\pi (2{\gamma }_{i}+1)}{{s}_{i}{\gamma }_{i}}-\frac{\pi }{{s}_{i-1}{\gamma }_{i-1}} < \hat{\xi } < \hat{\varphi }-\frac{\pi (2{\gamma }_{i}-1)}{{s}_{i}{\gamma }_{i}}+\frac{\pi }{{s}_{i-1}{\gamma }_{i-1}}\) then
10: \(\hat{\varphi }\leftarrow \hat{\xi }+\frac{2\pi }{{s}_{i}}\)
11: else
12: \(\hat{\varphi }\leftarrow \hat{\xi }\)
13: end if
14: \(\hat{\varphi }\leftarrow \hat{\varphi }-2\pi \left\lfloor \frac{\hat{\varphi }}{2\pi }\right\rfloor\)
15: end for
We can upper bound the probability of choosing the wrong interval through the probability for the distance of the estimator \(\widehat{{s}_{i}\varphi }\) from φ to exceed π/γi, that is
where ni is the number of photons employed in the stage, \(C(\gamma )=\exp \left[b{\sin }^{2}\left(\frac{\pi }{\gamma }\right)\right]\), and A is an unimportant numerical constant. This form for C(γ) was suggested by Hoeffding’s inequality, and we set b = 0.7357 as indicated by numerical evaluations for ni ≤ 40. By applying the upper bound in Eq. (11) we can write a bound on the precision of the final estimator \(\hat{\varphi }\), as measured by the RMSE with the circular distance, that reads
where \({C}_{i}=C\left({\gamma }_{i}\right)\), and Di are
If \(\frac{2\pi {D}_{i}}{{\gamma }_{i-1}{s}_{i-1}}\ge \pi\) then we redefine \({D}_{i}=\frac{{\gamma }_{i-1}{s}_{i-1}}{2}\). These steps are analogous to those in ref. 41. The last stage of the estimation is different from the previous ones, as it is no more a step of the localization process. This difference can be clearly seen in how the error contribution is treated in Eq. (12). We optimize this upper bound while fixing the total number of used resources by writing
Through the optimization of this Lagrangian, we found the resource distribution ni optimal for the given sequence of si and N. Substituting back the obtained ni in the error expression, we get
where α depends on the total resource number N. In an experiment we have at disposal, or we have selected, a certain sequence of quantum resources s = 1; s2; s3; …; sK, but it is not convenient for every N to use the whole sequence. A better strategy is to add one at a time a new quantum resource as the total number of available resources N grows, and therefore slowly building the complete sequence. For small N we do not employ any quantum resource, so that s = 1. The first upgrade prescribes the use of the 2-stage strategy s = 1; s2, then, as N reaches a certain value we upgrade again to a 3-stage strategy s = 1; s2; s3, and so on until we get to s = 1; s2; s3; …; sK, which will be valid asymptotically in N. The optimal points at which these upgrades should be performed can be found by comparing the error upper bounds given in Eq. (15) or via numerical simulations. The sequence s = 1; s2; s3; …, sK might not be the complete set of all the quantum resources that are experimentally available. In our experiment s = 1; 2; 11; 51 were all the available quantum resources, but the here-described procedure of adding one stage at a time might work better with only a subset of the available si. We are therefore in need of comparing many sets of quantum resources s = 1; s2; s3; …; sK. The numerical simulations suggested that a comparison of the summations
with optimized γ1, which appears in Eq. (15), is a quick and reliable way to establish the best set of quantum resources. We can treat the non-perfect visibility of the apparatus by rescaling the parameters b and Cj in the Lagrangian (14). Given vi the visibility in the ith stage, the rescaling requires \({C}_{i}\to {C}_{i}^{{v}_{i}^{2}}\), and for the last stage \(b\to b{v}_{K}^{2}\).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
All the custom code developed for this study is available from the corresponding author upon reasonable request.
References
Berry, D. W., Wiseman, H. & Breslin, J. Optimal input states and feedback for interferometric phase estimation. Phys. Rev. A 63, 053804 (2001).
Górecki, W., Demkowicz-Dobrzański, R., Wiseman, H. M. & Berry, D. W. π-corrected Heisenberg limit. Phys. Rev. Lett. 124, 030501 (2020).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330–1336 (2004).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photonics 5, 222–229 (2011).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).
Berni, A. A. et al. Ab initio quantum-enhanced optical phase estimation using real-time feedback control. Nat. Photonics 9, 577–581 (2015).
Lee, H., Kok, P. & Dowling, J. P. A quantum rosetta stone for interferometry. J. Mod. Opt. 49, 2325–2338 (2002).
Bollinger, J. J., Itano, W. M., Wineland, D. J. & Heinzen, D. J. Optimal frequency measurements with maximally correlated states. Phys. Rev. A 54, R4649 (1996).
Polino, E., Valeri, M., Spagnolo, N. & Sciarrino, F. Photonic quantum metrology. AVS Quantum Sci. 2, 024703 (2020).
Boto, A. N. et al. Quantum interferometric optical lithography: exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 85, 2733–2736 (2000).
Wolfgramm, F., Vitelli, C., Beduini, F. A., Godbout, N. & Mitchell, M. W. Entanglement-enhanced probing of a delicate material system. Nat. Photonics 7, 1749–4893 (2013).
Cimini, V. et al. Adaptive tracking of enzymatic reactions with quantum light. Opt. Express 27, 35245–35256 (2019).
Mitchell, M. W., Lundeen, J. S. & Steinberg, A. M. Super-resolving phase measurements with a multiphoton entangled state. Nature 429, 161–164 (2004).
Nagata, T., Okamoto, R., O’Brien, J. L., Sasaki, K. & Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 316, 726–729 (2007).
Daryanoosh, S., Slussarenko, S., Berry, D. W., Wiseman, H. M. & Pryde, G. J. Experimental optical phase measurement approaching the exact Heisenberg limit. Nat. Commun. 9, 4606 (2018).
Roccia, E. et al. Multiparameter approach to quantum phase estimation with limited visibility. Optica 5, 1171–1176 (2018).
Rozema, L. A. et al. Scalable spatial superresolution using entangled photons. Phys. Rev. Lett. 112, 223602 (2014).
Afek, I., Ambar, O. & Silberberg, Y. High-noon states by mixing quantum and classical light. Science 328, 879–881 (2010).
Wang, X.-L. et al. Experimental ten-photon entanglement. Phys. Rev. Lett. 117, 210502 (2016).
Israel, Y., Afek, I., Rosen, S., Ambar, O. & Silberberg, Y. Experimental tomography of noon states with large photon numbers. Phys. Rev. A 85, 022115 (2012).
Zhong, H.-S. et al. 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion. Phys. Rev. Lett. 121, 250505 (2018).
Slussarenko, S. et al. Unconditional violation of the shot-noise limit in photonic quantum metrology. Nat. Photonics 11, 700–703 (2017).
Higgins, B. L. et al. Demonstrating Heisenberg-limited unambiguous phase estimation without adaptive measurements. N. J. Phys. 11, 073023 (2009).
Grinko, D., Gacon, J., Zoufal, C. & Woerner, S. Iterative quantum amplitude estimation. npj Quantum Inf. 7, 1–6 (2021).
Gebhart, V., Smerzi, A. & Pezzè, L. Bayesian quantum multiphase estimation algorithm. Phys. Rev. Appl. 16, 014035 (2021).
Liu, L.-Z. et al. Distributed quantum phase estimation with entangled photons. Nat. Photonics 15, 137–142 (2021).
Hong, S. et al. Quantum enhanced multiple-phase estimation with multi-mode n00n states. Nat. Commun. 12, 1–8 (2021).
Valeri, M. et al. Experimental multiparameter quantum metrology in adaptive regime. Phys. Rev. Res. 5, 013138 (2023).
Cimini, V. et al. Deep reinforcement learning for quantum multiparameter estimation. Adv. Photonics 5, 016005 (2003).
Krisnanda, T., Ghosh, S., Paterek, T., Laskowski, W. & Liew, T. C. Phase measurement beyond the standard quantum limit using a quantum neuromorphic platform. Phys. Rev. Appl. 18, 034011 (2022).
Lin, L. & Tong, Y. Heisenberg-limited ground-state energy estimation for early fault-tolerant quantum computers. PRX Quantum 3, 010318 (2022).
Hou, Z. et al. "Super-Heisenberg” and Heisenberg scalings achieved simultaneously in the estimation of a rotating field. Phys. Rev. Lett. 126, 070503 (2021).
Escher, B. M., de Matos Filho, R. L. & Davidovich, L. General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology. Nat. Phys. 7, 406–411 (2011).
Knysh, S., Smelyanskiy, V. N. & Durkin, G. A. Scaling laws for precision in quantum interferometry and the bifurcation landscape of the optimal state. Phys. Rev. A 83, 021804 (2011).
Dorner, U. et al. Optimal quantum phase estimation. Phys. Rev. Lett. 102, 040403 (2009).
Xiang, G. Y., Higgins, B. L., Berry, D. W., Wiseman, H. M. & Pryde, G. J. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photonics 5, 43–47 (2011).
D’Ambrosio, V. et al. Photonic polarization gears for ultra-sensitive angular measurements. Nat. Comm. 4, 2432 (2013).
Kitaev, A. Y. Quantum measurements and the abelian stabilizer problem. arXiv preprint quant-ph/9511026 (1995).
Griffiths, R. B. & Niu, C.-S. Semiclassical Fourier transform for quantum computation. Phys. Rev. Lett. 76, 3228 (1996).
Kimmel, S., Low, G. H. & Yoder, T. J. Robust calibration of a universal single-qubit gate set via robust phase estimation. Phys. Rev. A 92, 062315 (2015).
Belliardo, F. & Giovannetti, V. Achieving Heisenberg scaling with maximally entangled states: an analytic upper bound for the attainable root-mean-square error. Phys. Rev. A 102, 042613 (2020).
Higgins, B. L., Berry, D. W., Bartlett, S. D., Wiseman, H. M. & Pryde, G. J. Entanglement-free Heisenberg-limited phase estimation. Nature 450, 393–396 (2007).
Padgett, M., Courtial, J. & Allen, L. Light’s orbital angular momentum. Phys. Today 57, 35–40 (2004).
Erhard, M., Fickler, R., Krenn, M. & Zeilinger, A. Twisted photons: new quantum perspectives in high dimensions. Light Sci. Appl. 7, 17146 (2018).
Cardano, F. et al. Statistical moments of quantum-walk dynamics reveal topological quantum transitions. Nat. Commun. 7, 11439 (2016).
Cardano, F. et al. Detection of zak phases and topological invariants in a chiral quantum walk of twisted photons. Nat. Commun. 8, 15516 (2017).
Buluta, I. & Nori, F. Quantum simulators. Science 326, 108–111 (2009).
Bartlett, S. D., deGuise, H. & Sanders, B. C. Quantum encodings in spin systems and harmonic oscillators. Phys. Rev. A 65, 052316 (2002).
Ralph, T. C., Resch, K. J. & Gilchrist, A. Efficient Toffoli gates using qudits. Phys. Rev. A 75, 022313 (2007).
Lanyon, B. P. et al. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nat. Phys. 5, 134–140 (2009).
Michael, M. H. et al. New class of quantum error-correcting codes for a bosonic mode. Phys. Rev. X 6, 031006 (2016).
Wang, X.-L. et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516 (2015).
Mirhosseini, M. et al. High-dimensional quantum cryptography with twisted light. N. J. Phys. 17, 033033 (2015).
Krenn, M., Handsteiner, J., Fink, M., Fickler, R. & Zeilinger, A. Twisted photon entanglement through turbulent air across Vienna. Proc. Natl Acad. Sci. USA 112, 14197–14201 (2015).
Malik, M. et al. Multi-photon entanglement in high dimensions. Nat. Photonics 10, 248–252 (2016).
Sit, A. et al. High-dimensional intracity quantum cryptography with structured photons. Optica 4, 1006–1010 (2017).
Cozzolino, D. et al. Orbital angular momentum states enabling fiber-based high-dimensional quantum communication. Phys. Rev. Appl. 11, 064058 (2019).
Wang, J. Advances in communications using optical vortices. Photonics Res. 4, B14–B28 (2016).
Cozzolino, D. et al. Air-core fiber distribution of hybrid vector vortex-polarization entangled states. Adv. Photonics 1, 046005 (2019).
Fickler, R., Campbell, G., Buchler, B., Lam, P. K. & Zeilinger, A. Quantum entanglement of angular momentum states with quantum numbers up to 10,010. Proc. Natl Acad. Sci. USA 113, 13642–13647 (2016).
Barnett, S. M. & Zambrini, R. Resolution in rotation measurements. J. Mod. Opt. 53, 613–625 (2006).
Jha, A. K., Agarwal, G. S. & Boyd, R. W. Supersensitive measurement of angular displacements using entangled photons. Phys. Rev. A 83, 053829 (2011).
Fickler, R. et al. Quantum entanglement of high angular momenta. Science 338, 640–643 (2012).
Hiekkamäki, M., Bouchard, F. & Fickler, R. Photonic angular superresolution using twisted N00N states. Phys. Rev. Lett. 127, 263601 (2021).
Marrucci, L., Manzo, C. & Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 96, 163905 (2006).
Acknowledgements
This work is supported by the ERC Advanced grant PHOSPhOR (Photonics of Spin-Orbit Optical Phenomena; Grant Agreement No. 828978), by the Amaldi Research Center funded by the Ministero dell’Istruzione dell’Università e della Ricerca (Ministry of Education, University and Research) program “Dipartimento di Eccellenza” (CUP:B81I18001170001) and by MIUR (Ministero dell’Istruzione, dell’Università e della Ricerca) via project PRIN 2017 “Taming complexity via QUantum Strategies a Hybrid Integrated Photonic approach” (QUSHIP) Id. 2017SRNBRK.
Author information
Authors and Affiliations
Contributions
V.C., E.P., F.B., F.H., N.S., V.G., and F.S. conceived the experiment. V.C., E.P., F.H., N.S., and F.S. carried out the experiment. V.C., E.P., F.B., F.H., N.S., V.G., and F.S. performed the data analysis. F.B. and V.G. developed the estimation protocol and performed the simulations. B.P. participated in the design and fabrication of the Q-Plate devices. All the authors discussed the results and contributed to the writing of the paper. N.S., V.G., and F.S. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cimini, V., Polino, E., Belliardo, F. et al. Experimental metrology beyond the standard quantum limit for a wide resources range. npj Quantum Inf 9, 20 (2023). https://doi.org/10.1038/s41534-023-00691-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-023-00691-y