A neural network assisted ¹⁷¹Yb⁺ quantum magnetometer

Abstract

A versatile magnetometer must deliver a readable response when exposed to target fields in a wide range of parameters. In this work, we experimentally demonstrate that the combination of¹⁷¹Yb⁺ atomic sensors with adequately trained neural networks enables us to investigate target fields in distinct challenging scenarios. In particular, we characterize radio frequency (RF) fields in the presence of large shot noise, including the limit case of continuous data acquisition via single-shot measurements. Furthermore, by incorporating neural networks we significantly extend the working regime of atomic magnetometers into scenarios in which the RF driving induces responses beyond their standard harmonic behavior. Our results indicate the benefits to integrate neural networks at the data processing stage of general quantum sensing tasks to decipher the information contained in the sensor responses.

Introduction

Quantum sensing¹ and metrology² are important branches of modern quantum technologies with applications in different areas such as imaging^3,4 and spectroscopy^5,6,7. In this scenario, atomic-sized sensors encoded in¹⁷¹Yb^{+8,9,10,11,12} and ⁴⁰Ca⁺¹³ ions provide spatial resolution and sensitivity for the detection of external/target fields. In addition, ¹⁷¹Yb⁺ ions exhibit negligible emission rates¹¹ and extended coherence times due to the stabilization provided by dynamical decoupling (DD) techniques^14,15,16. In particular, DD methods that exploit the multi-level structure in the${}^{2}{S}_{\frac{1}{2}}$ manifold of the ¹⁷¹Yb⁺ ion have to lead to the detection of radio frequency (RF) fields with sensitivity close to the standard quantum limit⁹, while the resulting dressed state qubit was proposed as a robust register for quantum information processing^8,10. However, this approach is restricted to a narrow working regime leading to harmonic sensor responses where RF target parameters are encoded. A departure from such a range leads to complex sensor responses where standard inference of the external fields gets challenging. In another vein, machine learning (ML) tools are incorporated to address distinct problems in quantum technologies. In particular, neural networks (NNs) are valuable in distinct quantum sensing scenarios leading to adaptive protocols for phase estimation^17,18,19, parameter estimation^{20,21,22,23,24}, and quantum sensors calibration^25,26,27.

In this article, we experimentally demonstrate the ability of NNs to decode complex sensor responses, thus significantly extending the operational regime of quantum detectors. In particular, we infer RF target parameters from the measured response of an ¹⁷¹Yb⁺ atomic sensor in distinct challenging scenarios. These comprise the regime of non-harmonic sensor responses with large shot noise, and the continous interrogation of the sensor (via single-shot measurements) under always-on RF fields. With careful modeling of the sensor-target dynamics, we train NNs to relate intricate responses of the sensor with RF parameters leading to estimations of the latter with high accuracy.

Results

The quantum sensor

The sensor consists of four hyperfine levels ($\left\vert 0\right\rangle ,\left\vert \acute{0}\right\rangle ,\left\vert 1\right\rangle$, and $\left\vert -1\right\rangle$) in the ${}^{2}{S}_{\frac{1}{2}}$ manifold of the ¹⁷¹Yb⁺ ion, and in a static magnetic field B_z. To enhance the coherence of the sensor, we use two microwave (MW) fields with Rabi frequency Ω leading to the dressed basis set $\{\left\vert u\right\rangle ,\left\vert d\right\rangle ,\left\vert D\right\rangle ,\left\vert \acute{0}\right\rangle \}$ with $\left\vert u\right\rangle =(\left\vert B\right\rangle +\left\vert 0\right\rangle )/\sqrt{2}$, $\left\vert d\right\rangle =(\left\vert B\right\rangle -\left\vert 0\right\rangle )/\sqrt{2}$, $\left\vert D\right\rangle =(\left\vert -1\right\rangle -\left\vert 1\right\rangle )/\sqrt{2}$, and $\left\vert B\right\rangle =(\left\vert -1\right\rangle +\left\vert 1\right\rangle )/\sqrt{2}$ which is insensitive to magnetic field fluctuations^8,9, see Fig. 1a, b.

Fig. 1: Schematic levels of the ¹⁷¹Yb⁺ atomic sensor and the experimental setup.

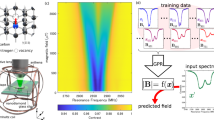
a Relevant levels of the ¹⁷¹Yb⁺ atomic sensor. Two resonant MW fields drive the sensor with a Rabi frequency Ω leading to the configuration in (b) which is defined in the dressed state basis $\{\left\vert u\right\rangle ,\left\vert d\right\rangle ,\left\vert \acute{0}\right\rangle ,\left\vert D\right\rangle \}$⁹. c Schematic configuration of the experimental setup. The ion is trapped in a needle trap which consists of a pair of RF electrodes and four DC electrodes. The MW fields for state manipulation are generated by mixing a 12.4428 GHz signal with the signal from an arbitrary waveform generator (AWG1). The 12.6 GHz signal after a high pass filter (HPF) is amplified by an amplifier (Amp1) and sent to the ion using a MW horn outside the vacuum chamber. The target field around 10 MHz is generated by another arbitrary waveform generator (AWG2) controlled by the computer and broadcast to the ion through a coil after amplification. We place an extra RF switch after AWG2, which can be used to remove the target field from the trap while keeping the signal from AWG2 continuous. A photomultiplier tube (PMT) is used to detect the state-dependent fluorescence. d Scheme of the NN. The response from PMT, i.e., X, is processed by a number of hidden layers (HL₁... HL_k) leading to the outputs Y.

Once a target field ${\Omega }_{{{{\rm{tg}}}}}\cos ({\omega }_{{{{\rm{tg}}}}}t+{\phi }_{{{{\rm{tg}}}}})$ is applied, one measures the dark state ($\left\vert D\right\rangle$) survival probability P_D(t) considered here as the sensor response. The standard working regime of the sensor (leading to harmonic responses) implies Ω_tg ≪ Ω ≪ ω_tg with ω_tg resonant with, e.g., the $\left\vert \acute{0}\right\rangle \leftrightarrow \left\vert 1\right\rangle$ transition⁹. This simplifies the total Hamiltonian (see Supplementary Note 1) into

$$H=-\frac{{\Omega }_{{{{\rm{tg}}}}}}{2\sqrt{2}}(\left\vert D\right\rangle \langle \acute{0}| +| \acute{0}\rangle \left\langle D\right\vert ).$$

(1)

From Eq. (1) one finds the harmonic sensor response ${P}_{D}(t)={\cos }^{2}(\pi t/{t}_{{{{\rm{R}}}}})$, with ${t}_{{{{\rm{R}}}}}=2\pi \sqrt{2}/{\Omega }_{{{{\rm{tg}}}}}$ establishing a simple relation between t_R and the target field parameter Ω_tg. In contrast, a departure from the standard working regime leads to the loss of this type of simple dependencies between sensor responses and target parameters, thus posing serious challenges for reliable field characterization. We demonstrate that our setup combining a quantum sensor and NNs can extract RF fields parameters from complex sensor responses.

Experimental setup

As schematically shown in Fig. 1c, our protocol is executed on a single ¹⁷¹Yb⁺ ion confined in a Paul trap which is shielded by permalloy to reduce the surrounding magnetic noise^28,29. A magnetic field B_z is applied to the ion leading to a Zeeman shift ≈10.0 MHz between $\left\vert \acute{0}\right\rangle$ and $\left\vert 1\right\rangle$. Two ~12.6 GHz MW fields ${\Omega }_{j}\cos ({\omega }_{j}t+{\phi }_{j})(j=1,2)$, respectively resonant with transitions $\left\vert 0\right\rangle \leftrightarrow \left\vert 1\right\rangle$ and $\left\vert 0\right\rangle \leftrightarrow \left\vert -1\right\rangle$ are used for state manipulation. To generate the dark state $\left\vert D\right\rangle$, we design pulses with the amplitudes Ω₁ and Ω₂ evolving in the form of a hyperbolic tangent (details available in Supplementary Note 2). During the sensing window, the amplitudes of dressing fields are kept constant at Ω₁ = Ω₂ = (2π) × 5.5 kHz. Afterwards the state remaining in $\left\vert D\right\rangle$ is transferred to $\left\vert 0\right\rangle$ for detection.

A copper coil placed under the trap generates the target field once an RF current is sent to the coil. As the original RF signal is produced by an arbitrary waveform generator (AWG2), the amplitude, frequency, and the initial phase of the target field can be set by adjusting the parameters of AWG2. An RF switch is placed after the AWG2 output in order to remove interaction between the field and the ion if necessary while keeping the signal source continuously on. After amplification, the RF target field generated by the coil has a maximum amplitude of ${\Omega }_{{{{\rm{tg}}}}}^{\max }=(2\pi )\times 9.0$ kHz. A photomultiplier tube (PMT) is used to detect the state-dependent fluorescence. As schematically shown in Fig. 1d, the response from PMT, i.e., X, is processed through the well-trained NN leading to the outputs Y which approach the targets A. We use data generated from numerical simulations to create the NN. Then, by inputting experimentally collected responses into the NN, we estimate the RF parameters.

Now, we demonstrate the good performance of an ¹⁷¹Yb⁺-magnetometer assisted by a NN in two scenarios in which input data comprise (i) average values obtained from a reduced number of measurements, and (ii) binary sequences (including only 0, or 1) continuously acquired from single-shot measurements. Both cases are demonstrated in regimes where the sensor delivers complex responses that depart from the standard harmonic regime. Hence, we prove that NNs significantly extends the versatility of quantum sensors.

Scenario i: Parameter estimation with a reduced number of measurements

We aim to estimate the Rabi frequency of a target field. In this case, the input data string ${{{\bf{X}}}}=\{{P}_{1},{P}_{2},...,{P}_{{N}_{p}}\}$ consist of the average values P_i (i ∈ [1, N_p]) collected at N_p time instants t = t_i distributed in a time interval [0, t_f] for a specific Ω_tg. We use the Hamiltonian in Supplementary Note 1 to numerically compute P_D(t_i), as each P_i does not follow the expression ${P}_{D}({t}_{i})={\cos }^{2}(\pi {t}_{i}/{t}_{{{{\rm{R}}}}})$ in cases that depart from the standard working regime. In addition, the binary outcome is drawn from a Bernoulli distribution ${z}_{n}^{i} \sim B(1,{P}_{D}({t}_{i}))\in \{0,1\}$ such that each simulated average value is ${P}_{i}=\mathop{\sum }\nolimits_{n = 1}^{{N}_{m}}{z}_{n}^{i}/{N}_{m}$ for a number of shots N_m. We choose N_p = 151, N_m = 100 and t_f = 2.828 ms (note that this value of t_f corresponds to one period of the sensor response for Ω_tg = (2π) × 0.5 kHz, i.e., in the harmonic case). The examples (i.e., the data strings X, Y, and A) are computed by selecting 96 values for Ω_tg/(2π) in the range [0.5–10] kHz. In addition, as each P_i fluctuates owing to the reduced number of measurements, we perform 100 repetitions for each simulated experimental acquisition (i.e., for each Ω_tg). Therefore, our dataset contains 96 × 100 examples of which 70%/15%/15% lead to the training/validation/test datasets. After training the NN (details are available in Methods and Supplementary Note 3) we can estimate the Rabi frequency Ω_tg of experimentally collected responses by inputting them into the NN.

In particular, we harvest sensor responses for N = 15 values of Ω_tg (while we select other RF parameters as ϕ_tg = 0 and ω_tg = (2π) × 10.56 MHz) which do not belong to the training/validation/test datasets, and for a number of shots N_m = 100, and N_m = 30. In Table 1, we list the estimations y₁ from the NN for each target a₁ ≡ Ω_tg. Each output y₁ is obtained after feeding the NN with the experimentally acquired response consisting of average values measured during t ∈ [0, t_f] with N_p = 151. We show the results for a number of shots N_m = 100 and N_m = 30. The regressions of the NN outputs with respect to Ω_tg are shown in Fig. 2a, b.

Table 1 Outputs y₁ obtained from the NN in Scenario i.

Fig. 2: Estimation results from Scenario i, a reduced number of measurements.

a, b Regression of the NN outputs (y₁) with respect to the targets a₁ ≡ Ω_tg for a number of shots N_m = 100 (a) and N_m = 30 (b). The fit (solid-blue) overlaps with the line y₁ = a₁, while R is the correlation coefficient³⁰ of y₁ and a₁. This is R = 0.9996 (a), and 0.9994 (b). c–e Sensor response (diamonds) for the targets Ω_tg = (2π) × 1.1487 kHz (c) and Ω_tg = (2π) × 8.9493 kHz (d, e) experimentally obtained for N_m = 30 shots. For comparison, in (c, d) the harmonic response ${P}_{D}(t)={\cos }^{2}(\pi t/{t}_{{{{\rm{R}}}}})$ (solid-blue) is included. The plot in c shows the case with Ω_tg = (2π) × 1.1487 kHz lying in the harmonic regime, while in (d) the response for Ω_tg = (2π) × 8.9493 kHz significantly deviates from the harmonic behavior. In e, we observe that the curve obtained from numerical simulations (solid-red) fits experimental data for Ω_tg = (2π) × 8.9493 kHz. Error bars in c–e represent the standard error of the mean.

The average accuracy in the estimation of the different Ω_tg is defined as $\bar{F}=\frac{1}{N}\mathop{\sum }\nolimits_{j = 1}^{N}{F}_{j}$, with ${F}_{j}=1-| {y}_{1}^{j}-{a}_{1}^{j}| /{a}_{1}^{j}$, and a₁ = Ω_tg. With the values in Table 1 we find the results $\bar{F}=98.76 \%$ for N_m = 100 with a standard deviation (SD) of the F_j set SD = 0.7762%. In the case of N_m = 30, we find $\bar{F}=98.31 \%$ with SD = 1.1483%. We remark that these highly accurate estimations were obtained with examples that comprise values of Ω_tg leading to sensor responses that depart from the harmonic case. In particular, in Fig. 2 (c,d,e) we show the cases for Ω_tg = (2π) × 1.1487 kHz (c) and Ω_tg = (2π) × 8.9493 kHz (d, e), leading to harmonic and non-harmonic responses respectively (both cases comprise N_m = 30). On the one hand, in Fig. 2c, we show that the sensor response (diamonds) follows the harmonic function ${P}_{D}(t)={\cos }^{2}(\pi t/{t}_{{{{\rm{R}}}}})$ (blue-solid line). On the other hand, in Fig. 2d, one can observe that the response (diamonds) deviates from the harmonic case, while Fig. 2e shows that the same response fits to a non-harmonic function (red-solid curve) obtained via numerical simulations of the Hamiltonian (see Supplementary Note 1). By introducing these two responses into our NN, we get the outputs y₁ = (2π) × 1.1731 kHz and y₁ = (2π) × 8.7825 kHz which result in large accuracies F = ∣y₁ − a₁∣/a₁ = 97.84%, 98.14%, respectively. In Supplementary Note 4, we show further examples including both Rabi frequency Ω_tg and potential detunings ξ between the target frequency and the sensor hyperfine transition.

Scenario ii: Continuous data acquisition

Now, we consider a scenario that comprises single-shot measurements on the ion (i.e., N_m = 1). This scheme is relevant in situations where no reinitialization of the RF field is possible. We demonstrate that the estimation of RF parameters is still feasible in these conditions.

We get one binary value from the atomic sensor (0 or 1) after completing the three experimental stages illustrated in Fig. 3a. More specifically, at stage 1 we cool the ion and prepare the $\left\vert D\right\rangle$ state in a time t₁ = 6.097 ms. At stage 2 the ion is allowed to interact with the target field for a time t₂ ∈ [0, 6] ms. At stage 3, we readout the ion in a time t₃ = 2.447 ms. We repeat these three stages 251 times (leading to a binary string comprising 251 numbers) where t₂ varies in the interval [0, 6] ms with a step 0.024 ms. Note that during the three stages the RF source is always on, thus to avoid potential damage on initialization and readout we switch the RF signal to a dummy load at stages 1 and 3.

Fig. 3: Estimation results from Scenario ii, continuous data acquisition.

a Schematic configuration of the continuous data acquisition scheme. Each binary value is obtained after completing the preparation, interaction, and measurement stages. b–d Regression of the rescaled outputs ${y}_{1}^{r}$ from the NN with respect to the targets ${a}_{1}^{r}={\Omega }_{{{{\rm{tg}}}}}^{r}$. The regression lines ${y}_{1}^{r}=\alpha {a}_{1}^{r}+\beta$ comprise b α = 0.9946, β = 0.0032, c α = 0.9932, β = 0.0040, d α = 0.9925, β = 0.0041, while the correlation coefficients R between the outputs and the targets are all larger than 0.999. All inputs X^r, outputs ${{{{\bf{Y}}}}}^{r}=\{{y}_{1}^{r}\}$, and targets ${{{{\bf{A}}}}}^{r}=\{{a}_{1}^{r}\}$ are rescaled into the range [0, 1].

Via numerical simulations, we train a NN in accordance with the scheme in Fig. 3a. In particular, we use 96 values for Ω_tg in the range (2π) × [0.5, 10] kHz (with a step of (2π) × 0.1 kHz) and repeat the data acquisition process 1800 times for each Ω_tg. Thus we generate 96 × 1800 = 172,800 examples, of which 70%/15%/15% are used to build the training/validation/test datasets. After training the NN, we find the regression accuracy of the training/validation/test datasets shown in Fig. 3b–d. Note that data in Fig. 3b–d is rescaled into [0, 1] as this is a standardized procedure in NNs.

Now, we experimentally obtain the sensor responses for 8 randomly chosen values of Ω_tg in the range (2π) × [0.5, 10] kHz, which do not belong to the training/validation/test datasets (in addition, we select other RF parameters as ϕ_tg = 0 and ω_tg = (2π) × 10.03 MHz). We remark that the obtained responses range from the harmonic shape to those deviating from it. After 251 measurements for each Ω_tg, we get binary strings including 251 numbers (0 or 1), where each number is obtained according to the scheme in Fig. 3a. When inputting each string into the trained NN, we get one output y₁ from the NN. In order to study the stability of the NN prediction, we have repeated 20 times the data acquisition for each Ω_tg. In Table 2, we show the average value ${\bar{y}}_{1}$ of the results from the NN and the SD based on 20 experimentally obtained strings.

Table 2 Estimation results from the NN in Scenario ii.

In addition, the regression of the outputs ${\bar{y}}_{1}$ with respect to the targets is in Fig. 4a. Finally, in Fig. 4b, we illustrate for a₁ = (2π) × 2.1572 kHz the histogram of the NN outputs y₁ obtained after feeding the NN with 20 strings of experimental data. The above analysis illustrates the ability of NNs to achieve accurate estimations in scenarios involving single-shot measurements (thus, when the RF field is not controllable), leading to highly versatile quantum sensors.

Fig. 4: Accuracy analysis for continuous data acquisition.

a Regression of ${\bar{y}}_{1}$ obtained from the NN with respect to each target. In addition, the fit line (blue) and the correlation coefficient R are shown. b Histogram of 20 outputs y₁ from the NN for the case a₁ = (2π) × 2.1572 kHz denoted with a vertical red line.

Discussion

One can resort to other estimators for predicting parameters, e.g., using Bayesian inference. Following the well-known Bayes theorem, one may compute the posterior distribution p(Θ∣X) ∝ p(X∣Θ)p(Θ) where p(Θ), p(X∣Θ) denote the prior and likelihood, respectively, while X refers to the data obtained by interrogating the quantum sensor at different time instances, and Θ = {θ₁, . . . , θ_k} denotes k unknown parameters which we aim to estimate by our quantum sensor. For a Bayesian estimator, an accurate microscopic model is needed in order to calculate the likelihood p(X∣Θ). More specifically, this is

$$\begin{array}{rcl}&&p({{{\bf{X}}}}| \Theta )={\Pi }_{i = 1}^{{N}_{p}}f({X}_{i},{N}_{m},{\tilde{P}}_{i}({t}_{i};\Theta ))\\ &{{{\rm{with}}}}&f(x,n,p)=\frac{n!}{x!(n-x)!{p}^{x}{(1-p)}^{(n-x)}},\end{array}$$

(2)

where the function f(x, n, p) refers to the probability of observing x success outcomes through n trials from the Binomial distribution with success probability p. ${\tilde{P}}_{i}({t}_{i};\Theta )$ is the survival probability P_D computed using the total Hamiltonian H (see Supplementary Note 1: Eq. (3)) at time t_i whose obtention requires to load a string of values for the Θ parameters in the microscopic model and then compute its dynamical evolution. Note this is a procedure that has to be repeated for each value of the Θ parameters. Finally, via the marginal distribution p(θ_j∣X) = ∫Π_i≠jdθ_ip(Θ∣X), one could derive the average value and SD as

$$\begin{array}{c}{\theta }_{j}^{{{{\rm{est}}}}}=\int\,d{\theta }_{j}{\theta }_{j}p({\theta }_{j}| {{{\bf{X}}}}),\\ {(\delta {\theta }_{j}^{{{{\rm{est}}}}})}^{2}=\int\,d{\theta }_{j}{({\theta }_{j}-{\theta }_{j}^{{{{\rm{est}}}}})}^{2}p({\theta }_{j}| {{{\bf{X}}}}).\end{array}$$

(3)

In contrast, less prior knowledge of the microscopic model is needed when using NNs. This owes to NNs learning the input–output relation from the training/validation/test datasets that can be obtained from numerical simulations, or directly from experiments. The latter is especially useful when numerical simulation of the system dynamics becomes challenging (for instance, in a sensor that consists of several entangled ions).

In this manner, our work demonstrates the good performance in parameter estimation that results from an appropriate hybridization of ML tools with quantum sensing techniques. This is a strategy that can be easily extended to other quantum platforms, such as, e.g., nitrogen-vacancy (NV) centers in diamond, to decipher complex NV responses emerging from dense nuclear samples comprising nuclear spins which are strongly coupled to the sensor and/or among them.

Methods

NN-based magnetometer

A NN enables to find the relation between N_p measured data ${{{\bf{X}}}}=\{{x}_{1},{x}_{2},...,{x}_{{N}_{p}}\}$, and n output data Y = {y₁, y₂, . . . y_n} that approach the targets A = {a₁, a₂, . . . , a_n}. During the training stage of the NN, the following cost function

$$C=\frac{1}{nN}\mathop{\sum }\limits_{j=1}^{N}\mathop{\sum }\limits_{i=1}^{n}{({y}_{i}^{j}-{a}_{i}^{j})}^{2}$$

(4)

is minimized for a training set that comprises N examples. This is done by using gradient descent methods such that the NN parameters (i.e., weights and biases) are adjusted to satisfy F(X) = Y ≈ A.

In our case, we deal with an ¹⁷¹Yb⁺-magnetometer where we aim to estimate RF parameters from experimentally collected responses by inputting them into the NN. The input data contains, in Scenario i, average values obtained from a reduced number of measurements and, in Scenario ii, a sequence containing binary values continuously acquired from single-shot measurements. For the first case, the input data string ${{{\bf{X}}}}=\{{P}_{1},{P}_{2},...,{P}_{{N}_{p}}\}$ consist on the average values P_i (i ∈ [1, N_p]) collected in a time interval [0, t_f] for a specific set of targets A. The simulated average value is ${P}_{i}=\mathop{\sum }\nolimits_{n = 1}^{{N}_{m}}{z}_{n}^{i}/{N}_{m}$ for a number of shots N_m, where the binary outcome is drawn from a Bernoulli distribution ${z}_{n}^{i} \sim B(1,{P}_{D}({t}_{i}))\in \{0,1\}$. In the second scenario that comprises continuous data acquisition, the input data string X is made of binary numbers, 0 and 1, which are obtained according to the scheme in Fig. 3a. Repeating this procedure N times, we achieve the whole dataset that comprises N examples. In both cases, the examples with the data strings X, Y, and A are computed by selecting a number of values of the targets in, and beyond, the regime leading to harmonic sensor responses. Among all the examples of the total datasets, 70%/15%/15% lead to the training/validation/test sets. A number of repetitions for each data acquisition are repeated such that the NN learns the statistical fluctuations resulting from a reduced number of measurements.

Experimental timing sequence

As shown in Fig. 5, in each cycle (each period to obtain one value P_i (i ∈ [1, N_P]) of a response / input data string), the ion is cooled down approximately in the Doppler limit by a red-detuning 369.5 nm laser starting from stage 1. After that, the state of the ion is initialized to $\left\vert 0\right\rangle$ by an optical pumping process. After a 0.5 μs ‘MW trigger’ signal, a MW π-pulse resonant with $\left\vert 0\right\rangle \leftrightarrow \left\vert 1\right\rangle$ transfers the state from $\left\vert 0\right\rangle$ to $\left\vert 1\right\rangle$. Subsequently, the STIRAP pulses drive the system from the state $\left\vert 1\right\rangle$ to the dark state $\left\vert D\right\rangle$. At stage 2, the amplitudes of MW fields are held at a constant Ω within the fixed time interval [0, t_D]. Simultaneously, the target RF field is applied for the time interval [0, t₂], where t₂ ≤ t_D. For the scheme of a finite number of measurements (Scenario i), after the time instant t₂, the RF field is removed by turning off the AWG2 output. The RF target field is restarted at the next cycle such that the repetition of measurement can be done. For the scheme of single-shot measurement, Scenario ii, the RF signal is switched to a dummy load after the time instant t₂ while the origin RF source is always on. At stage 3, the STIRAP pulses transfer the rest of population of $\left\vert D\right\rangle$ back to $\left\vert 1\right\rangle$. Another π-pulse transfers the population of state $\left\vert 1\right\rangle$ to $\left\vert 0\right\rangle$. Thus, we can get the response of $\left\vert D\right\rangle$ by measuring the probability of $\left\vert 0\right\rangle$, and a state dependent fluorescence detection could be used to determine it. Before and after the cycle, there are extra ‘idle’ steps (1 μs) needed to end this cycle and start the next cycle. In our experiments, the timings are all controlled by a TTL pulse generator (Spincore PB24-100-4k-PCIe) see Table 3 for the specific values of the time intervals invested in each process.

Fig. 5: The sequence diagram of the experiment.

The whole cycle could be divided into three stages. Stage 1 consists of cooling, initialization, and preparation of the state $\left\vert 1\right\rangle$ (the first blue zone) and the state $\left\vert D\right\rangle$ (the first green zone). At Stage 2 (the pink zone of length t_D), we allow the ion interacts with the target field at the interval [0, t₂] (the yellow zone), where t₂ ≤ t_D. In stage 3, we transfer the state $\left\vert D\right\rangle$ back to $\left\vert 0\right\rangle$ and detect the probability of $\left\vert 0\right\rangle$.

Table 3 Experimental timings for two scenarios (‘Idle’ and ‘MW trigger’ are not shown).