Abstract
Technical noise present in laser systems can limit their ability to perform high fidelity quantum control of atomic qubits. The ultimate fidelity floor for atomic qubits driven with laser radiation is due to spontaneous emission from excited energy levels. The goal is to suppress the technical noise from the laser source to below the spontaneous emission floor such that it is no longer a limiting factor. It has been shown that the spectral structure of control noise can have a large influence on achievable control fidelities, while prior studies of laser noise contributions have been restricted to noise magnitudes. Here, we study the unique spectral structure of laser noise and introduce a metric that determines when a stabilised laser source has been optimised for quantum control of atomic qubits. We find requirements on stabilisation bandwidths that can be orders of magnitude higher than those required to simply narrow the linewidth of a laser. The introduced metric, the χ-separation line, provides a tool for the study and engineering of laser sources for quantum control of atomic qubits below the spontaneous emission floor.
Similar content being viewed by others
Introduction
The laser has become an invaluable tool in the control of atomic systems due to electronic transitions in atoms typically having optical wavelengths. The application of the laser to the field of quantum information has been particularly effectual1,2,3,4, and single atomic qubit control at the 10−4 error level has been demonstrated5,6. The use of laser radiation for manipulating atomic energy levels will be fundamentally limited by spontaneous emission (SE), either due to the finite lifetime of qubits stored in optical transitions, or due to off-resonant scattering during two-photon Raman transitions. However, experimental demonstrations at the SE error floor have not been forthcoming due in part to technical noise sources dominating qubit errors. It is of interest to understand and reduce the technical error to the SE floor to enable low-overhead fault tolerant quantum computation.
One dominant technical noise source is the local oscillator (LO) interacting with the qubit for quantum control. In this paper, we consider LOs derived from laser radiation. Previous studies have connected qubit fidelities to the total magnitude of laser noise7,8,9,10,11,12, and it has been demonstrated that the spectral structure of LO noise fields can have a critical influence in qubit fidelities through a study of phase noise in microwave sources13. The effect of specific laser noise spectra on Rydberg excitation has also been investigated14. Here, we identify general conditions on the spectral structure of frequency and intensity noise of laser radiation to reduce these technical errors to, or below, the SE floor. We focus strictly on the influence of laser noise on the qubit transition in the absence of other neighbouring transitions that could lead to additional error pathways. It has been previously acknowledged that the spectral structure of laser noise can interact with the motional modes of trapped ions10,15.
We find that, contrary to common belief10,16,17, narrowing the LO linewidth alone is not sufficient for high fidelity qubit control. The effective linewidth the qubit experiences is larger than the one given by a simple full-width-half-maximum (FWHM) measurement of the LO linewidth. This is because high frequency sideband noise on the LO carrier can have a sizeable effect on qubit fidelities, and stabilisation techniques are limited in their control bandwidth15,18,19,20.
We find that laser frequency noise is a primary consideration, as we show that the qubit infidelity from shot-noise limited laser intensity noise is always below the SE floor, across all commonly-used atomic species and qubit types. In practice, laser sources are rarely shot noise limited and we outline requirements on intensity noise stabilisation bandwidths to suppress these errors below the SE floor.
The results presented in this manuscript provide a roadmap to suppress qubit errors from technical laser noise to below the fundamental limit of atomic spontaneous emission. The findings guide the choice of laser source and requirements for laser stabilisation. We find that for a stabilised laser source, there are three primary regimes. In the first regime, the stabilisation is insufficient to reduce qubit control errors. In the second regime, the stabilisation reduces control errors, but the unstabilised noise still dominates the error. In the third regime, the stabilisation is sufficient such that the errors are dominated by the stabilised noise amplitude. We develop a metric, called the χ-separation line, that determines when the third regime is satisfied, and that can be easily used to analyse realistic laser noise spectra. Critically, the χ-separation line places stricter requirements on stabilisation loops than those for simply narrowing the laser linewidth. For a laser operating in the third regime we outline the requirements to operate below the SE floor for both laser frequency and intensity noise and find no fundamental obstacles to this goal. The results are derived for a general Hamiltonian of a two-level system interacting with a LO, and apply broadly to optical and hyperfine qubits in both trapped ions and neutral atoms. The results also apply to cascaded qubits, such as in Rydberg excitation, under some assumptions we outline below. Extensions beyond the two-level Hamiltonian used here are outlined in the discussion.
Results
Background
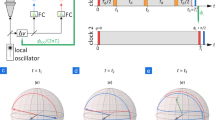
Atomic qubits are typically encoded in energy levels separated by either optical or microwave transition frequencies. One or more lasers can be used to drive transitions with either one-photon or multi-photon processes, where we restrict our analysis to one- and two-photon transitions. For optical transition frequencies (Fig. 1a), narrow-linewidth laser radiation can be directly used to coherently rotate the qubit state10 with a one-photon process, which we refer to as an optical qubit. Alternatively, if there is an intermediate transition between the ground and excited state, two lasers of different wavelengths can be used to drive a two-photon transition to coherently rotate the qubit state. We refer to these as cascaded qubits, and are typically used for Rydberg excitation. For microwave transitions (Fig. 1b), two phase-coherent optical fields offset by the qubit frequency can be used to control the qubit state through a two-photon Raman transition5,21. One way to generate the beatnote for hyperfine qubit control is to phase-lock two continuous-wave (CW) lasers and interfere them at the atom position. A more recent approach is to use the output of a mode-locked (ML) laser. The pulse train of an ML laser forms a comb of optical frequencies, with each comb tooth separated by the repetition rate of the laser22. The mode-locking process ensures all comb teeth are phase coherent, and when the comb is split into two paths and interfered at the atom position, a series of beatnotes are generated. By placing a frequency shifter, such as an acousto-optical modulator (AOM), in one arm of the interferometer, beatnote harmonics can be finely tuned to the qubit frequency21,23. We note that for the purpose of our analysis both cascaded and hyperfine qubits are analogous, with the difference between them being contained in how the laser noise is manifested in LO noise. For clarity, we concentrate on hyperfine qubits and comment under what approximations our results also hold for cascaded qubits as applicable.
a For optical qubits, the laser light is resonant with the qubit transition. b For hyperfine qubits, the LO is derived from the beatnote between two closely spaced optical frequencies. For continuous-wave (CW) lasers, this is performed by off-set phase locking two lasers by the qubit frequency. For modelocked (ML) lasers, this is performed by interfering two frequency combs at the atom position, with one comb shifted in frequency such that the qubit is driven by the frequency difference between comb pairs. c Noise away from the laser carrier frequency leads to a time-dependent variation in the LO control field, which can itself be expressed as a power spectral density, as shown in (d). e The time-dependent noise causes perturbations in qubit evolution on the Bloch sphere. f Example servo loops for stabilising laser frequency noise. g The servo loops act to reduce noise within the servo bandwidth, while free-running noise at higher frequencies is unaffected.
Noise in the laser sources used for optical and hyperfine qubit control (Fig. 1c, d) leads to noisy evolution of the qubit on the Bloch sphere (Fig. 1e). Frequency noise causes unwanted rotations around the Z axis, while intensity noise causes unwanted rotations around the X and Y axes. The accumulation of these perturbations leads to an imperfect overlap of the final quantum state with the target state. The overlap can be quantified by the fidelity, which can be calculated using filter function theory. For sufficiently small noise, the fidelity can be expressed as24,25,26
where the fidelity decay constant, χ(u), is a spectral overlap of the laser noise power spectral density (PSD) with the filter function of the target operation, u, of duration τ (see Methods). In this paper we derive our results for general filter functions and present examples for a primitive π-pulse between the ground and excited state in an ideal two-level atom with a Rabi frequency Ω = π/τ. The fidelity of a π-pulse is chosen for ease of interpretation, and we note that fidelities of other common operations, such as a Ramsey sequence, are within an order of magnitude of the π − pulse for the same operation times13.
The connection of the laser noise PSDs to the operation fidelity motivates the suppression of noise in the laser sidebands. As shown in Fig. 1f, g for frequency noise, this is typically performed using active stabilisation (servo) loops of a finite bandwidth. We use Eq. 1 to investigate the requirements on these stabilisation loops for maximising operation fidelities.
Models of laser noise
Noise processes in laser systems, which depend on properties of both the gain medium and the laser cavity, are typically expressed as either double- or single-sided PSDs27,28,29,30,31,32,33,34,35. For consistency, results presented here are in terms of single-sided PSDs. All laser systems have similar structural features in their PSDs, with the exact placement and magnitude of these features varying between laser technologies. Further, free-running relative intensity noise PSD, SRIN(ω), and frequency noise PSD, \({S}_{{\omega }_{{{{\rm{opt}}}}}}(\omega )\), follow a similar structure (as shown in Fig. 2), and therefore we introduce them together.
a The RIN PSD, demonstrating the low frequency 1/ω (flicker) noise, mid-frequency white noise, the relaxation oscillation peak, and shot noise. b The frequency noise PSD with the same general features as RIN with a fundamental limit of quantum noise. The noise above the β-separation line contributes to the linewidth of the laser, while the noise below the β-separation line contributes to the wings of the laser lineshape.
The fundamental limits of intensity and frequency noise PSDs take the form of white noise (i.e. constant for all Fourier frequencies, ω)36. For relative intensity noise, this limit is the shot noise limit (SNL)37
arising due to the Poisson statistics of the number of photons in the laser beam. Here, ωopt is the optical frequency and \(\bar{P}\) is the mean power in the optical field. For frequency noise, the white noise floor is given by the quantum noise limit, setting a minimum linewidth of the laser (often called the modified Schawlow-Townes linewidth). The PSD of the quantum noise limit (QNL) takes the value (see Supplementary Note 1)
where γc is the bandwidth of the laser cavity, which is inversely proportional to the cavity length.
In practice, lasers do not typically exhibit fundamentally limited noise PSDs. We refer to all noise processes above the fundamental limit as technical noise. The Fourier frequency response (modulation transfer function) of the gain medium inside a laser cavity acts as a low pass filter for pump noise36. The filter bandwidth is approximately set by the inverse of the upper-state lifetime of the laser gain medium, often called the relaxation frequency, ωrlx. Below ωrlx, the laser has a flat frequency response. Around ωrlx, the laser has a resonant response to modulation and undergoes relaxation oscillations. Above ωrlx, the relaxation oscillations are damped. The modulation response predominantly transfers pump noise into laser intensity noise. Intensity noise can modulate the refractive index of the gain medium, which alters the phase of the laser light. Therefore, the frequency noise is increased due to the intensity noise, with the increase characterised by the linewidth enhancement factor, α36.
At low Fourier frequencies, the technical noise from the pump takes the form of 1/ωa-type noise (commonly referred to as 1/f noise). For low-noise pumps, 1/ωa-type noise is dominated by 1/ω1 (flicker) noise, with higher order a noise being restricted to Fourier frequencies ω < 2π × 100 Hz. In all scenarios of interest, we find that these higher order noise terms do not contribute significantly to qubit fidelities unless they span the Rabi frequency of the quantum operation. Therefore, for simplicity, we restrict our study to pure flicker noise.
At the flicker corner frequency, ωflk, the flicker noise reaches a white noise floor. For intensity noise, this floor is given by the higher of the pump noise and the SNL. In realistic laser sources, the frequency noise floor for Fourier frequencies from ωflk to ωrlx is enhanced from the QNL by the coupling to intensity noise by a factor of α2 36. For Fourier frequencies above the relaxation oscillation peak, pump noise is increasingly damped and the noise amplitude approaches the SNL or QNL accordingly.
In this study we concentrate on two common laser sources used for qubit control: the external cavity diode laser (ECDL) and the optically-pumped solid state laser (OPSSL), where most contemporary OPSSLs are diode-pumped. A OPSSL typically has higher intensity noise than an ECDL due to pump noise amplification, and lower frequency noise due to a longer laser cavity. ECDLs typically have relaxation oscillation frequencies, ωrlx, of order GHz27, whereas for OPSSL they are sub-MHz29,30,31.
For ECDLs, the semiconductor’s asymmetric gain profile leads to α having typical values between 3 and 638. For OPSSL, the gain profile is more symmetric and typically α ≈ 0.339,40 and therefore is not a dominant contribution to frequency noise. Enhanced frequency instability in OPSSL typically occurs due to mechanical and thermal effects41.
In addition to the general structural trends of laser noise PSDs, for realistic laser sources there are bumps and spurs present in the laser spectrum. These features typically occur due to mechanical instabilities and actuator resonances in the laser cavity. For well designed laser cavities (e.g. Toptica DL Pro42), relatively smooth laser noise PSDs can be achieved. In this study, we focus on the gross structural features of laser noise PSDs due to the lasing process itself. Uncontrolled spurs in laser noise PSDs will affect qubit fidelities, however their influence is limited to when the Rabi frequency is close to the spur frequency. Calculations of qubit control fidelities for a measured laser frequency noise PSD are presented in the following section.
The technical noise present in both intensity and frequency noise of laser sources often requires the stabilisation of laser sources for use in quantum control. We model the PSDs of stabilised laser sources with the simplified model
such that ha is a constant white noise amplitude within the stabilisation bandwidth, ωsrv, and hb is the residual free-running white noise amplitude outside the stabilisation bandwidth. The approximation that hb is constant simplifies our derivations, and we demonstrate that our results typically hold even when this is not the case. We assume that ha < hb, and we address the case where this is not automatically valid (e.g. solid state lasers) in the Discussion. Such a model has previously been used to explore the effect of stabilisation bandwidths on laser linewidth reduction43. In the followings section we connect this general PSD to qubit fidelities and derive requirements on laser frequency and intensity noise to achieve high fidelity qubit control.
Frequency noise stabilisation requirements
For LOs derived from laser radiation, the frequency noise of the LO directly results from noise in the laser source. In this instance the PSD of LO frequency noise, \({S}_{{\omega }_{{{{\rm{LO}}}}}}(\omega )\), is equivalent to the stabilised laser frequency noise, which we approximate with the simple expression in Eq. 4. For the purposes of a general discussion on how stabilised frequency noise affects qubit control, we express all results in terms of the parameters ha, hb and ωsrv. For an exposition of the specific way that laser noise processes connect to these parameters for different qubit and laser types, see the Supplementary Information.
To connect laser noise parameters to qubit fidelities for arbitrary single-qubit operations, we require a general expression for single-qubit filter functions. We approximate a general filter function of a quantum operation as the piece-wise function
such that the qubit has a flat response to control noise above the cut-off frequency, \({\omega }_{{{{\rm{cut}}}}}^{(u)}\), and noise below the cut-off is damped at \(10{\log }_{10}({n}_{u})\) dB per decade, where nu is the order of the filter function. The condition of continuity sets the requirement \({c}_{b}^{(u)}={c}_{a}^{(u)}{({\omega }_{{{{\rm{cut}}}}}^{(u)})}^{{n}_{u}}\), and ca,b are constants set by the form of the filter function. Such a general model can approximate a wide range of quantum operations, including composite pulse sequences designed to correct for control errors and noise24,44. The use of filter functions over numerically solving the Schrödinger equation in the presence of noise allows the analytical derivation of conditions on arbitrary laser noise PSDs. A thorough exposition on the use of filter function theory for assessing qubit control in the presence of noise is given in Ref. 26.
We find that to improve qubit control over using a free-running laser, the servo bandwidth must be above the filter function cut-off frequency, which in the case of a primitive π − pulse is the Rabi frequency. Substituting the piece-wise expressions for the frequency noise PSD (Eq. 4) and the general filter function into Eq. 1 (see Supplementary Note 3), we can derive an approximate expression for the fidelity decay constant, χ(u), of a general single-qubit operation. In the regime that the servo bandwidth is below the filter function cut-off frequency, ωsrv < ωcut, we find \({\chi }^{(u)}\approx n{c}_{b}^{(u)}{h}_{{{{\rm{b}}}}}/(4\pi (n-1){\omega }_{{{{\rm{cut}}}}})\). In this instance, the qubit fidelity is dominated by the free-running noise of the laser, hb, and the contribution from ha has negligible influence on qubit errors. We refer to this regime as hb-limited.
In the regime ωsrv > ωcut, the expression for the fidelity decay constant becomes
The first term contains the ratio of the stabilised frequency noise ha to the cut-off frequency of the quantum operation, \({\omega }_{{{{\rm{cut}}}}}^{(u)}\), which determines a fundamental limit to the fidelity based on the stabilised laser noise. The second term places a limit on the fidelity from the free-running noise, hb, and the servo bandwidth, ωsrv. For servo bandwidths
the first term in Eq. 6 exceeds the second term such that ha is the dominant contribution to the qubit fidelity (ha-limited). For servo bandwidths below this frequency, the fidelity is limited by the insufficient suppression of the free-running noise (servo-limited). Here, \({\omega }_{\chi }^{(u)}\) defines the cutoff between the ha-limited and servo-limited regions.
As an example, we consider the filter function for the primitive π-pulse with Rabi frequency Ω. In this instance, \({c}_{b}^{(\pi )}=4\), nπ = 2 and \({\omega }_{{{{\rm{cut}}}}}^{(\pi )}={{\Omega }}\) (see Methods), such that Eq. 6 becomes
and Eq. 7 becomes
Eq. 9 can be reformulated as a bound on the PSD (see Supplementary Note 3) such that the π-pulse error from laser noise is dominated by residual noise in the region
We define the boundary of this region as the χ-separation line. The requirement on the servo bandwidth is therefore to suppress all free-running noise to below the χ-separation line. For typical values of ha and Ω, this limitation is stricter than the requirement on narrowing the linewidth of a laser source from the β-separation line (see Supplementary Note 4)
The β-separation line divides the frequency noise PSD into a region that contributes to the laser linewidth and a region that only contributes to the lineshape wings (see Fig. 2b). The required servo bandwidth to narrow the linewidth of the laser is the one that suppresses all free-running noise to below this β-separation line, while a much higher servo bandwidth is needed to suppress noise below the χ-separation line to minimise π-pulse control errors. The χ-separation line can be applied to LO frequency noise spectra for optical and hyperfine qubits, as well as cascaded qubits when each laser is stabilised with the same servo bandwidth, ωsrv.
To illustrate the above findings and confirm that the χ-separation line provides a useful measure of fidelity optimization, we show numerical calculations of primitive qubit infidelities in Fig. 3. We use the the frequency noise PSD shown in Fig. 3a and the exact expression for the first-order filter function of a π − pulse (see Methods, Eq. 34). Such a PSD applies equally to a single servoed ECDL addressing an optical qubit, or two phase-locked ECDLs addressing a hyperfine qubit. In contrast to the simplified-model PSD used to derive Eq. 6, we have included the relaxation oscillation peak found in ECDLs.
a The frequency noise PSD of a LO generated from a servoed diode laser. Within the servo loop, the noise amplitude takes the value of ha. Above the servo bandwidth, ωsrv, the LO takes on the free-running laser noise including a relaxation oscillation peak of 20dB at 2π × 1GHz. b The infidelity landscape as the Rabi frequency and servo bandwidth are varied, demonstrating three main regions (detailed in text). The hb-limited region is separated by Ω = ωsrv (solid line) from the servo-limited region, with the χ-separation line (dashed) delineating the ha-limited region. c A 1D cross-section of (b) at Ω = π/2 × 105Hz. d A diagrammatic representation of noise spectral densities in each of the three regions, with the π − pulse filter function (in arbitrary units) overlaid for comparison. e The infidelity landscape as the above-servo noise amplitude, hb, and the servo bandwidth are varied for Ω = 2π × 10kHz. The β-separation line (dotted), does not guarantee qubit coherence, while the χ-separation line (dashed) again bounds the ha-limited region. f A cross-section of (e) at ωsrv = 300kHz. f A diagrammatic representation of the PSDs in each of the three regions with respect to the β- and χ-separation lines. The χ-separation line in Fourier space is given by Eq. 10.
Our simulations confirm the existence of the three regions – hb-limited, servo-limited, and ha-limited – that were identified in our analysis using piece-wise approximations. These regions can be seen in Fig. 3b and c as the servo bandwidth, ωsrv is varied. For ωsrv < Ω (the hb-limited region), changing the servo bandwidth has little effect on the fidelity. The reason for this is illustrated by Fig. 3d, where the filter function in frequency space is shown for a primitive operation. The response of the filter function is flat for Fourier frequencies above Ω, and free-running noise in this region dominates the qubit errors. For \({{\Omega }}\, <\, {\omega }_{{{{\rm{srv}}}}} \,< \,{\omega }_{\chi }^{(\pi )}\) (the servo-limited region), the contribution of hb is reduced by the stabilisation loop; however, it can still have a sizeable effect compared to the contribution to the error from ha. To improve fidelity in this regime, the servo bandwidth must be increased, as the fidelity is largely independent of Ω. For \({\omega }_{{{{\rm{srv}}}}} \,>\, {\omega }_{\chi }^{(\pi )}\) (the ha-limited region), the contribution to the fidelity from ha becomes dominant, as hb is suppressed below the χ-separation line and increasing the servo bandwidth further provides diminishing returns.
We also confirm numerically the importance of the χ-separation line to qubit fidelities. In Fig. 3e and f the β- and χ-separation lines are directly compared. For high values of hb and low servo bandwidths, there is no coherence between the laser source and the qubit, indicated by fidelities of \({{{\mathcal{F}}}}=0.5\). The β-separation line relates only to properties of the laser, and therefore does not necessarily imply qubit coherence, as seen in the case shown in Fig. 3e and f. As hb decreases and/or ωsrv increases, fidelities improve up until the χ-separation line where the fidelity becomes limited by ha. These trends are further illustrated in Fig. 3g. In the instance that any part of the free-running noise is above the β-separation line, this free-running noise dominates the FWHM linewidth. Similarly, when any part of the free-running noise is above the χ-separation line, that free-running noise reduces the fidelity compared with an idealized white-noise LO of the same FWHM linewidth.
To demonstrate that the χ − separation line is a useful metric for realistic laser sources, we use it to analyse the frequency noise of an ultra-stable laser from Menlo Systems. As shown in Fig. 4a, the laser is stabilized to a sub-Hz linewidth (as defined by the β-separation line), with a servo bump at ω = 105Hz from the slow integrator that provides feedback to the piezo element in the ECDL cavity. The total servo loop has an approximate servo bandwidth of ωsrv = 3MHz, and we have extrapolated the free-running noise of the laser outside the measurement band as white noise. The χ − separation line for ha = (4π)−1 Hz is plotted with the Rabi frequency of Ω = 1.5kHz, selected such that the high frequency noise falls below the line. The value of ha corresponds to the low Fourier frequency white-noise of the PSD.
a Laser frequency noise of a Menlo Systems ORS-Compact at a wavelength of 1397 nm. The β-separation line indicates an ultra-narrow, sub-Hz linewidth. A χ-seperation line corresponding to the white noise at low Fourier frequency has been plotted, with a Rabi frequency chosen such that the high frequency noise is bounded by the line. b The calculated π-pulse error corresponding to driving an optical transition with the measured laser noise. The laser exhibits the three regimes of operation identified in our analysis, demonstrating that the χ-separation line is a useful tool for analysing real laser noise.
In Fig. 4b we calculate the π-pulse error for the Menlo laser driving an optical qubit transition over a range of typical Rabi frequencies. At low Rabi frequencies, the error approximately follows the ha-limit line (ha-limited operation), before starting to plateau at around Ω = 1.5kHz as the high frequency noise crosses the χ − separation line (servo-limited operation). The slow integrator servo bump appears as an increased error rate for when ωsrv ≈ Ω. At high Rabi frequencies, the error trends to the hb-limit (hb-limited operation). This analysis shows that the χ-separation line is a useful tool for the analysis of laser sources even when spurs and bumps are present, and when there is a gradual, rather than step, transition between the stabilised and free-running noise.
The demonstration that the χ-separation line is a useful tool for non-ideal frequency noise PSDs suggests that it can be applied to the cases of cascaded qubits even in the instance that their servo parameters are non-identical. In this case, the LO noise PSD -which is the summation of the individual, servoed noise PSDs - can be bounded by the χ − separation line. Each laser can then be optimised by reducing its individual contribution to any noise above the line that would then limit qubit fidelities.
To determine the conditions under which the error from an ha-limited laser source is smaller than the fundamental SE error, we set the requirement ϵSE > χ(u)/2. Here, ϵSE is the spontaneous emission error (see Methods for definition). In the asymptotic limit, ωsrv → ∞, this rearranges to the requirement
which for a π-pulse reduces to ha < πϵSEΩ. For a finite value of ωsrv, the fidelity does not appreciably change from this asymptote in the ha-limited region, as seen in Fig. 3c. The maximum value of ha that saturates this bound is plotted in Fig. 5 for both optical and hyperfine qubits with varying spontaneous emission floors. For optical qubits, the spontaneous emission error is inversely proportional to the Rabi frequency (see Methods), setting a constant requirement on ha for all Ω. For hyperfine and cascaded qubits, the spontaneous emission error is constant with Rabi frequency; thus, increasing Ω allows higher values of ha to satisfy the inequality in Eq. 12.
In this limit the linewidth of the LO is approximately equivalent to ΓFWHM = ha/4π. a Optical qubits, where the SE floor is given by the lifetime of the qubit state. Typical lifetimes of metastable atomic states are used, which approximately correspond to SE errors, ϵSE, of 6 × 10−6, 6 × 10−5, 6 × 10−5, and 6 × 10−3, from longest to shortest respectively. The SE floors of S1/2 → D5/2 transitions in a selection of optical qubit candidates are shown for reference16,52. b Hyperfine qubits, where the SE floor is given by off-resonant scattering. We define \(\epsilon =1-{{{\mathcal{F}}}}\). The requirement on laser noise is relaxed for higher Rabi frequency as less noise is sampled by the qubit and the SE error is constant with Rabi frequency. The value of ha corresponding to the minimum value of ϵSE for a selection of hyperfine trapped ion and neutral atom qubit candidates at Ω = 1MHz are shown for reference.
Intensity noise
The results presented for the effect of laser frequency noise on qubit control share many similarities with the effect of laser intensity noise. For stabilised intensity noise, we approximate the PSD, SRIN(ω), using the simple model of Eq. 4, with noise amplitudes \({h}_{{{{\rm{a}}}}}^{\prime}\) and \({h}_{{{{\rm{b}}}}}^{\prime}\) replacing ha and hb, respectively. Here, \({h}_{{{{\rm{a}}}}}^{\prime}\) and \({h}_{{{{\rm{b}}}}}^{\prime}\) have different physical units than ha and hb. Similar to our analysis for frequency noise, the fidelity decay constant, χ(u), for intensity noise takes the form
with the constant κ = 1/4 for optical qubits and κ = 1 for hyperfine and cascaded qubits. For simplicity, in the case that two separate laser sources are used to generate the LO, we assume that they have identical intensity noise PSDs. The additional factor of κΩ2 over the fidelity decay constant for frequency noise in Eq. 6 comes from the conversion of intensity noise to Rabi frequency noise (see Methods). Thus, the servo bandwidth requirement and the χ-separation line take the same form as for frequency noise in Eqs. 7 and 10 respectively.
Similarly to frequency noise, we derive the requirement for the intensity noise error to be below the fundamental SE floor by enforcing the constraint ϵSE > χ(u)/2. In the asymptotic limit, ωsrv → ∞, this becomes
which simplifies to \({h}_{{{{\rm{a}}}}}^{\prime} \,<\, 2{\epsilon }_{{{{\rm{SE}}}}}/(\kappa {{\Omega }})\) for a π-pulse.
The fundamental limit of laser intensity noise, and therefore \({h}_{{{{\rm{a}}}}}^{\prime}\), is the SNL (Eq. 2). Therefore, the lowest achievable error depends on the SNL, which is inversely proportional to laser power. As Ω increases with increasing laser intensity, the condition of Eq. 14 can be reduced to involve only the beam size, which is determined by the usable numerical aperture (NA) of the addressing beam. We find (see Supplementary Note 6) that for hyperfine, cascaded and optical qubits, the condition is satisfied for all physical numerical apertures up to the Abbe limit in vacuum (NA = 1). Therefore, the intensity noise error from SNL laser light is always below the SE floor. For hyperfine and cascaded qubits, this result is true for all single-valence electron ions and neutral atoms where the lower qubit state is defined in the ground state manifold. For optical qubits, this result is true for all quadrupole transitions in ions and neutral atoms. The reason for this universality is that changes from system to system are contained within ϵSE (see Supplementary Note 6).
As well as contributing to Rabi noise, the intensity noise can couple to an effective dephasing noise through AC Stark shifts. The varying laser intensity changes the effective electric field strength at the atomic position, leading to a time-varying change in the qubit frequency. Assuming a static laser frequency, this causes an effective detuning that can lead to a non-trivial error contribution from dephasing. We neglect the contribution of AC Stark shift for optical qubits driven on resonance, and the following results apply to hyperfine qubits.
For CW laser radiation, the Stark shift, \({{{\Delta }}}_{{{{\rm{AC}}}}}^{{{{\rm{(cw)}}}}}\), depends on the two-photon Rabi frequency, Ω2γ, as \({{{\Delta }}}_{{{{\rm{AC}}}}}^{{{{\rm{(cw)}}}}}={\mu }_{{{{\rm{cw}}}}}{{{\Omega }}}_{2\gamma }\). Here, the dimensionless proportionality constant, μcw, can be calculated from atomic and laser parameters and its value typically takes an order of magnitude of 10−3 45. We find that Stark shift noise from CW laser radiation causes less infidelity than Rabi noise for \({\mu }_{{{{\rm{cw}}}}} < \sqrt{({\pi }^{2}+4)/8}\approx 1.3\) (see Supplementary Note 9), and is therefore typically negligible.
When the laser radiation is a frequency comb, each comb tooth frequency contributes to the Stark shift, \({{{\Delta }}}_{{{{\rm{AC}}}}}^{{{{\rm{(fc)}}}}}\), and its magnitude depends quadratically on the two-photon Rabi frequency as \({{{\Delta }}}_{{{{\rm{AC}}}}}^{{{{\rm{(fc)}}}}}={\mu }_{{{{\rm{fc}}}}}{{{\Omega }}}_{2\gamma }^{2}\). The proportionality constant, μfc, is again calculated from atomic and laser parameters, typically taking the value of ~ 10−9Hz−1 (see Supplementary Table 2). We find that infidelities from frequency comb Stark shifts are below those of Rabi noise for \({\mu }_{{{{\rm{fc}}}}} < \sqrt{({\pi }^{2}+4)/(32{{{\Omega }}}_{2\gamma }^{2})}\approx 0.65/({{{\Omega }}}_{2\gamma })\). Therefore, for typical Stark shift values and Rabi frequencies, AC Stark shift noise from intensity noise is not a dominant contribution.
In the above analysis we have concentrated on the noise from the lasing process itself. There are other sources of intensity noise between the laser head and the atom position, such as AOM diffraction efficiency noise, polarisation-to-intensity noise and beam pointing jitter. These effects may contribute a greater source of intensity noise than the laser itself, especially for tightly focused individual addressing beams. However we consider these technical, and not fundamental, limits to qubit fidelities and their consideration is beyond the scope of our present analysis.
Discussion
We have outlined the requirements for laser sources to perform quantum control with errors below the SE floor. The noise of a free-running laser necessitates the use of stabilisation loops to reach this fundamental floor, and we have shown how the specific details of this loop are important for fidelity optimisation. Specifically, there is an interplay between the stabilized noise amplitude, ha, the servo bandwidth, ωsrv, the Rabi frequency, Ω, and the residual free-running noise of the noise spectrum, hb. The interplay can be summarised in the introduced concept of the χ-separation line, such that when free-running noise is suppressed below this line, the fidelity of qubit operations will be approximately limited at a fundamental level by the value of ha. Within this ha-limited regime, noise from the laser source can become non-dominant by appropriately minimising the value of ha, which can be below the SE floor. Therefore, the task of performing optimal quantum control using laser LOs is first to determine the required value of ha such that errors are below the SE floor, and then to determine the appropriate servo bandwidth to suppress free-running noise such that ha-limited operation is achieved.
The simple PSD used to model stabilised laser sources does not capture some non-universal features of realistic laser noise spectra, such as spurs and servo bumps. However, we find numerically that deviations from the simple model do not compromise the use of the χ-separation line as a metric for laser noise optimisation. For example, when we introduce a servo bump at ωsrv, we find that if the noise is below the χ-separation line, its influence is negligible. Similarly, for the relaxation oscillation peak we numerically find that in the regime where the ωrlx is close to ωsrv, the relaxation peak has a negligible influence as long as it sits below the χ-separation line. These examples suggest that any noise below the χ-separation line has little influence on qubit fidelities, irrespective of its exact structure. This conclusion is further supported by the application of the χ-separation line to the frequency noise PSD of an ultra-stable laser from Menlo Systems, where the χ-separation line correctly predicts the numerically calculated π − pulse error despite spurs and servo bumps being present.
Our results on the influence of LO noise from a laser source perspective also provide informative design constraints on LOs derived from microwave sources. It has previously been shown that lab-grade microwave oscillators can cause significant fidelity limitations on qubit operations, and that composite pulse sequences provide a negligible improvement in achievable fidelities13. These lab-grade oscillators have a remarkably similar frequency noise PSD to a diode laser locked to a high finesse cavity (ha ~ 10−1Hz), with a servo bandwidth of approximately 2π × 104Hz. As we have shown, such a servo bandwidth is insufficient to narrow the effective linewidth the qubit experiences. Similarly, it was shown that a precision LO has a smaller low-frequency noise (ha ~ 10−4Hz), but is still servo-limited in its operation. Therefore, to improve the use of microwave oscillators for driving qubit operations, either the phase-locked-loop bandwidth must be increased, or the intrinsic phase noise of the variable oscillator must be improved. For microwave oscillators with Ω = 100kHz, servo bandwidths would have to be increased to approximately 5MHz to achieve ha-limited operation.
The simple PSD model used in this manuscript does not match the typical noise spectra of stabilised OPSSLs. Solid state gain media typically have long relaxation times, and therefore low values of ωrlx (of order 2π × 105kHz), and it is possible for ωsrv < ωrlx such that the relaxation peak is suppressed. In this instance the free running frequency noise is actually the QNL, such that ha > hb. In this case, the qubit fidelities are automatically limited by the value of ha without the servo bandwidth having to satisfy the requirement from the χ-separation line. Therefore, OPSSLs have a distinct advantage over ECDLs in that ha-limited operation can be achieved with comparably relaxed servo bandwidth requirements.
In the instance where active stabilisation bandwidths needed to achieve ha-limited fidelities are technologically demanding, or even prohibitive, it may be preferable to use passive stabilisation techniques. For an LO of an optical qubit, this can be performed using the transmitted light of a high-finesse cavity, such that the resulting laser frequency noise is low-pass filtered by the cavity linewidth15. Offset injection locking can be used to passively lock two diode lasers, where the light of a primary laser is shifted in frequency by the qubit frequency and injected into a secondary laser46. The effective bandwidth of the phase locking is that of the cavity bandwidth, which, for the short cavity lengths present in ECDLs, can be of order GHz. Similar to frequency noise, the suppression of intensity noise could be performed passively to avoid the demanding requirements on servo bandwidths. The use of a saturated optical amplifier can generate SNL light with watts of optical power over at least a 50MHz bandwidth47. Alternatively, collinear balanced detection can be used as a notch filter on laser intensity noise, with center frequencies of the notch filter being able to be passively selected from MHz to GHz48. Therefore, this technique can be used to suppress noise around ωcut.
The interplay between laser noise and an arbitrary filter function was derived. In the general expressions of Eqs. 6 and 7, the order of the filter function, nu, plays an important role in both the achievable fidelity and the required servo bandwidth. As nu is increased (better low frequency filtering), the fidelity is improved. However, filter functions of higher order nu are constructed using concatenated pulses. For the same laser power, these concatenated sequences are longer in duration than a primitive π-pulse, reducing ωcut. Therefore, there is a competing effect between the increasing order of nu and decreasing value of ωcut. This result is reflected in the previous finding of an unreliable improvement in fidelity of a dynamically corrected gate (DCG) for typical microwave oscillators that have approximately the same frequency PSD as Eq. 413. We have confirmed these findings for the simple model PSD using a fixed laser power, and find negligible improvement in fidelity of a DCG over a π − pulse. A slight improvement is only found in the instance that noise is suppressed below the χ-separation line. Further investigations are required to explore whether these improvements are maintained for actual laser noise PSDs.
The analysis presented here has focused on single-qubit gates, where the sideband noise causes infidelities on the qubit carrier transition. In physical atomic systems of interest, there are often other nearby transitions that the sideband noise could interact with, such as Zeeman states, or motional modes due to confinement. The coupling of sideband noise to these transitions could lead to additional infidelity pathways not quantified here10. In particular, when the motional modes are used for two-qubit entangling operations, such as the Mølmer-Sorensen gate in trapped ion chains, excess phase noise at the carrier transition frequency will cause two-qubit gate infidelities. The analysis here should therefore be extended to Hamiltonians beyond the two-level qubit to include additional transitions and quantum operations. These further analyses would require extensions to the filter function theory formalism employed here, which has previously been performed for the Mølmer-Sorensen gate49. These extensions would allow for the studies to be applied more broadly to other fields, such as quantum simulation experiments, with the Ising Hamiltonian as one example. Such analyses would allow for the appropriate choice and tailoring of LOs for a vast array of quantum systems of interest, to maximise the fidelity and usefulness of these apparatus.
Methods
Spontaneous emission
For optical qubits, the fundamental limit to qubit fidelities is from the finite upper-state lifetime. The fidelity of a primitive pulse to an excited state of finite lifetime,τe, is given by50
such that higher Rabi frequency and longer state lifetimes leads to higher gate fidelities.
For two-photon transitions, the spontaneous emission is due to photons off-resonantly scattering from the intermediate state. For equal intensity laser beams driving σ± transitions, the scattering probability is independent of the Rabi frequency, such that51
where Γ is the linewidth of the intermediate transition, ωF is the splitting to the next closest excited state to the intermediate transition, and Δ is the detuning of the laser light from the intermediate transition. The off-resonant scattering probability can be minimised for Δ ≈ 0.4ωF, and its exact value is strongly dependent on the atomic species used, due to different values of Γ and ωF that can vary over orders of magnitude. Typical values of the SE error are presented in the Supplementary Information.
The Hamiltonian
We consider the Hamiltonian of an atom interacting with a LO field and subject to time-dependent errors in its frequency and Rabi frequency13,25,26,
where \({\sigma }_{\theta }=\{\cos [{\phi }_{c}(t)]{\sigma }_{x}+\sin [{\phi }_{c}(t)]{\sigma }_{y}\}\), Ωc(t) and ϕc(t) are the Rabi frequency and phase of the control field respectively, δΔ(t) describes the time-varying detuning of the LO frequency from the qubit frequency, and δΩ(t) is the time-varying fluctuations of the Rabi frequency. The Hamiltonian can be used to represent both optical and two-photon Raman transitions.
For optical transitions \({{{\Omega }}}_{c}\propto \sqrt{I}\), where I is the laser intensity, the relationship between RIN and Rabi frequency noise is given by
where δI(t) is the time-varying intensity noise of the laser field.
For two-photon Raman transitions \({{\Omega }}\propto \sqrt{{I}_{1}}\sqrt{{I}_{2}}\), where I1 and I2 are the intensities of each laser beam. Making the assumption that I1 = I2 = I, and the Rabi frequency noise is then related to the RIN by
In the instance of the detuning of the LO field from the qubit resonance being entirely due to LO frequency noise, δΔ = δωLO.
For CW Raman transitions, the intensity-to-frequency conversion of AC Stark shifts enters the Hamiltonian as an effective frequency detuning term, \({{{\Delta }}}_{{{{\rm{AC}}}}}^{{{{\rm{(cw)}}}}}\propto {g}^{2}\), where \(g\propto \sqrt{I}\) is the contribution of one laser beam’s intensity to the two-photon Rabi frequency. As Ω2γ ∝ I, variations in the AC Stark shift with intensity noise lead to a noise field of
where \({{{\Delta }}}_{{{{\rm{AC}}}}}^{{{{\rm{(cw)}}}}}={\mu }_{{{{\rm{cw}}}}}{{{\Omega }}}_{2\gamma }\). Similarly, for a ML laser, where all comb lines contribute to the AC Stark shift such that
where \({{{\Delta }}}_{{{{\rm{AC}}}}}^{{{{\rm{(fc)}}}}}={\mu }_{{{{\rm{fc}}}}}{({{{\Omega }}}_{2\gamma }^{\prime})}^{2}\). Typical values of μcw and μfc are presented in the Supplementary Information.
Filter function theory
Consider a classical noise field βj(t) such that it contributes an error term to the Hamiltonian
where j = {z, θ}. The single-sided PSD of βj(t) is defined through the Weiner-Khinchin theorem as
where 〈⋅〉 denotes ensemble-averaging. The total fidelity of a unitary operation, defined by its filter function \({F}_{j}^{(u)}(\omega )\) can be calculated to first order as24,25,26
with
such that Sz and Sθ determine the dephasing and amplitude noise errors. These PSDs can be related to physical noise processes by again considering the Weiner-Khinchin theorem. Expressing the noise field as βj = αfj(t), where α is constant and fj(t) is a time-varying function. Through the linearity of the ensemble-averaging operation
such that \({S}_{j}(\omega )={\alpha }^{2}{S}_{{f}_{j}}(\omega )\), providing a way to convert between PSDs given their functional relation of the corresponding parameters.
Inspecting the full Hamiltonian (Eq. 17) the noise fields are given by
such that the relation between the PSDs of these parameters are
The PSDs for dephasing and amplitude errors can then be related to physical noise processes using the expressions in Eqs. 18–21. For example, for optical transitions, \({S}_{{{\Omega }}}(\omega )=\frac{1}{4}{{{\Omega }}}_{c}^{2}{S}_{{{{\rm{RIN}}}}}(\omega )\) such that
and for LO frequency noise \({S}_{{{\Delta }}}(\omega )={S}_{{\omega }_{{{{\rm{LO}}}}}}(\omega )\), such that
which is the expression previously used in Ref. 13.
Once the PSDs are well defined, the fidelity can be calculated using knowledge of the corresponding filter functions, \({F}_{z}^{(u)}(\omega )\) and \({F}_{\theta }^{(u)}(\omega )\), for the desired operation. For a π-pulse around X, the dephasing filter function is given by
where τπ = π/Ω. By Taylor expanding \({F}_{z}^{(\pi )}(\omega )\) and taking the leading order, \({F}_{z}^{(\pi )}(\omega )\) can be approximated by the piecewise function
such that the approximate analytic fidelity in Eq. 6 can be derived. The filter function for amplitude noise is the same for all values of ϕc such that the fidelity of an arbitrary π-pulse can be calculated using the filter function
which on Taylor expansion can be approximated by
These Taylor expansions provide the values of \({c}_{b}^{(\pi )}\) and nπ used in the results.
Data availability
The numerical data for generating the plots in this manuscript are available upon reasonable request. Data supplied by third parties is available by consent of the third party.
Code availability
The codes used for generating the results in this manuscript are available upon reasonable request.
References
Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63–66 (2016).
Wright, K. et al. Benchmarking an 11-qubit quantum computer. Nat. Commun. 10, 1–6 (2019).
Madjarov, I. S. et al. High-fidelity entanglement and detection of alkaline-earth Rydberg atoms. Nat. Phys 16, 857–861 (2020).
Levine, H. et al. Parallel implementation of high-fidelity multiqubit gates with neutral atoms. Phys. Rev. Lett. 123, 170503 (2019).
Ballance, C., Harty, T., Linke, N., Sepiol, M. & Lucas, D. High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett. 117, 060504 (2016).
Pino, J.M. et al. Demonstration of the trapped-ion quantum CCD computer architecture. Nature 592, 209–213 (2021).
Wineland, D. J. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. NIST 103, 259 (1998).
Benhelm, J., Kirchmair, G., Roos, C. F. & Blatt, R. Towards fault-tolerant quantum computing with trapped ions. Nat. Phys. 4, 463–466 (2008).
Schindler, P. et al. A quantum information processor with trapped ions. New J. Phys. 15, 123012 (2013).
Akerman, N., Navon, N., Kotler, S., Glickman, Y. & Ozeri, R. Universal gate-set for trapped-ion qubits using a narrow linewidth diode laser. New J. Phys. 17, 113060 (2015).
Gaebler, J. P. et al. High-fidelity universal gate set for 9Be+ ion qubits. Phys. Rev. Lett. 117, 060505 (2016).
Thom, J., Yuen, B., Wilpers, G., Riis, E. & Sinclair, A. G. Intensity stabilisation of optical pulse sequences for coherent control of laser-driven qubits. Appl. Phys. B 124, 90 (2018).
Ball, H., Oliver, W. D. & Biercuk, M. J. The role of master clock stability in quantum information processing. npj Quantum Inf. 2, 1–8 (2016).
De Léséleuc, S., Barredo, D., Lienhard, V., Browaeys, A. & Lahaye, T. Analysis of imperfections in the coherent optical excitation of single atoms to Rydberg states. Phys. Rev. A 97, 053803 (2018).
Gerster, L. Spectral filtering and laser diode injection for multi-qubit trapped ion gates (ETH Zurich, 2015).
Bruzewicz, C. D., Chiaverini, J., McConnell, R. & Sage, J. M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 6, 021314 (2019).
Yum, D., De Munshi, D., Dutta, T. & Mukherjee, M. Optical barium ion qubit. JOSA B 34, 1632–1636 (2017).
Stoehr, H., Mensing, F., Helmcke, J. & Sterr, U. Diode laser with 1 Hz linewidth. Opt. Lett. 31, 736–738 (2006).
Kirchmair, G. Frequency stabilization of a Titanium-Sapphire laser for precision spectroscopy on Calcium ions (Thesis, 2006).
Chang, P., Zhang, S., Shang, H. & Chen, J. Stabilizing diode laser to 1 Hz-level Allan deviation with atomic spectroscopy for Rb four-level active optical frequency standard. Appl. Phys. B 125, 196 (2019).
Mizrahi, J. et al. Quantum control of qubits and atomic motion using ultrafast laser pulses. Appl. Phys. B 114, 45–61 (2014).
Stowe, M. C. et al. Direct frequency comb spectroscopy. Adv. At. Mol. Opt. Phys. 55, 1–60 (2008).
Islam, R. et al. Beat note stabilization of mode-locked lasers for quantum information processing. Opt. Lett. 39, 3238–3241 (2014).
Ball, H. & Biercuk, M. J. Walsh-synthesized noise filters for quantum logic. EPJ Quantum Technol. 2, 1–45 (2015).
Kabytayev, C. et al. Robustness of composite pulses to time-dependent control noise. Phys. Rev. A 90, 012316 (2014).
Green, T. J., Sastrawan, J., Uys, H. & Biercuk, M. J. Arbitrary quantum control of qubits in the presence of universal noise. New J. Phys. 15, 095004 (2013).
Darman, M. & Fasihi, K. A new compact circuit-level model of semiconductor lasers: investigation of relative intensity noise and frequency noise spectra. J. Mod. Opt. 64, 1839–1845 (2017).
Ahmed, M. Theoretical modeling of intensity noise in InGan semiconductor lasers. Sci. World J 2014, 475423 (2014).
Lu, H., Su, J., Xie, C. & Peng, K. Experimental investigation about influences of longitudinal-mode structure of pumping source on a Ti:sapphire laser. Opt. Express 19, 1344–1353 (2011).
Wei-Nan, Z. et al. A compact low noise single frequency linearly polarized dbr fiber laser at 1550 nm. Chin. Phys. Lett. 29, 084205 (2012).
Galzerano, G., Laporta, P., Bonelli, L., Toncelli, A. & Tonelli, M. Single-frequency diode-pumped Yb: KYF4 laser around 1030 nm. Opt. Express 15, 3257–3264 (2007).
Loh, W., Papp, S. B. & Diddams, S. A. Noise and dynamics of stimulated-brillouin-scattering microresonator lasers. Phys. Rev. A 91, 053843 (2015).
Camatel, S. & Ferrero, V. Narrow linewidth cw laser phase noise characterization methods for coherent transmission system applications. J. Light. Technol. 26, 3048–3055 (2008).
Tran, M. A., Huang, D. & Bowers, J. E. Tutorial on narrow linewidth tunable semiconductor lasers using Si/III-V heterogeneous integration. APL Photonics 4,111101 (2019)
Kim, J. & Song, Y. Ultralow-noise mode-locked fiber lasers and frequency combs: principles, status, and applications. Adv. Opt. Photonics 8, 465–540 (2016).
Coldren, L. A., Corzine, S. W. & Mashanovitch, M. L. Diode lasers and photonic integrated circuits (John Wiley & Sons, 2012).
Obarski, G. E. & Splett, J. D. Transfer standard for the spectral density of relative intensity noise of optical fiber sources near 1550 nm. JOSA B 18, 750–761 (2001).
Giuliani, G. The linewidth enhancement factor of semiconductor lasers: usefulness, limitations, and measurements. In 2010 23rd Annual Meeting of the IEEE Photonics Society, 423-424 (IEEE, 2010).
Fordell, T., Valling, S. & Lindberg, ÅM. Modulation and the linewidth enhancement factor of a diode-pumped Nd:YVO4 laser. Opt. Lett. 30, 3036–3038 (2005).
Thorette, A., Romanelli, M. & Vallet, M. Linewidth enhancement factor measurement based on fm-modulated optical injection: application to rare-earth-doped active medium. Opt. Lett. 42, 1480–1483 (2017).
Zhou, B., Kane, T. J., Dixon, G. J. & Byer, R. L. Efficient, frequency-stable laser-diode-pumped Nd: YAG laser. Opt. Lett. 10, 62–64 (1985).
Toptica. Tuneable Diode Laser DL Pro Datasheet. https://www.toptica.com/products/tunable-diode-lasers/ecdl-dfb-lasers/dl-pro/ (2021). Online; accessed 1 December 2021.
Di Domenico, G., Schilt, S. & Thomann, P. Simple approach to the relation between laser frequency noise and laser line shape. Appl. Optics 49, 4801–4807 (2010).
Bermudez, A. et al. Assessing the progress of trapped-ion processors towards fault-tolerant quantum computation. Phys. Rev. X 7, 041061 (2017).
Wineland, D. J. et al. Quantum information processing with trapped ions. Philos. Trans. Royal Soc. A . 361, 1349–1361 (2003).
Linke, N., Ballance, C. & Lucas, D. Injection locking of two frequency-doubled lasers with 3.2 GHz offset for driving Raman transitions with low photon scattering in 43Ca+. Opt. Lett. 38, 5087–5089 (2013).
Yang, C. et al. High-power and near-shot-noise-limited intensity noise all-fiber single-frequency 1.5 μm mopa laser. Opt. Express 25, 13324–13331 (2017).
Allen, E. J. et al. Passive, broadband, and low-frequency suppression of laser amplitude noise to the shot-noise limit using a hollow-core fiber. Phys. Rev. Appl. 12, 044073 (2019).
Milne, A. R. et al. Phase-modulated entangling gates robust to static and time-varying errors. Phys. Rev. Appl. 13, 024022 (2020).
Loudon, R. The quantum theory of light (OUP Oxford, 2000).
Campbell, W. et al. Ultrafast gates for single atomic qubits. Phys. Rev. Lett. 105, 090502 (2010).
Barakhshan, P., Marrs, A., Arora, B., Eigenmann, R. & Safronova, M. S. Portal for High-Precision Atomic Data and Computation (version 1.0). University of Delaware, Newark, DE, USA. URL: https://www.udel.edu/atom [December 2021].
Acknowledgements
We would like to thank Virginia Frey for useful discussions on filter functions. This research was supported in part by the Natural Sciences and Engineering Research Council of Canada (NSERC), Grant Nos. RGPIN-2018-05253 and RGPIN-2018-05250, and the Canada First Research Excellence Fund (CFREF), Grant No. CFREF-2015-00011. CS is also supported by a Canada Research Chair.
Author information
Authors and Affiliations
Contributions
MLD conceived and the derived the main theoretical results of the manuscript with assistance from PJL and BW. MLD, PJL, and BW contributed the supporting derivations in the supplementary information. RI and CS both supervised the project. All authors discussed and checked the results and contributed to the final writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Day, M.L., Low, P.J., White, B. et al. Limits on atomic qubit control from laser noise. npj Quantum Inf 8, 72 (2022). https://doi.org/10.1038/s41534-022-00586-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00586-4