Abstract
We study the dissipative Bose-Hubbard model on a small ring of sites in the presence of a chiral drive and explore its long-time dynamical structure using the mean-field equations and by simulating the quantum master equation. Remarkably, for large enough drivings, we find that the system admits, in a wide range of parameters, a chaotic attractor at the mean-field level, which manifests as a complex Wigner function on the quantum level. The latter is shown to have the largest weight around the approximate region of phase space occupied by the chaotic attractor. We demonstrate that this behavior could be revealed via measurement of various bosonic correlation functions. In particular, we employ open system methods to calculate the out-of-time-ordered correlator, whose exponential growth signifies a positive quantum Lyapunov exponent in our system. This can open a pathway to the study of chaotic dynamics in interacting systems of photons.
Similar content being viewed by others
Introduction
Methods to confine and control photons using solid-state materials have opened a pathway to the generation of novel liquids of light1, exhibiting a wide range of phenomena, from superfluidity2 to topological states3. Coupled cavity arrays evolved into a valuable experimental framework for the study of lattices of photons in the presence of interactions, drive, and dissipation4,5,6. Such systems benefit from the exquisite fabrication techniques of solid-state materials as well as from the high coherence properties of the photons, making them an attractive venue for future applications7.
Even a small number of driven coupled cavities can exhibit rich behavior: a single cavity gives rise to regions of bistability and to critical slowing down8; cavity dimers demonstrate Josephson oscillations9 and parametric instabilities10 and could be driven into a more exotic quantum limit-cycle if the dissipation is further engineered11; the levels of a six cavity ring were demonstrated to be individually excitable, generating chirality, with their population exhibiting hysteretic behavior, indicative of a bistability12; and many more. These phenomena explore at most a quasi-two-dimensional manifold of phase space. Yet, on the classical, mean-field level such coupled cavities are described as driven-dissipative coupled nonlinear oscillators, that are in principle capable of exhibiting chaotic behavior13,14,15. However, it remains unclear what are the key ingredients which are required to generate chaotic behavior in such systems. Further, once the interactions increase and the system crosses into a more quantum regime, what implications does the emergence of classical chaos carry for the quantum behavior of the system?
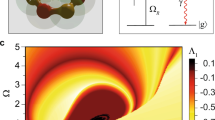
In this paper, we consider a ring of three coupled cavities, driven by finite orbital momentum light16,17,18 (illustrated in Fig. 1). We demonstrate that as a direct result of the chirality of the applied drive, the system exhibits robust chaotic dynamics over a large part of its mean-field phase diagram. On this level, the chaos is manifested as a dense, compact attractor in phase space. For the quantum problem, a full quantum trajectory approach19 reveals a complex Wigner function, indicative of the underlying chaos. The g(1) correlator places the system on the chaotic attractor, while the g(2) correlator reveals signatures of the chaotic behavior. We find that, most prominently, the out-of-time-ordered correlator (OTOC) reveals the onset of chaos via an exponential sensitivity to the application of a weak perturbation. These predictions could pave the way to the study of the interplay of classical and quantum chaotic dynamics and their properties in coupled cavity arrays of photons.
Results
Proposed setup and model
We consider the Bose-Hubbard Hamiltonian for M sites (cavities) on a ring in the presence of drive and dissipation, with a driving term that is coherent with respect to both frequency and momentum,
Here \({\hat{b}}_{j}^{{\dagger} }\) (\({\hat{b}}_{j}\)) creates (annihilates) a boson at site \(j\,{{\mathrm{mod}}}\,\,M\) (j ∈ {0, …, M − 1} where M is the number of sites), \({x}_{j}=j\,{{\mathrm{mod}}}\,\,M\) is the position of the site (choosing the units such that the lattice spacing a = 1), U > 0 is the on-site interaction strength, J is the tunneling amplitude and D, Ω and \(p=\frac{2\pi }{M}m\) (m ∈ {0, …, M − 1}) are the amplitude, detuning, and momentum of the drive. The Lindblad master equation governs the dynamics of the density matrix \(\hat{\rho }\) in the presence of a boson loss rate Γ
It prescribes the non-Hermitian effective Hamiltonian \({\hat{{{{\mathcal{H}}}}}}_{{{\rm{eff}}}}=\hat{{{{\mathcal{H}}}}}-{{{\rm{i}}}}\frac{{{\Gamma }}}{2}\mathop{\sum }\nolimits_{j = 0}^{M-1}{\hat{b}}_{j}^{{\dagger} }{\hat{b}}_{j}\) which is the deterministic part of the Lindblad evolution; as well as the so-called “recycling” term, \({{\Gamma }}{\sum }_{j}{\hat{b}}_{j}\hat{\rho }{\hat{b}}_{j}^{{\dagger} }\). In the following we use the rescaled parameters u = U/J, d = D/J, ω = Ω/J, and γ = Γ/J.
Mean-field phase diagram
We start by analysing the mean-field equations of motion, derived from the hamiltonian \({\hat{{{{\mathcal{H}}}}}}_{{{\rm{eff}}}}\). We analyze the fixed points using the ansatz that only a single-mode participates in the dynamics, \({\hat{b}}_{p}=\frac{1}{\sqrt{M}}{\sum }_{j}{{{{\rm{e}}}}}^{{{{\rm{i}}}}p{x}_{j}}{\hat{b}}_{j}\), with the operators replaced by c-numbers. The regimes of existence and stability of the resulting fixed points are delineated by black lines in Fig. 2a, b (note that the shading has different meaning as we explain in the next paragraphs). These include ‘dim’ (denoted by I and II, depending on the existence and stability of the other fixed points) and ‘bright’ (denoted by III) regimes which are each dominated by the effect of a single fixed point with low and high bosonic occupation, respectively, as well as a bistable regime (denoted ‘Bi’) where both fixed points are stable, and a region where no fixed point is stable (denoted ‘NFP’).
Panels a and b display the phase diagram for zero momentum drive (a) and a finite p = 2π/3 momentum drive (b), the latter giving rise to a chaotic regime. The phase diagrams are displayed as function of the strength of the drive (d) and its frequency (ω) with respect to the non-interacting resonant frequency (\({\omega }_{{{\rm{res}}}}=-\!\cos p\)). The black lines delineate the bright (III), dim (I and II), and bistable (Bi) regimes, while for p = 2π/3 a new regime appears where no fixed point (NFP) remains stable. The shading of each point is determined by the long-time dynamical behavior when starting from the vacuum state, with most of the points in the NFP regime ending in chaotic dynamics. Panels c–h visualize the basins of attraction of the different attractors for a finite chiral drive: the chaotic basins (light blue), the bright fixed point basin (yellow), and the dim fixed point basin (gray) [see the red asterisks in (b) for the corresponding parameters]. The ending points of the sampled trajectory (for Jtm = 2000) are projected onto the resonant plane (red). The green × (+) markers correspond to the dim (bright) stable fixed point solution. Here u = 0.1 and γ = 0.05.
The difference between a uniform and a chiral drive is already exposed in this mean-field level. These two types of drive lead to the two dramatically different phase diagrams, presented in Fig. 2, with panel (a) describing the uniform case and (b) the chiral case. In between the dim and bright regimes, for the uniform drive and for the chiral drive at low amplitudes, there exist bistability regimes. This picture changes considerably for the chiral drive at higher amplitudes, where a large regime where no fixed point remains stable appears in the phase diagram.
To gain further intuition into the nature of this regime, we note that the actual steady state the system attains is decided by the initial condition. When we start from the vacuum state \(\left|0\right\rangle\) with zero bosonic occupation, the resulting steady state is depicted by the shading in Fig. 2a, b. In particular, in most of the bistable regime, the system reaches the dim fixed point. In the region NFP it turns out that the system reaches no particular fixed point, but the long-time dynamics remains confined in a certain dense region of phase space. In order to analyze it, we have to go beyond the single-mode ansatz (see the “Methods” section).
We next relax the requirement that we start from the \(\left|0\right\rangle\) state and consider the two-dimensional phase plane of initial conditions associated with bp. Each initial condition is color-coded according to the attractor the system eventually reaches. The result is described in Fig. 2c–h, and defines the basins of attraction of the relevant attractors. In addition, the long-time trajectories of bp are superimposed in red.
The spiral shape of the basins was highlighted in ref. 20 for the case of a single cavity. Our case is richer since the higher dimensional phase space allows for the possibility of classical chaos, which in our system is accessible due to the operation of a chiral drive. The onset of chaos is marked by an exponential sensitivity to initial conditions and is characterized by a positive (classical) Lyapunov exponent. For the NFP regime, we find that the system ends up in either a limit cycle or in a strange attractor (SA), the latter depicted by the red shape in Fig. 2e–h. In fact, the SA also exists beyond the region marked by NFP, and when the vacuum is contained in its basin of attraction the system will flow into this steady state, see e.g., Fig. 2d. Technically, we identify the limit cycles by the occurrence of finite frequencies in the Fourier transform of the time-dependence of the occupation combined with a vanishing maximum Lyapunov exponent.
Once the interaction in the system increases the system will characteristically hold lower bosonic occupations and can cross into the quantum regime. In the next section, we will investigate the quantum behavior of the system within and in the vicinity of the NFP region, and explore its properties.
Quantum approach to chaos
We now turn to study the full quantum evolution of Eq. (2) using the method of quantum trajectories19, and compare with the classical equation of motion analysis. The quantum trajectories are visualized in Fig. 3 using a histogram, which depicts the formation and interplay of the various fixed points and their exploration by the quantum dynamics. In Fig. 3a–c, the trajectories explore the vicinity of the bright fixed point but as the frequency increases a larger portion of the chaotic basin is traversed quantum mechanically. Figure 3c, d depicts a regime where the full classical chaotic basin is explored. Curiously, in Fig. 3d the trajectories initially tend towards the newly nucleated dim fixed point but eventually flow past it and end up in the chaotic attractor. Figure 3e, f shows the coexistence of two attractors, a chaotic one and a dim fixed point, as the weight of the former decreases with increasing frequency.
We employ a 2D histogram showing the full-time evolution of 2000 trajectories, presented in log scale, with the quantum trajectories projected to the resonant plane. Each trajectory starts from the vacuum state \(\left|0\right\rangle\), corresponding to the point (0,0) at the intersection of the two grid lines. The evolution and interplay of the various fixed points are clearly visible as the frequency of the drive increases, including the emergence of the chaotic attractor replacing the bright fixed point and the nucleation of the dim fixed point at higher frequencies. Here u = 0.1, γ = 0.05, and d = 0.3.
The state the system attains at long times can be characterized by the Wigner function \(W({\boldsymbol{\beta}}; t)\) in the momentum-space coherent state representation \(\left|{\boldsymbol{\beta} }\right\rangle\), of which we display only the two-dimensional cut with finite βp (and βk = 0 for k ≠ p) in Fig. 4a–e (see the “Methods” section for details of the calculation). When the system flows into a fixed point it generates a Wigner function that is localized around this fixed point, forming an approximate coherent state, see e.g. Fig. 4e. In contrast, in the NFP regime, the Wigner function exhibits a pattern of islands of positive and negative values which aggregate around the SA, see Fig. 4b–d. When projected onto the resonant plane, we introduce the Wigner function which characterizes the associated reduced density matrix, which becomes strictly positive, see Fig. 4f–j. Remarkably, it admits the greatest support around the region of the classical SA in phase space, Fig. 4h, i21.
The Wigner functions for frequencies below and within the strange attractor regime are presented for time tm = 2000/J. Panels a–e display the Wigner functions on a cut depicting the resonant (βp) plane. Panels f–j display the Wigner function for the reduced density matrix associated with the same plane. The classical attractor is superimposed in green. The different fixed points are displayed using green markers. Here u = 0.1, γ = 0.05, and d = 0.3.
Next, we consider photonic correlation measurements and weigh their relevance in unveiling the presence of quantum chaos in our system, starting with the standard photonic correlators g(1) and g(2), obtained by the quantum trajectories procedure (see “Methods” for details).
First, the correlator \({g}_{p}^{(1)}(t)=\langle {\hat{b}}_{p}^{{\dagger} }(t){\hat{b}}_{p}(t)\rangle\) is associated with the photonic occupation and is presented in the inset of Fig. 5a. As the frequency increases, it is shown to reach a steady-state value that progressively deviates from the value of the bright fixed point towards a mean value associated with the chaotic attractor (see the main panel of Fig. 5a). When the frequency further increases, the value of the g(1) correlator rapidly drops into the dim fixed point.
The main panels show the dependence on the drive frequency ω of: a the \({g}_{p}^{(1)}(J{t}_{\rm{m}})\) photonic correlator (colored points) versus the analytical stable (solid line) and unstable (dashed line) fixed points \({N}_{0}^{(\nu )},\) with ν = 1, 2, 3; b the uncertainty of the occupation \({{\Delta }}{N}_{p}^{2}(J{t}_{{{\rm{m}}}})\); c the OTOC \({{{\mathcal{O}}}}(J{t}_{{{\rm{m}}}};J{\tau }_{{{\rm{m}}}})\) saturation value; (d) the trajectory-averaged entanglement entropy \({\overline{S}}_{p}(J{t}_{{{\rm{m}}}})\) (black line), with the contribution of individual trajectories denoted by colored points. The classical chaos region is shaded in blue. The insets show: a the \({g}_{p}^{(1)}(Jt)\) correlator as function of Jt; b the left side (with respect to the dashed vertical line) presents \({g}_{p}^{(2)}(Jt;0)\) correlator as function of Jt while the right side presents \({g}_{p}^{(2)}(J{t}_{\rm{m}};J\tau )\) as function of Jτ; c the time-dependence of \({{{\mathcal{O}}}}(J{t}_{{{\rm{m}}}};J\tau )\) as function of Jτ; d the variance over different trajectories of the entanglement entropy δSp(Jtm) as function of the drive frequency ω. Here u = 0.1, γ = 0.05, d = 0.3, tm = 2000/J (corresponding to steady state) and τm = 10/J (corresponding to saturation).
The correlator \({g}_{p}^{(2)}(t;\tau )=\langle {\hat{b}}_{p}^{{\dagger} }(t){\hat{b}}_{p}^{{\dagger} }(t+\tau ){\hat{b}}_{p}(t+\tau ){\hat{b}}_{p}(t)\rangle /\langle {\hat{b}}_{p}^{{\dagger} }(t){\hat{b}}_{p}(t)\rangle^{2} \) is presented in the inset of Fig. 5b and is shown to be sensitive to the presence of the SA as is demonstrated by the larger value it attains at τ = 0. This value is indicative of the increased fluctuations of the light generated by the chaotic phase space. The correlator \({g}_{p}^{(2)}\) becomes numerically unstable when the \({g}_{p}^{(1)}\) correlator becomes low, i.e., at low and high frequencies. As it is proportional to the uncertainty of the occupation \({{\Delta }}{N}_{p}^{2}(t)=\langle {\hat{b}}_{p}^{{\dagger} }(t){\hat{b}}_{p}(t){\hat{b}}_{p}^{{\dagger} }(t){\hat{b}}_{p}(t)\rangle -\langle {\hat{b}}_{p}^{{\dagger} }(t){\hat{b}}_{p}(t)\rangle^{2}\), we plot the latter instead at long times for the resonating momentum p in the main panel of Fig. 5b. In addition, the fluctuations of the quantum trajectories around the mean value could indicate the presence of the SA if the quantum trajectories are individually measured22.
The most prominent indicator of quantum chaos in our system turns out to be the OTOC23,24, defined by,
where \(\hat{Q}=({\hat{b}}_{p}+{\hat{b}}_{p}^{{\dagger} })/\sqrt{2}\) and \(\hat{P}={{{\rm{i}}}}({\hat{b}}_{p}^{{\dagger} }-{\hat{b}}_{p})/\sqrt{2}\) are the dimensionless position and momentum operators associated with \({\hat{b}}_{p}\). The OTOC generalizes the concept of a Lyapunov exponent to the quantum regime, i.e., \(\mathop{\lim }\nolimits_{t\to \infty }{{{\mathcal{O}}}}(t;\tau ) \sim {{{{\rm{e}}}}}^{{\lambda }_{q}\tau }\) where λq is the quantum Lyapunov exponent and τ is in some intermediate regime: for small enough τ the commutator is set by its equal-time value while for large enough τ it saturates25. The saturation value of \(\mathop{\lim }\nolimits_{t,\tau \to \infty }{{{\mathcal{O}}}}(t;\tau )\) is related to the size of the available phase space in the chaotic basin26 and its relation to chaos was demonstrated for the periodically kicked Dicke model27. A version of the OTOC was measured in a trapped ion quantum magnet28. In the “Methods” we detail a procedure to calculate it for a dissipative system.
The result, presented in the inset of Fig. 5c, exhibits the anticipated exponential increase within the chaotic regime. Remarkably, we find a non-monotonic behavior of the saturation value of the OTOC as function of the drive frequency ω (see the main panel of Fig. 5c). It is interesting to note that a positive quantum Lyapunov exponent is detected for lower values of ω as compared to the classical phase diagram. At higher frequencies, once the frequency crosses into the classical dim fixed point regime, a dramatic reduction in the quantum Lyapunov exponent occurs. It therefore turns out that the quantum chaotic regime extends beyond the classical one into the lower frequency regime; see main panel of Fig. 5c where the classical chaotic regime is depicted by blue shading. The higher frequency regime is marked by a coexistence of the dim and chaotic fixed points. The main panel of Fig. 5d displays, using colored points, the entanglement entropy associated with the resonant mode calculated for individual trajectories, \({S}_{p}(t)=-{{{\rm{Tr}}}}\left[{\hat{\rho }}_{p}(t){{\mathrm{log}}}\,{\hat{\rho }}_{p}(t)\right]\), with \({\hat{\rho }}_{p}(t)={{{{\rm{Tr}}}}}_{k\ne p}\left|\psi (t)\right\rangle \left\langle \psi (t)\right|\) the reduced density matrix. For each trajectory Sp(t) is well defined, and the average over trajectories \({\overline{S}}_{p}(t)\) is displayed as a black line. In addition, the variance of the entanglement entropy over trajectories, quantified by \(\delta {S}_{p}=({{\bar{S}}_p^2}-{{\bar{S}}_p^2})^{1/2}\), appears to be sensitive to the presence of the chaotic regime, see inset of Fig. 5d. The similarity of the two graphs in panel (d) to the one in main panel (c) indicates relations between the entanglement entropy and the OTOC29, that characterize the chaotic attractor.
Discussion
We have demonstrated that the driven-dissipative Bose-Hubbard model with a small number of sites on a ring, once chirally-driven, could lead to the generation of chaotic regimes in both the mean-field analysis and at the full quantum level. To characterize the quantum chaos, we have calculated the Wigner function on a cut through the 6-dimensional phase space and projected it onto the 2-dimensional resonant plane, where it is shown to spread over the approximate region of the classical chaotic phase space. Next, we extended the Monte-Carlo method to calculate the OTOC in driven-dissipative systems (see “Methods” section), and demonstrated its sensitivity to the onset of quantum chaos in our model. Finally, we calculated the measurable correlators g(1) and g(2) and extracted the relevant signatures of the chaotic attractor. The results could prove relevant for photons in coupled cavity arrays and may lead to a study of chaos in such systems.
Methods
Mean-field analysis
To study the mean-field fixed points we employ above the ansatz that only the single mode that shares its momentum with the drive is macroscopically occupied, i.e. bk = 0 for k ≠ p. The equation of motion for bp is given in this case by
Denoting the steady-state solution as \({b}_{p}(t\to \infty )=\sqrt{{N}_{0}}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}\theta }\) we arrive at the following equation for the occupation of the condensate, n0 = N0/M,
and its phase \(\theta ={\sin }^{-1}(\gamma \sqrt{{n}_{0}}/2d)\). Equation (5) has three roots for n0, which determine three fixed points \({b}_{p}^{(\nu )}=\sqrt{{n}_{0}^{(\nu )}}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}{\theta }^{(\nu )}}\), with ν = 1, 2, 3. The stability of \({b}_{p}^{(\nu )}\) is then determined by perturbing \({b}_{j}={b}_{j}^{(\nu )}+\delta {b}_{j}^{(\nu )}\), where \({b}_{j}^{(\nu )}={b}_{p}^{(\nu )}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}p{x}_{j}}/\sqrt{M}\) is the steady-state solution and \(\delta {b}_{j}^{(\nu )}={{{{\rm{e}}}}}^{-\gamma s/2}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}{\theta }^{(\nu )}}\delta {\zeta }_{j}\) with s = Jt the rescaled time. Taking into account only the leading terms in \(\delta {\zeta }_{j}={{{{\rm{e}}}}}^{-{{{\rm{i}}}}p{x}_{j}}({v}_{j}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}\mu s}-{u}_{j}^{* }{{{{\rm{e}}}}}^{{{{\rm{i}}}}{\mu }^{* }s})\), the equations of motion in the momentum basis q prescribe
Here \({{{{\mathcal{L}}}}}_{q}=-{\epsilon }_{0}(q)+{{{\rm{i}}}}{\sigma }_{y}{\epsilon }_{y}+{\sigma }_{z}{\epsilon }_{z}(q)\), where \({\epsilon }_{0}(q)=\sin (q)\sin (p)\), ϵy = n0u, \({\epsilon }_{z}(q)=2{n}_{0}u-\cos (q)\cos (p)-\omega\), σi are the Pauli matrices and μq is the Bogoliubov dispersion, given by \({\mu }_{q}=-{\epsilon }_{0}(q)\pm \sqrt{{\epsilon }_{z}^{2}(q)-{\epsilon }_{y}^{2}}\). For a solution to be stable we require δbj to decay with time, thus stability is contingent upon ∣Imμq∣ ≤ γ/2 for all values of \(q=\frac{2\pi }{M}m\), m ∈ {0, 1, . . , M − 1}. This is an extension1 of the more familiar case without loss (γ = 0).
In the main text, we describe the resulting phase diagram, which is presented in Fig. 2a, b. Here we describe the phase diagram in terms of existence and stability of the fixed points. In region I (III) there exists only a single fixed point that is also stable: the dim (bright), ν = 1 (ν = 3), is the low (high) occupation fixed point (the intermediate fixed point, ν = 2, is always unstable). Whereas, in region II there exist three fixed points of which only the dim (ν = 1) one is stable. In addition, there are the bistable regime (denoted by “Bi”) in which both ν = 1 and ν = 3 are stable, and the regime where no fixed point is stable (denoted by “NFP”) in which the system flows into the chaotic attractor, which is not revealed by the linear analysis above.
Quantum analysis
We calculate the Wigner function displayed in Fig. 4 using the formula
where \({\rho }_{{\boldsymbol{\beta}};{\boldsymbol{\eta}}}(t)=\left\langle {\boldsymbol{\beta} }-\frac{\boldsymbol{\eta} }{2}| \hat{\rho }(t)| {\boldsymbol{\beta} }+\frac{\boldsymbol{\eta} }{2}\right\rangle\). Here \(\left|{\boldsymbol{\beta} }\right\rangle\) represents a product of momentum coherent states, i.e., \(\left|{\boldsymbol{\beta} }\right\rangle { = \bigotimes }_{k}\left|{\beta }_{k}\right\rangle ,\) satisfying \({\hat{b}}_{k}\left|{\boldsymbol{\beta} }\right\rangle ={\beta }_{k}\left|{\boldsymbol{\beta} }\right\rangle\). Expressing the density matrix using momentum occupation states \(\left|{{{{\mathbf{n}}}}}\right\rangle { = \bigotimes }_{k}\left|{n}_{k}\right\rangle\), we get the following transform
where
with U(a, b, c) denoting the confluent hypergeometric function. The density matrix \({\rho }_{{{{\mathbf{n}}}},{{{\mathbf{n}}}}^{\prime} }(t)\) is then calculated employing 2000 quantum trajectories. In the main text we considered two types of Wigner functions. The first was the full 6-dimensional Wigner function of Eq. (8) of which we displayed only the 2-dimensional cut representing the resonant plane (βk = 0 for k ≠ p) at time Jtm (see Fig. 4a–e). Second, we consider the reduced density matrix relevant to the resonant momentum, i.e, the density matrix in Eq. (8) is replaced with \({\hat{\rho }}_{p}(t)={{{{\rm{Tr}}}}}_{k\ne p}\hat{\rho} (t)\) (see Fig. 4f–j). All quantum trajectory simulations are performed by truncating each of the three bosonic modes to 30 occupations states.
Using the same quantum trajectory Monte-Carlo formalism, we calculate the different photonic correlation functions as we now describe.
To calculate the \({g}_{p}^{(2)}(t;\tau )=\langle {\hat{b}}_{p}^{{\dagger} }(t){\hat{b}}_{p}^{{\dagger} }(t+\tau ){\hat{b}}_{p}(t+\tau ){\hat{b}}_{p}(t)\rangle /\langle {\hat{b}}_{p}^{{\dagger} }(t){\hat{b}}_{p}(t)\rangle^{2}\) correlator, we employ the usual method of first enforcing a quantum a jump at t and then finding the evolution along τ following the same Monte-Carlo procedure.
Calculating the OTOC in a dissipative-driven system is more challenging. The OTOC can be expanded into a sum of four two-time correlators with both forward and backward time evolutions. For each of these correlators, let t1 be the time associated with the rightmost operator, and let t2 be the other time. We proceed according to the following steps: (i), we evolve the wavefunction to t1 (i.e. either t or t + τ); (ii), we apply the operators associated with t1 on both the evolved ket and bra or, where this is not possible, we define four helper states following Mølmer et al.19; next, (iii), we apply either forward or backward evolution in time from t1 to t2, as necessary (i.e., forward evolution from t1 = t to t2 = t + τ or backward evolution from t1 = t + τ to t2 = t). The latter is done according to \(\hat{{{{\mathcal{H}}}}}\to -\hat{{{{\mathcal{H}}}}}\) but with the dissipative part of the Lindblad evolution remaining the same30; finally, (iv), we find the expectation value of the operator or product of operators associated with time t2.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The codes that support the findings of this study are available from the corresponding author upon reasonable request.
References
Carusotto, I. & Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 85, 299 (2013).
Amo, A. et al. Superfluidity of polaritons in semiconductor microcavities. Nat. Phys. 5, 805 (2009).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Deng, H., Weihs, G., Santori, C., Bloch, J. & Yamamoto, Y. Condensation of semiconductor microcavity exciton polaritons. Science 298, 199 (2002).
Schmidt, S. & Koch, J. Circuit QED lattices: towards quantum simulation with superconducting circuits. Ann. Phys. 525, 395 (2013).
Fitzpatrick, M., Sundaresan, N. M., Li, A. C. Y., Koch, J. & Houck, A. A. Observation of a dissipative phase transition in a one-dimensional circuit QED lattice. Phys. Rev. X 7, 011016 (2017).
Amo, A. & Bloch, J. Exciton-polaritons in lattices: a non-linear photonic simulator. C. R. Phys. 17, 934 (2016).
Fink, T., Schade, A., Höfling, S., Schneider, C. & Imamoglu, A. Signatures of a dissipative phase transition in photon correlation measurements. Nat. Phys. 14, 365 (2018).
Abbarchi, M. et al. Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. Nat. Phys. 9, 275 (2013).
Carlon Zambon, N. et al. Parametric instability in coupled nonlinear microcavities. Phys. Rev. A 102, 023526 (2020).
Lledó, C., Mavrogordatos, T. K. & Szymańska, M. H. Driven Bose-Hubbard dimer under nonlocal dissipation: a bistable time crystal. Phys. Rev. B 100, 054303 (2019).
Sala, V. G. et al. Spin-orbit coupling for photons and polaritons in microstructures. Phys. Rev. X 5, 011034 (2015).
Solnyshkov, D. D., Johne, R., Shelykh, I. A. & Malpuech, G. Chaotic Josephson oscillations of exciton-polaritons and their applications. Phys. Rev. B 80, 235303 (2009).
Gavrilov, S. S. Towards spin turbulence of light: spontaneous disorder and chaos in cavity-polariton systems. Phys. Rev. B 94, 195310 (2016).
Ruiz-Sánchez, R., Rechtman, R. & Rubo, Y. G. Autonomous chaos of exciton-polariton condensates. Phys. Rev. B 101, 155305 (2020).
Dholakia, K., Simpson, N. B., Padgett, M. J. & Allen, L. Second-harmonic generation and the orbital angular momentum of light. Phys. Rev. A 54, R3742 (1996).
Martinelli, M., Huguenin, J. A. O., Nussenzveig, P. & Khoury, A. Z. Orbital angular momentum exchange in an optical parametric oscillator. Phys. Rev. A 70, 013812 (2004).
Zambon, N. C. et al. Orbital angular momentum bistability in a microlaser. Opt. Lett. 44, 4531 (2019).
Mølmer, K., Castin, Y. & Dalibard, J. Monte Carlo wave-function method in quantum optics. J. Opt. Soc. Am. B. 10, 524 (1993).
Kolovsky, A. R. Bistability in the dissipative quantum systems I: damped and driven nonlinear oscillator. Preprint at https://arXiv.org/abs/2002.11373 (2020).
Lee, S. & Feit, M. Signatures of quantum chaos in Wigner and Husimi representations. Phys. Rev. E. 47, 4552 (1993).
Murch, K., Weber, S., Macklin, C. & Siddiqi, I. Observing single quantum trajectories of a superconducting quantum bit. Nature 502, 211 (2013).
Larkin, A. I. & Ovchinnikov, Y. N. Quasiclassical method in the theory of superconductivity. J. Exp. Theor. Phys. 28, 1200 (1969).
Maldacena, J., Shenker, S. H. & Stanford, D. A bound on chaos. J. High. Energy Phys. 2016, 106 (2016).
Hashimoto, K., Murata, K. & Yoshii, R. Out-of-time-order correlators in quantum mechanics. J. High. Energy Phys. 2017, 1 (2017).
Chávez-Carlos, J. et al. Quantum and classical Lyapunov exponents in atom-field interaction systems. Phys. Rev. Lett. 122, 024101 (2019).
Sinha, S., Ray, S. & Sinha, S. Fingerprint of chaos and quantum scars in kicked Dicke model: an out-of-time-order correlator study. J. Condens. Matter Phys. 33, 174005 (2021).
Gärttner, M. et al. Measuring out-of-time-order correlations and multiple quantum spectra in a trapped-ion quantum magnet. Nat. Phys. 13, 781 (2017).
Lewis-Swan, R., Safavi-Naini, A., Bollinger, J. J. & Rey, A. M. Unifying scrambling, thermalization and entanglement through measurement of fidelity out-of-time-order correlators in the Dicke model. Nat. Commun. 10, 1 (2019).
Tuziemski, J. Out-of-time-ordered correlation functions in open systems: a Feynman-Vernon influence functional approach. Phys. Rev. A. 100, 062106 (2019).
Acknowledgements
We thank D. Cohen for the discussions. This research was funded by the Israel Innovation Authority under the Kamin program as part of the QuantERA project InterPol, and by the Israel Science Foundation under grant 1626/16.
Author information
Authors and Affiliations
Contributions
All authors devised the research and contributed to the writing of the manuscript. All the numerical work was performed by D. Dahan.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dahan, D., Arwas, G. & Grosfeld, E. Classical and quantum chaos in chirally-driven, dissipative Bose-Hubbard systems. npj Quantum Inf 8, 14 (2022). https://doi.org/10.1038/s41534-022-00518-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00518-2
This article is cited by
-
Bloch theorem dictated wave chaos in microcavity crystals
Light: Science & Applications (2023)