Abstract
Device-independent quantum key distribution (DIQKD) provides the strongest form of secure key exchange, using only the input–output statistics of the devices to achieve information-theoretic security. Although the basic security principles of DIQKD are now well understood, it remains a technical challenge to derive reliable and robust security bounds for advanced DIQKD protocols that go beyond the previous results based on violations of the CHSH inequality. In this work, we present a framework based on semidefinite programming that gives reliable lower bounds on the asymptotic secret key rate of any QKD protocol using untrusted devices. In particular, our method can in principle be utilized to find achievable secret key rates for any DIQKD protocol, based on the full input–output probability distribution or any choice of Bell inequality. Our method also extends to other DI cryptographic tasks.
Similar content being viewed by others
Introduction
Device-independent quantum key distribution (DIQKD) considers the problem of secure key exchange using devices which are untrusted or uncharacterized1,2,3. In this setting, security is based entirely on the observation of nonlocal correlations, which are typically measured by a Bell inequality4,5. In particular, if the correlations violate a Bell inequality, then we say that they are nonlocal. This is necessary for secure key distribution, for it certifies that the key must come from measurements on an entangled state6,7,8. While the basic principle behind the security of DIQKD is well understood from the monogamy property of nonlocal correlations9, an explicit security analysis is rather involved and tricky. This is mainly because the dimension of the underlying shared quantum state is unknown and therefore the usual security proof techniques cannot be applied.
Recently, security proof techniques based on semidefinite programming (SDP) have been proposed for standard QKD10,11,12,13,14. In this so-called device-dependent (DD) setting, the underlying QKD devices are assumed to be suitably characterized. Our main result extends this approach to a wider range of settings, adapting to different levels of device characterization (see Fig. 1). Previously, to prove the security of DIQKD, the existing approaches were to either employ a reduction to qubit-level systems1, or to bound the adversary’s guessing probability15,16,17. However, the former is restricted to protocols based on the CHSH inequality or similar Bell inequalities with binary inputs and outputs, while the latter only bounds the min-entropy, which typically leads to suboptimal bounds on the von Neumann entropy (the relevant quantity for computing secret key rates against general attacks in the asymptotic limit3). The direct computation of DIQKD secret key rates is therefore an important task to address18.
Under device-dependent (DD) assumptions, all measurements and their underlying Hilbert spaces are characterized. Under fully device-independent (DI) assumptions, none of these are known, and we only assume the validity of quantum mechanics. One-sided device-independent (1sDI) assumptions lie between these two cases. For the 1sDI setting, we consider the case where one party’s measurements are fully characterized while the others’ are unknown (e.g., see Refs. 58,59).
Here, we approach this problem with a universal computational toolbox that directly bounds the von Neumann entropy using the complete measurement statistics of a device-independent (DI) cryptographic protocol. Given this, our method not only applies to QKD, but also to some other DI cryptographic tasks such as randomness expansion19,20,21,22,23. Importantly, this computational approach liberates the scope of DI cryptography to more complex scenarios, which could prove useful in analyzing the security of non-standard protocols which are known to be more robust against noise and loss24,25,26,27,28, as well as multipartite protocols29.
The main mechanism of our toolbox is a technique for estimating the entropy production of a quantum channel acting on an unknown state under algebraic constraints. Entropy production30,31,32,33 is a fundamental concept traditionally used to study non-equilibrium thermodynamic processes, but here we show that it has an intrinsic connection to quantum cryptography as well. The simplest way to understand entropy production is to view it as the amount of entropy introduced to a system after performing some action on it. For instance, in the case of projective measurement, the entropy production is the entropy difference between the post-measurement system and the initial system.
Our toolbox bounds this entropy production via a (noncommutative) polynomial optimization over the measurement operators in the protocol. This can be evaluated using the SDPs in the Navascués-Pironio-Acín (NPA) hierarchy34. In this context, switching from DI to 1sDI or DD scenarios translates to adding more constraints on the SDPs and thus higher values for the final secret key rates. We present the key ideas used to derive this bound in the “Methods” section, and more specific details in Sections I–III of the Supplement.
(After the release of this preprint, other approaches to solve the same optimization problem were separately developed in35,36, with the technique in the latter yielding arbitrarily tight bounds in principle. We refer the interested reader to those works for comparisons and further details.)
Results
Main theorem
We focus mainly on describing our results for DIQKD, with results for other DI cryptographic tasks elaborated on in Sections I–IV of the Supplement.
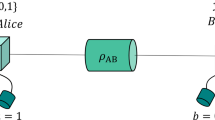
To assess the security performance of QKD, one can start by finding the asymptotic key rate under the assumption of independent and identically distributed (IID) states. In this setting, we consider protocols that are modeled as follows: in each round, Alice and Bob share a quantum state ρAB, and Eve’s side-information E is described by the purification ψABE of ρAB (see Fig. 2). Qualitatively, this means Eve controls all systems that are not in the labs of Alice and Bob. In each round, Alice (resp. Bob) performs one measurement from a set \(\{{A}_{0},{A}_{1},\ldots \ {A}_{{{{\mathcal{X}}}}-1}\}\) (resp. \(\{{B}_{0},{B}_{1},\ldots ,{B}_{{{{\mathcal{Y}}}}-1}\}\)) on their local system. The raw key will be produced from the measurements (A0, B0). This model describes entanglement-based protocols, but can be easily converted to security proofs for prepare-and-measure protocols13,37,38. Here, we focus on protocols that use one-way error correction. In this case, the asymptotic key rate r∞ is lower bounded by the Devetak-Winter formula39:
where H is the von Neumann entropy (which reduces to the Shannon entropy for H(A0∣B0)). This can be intuitively interpreted as the difference between Eve’s and Bob’s uncertainty about Alice’s measurement A0.
By measuring her share of the joint state ψABE with measurement A0, Alice is (virtually) sending a raw key to Bob who (virtually) receives it by measuring B0. Bob’s uncertainty about Alice’s bit values is quantified by the classical entropy H(A0∣B0). We assume that Eve has access to all classical communication and her share of the joint quantum state, which gives her some partial information on A0 as well. This is quantified by the classical-quantum entropy H(A0∣E).
The H(A0∣B0) term in Eq. (1) can be computed based on the expected behavior of the devices (see 3 for more details), so the main challenge here is to reliably bound H(A0∣E) using the observed statistics. More specifically, suppose the protocol estimates parameters of the form \({l}_{j}={\sum }_{abxy}{c}_{abxy}^{(j)}\Pr (ab| xy)\) for some coefficients \({c}_{abxy}^{(j)}\), where Pr(ab∣xy) is the probability of obtaining outcomes (a, b) from measurements (Ax, By) (e.g., these parameters could be Bell inequalities in a DI scenario). Without loss of generality (see Section V of the Supplement), we assume all measurements are projective by taking an appropriate Naimark dilation. For simplicity, we take the systems to be finite-dimensional; however, we do not impose any upper bound on the dimension. Let Pa∣x denote the projector corresponding to an outcome a of Alice’s measurement Ax, and analogously, let Pb∣y denote Bob’s measurement projectors. Our task is to find lower bounds on
where \({L}_{j}={\sum }_{abxy}{c}_{abxy}^{(j)}{P}_{a| x}\otimes {P}_{b| y}\), and the infimum takes place over ψABE and any uncharacterized measurements (which may be some or all of the measurements, for 1sDI or DI scenarios). This is a non-convex optimization (even after applying the approach from10), and the dimensions of any uncharacterized measurements could be arbitrarily large, hence there is no a priori guarantee that any specific dimension suffices to find the minimum. Our central result is a method to tackle this task despite its challenges, which we achieve by proving the following theorem:
Theorem 1
For a DI scenario as described, the minimum value of H(A0∣E) (in base e), subject to constraints \({\langle {L}_{j}\rangle }_{{\rho }_{AB}}={l}_{j}\) with \({L}_{j}={\sum }_{abxy}{c}_{abxy}^{(j)}{P}_{a| x}\otimes {P}_{b| y}\), is lower-bounded by
where
with \(T[{\sigma }_{AB}]={\sum }_{a}({P}_{a| 0}\otimes {{\mathbb{I}}}_{B}){\sigma }_{AB}({P}_{a| 0}\otimes {{\mathbb{I}}}_{B})\), \(\beta (t)=(\pi /2){(\cosh (\pi t)+1)}^{-1}\), and \({\kappa }_{abxy}=(1+it){\sum }_{j}{\lambda }_{j}{c}_{abxy}^{(j)}/2\). The integrals can be evaluated in closed form (we give the explicit expressions in Section II of the Supplement).
Importantly, Eq. (4) is a noncommutative polynomial in the measurement operators, and thus the task of bounding 〈K〉ρ can now be tackled using the well-established NPA hierarchy34. We can also study 1sDI scenarios by imposing additional algebraic constraints corresponding to those satisfied by the characterized measurements. We highlight that since the optimization over \(\vec{\lambda }\) is a supremum, any value of \(\vec{\lambda }\) yields a secure lower bound, without needing to identify the optimal \(\vec{\lambda }\).
To go beyond the asymptotic IID scenario, one could apply the recently developed “entropy accumulation theorem”3,40. This technique is applicable to DD, 1sDI, and DI scenarios, and shows that the key rate against general attacks is still of a form essentially similar to Eq. (1). It inherently accounts for finite-size and non-IID effects, and reduces the main challenge in a security proof to an IID problem, namely, finding lower bounds on the optimization problem in Eq. (2) (see3,40,41 for more details). Specifically, our technique allows us to bound the min-tradeoff function in the statement of the entropy accumulation theorem. Hence our approach could also be used to compute finite key lengths against general attacks, by applying the entropy accumulation theorem.
Computed key rates
We apply our method to two commonly studied DI scenarios, in which Alice and Bob each perform parameter estimation on two binary-outcome measurements. (For QKD purposes, Bob will need to perform a third measurement for key generation, corresponding to B0 in Eq. (1), but we do not use this when bounding H(A0∣E).) Our results are shown in Fig. 3. The results in some other scenarios, including distributions optimized for tilted CHSH inequalities42, are presented in Section IV of the Supplement. The first scenario is parametrized by a depolarizing-noise value q ∈ [0, 1/2], and corresponds to performing the ideal CHSH measurements (i.e., A0 = Z, A1 = X, \({B}_{0}=(Z+X)/\sqrt{2}\)) and \(\left.{B}_{1}=(Z-X)/\sqrt{2}\right)\) on the Werner state \((1-2q)\left|{{{\Phi }}}^{+}\right\rangle \left\langle {{{\Phi }}}^{+}\right|+(q/2){{\mathbb{I}}}\), where \(\left|{{{\Phi }}}^{+}\right\rangle\) is the Bell state \((\left|00\right\rangle +\left|11\right\rangle )/\sqrt{2}\) and Z and X are Pauli operators. The second scenario is a limited-detection-efficiency model parametrized by η ∈ [0, 1], where for every measurement the outcome 1 is flipped to 0 with probability 1 − η. This is a simplistic model for a photonic setup where all non-detection events are mapped to the outcome 043. For this scenario, we use different states and measurements for each value of η, as follows: to compute the H(A0∣E) bound, we first optimize the state and parameter-estimation measurements to maximize the CHSH value the same way as in43; then to compute the r∞ curves, we optimized the key-generating measurement B0 on its own without changing the state or other measurements. In principle, this yields parameter choices that may be suboptimal for maximizing H(A0∣E) or r∞, since maximizing either of these quantities is not necessarily equivalent to maximizing CHSH value (this was later confirmed in35,36, which aimed to optimize the rates directly). However, our method is too computationally intensive to attempt to maximize H(A0∣E) or r∞ directly, so we use the CHSH value as an indirect proxy (since it can be optimized independently of our bounds).
Lower bounds on entropy H(A0∣E) and key rate r∞, as a function of depolarizing noise (for the scenario studied in 1) or detection efficiency (for the scenario studied in43, which optimizes the state and measurements to achieve maximal CHSH value). For the latter, r∞ was computed by optimizing the key-generating measurement B0 alone to minimize the value H(A0∣B0), without changing the state and other measurements from those in43. Also, to yield higher key rates, the key-generating measurement B0 was preserved as a 3-outcome measurement (following60) rather than postprocessing it to 2 outcomes. It can be seen from the graph that our bounds are either close to or slightly better than the best previous result1 for these scenarios, which was based on the CHSH value alone. For comparison, we also show the indirect bounds obtained by using the inequality H(A0∣E) ≥ 2(1 − Pg(A0∣E)) (in base 2).
The previous best bound on H(A0∣E) in these scenarios (see Section IV of the Supplement for the known results in other cases) was that derived in Ref. 1, which uses only the CHSH value instead of the full probability distribution. To make use of the latter, the only preceding approach was to first bound the guessing probability Pg(A0∣E) and then apply the inequality \(H({A}_{0}| E)\ge -{{\mathrm{ln}}}\,{P}_{g}({A}_{0}| E)\)15,16,17 (all entropies are in base e unless otherwise specified). We note that if the marginal distribution of A0 is uniform and binary-valued, then in fact the tighter inequality44\(H({A}_{0}| E)\ge (2{{\mathrm{ln}}}\,2)(1-{P}_{g}({A}_{0}| E))\) holds, and we plot this bound in Fig. 3. (See Section IV of the Supplement for details on how it applies in the limited-detection-efficiency model.) However, approaches based on guessing probability do not outperform the bound in1 for the two scenarios considered here.
Our method uses the full input–output distribution to bound H(A0∣E) directly. As shown in Fig. 3, it gives results that are close to or slightly outperform the bound from Ref. 1. Roughly speaking, our approach tends to perform well for moderate noise values, which is useful since many Bell-test implementations are currently in such noise regimes45,46,47,48,49. Our results prove that for the limited-detection-efficiency scenario, better bounds on H(A0∣E) can be obtained by considering the full distribution rather than just the CHSH value (since the CHSH-based bound1 is tight). This suggests it may not be optimal to simply choose experimental parameters that maximize the CHSH value—maximizing a different Bell value may allow our method to yield a further improvement over the results in Fig. 3.
With minor modifications (see Section I of the Supplement) our method can also bound the “two-party entropy” H(A0B0∣E), which is relevant for DI randomness expansion19,20,21,22,23. The previous approaches for this were similar to those for H(A0∣E): firstly, simply noting that H(A0B0∣E) ≥ H(A0∣E) and then applying the bound from1; secondly, bounding it via \(H({A}_{0}{B}_{0}| E)\ge -{{\mathrm{ln}}}\,{P}_{g}({A}_{0}{B}_{0}| E)\). These approaches are suboptimal for similar reasons as before, though here the former is further limited by the fact that it ignores the register B0. As shown in Fig. 4, our method clearly outperforms both of these approaches, which could improve the key rates for DI randomness expansion.
Lower bounds on H(A0B0∣E) as a function of depolarizing noise (for the scenario studied in1) or detection efficiency (for the scenario studied in43). Our approach outperforms both previous approaches, namely indirect bounds via the one-party entropy H(A0∣E) (using the bound in1) or the guessing probability. We also show a curve obtained when applying our method with only the CHSH value as the constraint, instead of the full output distribution.
We also analyze a 1sDI version of the six-state protocol50, where Bob’s measurement device is uncharacterized. As mentioned earlier, the characterization of Alice’s device translates to algebraic relations between the operators Pa∣x, which we impose as additional constraints on top of the NPA hierarchy. We see that in Fig. 5, the resulting bound coincides with the bound for the BB84 protocol. This supports a conjecture51 that when Bob’s measurements are uncharacterized, performing three measurements does not offer any advantage over performing only two measurements.
Lower bounds on H(A0∣E) for a 1sDI version of the six-state protocol50. Interestingly, the bound we obtain from our method coincides with that for the BB84 protocol. For reference, we also show the bound that could be obtained from a tomographically complete characterization of the state, such as via the measurements in the standard (device-dependent) six-state protocol.
Discussion
Here, we have developed a universal toolbox to obtain reliable secret key rates for QKD with untrusted devices. The main advantage of our method is that it can be applied not only to those based on specialized Bell inequalities, but also to any DIQKD protocol. The only previous known approach that could be applied to DIQKD with such generality is that based on bounding the guessing probability15,16,17, which is generally not optimal. Our method outperforms all earlier results in some cases, as shown in Figs. 3 and 4. Importantly, it seems to give good bounds in regimes with substantial noise, which are likely to be experimentally relevant.
Currently, our method scales rapidly in computational difficulty as the number of inputs or outputs for the protocol increases—the polynomial in Eq. (4) is generally of high order, hence a high NPA hierarchy level34 is needed to bound 〈K〉ρ. Because of this, we currently do not have good bounds for DI scenarios with large numbers of inputs or outputs (though we find suboptimal bounds for some such cases; see Section IV of the Supplement). An important goal now would be to find ways to improve the tractability of our approach, perhaps by following reductions along the lines of those described in Ref. 52. This would enable the computation of key rates for DIQKD protocols (or other DI protocols) with more measurement settings and/or outcomes.
With our toolbox in hand, one can now explore DI protocols based on maximizing a variety of Bell expressions (or maximizing the key rate directly) instead of being restricted to CHSH. While the scaling issues currently impose some limitations, we observe that there remains substantial unexplored territory even within 2-input 2-output DI protocols. For instance, the tilted CHSH inequalities42 can certify higher two-party entropies than CHSH in the absence of noise, but the previous bounds were based on min-entropy and not very noise robust. Using our approach to improve these bounds (see Section IV of the Supplement) would be relevant for experimental implementations of DI protocols such as randomness expansion22,23.
Methods
Bounding the von Neumann entropy
The advantage of quantum over classical cryptography stems from the fact that for the former, it is possible to bound Eve’s knowledge using only Alice’s and Bob’s systems (essentially, using the monogamy property of entanglement). To make this precise for H(A0∣E), one can regard the key-generating measurement as a quantum-to-classical channel that maps Alice’s (quantum) system A to a memory register A0 which stores the (classical) measurement outcomes. By Stinepring’s theorem53, this channel can be described via an isometry V to an extended system \({A}_{0}A^{\prime}\). This isometry maps the pure initial state ΨABE to a pure final state \({{{\Psi }}}_{A^{\prime} BE{A}_{0}}\) (see Fig. 6).
The key-generating measurement is regarded as an isometry to a larger Hilbert space, by expanding the classical memory A0 with an ancilla \({A}^{\prime}\). From this perspective the initial and final states are pure, and thus the entropy change ΔH on the memory-Eve subsystem equals the entropy change on the Alice–Bob subsystem.
Since the entropies of the marginal states of a pure bipartite state are equal, this gives
where \(T[{\rho }_{AB}]={{{{\rm{tr}}}}}_{{A}_{0}}((V\otimes {{\mathbb{I}}}_{B}){\rho }_{AB}{(V\otimes {{\mathbb{I}}}_{B})}^{{\dagger} })\). (We remark that this approach was used in Ref. 54.) The last line can be interpreted as entropy production, ΔH, resulting from the transformation \(AB\to A^{\prime} B\). Since it only depends on the reduced states of Alice and Bob, they can be used to bound Eve’s knowledge using only their own systems. For projective measurements, V can be chosen54 such that T is the pinching channel
Besides its application to QKD, the amount of entropy that is produced or consumed by a quantum operation T is one of the central quantities of a physical system. However, computing this entropy quantity is technically challenging, since the entropy of a quantum state is not directly accessible. Instead, the quantities that are directly accessible are typically the expectation values of certain observables, i.e., expressions of the form \({\langle {L}_{j}\rangle }_{\rho }={{{\rm{tr}}}}(\rho {L}_{j})\) for operators Lj (which in QKD scenarios have the form described earlier). Following this perspective, we have to study the following problem: find bounds on ΔH that hold for all states consistent with the observed constraints \({\langle {L}_{j}\rangle }_{\rho }={l}_{j}\). For QKD, these bounds have to be lower bounds, since we consider the “worst-case scenario” for the honest parties.
To solve this problem, we propose the following ansatz: for coefficients \({\lambda }_{j}\in {\mathbb{R}}\), we define L = ∑jλjLj and aim to find an operator K such that
holds for all states. To find such a K, we note that Jensen’s operator inequality and the Gibbs variational principle imply (see Section III of the Supplement for details)
where T* is the adjoint channel of T. Applying a recently discovered generalization of the Golden–Thompson inequality55, it follows that for any self-adjoint \({\tilde{L}}_{k}\) such that \(L={\sum }_{k}{\tilde{L}}_{k}\), we can choose
where \(\beta (t)=(\pi /2){(\cosh (\pi t)+1)}^{-1}\). Thus, this yields a family of lower bounds on \(H\left(T[\rho ]\right)-H(\rho )\), characterized by λj and \({\tilde{L}}_{k}\).
Our task is now reduced to finding upper bounds on 〈K〉ρ. If the explicit matrix representation of K is known, such as in a DD scenario, this is an SDP in a standard form and can be solved directly (see, e.g.,10). However, 1sDI and DI scenarios appear much more challenging, because one does not have an explicit form for K. This reveals the key breakthrough allowed by our approach: a careful choice of \({\tilde{L}}_{xy}\) lets us bound 〈K〉ρ without an explicit matrix representation. Specifically, by setting
we obtain (see Section III of the Supplement) Theorem 1 as stated above. For the DI scenario, the channel T is self-adjoint and idempotent, so T*T = T. With this choice of \({\tilde{L}}_{xy}\), we achieved the critical goal of reducing 〈K〉ρ to a form that can be bounded using the NPA hierarchy.
Data availability
The data produced in this work is available from the corresponding authors upon reasonable request.
Code availability
The code used in this work is available from the corresponding authors upon reasonable request.
References
Pironio, S. et al. Device-independent quantum key distribution secure against collective attacks. New J. Phys. 11, 045021 (2009).
Vazirani, U. & Vidick, T. Fully device-independent quantum key distribution. Phys. Rev. Lett. 113, 140501 (2014).
Arnon-Friedman, R., Dupuis, F., Fawzi, O., Renner, R. & Vidick, T. Practical device-independent quantum cryptography via entropy accumulation. Nat. Commun. 9, 459 (2018).
Bell, J. S. On the Einstein-Podolsky-Rosen paradox. Physics 1, 195–200 (1964).
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Bell nonlocality. Rev. Mod. Phys. 86, 419–478 (2014).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Curty, M., Lewenstein, M. & Lütkenhaus, N. Entanglement as a precondition for secure quantum key distribution. Phys. Rev. Lett. 92, 217903 (2004).
Acin, A. & Gisin, N. Quantum correlations and secret bits. Phys. Rev. Lett. 94, 020501 (2005).
Barrett, J., Kent, A. & Pironio, S. Maximally nonlocal and monogamous quantum correlations. Phys. Rev. Lett. 97, 170409 (2006).
Coles, P. J., Metodiev, E. M. & Lütkenhaus, N. Numerical approach for unstructured quantum key distribution. Nat. Commun. 7, 11712 (2016).
Winick, A., Lütkenhaus, N. & Coles, P. J. Reliable numerical key rates for quantum key distribution. Quantum 2, 77 (2018).
Lin, J., Upadhyaya, T. & Lütkenhaus, N. Asymptotic security analysis of discrete-modulated continuous-variable quantum key distribution. Phys. Rev. X 9, 041064 (2019).
Wang, Y., Primaatmaja, I. W., Lavie, E., Varvitsiotis, A. & Lim, C. C. W. Characterising the correlations of prepare-and-measure quantum networks. npj Quantum Inf. 5, 17 (2019).
Primaatmaja, I. W., Lavie, E., Goh, K. T., Wang, C. & Lim, C. C. W. Versatile security analysis of measurement-device-independent quantum key distribution. Phys. Rev. A 99, 062332 (2019).
Masanes, L., Pironio, S. & Acín, A. Secure device-independent quantum key distribution with causally independent measurement devices. Nat. Commun. 2, 238 (2011).
Bancal, J.-D., Sheridan, L. & Scarani, V. More randomness from the same data. New J. Phys. 16, 033011 (2014).
Nieto-Silleras, O., Pironio, S. & Silman, J. Using complete measurement statistics for optimal device-independent randomness evaluation. New J. Phys. 16, 013035 (2014).
Pirandola, S. et al. Advances in quantum cryptography (2019). Adv. Opt. Photonics 12, 1012–1236 (2020).
Acín, A. & Masanes, L. Certified randomness in quantum physics. Nature 540, 213–219 (2016).
Pironio, S. et al. Random numbers certified by Bell’s theorem. Nature 464, 1021–1024 (2010).
Colbeck, R.Quantum And Relativistic Protocols For Secure Multi-Party Computation. Ph.D. thesis, University of Cambridge (2006).
Liu, W.-Z. et al. Device-independent randomness expansion against quantum side information. Nat. Phys. 17, 488 (2021).
Shalm, L. K. et al. Device-independent randomness expansion with entangled photons. Nat. Phys. 17, 452–456 (2021).
Vértesi, T., Pironio, S. & Brunner, N. Closing the detection loophole in Bell experiments using qudits. Phys. Rev. Lett. 104, 060401 (2010).
Froissart, M. Constructive generalization of Bell’s inequalities. Nuov. Cim. B (1971-1996) 64, 241–251 (1981).
Śliwa, C. Symmetries of the Bell correlation inequalities. Phys. Lett. A 317, 165–168 (2003).
Collins, D. & Gisin, N. A relevant two qubit Bell inequality inequivalent to the CHSH inequality. J. Phys. A 37, 1775 (2004).
Gisin, N. Bell inequalities: many questions, a few answers. In Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle, The Western Ontario Series in Philosophy of Science Vol. 73 (eds. Myrvold, W.C. & Christian, J.) 125–138 (Springer, 2009).
Ribeiro, J., Murta, G. & Wehner, S. Fully device-independent conference key agreement. Phys. Rev. A 97, 022307 (2018).
Reeb, D. & Wolf, M. M. An improved Landauer principle with finite-size corrections. New J. Phys. 16, 103011 (2014).
Jarzynski, C. Equalities and inequalities: irreversibility and the second law of thermodynamics at the nanoscale. Annu. Rev. Condens. Matter Phys. 2, 329–351 (2011).
Clausius, R.The Mechanical Theory of Heat – With its Applications to the Steam Engine and to Physical Properties of Bodies (John van der Voorst, 1867).
Bekenstein, J. D. Black holes and entropy. Phys. Rev. D 7, 2333 (1973).
Navascués, M., Pironio, S. & Acín, A. A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations. New J. Phys. 10, 073013 (2008).
Brown, P., Fawzi, H. & Fawzi, O. Computing conditional entropies for quantum correlations. Nat. Commun. 12, 575 (2021).
Brown, P., Fawzi, H. & Fawzi, O. Device-independent lower bounds on the conditional von Neumann entropy. Preprint at https://arxiv.org/abs/2106.13692 (2021).
Shor, P. W. & Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441 (2000).
Bennett, C. H., Brassard, G. & Mermin, N. D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 68, 557 (1992).
Devetak, I. & Winter, A. Distillation of secret key and entanglement from quantum states. Proc. Roy. Soc. A 461, 207–235 (2005).
Dupuis, F., Fawzi, O. & Renner, R. Entropy accumulation. Commun. Math. Phys. 379, 867–913 (2020).
Brown, P. J., Ragy, S. & Colbeck, R. A framework for quantum-secure device-independent randomness expansion. IEEE Trans. Inf. Theory 66, 2964–2987 (2020).
Acín, A., Massar, S. & Pironio, S. Randomness versus nonlocality and entanglement. Phys. Rev. Lett. 108, 100402 (2012).
Eberhard, P. H. Background level and counter efficiencies required for a loophole-free Einstein-Podolsky-Rosen experiment. Phys. Rev. A 47, R747–R750 (1993).
Briët, J. & Harremoës, P. Properties of classical and quantum Jensen-Shannon divergence. Phys. Rev. A 79, 052311 (2009).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Giustina, M. et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).
Shalm, L. K. et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).
Rosenfeld, W. et al. Event-ready Bell test using entangled atoms simultaneously closing detection and locality loopholes. Phys. Rev. Lett. 119, 010402 (2017).
Murta, G., van Dam, S. B., Ribeiro, J., Hanson, R. & Wehner, S. Towards a realization of device-independent quantum key distribution. Quantum Sci. Technol. 4, 035011 (2019).
Bruß, D. Optimal eavesdropping in quantum cryptography with six states. Phys. Rev. Lett. 81, 3018 (1998).
Goh, K. T., Bancal, J.-D. & Scarani, V. Measurement-device-independent quantification of entanglement for given Hilbert space dimension. New J. Phys. 18, 045022 (2016).
Tavakoli, A., Rosset, D. & Renou, M.-O. Enabling computation of correlation bounds for finite-dimensional quantum systems via symmetrization. Phys. Rev. Lett. 122, 070501 (2019).
Stinespring, W. F. Positive functions on C*-algebras. Proc. Am. Math. Soc. 6, 211–216 (1955).
Coles, P. J. Unification of different views of decoherence and discord. Phys. Rev. A 85, 042103 (2012).
Sutter, D., Berta, M. & Tomamichel, M. Multivariate trace inequalities. Commun. Math. Phys. 352, 37–58 (2017).
Löfberg, J. YALMIP: a toolbox for modeling and optimization in MATLAB. In IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508) 284–289 (IEEE, 2004). https://ieeexplore.ieee.org/document/1393890?arnumber=1393890.
MOSEK ApS. The MOSEK Optimization Toolbox for MATLAB Manual. Version 8.1 (MOSEK, 2019).
Branciard, C., Cavalcanti, E. G., Walborn, S. P., Scarani, V. & Wiseman, H. M. One-sided device-independent quantum key distribution: security, feasibility, and the connection with steering. Phys. Rev. A 85, 010301 (2012).
Tomamichel, M., Fehr, S., Kaniewski, J. & Wehner, S. A monogamy-of-entanglement game with applications to device-independent quantum cryptography. New J. Phys. 15, 103002 (2013).
Ma, X. & Lütkenhaus, N. Improved data post-processing in quantum key distribution and application to loss thresholds in device independent QKD. Quantum Info. Comput. 12, 203–214 (2012).
Acknowledgements
We thank Otfried Gühne, Miriam Huang, Mathias Kleinmann, Jie Lin, Norbert Lütkenhaus, Tobias Osborne, Gláucia Murta, Miguel Navascués, Renato Renner, Valerio Scarani, Marco Tomamichel, Reinhard F. Werner, and Ramona Wolf for useful discussions. E. Y.-Z. T. was funded by the Swiss National Science Foundation via the National Center for Competence in Research for Quantum Science and Technology (QSIT), and by the Air Force Office of Scientific Research (AFOSR) via grant FA9550-19-1-0202. C. C.-W. L. acknowledges support from the National Research Foundation (NRF) Singapore, under its NRF Fellowship programme (NRFF11-2019-0001) and Quantum Engineering Programme (QEP-P2), and the Asian Office of Aerospace Research and Development (FA2386-18-1-4033). Computations were performed using the MATLAB package YALMIP56 with solver MOSEK57. Some of the calculations reported here were performed using the Euler cluster at ETH Zürich.
Author information
Authors and Affiliations
Contributions
E.Y.-Z.T. and R.S. are co-first authors on this work. Both contributed to the derivation of the main theorem, with inputs from all other authors. E.Y.-Z.T. implemented the computations for DI scenarios, and R.S., K.T.G., I.W.P., and C.C.-W.L. studied 1sDI scenarios. C.C.-W.L. and E.Y.-Z.T. proposed the project and structured the overall concept. All authors contributed to writing the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tan, E.YZ., Schwonnek, R., Goh, K.T. et al. Computing secure key rates for quantum cryptography with untrusted devices. npj Quantum Inf 7, 158 (2021). https://doi.org/10.1038/s41534-021-00494-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00494-z
This article is cited by
-
The Schmidt Rank for the Commuting Operator Framework
Communications in Mathematical Physics (2024)
-
Complete classification of steerability under local filters and its relation with measurement incompatibility
Nature Communications (2022)
-
Neural network-based prediction of the secret-key rate of quantum key distribution
Scientific Reports (2022)