Full monitoring of ensemble trajectories with 10 dB-sub-Heisenberg imprecision

Abstract

The change of a quantum state can generally only be fully monitored through simultaneous measurements of two non-commuting observables $\hat{X}$ and $\hat{Y}$ spanning a phase space. A measurement device that is coupled to the thermal environment provides at a time a pair of values that have a minimal uncertainty product set by the Heisenberg uncertainty relation, which limits the precision of the monitoring. Here, we report on an optical ensemble measurement setup that is able to monitor the time-dependent change of the quantum state’s displacement in phase space ($\langle \hat{X}(t)\rangle ;\langle \hat{Y}(t)\rangle$) with an imprecision 10 dB below the Heisenberg uncertainty limit. Our setup provides pairs of values (X(t_i); Y(t_i)) from simultaneous measurements at subsequent times t_i. The measurement references are not coupled to the thermal environment but are established by an entangled quantum state. Our achievement of a tenfold reduced quantum imprecision in monitoring arbitrary time-dependent displacements supports the potential of the quantum technology required for entanglement-enhanced metrology and sensing as well as measurement-based quantum computing.

Introduction

Quantum sensing and measurement-based quantum computing utilise quantum correlated states^1,2. The most mature technology for these applications is based on quantum states of the electro-magnetic field. Laser interferometers that are used as telescopes for gravitational-wave astronomy achieve unprecedented sensitivities based on states having a squeezed photon counting statistic^3,4,5,6. It was proposed to further improve them by bipartite Gaussian entangled states^7,8,9,10. Optical measurement-based quantum computing based on multi-partite entangled cluster states^11,12 was pushed forward recently¹³.

Measurements in the regime of Gaussian quantum statistics concern two non-commuting observables. In terms of dimensionless operators that are normalised to the variance of the ground state, they are often named $\hat{X}$ and $\hat{Y}$. They need to be measured both in order to determine the full energy of a quantised harmonic oscillator, similar to position and momentum. The Heisenberg uncertainty relation^14,15,16,17 is a useful reference to distinguish between semi-classical measurements¹⁸ and those that exploit entanglement¹⁹. Experimentally achievable Gaussian entanglement has been characterised by co-variances derived from ensemble measurements in stationary settings^8,20,21,22. So far, Gaussian entanglement was not used to improve measurements of phase space displacements that changed after a single measurement window. In such a time-dependent setting, averaging would not constitute a suitable approach for improving the signal-to-noise ratio.

Here, we present the monitoring of a dynamical phase space trajectory α(t) through the simultaneous measurements of two non-commuting observables (X(t_i); Y(t_i)) at subsequent times t_i with an imprecision much lower than the reference limit as given by the Heisenberg uncertainty relation. The non-classical improvement provides the same benefit as ten times averaging, which, however, is possible only in a stationary setting. The experimental achievements presented here are entirely based on individually sampled two-dimensional data points.

Results

Uncertainty relations

Our experiment uses quantities that are also used in optical communication and optical quantum computing¹³, namely phase and amplitude modulation depths carried by quasi-monochromatic laser light of optical frequency ν, see the figure in Supplementary Information. The depth of the amplitude modulation (amplitude modulation index) in the frequency band f ± Δf, with ν ≫ f > Δf, is quantified by the dimensionless operator ${\hat{X}}_{f,{{\Delta }}f}$²³. This operator is also known as ‘amplitude quadrature amplitude’. The corresponding depth of phase modulations is (in the limit of weak phase modulations) quantified by the operator ${\hat{Y}}_{f,{{\Delta }}f}$. This operator is also known as ‘phase quadrature amplitude’ ²⁴. ${\hat{X}}_{f,{{\Delta }}f}$ and ${\hat{Y}}_{f,{{\Delta }}f}$ do not commute. In the following, we skip the indices and normalise the commutator to $[\hat{X},\hat{Y}]=2{{{{{\rm{i}}}}}}$, which results in the Heisenberg uncertainty relation

$${{\Delta }}\hat{X}{{\Delta }}\hat{Y}\ge 1,$$

(1)

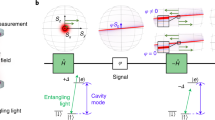
where Δ denotes the standard deviation of the measured eigenvalues of the respective operator. $\hat{X}$ and $\hat{Y}$ span a phase space, in which the uncertainty area is bounded from below accordingly. The lower bound in Eq. (1) refers to ‘ideal’ measurements performed with semi-classical devices, which do not use quantum correlations. ‘Ideal’ means that $\hat{X}$ is measured on a first copy and $\hat{Y}$ is measured on a second copy of the system. Ideal measurements are only possible in (quasi-)stationary settings. If the quantities $\hat{X}$ and $\hat{Y}$ change on time scales that are not much longer than 1/Δf, they need to be measured simultaneously. In this case, splitting the system into two independently measured subsystems is required (beam splitter in Fig. 1, and BS₃ in Fig. 2). Furthermore, averaging is not possible unless the trajectory repeats after some time. The splitting reduces the signal-to-noise ratio in comparison with ideal measurements. The splitting can be described as opening a new port through which vacuum uncertainty couples to the measurement (port B in Fig. 1, left), if not an entangled reference system is superimposed via this port, as shown in in Figs. 1b and 2. In the absence of quantum correlations, simultaneous measurements at times t_i need to cope with at least doubled minimal quantum uncertainty, which increases standard deviations by at least the factor $\sqrt{2}$¹⁸, yielding

$${{\Delta }}\left(\hat{X}({t}_{i})\right){{\Delta }}\left(\hat{Y}({t}_{i})\right)\ge 2.$$

(2)

The above inequality represents the fundamental precision limit when two conjugate observables are measured simultaneously on a single system with respect to reference values of a semi-classical measurement device. Note that inequality (2) relates to a Gaussian state in the Husimi Q representation²⁵, whereas inequality (1) relates to the Wigner representation²⁶.

Fig. 1: Monitoring of quantum state displacement α(t).

The phase space observables are the real and imaginary parts $\alpha (t)=\langle \hat{X}(t)\rangle +i\langle \hat{Y}(t)\rangle$. a The simultaneous (semi-classical) monitoring of the displacement is hampered by quantum uncertainty, which can be illustrated by ground states entering the measurement device at inputs A and B. b Exploiting an entangled state ${\left|0,{X}_{{{{{{\rm{diff}}}}}}},{Y}_{{{{{{\rm{sum}}}}}}},r\right\rangle }_{A,B}$ reduces the quantum noise imprecision of a single measurement pair (X(t_i); Y(t_i)) at time t_i in principle to arbitrarily low values. Here, ‘0' refers to the average displacements at inputs A and B, X_diff, Y_sum to the kind of quantum correlations, and r to the joint strength of the quantum correlations. In practice, decoherence on the entangled state that reduces r is the major problem.

Fig. 2: Schematics of the experiment.

Shown are optical paths of laser beams at wavelength 1550 nm. The phase space pictures show the quantum uncertainty of the laser beams' modulations at f = 5 MHz at several instances in the Wigner representation. From bottom left to top right: balanced beam splitter BS₁ converted two squeezed vacuum states into a bipartite EPR entangled state. One part served as a quantum entangled reference (subscript 0). The other part was displaced by $(\langle \hat{X}\rangle ;\,\langle \hat{Y}\rangle )(t)$ (illustrated by the arrow) by overlapping modulated light transmitted through BS₂. The two projections of the arrow were simultaneous monitored with respect to the entangled reference system by superposition at BS₃ and by detecting the outputs with balanced homodyne detectors. BHD₁ provided eigenvalues of $(\hat{X}\,-\,{\hat{X}}_{0})({t}_{i})/\sqrt{2}$, while BHD₂ provided eigenvalues of $(\hat{Y}\,+\,{\hat{Y}}_{0})({t}_{i})/\sqrt{2}$, with $\langle {\hat{X}}_{0}\rangle \,=\,\langle {\hat{Y}}_{0}\rangle \,=\,0$. EOM electro-optical modulator, AFG arbitrary function generator, DAQ data acquisition, LO local oscillator.

Measurements with respect to quantum entangled references

Let $[\hat{X},\hat{Y}]\,=\,2{{{{{\rm{i}}}}}}$ describe a quantum system of interest and $[{\hat{X}}_{0},{\hat{Y}}_{0}]\,=\,2{{{{{\rm{i}}}}}}$ another quantum system. A short calculation leads to the zero-commutator $[\hat{X}\,\pm \,{\hat{X}}_{0},\hat{Y}\,\mp \,{\hat{Y}}_{0}]\,=\,0$, which results in

$${{\Delta }}(\hat{X}\pm {\hat{X}}_{0})\ {{\Delta }}(\hat{Y}\mp {\hat{Y}}_{0})\ge 0.$$

(3)

This inequality describes the fact that X and Y of a system can be measured simultaneously with arbitrary precision with respect to the corresponding quantities X₀ and Y₀ of a reference system. Usually, a reference system has its own quantum uncertainty. If, however, an ensemble of quantum systems is available that are all entangled with a reference system at hand, the measurement of a phase space trajectory $(\langle \hat{X}\rangle ;\,\langle \hat{Y}\rangle )(t)$ with a sub-Heisenberg imprecision is possible.

Experimental setup

Figure 2 shows the schematics of our experiment. A commercial erbium-doped fibre laser generated 1 W of quasi-monochromatic light at the wavelength of 1550 nm. About half of the light was frequency doubled to provide the pump light for two squeezed-light resonators. The latter used resonator-enhanced degenerate type 0 optical-parametric amplification in periodically poled potassium titanyl phosphate. The two output fields carried modulation spectra around 5 MHz in squeezed vacuum states and were overlapped at balanced beam splitter BS₁. The results were two fields whose modulations were strongly EPR entangled, which was characterised in a precursor experiment²⁰. Here, we recombined the entangled beams on a second balanced splitter (BS₃). The optical path length difference was controlled to convert them back to two squeezed beams. Due to necessarily imperfect interference contrasts at the two beam splitters, the final squeeze factors could only be lower than the initial squeeze factors of the input modes (subscripts 1 and 2). The BHDs used optical local oscillators (LOs) of about 10 mW from the joint fibre laser. The phase differences between the LOs and the squeezed fields were stably controlled to 0° and 90°, respectively. BHD₁ at 0° sampled values of a squeezed amplitude quadrature amplitude and BHD₂ at 90° sampled values of a squeezed phase quadrature amplitude, both with a sampling frequency of 200 MHz. To avoid aliasing, we applied an analogue lowpass filter with a corner frequency of 50 MHz to each channel. Post processing was done with a self-written Python script, which was used to digitally demodulate the data at f = 5 MHz and subsequent finite impulse response-lowpass filtering with a cut-off frequency of Δf/2 = 10 kHz. Figure 3 represents the entanglement quality of our setup in terms of variances.

Fig. 3: Variances of our X(t_i) data and Y(t_i) data.

Shown is the example of stationary zero displacement, i.e. $\langle \hat{X(t)}\rangle =\langle \hat{Y(t)}\rangle =0$. Solid lines correspond to the variance of 2600 measuring points each, without entanglement (top lines) and with entanglement (bottom lines). The latter represents 10 dB two-mode squeezing. Dots represent variances calculated over 260 consecutive measuring points. The variances characterise the quality of our data sampling with respect to the entangled reference. The two types of modulations (X: left panel; Y: right panel) can be measured simultaneously with an uncertainty product of ${{\Delta }}(\hat{X}({t}_{i})){{\Delta }}(\hat{Y}({t}_{i}))\approx 0.2$ violating Inequality (2) by a factor of ~10. Here, f = 5 MHz and Δf = 20 kHz.

The time-dependent displacement α(t) in our setup corresponded to the time-dependent modulation at f = 5 MHz of a coherent carrier field that was transmitted through the high reflectivity mirror BS₂ (R = 99.99%). The high reflectivity minimised decoherence, i.e. optical loss to the entanglement. Changing the peak voltage to the electro-optical modulator (EOM, as shown in Fig. 2), changed the absolute value of the displacement ∣α∣. Changing the DC voltage to the piezo-actuated phase-shifter (U₁) changed the differential excitation in $\langle \hat{X}\rangle$ and $\langle \hat{Y}\rangle$. The time series produced at BHD₁ and BHD₂ represented simultaneous measurements of the system’s conjugate displacement components with respect to the corresponding values of the (entangled) reference. Since $\langle {\hat{X}}_{0}\rangle \,=\,\langle {\hat{Y}}_{0}\rangle \,=\,0$, the data serve for monitoring the trajectory $(\langle \hat{X}\rangle ;\,\langle \hat{Y}\rangle )(t)$.

Experimental results

Figure 4 shows two phase space trajectories $(\langle \hat{X}\rangle ;\,\langle \hat{Y}\rangle )(t)$ (solid lines) measured with precision suspending inequalities (1) and (2). Added are individual data points from simultaneous measurements of (X − X₀)(t_i) and (Y + Y₀)(t_i), when the interrogated system was entangled with the reference system. Also shown are individual data points from simultaneous measurements of (X − X₀)(t_i) and (Y + Y₀)(t_i), when the entanglement source was switched off and the modulations $\langle \hat{X}\rangle$ and $\langle \hat{Y}\rangle$ set to 0. These data points accumulated around the phase space origin and were used to derive the factor by which the inequalities (1) and (2) were surpassed. The standard deviations in (X − X₀)(t_i) and (Y + Y₀)(t_i) around the actual phase space trajectories $(\langle \hat{X}\rangle ;\,\langle \hat{Y}\rangle )(t)$ (solid line) were reduced by more than $\sqrt{10}$. This factor is highlighted by the different radii of the small circles. The phase space trajectories were thus tracked with an uncertainty product that violated inequality (2) by slightly more than a factor of 10. As expected, the factor by which Heisenberg’s uncertainty limit was surpassed directly corresponded to the strength of the entanglement. Increasing the entanglement strength requires further reduction of optical loss, including further increase of photo-electric detection efficiency²⁷.

Fig. 4: Example phase space trajectories.

Examples (a) and (b) have a duration of about 5 ms length and are measured with sub-Heisenberg imprecision (solid line surrounded by green dots) in comparison to measurements on ground states (centred, blue dots). The dots represent single measurements ((X − X₀)(t_i); (Y + Y₀)(t_i)) performed at subsequent times t_i, with t_i+1 − t_i = 10 μs. (To increase the number of points, we superposed 15 and 8 identical measurements, respectively.) The spreads of the data points in the two phase space directions represent the relevant standard deviations of quantum noise in estimating the trajectories. The sub-Heisenberg uncertainty area is revealed by comparing the small circles to larger ones in the centres, which represent the lower bound in inequality (2). The latter is surpassed by a factor of about 10. The upper trajectory represents a changing type of modulation at constant modulation depth. The bottom one additionally shows a continuously decreasing modulation depth.

Figure 4a represents a constant modulation depth, while the kind of modulation was continuously changed. The system had a pure amplitude modulation when $\langle \hat{Y}\rangle (t)=0$ and a pure phase quadrature modulation when $\langle \hat{X}\rangle (t)=0$. The amplitude of the AC voltage at the EOM (U₂) was constant and just the DC voltage at the piezo actuator (U₁) continuously changed. The trajectory started at about $(\langle \hat{X}\rangle ;\,\langle \hat{Y}\rangle )=(-3.7\sqrt{2};5.8\sqrt{2})$, completed almost a full cycle, returned and stopped at about $(-5.3\sqrt{2};-4.3\sqrt{2})$. The bottom panel shows another example trajectory whose modulation depth also changed, resulting in a phase and amplitude dependent trajectory.

Discussion

Our experiment demonstrates that any individual measurement of two non-commuting observables at the same time improved when entanglement is exploited. The observables considered are the real and imaginary parts of phase space displacement, which describe the depths of the amplitude modulation and the phase quadrature around a selected radio frequency of a continuous-wave quasi-monochromatic laser beam. The temporal change of the modulations depths corresponds to a trajectory in phase space. Our experiment shows that the trajectory can be monitored by a large number of individual measurement pairs with a tenfold reduced imprecision in each of the observables compared with the variances of measurements on the ground state (without entanglement). The reduction factors correspond to the squeeze factor in both observables (10 dB) realised by the entanglement resource. We conclude that the time-varying displacement can in principle be monitored with arbitrary precision without averaging, i.e. even for random walks. We thus further conclude that the often-quoted interpretation of Heisenberg’s uncertainty relation ‘two non-commuting observables of a quantum system cannot be measured simultaneously with arbitrary precision’ is incorrect. In light of our experiment, the statement becomes correct, if completed by ‘...with respect to a reference system that was or has been coupled to a thermal environment’, since in this case the reference system cannot be quantum correlated.

The phase space displacement in our experiment is overlapped with the entangled fields via a high reflectivity beam splitter. In principle, the displacement can also be produced directly in the beam path of one of the entangled states by a combination of an amplitude and a phase modulator, because the entangled states are carried by accompanying monochromatic fields. An important issue is to keep the entanglement decoupled from the environment before the measurement. The reduction factor in the quantum imprecision achieved is of practical significance and supports the emergent field of quantum sensing. In gravitational-wave observatories, entangled light provides additional sensitivity improvements compared to squeezed light^3,4,5,6 by mitigating disturbances from back-scattered light⁸ and from quantum radiation pressure^7,9,10. The setup realised constitutes state of the art quantum optics technology suitable for the generation and detection of Gaussian cluster states for measurement-based quantum computing^11,12,13.