Abstract
The recently demonstrated trapping and laser cooling of 133Ba+ has opened the door to the use of this nearly ideal atom for quantum information processing. However, before high-fidelity qubit operations can be performed, a number of unknown state energies are needed. Here, we report measurements of the 2P3/2 and 2D5/2 hyperfine splittings, as well as the 2P3/2 ↔ 2S1/2 and 2P3/2 ↔ 2D5/2 transition frequencies. Using these transitions, we demonstrate high-fidelity 133Ba+ hyperfine qubit manipulation with electron shelving detection to benchmark qubit state preparation and measurement (SPAM). Using single-shot, threshold discrimination, we measure an average SPAM fidelity of \({\mathcal{F}}=0.99971(3)\), a factor of ≈2 improvement over the best reported performance of any qubit.
Similar content being viewed by others
Introduction
Quantum error correction allows an imperfect quantum computer to perform reliable calculations beyond the capability of classical computers1,2,3. However, even with the lowest reported error rates4,5,6,7,8,9,10,11,12, the number of qubits (Nq) required to achieve fault tolerance is projected13 to be significantly larger than the state of the art14,15,16. Nonetheless, noisy intermediate-scale quantum (NISQ) devices17 are currently being employed to tackle important problems without fault tolerance18,19,20,21,22,23,24.
For these NISQ devices, single-shot state preparation and measurement (SPAM) infidelity (ϵs) causes a reduction in computational fidelity that is exponential in qubit number, \({{\mathcal{F}}}_{s}={(1-{\epsilon }_{\mathrm s})}^{{N}_{\mathrm q}}\) (uncorrelated errors). The requirement to perform faithful SPAM therefore limits the number of qubits to \({N}_{\mathrm {q}}\,<\,{\mathrm{ln}}\,(2)/{\epsilon }_{\mathrm {s}}\). While state readout error correction techniques can effectively lower measurement infidelity, they generally require a number of measurements that grows exponentially with Nq and single-shot readout infidelity25. For these reasons, and given the desire to increase Nq to tackle problems beyond the reach of classical computers, it is important to develop new means to improve ϵs.
The A = 133 isotope of barium provides a potential path to improving fidelities in atomic ion quantum computing, as this isotope combines the advantages of many different ion qubits into a single system26. 133Ba+ has nuclear spin I = 1/2, which as we show here, allows fast, robust state preparation and readout of the hyperfine qubit. It possesses both hyperfine and optical mF = 0 “clock” state qubits, which are relatively insensitive to magnetic fields (mF is the projection quantum number of the total angular momentum F)27. It also possesses metastable 2DJ states (τ ~ 1 min), allowing high-fidelity readout, and long-wavelength transitions enabling the use of photonic technologies developed for the visible and near-infrared spectrum. However, before these advantages can be realized, a number of unknown hyperfine and electronic transition frequencies must be determined.
Here, we measure the previously unknown 2P3/2 and 2D5/2 hyperfine structure, as well as the 2P3/2 ↔ 2S1/2 and 2P3/2 ↔ 2D5/2 electronic transition frequencies. Using this knowledge, we demonstrate 133Ba+ hyperfine qubit manipulation and electron shelving detection. Employing a threshold discrimination and modest fluorescence collection optics (0.28 NA), we measure an average single-shot SPAM fidelity of \({\mathcal{F}}=0.99971(3)\), the highest reported for any qubit.
In what follows, we first present qubit SPAM using standard hyperfine-selective optical cycling28,29 combined with arbitrary qubit rotations and a composite pulse sequence for high-fidelity state transfer. We then present measurement of the unknown hyperfine and electronic transition frequencies. Finally, we use this information to demonstrate high-fidelity SPAM using electron shelving.
Results
Qubit manipulation and hyperfine-selective SPAM
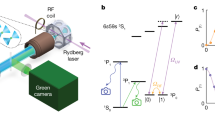
The hyperfine qubit is defined on the pair of mF = 0 “clock” states in the 2S1/2 manifold as \(\left|0\right\rangle\) \(\equiv \left|F=0\right\rangle\) and \(\left|1\right\rangle\) \(\equiv \left|F=1;{m}_{F}=0\right\rangle\). This hyperfine qubit is initialized to the \(\left|0\right\rangle\) state after Doppler cooling via optical pumping by applying frequencies \({\nu }_{493}^{\mathrm c}\), \({\nu }_{493}^{\mathrm {op}}\), \({\nu }_{650}^{\mathrm c}\), and \({\nu }_{650}^{\mathrm {sb}}\) (Fig. 1). Rotations of the qubit Bloch vector about \(\cos (\phi )\hat{x}+\sin (\phi )\hat{y}\) through angle θ, R(θ, ϕ), are accomplished by using microwave radiation near 9.925 GHz30 controlled by a modular digital synthesis platform31. An example rotation of the form R(ΩRt, 0) is shown in Fig. 2a, where the average population in state \(\left|1\right\rangle\) found in 200 trials, measured with a technique described later, is plotted versus the duration of microwave radiation with Rabi frequency ΩR = 2π × 57.03(3) kHz. The \(\left|1\right\rangle\) state can be prepared after initialization into \(\left|0\right\rangle\) by R(π, 0); however, we employ a composite pulse sequence, referred to as the CP Robust 180 sequence (attributed to E. Knill)32, consisting of the five π-pulses \(R(\pi ,\frac{\pi }{6})R(\pi ,0)R(\pi ,\frac{\pi }{2})R(\pi ,0)R(\pi ,\frac{\pi }{6})\). As shown in Fig. 2b, c, the broad flat features in both curves near zero detuning and θ = π demonstrate resiliency to both pulse area and detuning errors as compared to single π-pulses, enabling robust day-to-day operation.
Laser cooling is accomplished using lasers near 493 and 650 nm (\({\nu }_{493}^{{\mathrm c}}\) and \({\nu }_{650}^{{\mathrm c}}\)), and fiber EOMs for repumping sidebands (\({\nu }_{493}^{{\mathrm {sb}}}\), and \({\nu }_{650}^{{\mathrm {sb}}}\)). The \(\left|0\right\rangle\) state is initialized by removing \({\nu }_{493}^{{\mathrm {sb}}}\) and adding \({\nu }_{493}^{{\mathrm {op}}}\) with the 493 nm fiber EOM. Microwave radiation at Δ1 ≈ 9.925 GHz30 allows for arbitrary rotations on the qubit Bloch sphere. Electron shelving of the \(\left|1\right\rangle\) state to the metastable 2D5/2 state is accomplished with lasers near 455, 585, and 650 nm (ν455, ν585, and ν650). A laser near 614 nm (ν614) is used to depopulate the 2D5/2 manifold after state detection. Measurements from this work include Δ3 = 623(20) MHz and Δ5 = 83(20) MHz, with Δ2 = 1840(11) MHz40 and Δ4 = 937(20) MHz26 previously reported. In future experiments, a laser near 1762 nm (ν1762) can be used to directly manipulate the optical qubit clock-states \(\left|1\right\rangle\) and \(\left|2\right\rangle\).
a Probability of shelving \(\left|1\right\rangle\) after microwave rotations of the form R(ΩRt, 0), where ΩR = 2π × 57.03(3) kHz. b, c To prepare the \(\left|1\right\rangle\) state, the five π-pulse CP Robust 180 sequence \(R(\pi ,\frac{\pi }{6})R(\pi ,0)R(\pi ,\frac{\pi }{2})R(\pi ,0)R(\pi ,\frac{\pi }{6})\) transfers population from the initially prepared \(\left|0\right\rangle\) state. b Probability of shelving \(\left|1\right\rangle\) vs. microwave detuning using the CP Robust 180 sequence with ΩR = 2π × 35.4(1) kHz. Points are experimental data and solid line represents theoretical prediction for this composite pulse sequence with no fit parameters. c Pulse area (\(t=\frac{\theta }{{\Omega }_{R}}\)) scan at zero detuning using the CP Robust 180 sequence. Dashed dotted lines in b, c are theory for a single π-pulse, R(π, 0). Statistical error bars on individual data points are smaller than markers.
Typically, for nuclear spin-1/2 hyperfine qubits, single-shot state readout is accomplished via hyperfine-selective optical cycling (\({\nu }_{493}^{\mathrm c}\) and \({\nu }_{650}^{\mathrm c}\) in Fig. 1) and collection of any resulting fluorescence. The \(\vert0\rangle\) and \(\left|1\right\rangle\) states are determined by threshold discrimination on the number of collected photons, as an atom in the \(\left|1\right\rangle\) state scatters many photons, while an atom in the \(\left|0\right\rangle\) state does not28,29. Using this hyperfine-selective optical cycling for SPAM, we measure the fraction of events in which an ion prepared in the \(\left|0\right\rangle\) state was determined to be \(\left|1\right\rangle\), \({\epsilon }_{\left|0\right\rangle }=3.03(4)\times 1{0}^{-2}\), and the fraction of experiments in which an ion prepared in the \(\left|1\right\rangle\) state was determined to be \(\left|0\right\rangle\), \({\epsilon }_{\left|1\right\rangle }=8.65(9)\times 1{0}^{-2}\). The average SPAM fidelity is defined as \({\mathcal{F}}=1-\epsilon =1-\frac{1}{2}({\epsilon }_{\vert 0 \rangle }+{\epsilon }_{\vert 1\rangle })=0.9415(5)\). The fidelity of this technique is limited by off-resonant excitation to the \(\vert{}^{2}{\text{P}}_{1/2},F=1 \rangle\) manifold during readout, which can decay to either \(\left|0\right\rangle\) or \(\left|1\right\rangle\), thereby causing misidentification of the original qubit state28. This readout fidelity could be improved with increased light collection efficiency12,33.
Spectroscopy
For high-fidelity SPAM, 133Ba+ offers another path to state detection. The \(\left|1\right\rangle\) qubit state can be shelved34 to the long-lived (τ ≈ 30 s) metastable 2D5/2 state via the 2D5/2 ↔ 2S1/2 transition, or optically pumped via the 2P3/2 state (Fig. 1), followed by Doppler cooling for state readout. Projection into the \(\left|0\right\rangle\) or \(\left|1\right\rangle\) state is then determined by threshold discrimination on the number of collected photons, as an atom in the \(\left|0\right\rangle\) state scatters many photons, while an atom in the 2D5/2 state, indicating \(\left|1\right\rangle\), does not. Off-resonant scatter is negligible in this case as the Doppler cooling lasers are detuned by many THz from any 2D5/2 state transitions.
In principle, shelving of the \(\left|1\right\rangle\) qubit state is possible via the 2D5/2 ↔ 2S1/2 electric quadrupole transition near 1762 nm (ν1762, currently unknown). However, as we demonstrate below, fast, high-fidelity shelving of the \(\left|1\right\rangle\) state can be achieved with optical pumping by application of the frequencies ν455, ν585, and \({\nu }_{650}^{\mathrm c}\) (and ν614 for deshelving). Of these, only \({\nu }_{650}^{\mathrm c}\) has been previously measured26. To determine these unknown frequencies, we measure the 2P3/2 ↔ 2S1/2 and 2P3/2 ↔ 2D5/2 isotope shifts relative to 138Ba+ (\(\delta {\nu }_{133,138}^{455}\) and \(\delta {\nu }_{133,138}^{614}\)) and hyperfine splittings Δ3 and Δ5 (Fig. 1). To measure Δ3 and \(\delta {\nu }_{133,138}^{455}\), the atom is prepared in the \(\left|{}^{2}{\text{S}}_{1/2};F=1\right\rangle\) manifold by optical pumping with \({\nu }_{650}^{\mathrm c}\) and \({\nu }_{650}^{\mathrm {sb}}\) after Doppler cooling. A tunable laser near 455 nm (ν455) is applied for 50 μs. When the frequency is near one of the two allowed transitions, excitation followed by spontaneous emission from the 2P3/2 with branching ratios35 0.74, 0.23, and 0.03 to the 2S1/2, 2D5/2, and 2D3/2 states, respectively, optically pumps the ion to the 2D5/2 state. The population remaining in the 2S1/2 and 2D3/2 states is then detected by collecting fluorescence while Doppler cooling and using threshold discrimination on the number of collected photons to decide if the atom was in the 2D5/2 state. This sequence (see Supplementary Information) is repeated 200 times per laser frequency, and the average population is shown Fig. 3a as a function of frequency. From these data, we find Δ3 = 623(20) MHz, and \(\delta {\nu }_{133,138}^{455}\) = +358(28) MHz relative to 138Ba+ .
a Measurement of the 2P3/2 hyperfine splitting by tuning the 455nm laser. The left (right) peak corresponds to F=2 (F=1) in 2P3/2. b Measurement of the 2D5/2 hyperfine splitting by tuning the 614nm laser. Triangles are data for the \(\vert{}^{2}{\text{P}}_{3/2};F=2\rangle\,\leftrightarrow\,\vert{}^{2}{\text{D}}_{5/2};F=3\rangle\) transition, circles are for the \(\vert{}^{2}{\text{P}}_{3/2};F=2\rangle\, \leftrightarrow \,\vert{}^{2}{\text{D}}_{5/2};F=2\rangle\) transition. Solid lines are Lorentzian fits. Statistical error bars on individual data points are smaller than markers.
To measure Δ5 and \(\delta {\nu }_{133,138}^{614}\), the atom is Doppler cooled and shelved to the 2D5/2 state via one of the 2P3/2 hyperfine manifolds. The \(\left|{}^{2}{\text{D}}_{5/2};F=2\right\rangle\) manifold is prepared via shelving on the \(\left|{}^{2}{\text{P}}_{3/2};F=1\right\rangle \leftrightarrow \left|{}^{2}{\text{S}}_{1/2};F=1\right\rangle\) transition, as dipole selection rules forbid decay to the \(\left|{}^{2}{\text{D}}_{5/2};F=3\right\rangle\) state. Similarly, the \(\left|{}^{2}{\text{D}}_{5/2};F=3\right\rangle\) manifold is prepared by shelving on the \(\left|{}^{2}{\text{P}}_{3/2};F=2\right\rangle \leftrightarrow \left|{}^{2}{\text{S}}_{1/2},F=1\right\rangle\) transition, where 0.93 of decays to the 2D5/2 are to the \(\left|{}^{2}{\text{D}}_{5/2};F=3\right\rangle\) manifold. Next, a tunable laser near 614 nm is applied for 100 μs. When the frequency is near the \(\left|{}^{2}{\text{P}}_{3/2};F=2\right\rangle \leftrightarrow \left|{}^{2}{\text{D}}_{5/2};F=3\right\rangle\) or \(\left|{}^{2}{\text{P}}_{3/2};F=2\right\rangle \leftrightarrow \left|{}^{2}{\text{D}}_{5/2};F=2\right\rangle\) transition, spontaneous emission from the 2P3/2 state quickly deshelves the ion to the \(\left|{}^{2}{\text{S}}_{1/2};F=1\right\rangle\) and 2D3/2 states. This deshelved population is then detected via Doppler cooling. This sequence is repeated 200 times per laser frequency, and the average population is shown Fig. 3b as a function of frequency. From these data, we find the 2D5/2 hyperfine splitting Δ5 = 83(20) MHz, and isotope shift \(\delta {\nu }_{133,138}^{614}\) = +216(28) MHz.
High-fidelity SPAM
With the required spectroscopy known, we can calculate the expected fidelity of optically pumped electron shelving detection of the hyperfine qubit as follows. For SPAM of the \(\left|1\right\rangle\) state, the initial state is prepared as described above, followed by illumination with a laser resonant with the \(\left|{}^{2}{\text{P}}_{3/2};F=2\right\rangle \leftrightarrow\)\(\left|{}^{2}{\text{S}}_{1/2};F=1\right\rangle\) transition (ν455) at an intensity below saturation (Fig. 1 and Methods). After excitation of the atom, the 2P3/2 state quickly (τ ≈ 10 ns) spontaneously decays to either the 2S1/2, 2D5/2, or 2D3/2 state. Dipole selection rules forbid decay to the \(\left|{}^{2}{\text{S}}_{1/2};F=0\right\rangle\) (\(\left|0\right\rangle\)) state, resulting in \({\mathcal{F}}=0.88\) shelving fidelity, limited by population stranded in the 2D3/2 states. To further increase the shelving fidelity, a 650 nm laser near resonant with the \(\left|{}^{2}{\text{P}}_{1/2};F=0\right\rangle \leftrightarrow\)\(\left|{}^{2}{\text{D}}_{3/2};F=1\right\rangle\) transition (\({\nu }_{650}^{\mathrm c}\)), and a laser near 585 nm (ν585) resonant with the \(\left|{}^{2}{\text{P}}_{3/2};F=2\right\rangle \leftrightarrow\)\(\left|{}^{2}{\text{D}}_{3/2};F=2\right\rangle\) transition can be applied at an intensity below saturation. The hyperfine structure of 133Ba+ allows for concurrent repumping of the 2D3/2 states (ν585 and \({\nu }_{650}^{\mathrm c}\)) with all polarization components during the application of ν455, simplifying the shelving sequence (see Supplementary Information) compared with other species7. Dipole selection rules forbid spontaneous emission to the \(\left|{}^{2}{\text{S}}_{1/2};F=0\right\rangle\) (\(\left|0\right\rangle\)) state resulting in a fidelity of \({\mathcal{F}}\approx 0.999\). This scheme is limited by off-resonant scatter of ν455 to the \(\left|{}^{2}{\text{P}}_{3/2};F=1\right\rangle\) state, where 0.44 of decays to the 2S1/2 are to the \(\left|{}^{2}{\text{S}}_{1/2};F=0\right\rangle\). If ν455 is linearly polarized parallel to the magnetic field direction (π-light), dipole selection rules forbid excitation from the \(\left|{}^{2}{\text{P}}_{3/2};F=1;{m}_{F}=0\right\rangle \leftrightarrow\)\(\left|{}^{2}{\text{S}}_{1/2};F=1;{m}_{F}=0\right\rangle\) for the first scattered photon, and the expected fidelity increases to \({\mathcal{F}}=0.9998\).
For SPAM of the \(\left|0\right\rangle\) state, initialization with optical pumping proceeds as described above. After preparation, the \(\left|1\right\rangle\) state is shelved as previously described, and the state is read out via Doppler cooling. During \(\left|1\right\rangle\) state shelving, off-resonant excitation to the \(\left|{}^{2}{\text{P}}_{3/2};F=1\right\rangle\) followed by spontaneous emission can shelve the ion to the 2D5/2state. This results in an expected SPAM fidelity of \({\mathcal{F}}=0.9998\).
To experimentally test these predictions, state preparation of each qubit state is applied to a single trapped 133Ba+ ion and read out using the highest fidelity optically pumped shelving scheme (see Methods for experimental parameters). Before each SPAM attempt, the Doppler cooling fluorescence is monitored to determine if an SPAM attempt can be made. If the count rate does not reach a predetermined threshold of 2σ below the Doppler cooling mean count rate, chosen before the experiment begins and constant for all SPAM measurements, the subsequent SPAM attempt is not included and deshelving and Doppler cooling are repeated until the threshold is met. Each qubit state is attempted in blocks of 200 consecutive trials, followed by the other qubit state, for a combined total of 313,792 trials. The number of photons detected after each experiment is plotted in Fig. 4, and a threshold at nth ≤ 12 photons maximally discriminates between \(\left|0\right\rangle\) and \(\left|1\right\rangle\) . The fraction of events in which an attempt to prepare the \(\left|0\right\rangle\) state was measured to be \(\left|1\right\rangle\) is \({\epsilon }_{\left|0\right\rangle }=1.9(4)\times 1{0}^{-4}\), while the fraction of experiments in which an attempt to prepare the \(\left|1\right\rangle\) state was measured to be \(\left|0\right\rangle\) is \({\epsilon }_{\left|1\right\rangle }=3.8(5)\times 1{0}^{-4}\). The average SPAM fidelity is \({\mathcal{F}}=1-\frac{1}{2}({\epsilon }_{\left|0\right\rangle }+{\epsilon }_{\left|1\right\rangle })=0.99971(3)\).
Detection of the \(\left|0\right\rangle\) (bright) states returns an average of 39 collected photons, while detection of the \(\left|1\right\rangle\) (dark) state returns an average of 1 collected photon. Using standard spin-1/2 techniques for \(\left|0\right\rangle\) state preparation28,29, a five π-pulse composite pulse sequence32 to prepare the \(\left|1\right\rangle\) state, and electron shelving for high-fidelity readout, we measure an average SPAM error of ϵ = 2.9(3) × 10−4.
Table 1 provides an error budget with estimates of the individual sources of error that comprise the observed infidelity. In addition to the previously discussed errors, we have experimentally determined several sources of infidelity. The CP Robust 180 sequence is found to have an error of ϵ = 9(1) × 10−5, determined by measuring the \(\left|1\right\rangle\) state SPAM infidelity as a function of the number of concatenated CP Robust 180 sequences. The state readout duration is determined by the need to statistically separate the \(\left|0\right\rangle\) and \(\left|1\right\rangle\) state photon distributions. Our limited numerical aperture requires detection for 4.5 ms, leading to an error due to spontaneous emission from the 2D5/2 state of \(1-\exp(\frac{4.5\times 1{0}^{-3}}{30})\approx 1.5\times 1{0}^{-4}\). This could be reduced with maximum likelihood methods36,37 or higher efficiency light collection33. Finally, the readout of the 2S1/2 manifold is limited by background gas collisions, characterized by the preparation and readout fidelities of the 2S1/2 and 2D5/2 manifolds in 138Ba+, for which we achieve \({\mathcal{F}}=0.99997(1)\).
It should be possible to further improve the fidelity to \({\mathcal{F}}\,>\,0.9999\). Errors due to \(\left|0\right\rangle\) → \(\left|1\right\rangle\) state transfer and spontaneous emission during readout could be reduced with higher fidelity population transfer and improved light collection efficiency7,33. The shelving fidelity could be improved using a pulsed shelving scheme37, or by addition of a 1762 nm transfer step before optical pumping (Fig. 1) in two ways. First, optical-frequency qubit manipulations have been demonstrated (in other species) with a π-pulse fidelity of \({\mathcal{F}}=0.99995\)4, suggesting that high-fidelity, unitary transfer to 2D5/2 may be possible. Second, even without the narrow-band laser used for coherent transfer on the electric quadrupole transition, a broad-band 1762 nm laser could be used to saturate the transition to achieve 50% population transfer. Performing these operations to each of the ten available Zeeman sublevels will transfer the majority of the population to the 2D5/2 state. If either method via 1762 nm is followed with the optically pumped shelving scheme, we expect a shelving infidelity below 10−6.
Discussion
In summary, we report measurements in 133Ba+ of the 2P3/2 and 2D5/2 hyperfine splittings and 2P3/2 ↔ 2S1/2 and 2P3/2 ↔ 2D5/2 transition frequencies, which are required for high-fidelity state readout and optical qubit manipulations. Using these measurements, we have demonstrated operation of the 133Ba+ hyperfine qubit, including use of the CP Robust 180 composite pulse sequence, to realize an average single-shot SPAM error of ϵs = 2.9(3) × 10−4 via threshold discrimination. This represents a ≈2× reduction of SPAM error for any qubit7, and is sufficient for single-shot, projective readout of a register of ≈2000 individually resolved qubits.
Methods
We trap and laser cool 133Ba+ ions as described in ref. 26. 133Ba+ ions are loaded into a linear Paul trap (ωsec ≈ 2π × 100 kHz) by laser ablating an enriched BaCl2 salt (see Supplementary Notes) deposited on a platinum substrate. Laser cooling is accomplished using external cavity diode lasers (ECDLs) near 493 and 650 nm detuned approximately half an atomic linewidth from the resonant transitions (\({\nu }_{493}^{\mathrm c}\) and \({\nu }_{650}^{\mathrm c}\)) with saturation parameter s ≈ 10. Fiber electro-optic modulators (EOMs) are used to add repumping sidebands resonant with \({\nu }_{493}^{{\mathrm {sb}}}\), \({\nu }_{493}^{\mathrm {op}}\), and \({\nu }_{650}^{\mathrm {sb}}\) (Fig. 1). An applied magnetic field (B ≈ 5G) applied along a radial direction of the ion trap, with laser beams linearly polarized ≈45° from the magnetic field direction, are used to destabilize dark states that result from coherent population trapping (CPT)38.
State preparation of the \(\left|0\right\rangle\) state is accomplished by removing \({\nu }_{493}^{\mathrm {sb}}\) and adding \({\nu }_{493}^{\mathrm {op}}\) for 100 μs after Doppler cooling. The \(\left|1\right\rangle\) state is prepared via the CP Robust 180 sequence with approximately 3 W of microwave power directed with a microwave horn for ≈15 μs.
Electron shelving is accomplished by simultaneously applying three lasers near 455, 585, and 650 nm for 300 μs. The ECDL laser near 455 nm tuned resonant with the \(\left|{}^{2}{\text{P}}_{3/2};F=2\right\rangle \leftrightarrow\)\(\left|{}^{2}{\text{S}}_{1/2};F=1\right\rangle\) transition (ν455) is linearly polarized parallel to the magnetic field (π-light) with saturation parameter s ≈ 1 × 10−3. The ECDL near 1171 nm frequency doubled using a periodically poled lithium niobate (PPLN) waveguide is tuned resonant with \(\left|{}^{2}{\text{P}}_{3/2};F=2\right\rangle \leftrightarrow\)\(\left|{}^{2}{\text{D}}_{3/2};F=2\right\rangle\) transition (ν585). The laser is linearly polarized ≈45° from the magnetic field direction with saturation parameter s ≈ 1 × 10−2. The ECDL near 650 nm is tuned to the same parameters as Doppler cooling except for the reduction of saturation parameter to s ≈ 1. Deshelving of the 2D5/2 manifold back to the cooling cycle is accomplished with an ECDL near 1228 nm frequency doubled with a PPLN waveguide and linearly polarized ≈45° from the magnetic field direction. The frequency is red-detuned approximately 40 MHz from the \(\left|{}^{2}{\text{P}}_{3/2};F=2\right\rangle \leftrightarrow\)\(\left|{}^{2}{\text{D}}_{5/2};F=2\right\rangle\) transition and applied for 500 μs with saturation parameter s ≈ 1.
State detection is accomplished by collecting only 493 nm photons for 4.5 ms using a 0.28 NA commercial objective and photomultiplier tube with approximately 15% quantum efficiency. The 493 and 650 nm lasers have the same parameters as Doppler cooling during detection. The collection efficiency, laser parameters, 2P1/2 branching ratio of approximately 3:1, and CPT of the lambda cooling system result in a 493 nm photon count rate of approximately 10 kHz. Background counts of approximately 150 Hz are dominated by 493 nm laser scatter from the 493 nm Doppler cooling beam.
To measure the 2P3/2 hyperfine splitting and 2P3/2 ↔ 2S1/2 isotope shift, Doppler cooling followed by optical pumping with \({\nu }_{650}^{\mathrm c}\) and \({\nu }_{650}^{{\mathrm {sb}}}\) prepares the \(\left|{S}_{1/2};F=1\right\rangle\) manifold. A laser near 455 nm (ν455) is applied for 50 μs with saturation parameter s ≈ 1 × 10−3. Doppler cooling then determines population in the 2D5/2 states via fluorescence detection, followed by deshelving to reset the ion to the cooling cycle. The sequence is repeated 200 times per frequency, and the frequency scanned over the 2P3/2 hyperfine splitting. All lasers are linearly polarized ≈45° from the magnetic field direction.
To measure the 2D5/2 hyperfine splitting and 2P3/2 ↔ 2D5/2 isotope shift, the 2D5/2 F = 3 or F = 2 manifold is prepared by Doppler cooling and applying ν455. A laser near 614 nm (ν614) is applied for 100 μs with saturation parameter s ≈ 1. Doppler cooling then determines population in the 2D5/2 states via fluorescence detection, followed by deshelving to reset the ion to the cooling cycle. The sequence is repeated 200 times per frequency, and the frequency scanned between the \(\left|{P}_{3/2};F=2\right\rangle\) and 2D5/2 hyperfine splitting. All lasers are linearly polarized ≈45° from the magnetic field direction.
All lasers are stabilized via a software lock to a High Finesse WSU-2 wavemeter39. Reported hyperfine measurements (see Supplementary Information) include a systematic uncertainty of 20 MHz due to unresolved Zeeman structure. For isotope shifts, the relevant 133Ba+ centroid frequency is determined from the hyperfine splitting measurements and then compared to measurements of the corresponding 138Ba+ transition. All 133Ba+ and 138Ba+ measurements use the same experimental hardware and wavemeter. Reported isotope shifts include a 28 MHz systematic uncertainty due to wavemeter drift and unresolved Zeeman structure.
Data availability
Data are available upon request.
References
Steane, A. Quantum computing. Rep. Prog. Phys. 61, 117–173 (1998).
Preskill, J. Fault-Tolerant Quantum Computation. Introduction to Quantum computation and Information. 213–269 (1997).
Gottesman, D. An introduction to quantum error correction and fault-tolerant quantum computation. Quantum Information Science and Its Contributions to Mathematics, Proceedings of Symposia in Applied Mathematics. 68, 13–58 (2010).
Gaebler, J. P. et al. High-fidelity universal gate set for 9 Be+ ion qubits. Phys. Rev. Lett. 117, 060505 (2016).
Hume, D. B., Rosenband, T. & Wineland, D. J. High-fidelity adaptive qubit detection through repetitive quantum nondemolition measurements. Phys. Rev. Lett. 99, 120502 (2007).
Jeffrey, E. et al. Fast accurate state measurement with superconducting qubits. Phys. Rev. Lett. 112, 190504 (2014).
Harty, T. P. et al. High-fidelity preparation, gates, memory, and readout of a trapped-ion quantum bit. Phys. Rev. Lett. 113, 220501 (2014).
Ballance, C. J., Harty, T. P., Linke, N. M., Sepiol, M. A. & Lucas, D. M. High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett. 117, 060504 (2016).
Bermudez, A. et al. Assessing the progress of trapped-ion processors towards fault-tolerant quantum computation. Phys. Rev. X 7, 041061 (2017).
Erhard, A. et al. Characterizing large-scale quantum computers via cycle benchmarking. Nat. Commun. 10, 5347 (2019).
Wu, T., Kumar, A., Giraldo, F. & Weiss, D. S. Stern-gerlach detection of neutral-atom qubits in a state-dependent optical lattice. Nat. Phys. 15, 538–542 (2019).
Crain, Sea High-speed low-crosstalk detection of a 171yb+ qubit using superconducting nanowire single photon detectors. Commun. Phys. 2, 97 (2019).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Wright, K. et al. Benchmarking an 11-qubit quantum computer. Nat. Commun. 10, 5464 (2019).
Friis, N. et al. Observation of entangled states of a fully controlled 20-qubit system. Phys. Rev. X 8, 021012 (2018).
Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63 (2016).
Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).
Nam, Y. et al. Ground-state energy estimation of the water molecule on a trapped ion quantum computer. Preprint at https://arxiv.org/abs/1902.10171 (2019).
Zhang, J. et al. Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator. Nature 543, 217 (2017).
Hempel, C. et al. Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X 8, 031022 (2018).
Gorman, D. J. et al. Engineering vibrationally assisted energy transfer in a trapped-ion quantum simulator. Phys. Rev. X 8, 011038 (2018).
Landsman, K. A. et al. Verified quantum information scrambling. Nature 567, 61–65 (2019).
Hucul, D. et al. Modular entanglement of atomic qubits using photons and phonons. Nat. Phys. 11, 37 (2015).
Kokail, C. et al. Self-verifying variational quantum simulation of lattice models. Nature 569, 355–360 (2019).
Shen, C. & Duan, L.-M. Correcting detection errors in quantum state engineering through data processing. N. J. Phys. 14, 053053 (2012).
Hucul, D., Christensen, J. E., Hudson, E. R. & Campbell, W. C. Spectroscopy of a synthetic trapped ion qubit. Phys. Rev. Lett. 119, 100501 (2017).
Wang, Y. et al. Single-qubit quantum memory exceeding ten-minute coherence time. Nat. Photon. 11, 646–650 (2017).
Olmschenk, S. et al. Manipulation and detection of a trapped yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Acton, M. et al. Near-perfect simultaneous measurement of a qubit register. Quantum Inf. Comp. 6, 465 (2006).
Knab, H., Schupp, M. & Werth, G. Precision spectroscopy on trapped radioactive ions: ground-state hyperfine splittings of 133 ba+ and 131 ba+. Europhys. Lett. 4, 1361 (1987).
Pruttivarasin, T. & Katori, H. Compact field programmable gate array-based pulse-sequencer and radio-frequency generator for experiments with trapped atoms. Rev. Sci. Instrum. 86, 115106 (2015).
Ryan, C. A., Hodges, J. S. & Cory, D. G. Robust decoupling techniques to extend quantum coherence in diamond. Phys. Rev. Lett. 105, 200402 (2010).
Noek, R. et al. High speed, high fidelity detection of an atomic hyperfine qubit. Opt. Lett. 38, 4735–4738 (2013).
Dehmelt, H. G. Bull. Am. Phys. Soc. 20, 60 (1975).
Dutta, T., De Munshi, D., Yum, D., Rebhi, R. & Mukherjee, M. An exacting transition probability measurement—a direct test of atomic many-body theories. Sci. Rep. 6, 29772 (2016).
Langer, C. High-Fidelity Quantum Information Processing with Trapped Ions. Ph.D. Thesis, University of Colorado, Boulder (2006).
Myerson, A. H. et al. High-fidelity readout of trapped-ion qubits. Phys. Rev. Lett. 100, 200502 (2008).
Berkeland, D. J. & Boshier, M. G. Destabilization of dark states and optical spectroscopy in zeeman-degenerate atomic systems. Phys. Rev. A 65, 033413 (2002).
High Finesse. WS Ultimate 2 User Manual (High Finesse, 2014).
Höhle, C., Hühnermann, H., Meier, T., Ihle, H. & Wagner, R. Nuclear moments and optical isotope shift of radioactive 133ba. Phys. Lett. B 62, 390–392 (1976).
Acknowledgements
This work was supported by the US Army Research Office under award W911NF-18-1-0097. We thank Anthony Ransford, Christian Schneider, Conrad Roman and Paul Hamilton for helpful discussions. We thank Peter Yu for technical assistance. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the AFRL.
Author information
Authors and Affiliations
Contributions
J.E.C. and D.H. conducted the experiment. J.E.C., D.H., W.C.C., and E.R.H. analyzed the results. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Christensen, J.E., Hucul, D., Campbell, W.C. et al. High-fidelity manipulation of a qubit enabled by a manufactured nucleus. npj Quantum Inf 6, 35 (2020). https://doi.org/10.1038/s41534-020-0265-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-0265-5
This article is cited by
-
Seeking a quantum advantage with trapped-ion quantum simulations of condensed-phase chemical dynamics
Nature Reviews Chemistry (2024)
-
Realization of a crosstalk-avoided quantum network node using dual-type qubits of the same ion species
Nature Communications (2024)
-
Entangling gates for trapped-ion quantum computation and quantum simulation
Journal of the Korean Physical Society (2023)
-
Resonant and non-resonant optimizations by multi-constraint quantum control theory in molecular rotational states
Scientific Reports (2022)
-
Realizing coherently convertible dual-type qubits with the same ion species
Nature Physics (2022)