Introduction

Quantum Fourier Transform (QFT) is one of the most important operations in quantum computing. It can extract the periodicity encoded in the amplitudes of a quantum state, which is employed by an efficient algorithm for integer number factoring, widely known as Shor’s algorithm1. Shor’s integer factoring algorithm can be generalized (while still relying on the QFT) into a polynomial-time algorithm for the discrete logarithm problem over Abelian groups1. The importance of the above is witnessed through the threat such algorithms pose to modern public-key cryptosystems, such as the RSA or the ECC. Using the QFT as a subroutine, the eigenphase of a black-box unitary can be estimated up to an arbitrary precision2, which may be used to estimate quantum amplitudes3,4, simulate quantum chemistry/dynamics5, find the ground state/energy of a Hamiltonian6, compute Hessian to optimize molecular geometry7, exponentiate unitaries8, construct fractional powers of the QFT using constantly many copies of the controlled-QFT8,9, extract features of the solution of linear systems10, and more. QFT has also been used in quantum arithmetics11,12 and quantum cryptography13.

QFT can be implemented approximately by removing all rotation gates with angles smaller than a certain threshold value, resulting in the Approximate QFT (AQFT). In practice, it was shown that it suffices to apply AQFT with ~5.3 × 104 controlled rotation gates to factor 2048-digit numbers (reflecting the de facto key size for today’s standard14) with a high expected algorithmic accuracy (≳99.992%)15. AQFT has been studied extensively in the literature. The robustness of the quantum computer equipped with the AQFT was investigated in detail16,17,18,19,20. A study of the optimal level of the approximation of the AQFT in the presence of certain errors may be found in ref. 21. Implementation of the QFT and its approximate version over restricted architectures was addressed in refs 22,23. An efficient approximate implementation of the AQFT that harnesses certain quantum hardware features was also investigated24.

Quantum information is fragile, and it is generally accepted that the implementation of large quantum algorithms must rely on the fault-tolerant computations. Fault tolerance suppresses the errors at the cost of using multiple physical qubits to encode a single logical qubit. Fault-tolerant computations must furthermore rely on a quantum gate library consisting of those gates that are constructible fault tolerantly. A standard choice for such a computationally universal gate library is Clifford+T. Within known fault tolerance approaches, Clifford gates can generally be implemented with the relative ease, frequently transversally. On the other hand, a non-Clifford gate typically does not admit such an implementation; for instance, a T gate may be implemented fault tolerantly by distilling a certain quantum state and then teleporting it into the gate25. A T gate is indeed far more costly than any of the Clifford gates, and therefore efficient fault-tolerant circuits must minimize the T-count.

To implement an n-qubit AQFT to within a certain fixed error fault-tolerantly, the standard approach is to approximate the desired transformation by removing small-angle controlled rotations to bring down the gate count from O(n2) [ref. 26, page 219] to \(O\left(n\ {\mathrm{log}}\,(n)\right)\), and then replace the remaining \(O(n\ {\mathrm{log}}\,(n))\) controlled rotations with their Clifford+T implementations. The resulting circuit has the T-count of \(O(n\,{\mathrm{log}\,}^{2}(n))\). Only in the special case of the semiclassical version of AQFT27, where the AQFT transform is followed by the measurement, the T-count of \(O(n\ \,{\mathrm{log}}\,(n))\) implementation is known28. In contrast, in this paper, we focus on the fully coherent AQFT.

We develop a more efficient implementation with the T-count complexity of \(O(n \,{\mathrm{log}}\,({\it{n}}))\) for the general case of fully coherent AQFT, improving over the standard construction by a factor of \(O({\mathrm{log}}\,({\it{n}}))\). Including the dependence on the approximating error ε results in the reduction of complexity from \(O(n\,{\mathrm{log}}\,(n/\varepsilon ){\mathrm{log}}\,(\frac{n\ {\mathrm{log}}\,(n/\varepsilon )}{\varepsilon }))\), assuming the error budget is split equally between the approximation of the QFT itself and the approximation by Clifford+T library, and evenly across gates needing the decomposition into Clifford+T, to \(O(n\ {\mathrm{log}}\,(n/\varepsilon )+{\mathrm{log}}\,(n/\varepsilon ){\mathrm{log}}\,(\frac{{\log}(n/\varepsilon)}{\varepsilon }))\). We drop the dependence on ε in most discussions to improve the readability. Our results show that, in general and regardless of the amenability to the semiclassical approach, the AQFT may be implemented with \(O(n\, {\mathrm{log}}\,(n))\) T gates. This allows for the efficient implementation of the AQFT in any quantum algorithm, including those that use the AQFT as subroutines in the midst of the quantum computation5,7,10,12,13. Since our implementation is more involved compared to the standard, we also make a separate effort to show that the constant factor and small-order additive terms missing in the asymptotic analyses but otherwise present in our construction do not prevent it from achieving a significant practical advantage.

Results and discussion

We start with a high-level description of our result, and delay the detailed discussion of algorithmic advantages and further low-level optimizations offered by the final circuits to the following subsections.

The entry point for our construction is the standard textbook implementation of the QFT circuit [ref. 26, page 219] using O(n2) parametrized controlled-Za rotations, where a ∈ {1∕2, 1∕4, . . ., 1∕2n−1}, and n Hadamard gates. Recall that the AQFT may be obtained from the textbook circuit by simply discarding the rotations with parameter a below a certain threshold, keeping only b controlled rotations per layer, with parameter b scaling logarithmically with n (see Fig. 1 for an illustration). A standard fault-tolerant implementation of AQFT with \(\sim \!n\ {\mathrm{log}}\,(n)\) (removing lower order terms, and for simplicity furthermore assuming n stages of \({\mathrm{log}}\,(n)\) gates) parametrized controlled rotations, choosing \(b={\mathrm{log}}\,(n)\) for simplicity and to remove the dependence on the approximation error, uses \(\sim \!24n\ {\mathrm{log}\,}^{2}(n)\) T gates since 8 T gates are employed to map controlled rotations into uncontrolled ones [ref. 30, Fig. 10], and \(\sim \!3\,{\mathrm{log}}\,(n)\) T gates are needed to approximate the uncontrolled rotations35.

Fig. 1: AQFT with n = 6 and b = 3.
figure 1

Note that each of the n − 1 sets of controlled-za gates are separated by the H gates.

Full size image

We optimize the above implementation by first noting that mapping controlled rotations into uncontrolled ones may be done using only 4 T gates. This reduces the T gate count to \(\sim\!\! 12n\ {\mathrm{log}\,}^{2}(n)\). We next notice that the uncontrolled rotations come in layers, and thus can be induced via adder, given access to a \({\mathrm{log}}\,(n)\)-qubit gradient state32. Using an efficient b-bit integer adder31 with ~4b T gates allows to reduce the T gate requirement from \(\sim\!\! 12n\ {\mathrm{log}\,}^{2}(n)\) to \(\sim \!\!8n\ {\mathrm{log}}\,(n)+{3}\,{\mathrm{log}\,}^{2}(n)\), where 8 = 4 + 4 T gates are employed to remove the control (4 T gates) and integer-add the target (4 T gates) per each controlled rotation, and \(3\,{\mathrm{log}}\,(n)\) T gates35 are used on each of \({\mathrm{log}}\,(n)\) qubits to synthesize the \({\mathrm{log}}\,(n)\)-qubit gradient state, that is then reused. This is the most significant reduction giving improvements in both asymptotic analysis and gate counts. We next apply RUS circuits to reduce the cost of state generation by a factor of about 2.533, leading to \(\sim \!\!8n\ {\mathrm{log}}\,(n)+{1.2}\,{\mathrm{log}}^{2}({\it{n}})\) T gates and find local optimizations worth of ~8n T gates further bringing down the T gate cost to the final figure of \(\sim \!\!8n({\mathrm{log}}\,({\it{n}})-2)+{1.2}\,{\mathrm{log}\,}^{2}({\it{n}})\), compared to the original \(\sim \!\!24n\ {\mathrm{log}\,}^{2}(n)\).

Details of the construction

We start with an n-qubit AQFT whose construction relies on O(nb) controlled-Za gates with

$${{\rm{Z}}}^{a}:=\left[\begin{array}{ll}1&0\\ 0&{e}^{i\pi a}\end{array}\right],$$

where a ∈ {1∕2, 1∕4, . . ., 1∕2b}, for \(b:=\lceil {\mathrm{log}}\,{\it{n}}\rceil\), and n Hadamard (H) gates (see Fig. 1 for an illustration with n = 6 and b = 3). Such a choice of b implies a very specific approximation error ε, whose analysis will be detailed in the next section. We unite the individual controlled rotations into n − 1 sets separated by the H gates, such as illustrated in Fig. 1.

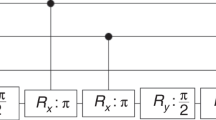
To implement a given controlled-Za rotation, we map its real-valued degree of freedom into that of the uncontrolled power of Pauli-Z, such as shown in Fig. 2. This implementation was developed by combining Kitaev’s trick2 with Toffoli-measurement construction of Jones 29 with our own choice of the relative the phase Toffoli gate, and custom circuit simplifications. Our circuit improves over the one reported in [ref. 30, Fig. 10] (note that the middle T gate in [ref. 30, Fig. 10] can be replaced with the Za gate) by 4 T gates (8 ↦ 4), 9 CNOT gates (12 ↦ 3), 1 H gate (4 ↦ 3), and 1 Phase (P) gate (2 ↦ 1) at the cost of introducing 1 measurement and 1 classically-controlled controlled-Z operation. Note that the fault-tolerant cost of those operations introduced is significantly lower than that of a single T gate, as the construction of the T gate itself requires both a measurement and a classically controlled quantum correction25.

Fig. 2: Ancilla-aided, measurement/feedforward-based fault-tolerant controlled-Za gate.
figure 2

This construction improves on the known state-of-the-art in the quantum resource requirement (see main text for detail), while enabling to decouple the control from the target, important for further optimization.

Full size image

We now group the uncontrolled Za rotations into one layer (time slice), as shown in Fig. 3. This layer applies the transformation that was coined the phase gradient operation in31, the induction of which by the addition circuit was first reported in ref. 32. Such a transformation can be implemented by a b-bit adder at the cost of 4b + O(1) T gates31, so long as one has access to a special quantum state \(\left|{\psi }_{b+1}\right\rangle :=\frac{1}{\sqrt{{2}^{b+1}}}{\sum }_{j = 0}^{{2}^{b+1}-1}{e}^{-2\pi ij/{2}^{b+1}}\left|j\right\rangle\). The quantum state \(\left|{\psi }_{b+1}\right\rangle\) can be reused to induce phase gradient transformations in all n − 1 sets of controlled-Za rotations. A schematic circuit diagram of our AQFT implementation is shown in Fig. 4.

Fig. 3: A 4-qubit example of the layer of controlled-za gates.
figure 3

The uncontrolled rotations are grouped together to induce the phase gradient operation31,32.

Full size image
Fig. 4: A schematic diagram of the full implementation of the fault-tolerant AQFT.
figure 4

ψ denotes the preparation of the special state \(\left|{\psi }_{b+1}\right\rangle\). Ui illustrate the operations that precede the ith adder, including H gates and the relative phase Toffoli gates used to map controlled-Za into uncontrolled Za rotations. \({U}_{i}^{\prime}\) denotes the operations that follow the adder up to the in-circuit measurements. ADDERi denotes the ith adder. \({U}_{i}^{^{\prime\prime} }\) are the classically controlled controlled-Z gates, applied at the ith step.

Full size image

To construct the special (b + 1)-qubit state \(\left|{\psi }_{b+1}\right\rangle\), we first apply H gates to the quantum register \(\left|00...0\right\rangle\) and then exercise the gates Z, Z−1∕2, …, Z\(^{-1/{2}^{b}}\). The latter step is accomplished via approximating each Za by RUS circuits33. Specifically, we approximate complex number eiπa by z*∕z, where \(z\in {\mathbb{Z}}[\omega ]\) with ω := eiπ∕4 being the cyclotomic integer obtained from the PSLQ Algorithm34. We choose \(r\in {\mathbb{Z}}[\sqrt{2}]\) randomly and search the solution \(y\in {\mathbb{Z}}[\omega ]\) of the norm equation ∣y∣2 = 2L − ∣rz∣2 with \(L=\lceil \mathrm{log}\,(| rz{| }^{2})\rceil\)35, such that \(V:=\frac{1}{{\sqrt{2}}^{L}}(\begin{array}{ll}rz&y\\ -{y}^{* }&r{z}^{* }\end{array})\) is a unitary. We exactly synthesize the two-qubit gate \((\begin{array}{ll}V&0\\ 0&{V}^{\dagger }\end{array})\)into a Clifford+T circuit33,36. Upon measuring the second qubit and obtaining 0, the gate Za is successfully implemented. Otherwise, a Z error takes place and can be reversed at zero cost in the T gate count. The expected number of repetitions until success is 2L∕∣rz∣2. We resorted to using this more complex algorithm as opposed to the simpler one given by refs 35,36, as we already use quantum circuits with measurements and feedforward elsewhere in our constructions, and the RUS approach results in about 2.5-fold improvement33 in the number of the T gates required to obtain the desired Za.

Local optimization

Here we describe a local optimization of the AQFT circuit developed above, exploiting the fact that controlled-P and controlled-T gates have a special implementation, due to both P and T gates being a part of the Clifford+T library.

We start by noting that the controlled-P gate may be implemented by two CNOT gates and three T gates (including inverses) as shown in Fig. 5. We know from our construction above that each controlled-Za gate in the AQFT is implemented using 8 T gates (of which 4 are used to remove the control, and 4 to implement the target via the adder). Therefore, instead of relying on inducing the gradient operation through the adder, we implement controlled-P gates directly, according to Fig. 5.

Fig. 5: Direct implementation of the controlled-P gate.
figure 5

These constructions also work when all Z-axis gates are replaced by their complex conjugates.

Full size image

Next, we consider controlled-T gates. As per Fig. 1, we see that each controlled-T gate in the AQFT neighbors a controlled-P gate in the following layer of controlled-Za gates in the target qubit line. Since we implement controlled-P gates according to Fig. 5, we may obtain T-count savings via gate cancellation (TT† = Id) by rewriting the controlled-T gate as the controlled-Z3∕4 gate followed by the controlled-Z−1∕2, where the controlled-Z−1∕2 gate is implemented according to Fig. 5, inducing T-count reduction by 2 on the ‘target’ of controlled-Z−1∕2 and controlled-T gates, and by another 2 for each layer of controlled-Za gates by cancellations on the ‘control’ line, and the controlled-Z3∕4 gate is implemented directly as per the top panel of Fig. 2, which costs 5 T gates.

Altogether, the above implementation of the controlled-T and controlled-P gate pair requires 7(= 5 + 3 + 3 − 2 − 2) T gates. This is in comparison to 16 T gates that would otherwise have been used by the implementation based on the adder. What remains to be investigated at this point is the modification that needs to be made to the gradient operation so as to induce a partial gradient operation, i.e., \(\left|k\right\rangle \left|{\psi }_{d+1,b+1}\right\rangle\, \mapsto \,{e}^{2\pi ik/{2}^{b+1}}\left|k\right\rangle \left|{\psi }_{d+1,b+1}\right\rangle\), where k < 2b−d, d ≤ b, and \(\left|{\psi }_{d+1,b+1}\right\rangle\) is the state \(\left|{\psi }_{b+1}\right\rangle\) without first d + 1 qubits, to implement the remaining Za gates in a layer.

To obtain the partial gradient operation, we analyze how the gradient operation works. Firstly, we formally define the state \(\left|{\psi }_{d+1,b+1}\right\rangle :=\frac{1}{\sqrt{{2}^{b-d}}}{\sum }_{j = 0}^{{2}^{b-d}-1}{e}^{-2\pi ij/{2}^{b+1}}\left|j\right\rangle\). The application of (b − d)-bit addition (see ref. 31) to \(\left|k\right\rangle \left|{\psi }_{d+1,b+1}\right\rangle\) results in two cases: k + j < 2b−d and k + j ≥ 2b−d. In order for the partial gradient operation to work, we need k + j ↦ k + j mod2b−d. This may be achieved by applying Z\(^{1/{2}^{d}}\) gate to the most significant bit of the modular addition circuit. Since in our case d = 2, this amounts to applying a T gate for each gradient operation. This means that the overall result of our optimization detailed in this section is by about 8(n − 2) T gates.

Comparisons to prior work

Our improved implementation of AQFTn with n > b > 2 requires the qubit count of nq = n + 3b − 4, the CNOT-gate count of \(7.5n\ -\ 13+{\sum }_{l = 3}^{n-1}\) (\(16\min\)(b − 2, l − 2) − 5)\(\,+\,{\sum }_{b^{\prime} = 3}^{\min (b,n-1)}{C}_{{\rm{CNOT}}}({{\rm{RUS}}}_{b^{\prime} })/{p}_{b^{\prime} }\), and the T-count of \(7n-11+{\sum }_{l = 3}^{n-1}(8\min (b-2,l-2)+1)+{\sum }_{b^{\prime} = 3}^{\min (b,n-1)}{C}_{{\rm{T}}}({{\rm{RUS}}}_{b^{\prime} })/{p}_{b^{\prime} }\), where \({C}_{g}({{\rm{RUS}}}_{b^{\prime} })\) denotes the count of the fault-tolerant gate g in the RUS circuit synthesizing \({z}^{-1/{2}^{b^{\prime} }}\), and \({p}_{b^{\prime} }\) denotes the success probability of the RUS circuit. As follows from our constructions, the T gate count can be fairly accurately approximated by the simple formula 8n(b − 1). This may be compared to the previous state of the art that uses a variant of [ref. 30, Fig. 10] to implement the controlled-Za, which requires nq = n + 1 qubits, the CNOT gate count of \(12\cdot {\sum }_{l = 0}^{n-1}\min (b,l)\), and the T-count of \(3(n-1)+{\sum }_{b^{\prime} = 2}^{\min (b,n-1)}(n-b^{\prime} )[{C}_{{\rm{T}}}({{\rm{Gridsynth}}}_{b^{\prime} })+8]\), where CT(Gridsynth) is the T-count of the Gridsynth algorithm 35 synthesizing \({z}^{1/{2}^{b^{\prime} }}\) and CT = 1 when considering z±1∕4 gate.

For a concrete comparison with the previous state of the art30,37 at the gate-by-gate level, we implemented our improved fault-tolerant construction as described in Section II B in software. We synthesized the RUS circuits for za gates with a ∈ { − 1∕23, − 1∕24, . . ., − 1∕213}, motivating the choice of the smallest angle π∕2b by that sufficient to launch a quantum attack on the classically-infeasible instance of the integer factoring problem corresponding to cracking the RSA-2048. We also chose the overall fault-tolerance error that arises from the gate synthesis to be below 1.1 × 10−4 for all sizes of the AQFT (n ≤ 4096 and b = 13) we considered. In particular, we chose the error 10−5 per za gate approximation for our improved construction. This amounts to the gate-synthesis error budget of ~10−5∕n per rotation for the previous state-of-the-art AQFT circuit. The improvement of the accuracy per Za gate is justified by the fact that our implementation of the AQFT requires the approximation of only O(b) rotations instead of O(nb) in the previous constructions.

Summary of the resulting quantum resource cost of our improved AQFT implementation is shown in Table 1. We included a comparison of the gate costs of our implementation to those circuits known previously: first set relying on [ref. 30, Fig. 10] to implement controlled-Za gates in the AQFT and the second set resulting from an automated AQFT circuit optimization37. For both implementations, we used Gridsynth algorithm35 to synthesize Za gates. Note that our implementation carries a significant practical advantage, saving quantum resource cost in the form of the T-count by a factor of as large as 12 (AQFT4096 with b = 13). The slight increase in nq and the CNOT gate counts are completely offset by the savings in the T-count in the fault-tolerant regime.

Table 1 Quantum resource counts for implementing an n-qubit AQFT with b = 13. nq denotes the number of qubits required to execute the corresponding circuit. Columns CNOT and T report the number of respective gates in the circuits. All circuits are available in ref. 38.
Full size table

Complexity analysis

The total T-count in our AQFT circuit is \(8n(b-1)+O(b\,{\mathrm{log}}\,({\it{b}}/\varepsilon ))\). This is because each of the nb − b(b + 1)∕2 = nb + O(b2) controlled-Za gates consumes 4 T gates to be first mapped into an uncontrolled Za and another 4 T gates for the Za to be implemented as a part of the adder circuit, except for controlled-Z1∕2 and controlled-Z1∕4 gates; the two require 7 T gates to implement and 1 T gate to correct for the phase in the partial gradient operation. The construction of the special state \(\left|{\psi }_{d+1,b+1}\right\rangle\) requires implementation of O(b) Za rotations, and we approximate each rotation with \(O({\mathrm{log}}\,({\it{b}}/\varepsilon ))\) T gates33 to achieve accuracy ε∕b per rotation.

There are two sources of approximation errors in our construction. Our circuit differs from the ideal AQFT circuit only in the preparation of the special state \(\left|{\psi }_{d+1,b+1}\right\rangle\). Therefore, the spectral norm distance between our AQFT circuit and the ideal AQFT is O(b ⋅ ε∕b) = O(ε). This ensures that, with 1 − O(ε2) probability, regardless of how many operations to follow from the \(\left|{\psi }_{d+1,b+1}\right\rangle\) state preparation stage, our circuit implements the ideal AQFT. If we choose \(b=O({\mathrm{log}}\,({\it{n}}/\varepsilon ))\), the spectral norm error of the ideal AQFT circuit will be O(ε). Due to the triangle inequality, the total error can be upper bounded by adding the error of the Clifford+T synthesis and the error of AQFT, which is still O(ε).

The above error analysis shows that for all effective purposes (specifically, when ε ≻ n∕2n) we can drop the dependence on the approximation error ε, resulting in the claimed T-count of \(O(n\,{\mathrm{log}}\,{\it{n}})\).

Future work

Future lines of inquiry may include laying out our circuit in restricted architectures and the optimization of depth. To address former, both the basic QFT22,23 and the adder31 we rely on (being the long adder) can be laid out in the Linear Nearest Neighbor architecture with a constant SWAP overhead. Thus, the increase in the CNOT gate count due to SWAP operations will remain under control, and the overall cost of the implementation is expected to continue being dominated by the cost of the T gates (note that the introduction of SWAP gates does not increase the number of T gates), although the cost of the CNOTS will start to matter more. To address depth, we first note that everything but the adder is already parallelized. To optimize depth, one may choose to rely on a fast logarithmic-depth adder and lay it out in 2D Square Lattice (a natural architecture for superconducting circuit quantum information processors) using the H-tree – an H-tree, popular in VLSI design, is a fractal tree, embedded in a 2D square lattice, constructed from a repeating pattern that resembles the letter H. This will introduce additional gates and require more space, but it may reduce the depth. Note that for small numbers such as those used in our result (b = 13) the H-tree remains compact and requires few SWAP operations.

Conclusion

Before our contribution, the best known coherent approximation of the n-qubit QFT to an error ε by a quantum fault-tolerant Clifford+T circuit featured the T-count of \(O(n\,{\mathrm{log}}\,(n/\varepsilon ){\mathrm{log}}\,(\frac{n\ {\mathrm{log}}\,(n/\varepsilon )}{\varepsilon }))\), with the term \(O(n\ {\mathrm{log}}\,({\it{n}}/\varepsilon ))\) originating from the standard AQFT construction using controlled rotations, and term \(O({\mathrm{log}}\,(\frac{\it{n}} {\mathrm{log}\,({\it{n}}/\varepsilon )}{\varepsilon }))\) coming from the fault-tolerance overhead. In this paper we reported an improved approximation of the QFT by a quantum Clifford+T circuit with the T-count of \(O(n\ {\mathrm{log}}\,({\it{n}}/\varepsilon )+{\mathrm{log}}\,({\it{n}}/\varepsilon ){\mathrm{log}}\,(\frac{\mathrm{log}\,({\it{n}}/\varepsilon )}{\varepsilon }))\). Our improvement is twofold: first, we reduce the dependence on n from \(O(n\ {\mathrm{log}\,}^{2}(n))\) to \(O(n\ {\mathrm{log}}\,({\it{n}}))\), and second, we moved the dependence on ε from the leading term into a lower order additive term. This means that the smaller the desired approximation error the more efficient our construction is compared to those known previously.

Our implementation includes constant factor improvements that are not captured by the asymptotics. We report significant practical advantages from applying our construction, as is evidenced by the numbers in Table 1, showing the improvement by a factor of 10 to 12 in the T-count for values of n of the size expected in practical applications of quantum computers. This shows that our result carries both theoretical and practical value.

Methods

Descriptions of the methods used to construct the AQFT circuit, the central result of our paper, are available in Section II. See Section II A for the detailed methods of the circuit construction. See Section II B for further circuit optimization methods used to improve the T-gate counts.