Feasibility of satellite-to-ground continuous-variable quantum key distribution

Abstract

Establishing secure communication links at a global scale is a major potential application of quantum information science but also extremely challenging for the underlying technology. Although milestone experiments using satellite-to-ground links and exploiting singe-photon encoding for implementing quantum key distribution have shown recently that this goal is achievable, it is still necessary to further investigate practical solutions compatible with classical optical communication systems. Here, we examine the feasibility of establishing secret keys in a satellite-to-ground downlink configuration using continuous-variable encoding, which can be implemented using standard telecommunication components certified for space environment and able to operate at high symbol rates. Considering a realistic channel model and state-of-the-art technology, and exploiting an orbit subdivision technique for mitigating fluctuations in the transmission efficiency, we find positive secret key rates for a low-Earth-orbit scenario, whereas finite-size effects can be a limiting factor for higher orbits. Our analysis determines regions of values for important experimental parameters where secret key exchange is possible and can be used as a guideline for experimental efforts in this direction.

Introduction

Quantum key distribution (QKD) exploits the fundamental principles of physics to exchange cryptographic keys between two parties. It can guarantee information-theoretic security, in the sense that the security of the protocol does not depend on the complexity of some mathematical problem and hence the computational power of a possible adversary does not have to be bounded. QKD represents today one of the most successful applications of quantum information^1,2.

The rapid evolution in QKD implementations has resulted in extending the communication range from few centimeters of the first test to several hundreds of kilometers obtained with modern technology^3,4,5,6. However, this evolution in ground-based implementations faces a fundamental limitation related to the attenuation of the quantum signal in optical fibers, which increases exponentially with the distance. With this scaling law, covering several thousands of kilometers, as required for the realization of an intercontinental QKD link, would be impossible even with the most advanced technology, if only repeaterless architectures are considered⁷. Quantum repeaters^8,9,10,11,12, whose functioning relies on entanglement distribution and in most cases on quantum memories, might solve the problem of extending the communication range. However, despite progress in the field^13,14, the technology is still far from being applicable to intercontinental quantum communication.

To overcome this limitation, a possible solution is the use of orbiting terminals to distribute cryptographic keys among ground stations. Studies investigating the feasibility of quantum communication using satellites have been ongoing for a decade^{15,16,17,18,19,20,21}, but a milestone was reached in 2017 with the first complete satellite-to-ground QKD implementations realized with the Chinese satellite Micius^22,23. Later the same year, QKD from satellite was also implemented by means of a small payload on-board of the Tiangong-2 space laboratory²⁴. Soon after these demonstrations, the Micius satellite was used for the realization of the first intercontinental quantum-secured communication²⁵, thus opening the era of satellite QKD.

Although these results represent a major step in the field, several issues still need to be addressed for the realization of a global QKD network based on satellite communication. In this framework, an important aspect is related to the development of high-performance space-qualified terminals that will allow for stable, high-throughput QKD links from a constellation of satellites to a network of ground stations. To this end, a possible breakthrough may come from the implementation of continuous-variable QKD protocols (CV-QKD)^26,27,28,29. These protocols have the main advantage of using standard telecommunication components, such as IQ or amplitude and phase modulators for state preparation and coherent receivers for state detection, thus allowing to exploit the heritage of classical optical communication both in terms of high-speed components and of their space qualification. The possibility of free-space and satellite CV-QKD has been investigated theoretically^30,31,32,33 and some preliminary experimental studies have been performed on signal transmission along free-space and satellite-to-ground links^34,35. Moreover, recent studies have summarized the main characteristics of a satellite-based CV-QKD link³⁶ and have provided the secret key rate for some specific scenarios, which however do not include crucial link aspects, such as beam divergence, satellite pointing error, satellite motion, and finite-size effects^37,38,39. Therefore, whether this technology can be used for secret key generation in a realistic satellite-based scenario remains an open question.

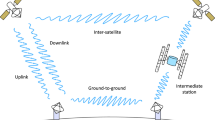
Here, we present a feasibility study of satellite-to-ground CV-QKD, taking into consideration state-of-the-art technology for the quantum state generation, transmission, and detection, a realistic channel model and various orbit configurations. Our analysis follows the trusted node approach, where the satellite establishes a separate QKD link with each ground station and hence has access to the keys^22,25, rather than the untrusted one, where entangled photons are provided by the satellite to the ground stations, which subsequently establish the secret key⁴⁰. Furthermore, we calculate the secret key rate in the downlink scenario, where the emitter is on the satellite and the receiver on the ground, as it is more favorable for the optical signal transmission. The receiver uses a coherent detector with a free running local oscillator (local LO) and reference symbols (pilots) are transmitted for phase recovery. A schematic diagram of the configuration we are considering is shown in Fig. 1.

Fig. 1: Schematic diagram of the CV-QKD communication scheme analyzed in this work.

A fixed ground station (Bob) follows the trajectory of a satellite (Alice), equipped with a tracking system, passing over its zenith point. An adaptive optics (AO) system is required in order to correct the wavefront distortions due to the atmosphere and maximize the signal to noise ratio at the receiver. The exact implementation of this system is beyond the scope of this work. The parameters θ_p, θ_d are explained in the text.

Adopting a technique based on orbit subdivision to mitigate the effects of transmission fluctuations, we find that continuous-variable technology is a viable option for satellite QKD on low-Earth orbits and identify experimental parameter regions that allow for secret key exchange. For higher orbits, the key generation is affected by finite-size effects due to the limited number of symbols exchanged in a single satellite pass for such high-loss channels. These may be mitigated by achieving higher transmission rates or by considering multiple satellite passes.

Results

In our study, we first provide a general model of the satellite-to-ground transmission channel, taking into account the beam propagation as well as the satellite orbit. We then examine the effect of channel fluctuations in CV-QKD and derive an equation for the secret key rate over generic fading channels. We subsequently use this equation for estimating the key rate in the case of downlink transmission, both in the asymptotic limit and considering finite-size effects.

Channel model

We start our analysis by investigating the statistical properties of the satellite-to-ground transmission channel, which are critical for the assessment of the possibility to establish a QKD link in this configuration. In the downlink scenario that we are considering here, the beam travels from the satellite to the ground station and undergoes the disturbance and loss effects owing to the atmosphere at the end of its path, resulting in a more favorable situation for key generation with respect to an uplink configuration⁴¹. Indeed, in downlink most of the beam propagation occurs in vacuum, where the beam maintains its diffraction limit properties, whereas the turbulent atmosphere is encountered only during the last ≃20 km of its path. On the contrary, for uplink the wavefront is distorted at the beginning of its path, resulting in a stronger impact on the beam propagation.

There are several disturbance effects that occur during beam propagation, which can be classified as systematic or of random nature.

The systematic effects are theoretically predictable physical processes that perturb and attenuate the signal, and they include the refraction of the beam in the different atmospheric layers and the extinction of light owing to absorption or scattering by air molecules or aerosols. The former is owing to the variation in the optical refractive index of the atmosphere as a function of altitude and it causes the light to deviate from a straight line, resulting in an elongation of its physical path. Reference⁴² provides a detailed calculation of the elongation factor—the ratio of the total length of the beam trajectory to the geometric path length—as a function of the apparent elevation angle of the satellite, i.e., the angle with respect to the horizon at which the satellite appears owing to refraction and which differs from the real elevation angle. In this work, we restrict our analysis to elevation angles above 20 degrees, where the elongation factor remains close to 1 and therefore this effect can be neglected (see Fig. 1). The latter effect, namely extinction owing to absorption and scattering, depends on the link length and on the molecule and aerosol distribution model⁴². It also strongly depends on the sky condition and the transmission wavelength. For elevation angles above 20 degrees, the atmospheric transmission efficiency τ_atm scales as:

$${\tau }_{{\rm{atm}}}={\tau }_{{\rm{zen}}}^{\sec ({\theta }_{{\rm{zen}}})},$$

(1)

where θ_zen is the zenith angle and τ_zen is the transmission efficiency at zenith⁴³. The estimation of the zenith transmission efficiency relies on the MODTRAN code⁴⁴, a widely used atmospheric transmittance and radiance simulator. Considering a 1550 nm wavelength, mid-latitude summer atmospheric model with visibility of 23 km (corresponding to clear sky condition), the MODTRAN web app calculator gives τ_zen = 0.91 for both rural and urban aerosol models⁴⁵. We remark that the main parameter that affects the transmission efficiency is the sky visibility; in particular, we find τ_zen = 0.85, 0.75, 0.53 for a 10, 5, 2 km visibility, respectively.

In addition to such systematic effects, random variations in the atmospheric temperature lead to fluctuations in the refractive index that have the statistical properties of turbulent scalar fields. The most important consequence of this atmospheric turbulence are intensity fluctuations (scintillation), beam wandering and beam broadening, which induce fading, namely fluctuations in the received optical power and hence in the transmissivity of the channel. The strength of these effects also depends on the altitude and hence on the elevation angle, as discussed in detail in ref. ⁴². The atmospheric turbulence is also responsible for the deformation of the beam profile. This is crucial, especially in the context of CV-QKD, where mode matching between the received signal and the phase reference (LO) is important for the coherent detection³⁵. To avoid mode mismatch, we assume the use of single-mode fibers as spatial-mode filters of the incoming beam, together with an advanced adaptive optics system⁴⁶ to improve the coupling efficiency of the incoming light into the single-mode fiber core. Acting as a spatial-mode filter, the coupling to a single-mode fiber removes components of the signal that would not interact with the LO and contribute to the detected signal. This filtering hence reduces the noise in the detection apparatus and also facilitates the use of components like integrated coherent receivers, which are typically available as commercial off-the-shelf and standardized devices. We remark that recent advances in this field have experimentally demonstrated a coupling efficiency in a single-mode fiber exceeding 50% for a large aperture telescope⁴⁷.

Besides turbulence effects, the beam propagation is affected by wandering owing to the pointing error of the satellite. This is characterized by the angle θ_p, which is defined as the standard deviation of the angle between the direction of the center of the beam and the imaginary line joining the emitter and receiver telescopes, so that in the case of no pointing error we would have θ_p = 0 μrad. A pointing error of the order of 1 μrad has been obtained in low-Earth-orbit (LEO) satellite-to-ground communication links²². This is used as a nominal value in our analysis. Similarly, the divergence of the beam is characterized by the angle θ_d, for which we use the nominal value of 10 μrad, which has been demonstrated with a 300 mm aperture telescope on-board of the Micius satellite.

We are now ready to analyze the statistical properties of our channel, which will be necessary for assessing the effect of fading on the CV-QKD link, under the above assumptions. To do this, we follow the approach of ref. ³⁰ and calculate the probability distribution of the transmission efficiency (PDTE), as it characterizes completely the statistics of the quantum channel for a given satellite orbit. Indeed, the transmission of coherent states of light through the atmosphere can be modeled by the input/output relation of the annihilation operators, ${\hat{a}}_{{\rm{out}}/{\rm{in}}}$. The transformation should preserve the commutation relation, so that we can write:

$${\hat{a}}_{{\rm{out}}}=T{\hat{a}}_{{\rm{in}}}+\sqrt{1-{T}^{2}}\hat{c},$$

(2)

where $\hat{c}$ are environmental modes and T is the transmission coefficient (with the transmission efficiency being τ = T²). Within this model, we can obtain the P-function characterizing the statistics of the quantum state; it is then possible to show that the PDTE is sufficient to characterize the state at the receiving telescope³⁰. In the following, we first calculate the probability distribution obtained at a fixed distance between the satellite and the ground station, and then we take into account the satellite’s orbit to compute the total probability distribution, i.e., the PDTE of the entire orbit.

We start by considering a fixed distance R between the satellite and the ground station. The overall transmission efficiency can be divided into a fixed and a time-varying term. We estimate the fixed attenuation term to be 3.8 dB, including 3 dB of losses for fiber coupling and an additional 0.8 dB for taking into account the fact that we are only considering the main peak of the Airy diffraction pattern. As discussed previously, the main dynamic effects affecting the transmission in our analysis are the pointing error of the satellite and the divergence of the beam, characterized by the angles θ_p and θ_d, respectively.

Following ref. ³⁰, to calculate the PDTE we first consider the deflection distance, r, and its standard deviation, σ_r. As shown in Fig. 2a, r is the instantaneous distance between the center of the receiving telescope and the center of the beam. Its standard deviation depends on the pointing and on the atmospheric turbulence as:

$${\sigma }_{{\rm{r}}}=\sqrt{{\left(R{\theta }_{{\rm{p}}}\right)}^{2}+{\sigma }_{{\rm{turb}}}^{2}}\simeq R{\theta }_{{\rm{p}}}.$$

(3)

Fig. 2: Channel characterization.

Example of the characterization of an atmospheric channel at a fixed satellite-to-ground slant distance of R = 400 km. The values for the variables are θ_p = 1 μrad, θ_d = 10 μrad, a = 0.75 m. a Schematic of the beam and receiver telescope aperture. b Transmission coefficient as a function of the deflection distance. c Probability distribution of the deflection distance. d Probability distribution of the transmission efficiency (PDTE).

In the weak turbulence regime, the variance of the beam center owing to turbulence is given by ${\sigma }_{{\rm{turb}}}^{2}\simeq 1.919\ {C}_{n}^{2}{z}^{3}{(2{W}_{0})}^{-1/3}$ and depends on the distance traveled by the beam in the atmosphere, z, and on the beam waist when entering the atmosphere, W₀. For stronger turbulence, this expression represents an upper bound, as ${\sigma }_{{\rm{turb}}}^{2}$ saturates and an increase of the path length or turbulence strength will not increase its value⁴⁸. The parameter ${C}_{n}^{2}$ is the refractive index structure parameter that characterizes the strength of the atmospheric turbulence. In case of moderate turbulence and considering a wavelength of 1550 nm, we have ${C}_{n}^{2}\simeq 1{0}^{-15}-1{0}^{-14}\,{{\rm{m}}}^{-2/3}$, which gives ${\sigma }_{{\rm{turb}}}^{2}$ ≲ $1{0}^{-4}\,{{\rm{m}}}^{2}\, << \,{(R{\theta }_{p})}^{2}\simeq 1{0}^{-1}\,{{\rm{m}}}^{2}$, corresponding to a pointing error of ≃ 1 μrad and a satellite altitude of 300 km. This justifies the approximation in the right hand side of Eq. (3) for all satellite altitudes above 300 km.

Under this approximation, the probability distribution of the deflection distance follows the Weibull distribution:

$$P(r;{\sigma }_{r})=\frac{r}{{\sigma }_{r}^{2}}\exp \left(-{\left(\frac{r}{\sqrt{2}{\sigma }_{r}}\right)}^{2}\right).$$

(4)

An example of this distribution is shown in Fig. 2c. Given now a distance r, the transmission coefficient can be obtained from geometrical considerations. An approximate but sufficiently accurate analytic relation between r and T can be calculated as³⁰:

$${T}^{2}(r)={T}_{0}^{2}\exp \left(-{\left(\frac{r}{S}\right)}^{\lambda }\right).$$

(5)

T₀ is the maximum transmission coefficient possible, and S and λ are the scale and shape parameters, respectively, given by:

$$S=a{\left[ln\left(\frac{2{T}_{0}^{2}}{1-exp[-4\frac{{a}^{2}}{{W}^{2}}]{I}_{0}(4\frac{{a}^{2}}{{W}^{2}})}\right)\right]}^{-(1/\lambda )},$$

(6)

$$\begin{array}{l}\lambda = 8\frac{{a}^{2}}{{W}^{2}}\frac{\exp [-4\frac{{a}^{2}}{{W}^{2}}]{I}_{1}\left(4\frac{{a}^{2}}{{W}^{2}}\right)}{1-\exp [-4\frac{{a}^{2}}{{W}^{2}}]{I}_{0}(4\frac{{a}^{2}}{{W}^{2}})}\\ \times {\left[ln\left(\frac{2{T}_{0}^{2}}{1-\exp [-4\frac{{a}^{2}}{{W}^{2}}]{I}_{0}\left(4\frac{{a}^{2}}{{W}^{2}}\right)}\right)\right]}^{-1},\end{array}$$

(7)

where I_n is the n-th order modified Bessel function.

All three are given functions of the beam waist on the ground, W = Rθ_d > 4 m for satellites above 400 km, and of the telescope aperture radius, a, here considered 0.75 m. Hence, we can write T₀ = T₀(W, a), λ = λ(W, a), and S = S(W, a). The relation between T and r/a for these values is shown in Fig. 2b.

We can then substitute Eq. (5) into Eq. (4) and use the chain rule to obtain the probability distribution of the transmission coefficient, PDTC. The PDTE is obtained from the PDTC using the chain rule with τ = T². Fig. 2d gives an example of the characterization of an atmospheric channel of fixed distance following our model for the same parameters as discussed above.

We now obtain the PDTE for the entire satellite pass. In our analysis, we consider circular orbits that are passing at the zenith of the ground station (which is assumed not to move during the pass). We can write the radius of such orbits as R_O = R_E + h_s, were R_E is the Earth’s radius and h_s the satellite’s altitude with respect to the ground. The angular velocity of the satellite is ${\omega }^{2}=G{M}_{{\rm{T}}}/{R}_{{\rm{O}}}^{3}$, where M_T is the Earth’s mass and G is the gravitational constant. The distance between the satellite and the ground station during the satellite’s visibility time, that we denote R(t), then reads:

$$R(t)=\sqrt{{R}_{{\rm{E}}}^{2}+{R}_{{\rm{O}}}^{2}-2{R}_{{\rm{E}}}{R}_{{\rm{O}}}\cos (\omega t)}.$$

(8)

We then proceed as follows:

• The orbit is divided into a set of points defined by the position of the satellite at a certain time, R(t_i) (i runs with the number of points), given by the orbital equation, Eq. (8).

• For each one of these points, both the PDTE(R(t_i)) and the time difference between consecutive points of the orbit, denoted Δt_i = t_i − t_i−1, are computed. The PDTE(R(t_i)) includes as a multiplicative factor the atmospheric transmission efficiency, Eq. (1), for the elevation angle corresponding to R(t_i). The value PDTE(R(t_i)) ⋅ Δt_i gives the distribution of the times with different transmission efficiencies inside the computed interval.

• Therefore, if we sum PDTE ⋅ Δt_i overall the points we obtain the final distribution for the time spent by the satellite with a certain transmission efficiency τ. Indeed, we are mimicking the integral over the flight time:

  $$\frac{1}{{\rm{FT}}}\sum \limits_{i}{\rm{PDTE}}(\tau ,R({t}_{i}))\Delta {t}_{i}\,\longrightarrow \,\frac{1}{{\rm{FT}}}\int \ {\rm{PDTE}}(\tau ,t){\rm{dt}},$$

  (9)

where the flight time, FT, is the normalization factor. Because we are considering circular orbits, we can label each orbit with its altitude, which is the minimum distance of the orbit, coinciding with the moment at which the satellite is exactly above the ground station. For such orbits and following the procedure described above, we show in Fig. 3 the PDTE for three different orbits of increasing altitude for a telescope with aperture radius a = 0.75 m. We remark that for higher orbits the variance of the distribution decreases. As described in the following, this fact has an impact on the noise introduced in time-varying channels.

Fig. 3: PDTE for three different orbits of increasing satellite altitude.

The values of the variables for each orbit are the same as in Fig. 2.

We note that the conclusions that we have drawn for the downlink characterization are in agreement with the recent analysis of ref. ⁴⁹. Interestingly however the authors there use the elliptical model rather than the circular one, which means that the ellipticity does not affect the probability distributions. For completeness, we also show in Fig. 4 the average attenuation encountered in a pass as a function of the satellite altitude.

Fig. 4: Average attenuation.

Average attenuation per pass as a function of satellite altitude.

Key rate estimation

Let us now describe the procedure we follow to estimate the key rate over a fading channel in the asymptotic regime, i.e., when no finite-size effects are taken into account. For this estimation, we consider the no-switching CV-QKD protocol⁵⁰ in its prepare and measure version (PM). Alice starts by sampling 2N real random variables X₁, . . ., X_2N according to a Gaussian distribution with variance V_A, that is, ${X}_{k} \sim {\mathcal{N}}(0,{V}_{{\rm{A}}})$ and prepares the corresponding N coherent states $\left|{\alpha }_{1}\right\rangle ,...,\left|{\alpha }_{N}\right\rangle$, where ${\alpha }_{k}={X}_{2k-1}+i{X}_{2k}\in {\mathbb{C}}$. Each of these states is sent through the quantum channel to Bob, who performs measurements in both quadratures simultaneously (heterodyne detection)¹. For the kth use of the channel, he obtains two results Y_2k−1 and Y_2k which are supposed to be correlated to X_2k−1 and X_2k. The string Y = (Y₁, …Y_2N) forms the raw key since we consider the reverse reconciliation setting⁵¹, which is advantageous in case of low transmission efficiency. Note that in a practical protocol, Bob will discretize his data, for instance, by dividing the real axis into bins of small width. Asymptotic values are obtained in the limit N → ∞.

The standard formula to compute the asymptotic value of the secret key rate, in the case of reverse reconciliation, is the so-called Devetak-Winter bound⁵²:

$${K}_{{\rm{DW}}}=\beta {I}_{{\rm{AB}}}-{\chi }_{{\rm{BE}}},$$

(10)

where βI_AB quantifies the correlations between Alice and Bob’s data (here, the imperfect efficiency of the error correction procedure is taken into account thanks to parameter β ≤ 1) and χ_BE quantifies how much information the adversary holds about the raw key corresponding to Bob’s string. The Devetak-Winter bound is valid against collective attacks and remains true even against general attacks for QKD protocols with sufficient symmetry, including for the no-switching protocol, more precisely when de Finetti reductions are applicable^53,54,55.

In order to assess the performance of a protocol for a given quantum channel, one simply needs to estimate the value of βI_AB and χ_BE. For the first term, as we are dealing with the reverse reconciliation scenario, one should provide a model of the classical channel {Y_k → X_k} as well as an error correction procedure allowing Alice to recover the value of Y_k from her observations and from additional side information sent by Bob. In order to obtain χ_BE, one should similarly model the parameter estimation procedure and compute the expected value that Alice and Bob would observe for our specific channel model. Although these computations are fairly standard in the case of a fixed Gaussian channel with constant transmission efficiency and excess noise, the situation becomes more subtle in the case of a fading quantum channel and indeed conflicting results have appeared in the literature^56,57 (see Methods for details).

Here, we find it useful to recall the derivation of the asymptotic secret key rate from the non-asymptotic case. According to refs. ^55,58, the protocol we are considering is secure against general attacks, even in the finite-size regime, and the asymptotic secret key rate is given by

$$K={\mathop{\lim} \limits_{N\to \infty}}\frac{1}{N}\left(H({{\bf{Y}}}^{(N)})-\left.{{\rm{leak}}}_{{\rm{EC}}}^{(N)}\right)\right)-f({\Gamma }^{(N)}).$$

(11)

In this expression, H(Y^(N)) refers to the empirical entropy of the string Y^(N) and the superscript N is explicitly written to emphasize that each of these quantities depends on the block length. As we are only interested in the asymptotic behavior of the secret key rate, we neglect discretization effects here. The quantity ${{\rm{leak}}}_{{\rm{EC}}}^{(N)}$ is the number of bits that are leaked in the error correction procedure during which Bob sends some side information to Alice to help her guess the value of Y. The term f(Γ^(N)) quantifies the information available to Eve and will be described later.

The advantage of Eq. (11) is that it tells us how to compute βI_AB and χ_BE in the Devetak-Winter bound, namely

$$\begin{array}{l}\beta {I}_{{\rm{AB}}}={\mathop{\lim}\limits_{N\to \infty }}\frac{1}{N}\left(H({{\bf{Y}}}^{(N)})-\left.{{\rm{leak}}}_{{\rm{EC}}}^{(N)}\right)\right),\\ {\chi }_{{\rm{BE}}}={\mathop{\lim}\limits_{N\to \infty }}f({\Gamma }^{(N)}).\end{array}$$

(12)

Let us first consider the first term. Here we model the quantum channel between Alice and Bob as a phase-insensitive noisy bosonic channel with transmission efficiency given by a random variable τ_k ∈ [0, 1], whose probability distribution is the one calculated previously. The channel noise will be treated with the so-called excess noise, ξ, whose full derivation will be given in the following. We will additionally model the imperfections in Bob’s detectors by two parameters: their detection efficiency η and the electronic noise ν_el. In particular, this implies that the random variables X_k corresponding to Alice’s inputs and Y_k for Bob’s measurement results satisfy:

$${Y}_{k}={T}_{k}{X}_{k}+{Z}_{k},$$

(13)

where T_k is the overall transmission coefficient for the kth channel use, ${T}_{k}^{2}={\tau }_{k}$, and ${Z}_{k} \sim {\mathcal{N}}(0,{\sigma }^{2})$ is a Gaussian noise of variance σ² assumed to be constant.

In order to compute the key rate of Eq. (11), it is important to understand how fast the fading process is. The main idea here is that this process, whose timescale is typically of the order of 1–10 ms owing to atmospheric turbulence, is much faster than the time needed to distill a secret key, which in our case corresponds to a complete satellite pass. In other words, the channel transmission coefficient fluctuates significantly over N uses of the channel, but this coefficient is relatively stable over consecutive uses of the channel, which occur with ns separation. As a consequence, Alice and Bob can exploit classical signals to roughly monitor the current transmission value of the channel and adapt their error correction procedure accordingly. This implies notably that for the error correction procedure, we can assume that Alice and Bob know (approximately) the value of T_k. This allows them to use good error-correcting techniques developed for the fading channel where the fading process T_k is known to the receiver. In particular, the Gaussian modulation permits to achieve the capacity of this channel up to a reconciliation efficiency factor β and one expects⁵⁹

$$\beta {I}_{{\rm{AB}}}=\beta {\bf{E}}\left[{\mathrm{log}\,}_{2}\left(1+\frac{{T}^{2}{V}_{{\rm{A}}}}{{\sigma }^{2}}\right)\right],$$

(14)

where E[⋅] is the expectation with respect to the fading process. Here and in the following, we write T instead of T_k and replace averages of the form $\frac{1}{N}\mathop{\sum }\nolimits_{k = 1}^{N}$ by the expectation E for simplicity. Note that since the $\mathrm{log}\,$ function is concave, the value we find for βI_AB is smaller than the one computed for a channel with a fixed transmittance E[T²]. To numerically compute the value of Eq. (14), it is possible to use the expressions given in Ref. ⁶⁰ for a fixed-transmission channel, and take their expection value.

Let us now turn to the second term of Eq. (11), namely f(Γ^(N)), which quantifies the information available to Eve. More precisely, Γ^(N) is a worst case estimate of the (average) covariance matrix of the state Alice and Bob would share in the entanglement-based version of the protocol and the function f is defined as

$$f(\Gamma )=g({\nu }_{1})+g({\nu }_{2})-g({\nu }_{3})-g({\nu }_{4}),$$

(15)

where g is the entropy function $g(z)=\frac{z+1}{2}{\mathrm{log}\,}_{2}\frac{z+1}{2}-\frac{z-1}{2}{\mathrm{log}\,}_{2}\frac{z-1}{2}$, ν₁ and ν₂ are the symplectic eigenvalues of Γ^(N) and ν₃ and ν₄ are the symplectic eigenvalues of the matrix describing Eve’s system conditional on Bob’s measurement outcome⁶¹. The interpretation of the function f is that it coincides with the Holevo information between the raw key and Eve’s quantum memory computed for a Gaussian state ${\rho }_{{\rm{ABE}}}^{G}$ with covariance matrix coinciding with Γ^(N) on Alice and Bob’s systems.

In order to compute the covariance matrix Γ^(N) that Alice and Bob would infer from their data, we note first that for a fixed transmittance value T, the covariance matrix of the bipartite quantum state they would hold in the entanglement-based version of the protocol reads

$$\Gamma (T)=\left[\begin{array}{cc}V{{\mathbb{1}}}_{2}&T\sqrt{{V}^{2}-1}{\sigma }_{Z}\\ T\sqrt{{V}^{2}-1}{\sigma }_{Z}&({T}^{2}(V-1)+{\sigma }^{2}){{\mathbb{1}}}_{2}\end{array}\right],$$

(16)

with V = V_A + 1, ${\mathbb{1}}$₂ = diag(1, 1) and σ_Z = diag(1, − 1).

As observed in ref. ⁵⁶, when the fluctuation of the transmission efficiency is considered, the resulting state is a mixture of the individual fixed-transmission states, giving an overall covariance matrix equal to Γ^(N) = E[Γ(T)], that is:

$${\Gamma }^{(N)}=\left[\begin{array}{cc}V{{\mathbb{1}}}_{2}&{\bf{E}}[T]\sqrt{{V}^{2}-1}{\sigma }_{Z}\\ {\bf{E}}[T]\sqrt{{V}^{2}-1}{\sigma }_{Z}&({\bf{E}}[{T}^{2}](V-1)+{\sigma }^{2}){{\mathbb{1}}}_{2}\end{array}\right].$$

(17)

If we compare the covariance terms in Eqs. (16) and (17), we can identify an effective transmission for the fading channel equal to E[T]². In particular, the variance of Bob’s system can be written

$${\bf{E}}[{T}^{2}](V-1)+{\sigma }^{2}={\bf{E}}{[T]}^{2}(V-1+{\xi }_{{\rm{fad}}})+{\sigma }^{2},$$

where

$${\xi }_{{\rm{fad}}}=\frac{({\bf{E}}[{T}^{2}]-{\bf{E}}{[T]}^{2})}{{\bf{E}}{[T]}^{2}}(V-1)=\frac{{\rm{Var}}(T)}{{\bf{E}}{[T]}^{2}}(V-1)$$

(18)

corresponds to noise exclusively owing to fading. In other words, Eve’s information in the presence of fading corresponds to her information for a fixed Gaussian channel with transmission efficiency E[T]² and an added noise given by (V − 1)Var(T)/E[T]². This extra noise will be detrimental to the performance of the QKD system unless ${\rm{Var}}(T)\ll \frac{1}{V-1}$. By re-writing the fading case as a fixed case with an effective transmission efficiency and excess noise, it is possible to use the equations reported in ref. ⁶⁰ for calculating the eigenvalues in Eq. (15).

To summarize, by putting together the two terms of Eq. (11), our expression for the secret key rate in the presence of fading becomes:

$${K}_{{\rm{fad}}}=\beta {\bf{E}}\left[{\mathrm{log}\,}_{2}\left(1+\frac{{T}^{2}{V}_{{\rm{A}}}}{{\sigma }^{2}}\right)\right]-f({\bf{E}}[\Gamma (T)]).$$

(19)

Simulation results

We are now ready to use the results derived above to estimate the expected key rate achievable for a satellite-to-ground CV-QKD link under our assumptions. To properly account for the expected noise, we include in our modeling the noise contribution related to the phase recovery between the signals generated by Alice and measured by Bob. The technique that we consider here has been proposed in refs. ^62,63 and consists in sending periodic reference symbols (pilots) along with the quantum signal. At the receiver side, Bob uses a free running LO, which must be tuned to compensate for the Doppler frequency shift introduced by the satellite motion, to measure both the pilot and the quantum signals, in a so-called “local” LO configuration. As described in the Methods section, two noise contributions arise from this technique, which are due to laser instability and shot noise.

We remark that at telecom wavelength, the Doppler shift ranges from several GHz for LEO to several hundreds of MHz for MEO⁶⁴. This problem is well known in classical laser communication and several solutions have been proposed, such as optical⁶⁵ or digital⁶⁶ phase-locked loops. An alternative solution could come from precise orbit determination (POD) based on additional satellite payloads, such as retroreflectors, GPS receivers or DORIS antennas. With these techniques, it is possible to achieve an a posteriori determination of the satellite velocity with a precision of <1 mm/s, which would correspond to a residual frequency shift of <1 kHz^67,68. Moreover, in the case of “local” LO CV-QKD, an alternative solution is to exploit the pilots to measure the residual Doppler shift. In fact, by using ephemeris data, it is possible to pre-compensate the Doppler shift with an a priori residual error of tens of MHz, much smaller than the pilot repetition rate. Under these conditions, it would be possible to retrieve the residual Doppler shift by analyzing the trend of the pilot phase. This possible Doppler correction technique will need further experimental investigation, which is however outside the scope of this work.

The overall excess noise ξ, here referred to as the channel input, is given by the above-mentioned contributions, the fading noise, described in the previous section, and an additional fixed contribution owing to experimental imperfections, ξ_fix, which includes also other possible errors in the phase correction.

The main experimental parameters that influence the key rate generation are summarized in Table 1, together with their reference values. The reference values considered for the ground station and the satellite are similar to those reported in ref. ²² and represent a high-performance satellite optical communication system. A detailed analysis of the effect of individual parameters on the key rate is given in the Methods. Regarding the signal variance V_A, for each satellite altitude and for each set of parameters we choose the value that maximizes the key rate. These values are in general between 2 and 4 shot noise units (S.N.U.), depending on the configuration. Fig. 5 shows the fading noise given by the PDTE that we obtain for orbits going from 400 km to 22,000 km. As we see, an increase of the noise is present for LEO. This is due to the fact that in such orbits the variation of the slant range is more pronounced, thus, introducing a higher variance on τ (as we observe in Fig. 3). Moreover, it is worth noting that when the pointing error is much smaller than the beam divergence, the fading effect is mainly due to the variation on the satellite distance.

Table 1 Parameters summary.

Fig. 5: Fading noise vs. satellite altitude.

Trend of the fading excess noise, ξ_fad, in percentage of the shot noise units, as a function of the satellite altitude for several values of pointing error and a fixed value of the divergence angle.

To reduce the effect of fading excess noise, a natural strategy is to reduce the variance of the fading process. This can be achieved as follows: Alice and Bob can approximately monitor the value of the transmission efficiency of the channel seen by the quantum symbols τ_k by multiplexing in some degree of freedom an intense optical signal that serves as beacon and experiences a transmission efficiency τ_b. An intensity detection of the beacon at Bob’s, sampled at rates higher than the atmospheric coherence time (typically ~1 kHz), can provide an accurate estimation of the channel transmittance evolution with time τ_b(t). This information can be used to classify the detected quantum symbols in groups as a function of the expected transmittance so that for each group g the PDTE is reduced to a transmittance interval PDTE(g) for which the contribution of the fading is less detrimental. The CV-QKD protocol can be performed independently for each of these groups to obtain a secret key rate per symbol K_fad(PDTE(g)) and an aggregated secret key rate per symbol of

$${{\rm{K}}}_{{\rm{agg}}}= \sum \limits_{g}P({\tau }_{b}\in {\rm{PDTE}}(g)){K}_{{\rm{fad}}}({\rm{PDTE}}(g)).$$

(20)

A similar idea has been proposed in ref. ³³, however here we propose to use a beacon signal to estimate the instantaneous channel transmission efficiency, instead of relying on the quantum data. This allows for a more precise estimation, also for a fast-fading process. The classical beacon does not transport information related to the quantum signal and K_fad(PDTE(g)) is obtained using only the quantum symbols. For this reason, if the signal is tampered within order to falsify the group classification (alter the correlation between τ_k and τ_b) only a denial of service would be experienced, as the secret key rate would be reduced, as the manipulated group would suffer higher fading and more excess noise would be estimated.

In order to reduce the effect of fading, narrow PDTE intervals are desirable, but this can magnify finite-size effects, since the number of symbols per group will be reduced. This compromise between PDTE interval width and the number of symbols per group can be taken into account in order to optimize the division of the PDTE so that K_agg is maximal for a given PDTE and orbit duration. Technical restrictions such as the resolution available for determining τ_b can also play a role in the ideal division of the PDTE in groups.

In our analysis, we have chosen a uniform division of the PDTE and we do not treat the problem of the PDTE division optimization. We divided the whole range of transmission values in equally spaced intervals, going from a single group (corresponding to analyzing the data altogether) to 100 intervals (i.e., close to the asymptotic limit). The results are reported in Fig. 6 for a satellite at 400 km and for three values of fixed excess noise. We note that without channel subdivision no key would be possible for a 400 km orbit. To analyze the effect of the channel subdivision for all the orbits, we selected subdivisions of 3, 10, and 100 intervals for all the satellite altitudes. As shown in Fig. 7, the division of the channel transmission efficiency in 10 groups gives a total rate close to the asymptotic limit for all satellite altitudes. We underline that for this simulation the same values of beam divergence and pointing error have been used in all cases, to emphasize the impact of the orbit altitude on the key generation rate. However, owing to the different satellite size and environmental disturbance, MEO satellites could in general reach better performance in terms of beam quality.

Fig. 6: Asymptotic key rate vs group factor.

Secret key rate for channel subdivision from 1 to 100 equally spaced intervals for a 400 km altitude satellite. The fixed excess noise, ξ_fix, is, in S.N.U, 1 % (red), 3% (blue) and 5% (green), respectively.

Fig. 7: Asymptotic key rate vs satellite altitude.

Secret key rate for channel subdivision in 3, 10, and 100 groups and different values of the fixed excess noise, ξ_fix: (in S.N.U), 1% (red), 3% (blue), and 5% (green). The key rate in bits/s can be calculated by multiplying by the transmission symbol rate.

Finite-size analysis

We complete our analysis by considering the issue of finite-size effects on the estimation of parameters. It is worth noting that in satellite communication the maximum amount of time for transmission is given by the orbital parameters and can range from a few minutes to hours, depending on the satellite altitude. Moreover, as discussed previously an optimization is required if we consider the subdivision of the channel transmission efficiency for reducing the fading noise. A denser subdivision will decrease the fading noise, but will result in less populated groups, thus, making the finite-size effects more detrimental.

Here, we consider the uncertainty of the parameter estimation owing to the limited statistics. As described in ref. ⁶⁹, it is possible to account for this effect by considering a lower bound on the transmission coefficient $T=\sqrt{\tau }$ and an upper bound of the parameter σ² = 1 + τξ:

$${T}_{\min }\simeq \sqrt{\tau }-{z}_{{\epsilon }_{{\rm{PE}}}/2}\sqrt{\frac{1+\tau \xi }{m{V}_{{\rm{A}}}}}$$

(21)

$${\sigma }_{\max }^{2}\simeq 1+\tau \xi +{z}_{{\epsilon }_{{\rm{PE}}}/2}\frac{(1+\tau \xi )\sqrt{2}}{\sqrt{m}},$$

(22)

where m is the number of symbols used for parameter estimation and ${z}_{{\epsilon }_{{\rm{PE}}}/2}$ is a parameter related to the failing probability of the parameter estimation ϵ_PE. Here we consider ϵ_PE = 10⁻¹⁰, which gives ${z}_{{\epsilon }_{{\rm{PE}}}/2}=\sqrt{2}\ {{\rm{erf}}}^{-1}(1-{\epsilon }_{{\rm{PE}}})=6.5$, where ${{\rm{erf}}}^{-1}$ is the inverse error function. We consider the situation in which half of the symbols are used for parameter estimation and the orbit is divided into 10 intervals. This choice is not optimized and should be tailored to a specific experimental setup, however such optimization is beyond the scope of this work.

The results for the given parameters are shown in Fig. 8 and highlight how the finite-size effects have a remarkable impact on higher orbits, effectively precluding CV-QKD operation beyond 2000 km when the key distillation is performed on a single satellite pass. For lower orbits, below 800 km, the effect is only limited to a drop in the key rate. The finite-size effects could be reduced by increasing the transmission rate and optimizing the orbit subdivision, as well as accumulating multiple satellite passes.

Fig. 8: Finite-size vs asymptotic key rate.

Comparison of the key rate for LEO between the asymptotic regime (solid line) and considering finite-size effects (dashed line), which have been calculated for a symbol rate of 1 Gsymbol/s. The fixed excess noise, ξ_fix, is 1% (red), 3% (blue) 5% (green).

Discussion

In this work, we analyzed the feasibility of CV-QKD from satellite to a ground station. By modeling the transmission channel along a complete circular orbit, it has been possible to obtain the PDTE of the quantum channel, from which we derived the secret key generation rate both in the asymptotic case and when finite-size effects are considered in the parameter estimation. To cope with channel fluctuations, typical of the satellite signal transmission, we proposed a method of data analysis based on orbit subdivision and proved its effectiveness in improving secret key generation. The analysis provides an estimate of the expected key rate of satellite-to-ground CV-QKD and allows to constraint of the experimental parameters for its realization. The obtained results show that coherent state modulation and detection is a viable option for quantum communication with LEO satellites. The communication with higher orbits, achievable in the asymptotic limit, can be affected by finite-size effects if the transmission rate is low or the orbit subdivision is not optimized. We note however that by merging multiple satellite passes, or with the implementation of higher repetition rate systems, it would be possible to extend the communication range beyond 2000 km. Further work is required for the comparison of the key rates achievable with continuous and discrete variable encodings in different communication scenarios.

Methods

Parameter analysis

Here, we analyze the dependence of the secret key rate on several parameters, to obtain a better insight into which parameters affect the most the overall performance. To reduce the complexity of this multiparameter analysis, we consider here the key rate that can be obtained if the instantaneous value of the transmission efficiency is known. This case occurs when a sufficient number of symbols is exchanged within the timescale of the channel fluctuation (typically of the order of few ms) and it upper bounds the rate given by Eq. (19). Such a situation is unrealistic in practice, however, it will give us a reference for estimating the efficiency of the realistic scenario.

In this scenario, the key rate can be calculated as a weighted average, considering as weight the PDTE calculated from our channel model analysis:

$${K}_{UB}={\left\langle \min (0,\beta {I}_{{\rm{AB}}}(\tau )-{\chi }_{{\rm{BE}}}(\tau ))\right\rangle }_{\tau }.$$

(23)

The parameters will be changed one by one, keeping the others to their reference values, expressed in Table 1. The color code reflects the value of the fixed excess noise and is the same used in the main text: red, blue, and green for ξ_fix = 1, 3, 5% (in S.N.U.), respectively.

In Fig. 9, we vary the electronic noise of the detectors from 0.01 to 0.1 S.N.U. We notice that even with one order of magnitude increase in noise, the key rate is almost unaffected for all cases. This is mainly due to the fact that in this analysis we consider the so-called "trusted” or "calibrated” scenario, in which the electronic noise is known to Bob via a constant calibration and cannot be exploited by Eve.

Fig. 9: Impact of the electronic noise on key rate.

Comparison of secret key rate for two different electronic noise ν_el and three different excess noise values.

The second effect considered is the energy of the reference symbols used for phase recovery. We will illustrate the problem considering a simple phase estimation scheme operating at 1 Gsymbol/s with alternating signal and reference symbols. The time between two such symbols, Δt = 1 ns, gives rise to a noise contribution ξ_t = V_A2πΔtΔf, where $\Delta f\simeq \frac{1}{\pi {\tau }_{c}}=10$ kHz is the linewidth of the two lasers and τ_c their coherence time (assumed equal for Alice and Bob). On the other hand, the phase measurement is affected by shot noise, introducing a noise of ${\xi }_{{\rm{sn}}}=\frac{{V}_{{\rm{A}}}}{2\eta {n}_{{\rm{ref}}}}$, where ${n}_{{\rm{ref}}}=\frac{{E}_{{\rm{ref}}}\tau }{{E}_{{\rm{photon}}}}$ is the total number of photons collected, E_ref is the energy of the reference symbols and E_photon is the photon energy. The effects for different reference symbol energies are shown in Fig. 10. Although the effect for LEO satellites is negligible for energies above 10 pJ, for higher orbits stronger values of the reference are required to avoid any detrimental effect owing to the phase alignment uncertainty, which might impose restrictions in the dynamic range of the modulators, as the optimal variance V_A decreases as attenuation increases.

Fig. 10: Impact of the reference pulse energy on key rate.

Comparison of secret key rate for different values of the reference symbol energy E_ref, for the three different excess noise values considered along the paper.

Next, we consider the impact of the downlink beam characteristics, namely the pointing error and the beam divergence, on the final key rate. As expected, these values have a strong impact in all the configurations shown in Fig. 11, underlying the importance of a high-quality beam propagation for satellite CV-QKD.

Fig. 11: Impact of the beam quality on key rate.

Comparison of secret key rate for different values of pointing error, θ_p, and divergence angle, θ_d at the three excess noise values.

Finally, we analyze the impact of atmospheric transmission efficiency, as given by Eq. (1). In particular, we calculate the key rate for visibility of 5 km and 2 km, corresponding to haze and mist conditions, respectively. In these two cases the atmospheric transmission efficiency at zenith, τ_zen, is, respectively, 0.75 and 0.53. The results, reported in Fig. 12, show that the key rate is affected slightly by haze condition, but drops significantly for mist condition.

Fig. 12: Impact of the sky visibility on key rate.

Comparison of secret key rate for different values of sky visibility at the three excess noise values.

Previous treatment of fading in the literature

Reference ⁵⁷ considers two scenarios: slow fading where the transmission efficiency fluctuates at a slower rate than the key establishment rate, and fast fading where the transmission value fluctuates significantly during a single key extraction procedure. The second scenario is similar to ours, but the expression of the authors for the secret key rate differs since they obtain

$${K}_{{\rm{fast}}{\rm{fading}}}=\beta {I}_{A}{B}^{{\eta }_{\min }}-\int \ d\tau {P}_{\tau }\chi (E;y),$$

(24)

where the transmission efficiency τ = T² is uniformly distributed with distribution P_τ over some interval $[{\tau }_{\min },{\tau }_{\max }]$. In other words, they take the most pessimistic value of I_AB (corresponding to the lowest transmission value) and consider the average of the Holevo information between Eve and the raw key, over the possible fading values.

In contrast, we agree with the estimate for the Holevo information from ref. ⁵⁶ but take a more conservative value for the mutual information I_AB since their value is computed for a Gaussian modulation that would yield the same covariance matrix. We have instead argued that one needs to carefully consider the classical channel mapping Y to X (in the reverse reconciliation procedure). This is a fading channel where one can take advantage of the pilot signals to get a rough estimate of the fading coefficient. This implies that one can approximate the capacity of that channel with the average of the capacities of an AWGN channel over the value of the fading parameter.