Abstract
Quantum key distribution (QKD) allows for secure communications safe against attacks by quantum computers. QKD protocols are performed by sending a sizeable, but finite, number of quantum signals between the distant parties involved. Many QKD experiments, however, predict their achievable key rates using asymptotic formulas, which assume the transmission of an infinite number of signals, partly because QKD proofs with finite transmissions (and finite-key lengths) can be difficult. Here we develop a robust numerical approach for calculating the key rates for QKD protocols in the finite-key regime in terms of two semi-definite programs (SDPs). The first uses the relation between conditional smooth min-entropy and quantum relative entropy through the quantum asymptotic equipartition property, and the second uses the relation between the smooth min-entropy and quantum fidelity. The numerical programs are formulated under the assumption of collective attacks from the eavesdropper and can be promoted to withstand coherent attacks using the postselection technique. We then solve these SDPs using convex optimization solvers and obtain numerical calculations of finite-key rates for several protocols difficult to analyze analytically, such as BB84 with unequal detector efficiencies, B92, and twin-field QKD. Our numerical approach democratizes the composable security proofs for QKD protocols where the derived keys can be used as an input to another cryptosystem.
Similar content being viewed by others
Introduction
Quantum key distribution (QKD), until today, remains the only quantum-resistant method of sharing secret keys and transmitting future-proof secret information at a distance1. Even after >30 years of development, QKD still does not see widespread adoption, primarily due to practical and theoretical difficulties.
Practically, QKD as a means of encryption requires a dramatic change to the existing classical fiber-optical communication infrastructure. QKD systems typically require the use of specialized quantum optical devices. For example, some QKD protocols need single photon detectors and dark fiber-optical channels without any classical repeater device, e.g., erbium-doped fiber amplifiers. In other words, the need for significant change to the current telecommunication infrastructure presents a challenge to QKD’s wide use today.
Theoretically, security proofs are typically complicated, and the key rate derived can be loose due to limited availability of analytical proof techniques. Validating a published security proof is an equally complicated task, and it is likely impractical to expect QKD users to be capable of verifying the security of a protocol.
The security of any QKD protocol is guaranteed when a detailed security analysis certifies that the protocol produces a non-zero secret key rate (in terms of either bits per second or bits per transmission). So far, development in key rate calculations has relied on analytical tools that can be limited in scope to specific protocols. In particular, oftentimes to simplify the analysis, the calculations invoke a high degree of symmetry. Indeed, for some protocols, such as the Bennett–Brassard 1984 (BB84) protocol2 or the six-state protocol3, analytical formulas for the key rates are known. However, in practical implementations of QKD, a lack of symmetry is the norm rather than the exception as experimental imperfections tend to break these symmetries4. This motivates the need to develop a method of analyzing the security of QKD protocols that may lack structure.
Recently, refs. 5,6 proposed two numerical techniques to obtain reliable secret key rate bounds for an arbitrary unstructured QKD protocol. The original technique, described in ref. 5, formulates the problem of calculating the secret key rate in terms of a mathematical optimization problem. Unfortunately, this original formulation resulted in a non-convex problem. The method was improved in ref. 6, which formulates the key rate problem in terms of convex optimization. Commercially available convex optimization tools, such as Mosek7, SeDuMi8, or SDPT39, can therefore be used to reliably solve the problem. A more recent technique opted to compute the secret key rate by directly bounding the quantum error rate of a protocol using the Gram matrix of the eavesdropper’s information10,11. Nevertheless, the problems formulated so far still assumed that Alice and Bob have exchanged an infinite number of signals (and an infinite-key length), which is practically impossible. In order to quantify the security of realistic QKD protocols, a new problem that includes the finite-key statistics of the QKD operations must be formulated.
Here we formulate the key rate problem in terms of a semidefinite program (SDP) that considers the practical case of only a finite number of transmitted signals. The program takes as inputs the measured statistics from the parameter estimation step and outputs the key rate as a function of the security parameter of the protocol: εqkd. The SDP computes a reliable, achievable lower bound on the actual value of the secret key rate assuming collective attacks from the eavesdropper. As SDP is a convex optimization problem, we can solve the problem using commercial solvers that often are able to find the global optima. Our problem formulation is reliable, such that even if the solver fails to find the global optimum, the SDP is guaranteed to output an achievable secret key rate. Lastly, since the problem takes into consideration the finite number of signals exchanged, the secret key guaranteed by the method is composable, i.e., can be used as an input to another cryptosystem.
In the following sections, we present our main result of reformulating the QKD finite-key problem under collective attacks into easily computable SDPs. We then implement the SDPs formulated in two example asymmetric protocols: BB84 with unequal detector efficiencies and B92. By asymmetric protocol, we mean the general situation where something about the protocol is unbalanced or biased. Examples include a non-uniform probability distribution of transmitted signal states and when the states of Alice and Bob experience different quantum channels. The difference in the quantum channels naturally occurs when Alice and Bob have unequal resources (e.g., imbalanced transmission loss, or unequal detector efficiency) or when the protocol dictates Alice and Bob perform different operations on their states (in the entanglement-based picture). These examples emphasize the robustness and usefulness of the numerical programs in analyzing protocols that are difficult to analyze analytically because of their lack of symmetry. We also implement the SDPs in the more recently developed twin-field QKD, demonstrating the broad applicability of our numerical programs to contemporary QKD.
Results
The key rate problem in the non-asymptotic regime
We describe the main steps of a typical QKD protocol and take note of the relevant security parameters at each step.
-
1.
Transmission. A QKD protocol starts with the transmission of quantum signals. Let us assume that N signals are successfully distributed from Alice to Bob. After this step, in the entanglement picture, they will share N entangled quantum states, whose joint state can be described as ρAB. They will then apply measurements to their respective quantum states to obtain classical data.
-
2.
Sifting. Sifting is often (but not always) performed at this stage. Alice and Bob discard those data where they have chosen a different measurement basis. We denote the number of signals they discard as s.
-
3.
Parameter estimation. Next, Alice and Bob perform parameter estimation where they reveal a random sample of m signals through the public classical communication channel to estimate the statistics of their data. At this step, they are left with n ≤ N − m number of signals, called the raw keys, from which they can eventually generate secret keys. Let us denote their raw keys by ZA and ZB, both of which have the length ∣ZA∣ = ∣ZB∣ = n. There is a small probability εPE that the raw keys obtained are not compatible with the estimated parameters, and it is related to the number of signals m that are used to estimate the relevant statistics of the overall data. (Relevant security parameter: εPE.)
-
4.
Reconciliation. Alice and Bob then perform key reconciliation (sometimes also referred to as error correction). The key reconciliation step, in which they correct for any possible error between their raw keys, reveals leakEC number of bits. This error correction step is performed with a certain failure probability εEC, which is the probability that one party computes the wrong guess of the other party’s raw keys. (Relevant security parameter: εEC.)
-
5.
Error verification. To ensure they have identical raw keys, they apply a two-universal hash function and publish \(\lceil {\mathrm{log}\,}_{2}1/{\varepsilon }_{\text{cor}}\rceil\) bits of information. Here εcor = εhash, which is the probability that two non-identical raw secret keys generate the same hash value. (Relevant security parameter: εcor.)
-
6.
Privacy amplification. Next, they apply another two-universal hash function (of different resulting hash length than the previous one in the error verification step) to extract a shorter secret key pair (SA, SB) of length ∣SA∣ = ∣SB∣ = ℓ. εPA measures how close the output of the hash function, i.e., the secret keys SA and SB are, from a uniform random bit string conditioned on the eavesdropper’s, Eve’s, knowledge. (Relevant security parameter: εPA.)
In this nonasymptotic regime, we use a generalization of the von Neumann entropy called smooth min-entropy, which was developed by ref. 12. The main significance of smooth min-entropy comes from the fact that it characterizes the number of uniform bits that can be extracted in the privacy amplification step of a QKD protocol. Now, let us take \({\bf{E}}^{\prime}\) to be the information that Eve gathered about Alice’s raw key ZA up to and including the error correction and verification steps. When Alice and Bob apply a two-universal hash function in the privacy amplification step, they can then extract a εsec-secret key of length:
for \(\overline{\varepsilon }+{\varepsilon }_{\text{PA}}\le {\varepsilon }_{\text{sec}}\) (proof is by the quantum leftover hash lemma in ref. 13). \({H}_{\min }^{\overline{\varepsilon }}({{\bf{Z}}}_{A}| {\bf{E}}^{\prime})\) is the conditional smoothed min-entropy that quantifies the average probability that Eve guesses ZA correctly using her optimal strategy based on her knowledge of the information \({\bf{E}}^{\prime}\).
During the error correction step, a maximum of leakEC bits of information are revealed about ZA. Alice has to send a syndrome bit string of length leakEC to Bob over the public channel, so that Bob can correct his raw key to match Alice’s. Furthermore, during the error verification step, \(\lceil {\mathrm{log}\,}_{2}(1/{\varepsilon }_{\text{cor}})\rceil \le {\mathrm{log}\,}_{2}(2/{\varepsilon }_{\text{cor}})\) bits of information are revealed. If we let E be the remaining quantum information Eve has on ZA, then
The QKD protocol is said to be εqkd ≥ εcor + εsec secure if it is correct with a probability higher than 1 − εcor and is secret with a probability higher than 1 − εsec.
Under the assumption of independent and identically distributed (i.i.d.) and collective attacks from Eve, the total state of Alice, Bob, and Eve admits a product form. The quantity \({H}_{\min }^{\overline{\varepsilon }}({{\bf{Z}}}_{A}| {\bf{E}})\) can then be further simplified in this case, as the state shared by Alice and Bob has the form \({\rho }_{{\bf{A}}{\bf{B}}}={\left({\rho }_{AB}\right)}^{\otimes N}\). In this case, we can also assume that \({\rho }_{{{\bf{Z}}}_{A}{\bf{E}}}={\left({\rho }_{{Z}_{A}E}\right)}^{\otimes n}\) since all purifications of ρAB are equivalent under a local unitary operation by Eve, and there exists a purification with this property14. In other words, after being presented with the tensor product states \({\left({\rho }_{AB}\right)}^{\otimes N}\), Eve is free to choose how to purify this state. (She wants to purify this state because this gives her the most information.) One obvious choice is to purify each transmission such that she has \({\left|\Psi \right\rangle }_{{\bf{A}}{\bf{B}}{\bf{E}}}={\left|\psi \right\rangle }_{{A}_{1}{B}_{1}{E}_{1}}\otimes {\left|\psi \right\rangle }_{{A}_{2}{B}_{2}{E}_{2}}\otimes \cdots \otimes {\left|\psi \right\rangle }_{{A}_{N}{B}_{N}{E}_{N}}\). It is from such a purification, we obtain the tensor product structure of \({\rho }_{{{\bf{Z}}}_{A}{\bf{E}}}={\left({\rho }_{{Z}_{A}E}\right)}^{\otimes n}\). The observed statistics of relative detection frequencies, however, only gives some knowledge about the state \({\rho }_{{Z}_{A}E}\). Given that the state \({\rho }_{{Z}_{A}E}\) is contained within a set that contains all \({\rho }_{{Z}_{A}E}\) compatible with the observed statistics, except with probability εPE, we have:
where \(\overline{\varepsilon }=\varepsilon +{\varepsilon }_{\text{PE}}\).
When the error correction step is performed with a failure probability of εEC, i.e., the probability that Bob computes the wrong guess for ZA, we can bound the quantity leakEC with Corollary 6.3.5 of ref. 12:
where d is the number of possible symbols in ZA, and fEC ≥ 1 characterizes the error correction (in)efficiency. Commonly, fEC is chosen to be ~1.2, which is based on the performance of real codes15. We note that ref. 15 also provides a tighter bound than Eq. (4) above using higher-order corrections.
To compute the key rate under the assumption of collective attacks, we therefore have to minimize the quantity:
Here the set \({{\mathcal{C}}}_{{\varepsilon }_{\text{PE}}}\) is the set of all density operators ρAB that are consistent with the statistics measured from the parameter estimation step, except with a probability εPE. Let Γi be the Hermitian observables for these measurements, then the average values of these operators are within the bounds: \({\gamma }_{i}^{LB}\le {\rm{Tr}}({\rho }_{AB}{\Gamma }_{i})\le {\gamma }_{i}^{\,\text{UB}\,}\), for i = 1, …, nPE, except with probability εPE. Along with the constraint that ρAB is a valid i.i.d. normalized density operator, i.e., ρAB ≽ 0 and \({\rm{Tr}}({\rho }_{AB})=1\), then ρAB is constrained to be in the set:
except with probability εPE.
To understand how one can obtain the bounds on the average values \({\gamma }_{i}\equiv {\rm{Tr}}({\rho }_{AB}{\Gamma }_{i})\), consider the parameter estimation step in a typical QKD protocol. Alice and Bob perform the measurements using the positive operator-valued measures (POVMs) \(\{{M}_{A}^{a}\}\) and \(\{{M}_{B}^{b}\}\) (in the entanglement-based picture) and use a fraction of their measurements to obtain \({\gamma }_{(a,b)}={\rm{Tr}}({\rho }_{AB}{M}_{A}^{a}\otimes {M}_{B}^{b})\). Then, we can make the identification \({\Gamma }_{i}\equiv {\Gamma }_{(a,b)}={M}_{A}^{a}\otimes {M}_{B}^{b}\) with γi ≡ γ(a, b). To find the relevant bounds, suppose that a total of mi signals have been used to estimate γi, then the deviation of the estimate \({\gamma }_{i}^{{m}_{i}}\) from the ideal estimate \({\gamma }_{i}^{\infty }\) can be quantified using the law of large numbers14,16:
except with a failure probability of \({\varepsilon }_{\,\text{PE}\,}^{i}\). Here d is the number of outcomes of the POVM Γi needed to estimate it (for error rates, d = 2 since the outcomes are either Alice = Bob or Alice ≠ Bob). The overall parameter estimation step fails with a probability of \({\varepsilon }_{\text{PE}}={\sum }_{i}{\varepsilon }_{\text{PE}\,}^{i}\). We can then obtain the upper and lower bounds:
as γi is a probability and must have values between 0 and 1. We note that the inequality (7) is not the only law of large numbers that can be used to find these bounds. Tighter (asymmetric) bounds can be achieved by applying both the Chernoff bound and the Hoeffding’s inequality17,18. Recently, even tighter bounds were obtained with clever usage of the Chernoff bound alone19.
The definition of Γi and γi above may be too fine-grained for a QKD protocol such that each individual \({\varepsilon }_{\,\text{PE}\,}^{i}\) may be too small for a given value of εPE. The security of a QKD protocol typically can be defined with only a few parameters; for example, the security of BB84 relies on only the bit error rates when both parties choose the Z-basis and the X-basis. Coarse-graining the constraints can be achieved by merging the constraints Γi together, e.g., by summing a subset of or by taking an average value of the constraints and the observed statistics. Coarse-graining, from an optimization perspective, loosens a constraint such that the guaranteed key rate can be lower than the optimal value of the calculations with fine-grained constraints. However, coarse-graining can provide tighter bounds on γis for the same value of εPE simply because there are there are fewer constraints to be bounded. Tighter bounds on γis can possibly result in a higher secret key rate.
We now use two methods to evaluate a reliable numerical lower bound on the quantity \({H}_{\min }^{\varepsilon }({\rho }_{{Z}_{A}E}^{\otimes n}| {\rho }_{E}^{\otimes n})\) that will allow us to eventually quantify the key length ℓ—hence the key rate r.
Key rate estimation using von Neumann entropy and the quantum asymptotic equipartition property
The smooth min-entropy of an independent and identically distributed product state \({\rho }_{{Z}_{A}E}^{\otimes n}\) converges to the von Neumann entropy through the quantum asymptotic equipartition property in the limit of large n:
For the case of finite number of signals n, these two entropic quantities are related via a correction factor obtained in Corollary 3.3.7 of ref. 12 that was further tightened in Theorem 9 of ref. 20, i.e.,
where \(\delta (n,\epsilon)=(2d+3)\sqrt{{\mathrm{log}\,}_{2}(2/\varepsilon)/n}\) is the correction factor. It is worth pointing out that the correction factor from the tighter bound in ref. 20 is independent of the dimensions d of ZA, which can be useful when considering high-dimensional protocols. It is also important to note that the right-hand side of Eq. (10) is an achievable secure lower bound in the asymptotic limit to estimate the key rate. We apply this result to obtain an εqkd-secure finite-key QKD protocol that is εcor-correct and εsec-secret (with εcor + εsec ≤ εqkd) at a secret key rate per transmission of:
which is in terms of the von Neumann entropy instead of the smooth min-entropy. The protocol is secret up to a failure probability of εsec ≥ ε + εPA + εPE + εEC.
In light of Eq. (11), the optimization problem that we have to solve is \(\mathop{\min }\limits_{{\rho }_{AB}\in {{\mathcal{C}}}_{{\varepsilon }_{\text{PE}}}}H({Z}_{A}| E)\). Reference 5 shows how to recast this as an optimization problem with the quantum relative entropy, rather than the von Neumann entropy, as the objective function. Reference 6 further developed a two-step method to obtain a secure lower bound. Simply put, this two-step method consists of finding an approximate minimum (step one) and then solving a linearized version of the SDP around this approximate minimum to obtain a secure lower bound (step two). In this work, we use the semidefinite approximation of the matrix logarithm and quantum relative entropy from ref. 21 to perform step one and then follow step two directly as described in ref. 6. The “Methods” section contains a review of the SDP developed in ref. 6 and a more detailed description of our approach to step one.
Key rate estimation using min-entropy
To compute the key rate via the min-entropy, we use the fact that the smooth min-entropy is a maximization of the min-entropy and is equal to the min-entropy when the smoothing parameter ε = 0, i.e.,
Then, using the additivity of min-entropy (derived in Lemma 3.1.6 of ref. 12) we have that:
which gives a lower bound on the smooth min-entropy in terms of the single-transmission min-entropy (The same result using different bounds of the smooth min-entropy is found in ref. 22.).
This approach guarantees an εqkd-secure QKD protocol that is εcor-correct and εsec-secret at a secret key rate per transmission of:
The secrecy of the protocol is found by composing the error terms εsec ≥ εPA + εPE + εEC (since ε = 0).
The optimization problem to be solved in this formulation is therefore \(\mathop{\min }\nolimits_{{\rho }_{AB}\in {{\mathcal{C}}}_{{\varepsilon }_{\text{PE}}}}[{H}_{\min }({Z}_{A}| E)]\). To solve this problem, we must show how the objective function \({H}_{\min }({Z}_{A}| E)\) can be expressed in terms of an optimization problem that does not include Eve’s state. We obtain the following relation by following a similar approach to ref. 23 (further detailed in “Methods”):
where
is the fidelity function and σAB is a valid density matrix. Finally, using the linear SDP developed in ref. 24 for the fidelity, we obtain a SDP that can be solved for a secure lower bound to the min-entropy, and therefore for the finite-key rate (see “Methods” for further details).
The lower bound to the key rate using the single-transmission min-entropy is typically not as tight as that using the von Neumann entropy. However, this formulation is computationally less expensive than the von Neumann approach and is therefore useful for protocols with signal states that have a large Hilbert space.
Both the von Neumann and min-entropy approaches described are amenable to protocols that require postselection. We outline how the general postselection framework developed in ref. 6 can be applied to these approaches in Supplementary Methods.
Outline of examples
We now illustrate our numerical approach for obtaining reliable lower bounds on the QKD secret key rate by applying it to some well-known protocols. We consider two asymmetric protocols: the BB84 protocol with unequal detector efficiencies and the B92 protocol25, where analytical solutions are not known in general. We also consider the recently developed Twin-Field QKD (TF-QKD) protocol26 that is able to beat the fundamental capacity for direct quantum communication without any repeaters27.
In the Supplementary Note 3, we benchmark our numerical method by studying two well-known protocols: BB842 and the measurement-device-independent (MDI)-QKD protocol28. Moreover, to show that the numerical approach can also be applied to prepare-and-measure protocols, we also study the BB84 protocol with a side-channel Trojan-horse attack in Supplementary Note 3.
Table 1 summarizes all examples we consider. For symmetric protocols, the numerical solutions match those of analytical QKD proofs against collective attacks. The numerical solutions, however, are amenable for providing a secure key rate bound for asymmetric protocols that are difficult for analytical methods. For all results presented, we used the Mosek7 SDP solver, with the SDPs programmed within a disciplined convex programming framework: cvxpy29,30 in Python or CVX31,32 in MATLAB.
BB84 with detector efficiency mismatch example: a direct, entanglement-based, asymmetric protocol
Let us start by considering the idealized entanglement-based version of the BB84 protocol2. Alice and Bob each receive a qubit from a maximally entangled state \(\left|{\Phi }^{+}\right\rangle =(\left|00\right\rangle +\left|11\right\rangle)/\sqrt{2}\) and measure their qubit with probability pZ in the Z-basis \(=\{\left|0\right\rangle ,\left|1\right\rangle \}\) or with probability pX = 1 − pZ in the X-basis \(=\{\left|+\right\rangle ,\left|-\right\rangle \}\). The X-basis states are defined as \(\left|\pm \right\rangle =(\left|0\right\rangle \pm \left|1\right\rangle)/\sqrt{2}\).
Alice and Bob postselect for the cases when they both measure their qubits in the same basis, discarding the outcomes when they measure in different bases. (We follow the method in ref. 6; see Supplementary Methods for the postselection framework). They then generate a secret key using the results when they both measured in either the Z-basis or X-basis.
We explicitly quantify the efficiency of each of Bob’s detectors. In the Z-basis, his detector efficiencies are \({\eta }_{{Z}_{0}}\) and \({\eta }_{{Z}_{1}}\), and in the X-basis, his detector efficiencies are \({\eta }_{{X}_{0}}\) and \({\eta }_{{X}_{1}}\). This is an asymmetric scenario that one often encounters with practical QKD systems: no two detectors have the same exact detection efficiency. As has been suggested in ref. 6, Bob’s measurement operators are the same as in the entanglement-based picture, except we now model his system as a qutrit, where the single photon exists in a single qubit subspace, and the third dimension describes the vacuum that will contribute to the no-click event. Bob’s Z-basis states are \(\{\left|0\right\rangle ,\left|1\right\rangle ,\left|{{\emptyset}}\right\rangle \}\) and his X-basis states are \(\{\left|+\right\rangle ,\left|-\right\rangle ,\left|{{\emptyset}}\right\rangle \}\), with \(\left\langle {{\emptyset}}| 0\right\rangle =\left\langle {{\emptyset}}| 1\right\rangle =0\).
We can model the problem with the following POVMs for Alice:
\({M}_{A}^{(\,\text{basis},\text{bit-value}\,)}\) | Basis | Bit-value |
|---|---|---|
\({p}_{Z}\left|0\right\rangle \left\langle 0\right|\) | Z | 0 |
\({p}_{Z}\left|1\right\rangle \left\langle 1\right|\) | Z | 1 |
\({p}_{X}\left|+\right\rangle \left\langle +\right|\) | X | 0 |
\({p}_{X}\left|-\right\rangle \left\langle -\right|\) | X | 1 |
Bob’s POVMs are
\({M}_{B}^{(\,\text{basis},\text{bit-value}\,)}\) | Basis | Bit-value |
|---|---|---|
\({p}_{Z}{\eta }_{{Z}_{0}}\left|0\right\rangle \left\langle 0\right|\) | Z | 0 |
\({p}_{Z}{\eta }_{{Z}_{1}}\left|1\right\rangle \left\langle 1\right|\) | Z | 1 |
\({p}_{X}{\eta }_{{X}_{0}}\left|+\right\rangle \left\langle +\right|\) | X | 0 |
\({p}_{X}{\eta }_{{X}_{1}}\left|-\right\rangle \left\langle -\right|\) | X | 1 |
\({M}_{B}^{{{\emptyset}}}\) | \({{\emptyset}}\) | \({{\emptyset}}\) |
Here,
The maximally entangled state \(\left|{\Phi }^{+}\right\rangle\) is generated in Alice’s laboratory so that only one part of the state is transmitted through the channel to Bob. To model this transmission through the quantum channel, we consider the depolarizing channel with a depolarizing probability p on Bob’s qubit33:
Therefore, for this protocol, we consider the statistics given by the state:
Due to the asymmetry in Bob’s measurements, in addition to the error constraints, we must also include the constraints in which both parties measure the same values in the same basis. Thus we have a total of four coarse-grained constraints:
Typically in QKD experiments, the key rates are determined by the quantum bit error rates: \({Q}_{Z}=\left\langle {E}_{Z}\right\rangle ={\rm{Tr}}({\rho }_{AB}^{\prime}{E}_{Z})\) and \({Q}_{X}=\left\langle {E}_{X}\right\rangle ={\rm{Tr}}({\rho }_{AB}^{\prime}{E}_{X})\). For the state defined in (19), one can show analytically that QZ = QX = Q = 2p.
The key rate in the asymptotic limit is simple if we assume all detectors have the same efficiency (see discussion in Supplementary Note 3). The situation is more interesting if we consider \({\eta }_{{Z}_{0}}={\eta }_{{X}_{0}}={\eta }_{0}\) and \({\eta }_{{Z}_{1}}={\eta }_{{X}_{1}}={\eta }_{1}\), in which there is detector efficiency mismatch within a single basis. This QKD configuration has been treated analytically by ref. 34 in the asymptotic regime, and the key rate analytical formula derived is
The numerical analysis in the asymptotic limit has been considered in ref. 6.
To simulate a realistic QKD system, we assume that Alice and Bob uses αPE = 10% of the signals (after postselection) for parameter estimation. We take the protocol to be correct up to εcor = 10−15 and to be secret up to εsec = 10−10. For simplicity, we assume equal security parameters of \(\varepsilon ^{\prime}\) for εPA, εEC, and ε. For parameter estimation, we assume each constraint is estimated with a failure probability up to \({\varepsilon }_{\,\text{PE}\,}^{i}=2\varepsilon ^{\prime}\). The values of the security parameters are tabulated in Table 2. Therefore, we have \(\varepsilon ^{\prime} ={\varepsilon }_{\text{sec}}/11\) for the calculation with von Neumann entropy (Eq. (11) with SDPs (35) and (36)) and \(\varepsilon ^{\prime} ={\varepsilon }_{\text{sec}}/10\) for the calculation with min-entropy (Eq. (14) with SDP (45)).
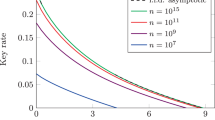
We consider the case where η0 = 1 and η1 = 25% or 75%. Figure 1 plots the secret key rate per pulse in terms of the number of pulses generated by Alice. We see that, in this case, the bound from von Neumann entropy consistently outperforms the bound from min-entropy.
The secret key rate per pulse is calculated using a the von Neumann entropy and b the min-entropy. We consider different values of error rate Q and efficiency of the “1” detector η1. We assume that the “0” detector has unit efficiency, i.e., η0 = 1. Note: the bound from the min-entropy method for Q = 5.0% and η1 = 25% is not greater than zero.
B92 example: a direct, entanglement-based, asymmetric protocol
The B92 protocol25 is a simple QKD protocol that is highly asymmetric. In this protocol, Alice prepares one of the two non-orthogonal states \(\{\left|{\phi }_{0}\right\rangle ,\left|{\phi }_{1}\right\rangle \}\), where \(\left\langle {\phi }_{0}| {\phi }_{1}\right\rangle =\cos (\theta /2)\)—each with a probability 1/2, which she will send to Bob. Alice therefore prepares the state:
Upon receiving the signals from Alice, Bob randomly measures either in the \({B}_{0}=\{\left|{\phi }_{0}\right\rangle ,\left|\overline{{\phi }_{0}}\right\rangle \}\) or in the \({B}_{1}=\{\left|{\phi }_{1}\right\rangle ,\left|\overline{{\phi }_{1}}\right\rangle \}\) basis, where \(\left\langle {\phi }_{0}| \overline{{\phi }_{0}}\right\rangle =\left\langle {\phi }_{1}| \overline{{\phi }_{1}}\right\rangle =0\). Bob postselects for those instances where he measures \(\left|\overline{{\phi }_{0}}\right\rangle\) or \(\left|\overline{{\phi }_{1}}\right\rangle\) and publicly announces “pass.” He then assigns a bit value 1 or 0, respectively, to his key. If he measures \(\left|{\phi }_{0}\right\rangle\) or \(\left|{\phi }_{1}\right\rangle\), he will announce “failure,” and both parties discard these signals.
As constraints for the problem, we use operators that describe (on the postselected state) both a successful outcome, where Bob’s measurement bit makes Alice’s prepared bit, and an unsuccessful one, where they do not agree:
In addition, since this is a prepare-and-measure protocol, we must add the constraints related to Alice’s knowledge of ρA, i.e., we add the constraints \({\Omega }_{A}^{j}\otimes {{\mathbb{I}}}_{B}=\left|{\psi }_{j}\right\rangle {\left\langle {\psi }_{j}\right|}_{A}\otimes {{\mathbb{I}}}_{B}\) obtained from the spectral decomposition of \({\rho }_{A}={\sum }_{j}{p}_{j}\left|{\psi }_{j}\right\rangle {\left\langle {\psi }_{j}\right|}_{A}\).
To simulate the channel, we again consider that the signal undergoes a depolarizing channel with probability p as it travels from Alice to Bob. Figure 2 shows the results of our numerical method in the asymptotic limit. We plot the secret key rate per pulse against the angle θ and against the depolarizing probability p after optimizing for the parameter θ. The asymptotic formula is obtained by taking the von Neumann formulation with N → ∞ (and n → ∞) and replacing the constraints \({\gamma }_{k}^{\,\text{LB}\,}\le {\rm{Tr}}({\rho }_{AB}{\Gamma }_{k})\le {\gamma }_{k}^{\,\text{LB}\,}\) with tight constraints \({\gamma }_{k}={\rm{Tr}}({\rho }_{AB}{\Gamma }_{k})\). This is a direct application of the formalism developed in ref. 6 and is not a development of this manuscript, though the results we show have not been reported elsewhere, and are a useful demonstration of the power of numerical QKD calculations.
Our results guarantee a non-zero key rate even up to p = 0.15 (with r1 = 0.00574 at θ = 64.8°), while previous analytical results predict a non-zero key rate only for p ≤ 0.06512,35,36. Furthermore, this numerical approach guarantees a higher secret key rate when compared to a previous numerical QKD approach described in ref. 5, which predicts a non-zero key rate for p ≤ 0.053. For noise levels where all methods guarantee finite-key rates, our results show tighter secure lower bounds than previous approaches. For example, for a depolarizing noise of p = 0.01, the method of ref. 6 predicts r1 = 0.248, while the previous method of ref. 5 only obtains r1 ≈ 0.21 per pulse. Now, we consider the security of the B92 protocol in the nonasymptotic regime, using the finite-key SDPs developed in the previous section. Figure 3 shows the secret key generation rate per pulse in terms of the number of signals that Alice has sent, for different values of p. For each curve, we choose the value of θ that maximizes the secret key rate. We consider the security parameters tabulated in Table 2 and assume that the protocol is εsec = 10−10-secret and εcor = 10−15-correct.
Our results provide a tighter bound than the analytic approach by ref. 36, which for example predicts a key rate of ~0.025 per pulse at 5% depolarizing noise and 108 signals. At the same depolarizing noise, our numerical approach predicts a key rate of 0.066 per pulse. Our analysis shows that the B92 protocol is a simple way of exchanging random secret keys with composable security.
TF-QKD example: an indirect, entanglement-based, symmetric protocol
TF-QKD is a recently developed variation of the MDI-QKD protocol that enables two parties to communicate through an intermediate untrusted node28. The main difference is that TF-QKD uses single-photon interference (instead of two-photon interference in MDI-QKD) and achieves a key rate that is expected to beat the fundamental information capacity for the repeaterless quantum communication rate, typically at long distances26. Because the protocol promises higher secret key rates than previous QKD protocols at long distances, it is a subject of extensive research both theoretically and experimentally. Theoretically, several security proofs of the protocol (and its variations) with asymptotic37,38,39,40 and non-asymptotic41,42,43 key rates have been proposed. Experimentally, the protocol has been demonstrated within the laboratory setting (with hundreds of kilometers of optical fibers)44,45,46,47,48, and future field tests of the protocol are to be expected.
In the entanglement-based description of TF-QKD presented in ref. 38, Alice and Bob each prepare the entangled state \(\left|{\Phi }_{q}\right\rangle =\sqrt{q}\left|00\right\rangle +\sqrt{1-q}\left|11\right\rangle\) for 0 ≤ q ≤ 1, where \(\left|0\right\rangle\) is the vacuum state (as opposed to the logical state 0) and \(\left|1\right\rangle\) is the single photon state. (In TF-QKD, the logical basis and the photon number or Fock basis coincide.) They then randomly choose to measure their qubits in the standard \(Z=\{\left|0\right\rangle ,\left|1\right\rangle \}\) basis with probability pZ or in the \(X=\{\left|+\right\rangle ,\left|-\right\rangle \}\) basis with probability pX = 1 − pZ.
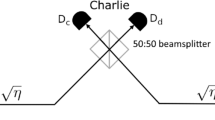
Alice and Bob send one part of their quantum signals (\(A^{\prime}\) for Alice and \(B^{\prime}\) for Bob) through optical channels with transmittance \(\sqrt{\eta }\) to Charlie. The total optical transmittance from Alice to Bob is η. Charlie then performs a Bell-state measurement on the combined state \(A^{\prime} B^{\prime}\) that he has received. One way to do so is to use a 50:50 beamsplitter to mix Alice and Bob’s signals and then route the outputs of this beamsplitter to two single-photon detectors. Charlie announces which of his two detectors fires, and Alice and Bob postselect for those events where one (and only one) detector fires. This is equivalent to postselecting for Charlie’s state being one of the Bell states \(\left|{\Psi }^{\pm }\right\rangle \,=(\left|01\right\rangle \pm \left|10\right\rangle)/\sqrt{2}\). We can postselect to \(\left|{\Psi }^{+}\right\rangle\) and \(\left|{\Psi }^{-}\right\rangle\) independently, and we focus our discussion henceforth on postselection to the single state \(\left|{\Psi }^{-}\right\rangle\) and the same arguments apply for postselection to the state \(\left|{\Psi }^{+}\right\rangle\).
The measurement POVMs for analyzing the TF-QKD protocol are
Alice’s POVM | Basis | Bit-value |
|---|---|---|
\({p}_{Z}\left|0\right\rangle {\left\langle 0\right|}_{A}\) | Z | 0 |
\({p}_{Z}\left|1\right\rangle {\left\langle 1\right|}_{A}\) | Z | 1 |
\({p}_{X}\left|+\right\rangle {\left\langle +\right|}_{A}\) | X | 0 |
\({p}_{X}\left|-\right\rangle {\left\langle -\right|}_{A}\) | X | 1 |
for Alice and
Bob’s POVM | Basis | Bit-value |
|---|---|---|
\({p}_{Z}\left|0\right\rangle {\left\langle 0\right|}_{B}\) | Z | 0 |
\({p}_{Z}\left|1\right\rangle {\left\langle 1\right|}_{B}\) | Z | 1 |
\({p}_{X}\left|+\right\rangle {\left\langle +\right|}_{B}\) | X | 0 |
\({p}_{X}\left|-\right\rangle {\left\langle -\right|}_{B}\) | X | 1 |
for Bob. In the simulation, the channel that the transmitted signal goes through is a pure-loss channel (or an amplitude damping channel for the single photon case33). We can describe the pure-loss channel \({{\mathcal{E}}}^{\text{loss}}(\sqrt{\eta })\) using a beam-splitter transformation with the help of an additional Hilbert space A0 starting in the vacuum state. For example, the photon creation operator for Alice’s transmitted signal \({\hat{a}}_{A^{\prime} }^{\dagger }\) undergoes the following transformation for a channel with transmittance \(\sqrt{\eta }\):
Here \({\hat{a}}_{{A}_{0}}^{\dagger }\) is the creation operator for the additional Hilbert space. In summary, to describe the transmitted state, Alice generates the entangled state:
which then undergoes a pure loss channel before being measured by Charlie. The state after the transmission is
We can also define a similar state for Bob:
and the overall state after both Alice’s and Bob’s transmissions is: \({\rho }_{AA^{\prime} BB^{\prime} }^{\prime}={\rho }_{AA^{\prime} }^{\prime}\otimes {\rho }_{BB^{\prime} }^{\prime}\).
Charlie, equipped with only threshold detectors, cannot distinguish between the click due to a only single photon arriving at his first detector and the click due to two photons arriving. Therefore, he is projecting the signals he receives to
We further assume that Charlie’s detectors have small but non-negligible dark counts. Let pd be the dark count probability for each clock cycle. We can modify Charlie’s projection operator above into the following POVM:
Alice and Bob postselect those cases, where Alice and Bob measure in the same basis and Charlie successfully measures \(|{\widetilde{\Psi }}_{\text{dark}}^{-}\rangle \langle {\widetilde{\Psi }}_{\text{dark}\,}^{-}|\).
The performance of the protocol in the asymptotic limit as a function of the overall loss between Alice and Bob is plotted in Fig. 4. At each loss value, we optimize for the value of q that gives the best key rate using the Brent’s method49,50. As shown in Fig. 5, the value of q increases monotonically to about ~0.93 at 40 dB loss and saturates at this value for higher losses. The high value of q suggests that a weakly pumped photon pair source, which uses spontaneous parametric down conversion or spontaneous four-wave mixing, would be ideal to generate the initial entangled states.
The rate per pulse is computed as a function of the overall loss between Alice and Bob. The different lines are for QKD operations with different dark count probability pd. The black dashed line corresponds to PLOB bound: the fundamental bound for direct repeaterless communications, calculated with η = 10−(Loss in dB)/10.
From Fig. 4, it is clear that the TF-QKD protocol—at sufficiently high losses (above ~40 dB)—can perform better than the capacity of direct repeaterless quantum communications, which we dub as the Pirandola–Laurenza–Ottaviani–Banchi (PLOB) bound after the original authors27. For a channel with a transmittance η, the bound, which is an achievable rate, is \(-{\mathrm{log}\,}_{2}(1-\eta)\) and scales linearly as ~η at low transmittance. As the dark count rate increases, the region of losses at which the TF-QKD protocol can beat the PLOB bound is reduced.
For the nonasymptotic regime, we evaluate the security of a protocol that is εsec-secret and εcor-correct with εsec = 10−10 and εcor = 10−15. We consider the values for the security parameters as in Table 2.
Figure 6 shows that the nonasymptotic bounds from von Neumann entropy can obtain better secret key rates than the PLOB bounds—even with the presence of dark counts. The plots also show that, to faithfully demonstrate a better rate than the PLOB bound in a TF-QKD experiment, both Alice and Bob must send a large number of transmissions to Charlie. For example, at 60 dB overall channel loss, they must send N ~ 1010 transmissions which are ~105 higher than the number of transmissions needed to obtain a substantial secret key in a BB84 QKD protocol (see Supplementary Fig. 1). We also compare the secret key rates calculated numerically against key rates calculated analytically in ref. 51 (see Supplementary Note 2). While this analytical approach, which makes use of entropic uncertainty relations, provides a tighter bound that beats the PLOB bound with about an order of magnitude fewer transmissions than our numerical bound, it requires expert knowledge and as such is less broadly applicable. Interestingly, our bounds from min-entropy are unable to beat the PLOB bound, but they do guarantee a substantial secret key rate even at orders of magnitude fewer transmissions.
The secret key rate per pulse is calculated at different values of dark count pd and overall channel loss. The key rates are obtained from a von Neumann entropy and from b min-entropy. The dashed lines with the same color are the PLOB bound at the different loss values, i.e., blue: 60 dB loss, orange: 80 dB loss, green: 100 dB loss. Note: For a, the dot-dashed lines are the key rates obtained using the analytical formula of ref. 51.
Discussion
We have developed SDPs for finding reliable lower bounds on the secret key rate of an arbitrary QKD protocol in the nonasymptotic regime. We presented two methods of calculating such bounds, one via an SDP for von Neumann entropy and one via an SDP for min-entropy. For some of the protocols we have considered, the bound from min-entropy provides a better key rate than the bound for von Neumann entropy at lower error rates and at lower numbers of transmissions. The computational advantage for solving the SDP for min-entropy is also clear since the problem is more tractable than that for von Neumann entropy. For a problem involving a density matrix between Alice and Bob of size q × q, the SDP (45) for min-entropy only requires us to solve for \({\mathcal{O}}({q}^{2})\) parameters while the SDP (35) for von Neumann entropy requires us to solve for \({\mathcal{O}}({q}^{4})\) parameters. Nevertheless, the nonasymptotic bound from von Neumann entropy guarantees a better secret key rate at higher numbers of transmission and, unlike the bound from min-entropy, can approach the asymptotic key rate. The supremum between these two methods should be considered as the tightest lower bound that our numerical approach offers.
So far, we have only considered security against collective attacks. Some protocols with high symmetry have been found to have the same secret key rates under collective attacks and under the more general coherent attacks. Examples of these protocols include popular protocols, such as BB84.
General methods for bounding the possible information advantage of coherent attacks over collective attacks has been outlined in multiple approaches. The first such approach uses the exponential de Finetti theorem52, but the overhead obtained by this theorem turns out to be heavy making the finite-key bounds unrealistically pessimistic. The de Finetti theorem is tight if one compares the attacks signal by signal. Reference 53 found that it suffices to only consider the entire collection of states. This method, known as the postselection technique, compares the distance between two maps: the map between the ideal protocol and an actual protocol under collective attacks and the map between the ideal protocol and an actual protocol under coherent attacks.
Using the postselection technique, we can define a new secrecy parameter under a coherent attack \({\varepsilon }_{\,\text{sec}}^{\text{coh}\,}\), which quantifies the probability the QKD protocol passes but is not secret to an eavesdropper with coherent-attack capabilities. \({\varepsilon }_{\,\text{sec}}^{\text{coh}\,}\) is related to the secrecy parameter under collective attack εsec in the following manner:
For the above value of secrecy, the key rate under coherent attack rcoh is related to the key rate under collective attack r by the following relation:
A more direct evaluation of the smoothed min-entropy using entropic uncertainty relations will produce a better key rate than our numerical method while being immediately secure against coherent attacks17,43,54,55,56. We were, however, unable to find a robust numerical reformulation of this approach.
Our numerical method is reliable and robust for calculating key rates involving single photon transmissions. Most practical implementations of QKD, however, have relied on the use of weak coherent states made by highly attenuated laser pulses. We hope to eventually evaluate such protocols numerically in the future. However, two main issues must be addressed when doing so. First, the probability of multiphoton emissions from a highly attenuated coherent light source, although small, is not negligible. Multiphoton signals are inherently insecure due to a class of attacks called the photon number splitting attack. One solution to combat the photon number splitting attack is to implement the decoy state protocol. In the decoy state protocol, Alice prepares an additional set of states—the decoy states—that are used to detect the presence of eavesdropping57,58. Therefore, we plan to incorporate decoy state analysis to the numerical method in the future.
Second, Alice’s coherent state transmission uses an infinite-dimensional Hilbert space. The calculation on this infinite-dimensional space is extremely challenging. For simple QKD protocols, there exist squashing maps that provide direct correlations between measurements in the infinite-dimensional optical implementation and measurements in the abstract low-dimensional protocol59,60,61. Therefore, the numerical method (or the user) must also be able to determine the appropriate squashing map to reduce the size of the problem. The numerical method presented in refs. 10,11 has been shown to be compatible with decoy states—obviating the use of squashing maps—by breaking the infinite-dimensional problem into the dimensions of the signals. This warrants a further study that combines this method with our approach of handling the finite-size statistics.
To conclude, our results extend the earlier numerical QKD approaches by presenting a general robust framework for calculating QKD key rates in nonasymptotic regimes. The numerical framework is especially useful when analyzing asymmetric QKD protocols that are difficult to study analytically. The source code for our numerical framework can be found in https://github.com/dbunandar/numerical_qkd, which we hope will be useful for democratizing the QKD security proofs that are needed to estimate the amount of secret key generated in any QKD operation.
Note added: We recently became aware of another proposal for calculating the finite-key rate of a QKD protocol numerically62,63.
Methods
Proof of the relationship between min-entropy and the fidelity function
We include the proof from ref. 23 here for completeness. In this proof, we consider the pure state shared between Alice, Bob, and Eve: ρABE, and will use the max-entropy, defined as:
The max-entropy is dual to the min-entropy, i.e., \({H}_{\min }(X| Y)=-{H}_{\max }(X| Z)\) for any pure state ρXYZ.
Now, consider the pure state \({\tilde{\rho }}_{{Z}_{A}ABE}={V}_{{Z}_{A}}{\rho }_{ABE}{V}_{{Z}_{A}}^{\dagger }\) with the isometry \({V}_{{Z}_{A}}={\sum }_{j}{\left|j\right\rangle }_{{Z}_{A}}\otimes {Z}_{A}^{j}\) representing Alice’s key map. We can derive the following series of equalities:
which relates the min-entropy to a maximization of the fidelity. The third line is true because an isometry must satisfy \({V}_{{Z}_{A}}{V}_{{Z}_{A}}^{\dagger }={\mathbb{I}}\), and the fourth line uses the fact that fidelity is invariant under isometries.
SDP for quantum relative entropy
Let us express the problem in terms of a convex optimization problem with quantum relative entropy as the objective function:
Here \({Z}_{A}^{j}\) are projectors onto the signal-state basis of the Hilbert space of A.
The SDP for the (m, k)-approximation of the quantum relative entropy in this case is21:
where wj and sj are the weights and nodes for the m-point Gauss–Legendre quadrature on interval [0, 1], respectively. Here, \(\left|e\right\rangle\) is the vector obtained by vertically stacking the columns of an identity matrix.
Solving the approximate problem above only gives us a density matrix \({\hat{\rho }}_{AB}\) that is close to the optimal matrix \({\rho }_{AB}^{* }\). However, as it pointed out by ref. 6, we can use this close-to-optimal density matrix \({\hat{\rho }}_{AB}\) and find a secure lower bound through linearization of the convex objective function: \(f(\rho)\equiv D(\rho | | {Z}_{A}^{j}\rho {Z}_{A}^{j})\). Using the fact that this objective function is convex and differentiable, we have:
where
The primal SDP for the last term in Eq. (36) is:
and the dual SDP is:
Key rate problems for some of the more well-known QKD protocols, e.g., the BB84 protocol, can be solved efficiently (within a second on a personal computer) with Eq. (35) using a commercial or an open-source SDP solver, e.g., Mosek7 or SeDuMi8. Some larger problems, such as the prepare-and-measure protocol or the MDI-QKD protocol, require simplification that makes use of the block diagonal structure of the density operator ρAB to be efficiently solved, see Supplementary Note 1 and refs. 64,65.
The main inefficiency in our formulation comes during step one. Suppose that ρAB is a q × q matrix, then X, Y, Z, and Mi matrices are of size q2 × q2. Therefore, the problem needs to solve a total of k blocks of 2q2 × 2q2 positive semidefinite matrices along with another m blocks of (q2 + 1) × (q2 + 1) positive semidefinite matrices. It is therefore desirable to find another approximation method that requires a smaller number of parameters.
SDP for min-entropy and quantum fidelity
Ref. 24 shows how the fidelity can be expressed in terms of a simple linear SDP. The primal SDP for computing the \(\sqrt{F(P,Q)}\) between two operators P ≽ 0 and Q ≽ 0 is:
and the dual SDP is:
We can therefore formulate the following optimization problem:
In particular, we can compute the following quantity:
The primal SDP problem for the quantity \({2}^{-g({{\mathcal{C}}}_{{\varepsilon }_{\text{PE}}})/2}\) is
which can be transformed into the following dual problem:
Solving the dual problem (45) directly provides a reliable lower bound to the key rate. The min-entropy SDP derived here has a computational advantage over the von Neumann SDP, due to the fact that, other than the positive real numbers xi and yi, only two matrices Y11 and Y22—both of the same size as the density matrix ρAB—have to be computed.
Data availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Code availability
The numerical finite-key QKD codebase can be found in this repository: https://github.com/dbunandar/numerical_qkd.
References
Pirandola, S. et al. Advances in quantum cryptography. Preprint at http://arxiv.org/abs/1906.01645 (2019).
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proc. IEEE International Conference on Computers, Systems, and Signal Processing. 175–179 (IEEE, 1984).
Bruß, D. Optimal eavesdropping in quantum cryptography with six states. Phys. Rev. Lett. 81, 3018–3021 (1998).
Gottesman, D., Lo, H.-K., Lütkenhaus, N. & Preskill, J. Security of quantum key distribution with imperfect devices. Quantum Inf. Comput. 4, 325–360 (2004).
Coles, P. J., Metodiev, E. M. & Lütkenhaus, N. Numerical approach for unstructured quantum key distribution. Nat. Commun. 7, 11712 (2016).
Winick, A., Lütkenhaus, N. & Coles, P. J. Reliable numerical key rates for quantum key distribution. Quantum 2, 77 (2018).
MOSEK ApS. The MOSEK optimization toolbox for MATLAB manual. Version 8.1. http://docs.mosek.com/8.1/toolbox/index.html (2017).
Sturm, J. F. Using SeDuMi 1.02, a Matlab toolbox for optimization over symmetric cones. Optimization Methods Softw. 11, 625–653 (1999).
Tütüncü, R. H., Toh, K. C. & Todd, M. J. Solving semidefinite-quadratic-linear programs using SDPT3. Math. Program. 95, 189–217 (2003).
Wang, Y., Primaatmaja, I. W., Lavie, E., Varvitsiotis, A. & Lim, C. C. W. Characterising the correlations of prepare-and-measure quantum networks. npj Quantum Inf. 5, 17 (2019).
Primaatmaja, I. W., Lavie, E., Goh, K. T., Wang, C. & Lim, C. C. W. Versatile security analysis of measurement-device-independent quantum key distribution. Phys. Rev. A 99, 062332 (2019).
Renner, R. Security of quantum key distribution. Int. J. Quantum Inf. 06, 1–127 (2008).
Tomamichel, M., Schaffner, C., Smith, A. & Renner, R. Leftover hashing against quantum side information. IEEE Trans. Inform. Theory 57, 5524–5535 (2011).
Scarani, V. & Renner, R. Quantum cryptography with finite resources: unconditional security bound for discrete-variable protocols with one-way postprocessing. Phys. Rev. Lett. 100, 200501 (2008).
Tomamichel, M., Martinez-Mateo, J., Pacher, C. & Elkouss, D. Fundamental finite key limits for one-way information reconciliation in quantum key distribution. Quantum Inf. Process. 16, 280 (2017).
Cai, R. Y. Q. & Scarani, V. Finite-key analysis for practical implementations of quantum key distribution. New J. Phys. 11, 045024 (2009).
Curty, M. et al. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 5, 3732 (2014).
Lim, C. C. W., Curty, M., Walenta, N., Xu, F. & Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 89, 022307 (2014).
Zhang, Z., Zhao, Q., Razavi, M. & Ma, X. Improved key-rate bounds for practical decoy-state quantum-key-distribution systems. Phys. Rev. A 95, 012333 (2017).
Tomamichel, M., Colbeck, R. & Renner, R. A fully quantum asymptotic equipartition property. IEEE Trans. Inf. Theory 55, 5840–5847 (2009).
Fawzi, H., Saunderson, J. & Parrilo, P. A. Semidefinite approximations of the matrix logarithm. Found. Comput. Math. 19, 259–296 (2019).
Bratzik, S., Mertz, M., Kampermann, H. & Bruß, D. Min-entropy and quantum key distribution: Nonzero key rates for “small” numbers of signals. Phys. Rev. A 83, 022330 (2011).
Coles, P. J. Unification of different views of decoherence and discord. Phys. Rev. A 85, 042103 (2012).
Watrous, J. Simpler semidefinite programs for completely bounded norms. Theory Comput. 5, 217–238 (2012).
Bennett, C. H., Bessette, F., Brassard, G., Salvail, L. & Smolin, J. Experimental quantum cryptography. J. Cryptol. 5, 3–28 (1992).
Lucamarini, M., Yuan, Z. L., Dynes, J. F. & Shields, A. J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 557, 400–403 (2018).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Diamond, S. & Boyd, S. CVXPY: a Python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 17, 2909–2913 (2016).
Akshay Agrawal, S. D., Verschueren, R. & Boyd, S. A rewriting system for convex optimization problems. J. Control. Decis. 5, 42–60 (2018).
Grant, M. & Boyd, S. CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx (2014).
Grant, M. & Boyd, S. In Recent Advances in Learning and Control, Lecture Notes in Control and Information Sciences (eds Blondel, V., Boyd, S. & Kimura, H.). 95–110 (Springer-Verlag, 2008).
Nielsen, M. & Chuang, I. Quantum Computation and Quantum Information. Cambridge Series on Information and the Natural Sciences (Cambridge University Press, 2000).
Fung, C. C.-H. F., Tamaki, K., Qi, B., Lo, H.-K. H. & Ma, X. Security proof of quantum key distribution with detection efficiency mismatch. Quantum Inf. Comput. 9, 0131–0165 (2009).
Tamaki, K. & Lütkenhaus, N. Unconditional security of the Bennett 1992 quantum key-distribution protocol over a lossy and noisy channel. Phys. Rev. A 69, 032316 (2004).
Sasaki, H., Matsumoto, R. & Uyematsu, T. Key rate of the B92 quantum key distribution protocol with finite qubits. In 2015 IEEE International Symposium on Information Theory (ISIT). 696–699 (IEEE, 2015).
Tamaki, K., Lo, H.-K., Wang, W. & Lucamarini, M. Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. Preprint at http://arxiv.org/abs/1805.05511 (2018).
Curty, M., Azuma, K. & Lo, H.-K. Simple security proof of twin-field type quantum key distribution protocol. npj Quantum Inf. 5, 64 (2019).
Ma, X., Zeng, P. & Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 8, 031043 (2018).
Wang, X.-B., Yu, Z.-W. & Hu, X.-L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 98, 062323 (2018).
Jiang, C., Yu, Z.-W., Hu, X.-L. & Wang, X.-B. Unconditional security of sending or not sending twin-field quantum key distribution with finite pulses. Phys. Rev. Appl. 12, 024061 (2019).
He, S.-F., Wang, Y., Li, H.-W. & Bao, W.-S. Finite-key analysis for a practical decoy-state twin-field quantum key distribution. Preprint at http://arxiv.org/abs/1910.12416 (2019).
Lorenzo, G. C., Navarrete, A., Azuma, K., Curty, M. & Razavi, M. Tight finite-key security for twin-field quantum key distribution. Preprint at http://arxiv.org/abs/1910.11407 (2019).
Minder, M. et al. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat. Photonics 13, 334–338 (2019).
Wang, S. et al. Beating the fundamental rate-distance limit in a proof-of-principle quantum key distribution system. Phys. Rev. X 9, 021046 (2019).
Zhong, X., Hu, J., Curty, M., Qian, L. & Lo, H.-K. Proof-of-principle experimental demonstration of twin-field type quantum key distribution. Phys. Rev. Lett. 123, 100506 (2019).
Liu, Y. et al. Experimental twin-field quantum key distribution through sending or not sending. Phys. Rev. Lett. 123, 100505 (2019).
Chen, J.-P. et al. Sending-or-not-sending with independent lasers: Secure twin-field quantum key distribution over 509 km. Phys. Rev. Lett. 124, 070501 (2020).
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. Numerical Recipes in FORTRAN; The Art of Scientific Computing 2nd edn (Cambridge University Press, New York, NY, 1993).
Brent, R. Algorithms for Minimization Without Derivatives. Dover Books on Mathematics (Dover, 2013).
Yin, H.-L. & Chen, Z.-B. Finite-key analysis for twin-field quantum key distribution with composable security. Sci. Rep. 9, 17113 (2019).
Renner, R. Symmetry of large physical systems implies independence of subsystems. Nat. Phys. 3, 645–649 (2007).
Christandl, M., König, R. & Renner, R. Postselection technique for quantum channels with applications to quantum cryptography. Phys. Rev. Lett. 102, 020504 (2009).
Tomamichel, M. & Renner, R. Uncertainty relation for smooth entropies. Phys. Rev. Lett. 106, 110506 (2011).
Tomamichel, M., Lim, C. C. W., Gisin, N. & Renner, R. Tight finite-key analysis for quantum cryptography. Nat. Commun. 3, 634 (2012).
Furrer, F. et al. Continuous variable quantum key distribution: finite-key analysis of composable security against coherent attacks. Phys. Rev. Lett. 109, 100502 (2012).
Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Beaudry, N. J., Moroder, T. & Lütkenhaus, N. Squashing models for optical measurements in quantum communication. Phys. Rev. Lett. 101, 093601 (2008).
Tsurumaru, T. & Tamaki, K. Security proof for quantum-key-distribution systems with threshold detectors. Phys. Rev. A 78, 032302 (2008).
Gittsovich, O. et al. Squashing model for detectors and applications to quantum-key-distribution protocols. Phys. Rev. A 89, 012325 (2014).
George, I. & Lütkenhaus, N. Numerical calculations of finite key rate for general QKD protocols. In 9th International Conference on Quantum Cryptography (2019).
George, I., Lin, J. & Lütkenhaus, N. Numerical calculations of finite key rate for general quantum key distribution protocols. Preprint at http://arxiv.org/abs/2004.11865 (2020).
Lin, J., Upadhyaya, T. & Lütkenhaus, N. Asymptotic security analysis of discrete-modulated continuous-variable quantum key distribution. Phys. Rev. X 9, 041064 (2019).
Govia, L. C. G. et al. Clifford-group-restricted eavesdroppers in quantum key distribution. Phys. Rev. A 101, 062318 (2020).
Song, T.-T., Wen, Q.-Y., Guo, F.-Z. & Tan, X.-Q. Finite-key analysis for measurement-device-independent quantum key distribution. Phys. Rev. A 86, 022332 (2012).
Acknowledgements
We would like to thank Norbert Lütkenhaus (University of Waterloo) and Jie Lin (University of Waterloo) for their helpful feedback and their suggestions to include the analysis against coherent attacks. We acknowledge the support from the Office of Naval Research CONQUEST program N00014-16-C-2069. We thank members of the CONQUEST Team for their helpful inputs: Saikat Guha (University of Arizona), Jeffrey Shapiro (MIT), Mark Wilde (Louisiana State University), and Franco Wong (MIT). D.E. acknowledges the support from the NSF Center for Quantum Networks and from the Under Secretary of Defense for Research and Engineering administered through the MIT Lincoln Laboratory Technology Office. D.B. and D.E. also acknowledge the support from the Air Force Office of Scientific Research program FA9550-16-1-0391, supervised by Gernot Pomrenke.
Author information
Authors and Affiliations
Contributions
D.B. and D.E. contributed to the initial conception of the ideas. D.B. provided the initial security proofs, and L.C.G.G. and H.K. assisted with the simplifications and extensions to the proofs. D.B. and L.C.G.G. wrote the source code, and D.B. implemented the code for the different examples. All authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bunandar, D., Govia, L.C.G., Krovi, H. et al. Numerical finite-key analysis of quantum key distribution. npj Quantum Inf 6, 104 (2020). https://doi.org/10.1038/s41534-020-00322-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00322-w
This article is cited by
-
High-rate intercity quantum key distribution with a semiconductor single-photon source
Light: Science & Applications (2024)
-
Improved security bounds against the Trojan-horse attack in decoy-state quantum key distribution
Quantum Information Processing (2024)
-
Neural network-based prediction of the secret-key rate of quantum key distribution
Scientific Reports (2022)