Abstract
Nowadays the most intriguing features of wave-particle complementarity of single-photons are exemplified by the famous Wheeler’s delayed-choice experiment with linear optics, nuclear magnetic resonance, and integrated photonic device systems in the optical platform. Until now, the delayed-choice experiments are demonstrated by either massless photons or massive particles, such as atoms, however, there is no report demonstrating Wheeler’s ideas in a hybrid system which consists of photons and atoms simultaneously. Here, we demonstrate a Wheeler’s delayed-choice experiment in an interface of light and atomic memory, in which the cold atomic memory makes the heralded single-photon divided into a superposition of atomic collective excitation and leaked pulse, thus acting as memory-based beam-splitters. We observe the intermediate states between particle and wave behavior by changing the relative proportion of the quantum random number generator, the second memory efficiency, and the relative storage time of two memories. The reported results confirm Bohr’s view that it makes no sense to illustrate the wave-like or particle-like behavior of light and matter before the measurement happens, and are helpful for improving our comprehension of the complementarity principle under the interface of light-atom interaction.
Similar content being viewed by others
Introduction
The choice of measurement determining the behavior of light in Wheeler’s famous delayed-choice experiment1,2,3,4,5,6,7,8 exhibits the counterintuitive feature of quantum mechanics9. To date, delayed-choice experiments have been studied in various systems of linear optics7,10,11 and integrated photonic device12. In these experiments, the conventional spatial Mach-Zender interferometers (MZIs) are exploited, where a single-photon exhibiting wave- or particle-like behavior depends on the experimental apparatus it is confronted by. Based on the device-independent causal model, the researchers provide a complementary method to test wave-particle duality13,14,15,16. Recently, Wheeler’s delayed-choice experiment was implemented between satellite and ground stations17, extending quantum mechanism tests to space. Besides, a twofold quantum delayed-choice experiment in a superconducting circuit was reported18. Apart from the fundamental aspects of the delayed-choice experiments well studied in these systems, the delayed-choice entanglement swapping19,20 and delayed-choice decoherence suppression21 have been reported.
Generally, people test Wheeler’s ideas by using massless single-photon in most delayed-choice experiments. Recently, studying wave-particle complementarity with massive particles, such as metastable hydrogen, spin interferometers with neutrons and atoms5,22,23,24, has attracted many interests for a deeper understanding of Bohr’s complementarity principle towards macroscopic systems. In this regard, it is interesting to consider what will happen when we study the delayed-choice experiment under the picture of light-matter interaction, which extends the demonstration of Wheeler’s experiment towards a hybrid system including both massive particles and massless photons. As an intriguing phenomenon in light-matter interaction, atomic quantum memory (QM) can coherently transfer a single-photon to a quasiparticle25 consisting of a single atomic excitation shared among a large number of ground-state atoms. Moreover, the QM can also be exploited to construct a temporal beam splitter26,27. Therefore, testing Wheeler’s ideals with a QM enables us to extend the comprehension of complementarity associated with light and matter simultaneously.
Here, we demonstrate a Wheeler’s delayed-choice experiment based on atomic QM. Three cold 85Rb atomic ensembles trapped in three 2D magneto-optical traps (MOT) are used. The first ensemble is exploited to generate a heralded single-photon, and the other two acting as the Raman memory-based beam splitters (M-BSs)26,28,29,30 are utilized to configure a temporal MZI. The memory herein is a quantum device that divides the single-photon packet into atomic and photonic components when the memory efficiency is less than unitary. In the delayed-choice experiment, we observe an intermediate state between particle-like and wave-like behavior, indicating that particle and wave are not realistic physical properties but merely dependent on how we observe the photon, which denies the hidden-information theory. This demonstration of the delayed-choice experiment in the interface of light-atom interaction advances further fundamental tests of quantum mechanism towards macroscopic scale and maybe in favor of our comprehension of wave-particle properties of light and matter.
Results
Experimental setup and theoretical analysis
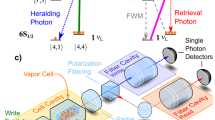
The simple energy level diagram is shown in Fig. 1a. We firstly generate a Stokes and anti-Stokes photon (signal 2 and signal 1) through spontaneously four-wave mixing (SFWM)31,32 process in MOT A, as shown in Fig. 1b. Here, pump 1 (795 nm, Rabi frequency 2π × 1.19 MHz) and pump 2 (780 nm, Rabi frequency 2π × 14.79 MHz) are orthogonal polarization and propagate counter collinearly in MOT A with optical depth (OD) of 40. The angle between pump lasers and signals is 2.8∘, and we collect the signal 2 (780 nm) and signal 1 (795 nm) by using the lens with a focal length of 300 mm. Since signal 2 is detected by a single-photon counting module (avalanche diode 2, PerkinElmer SPCM-AQR-15-FC, 50% efficiency, maximum dark count rate of 50/s), the heralded single-photon signal 1 is coupled into a 200-m single-mode fiber for further demonstration of the delayed-choice experiment.
a Energy level diagram. MOT A, B and C represent three magneto-optical traps. Single photons S 1 and S 2 are generated from MOT A using the SFWM process with single-photon detuning Δ/2π = 50 MHz. The MOT B/C acts as QM based on Raman storage protocol. States \(\left|1\right\rangle\), \(\left|2\right\rangle\), \(\left|3\right\rangle\) and \(\left|4\right\rangle\) correspond to 85Rb atomic levels of 5S1/2(F = 2), 5S1/2(F = 3), 5P1/2(F = 3) and 5P3/2(F = 3) respectively. b Simplified experimental setup. Pump 1/2 is pump light beam. Coupling 1/2 represents the coupling light beam. EOM is an electro-optic modulator to introduce a phase shift, and 200-m fiber is aimed for an optical delay of 1 μs. D 1/D 2, avalanche diode 1/2. c Schematic of the evolution of single-photon pulse in the delayed-choice experiment. d The wave-particle duality of single photons. When the M-BS 2 is inserted, the red experimental data dots are obtained and the interference curve is fitted with a sine function, which is a wave-like phenomenon. The black line is fitted with a constant function while M-BS 2 is moved out, the interference is vanished, revealing a particle-like phenomenon. The error bars in the experimental data are estimated from Poisson statistics and represent one standard deviation.
QM served as a quantum device in the synchronization of quantum information33 could enable the photon pulse separated in time, where the separated time interval and the amplitude of photons can be arbitrarily configured. Therefore, the QM can be considered as a dynamically configurable temporal BS26. Here we exploit two Raman memories B and C as M-BSs to construct a temporal interferometer. As depicted in Fig. 1c, we schematically present the evolution of single-photon pulse in the temporal domain. The implementation of the delayed-choice scheme is illustrated as follows. At first, the signal 1 photon is split into two parts by M-BS 1 with the following expressed state
here, η1con, is the conversion efficiency of optical signal to spin-wave in memory B. The right two terms in above equation represent the split states corresponding to the leaked part \(\left|L\right\rangle\) and stored part \(\left|{R}_{{\rm{a}}1}\right\rangle\) during the quantum storage process respectively, the coefficients \(\sqrt{1-{\eta }_{1{\rm{con}}}}\) and \(\sqrt{{\eta }_{1{\rm{con}}}}\) are the amplitude of these two parts. θ1 = w ⋅ ▵t is the relative phase between the states \(\left|L\right\rangle\) and \(\left|{R}_{{\rm{a}}1}\right\rangle\) with the storage time ▵t. The stored part \(\left|{R}_{{\rm{a}}1}\right\rangle\) corresponds to the atomic collective excited state (see “Methods” for more details), which is a state containing a large amount of massive atoms. The expression given by Eq. (1) corresponds to superposition state of photon and atom, and thus we do not know whether or not the photon is transformed to the atomic state.
After storage time of ▵t = 200 ns, we turn on the coupling laser to read the spin-wave in memory B out as \(\left|R\right\rangle\). Between memory B and C, we make signal travel through a 200-m fiber for an optical delay of about 1 μs to increase the length of interferometer (see “Methods”). Now the signal 1 photon is transformed into a photonic superposition state \(\left|{\psi }_{{\rm{1}}}\right\rangle \sim \sqrt{1-{\eta }_{1{\rm{c}}on}}\left|L\right\rangle +\sqrt{{\eta }_{1}}{e}^{i{\theta }_{1}}\left|R\right\rangle\), (here η1 = η1conη1stored, is the total storage efficiency of optical signal in memory B, including the efficiency of optical signal conversion to spin-wave and spin-wave retrieval to optical excitation η1stored). These two split photon packets separated in time domain are equivalent to the two arms of interferometer. We vary the relative phase between two interferometer arms by modulating a phase shift on \(\left|R\right\rangle\), which is controlled by an electro-optical modulation (EOM). The state becomes
here, φEOM is the added phase by EOM.
As soon as the leaked part arrives at M-BS 2 (memory C), a random choice to insert or remove the M-BS 2 has been made to realize the Wheeler’s delayed-choice experiment, which is controlled by a quantum random number generator (QRNG) (see “Methods” for more details). The whole system can be described by a density operator:
here, ξ represents the random probability of inserting M-BS 2. \(\left|{\psi }_{{\rm{2}}}\right\rangle\) and \(\left|{\psi }_{{\rm{1}}}\right\rangle\) can be considered as a wave-like and particle-like state respectively11, and whole system is a classical mixture of these two states. \(\left|{\psi }_{{\rm{2}}}\right\rangle\) corresponds to the case that M-BS 2 is inserted, and thus the whole setup forms a closed MZI. After switching off the coupling 2 light with Rabi frequency Ωc2 = 2π × 24.21 MHz, the leaked part is converted to the spin-wave in memory C. The \(\left|{\psi }_{{\rm{2}}}\right\rangle\) can be denoted by
η2con is the conversion efficiency of leaked part \(\left|L\right\rangle\) in Eq. (2) to spin-wave in memory C. After the same storage time of 200 ns (thus the relative phase θ1 = θ2 = ▵θ), we switch on the coupling 2 light to retrieve the spin-wave \(\left|{R}_{{\rm{a}}2}\right\rangle\) to optical signal, and check the photon’s behavior by projecting the density matrix ρ to the retrieved part \(\left|R\right\rangle\). Ultimately, the probability of photon has a function of
In analogy to η1, η2 = η2conη2stored is the total storage efficiency of optical signal in memory C, where η2stored is the efficiency of spin-wave retrieval to optical excitation. As depicted in Fig. 1d, the wave-like and particle-like behaviors are observed corresponding to ξ = 1/0 respectively. If M-BS 2 is inserted (for ξ = 1), the two arms of the interferometer are recombined and we can observe a wave-like phenomenon sketched in the red curve, in which the interference is necessary and sufficient for the demonstration of wave property of photons. On the contrary, while the M-BS 2 is removed (ξ = 0), corresponding to the situation that the leaked part is not converted to spin-wave and passes through the MOT C directly, the interferometer remains open. Hence, we observe no interference revealing the particle-like nature, as shown in the black line. To further confirm the particle nature of photons while the interferometer is open, we measure the heralded auto-correlation parameter α (see “Methods”) of photons after storage in memory B. The obtained α = 0.304 ± 0.055 < 0.5 clearly reflects the particle property of photons. Moreover, we measure a distinguishability parameter D = (NB − N0)/(NB + N0) to characterize the “which-way” information of photons7,8. At first, we block one arm by removing the memory C, then we measure the coincidence counts NB while the other arm is open (memory B is inserted) and N0 when the other arm is blocked (memory B is removed), respectively. Here, the value of N0 is mainly caused by the dark counts of the detector and residual background noise in the generation of photon pairs. The measured D is 0.92, the same value is obtained if we first remove the memory B, and then measure the coincidence counts while the memory C is inserted and removed respectively. This value shows the path-information of photons, further suggesting the particle-like behavior.
Observation of the intermediate state between particle-like and wave-like behaviors
We further investigate the behaviors of photons by changing the relative proportion of QRNG ξ = 0, 50%, 1. In Fig. 2, ξ takes different values and we observe a phenomenon from particle to wave. In the closed MZI as depicted in Fig. 2c, the calculated visibility of interference is not very high, and we attribute it to the mismatching of two retrieved signals, which is mainly caused by the different bandwidths of two memories. In Fig. 2a, the interference disappears, revealing the particle-like nature of photons. Foremost, we investigate the intermediate situation between wave- and particle-like behaviors, as described in Fig. 2b. This intermediate state reveals that particle and wave are not realistic physical properties, denying the hidden-information theory. Besides, as shown in Fig. 2d, we simulate the wave-like, particle-like behaviors and intermediate situations between them by using our experimental parameters to further illustrate the Wheeler’s delayed-choice experiment. All the results elucidate that the observed behavior of photons is intrinsically dependent on the measurement.
a–c The recorded coincidence counts against the EOM phase with a step of π/4. The red curves are fitted by \(N[\xi | \sqrt{1-{\eta }_{1{\rm{con}}}}\sqrt{{\eta }_{2}}+\sqrt{{\eta }_{1}}{e}^{i{\varphi }_{{\rm{EOM}}}}{| }^{2}+(1-\xi ){\eta }_{1}]\), N is the total photon counts N = 650 ± 10, η1 = 0.151 ± 0.002, η1con = 0.874 ± 0.011, η2 = 0.247 ± 0.005. The fitted ξ is 0.001, 0.530, 0.960 for (a)–(c) respectively. The error bars denote one standard deviation. d Simulated result of wave-like, particle-like behaviors and intermediate situations as a function of ξ with N = 650, η1 = 0.151, η1con = 0.874, η2 = 0.247.
The interference versus different storage efficiency
Next, we explore the relationship between interference ability of our apparatus and storage parameters (e.g., storage efficiency and storage time) in the interface of light-matter interaction. As illustrated in Fig. 3, the visibility is varied against different storage efficiencies in memory C. Here, we change the storage efficiency by varying the Rabi frequency of coupling 2 light from 2π × 27.86 to 0. To obtain perfect interference, we should balance the retrieved signals after two storage processes. In this regard, we choose a suitable storage efficiency of spin-wave in memory C. Aside from this, it is also crucial to the choose a suitable storage efficiency in memory B. Because if the storage efficiency in memory B is too large, the leaked part as the input of the second storage process is too little to obtain the enough retrieved signal after memory C. As a result, we optimize the storage efficiencies in memory B and C to achieve the best interference, as shown in Fig. 3a. The minimum visibility (Fig. 3e) corresponds to the storage efficiency of 0 in memory C, suggesting the particle behavior. Figure 3f is the simulated interference as a function of effective storage efficiency of memory C. All the results are in favor of our comprehension of Bohr’s complementarity principle in light-matter interaction with the aid of this flexible and controllable temporal MZI.
a–e The interference pattern with different storage efficiency of spin-wave in memory C. The red curves are fitted by \(N| \sqrt{1-{\eta }_{1{\rm{con}}}}\sqrt{{\eta }_{2}}+\sqrt{{\eta }_{1}}{e}^{i{\varphi }_{{\rm{EOM}}}}{| }^{2}\) (where N = 568 ± 40, η1 = 0.122 ± 0.011, η1con = 0.850, and η2 = 0.331, 0.259, 0.114, 0.015, 0 for (a)–(e) respectively). The error bars represent one standard deviation. f The simulated interference ability of interferometer with the change of η2 (where N = 568, η1 = 0.122, η1con = 0.850).
The controllable temporal interference with different storage time
In our scheme, it is intriguing to study the wave-particle complementarity by varying the storage time of spin wave in memory C, as sketched in Fig. 4. The best interference pattern is shown in Fig. 4c with the storage time of 200 ns, which is identical to the storage time in memory B. Intrinsically, the visibility of interference is positively correlated to the overlap among two retrieval signals. While we vary the storage time of spin wave in memory C, the degree of temporal overlap between two parts of signal 1 is also changing. There is no interference pattern in Fig. 4a/f with the storage time of 160/280 ns, in which the two retrieved signals are almost separated without overlap. The overlap time window is ~120 ns (=280–160 ns), which is closed to the coherence time (110 ns) of the retrieved optical mode. In addition, the overlap of two retrieved signals can also be controlled by adjusting the waveforms or bandwidth of two retrieval wave packets.
The coherence of temporal interferometer
The two signal parts \(\left|L\right\rangle ,\ \left|R\right\rangle\) (leaked and retrieved signals) marked in Fig. 1c are exploited to construct the two arms of the temporal MZI. To avoid the retrieved signal interfering with itself on M-BS 2, we enlarge the length of interferometer arms by inserting a 200-m optical fiber (corresponding to a time delay of ~1 μs) in the optical path of signal 1, which is longer than the coherence length of \(\left|R\right\rangle\) (~50 ns) determined by the time width of the signal 1 photon.
In Fig. 5a, the recorded coincidence counts with ΔΦ = 0 and ΔΦ = π are illustrated in red and purple data respectively. The demonstration of wave-particle duality is not only dependent on the storage efficiencies η1 and η2, but also the coherence of the M-BSs. Here, we measure the decoherence of two memories and interferometer respectively, as depicted in Fig. 5b. The red and black curves show the coherence of memory B and C with a coherence time of 420 ns and 893 ns respectively. The blue curve is the coherence (with coherence time 691 ns) of interferometer when the phase is ΔΦ = 0. Ultimately, we explore the relationship between OD of memory C and interference visibility. Essentially, the change of OD of memory C equally corresponds to the variation of storage efficiency of η2 in memory C. We vary the OD of memory C from 0 to 40, and meanwhile measure the η2. The visibility V containing η2 can be expressed as \(V=[{P}_{\max }-{P}_{\min }]/[{P}_{\max }+{P}_{\min }]\), and we fit it with our experimental data, as shown in Fig. 5c.
a The interference of two stored spin waves in memory B and C, when the modulated phase are 0 and π, respectively. b The recorded coincidence counts against storage time in memory B (red), and memory C (black). The red and black curves are fitted by Ae−t/T1 + g0 (where red curve, A = 503, T1 = 420, g0 = 58, and back curve, A = 457, T1 = 893, g0 = 51). The interference results (blue) with a modulated phase of ΔΦ = 0 against the storage time. Here, the storage time in memory B and C is identical. The blue curve is fitted by Ae−t/T2 + g0 (where A = 304, T2 = 691, g0 = 32). c The interference visibility against the OD of atoms in memory C. The red curve corresponds to theoretical fitting (where η1 = 0.132, η1con = 0.88). The error bars represent one standard deviation.
Discussion
Our Wheeler’s delayed-choice experiment relies on the key element of M-BS, its properties can be tuned arbitrarily which are very different from other works10,11,12. For example, the wave-particle duality demonstrated herein is dependent on the pulse matching in the temporal domain between two retrieved signals in the context. Furthermore, the utilized M-BS can configure a high-dimensional MZI with multiple temporal arms by addressing multipulse with a Raman QM26, by which one can demonstrate the Wheeler’s delayed-choice experiment with multiple photonic paths. In addition, a new quantum key distribution protocol (QKD)34 similar to the BB84 protocol has been proposed based on the single-photon quantum eraser, which uses a single photon encoded in the time-bin degree of freedom to achieve quantum cryptography. In our work, the time-bin qubits could be obtained by using QM, and the temporal MZI enables two paths combined in a single-mode fiber, which is promising for implementing such kind of QKD protocol in quantum information processing.
In summary, we have demonstrated a Wheeler’s delayed-choice experiment with a temporal MZI consisting of Raman M-BSs.The used flexible and configurable temporal interferometer not only work for constructing a hybrid system but also help for studying the intermediate situation between wave and particle behavior. By changing the relative proportion of QRNG, the storage efficiency and the storage time of QM, we observe the wave-like, particle-like behavior as well as intermediate states between them. The resulting Wheeler’s delayed-choice experiment under light-atom interaction gives a fundamental aspect that it makes no sense to illustrate the wave-like or particle-like behavior of light and matter before the measurement happens. This experiment paves the way for implementing other foundational-like tests and applications of quantum mechanics in the macroscopic interface of light-atom interaction.
Methods
Photon pair generation and single-photon character
The repetition rate of our experiment is 100 Hz, and the MOT trapping time is 8.7 ms. Moreover, the experimental window is 1.3 ms. The fields of pumps 1 and 2 are controlled by two acousto-optic modulators (AOMs) modulated by an arbitrary function generator (Tektronix, AFG3252). Two lenses L1 and L2, each with a focal length of 300 mm, are used to couple the signal fields into the atomic ensemble in MOT A. The fields of pumps 1 and 2 are collinear, and hence their respective signal fields are collinear. The vector matching condition kp1 − kS1 = kp2 − kS2 is satisfied in the SFWM process. The two signal photons are collected into their respective single-mode fibers and are detected by two single-photon detectors. Here, signal 1 photon is detected by avalanche diode (PerkinElmer SPCM-AQR-16-FC, 60 efficiency, maximum dark count rate of 25 s−1. The two detectors are gated in the experimental window. The gated signals from the two detectors are then sent to a time-correlated single-photon counting system (TimeHarp 260) to measure their time-correlated function. In our experiment, the detected coincidence count rate of photon pairs is 7 s−1. The total detecting efficiency of signal can be calculated by Etotal = EcollectEdet. Here, Ecollect and Edet represent the collecting efficiency of photons and efficiency of single-photon detector. For signal 1 (2), Ecollect and Edet are 25% (85%) and 60% (50%), respectively. Hence, the generating rate of photon pairs is estimated to be 7 s−1/(25% × 60% × 85% × 50%) = 110 s−1. The residual noise arose from the multi-photon event and detector dark count is 0.04 s−1. To characterize the single-photon nature of signal 1 photon, we measure the heralded auto-correlation parameter α = p1p123/p12p1335 by performing the Hanbury-Brown-Twiss (HBT) experiment. Here, p1 is the count of signal 2 photon. The signal 1 photon is separated into two equal parts by a fiber beam splitter and p12 (p13) is the twofold coincidence count between signal 2 photon and corresponding separated signal 1 photons. p123 is the threefold coincidence count. For a classical field, α > 1. For an ideal single-photon source, α = 0, and α = 0.5 corresponds to a two-photon state. Therefore, α < 0.5 indicates the character of single photons. The measured α = 0.031 ± 0.002 ≪ 0.5 suggests the near single-photon character.
Raman QM
Two atomic ensembles in MOT B and MOT C are served as Raman memories30. The specific storage process is illustrated as follow: The signal 1 photon is inputted into the memory B with OD of 35, and simultaneously we adiabatically switch off the coupling 1 light with Rabi frequency Ωc1 = 2π × 20.61 MHz and a beam waist of 2 mm, and then a stored atomic collective excitation is obtained given by \(1/\sqrt{m}\sum {e}^{i{k}_{{\rm{S}}}\cdot {r}_{i}}{\left|1\right\rangle }_{1}\cdots {\left|2\right\rangle }_{i}\cdots {\left|1\right\rangle }_{m}\)36, also called as spin wave. kS = kc1 − ks1 is the wave vector of atomic spin wave, kc1 and ks1 are the vectors of coupling and signal 1 fields, ri denotes the position of the i-th atom in atomic ensemble in memory B. This state consists of a large amount of massive atoms, corresponding to the atomic excited state which is different from the photonic state. After a programmable storage time, the spin wave is converted back into photonic excitation by switching on the coupling 1 light again. Because the Raman memory efficiency is significantly dependent on the OD of atoms37, a controllable leaked component of single photon after storage could be obtained by changing the OD.
Quantum random number generator
We generate the random number by performing a logic gate operation between the detection of Stokes photon and a 100 kHz transistor-transistor logic (TTL) signal generated by an arbitrary function generator. Intrinsically, the emission of a single photon is an SFWM process, thus the random number is generated in a quantum random process. The choice to insert or remove M-BS 2 is controlled by the switching of coupling 2 implemented by a AOM, which is randomly decided by the QRNG. In order to exhibit the Wheeler’s delayed experiment more strikingly, we measure an intermediate situation between wave and particle by changing the duty cycle of the TTL signal. The intermediate state reveals that the photon’s behavior is dependent on the measurement, denying the hidden-information theory.
The timing of the delayed-choice experiment
After we detect signal 2 by a single-photon detector, an electronic delay of 1.3 μs is added to delay the signal from the detector. Then we perform a logic gate operation between the delayed signal and TTL signal to obtain a random number. Signal 1 emitted from MOT A propagates through a 200-m fiber corresponding to an optical delay of 1 μs and enters the interferometer. Therefore, the random choice to insert or remove memory C is indeed delayed (~300 ns) with respect to the photon entering the interferometer, and it ensures that the signal 1 has passed through M-BS 1 when the random choice is made. Besides, we want to emphasize that the second 200-m fiber between MOT B and MOT C is aimed to construct a spacelike separation between the choice of the performed measurement and the entry of the photon into the interferometer. When the leaked part of signal 1 arrives at the memory C (~2 μs after emitting from MOT A), the implement of opening or closing the memory C is simultaneously made via the switching of coupling 2, which is achieved by an AOM with a switch-delay of ~700 ns since the random number is loaded onto the AOM. To summarize, the choice to insert or remove memory C is made when the photon is already inside the interferometer, which is the key to Wheeler’s gedanken experiment.
Data availability
Data are available from the authors upon reasonable request.
References
Wheeler, J. A In: A. R., Marlow (ed.) Mathematical Foundations of Quantum Theory. 9–48 Elsevier, 1978.
Scully, M. O. & Drühl, K. Quantum eraser: a proposed photon correlation experiment concerning observation and “delayed choice” in quantum mechanics. Phys. Rev. A 25, 2208 (1982).
Hellmuth, T., Walther, H., Zajonc, A. & Schleich, W. Delayed-choice experiments in quantum interference. Phys. Rev. A 35, 2532 (1987).
Baldzuhn, J., Mohler, E. & Martienssen, W. A wave-particle delayed-choice experiment with a single-photon state. Z. f.ür. Phys. B Condens. Matter 77, 347–352 (1989).
Lawson-Daku, B. et al. Delayed choices in atom stern-gerlach interferometry. Phys. Rev. A 54, 5042 (1996).
Kim, Y.-H., Yu, R., Kulik, S. P., Shih, Y. & Scully, M. O. Delayed “choice” quantum eraser. Phys. Rev. Lett. 84, 1 (2000).
Jacques, V. et al. Experimental realization of wheeler’s delayed-choice gedanken experiment. Science 315, 966–968 (2007).
Jacques, V. et al. Delayed-choice test of quantum complementarity with interfering single photons. Phys. Rev. Lett. 100, 220402 (2008).
Ma, X.-s, Kofler, J. & Zeilinger, A. Delayed-choice gedanken experiments and their realizations. Rev. Mod. Phys. 88, 015005 (2016).
Kaiser, F., Coudreau, T., Milman, P., Ostrowsky, D. B. & Tanzilli, S. Entanglement-enabled delayed-choice experiment. Science 338, 637–640 (2012).
Tang, J.-S. et al. Realization of quantum wheeler’s delayed-choice experiment. Nat. Photon. 6, 600 (2012).
Peruzzo, A., Shadbolt, P., Brunner, N., Popescu, S. & O’Brien, J. L. A quantum delayed-choice experiment. Science 338, 634–637 (2012).
Chaves, R., Lemos, G. B. & Pienaar, J. Causal modeling the delayed-choice experiment. Phys. Rev. Lett. 120, 190401 (2018).
Huang, H.-L. et al. Compatibility of causal hidden-variable theories with a delayed-choice experiment. Phys. Rev. A 100, 012114 (2019).
Polino, E. et al. Device-independent test of a delayed choice experiment. Phys. Rev. A 100, 022111 (2019).
Yu, S. et al. Realization of a causal-modeled delayed-choice experiment using single photons. Phys. Rev. A 100, 012115 (2019).
Vedovato, F. et al. Extending wheeler’s delayed-choice experiment to space. Sci. Adv. 3, e1701180 (2017).
Liu, K. et al. A twofold quantum delayed-choice experiment in a superconducting circuit. Sci. Adv. 3, e1603159 (2017).
Jennewein, T., Weihs, G., Pan, J.-W. & Zeilinger, A. Experimental nonlocality proof of quantum teleportation and entanglement swapping. Phys. Rev. Lett. 88, 017903 (2001).
Ma, X.-s. et al. Experimental delayed-choice entanglement swapping. Nat. Phys. 8, 479 (2012).
Lee, J.-C. et al. Experimental demonstration of delayed-choice decoherence suppression. Nat. commun. 5, 4522 (2014).
Kawai, Tea Realization of a delayed choice experiment using a multilayer cold neutron pulser. Nucl. Instrum. Methods Phys. Res. A 410, 259 (1998).
Manning, A. G., Khakimov, R. I., Dall, R. G. & Truscott, A. G. Wheeler’s delayed-choice gedanken experiment with a single atom. Nat. Phys. 11, 539 (2015).
Li, G., Zhang, P. & Zhang, T. Quantum delayed-choice experiment with a single neutral atom. Opt. Lett. 42, 3800–3803 (2017).
Kozhekin, A., Mølmer, K. & Polzik, E. Quantum memory for light. Phys. Rev. A 62, 033809 (2000).
Reim, K. F. et al. Multipulse addressing of a raman quantum memory: configurable beam splitting and efficient readout. Phys. Rev. Lett. 108, 263602 (2012).
Guo, X., Mei, Y. & Du, S. Single photon at a configurable quantum-memory-based beam splitter. Phys. Rev. A 97, 063805 (2018).
Nunn, J. et al. Mapping broadband single-photon wave packets into an atomic memory. Phys. Rev. A 75, 011401 (2007).
Reim, K. et al. Towards high-speed optical quantum memories. Nat. Photon. 4, 218 (2010).
Ding, D.-S. et al. Raman quantum memory of photonic polarized entanglement. Nat. Photon. 9, 332 (2015).
Balić, V., Braje, D. A., Kolchin, P., Yin, G. & Harris, S. E. Generation of paired photons with controllable waveforms. Phys. Rev. Lett. 94, 183601 (2005).
Du, S., Wen, J. & Rubin, M. H. Narrowband biphoton generation near atomic resonance. JOSA B 25, C98–C108 (2008).
Kimble, H. J. The quantum internet. Nature 453, 1023 (2008).
Elsayed, T. A. Quantum key distribution based on the quantum eraser. Preprint at https://arxiv.org/abs/1907.04221 (2019).
Grangier, P., Roger, G. & Aspect, A. Experimental evidence for a photon anticorrelation effect on a beam splitter: a new light on single-photon interferences. Europhys. Lett. 1, 173 (1986).
Fleischhauer, M. & Lukin, M. D. Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 84, 5094 (2000).
Guo, J. et al. High-performance raman quantum memory with optimal control in room temperature atoms. Nat. Commun. 10, 148 (2019).
Acknowledgements
This work was supported by National Key R&D Program of China (2017YFA0304800), the National Natural Science Foundation of China (Grant Nos. 61525504, 61722510, 61435011, 11604322, 11934013), and the Innovation Fund from CAS, Anhui Initiative in Quantum Information Technologies (AHY020200), and the Youth Innovation Pro motion Association of Chinese Academy of Sciences under Grant No. 2018490.
Author information
Authors and Affiliations
Contributions
M.X.D. and D.S.D. contribute to this paper equally. D.S.D. conceived the idea and experiment. M.X.D. designed and carried out the experiments with assistance from W.H.Z., E.Z.L., L.Z., Y.H.Y., Y.C.Y., K.Z., D.C.L. D.S.D. and M.X.D. wrote the manuscript with contributions from B.S.S. D.S.D., B.S.S. and G.C.G. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dong, MX., Ding, DS., Yu, YC. et al. Temporal Wheeler’s delayed-choice experiment based on cold atomic quantum memory. npj Quantum Inf 6, 72 (2020). https://doi.org/10.1038/s41534-020-00301-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00301-1