Abstract
Twin-field (TF) quantum key distribution (QKD) was conjectured to beat the private capacity of a point-to-point QKD link by using single-photon interference in a central measuring station. This remarkable conjecture has recently triggered an intense research activity to prove its security. Here, we introduce a TF-type QKD protocol which is conceptually simpler than the original proposal. It relies on the pre-selection of a global phase, instead of the post-selection of a global phase, which significantly simplifies its security analysis and is arguably less demanding experimentally. We demonstrate that the secure key rate of our protocol has a square-root improvement over the point-to-point private capacity, as conjectured by the original TF QKD.
Similar content being viewed by others
Introduction
There is a tremendous research interest towards developing a global quantum internet,1,2,3,4,5,6 as this could enable many useful applications of quantum technologies, including, for example, quantum key distribution (QKD),7,8 blind quantum computing,9,10 distributed quantum metrology11,12 and distributed quantum computing.13 Among these applications, QKD is certainly the most mature technology today. Experimentally, long-distance QKD has already been performed over 400 km of telecom fibers,14,15 as well as over 1000 km of free space through satellite to ground links.16,17 Nonetheless, optical loss in telecom fibers (typically about 0.2 dB/km) poses an important limit to the distance of secure QKD without trusted or quantum repeater nodes.18,19,20,21,22,23,24,25 Indeed, even with a GHz repetition rate, it would take about 100 years to send a single photon successfully over 1000 km of a telecom fiber.20 Besides, fundamental limits for the key rate vs distance for secure point-to-point QKD have been obtained recently.26,27 They essentially state that, in the absence of the repeater nodes, the key rate scales linearly with η, where η is the transmittance of the channel between Alice and Bob.
To overcome these limits, it is necessary to include intermediate nodes in the communication link. A possible solution is to modify the standard measurement-device-independent QKD (MDI QKD) protocol28 based on two-photon interference. For instance, one could add a feedback mechanism to ensure that the Bell-state measurement is performed between single-photon pulses from Alice and Bob which actually arrive at the intermediate note. This can be done, for example, by means of quantum memories29,30 or by using quantum non-demolition measurements in an all-optical solution.31 While these approaches are promising, they are far from practical with current technology.
Remarkably, Lucamarini et al.32 have recently proposed a new MDI QKD type protocol, called twin-field (TF) QKD, which is based on a simple single-photon interferometric measurement in a 50:50 beamsplitter, and is conjectured to beat the fundamental bounds in refs. 26,27 TF QKD is conceptually interesting because, for the single-photon component, it considers a single detection event in the middle node of a photon that has come from either Alice or Bob. In other words, the photon does not even come from a definite party, but bears the interference of the two possibilities that is used to generate a secret key. Indeed, by considering restricted eavesdropping strategies, the authors of ref. 32 showed that the secret key rate of TF QKD scales with \(\sqrt \eta\). Very recently, two proofs of security of variants of the seminal TF QKD scheme against general attacks have been proposed,33,34 which also show the \(\sqrt \eta\) scaling. However, none of them is entirely satisfactory. They are rather complicated and require a post-selection on the matching of the global phase of Alice and Bob, like in the original TF QKD scheme, which leads to nearly an order of magnitude of drop in the secret key rate.
In this paper, we introduce a modified TF QKD protocol and provide a simple proof of its information-theoretic security. Our protocol removes the requirement of post-selection on the matching of the global phase, thus simplifying the security proof and elucidating the concepts behind its security. We draw inspiration from quantum repeaters and connect the security of TF QKD to the study of quantum repeaters. In the key generation basis, the phases are pre-selected to be either 0 or π. For the security, we invoke a “complementarity” relation35 between the “phase” and the “number” of a bosonic mode. This contrasts the phase-encoding MDI QKD protocol introduced in ref.,36 which also relies on single-photon interference at a central station, but uses another complementary relation between rectangular phases. In particular, to prove the security of a bit encoded in the phase value, our protocol considers what happens if Alice and Bob send optical pulses in number states to the central station. Importantly, the statistics related to this scenario can be estimated by using the decoy-state method.37,38,39 As a result, our protocol can use only local phase randomization together with a pre-selection of a global phase, instead of post-selecting a phase value based on a global-phase matching condition. Our proof also has practical impact as it can deliver nearly an order of magnitude higher secret key rate, compared to the two previous proofs.40 Indeed, among the first proof-of-principle experimental demonstrations of TF QKD41,42,43,44 reported very recently, most of them41,42,43 are based on our Protocol 3 (to be presented below) in the present paper.
Results
The key idea originates from entanglement generation protocols19,21,23 based on single-photon interference in quantum repeaters. In particular, suppose that Alice and Bob are separated over a distance L and there is a station C right in the middle between them. This central station is connected to Alice (Bob) through an optical fiber with transmittance \(\sqrt \eta\). If Alice and Bob implement the original MDI QKD scheme in this scenario, it is clear that the key rate cannot scale better than η, as this protocol requires that two-photon coincidence events with one photon from Alice and one from Bob interfere in the node C. In comparison, TF QKD can provide a key rate scaling with \(\sqrt \eta\) because it only requires singles, i.e., one photon (either from Alice or from Bob) reaches the node C. Indeed, this scaling improvement is well-known in the field of quantum repeaters. For instance, the performance of entanglement generation protocols in the repeater schemes introduced in19,21,23 scales as \(\sqrt \eta\) essentially because they use single-photon interference in node C. Our starting point is then an ideal version of these entanglement generation protocols with an idealized photon source.
Protocol 1
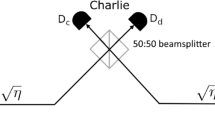
It consists of the following six steps. (i) Alice (Bob) first prepares an optical pulse a (b) in an entangled state \(\left| {\phi _q} \right\rangle _{Aa} = \sqrt q |0\rangle _A|0\rangle _a + \sqrt {1 - q} |1\rangle _A|1\rangle _a\) (|ϕq〉Bb) with 0 ≤ q ≤ 1, where |0〉a(b) is the vacuum state and |1〉a(b) is the single-photon state for optical pulse a (b), and system A (B) denotes a qubit in Alice’s (Bob’s) hands with {|0〉A(B), |1〉A(B)} representing the Z basis. (ii) Next, Alice and Bob send the optical pulses a and b through optical channels with transmittance \(\sqrt \eta\), respectively, to the middle node C in a synchronized manner. (iii) The node C applies to the incoming pulses a 50:50 beamsplitter, followed by two threshold detectors. Let Dc (Dd) denote the detector located at the output port c (d) of the beamsplitter associated to constructive (destructive) interference. (iv) The node C announces the measurement outcome kc (kd) corresponding to detector Dc (Dd), where kc = 0 and kc = 1 (kd = 0 and kd = 1) indicates a no-click event and a click event, respectively. (v) With probability pX Alice (Bob) chooses the X basis \(\{ | \pm \rangle _{A(B)}: = (|0\rangle _{A(B)} \pm |1\rangle _{A(B)})/\sqrt 2 \}\) as the key generation basis and performs the X-basis measurement on the qubit A (B), while with probability pZ she (he) chooses the Z basis and performs the Z-basis measurement. As a result, Alice (Bob) obtains the bit value bA (bB), where \(( - 1)^{b_A} = x\; (( - 1)^{b_B} = x)\) for the eigenvalues x = ±1 of the Pauli operators \(\hat X\) and \(\hat Z\). (vi) When node C reports kc = 1 and kd = 0 (kc = 0 and kd = 1) and Alice and Bob choose the X basis, bA and bB (bA and bB ⊕ 1) are regarded as their raw key. Note that in this protocol no phase randomization is applied.
We remark that step (iii) above actually corresponds to performing a “swap test” on the incoming signals. Such a swap test is commonly used in, for example, quantum digital signature schemes45 and quantum fingerprinting protocols.46,47,48
For simplicity and for the moment, let us neglect the effect of the dark counts in the detectors Dc and Dd and assume that their detection efficiency is perfect. Then, it is straightforward to show that the probability r with which node C observes only one click in say detector Dc (Dd) in step (iv) above is r = r1 + r2, where
That is, r1 (r2) corresponds to a detection event produced by a single-photon (two-photon) pulse.
Given only one detection click in say detector Dc (Dd), the joint state of Alice and Bob’s qubit systems A and B is denoted by \({\hat \rho _{AB}^+}\, (\hat \rho _{AB}^ - )\), where
with \(\left| {\Psi ^ \pm } \right\rangle _{AB}: = (|01\rangle _{AB} \pm |10\rangle _{AB})/\sqrt 2\).
According to Protocol 1, the bit-error rate, eX, is defined by the probability with which Alice’s and Bob’s X-basis measurement outcomes are different (i.e., bA ≠ bB) when kc = 1 and kd = 0, or they are equal (bA = bB) when kc = 0 and kd = 1. On the other hand, the phase-error rate, eZ, is defined by the probability with which Alice’s and Bob’s measurement outcomes in the Z basis coincide (bA = bB) when kc + kd = 1. From Eq. (3), we obtain that eX and eZ satisfy
The asymptotic key rate formula RX is then given by
where 2r represents the total success probability, f ≥ 1 is an inefficiency function for the error correction process, and h(x) is the binary entropy function, i.e., \(h(x): = - x\,{\mathrm{log}}_2x - (1 - x){\mathrm{log}}_2(1 - x)\). The parameter q is chosen such that RX is maximized for each given distance.
Protocol 2
We can also consider a prepare-and-measure version of Protocol 1. For this, we note that, without loss of generality, the measurement in step (v) of Protocol 1 can be done soon after its step (i). This is because this measurement operation commutes with all the operations performed in the other steps. So, the ordering of the steps is not relevant to the physics. Hence, Protocol 1 is mathematically equivalent to a prepare-and-measure protocol where one omits step (v) and replaces step (i) with the following step: (i′) Alice (Bob) prepares an optical pulse a (b) in the state \(\left| {X_0} \right\rangle _{a(b)}: = \sqrt q |0\rangle _{a(b)} + \sqrt {1 - q} |1\rangle _{a(b)}\) for bA = 0 (bB = 0) or in the state \(\left| {X_1} \right\rangle _{a(b)}: = \sqrt q |0\rangle _{a(b)} - \sqrt {1 - q} |1\rangle _{a(b)}\) for bA = 1 (bB = 1) at random when she (he) chooses the X basis with probability pX, while Alice (Bob) prepares the optical pulse a (b) in the state |Z0〉a(b) := |0〉a(b) for bA = 0 (bB = 0) with probability q or in the state |Z1〉a(b) := |1〉a(b) for bA = 1 (bB = 1) with probability 1 − q when she (he) chooses the Z basis with probability pZ. That is, Protocol 2 is composed of step (i′), as well as steps (ii)–(iv) and (vi) from Protocol 1.
In Fig. 1, we show the performance of these two protocols by maximizing RX over q as a function of the overall loss between Alice and Bob. According to our computation calculation, the optimal value of q = ∥a〈0∥ϕq〉Aa∥2 starts from about 0.88 at 0 dB, and then monotonically increases with the loss up to a value of about 0.94 at 20 dB, and afterwards remains basically constant. The high value of q suggests that the states |Xk〉 (k = 0, 1) could be replaced by coherent states |(−1)kα〉 by choosing an appropriate amplitude α (> 0), as their good approximation. Also, since the states |Zk〉 (k = 0, 1) are number states, Alice and Bob could estimate the phase-error rate eZ by using phase-randomized coherent states in combination with the decoy-state method. These two observations lead to the following practical protocol.
Secret key rate (per pulse) in logarithmic scale as a function of the overall loss between Alice and Bob, which includes the finite detection efficiency of the threshold detectors in node C. For simulation purposes, we set a misalignment of 2% in each channel Alice-C and Bob-C, and the inefficiency function for the error correction process f = 1.16. The dashed (solid) lines correspond to Protocol 1/Protocol 2 (Protocol 3) for different dark count rates, pd, of the detectors in node C. The solid red line illustrates the PLOB bound introduced in ref. 27 Our simulation results show clearly that, even in the presence of reasonably low values of dark counts of about 10−6 per pulse and misalignment, the Protocols could beat the PLOB bound
Protocol 3
It is composed of the following modified first step (i″) together with steps (ii)–(iv) and (vi) from Protocol 1: (i″) Alice (Bob) first chooses the X basis with probability pX and the Z basis with probability pZ. If her (his) choice is the X basis, she (he) prepares an optical pulse a (b) in a coherent state |α〉a(b) for bA = 0 (bB = 0) or | − α〉a(b) for bA = 1 (bB = 1) at random. If her (his) choice is the Z basis, she (he) prepares an optical pulse a (b) in a phase-randomized coherent state \(\hat \rho _{a,\beta _A}\,(\hat \rho _{b,\beta _B})\) whose amplitude βA (βB) is chosen from a set S = {βi}i of real nonnegative numbers βi ≥ 0, according to a probability distribution \(p_{\beta _A}\,(p_{\beta _B})\).
It is important to note that Protocol 3 requires synchronization of phase references for Alice and Bob. However, since in QKD Alice and Bob may use ancillary strong pulses generated by lasers to establish such a pulse reference, we believe that establishing the phase reference is practical. Indeed, as already mentioned in the introduction, this has already been accomplished in the recent TF QKD experiments reported in.41,42,44 In addition, Protocol 3 assumes that all the X-basis (key generation) states of Alice and Bob are either of the same or opposite phase, but no phase randomization is needed for the key generation states. That is, the global phase of the X-basis states is pre-selected by Alice and Bob before the execution of the protocol. This contrasts with the global-phase reconciliation procedure based on a post-selection step considered in refs. 32,33,34 Furthermore, all the Z-basis states (used for test for tampering) of Alice and Bob have random phases, which allows us to apply the decoy-state technique to these states to infer the contributions from the vacuum, single-photon, and multi-photon components. Also, note that pX can be chosen much higher than pZ to have a high key generation rate.
Security proof of Protocol 3
For simplicity we shall consider the asymptotic scenario where Alice and Bob emit an infinite number of signals, and the eavesdropper, Eve, performs a collective attack. The security against general attacks is presented in the Supplementary Information. We follow the loss-tolerant approach introduced in ref. 49 Also, without loss of generality, we shall assume that the node C is under the full control of Eve. After a QKD run, Alice and Bob can estimate the probability distribution pzz(kc, kd | βA, βB) (pxx (kc, kd | bA, bB)) over kc and kd given the choice of βA and βB (bA and bB) and the selection of the Z (X) basis. By noting that
where
we have that the bit-error rate, \(e_{X,k_ck_d}\), for Eve’s announcement of kc and kd is defined by
Next we consider the decoy-state method. In particular, since when Alice and Bob choose the Z basis in step (i″) of Protocol 3 they prepare phase-randomized coherent states, Eve cannot distinguish this step from the following fictitious scenario: Alice (Bob) prepares an optical pulse a (b) in a number state |nA〉a (|nB〉b) according to a Poissonian distribution \(P_{\beta _{A}^{2}}(n_{A})\,((P_{\beta _{B}^{2}}(n_{B}))\), where Pλ(n) = (e–λλn)/n!. In this fictitious scenario, Eve needs to return her measurement outcome by performing a measurement on the number states |nA〉 and |nB〉. This implies that Eve’s announcement of kc and kd follows a probability distribution pzz (kc, kd | nA, nB). Then, we have
for any βA and βB. That is, once Alice and Bob know pzz (kc, kd | βA, βB) for any βA and βB, they can use the decoy-state method to estimate pzz (kc, kd | nA, nB) based on their knowledge of \(P_{\beta _A^2}(n_A)\) and \(P_{\beta _B^2}(n_B)\).
The next step is to relate the conditional probabilities pzz (kc, kd | nA, nB) with the phase-error rate to prove security.35 For this, note that if Alice and Bob choose the X basis in step (i″) of Protocol 3, Eve cannot distinguish this step from the following fictitious step: Alice (Bob) prepares an optical pulse a (b) and a qubit A (B) in an entangled state \(\left| {\psi _X} \right\rangle _{A{a}} = (| + \rangle _A|\alpha \rangle _{a} + | - \rangle _A| - \alpha \rangle _{a})/\sqrt 2 \; \,(|\psi _X\rangle _{Bb})\). By running this, fictitious step together with steps (ii)–(iv) in order, Alice and Bob obtain a state
with probability pxx (kc, kd), where \(\hat M_{k_{c}k_{d}}^{ab}\) is the Kraus operator corresponding to the announcement of kc and kd. The phase-error rate, \(e_{Z,k_{c}k_{d}}\), is then defined by
Since A〈i||ψX〉Aa = |Ci〉a with unnormalized cat states
for nonnegative coefficients \(c_n^{(i)} \ge 0\), from Eq. (10) and for any i, j = 0, 1, we have
where we have used the Cauchy-Schwarz inequality and \(\left\| {\hat M_{k_{c}k_{d}}^{ab}|m_A\rangle _a|m_B\rangle _b} \right\|^2 = p_{ZZ}(k_{c},k_{d}|m_A,m_B)\). By combining these results with Eq. (11), we conclude
Notice that in the phase-error estimation process encapsulated in Eq. (15), it is important to estimate the yields pzz (kc, kd | nA, nB) for various photon-number components (nA, nB) (and for the various measurement outcomes (kc, kd) of node C). To do so, when Alice and Bob choose the Z basis, a decoy-state method is employed. For this reason, phase randomization is performed in the Z basis. The asymptotic key rate formula, \(R_{X,k_{c}k_{d}}\), can then be lower bounded as
which leads to the final key rate formula:
Discussion
The performance of Protocol 3 is illustrated in Fig. 1, where we maximize a further lower bound on \(R_X^{{\mathrm{low}}}\) over α as a function of the overall loss between Alice and Bob. In particular, here we assume the asymptotic scenario where Charlie behaves as he is supposed to do, Alice and Bob use an infinite number of decoy settings, and they can estimate the probabilities pzz (kc, kd | nA, nB), with (nA, nB) = (0, 0), (0, 2), (2, 0), (2, 2), (1, 1), (1, 3), (3, 1), precisely, while the remaining probabilities are simply upper bounded as pzz(kc, kd | nA, nB) ≤ 1 (although, clearly, the more probabilities \(\{ p_{ZZ}(k_{c},k_{d}|n_A,n_B)\} _{n_A,n_B}\) Alice and Bob tightly estimate, the higher the resulting key rate is). Notice that, in our protocol, secure key generation has contributions from not only the single-photon components, but also multi-photon components.50 Importantly, Fig. 1 demonstrates that \(R_X^{{\mathrm{low}}}\) has \(\sqrt \eta\) scaling. In the Supplementary Information, it is also confirmed that the use of three decoy states (that is, setting S = {βi}i=1,2,3 in Protocol 3), rather than infinite decoy states, is enough for Protocol 3 to achieve a similar performance to Fig. 1. Besides, remarkably, Protocol 3 is quite robust against phase mismatch between Alice-C and Bob-C channels. See Supplementary Information for the details.
The fact that the cases (nA, nB) = (0, 1) or (1, 0) do not contribute at all to the phase-error rate is remarkable. The reason for this behavior is the following. The even (odd) cat state corresponding to j = 0 (j = 1) in Eq. (12) (Eq. (13)) includes only even (odd) photons. And Eq. (14) considers what happens when Alice’s input and Bob’s input are both (phase-randomized) even cat states or both (phase-randomized) odd cat states. Thus, the terms (0, 1) and (1, 0) never contribute. This means that by lower bounding other contributions (such as (nA, nB) = (0, 0), (0, 2), (2, 0), …) with decoy states, one can severely limit the amount of information Eve has on the sifted key. Moreover, note that the signals contain mainly only one photon or less originating from either Alice or Bob. The net transmittance of the signal is thus of order \(\sqrt \eta\), which leads to a very high key rate for TF-type QKD at long distances. That is, it is mainly the interference between the single-photon component generated by either Alice or Bob that leads to security.
Finally, we note that since the structure of the security proof of Protocol 3 resembles that for the loss-tolerant QKD protocol,49 its extension to the finite-key scenario could be readily done by using similar techniques like those employed in,51,52,53 in combination with the decoy-state analysis employed in standard MDI QKD.54
In summary, we have introduced a novel TF-type QKD protocol, together with a simple proof of its security, which can beat the fundamental bounds on the private capacity of point-to-point QKD over a lossy optical channel presented in.26,27 Its secret key rate scales as \(\sqrt \eta\) rather than η, being η the transmittance of the quantum channel. This protocol could also be regarded as a phase-encoding MDI QKD scheme with single-photon interference. Indeed, it inherits the major advantage of standard MDI QKD, i.e., it is robust against any side channel in the measurement unit. Moreover, it has now been experimentally demonstrated in,41,42 thus showing its practicality.
Note added
During the preparation of this paper, three different pieces of research contributions considering variants of the TF QKD protocol have been posted on preprint servers55,56 or presented in a conference.57 While our formulation and discussion for security have similarities with these results, there are also differences in the methodology and our initial idea was conceived independently of these research contributions. Indeed, the quantum communication part of our protocol is equivalent to that of ref. 55 and the main difference between both schemes is merely the technique to prove the security.
Data Availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Azuma, K., Mizutani, A. & Lo, H.-K. Fundamental rate-loss trade-off for the quantum internet. Nat. Commun. 7, 13523 (2016).
Pirandola, S. Capacities of repeater-assisted quantum communications. Preprint at http://arxiv.org/abs/1601.00966 (2016).
Azuma, K. & Kato, G. Aggregating quantum repeaters for the quantum internet. Phys. Rev. A 96, 032332 (2017).
Bäuml, S. & Azuma, K. Fundamental limitation on quantum broadcast networks. Quantum Sci. Technol. 2, 024004 (2017).
Rigovacca, L. et al. Versatile relative entropy bounds for quantum networks. New J. Phys. 20, 013033 (2018).
Scarani, V. et al. The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301–1350 (2009).
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nat. Photon. 8, 595 (2014).
Broadbent, A., Fitzsimons, J. & Kashefi, E. Universal blind quantum computation. In Proc. of the 50th Annual IEEE Symposium on Foundations of Computer Science, 517–526 (IEEE, 2009).
Aharonov, D., Ben-Or, M., Eban, E. & Mahadev, U. Interactive proofs for quantum computations. Preprint at https://arxiv.org/abs/1704.04487 (2017).
Kómór, P. et al. A quantum network of clocks. Nat. Phys. 10, 582–587 (2014).
Gottesman, D., Jennewein, T. & Croke, S. Longer-baseline telescopes using quantum repeaters. Phys. Rev. Lett. 109, 070503 (2012).
Buhrman H. & Röhrig, H. in: Mathematical Foundations of Computer Science 2003 (MFCS 2003), Lecture Notes in Computer Science. Vol. 2747 (Rovan, B. & Vojtáš, P.) 1–20 (Springer, Berlin, Heidelberg, 2003).
Yin, H.-L. et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 117, 190501 (2016).
Boaron, A. et al. Secure quantum key distribution over 421 km of optical fiber. Phys. Rev. Lett. 121, 190502 (2018).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Takenaka, H. et al. Satellite-to-ground quantum-limited communication using a 50-kg-class microsatellite. Nat. Photon. 11, 502–508 (2017).
Briegel, H. J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Sangouard, N., Simon, C., de Riedmatten, N. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80 (2011).
Childress, L., Taylor, J. M., Sørensen, A. S. & Lukin, M. D. Fault-tolerant quantum communication based on solid-state photon emitters. Phys. Rev. Lett. 96, 070504 (2006).
Jiang, L. et al. Quantum repeater with encoding. Phys. Rev. A 79, 032325 (2009).
Azuma, K., Takeda, H., Koashi, M. & Imoto, N. Quantum repeaters and computation by a single module: Remote nondestructive parity measurement. Phys. Rev. A 85, 062309 (2012).
Munro, W. J., Stephens, A. M., Devitt, S. J., Harrison, K. A. & Nemoto, K. Quantum communication without the necessity of quantum memories. Nat. Photon. 6, 777–781 (2012).
Azuma, K., Tamaki, K. & Lo, H.-K. All-photonic quantum repeaters. Nat. Commun. 6, 6787 (2015).
Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat. Commun. 5, 5235 (2014).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Abruzzo, S., Kampermann, H. & Bruß, D. Measurement-device-independent quantum key distribution with quantum memories. Phys. Rev. A 89, 012301 (2014).
Panayi, C., Razavi, M., Ma, X. & Lütkenhaus, N. Memory-assisted measurement-device-independent quantum key distribution. New J. Phys. 16, 043005 (2014).
Azuma, K., Tamaki, K. & Munro, W. J. All-photonic intercity quantum key distribution. Nat. Commun. 6, 10171 (2015).
Lucamarini, M., Yuan, Z. L., Dynes, J. F. & Shields, A. J. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters. Nature 557, 400–403 (2018).
Tamaki, K., Lo, H.-K., Wang, W. & Lucamarini, M. Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. Preprint at http://arxiv.org/abs/1805.05511.
Ma, X., Zeng, P. & Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 8, 031043 (2018).
Koashi, M. Simple security proof of quantum key distribution based on complementarity. New J. Phys. 11, 045018 (2009).
Tamaki, K., Lo, H.-K., Fung, C.-H. F. & Qi, B. Phase encoding schemes for measurement-device-independent quantum key distribution with basis-dependent flaw. Phys. Rev. A 85, 042307 (2012).
Hwang, W.-Y. Quantum key distribution with high loss: Toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Lucamarini, M. Recent progress in MDI-QKD. 8th International Conference on Quantum Cryptography. http://2018.qcrypt.net (2018).
Minder, M. et al. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat. Photon. 13, 334–338 (2019).
Wang, S. et al. Beating the fundamental rate-distance limit in a proof-of-principle quantum key distribution system. Phys. Rev. X 9, 021046 (2019).
Zhong, X., Hu, J., Curty, M., Qian, L. & Lo, H-K. Proof-of-principle experimental demonstration of twin-field type quantum key distribution. Preprint at https://arxiv.org/abs/1902.10209 (2019).
Liu, Y. et al. Experimental twin-field quantum key distribution through sending-or-not-sending. Preprint at https://arxiv.org/abs/1902.06268 (2019).
Gottesman D. & Chuang, I. Quantum digital signatures. Preprint at http://arxiv.org/abs/quant-ph/0105032.
Arrazola, J. M. & Lütkenhaus, N. Quantum fingerprinting with coherent states and a constant mean number of photons. Phys. Rev. A 89, 062305 (2014).
Xu, F. et al. Experimental quantum fingerprinting with weak coherent pulses. Nat. Commun. 6, 87 (2015).
Guan, J.-Y. et al. Observation of quantum fingerprinting beating the classical limit. Phys. Rev. Lett. 116, 240502 (2016).
Tamaki, K., Curty, M., Kato, G., Lo, H.-K. & Azuma, K. Loss-tolerant quantum cryptography with imperfect sources. Phys. Rev. A 90, 052314 (2014).
Tamaki, K. & Lo, H.-K. Unconditionally secure key distillation from multiphotons. Phys. Rev. A 73, 010302(R) (2006).
Mizutani, A., Curty, M., Lim, C. C. W., Imoto, N. & Tamaki, K. Finite-key security analysis of quantum key distribution with imperfect light sources. New J. Phys. 17, 093011 (2015).
Nagamatsu, Y. et al. Security of quantum key distribution with light sources that are not independently and identically distributed. Phys. Rev. A 93, 042325 (2016).
Mizutani, A. et al. Quantum key distribution with setting-choice-independently correlated light sources. npj Quantum Information 5, 8 (2019).
Curty, M. et al. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 5, 3732 (2014).
Cui, C. et al. Twin-field quantum key distribution without phase post-selection. Phys. Rev. Appl. 11, 034053 (2019).
Wang, X.-B., Yu, Z.-W. & Hu, X.-L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 98, 062323 (2018).
Lin, J. & Lütkenhaus, N. Simple security analysis of phase-matching measurement-device-independent quantum key distribution. Phys. Rev. A 98, 042332 (2018).
Acknowledgements
We are especially thankful to G. Kato, M. Koashi, G. C. Lorenzo and Y. Zhang for giving us insightful comments and suggestions about the security proof of this paper, to M. Lucamarini and K. Tamaki for discussions related to the papers,32,33 to X. Ma and P. Zeng for discussions related to the paper,34 and to N. Lütkenhaus’ group for discussions regarding the results in ref.57 K.A. thanks support, in part, from PRESTO, JST JPMJPR1861. M.C. acknowledges support from the Spanish Ministry of Economy and Competitiveness (MINECO), the Fondo Europeo de Desarrollo Regional (FEDER) through grants TEC2014-54898-R and TEC2017-88243-R, and the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 675662 (project QCALL). H-K.L. thanks the US Office of Naval Research, NSERC, CFI, ORF, MITACS, Huawei Technologies Canada Co., Ltd, and the Royal Bank of Canada for financial support.
Author information
Authors and Affiliations
Contributions
M.C. and K.A. contributed equally to this work; M.C. contributed more to the protocol design and K.A. to its security proof. H-K.L. triggered the consideration of this research project. All authors contributed to the writing and generalization of the ideas.
Corresponding author
Ethics declarations
Competing interests
The authors declare no Competing Interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Curty, M., Azuma, K. & Lo, HK. Simple security proof of twin-field type quantum key distribution protocol. npj Quantum Inf 5, 64 (2019). https://doi.org/10.1038/s41534-019-0175-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0175-6
This article is cited by
-
Improving the performance of practical phase-matching quantum key distribution with advantage distillation
Quantum Information Processing (2024)
-
Twin-field quantum key distribution without optical frequency dissemination
Nature Communications (2023)
-
Surpassing the repeaterless bound with a photon-number encoded measurement-device-independent quantum key distribution protocol
npj Quantum Information (2023)
-
Coherent phase transfer for real-world twin-field quantum key distribution
Nature Communications (2022)
-
2×N twin-field quantum key distribution network configuration based on polarization, wavelength, and time division multiplexing
npj Quantum Information (2022)