Quantum reservoir processing

Abstract

The concurrent rise of artificial intelligence and quantum information poses an opportunity for creating interdisciplinary technologies like quantum neural networks. Quantum reservoir processing, introduced here, is a platform for quantum information processing developed on the principle of reservoir computing that is a form of an artificial neural network. A quantum reservoir processor can perform qualitative tasks like recognizing quantum states that are entangled as well as quantitative tasks like estimating a nonlinear function of an input quantum state (e.g., entropy, purity, or logarithmic negativity). In this way, experimental schemes that require measurements of multiple observables can be simplified to measurement of one observable on a trained quantum reservoir processor.

Introduction

Quantum neural networks are emerging technologies that combine the features of artificial neural networks and quantum information technologies.^1,2,3 While neural networks are biologically inspired computing systems that learn from example to perform complex tasks in the area of “big data” and machine learning,^4,5,6,7 quantum information technologies exploit quantum effects for practical applications like quantum computation, quantum cryptography, and long-distance quantum communications. The interaction between these two promising fields led to many advances. For instance, quantum effects in neural networks^8,9 enhance learning efficiency^10,11 and speed up solving many classical tasks.^12,13,14 Conversely, neural networks are used for solving complex quantum problems,^15,16 the control, and design of quantum experiments,^17,18,19 and considered as architectures, given a universal quantum computer^20,21 or quantum annealer.²²

Among the forms of neural networks, recurrent neural networks emerged as particularly suited for solving complex temporal machine-learning tasks. They achieve this by using feedback connections not present in more traditional feedforward neural networks to generate an internal temporal dynamic behavior. However, the training of recurrent neural networks is typically inefficient and computationally expensive.

In reservoir computing, a randomly connected network, called the reservoir, is used as a dynamical processing unit into which an input signal is fed. The training in reservoir computing takes place only at the readout weights that linearly map the readout of the reservoir state to the desired output. The training is conceptually simple and computationally inexpensive.²³ Furthermore, they are very suitable for hardware implementation in a wide variety of systems.^{24,25,26,27,28,29,30} Despite these advantages, reservoir computing is mostly used for tasks in the classical domain, like time-series prediction and speech recognition,^26,27,30,31 predicting the evolution of nonlinear dynamics³² and features of chaotic systems,³³ while quantum speedup of many of these classical tasks was also considered.³⁴

The idea of reservoir computing is based on the empirical observation that when the nonlinear expansion of the input data is performed randomly, but into a space with a very high dimensionality, one can find good linear cuts for virtually any classification problem. Here, we present a quantum reservoir processing platform designed on the same intuition, but operating on quantum information in a quantum Hilbert space. Our architecture does not require the pre-existence of a quantum computer and is nevertheless capable of performing quantum tasks on a quantum input. Specifically, we consider a 2D fermionic lattice with random intersite coupling excited by an incident quantum state in the form of an optical field, as illustrated in Fig. 1. The architecture is versatile and can perform both qualitative and quantitative tasks. Recognition of quantum entanglement of the input state is an example of a qualitative task. We find that the quantum reservoir processor (QRP) not only recognizes the entanglement of the same class of states as the training set, but is also able to make predictions on states beyond the training class, including bipartite bound entangled states. Our examples of quantitative tasks include estimation of logarithmic negativity, von Neumann entropy, purity, and the trace of any power of an input quantum state. Here, quantum coherence between reservoir nodes and nonlinearity are essential resources behind successful operation of QRP. We discuss the consequences of these findings to simplification of generic quantum experiments. In particular, we argue that measurements of multiple quantum observables can be replaced with a single measurement using QRP that has been suitably trained.

Fig. 1

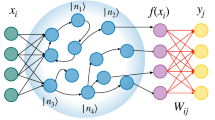
Schematic representation of a quantum reservoir processor. A quantum state in the form of an optical field excites a fermionic lattice with random couplings J_ij in an effective Fermi–Hubbard model. The occupation numbers of the fermionic sites are extracted and combined to give a final output. This generic architecture can perform various tasks, such as identifying separability of a quantum state and simultaneously estimating its various properties

Results

The model

Our considered quantum reservoir is a set of fermions (e.g., quantum dots) arranged in a 2D lattice with random nearest-neighbor hopping. The reservoir is defined by the Fermi–Hubbard Hamiltonian:

$$\hat H_R = \mathop {\sum}\limits_{ij} {J_{ij}} \left( {\hat b_i^\dagger \hat b_j + \hat b_j^\dagger \hat b_i} \right)$$

(1)

where $\hat b_i$ is the fermionic field operator of the site i and J_ij are the random hopping amplitudes uniformly distributed in the interval [−1, +1] and normalized, such that the spectral radius (largest modulus of the eigenvalues) of the Hamiltonian is $\tilde J$. Here, we considered nearest-neighbor coupling in the choice of J_ij. A comparison to the case of all-to-all coupling is included in the Supplementary Material (section VIII). Each site in the lattice is driven by an incoherent excitation (e.g., a nonresonant optical field) with the strength P.³⁵ In our scheme, an input bipartite state, in bosonic (e.g., optical) modes $\hat a_1$ and $\hat a_2$, is represented by the density matrix ρ_in. It is incident on the reservoir, interacting for a short time with all fermions. We consider that the two modes of the input state are coupled to the reservoir one at a time. This is to model the physical process, where wave packets are sequentially incident on the reservoir one after the other. The couplings of the input modes to the reservoir are realized via the “cascaded formalism”^35,36,37 which eliminates any feedback from the reservoir to the input modes. Due to this coupling, the input state merges to the reservoir. The incident state thus influences the evolution of the reservoir. As readout, we measure the occupation number of each fermionic site of the reservoir. This model can be practically realized in a variety of platforms, including arrays of semiconducting quantum dots or superconducting qubits.³⁸ We note that precise and deterministic quantum dots, which are typically a key challenge,³⁹ are unnecessary for our scheme, where random positioning and coupling are actually useful.

The whole phenomenon can be described by the combined density matrix ρ which includes the quantum reservoir and the incident modes. It follows the quantum master equation:

$$\begin{array}{*{20}{l}} {i\hbar \dot \rho } \hfill & = \hfill & {[\hat H_R,\rho ] + \frac{{i\gamma }}{2}\mathop {\sum}\limits_j {\cal{L}} (\hat b_j) + \frac{{iP}}{2}\mathop {\sum}\limits_j {\cal{L}} (\hat b_j^\dagger )} \hfill \\ {} \hfill & {} \hfill & { +\, i\mathop {\sum}\limits_{k,j} {f_k} (t)W_j^{{\mathrm{in}}}\left( {[\hat a_k\rho ,\hat b_j^\dagger ] + [\hat b_j,\rho \hat a_k^\dagger ]} \right)} \hfill \\ {} \hfill & {} \hfill & { + \,\frac{{i\eta }}{{2\gamma }}\mathop {\sum}\limits_k {f_k} (t){\cal{L}}(\hat a_k)} \hfill \end{array}$$

(2)

Here, the Lindblad operator ${\cal{L}}(\hat x) = 2\hat x\rho \hat x^\dagger - \hat x^\dagger \hat x\rho - \rho \hat x^\dagger \hat x$ for a field operator $\hat x$. On the right side of Eq. (2), the first term represents the coherent Hamiltonian evolution of the reservoir; the second term represents decay of the reservoir modes with a rate γ/ℏ; the third term represents the gain from a nonresonant optical field with strength P and the rest represents the cascade between the input modes $\hat a_k$ and the reservoir modes $\hat b_j$.^35,36 Here, the second line in Eq. (2) describes quantum excitation of the reservoir (target) by a source $(\hat a_k)$, while the last line in Eq. (2) describes the necessary loss of particles from the source due to the same process. This formalism is appropriate where the source corresponds to incident flying qubits or chiral optics is used to ensure unidirectional coupling.³⁵ Wⁱⁿ is an input weight vector with random components uniformly distributed in the interval [0,W] and $\eta = \mathop {\sum}\nolimits_j {(W_j^{{\mathrm{in}}})^2}$ is set to remove source photons that have excited the reservoir. The functions f_k(t) (for k = 1, 2) indicate that the input modes $\hat a_k$ are sequentially coupled to the reservoir for brief periods of time at different instances. We consider f₁(t) = 1 for t₁ < t < t₁ + τ when the first mode $\hat a_1$ is connected to the reservoir, whereas f₂(t) = 1 for t₁ + τ < t < t₁ + 2τ, when the second mode is connected to the reservoir; both f_1,2(t) = 0 at any other time. We express all energies and times using γ and ℏ/γ, which are natural scales for the respective quantities of our driven–dissipative reservoir. For our numerical simulations, we consider P/γ = 0.1 for the nonresonant optical field, $\tilde J/\gamma = 1$ for the random hopping amplitudes, W/γ = 1 for the random input weight matrix Wⁱⁿ, and τ = 1.5ℏ/γ. While the performance of a QRP weakly depends on P, the appropriate choice of other parameters is important (see Supplementary Material).

In our scheme, we start with an empty reservoir at time t = 0 and turn on the nonresonant optical field P. With P turned on, the reservoir reaches a steady state at time t = t₁. Then the input modes $\hat a_k$ are coupled in a temporal sequence into the reservoir, driving it out of its steady state. In this transient at time t = t₁ + 2τ, the occupation numbers $n_j = \langle \hat b_j^\dagger \hat b_j\rangle$ of the reservoir fermionic sites provide a readout. Our desired output can then be defined as $Y_i^{{\mathrm{out}}} = \mathop {\sum}\limits_j {W_{ij}^{{\mathrm{out}}}} n_j$, that is, a linear combination of the readout occupation numbers. Due to the fermionic nature of our considered reservoir, the occupation numbers n_j are nonlinear functions of the input state. We thus expect to recognize and estimate the nonlinear properties of the input state by linearly processing the readout n_j. The output weight matrix W^out is optimized using a training dataset, such that the Y^out is best fitted with known training data, corresponding to a particular task. We will now describe exemplary nonclassical tasks.

Recognition of quantum entanglement

We first train the QRP with a set of bipartite squeezed–thermal states that are randomly distributed between separable and entangled states. The two-mode squeezing operator $\hat {\cal{S}}(\alpha ) = {\mathrm{exp}}(\alpha \hat a_1^\dagger \hat a_2^\dagger - \alpha ^ \ast \hat a_1\hat a_2)$ is applied on bipartite thermal states ρ_th, with an average occupation number per mode $\bar n$, to obtain the squeezed–thermal input:

$$\rho _{{\mathrm{in}}} = \widehat {\cal{S}}(\alpha )\rho _{{\mathrm{th}}}\widehat {\cal{S}}^\dagger (\alpha )$$

(3)

where the squeezing parameter α = |α|e^iθ, and |α| and θ are chosen randomly, such that on average, 50% of states are entangled while others are separable (see Supplementary Material). The task is to find the states that are entangled.

For the considered supervised training, the input states must be unambiguously classified into entangled and separable. The squeezed–thermal states are bipartite Gaussian states, and can thus be unambiguously characterized by the logarithmic negativity.⁴⁰ We train the processor using a set of these states by assigning Y^out = (1, 0) if a state is entangled and Y^out = (0, 1) otherwise. The training determines the optimum output weights W^out by minimizing the prediction error using ridge regression.

For a performance test, we again prepare a set of random input states ρ_in which are then fed to the quantum reservoir processor. For each input ρ_in, the processor then provides an output Y^out, which is a 2D vector. If the first element of the vector is larger than the other element, then we assign the input state as entangled and otherwise as separable. In order to test the prediction efficiency, we calculate the logarithmic negativity N(ρ_in) (retaining the negative values, see Supplementary Material) to independently verify whether ρ_in is entangled. In an ideal situation, the processor predicts ρ_in as entangled whenever N(ρ_in) > 0. In Fig. 2, we represent the input states in a polar plot, where the radius gives the minimum symplectic eigenvalue $\tilde \nu _{{\mathrm{min}}}$ related to the log-negativity of the state $N(\rho _{{\mathrm{in}}}) = - {\mathrm{log}}(2\tilde \nu _{{\mathrm{min}}})$ and the angle gives the squeezing angle θ. The prediction of the reservoir processor is presented by the color of each point. The predicted entangled states are the magenta points and the predicted separable states are the blue points. We can see that the entangled states are clustered inside the circle $\tilde \nu _{{\mathrm{min}}}\, < \,0.5$ indicating that the predicted entangled states are of positive log-negativity.

Fig. 2

Quantum reservoir processor trained to recognize entangled squeezed–thermal states. A quantum reservoir processor of four fermions was trained with 200 squeezed–thermal states and tested with another set of squeezed–thermal states with squeezing parameters |α|e^iθ. Each point in the radial plot shows an input state ρ_in with radius being the minimum symplectic eigenvalue $\tilde \nu _{{\mathrm{min}}}$ related to the logarithmic negativity $N(\rho _{{\mathrm{in}}}) = - {\mathrm{log}}(2\tilde \nu _{{\mathrm{min}}})$ and angle being the squeezing angle θ. The solid black line represents the circle $\tilde \nu _{{\mathrm{min}}} = 0.5$. Clearly, the predicted entangled states are largely concentrated inside the circle $\left( {\tilde \nu _{{\mathrm{min}}} \,<\, 0.5} \right)$ and the separable states are largely on and outside the circle $\left( {\tilde \nu _{{\mathrm{min}}} \ge 0.5} \right)$. The overall prediction error is (3.7 ± 0.7)%

It turns out that the separability criterion recognized by the QRP is applicable to a wider class of input states beyond the training states. We consider frequently used non-Gaussian states (see the Methods section for detailed expressions): two-mode squeezed states with a photon added or subtracted (the mean photon number comparable to that in the training set), state c₀|00〉 + c₁|11〉, and bound entangled states introduced in ref. ⁴¹. We emphasize that QRP is trained only with the squeezed–thermal states. Surprisingly, it recognizes the non-Gaussian entangled states very efficiently. This suggests that the processor has truly identified the entanglement pattern from the considered Gaussian input states and has used that pattern to recognize the non-Gaussian entangled states, see Fig. 3.

Fig. 3

Quantum reservoir processor recognizes other classes of entangled states. In this simulation, the QRP consists of four fermions. The heights of the bars give the percentage of sampled states with correctly identified separability properties. The processor is trained with 200 examples of only squeezed–thermal states. The data are averaged over 10 different configurations of the random couplings J_ij between the fermions and input weights Wⁱⁿ, and the error bars are indicating the corresponding standard deviations

We show in the Supplementary Material that successful entanglement classification requires quantum coherence between reservoir nodes, confirming that QRP processed quantum rather than classical information.

Quantitative estimations and multiprocessing

QRP can also perform accurate quantitative estimations of nontrivial physical quantities. Furthermore, the method allows simultaneous estimation of many parameters and observables. Suppose we want to estimate M quantities of interest given an input state ρ_in. For this, we take Y^out as an M-dimensional vector. In the training phase, each element of the output vector, $Y_i^{{\mathrm{out}}}$, is taken as an estimate of the ith parameter. Once the optimum output weight matrix W^out is obtained from the training states, the QRP can predict the values of all M parameters at once. Notice that estimating one parameter at a time requires to repeat M times the same process of sending ρ_in to the reservoir and measuring n_j.

As an example, consider the following set of six parameters: log-negativity M₀ = N(ρ_in), von Neumann entropy M₁ = S(ρ_in), and $M_n = {\mathrm{Tr}}(\rho _{{\mathrm{in}}}^n)$ for n = 2…5. Clearly, any parameter with series expansion $\left\langle {\mathop {\sum}\nolimits_n {c_n} \rho ^n} \right\rangle$ can be estimated similarly. We again used the squeezed–thermal states as a training set in order to obtain the weight matrix W^out. Figure 4 shows the excellent capability of the QRP for predicting accurate and precise values of all parameters in one go. We find that increasing the size of the quantum reservoir improves estimation up to a limited amount (see Supplementary Material).

Fig. 4

Quantitative predictions for nonlinear functions of an input quantum state. Here, we demonstrate simultaneous estimation of six parameters. In each panel, we plot the true values versus the predicted values with reservoirs of two fermions (blue) and four fermions (orange). The solid black line corresponds to the ideal predictions. The predicted values became more precise and accurate when the number of fermionic sites in the reservoir is increased from 2 to 4. Panel a is for logarithmic negativity (where we retain negative values), panel b for von Neumann entropy, and the remaining panels for trace of higher powers of the input state. The processor is trained with 200 examples of squeezed–thermal states and the test states are also from this class

In this way, QRP provides a platform for simplification of quantum experiments. In a typical experiment, a good estimation of a nonlinear function of ρ_in requires measurements of multiple quantum observables. In the worst case, one has to perform full quantum state tomography. This is a consequence of the fact that the probability of the measurement result r is a linear function of ρ_in, i.e., p_r = Tr(ρ_inΠ_r), where Π_r is the corresponding POVM element. The advantage of QRP is that only one measurement is conducted (on the reservoir) and then different parameters are obtained by post-processing of the results. This comes at the expense of additional resources needed to train the processor. As seen in our example, the quality of prediction depends on the number of fermionic sites in the reservoir. If the required precision is obtained with a QRP small enough to be simulated on a classical computer, the training can be done by supplying density matrices likely to be produced in an experiment (or random mixed states in the case of no prior knowledge of the experiment). For a large QRP, the training requires supplying well-characterized physical input states, for which the parameters of interest can be calculated/measured independently and efficiently. Note that this needs to be done only once.

Discussion

We have presented a quantum reservoir processing platform for recognition of quantum entanglement and estimation of nonlinear functions of the input state. This architecture can be used both as a programmable quantum hardware device that can be programmed by training according to the need, or as a software architecture for quantum machine learning that can work for quantum tasks which are otherwise hard. For instance, a software implementation could be to use a quantum reservoir processing platform for identifying bound entangled states.

For hardware implementation, our considered reservoir, that is a 2D fermionic lattice, can be realized in a variety of systems, such as semiconductor quantum dots, NV centers in diamond, and trapped atoms. While here our considered quantum reservoir is a fermionic system, we have found that strongly interacting bosonic systems can also be used for quantum reservoir processing (see Supplementary Material). For instance, the model of our reservoir could be equivalently realized with an array of photonic crystal cavities⁴² or exciton–polaritons in semiconductor microcavities, which are now approaching the polariton blockade regime^43,44,45,46 and were shown to receive the entanglement of external optical fields.⁴⁷

Although we considered systems in which the source is cascade coupled into the reservoir without feedback, quantum reservoir processing should not be seen as model specific. Considering a system where the source and reservoir are coherently coupled (with feedback) we obtain similar results (see Supplementary Material). Also, our presented quantum-processing tasks are performed by a QRP of four fermions. While considering larger QRPs (if required) for processing quantum information, the sparsity of the reservoir parameters can be important (see Supplementary Material).

Methods

Squeezed–thermal states

A bipartite thermal state can be represented by the density matrix: $\rho _{{\mathrm{th}}} = \mathop {\sum}\nolimits_{n_1,n_2} {\rho _{n_1n_2}} |n_1,n_2\rangle \langle n_1,n_2|$ with the Fock space elements:

$$\rho _{n_1n_2} = \left( {\frac{1}{{1 + \bar n}}} \right)^2\left( {\frac{{\bar n}}{{1 + \bar n}}} \right)^{n_1 + n_2}$$

(4)

and $\bar n$ being the average occupation number per mode. The squeezed–thermal states are then obtained as $\rho _{{\mathrm{sq}}-{\mathrm{th}}} = \hat {\cal{S}}(\alpha )\rho _{{\mathrm{th}}}\hat {\cal{S}}^\dagger (\alpha )$ where the squeezing operator $\hat {\cal{S}}(\alpha ) = {\mathrm{exp}}(\alpha \hat a_1^\dagger \hat a_2^\dagger - \alpha ^ \ast \hat a_1\hat a_2)$. We write the squeezing parameter as α = |α|e^iθ and further |α| = s sinϕ and the average thermal occupation number $\bar n = s^2{\mathrm{cos}}^2\phi$. Thus, the parameters θ, s, and ϕ are the parameters characterizing the states ρ_sq-th. We take θ, s, and ϕ as random numbers uniformly distributed in the intervals [0, 2π], [0.8, 0.95], and 0.5 ± π/10, respectively. We have chosen the intervals for all the parameters such that 50% of the states are Gaussian entangled.

Photon-added squeezed states

The photon-added squeezed states are written as $\rho _{{\mathrm{sq}} - {\mathrm{add}}} = A_{{\mathrm{add}}}{\kern 1pt} \hat a_1^\dagger \hat a_2^\dagger \hat {\cal{S}}(\alpha )|00\rangle \langle 00|{\kern 1pt} \hat {\cal{S}}^\dagger (\alpha )\hat a_2\hat a_1$ where we have considered α = |α|e^iθ with |α| and θ uniformly distributed in [0.1, 0.25] and [0, 2π], respectively, and A_add is the normalization constant. The separability of these states is not always easy to recognize. For example, the Simon criterion does not detect the entanglement of these states for |α| < 0.378.^48,49 We have chosen the parameter α in such a way that the prepared states have an average occupation number close to that of the training squeezed–thermal states.

Photon-subtracted squeezed states

The photon-subtracted squeezed states are experimentally relevant.⁵⁰ These states are expressed as $\rho _{{\mathrm{sq}} - {\mathrm{sub}}} = A_{{\mathrm{sub}}}{\kern 1pt} \hat a_1\hat a_2\hat {\cal{S}}(\alpha )|00\rangle \langle 00|{\kern 1pt} \hat {\cal{S}}^\dagger (\alpha )\hat a_2^\dagger \hat a_1^\dagger$ where we have considered α = |α|e^iθ with |α| and θ uniformly distributed in [0.8, 0.95] and [0, 2π], respectively, and A_sub is the normalization constant. We have chosen the parameter α in such a way that the prepared states have an average occupation number close to that of the training states (squeezed–thermal).

The states c ₀|00〉 + c ₁|11〉

For these states, we have considered the parameterization c₀ = sinθ and c₁ = cosθe^iϕ, and we have sampled these states uniformly on a Bloch sphere.

Bound entangled states

We considered a family of bound entangled states defined by⁴¹

$$\rho _{{\mathrm{bn}}} = \frac{1}{{A_{\mathrm{b}}}}\left( {|\Psi \rangle \langle \Psi | + \mathop {\sum}\limits_{n = 1}^\infty \mathop {\sum}\limits_{m > n}^\infty |\Psi _{mn}\rangle \langle \Psi _{mn}|} \right)$$

(5)

where A_b is the normalization constant, $|\Psi \rangle = \mathop {\sum}\nolimits_{n = 1}^\infty {a^n} |n,n\rangle$, and |Ψ_mn〉 = c^maⁿ|n, m〉 + a^mc^−m|m, n〉. The two parameters a and c satisfy the condition 0 < a < c < 1 to impose finite A_b. c and a/c are chosen randomly in ranges [0.3, 0.6] and [0+, 0.1], respectively. These states are bound entangled in the infinite dimensional continuous variable limit as well as in finite dimensions.⁴¹ We achieve the continuous variable limit with a small a/c < 0.1 in a truncated Fock space.