Quantum key distribution with setting-choice-independently correlated light sources

Abstract

Despite the enormous theoretical and experimental progress made so far in quantum key distribution (QKD), the security of most existing practical QKD systems is not rigorously established yet. A critical obstacle is that almost all existing security proofs make ideal assumptions on the QKD devices. Problematically, such assumptions are hard to satisfy in the experiments, and therefore it is not obvious how to apply such security proofs to practical QKD systems. Fortunately, any imperfections and security-loopholes in the measurement devices can be perfectly closed by measurement-device-independent QKD (MDI-QKD), and thus we only need to consider how to secure the source devices. Among imperfections in the source devices, correlations between the sending pulses and modulation fluctuations are one of the principal problems, which unfortunately most of the existing security proofs do not consider. In this paper, we take into account these imperfections and enhance the implementation security of QKD. Specifically, we consider a setting-choice-independent correlation (SCIC) framework in which the sending pulses can present arbitrary correlations but they are independent of the previous setting choices such as the bit, the basis and the intensity settings. Within the framework of SCIC, we consider the dominant fluctuations of the sending states, such as the relative phases and the intensities, and provide a self-contained information-theoretic security proof for the loss-tolerant QKD protocol in the finite-key regime. We demonstrate the feasibility of secure quantum communication, and thus our work constitutes a crucial step towards guaranteeing the security of practical QKD systems.

Introduction

Quantum key distribution (QKD)¹ is one of the most promising applications of quantum information processing, and it is now on the verge of global commercialisation. Nonetheless, there are still several theoretical and experimental challenges² that need to be addressed before its wide-scale deployment. One such challenge is the lack of practical security proofs that bridge the gap between theory and practice. In the security proof of QKD, one typically assumes some mathematical models for Alice and Bob’s devices. However, if these models do not faithfully capture the physical properties of the actual QKD devices, the security of the systems is no longer guaranteed. In fact, such discrepancies between device models assumed in security proofs and the properties of actual devices could be exploited by Eve to attack both the source^3,4 and the detection apparatuses in refs ^{5,6,7,8,9,10,11,12}. It is therefore indispensable for realising secure QKD to develop security proof techniques that can be applied to actual devices.

One possible approach to close this gap is to use device-independent QKD.^13,14,15,16 Its main drawback is, however, that it delivers a quite low secret key rate with current technology, and it still requires some device characterisations. Note that device-independent QKD is known to be vulnerable to memory attacks.¹⁷ See also ref. ¹⁸ for experimentally feasible countermeasures against this type of attacks. An alternative solution is to use measurement-device-independent (MDI) QKD,¹⁹ which guarantees the security of QKD without making any assumption on the measurement device. That is, MDI-QKD completely closes the security loophole in the detection unit. This technique still requires, however, that certain assumptions on the source device are satisfied.

Unfortunately, the status of the security proofs with practical light sources is not fully satisfactory since most of the existing security proofs do not consider any imperfections (other than multiple photon emission) of the source devices. For instance, finite-key security analyses with a single-photon source^20,21,22 and those with a coherent light source^23,24,25 consider an unrealistic scenario in which there are no noises or imperfections in the QKD devices. As a result, the states of emitted pulses are identical and independent and the optical modulations are perfect, i.e., the phase modulation values are {0, π/2, π, 3π/2} and the intensity of a pulse is modulated exactly as prescribed by the protocol. A few finite-key security analyses^26,27 consider the imperfections, where in ref. ²⁷ nearest neighbour intensity correlations are accommodated, and in ref. ²⁶ imperfect IID (independent and identically distributed) phase modulation errors are accommodated.

Among the imperfections in the source, one of the crucial problems is the presence of correlations among the sending pulses. We categorise these correlations into two types: the first type is setting-choice-independent correlation (SCIC) where the correlation is independent of Alice’s choices of settings such as the bit, the basis, and the intensity settings, and the second type is setting-choice-dependent correlation (SCDC) where the correlation is dependent on Alice’s setting choices. For instance, the former case (SCIC) may arise when the temperature in the laser drifts slowly over time due to thermal effects, where such drift could depend on how long we have operated a device and the ambient temperature of the room. Another example may be found in modulation devices which are operated by power supply fluctuating in time. On the other hand, the latter case (SCDC) occurs when the i^th sending state could depend on the previous setting choices that Alice has made up to the (i − 1)^th pulse. That is to say, secret information encoded in the previous quantum signals sent by Alice could be leaked to subsequent quantum signals sent by Alice. In other words, subsequent signals could act as side channels for previous signals. Recently, the SCDC between intensities of different pulses has been observed experimentally.²⁷ Also, the authors of ref. ²⁷ conducted a security analysis which is valid for the restricted scenario where only the nearest neighbour intensity correlation is considered. More in general, however, the i^th state could be dependent on all the previous setting choices that Alice has made. This general correlation seems to be very hard to deal with theoretically, and even if we would have a theoretical countermeasure against it, the characterisation of the device might be highly non-trivial. Fortunately, it would be reasonable to assume that the SCDC could be eliminated if the modulation devices are initialised each time after Alice emits a pulse. For instance, before Alice sends the (i + 1)^th pulse, she applies a random voltage to the modulation devices several times until the setting-choice information up to the i^th pulse which is stored in the device is deleted. This potential solution may decrease the repetition rate of the source, but this could be overcome by multiplexing several sources, for instance by employing integrated silicon photonics.^28,29,30 With this reasonable solution, we are left with rigorously dealing with SCIC.

In this paper, we consider the dominant fluctuations of the sending state, such as the relative phase^26,31,32,33 and the intensity^26,27,34,35 within the framework of SCIC, and we provide an information-theoretic security proof in the finite-key regime. In particular, we consider the loss-tolerant QKD protocol³⁶ that is a BB84 type protocol which, unlike the standard BB84 protocol,³⁷ has the advantage of being robust against phase modulation errors. The loss-tolerant protocol is highly practical and has been experimentally demonstrated in both prepare & measure QKD^32,38,39 and MDI-QKD in ref. ³³. Our main contribution is to explicitly write down all the assumptions that we impose on QKD systems, and by using only these assumptions we give a self-contained security proof, which enhances implementation security of QKD. Our numerical simulations of the key generation rate show that provably secure keys can be distributed over long distances within a reasonable number of pulses sent, e.g. 10¹² pulses.

The paper is organised as follows. In the Results section, we introduce the assumptions on the devices and the protocol considered. Also, we present a formula for the key generation length of the protocol. This formula depends on the parameters that need to be estimated; the estimation results for these parameters are shown in this section. In the final part of the Results section, we present our numerical simulation results for the key generation rate. Here, we assume realistic intervals for the actual phases and intensities under the framework of SCIC, and we show that secure communication is possible within a reasonable time frame of signal transmission, say 10¹² signals.

Results

Here, we introduce the assumptions on Alice and Bob’s devices and the protocol we consider throughout this paper. To describe the assumptions, we use a shorthand notation Xⁱ: = Xⁱ, Xⁱ⁻¹, …, X¹ for a sequence of random variables $\{ X^j\} _{j = 1}^i$ and X⁰: = 0. In what follows, we first summarise the assumptions we make on the sending devices as well as those on the measurement devices, and then we move on to the description of the protocol.

Assumptions on Alice’s transmitter

(A-1) Assumption on the sending state $\hat \rho ^i(\theta ^i,\mu ^i)_{B^i}$

(A-1-i) Coherent-state assumption

Alice employs a coherent light source with a Poissonian photon number distribution in any basis, bit and intensity setting. Here we denote by $c^i \in {\cal C}: = \{ 0_Z,1_Z,0_X\}$ Alice’s bit and basis choice for the i^th pulse, and by $k^i \in {\cal K}: = \{ k_1,k_2,k_3\}$ Alice’s intensity setting choice for the i^th pulse. The method introduced in this paper is general and can be applied to many different protocols. To simplify the discussion, however, we consider the loss-tolerant three-state protocol³⁶ with two decoy states.

(A-1-ii) Single-mode assumption

The i^th signals are in a single-mode. The single-mode condition means that each i^th emitted signal can be mathematically characterised by a single creation operator. This creation operator can, however, be different for different pulses.

(A-1-iii) Phase-encoding assumption

Alice uses phase encoding, i.e., she encodes the i^th bit and basis information into the relative phase θⁱ between two pulses, a signal and a reference pulse. This assumption is for ease of discussion, and our proof can be applied to other encodings, such as a polarisation encoding.

(A-1-iv) Perfect phase randomisation assumption

A common phase δ ∈ [0, 2π) of signal and reference pulses is perfectly randomised.

(A-1-v) Same intensity assumption on signal and reference pulses

The intensities of the signal and the reference pulses are equal to μⁱ/2 where μⁱ denotes the i^th actual value of the intensity generated by Alice’s source. Note that this assumption is not mandatory. Even if the intensities of the i^th signal and reference pulses differ, the security proof can be established by introducing an additional filter operation in the security proof as explained in ref. ³⁶.

(A-1-vi) No side-channel assumption

There are no side-channels in Alice’s source and Eve can only manipulate Bob’s system B with her arbitrary prepared ancilla.

With above six assumptions (A-1-i)-(A-1-vi), given the phase and the intensity, the i^th sending state $\hat \rho ^i(\theta ^i,\mu ^i)_{B^i}$ to Bob in system Bⁱ can be described as

$$\hat \rho ^i(\theta ^i,\mu ^i)_{B^i} = \frac{1}{{2\pi }}{\int}_0^{2\pi } \hat P\left[ {\left| {e^{{\mathrm{i}}(\delta + \theta ^i)}\sqrt {\mu ^i/2} } \right\rangle _{S^i}\left| {e^{{\mathrm{i}}\delta }\sqrt {\mu ^i/2} } \right\rangle _{R^i}} \right]d\delta .$$

(1)

Here, we define $\hat P[| \cdot \rangle ]: = | \cdot \rangle \langle \cdot |$, the subscripts Sⁱ and Rⁱ respectively represent the optical modes of the i^th signal and reference pulse, and $\left| {e^{{\mathrm{i}}\theta }\sqrt \mu } \right\rangle _{S^i(R^i)}$ denotes a coherent state in mode Sⁱ(Rⁱ), i.e., $\left| {e^{{\mathrm{i}}\theta }\sqrt \mu } \right\rangle _{S^i(R^i)} = e^{ - \mu /2}\mathop {\sum}\nolimits_{n = 0}^\infty (e^{{\mathrm{i}}\theta }\sqrt \mu )^n|n\rangle _{S^i(R^i)}/\sqrt {n!}$ with $|n\rangle _{S^i(R^i)}$ being a Fock state with n photons in mode Sⁱ(Rⁱ). Eq. (1) can be rewritten as

$$\hat \rho ^i(\theta ^i,\mu ^i)_{B^i} = \mathop {\sum}\limits_{n^i = 0}^\infty p(n^i|\mu ^i)\hat P\left[ {\left| {\hat \Upsilon ^i(\theta ^i,n^i)} \right\rangle _{B^i}} \right],$$

(2)

where $p(n^i|\mu ^i): = e^{ - \mu ^i}(\mu ^i)^{n^i}/n^i!$ and the n-photon state $\hat P[|\hat \Upsilon ^i(\theta ^i,n^i)\rangle _{B^i}]$ of the i^th signal is defined as

$$\hat P[|\hat \Upsilon ^i(\theta ^i,n^i)\rangle _{B^i}]: = \frac{{\hat N_{B^i}^{n^i}\hat \rho ^i(\theta ^i,\mu ^i)_{B^i}\hat N_{B^i}^{n^i}}}{{{\mathrm{tr}}\left[ {\hat N_{B^i}^{n^i}\hat \rho ^i(\theta ^i,\mu ^i)_{B^i}} \right]}},$$

(3)

where $\hat N_{B^i}^{n^i}: = \mathop {\sum}\nolimits_{k = 0}^{n^i} \hat P\left[ {|n^i - k\rangle _{S^i}|k\rangle _{R^i}} \right]$.

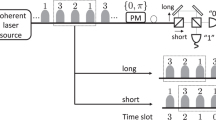
In the following, we first explain our correlation model for the source device, and we make assumptions on how the phases $\{ \theta ^i\} _{i = 1}^{N_{{\mathrm{sent}}}}$ and the intensities $\{ \mu ^i\} _{i = 1}^{N_{{\mathrm{sent}}}}$ are determined in the source device, where N_sent denotes the number of pulse pairs (signal and reference pulses) sent by Alice. See Fig. 1 for a schematic explanation of our correlation model of the source device. For illustration purposes, we exemplify in Fig. 2 setting-choice-dependent correlation (SCDC) that is not taken into account in our security analysis.

Fig. 1

A phase randomised coherent light source with SCIC (with N_sent = 3). The internal states of the source device $\{ g^i\} _{i = 1}^{N_{{\mathrm{s}}ent}}$ that determine $\{ \theta ^i\} _{i = 1}^{N_{{\mathrm{sent}}}}$ and $\{ \mu ^i\} _{i = 1}^{N_{{\mathrm{sent}}}}$ are setting-choice-independently correlated [see assumption (A-2)]. In each trial, Alice inputs cⁱ and kⁱ to the source device, and depending on these choices and gⁱ, the phase θⁱ and the intensity μⁱ are determined. Importantly, the internal states of the source device $\{ g^i\} _{i = 1}^{N_{{\mathrm{sent}}}}$ can be arbitrary correlated with each other. Note that the secret information contained in previous signals (namely, cⁱ⁻¹ and kⁱ⁻¹) is not leaked to subsequent signals. This avoids the side channel problem

Fig. 2

This figure exemplifies SCDC that is forbidden in our security assumptions (with N_sent = 3). It shows that the i^th internal state of the source device gⁱ depends on the previous outcomes θⁱ⁻¹ and μⁱ⁻¹. In this case, the secret information contained in the previous quantum signals (namely, cⁱ⁻¹ and kⁱ⁻¹) could be leaked to the i^th quantum signal sent by Alice. In other words, the i^th sending signal could act as a side channel for the previous (i − 1)^th signals

(A-2) Assumption on the correlation: setting-choice-independent correlation (SCIC)

The correlation model we consider is setting-choice-independent correlation (SCIC), which means that the internal state of the source device which determines the i^th sending state is arbitrarily correlated with the previous internal states of the source device but it does not depend on the previous setting choices made by Alice. We denote by gⁱ the classical random variable representing the i^th internal state of the source device; it determines the correspondence between the setting choices (cⁱ and kⁱ) and the output parameters from the source device (θⁱ and μⁱ). We suppose that gⁱ depends on the past internal state of the source device gⁱ⁻¹ and is independent of the past setting choices and output parameters. Note that since the output parameters (θⁱ and μⁱ) have the information of the setting choices (cⁱ and kⁱ), we also need to impose the independence of gⁱ from θⁱ⁻¹ and μⁱ⁻¹. Hence, if we denote the i^th setting choices and output parameters by

$${P^i}: = (\theta ^{i},{\mu} ^{i},c^{i},k^{i}),$$

(4)

the SCIC model can be mathematically expressed in terms of a probability distribution satisfying for any ${\boldsymbol{P}}^{i-1}$ and gⁱ⁻¹ the following

$$p(g^i|{\boldsymbol{g}}^{i - 1},{\boldsymbol{P}}^{i - 1}) = p(g^i|{\boldsymbol{g}}^{i - 1}).$$

(5)

For example, suppose that gⁱ is a temperature Tⁱ of the source device of the i^th pulse emission, and $\hat \rho (\theta ^i,\mu ^i)$ is determined once Tⁱ, cⁱ and kⁱ are fixed. Now, imagine a situation where θⁱ and μⁱ tend to deviate from ideal values when Tⁱ gets higher. Then, if a temperature Tⁱ is correlated with previous temperatures Tⁱ⁻¹, sets of sending states $\{ \hat \rho ^i(\theta ^i,\mu ^i)\} _{c^i,k^i}$ for different i are also correlated. But, Eq. (5) excludes a situation where Tⁱ depends on ${\boldsymbol{P}}^{i-1}$. This excludes, for instance, that if the previous setting choice is cⁱ⁻¹ = 0_Z, Tⁱ gets increased, but otherwise does not. With the constraint in Eq. (5), the sets of sending states $\{ \hat \rho ^i(\theta ^i,\mu ^i)\} _{c^i,k^i}$ for different i are correlated, but each i^th setting choice information is only encoded to the i^th sending pulse.

(A-3) Assumption on the random choice of cⁱ and kⁱ

We assume that conditioned on the past realisation ${\boldsymbol{P}}^{i-1}$ and gⁱ, then cⁱ and kⁱ are independent of each other and also independent of ${\boldsymbol{P}}^{i-1}$ and of gⁱ, which is expressed by the following condition

$$p(c^i,k^i|{\boldsymbol{g}}^i,{\boldsymbol{P}}^{i - 1}) = p(c^i)p(k^i).$$

(6)

(A-4) Assumption on the independence of θⁱ and μⁱ

We suppose that the phase θⁱ (intensity μⁱ) only depends on the setting choice cⁱ (kⁱ) and on gⁱ. Mathematically, this means that the probability distributions satisfy

$$p(\theta ^i,\mu ^i|c^i,k^i,{\boldsymbol{g}}^i,{\boldsymbol{P}}^{i - 1}) = p(\theta ^i|c^i,g^i)p(\mu ^i|k^i,g^i).$$

(7)

(A-5) Assumption on unique determination of θⁱ and μⁱ

The phase θⁱ (intensity μⁱ) is uniquely determined given gⁱ and the setting choice cⁱ (kⁱ) as $\theta _{c^i,g^i}^i$ $( {\mu _{k^i,g^i}^i} )$, that is, θⁱ (μⁱ) is a function of cⁱ (kⁱ) and gⁱ. This is expressed as

$$p(\theta ^i|c^i,g^i) = \delta (\theta ^i,\theta _{c^i,g^i}^i),\,p(\mu ^i|k^i,g^i) = \delta \left( {\mu ^i,\mu _{k^i,g^i}^i} \right),$$

(8)

where δ (x, y) denotes the Kronecker delta. Note that Eq. (8) does not impose any restriction on $\{ g^{i}\} _{i = 1}^{N_{{\mathrm{sent}}}}$ since there exists the information of θⁱ and μⁱ somewhere in the source device, and we can take the parameters $\{ g^{i}\} _{i = 1}^{N_{{\mathrm{sent}}}}$ such that $\{ g^{i}\} _{i = 1}^{N_{{\mathrm{sent}}}}$ uniquely determine the correspondence between $\{ c^{i}\} _{c^{i}\, \in \,{\cal C}}$ and $\{ \theta _{c^{i},g^{i}}^{i}\} _{c^{i}\, \in \,{\cal C}}$, and $\{ k^{i}\} _{k^{i}\, \in \,{\cal C}}$ and $\{ {\mu _{k^{i},g^{i}}^{i}} \}_{k^{i}\, \in \,{\cal C}}$.

For our security analysis, we define the random variable associated to tagged events as follows.

(D-1) Definition of a tagged random variable

For the internal state of the source device gⁱ, we define the untagged set ${\cal G}_{{\mathrm{unt}}}^i$ as

$${\cal G}_{{\mathrm{unt}}}^i = \{ g^i|\forall c^i \in {\cal C},\,\forall k^i \in {\cal K},\,\theta _{c^i,g^i}^i \in R_{{\mathrm{ph}}}^{c^i},\,\mu _{k^i,g^i}^i \in R_{{\mathrm{int}}}^{k^i}\} ,$$

(9)

and if $g^i \in ( \notin ){\cal G}_{{\mathrm{unt}}}^i$, we call the i^th pulse the untagged (tagged) signal, which we denote by tⁱ = u (t). In the above definition of the untagged set, $R_{{\mathrm{ph}}}^{c^i}$ and $R_{{\mathrm{int}}}^{k^i}$ respectively denote a possible interval of the phase for cⁱ and a possible interval of the intensity for kⁱ.

(A-6) Assumption on the intervals for the phase and intensity

The i^th interval of the phase $R_{{\mathrm{ph}}}^{c^i}$ is assumed to be given by

$$R_{{\mathrm{ph}}}^{0_Z} = \left[ {\theta _{0_Z}^{\mathrm{L}},\theta _{0_Z}^{\mathrm{U}}} \right],\,R_{{\mathrm{ph}}}^{1_Z} = \left[ {\theta _{1_Z}^{\mathrm{L}},\theta _{1_Z}^{\mathrm{U}}} \right],\,R_{{\mathrm{ph}}}^{0_X} = \left[ {\theta _{0_X}^{\mathrm{L}},\theta _{0_X}^{\mathrm{U}}} \right]$$

(10)

for all instances i, where $R_{{\mathrm{ph}}}^{0_Z}$, $R_{{\mathrm{ph}}}^{1_Z}$ and $R_{{\mathrm{ph}}}^{0_X}$ do not overlap each other and the parameters $\{ \theta _c^{\mathrm{L}}\} _{c\, \in \,{\cal C}}$ and $\{ \theta _c^{\mathrm{U}}\} _{c\, \in \,{\cal C}}$ must satisfy $- \frac{\pi }{6} < \theta _{0_Z}^{\mathrm{L}} \le 0$, $0 \le \theta _{0_Z}^{\mathrm{U}} < \frac{\pi }{6}$, $\frac{{5\pi }}{6} < \theta _{1_Z}^{\mathrm{L}} \le \pi$, $\pi \le \theta _{1_Z}^{\mathrm{U}} < \frac{{7\pi }}{6}$, $\frac{\pi }{3} < \theta _{0_X}^{\mathrm{L}} \le \frac{\pi }{2}$, and $\frac{\pi }{2} \le \theta _{0_X}^{\mathrm{U}} < \frac{{2\pi }}{3}$. Also, the i^th interval of the intensity $R_{{\mathrm{int}}}^{k^i}$ has the form

$$R_{{\mathrm{int}}}^k = [\mu _k^ - ,\mu _k^ + ],$$

(11)

for all instances i, and we suppose that the following three conditions are satisfied: $\mu _{k_3}^ + < \mu _{k_2}^ -$, $\mu _{k_2}^ + + \mu _{k_3}^ + < \mu _{k_1}^ -$ and $\mu _{k_1}^ + \le 1$. Note that these conditions are needed in the decoy-state method that is used for the parameter estimation (see Sec. IV in the Supplemental material for details).

(A-7) Assumption on the number of tagged signals

We define the good set ${\cal G}_{{\mathrm{good}}}^{N_{{\mathrm{sent}}}}$ of ${\boldsymbol{g}}^{N_{{\mathrm{sent}}}}$ as that whose number of tagged events $n_{{\mathrm{tag}}}: = |\{ i|g^i \notin {\cal G}_{{\mathrm{unt}}}^i\} |$ is upper bounded by a constant number N_tag as

$${\cal G}_{{\mathrm{good}}}^{N_{{\mathrm{sent}}}}: = \left\{ {{\boldsymbol{g}}^{N_{{\mathrm{sent}}}}|n_{{\mathrm{tag}}} \le N_{{\mathrm{tag}}}} \right\}.$$

(12)

We suppose that the probability of ${\boldsymbol{g}}^{N_{{\mathrm{sent}}}}$ not being an element of ${\cal G}_{{\mathrm{good}}}^{N_{{\mathrm{sent}}}}$ is upper bounded by p_fail, which is expressed as

$$\mathop {\sum}\limits_{{\boldsymbol{g}}^{N_{{\mathrm{sent}}}} \notin {\cal G}_{{\mathrm{good}}}^{N_{{\mathrm{sent}}}}} p({\boldsymbol{g}}^{N_{{\mathrm{sent}}}}) \le p_{{\mathrm{fail}}}.$$

(13)

Assumptions on Bob’s measurement unit

(B-1) Assumption on basis-independent detection efficiency

We denote by $\left\{ {\hat M_{y^i,b^i}} \right\}_{y^i \in \{ 0,1,\emptyset \} }$ the i^th POVM (positive operator-valued measure) for Bob’s measurement in the basis $b^i \in {\cal B}: = \{ Z,X\}$, where $\hat M_{0,b^i}$ $\left( {\hat M_{1,b^i}} \right)$ represents the POVM element associated to the detection of the bit value yⁱ = 0 (1) in the basis bⁱ, and the element $\hat M_{\emptyset ,b^i}$ represents the failure of outputting a bit value. We suppose that whether a detection occurs or not for each pulse pair does not depend on the chosen measurement basis bⁱ; this condition is represented as

$$\hat M_\emptyset : = \hat M_{\emptyset ,Z} = \hat M_{\emptyset ,X}.$$

(14)

(B-2) Assumption on the random choice of the measurement basis

We assume that Bob measures each incoming signal in a basis $b^i \in {\cal B}$ chosen independently of the previous basis choices and measurement outcomes. This condition is expressed in terms of the probability distribution as

$$p(b^i|{\boldsymbol{b}}^{i - 1},{\boldsymbol{y}}^{i - 1}) = p(b^i).$$

(15)

(B-3) Assumption on no side-channels

We suppose that there are no side-channels in Bob’s measurement device.

Let us remark that our security model allows the use of threshold detectors; this simply implies that Bob’s Z and X basis measurements are not necessarily measurements on a qubit space. Note also that any error in the detection apparatus (say, for example, modulation errors) can be accommodated in our security proof as long as the assumptions stated in (B-1)-(B-3) are satisfied.

Protocol description

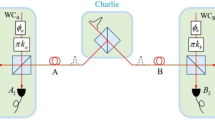
We describe the protocol of which we prove the security. See Fig. 3 for a typical setup of the actual protocol. In particular, we consider the loss-tolerant protocol in ref. ³⁶. Also, we suppose that Alice uses the decoy-state method^40,41,42 with one signal and two decoys, and we consider asymmetric coding, i.e., the Z and X bases are chosen with probabilities $p_Z^A: = \mathop {\sum}\nolimits_{c^i = 0_Z,1_Z} p(c^i)$ and $p_X^A: = p(c^i = 0_X)$, respectively. In addition, we assume that the secret key is generated from those events where both Alice and Bob select the Z basis regardless of their intensity settings.

Fig. 3

Description of the actual protocol with a typical measurement setup. In the i^th trial (with 1 ≤ i ≤ N_sent), Alice’s source device emits two consecutive coherent pulses: a signal and a reference pulse. Alice first inputs the basis and bit information $c^i \in {\cal C}$ and the intensity setting $k^i \in {\cal K}$ that she selects probabilistically. Let θⁱ and μⁱ denote the relative phase between the signal and the reference pulses and the total actual intensity of both pulses, respectively. On the receiving side, Bob uses a 50:50 beamsplitter (BS) to split the received pulses into two beams. Afterward, he applies a phase shift 0 or π/2 to one of them according to his basis choice bⁱ = Z or bⁱ = X, respectively. The pulses are then recombined at a 50:50 BS. A click in the detector D0 (D1) provides Bob the bit yⁱ = 0 (yⁱ = 1)

Next, we show in detail how the protocol runs. In its description, |A| represents the cardinality of a set or length of a bit string depending on whether A is a set or a bit string, respectively. The protocol is composed of the following steps:

(Step 0) Device characterisation and protocol parameter choice

First, Alice characterises her source to determine the value of the parameters $R_{{\mathrm{ph}}}^c$, $R_{{\mathrm{int}}}^k$ for all $c \in {\cal C}$ and $k \in {\cal K}$, N_tag and p_fail. Also, Alice and Bob decide the secrecy parameter ε_s given by Eq. (19), the correctness parameter ε_c, the upper bound on N_sent which we shall denote by N, and the quantity N_det that is associated to the termination condition.

After this characterisation step, Alice (Bob) repeats the following step 1 (step 2) and both Alice and Bob repeat step 3 for i = 1,..., N_sent until the condition in the sifting step is met. Note that we adopt the iterative sifting procedure with a basis independent termination condition, which has been recently analysed in ref. ⁴³. In this procedure, after each quantum transmission round, Bob announces whether or not the received signal produced a detection click in his measurement apparatus. And, in the case of a detection click, both Alice and Bob announce their basis choices, and Bob also declares his measurement outcome except for the event where both of them selected the Z basis. Then, the quantum communication part of the protocol terminates when the basis independent termination condition is satisfied.

(Step 1) Preparation

For each i, Alice randomly selects the intensity setting $k^i \in {\cal K}$ with probabilities $p_{k_1}: = p(k^i = k_1)$, $p_{k_2}: = p(k^i = k_2)$ and $p_{k_3}: = p(k^i = k_3)$, and the basis $a^i \in {\cal B}$ with probabilities $p_Z^A$ and $p_X^A = 1 - p_Z^A$. Afterward, if aⁱ = Z she chooses the bit information with probability 1/2; otherwise, she chooses cⁱ = 0_X. Finally, she generates the signal and reference pulses according to her choice of kⁱ and cⁱ, and sends them to Bob via a quantum channel.

(Step 2) Measurement

Bob measures the incoming signal and reference pulses using the measurement basis $b^{i} \in {\cal {B}}$, which he selects with probabilities $p_{Z}^{B}: = p(b^{i} = Z)$ and $p_{X}^{B}: = p(b^{i} = X)$. The outcome is recorded as {0, 1, ⊥, $\emptyset$}, where ⊥ and $\emptyset$ represent, respectively, a double click event, i.e., the two detectors click, and a no click event. If the outcome is ⊥, Bob assigns a random bit to the event. Note that this random assignment is not mandatory. Indeed, Bob can always choose a particular bit value, say 0, for the double click events. This deterministic procedure also preserves the basis-independence detection efficiency condition described in Eq. (14). As a result, Bob obtains yⁱ ∈ {0, 1, $\emptyset$}. The outcomes 0 and 1 will be called a detection event.

(Step 3) Sifting

Bob declares over an authenticated public channel whether or not he obtained a detection event. If yes, Alice and Bob announce their basis choices, and Alice identifies if the event can be assigned to the following sets for all $k \in {\cal K}$: ${\cal S}_{Z,Z,k,{\mathrm{det}}}: = \{ i|a^i = b^i = Z,\,k^i = k,\,y^i \ne \emptyset \}$. Moreover, if aⁱ ≠ Z or bⁱ ≠ Z, Alice asks Bob to also announce his measurement outcome, and Alice identifies if the event can be assigned to the following sets for all $c \in {\cal C}$, $k \in {\cal K}$, $b \in {\cal B}$ and y ∈ {0, 1}: ${\cal S}_{c,k,{\mathrm{det}},y,b}: = \{ i|c^i = c,k^i = k, b^i = b,y^i = y\}$. Then, Alice checks if the following termination condition is satisfied for a prefixed N_det: $S_{{\mathrm{det}}}: = |{\cal S}_{{\mathrm{det}}}|\, \ge \,N_{{\mathrm{det}}}$ for the set ${\cal S}_{{\mathrm{det}}} = \{ i|y^i \ne \emptyset \}$. Once this termination condition is met after sending N_sent pulses, the results associated to the set ${\cal S}_{Z,Z,{\mathrm{det}}}: = \cup _{k \in {\cal K}}{\cal S}_{Z,Z,k,{\mathrm{det}}}$ form Alice and Bob’s sifted keys ${\boldsymbol{\kappa }}_A^{{\mathrm{sift}}}$ and ${\boldsymbol{\kappa }}_B^{{\mathrm{sift}}}$. That is, the length of these sifted keys is $|{\boldsymbol{\kappa }}_A^{{\mathrm{sift}}}|\, = \,|{\boldsymbol{\kappa }}_B^{{\mathrm{sift}}}|\, = \,|{\cal S}_{Z,Z,{\mathrm{det}}}|$. If the termination condition is not met after sending N pulses, then Alice and Bob abort the protocol.

(Step 4) Parameter estimation

Alice calculates a lower bound for the parameter $S_{Z,Z,n = 1,u,{\mathrm{det}}}: = |{\cal S}_{Z,Z,n = 1,u,{\mathrm{det}}}|$, where ${\cal S}_{Z,Z,n,u,{\mathrm{det}}}: = \{ i|a^i = b^i = Z,n^i = n,t^i = u,y^i \ne \emptyset \}$ is a subset of ${\cal S}_{Z,Z,{\mathrm{det}}}$ composed of those elements where Alice emitted an untagged n-photon state. We call a lower bound on S_Z,Z,1,u,det as $S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}$, which is given by Eq. (21). Also, she calculates an upper-bound $N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{d}}et}^{\mathrm{U}}$ on the number of phase errors N_{ph,Z,Z,1,u,det} for the set ${\cal S}_{Z,Z,1,u,{\mathrm{det}}}$, whose quantity is given by Eq. (24). If the upper bound $e_{{\mathrm{ph}}|Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}: = N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}/S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}$ on the phase error rate e_{ph|Z,Z,1,u,det}: = N_{ph,Z,Z,1,u,det}/S_Z,Z,1,u,det satisfies $e_{{\mathrm{ph}}|Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}} \ge \overline {e_{{\mathrm{ph}}|Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}}$, where $\overline {e_{{\mathrm{ph}}|Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}}$ corresponds to the phase error rate associated with a zero secret key rate [see Eq. (20)], Alice and Bob abort the protocol. Otherwise, they proceed to step 5.

(Step 5) Bit error correction

Through public discussions, Bob corrects his sifted key ${\boldsymbol{\kappa }}_B^{{\mathrm{sift}}}$ to make it coincide with Alice’s key ${\boldsymbol{\kappa }}_A^{{\mathrm{sift}}}$ and obtains ${\boldsymbol{\kappa }}_B^{{\mathrm{cor}}}$ $\left( {|{\boldsymbol{\kappa }}_B^{{\mathrm{cor}}}|\, = \,|{\cal S}_{Z,Z,{\mathrm{det}}}|} \right)$.

(Step 6) Privacy amplification

Alice and Bob conduct privacy amplification by shortening ${\boldsymbol{\kappa }}_A^{{\mathrm{sift}}}$ and ${\boldsymbol{\kappa }}_B^{{\mathrm{cor}}}$ to obtain the final keys ${\boldsymbol{\kappa }}_A^{{\mathrm{fin}}}$ and ${\boldsymbol{\kappa }}_B^{{\mathrm{fin}}}$ of size $|{\boldsymbol{\kappa }}_A^{{\mathrm{fin}}}| = |{\boldsymbol{\kappa }}_B^{{\mathrm{fin}}}| = \ell$ with $\ell$ given by Eq. (20).

Secret key generation length

We present a formula to compute the secret key generation length $\ell$ that guarantees that the protocol introduced above is ε_sec-secure. According to the universal composable security framework,^44,45 we say that a protocol is ε_sec-secure if it is both ε_c-correct and ε_s-secret where ε_sec = ε_c + ε_s.⁴⁶ We say that the protocol is ε_c-correct if $p({\boldsymbol{\kappa }}_A^{{\mathrm{fin}}} \ne {\boldsymbol{\kappa }}_B^{{\mathrm{fin}}}) \le \varepsilon _{\mathrm{c}}$ holds. Also, we say that the protocol is ε_s-secret if

$$\frac{1}{2}||\hat \rho _{AE}^{{\mathrm{fin}}} - \hat \rho _{AE}^{{\mathrm{ideal}}}||\, \le \,\varepsilon _{\mathrm{s}}$$

(16)

holds in terms of the trace norm, where $\hat \rho _{AE}^{{\mathrm{fin}}} = \mathop {\sum}\nolimits_{{\boldsymbol{\kappa }}_A^{{\mathrm{fin}}}} p({\boldsymbol{\kappa }}_A^{{\mathrm{fin}}})|{\boldsymbol{\kappa }}_A^{{\mathrm{fin}}}\rangle \langle {\boldsymbol{\kappa }}_A^{{\mathrm{fin}}}| \otimes \hat \rho _E({\boldsymbol{\kappa }}_A^{{\mathrm{fin}}})$ is a classical-quantum state between Alice’s final key and Eve’s system after finishing the protocol and $\hat \rho _{AE}^{{\mathrm{ideal}}}$ is an ideal state in which Alice’s key is uniformly distributed over $2^{|{\boldsymbol{\kappa }}_A^{{\mathrm{fin}}}|}$ values and decoupled from Eve’s system. We suppose that the following two conditions for the random variables S_Z,Z,1,u,det and N_{ph,Z,Z,1,u,det} are satisfied

$$p(S_{Z,Z,1,u,{\mathrm{det}}}\, < \,S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}|S_{{\mathrm{det}}} = N_{{\mathrm{det}}}) \le \varepsilon _Z,$$

(17)

$$p(N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}\, > \,N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}|n_{{\mathrm{tag}}} \le N_{{\mathrm{tag}}},S_{{\mathrm{det}}} = N_{{\mathrm{det}}}) \le \varepsilon _{{\mathrm{PH}}}$$

(18)

regardless of Eve’s attack. In this case, for any ε_PA > 0, by setting^24,47

$$\varepsilon _{\mathrm{s}} = \sqrt 2 \sqrt {\varepsilon _{{\mathrm{PA}}} + \varepsilon _{{\mathrm{PH}}}} + \varepsilon _Z,$$

(19)

it can be shown that the protocol is ε_c-correct and ε_s-secret if the final key length $\ell$ satisfies

$$\ell \le \ell _{{\mathrm{SCIC}}}: = S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}\left[ {1 - h\left( {\frac{{N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}}}{{S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}}}} \right)} \right] - \mathrm{log}_2\frac{2}{{\varepsilon _{{\mathrm{PA}}}}} - \lambda _{{\mathrm{EC}}}(\varepsilon _{\mathrm{c}}),$$

(20)

where h(x) is the binary entropy function, and λ_EC(ε_c) is the cost of error correction to achieve ε_c-correctness. Note that the expressions of $S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}$ and $N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}$ are given in Eqs. (21) and (24), respectively.

Results of parameter estimation

Here, we summarise the estimation results of $S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}$ and $N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}$. All the detailed derivations of these quantities can be found in Secs. IV and V in the Supplemental material, respectively.

First, regarding the estimation of $S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}$, we employ the decoy-state method and we obtain the lower bound on S_Z,Z,1,u,det as

$$\begin{array}{*{20}{l}} {S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}} \hfill & = \hfill & {\frac{{\mu _{k_1}^ - \mathop {\sum}\nolimits_{k \in {\cal K}} {p_k\mu _k^ - e^{ - \mu _k^ - }} }}{{\left( {\mu _{k_2}^ +\,-\,\mu _{k_3}^ - } \right)\left( {\mu _{k_1}^{-} \,{-}\, \mu _{k_2}^ {+}\,{-}\,\mu _{k_3}^ - } \right)}}} \hfill \\ {} \hfill & {} \hfill & {\left\{ {\frac{{e^{\mu _{k_2}^ - }\left[ {S_{Z,Z,k_2,u,{\mathrm{det}}}^{-}\,{-}\, g_{{\mathrm{MA}}}(\varepsilon _{{\mathrm{MA}}}^{Z,k_2,u},p_Z^B,N_{{\mathrm{det}}})} \right]}}{{p_{k_2}}}} \right.} \hfill \\ {} \hfill & {} \hfill & { - \frac{{e^{\mu _{k_3}^ + }\left[ {S_{Z,Z,k_3,{\mathrm{det}}} \,{+}\, g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{Z,k_3,u},p_Z^B,N_{{\mathrm{det}}}} \right)} \right]}}{{p_{k_3}}} - \frac{{\left( {\mu _{k_2}^ + } \right)^2 - \left( {\mu _{k_3}^ - } \right)^2}}{{\left( {\mu _{k_1}^ - } \right)^2}}} \hfill \\ {} \hfill & {} \hfill & {\left. {\left( {\frac{{e^{\mu _{k_1}^ + }\left[ {S_{Z,Z,k_1,{\mathrm{det}}}\,{+}\,g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{Z,k_1,u},p_Z^B,N_{{\mathrm{det}}}} \right)} \right]}}{{p_{k_1}}}} \right)} \right\} + g_{{\mathrm{MA}}}(\varepsilon _{{\mathrm{MA}}}^{Z,1,u},p_Z^B,N_{{\mathrm{det}}})} \hfill \end{array}$$

(21)

except for error probability

$$\varepsilon _Z: = \mathop {\sum}\limits_{k \in {\cal K}} \varepsilon _{{\mathrm{MA}}}^{Z,k,u} + \varepsilon _{{\mathrm{MA}}}^{Z,1,u} + p_{{\mathrm{fail}}}$$

(22)

for any $\varepsilon _{{\mathrm{MA}}}^{Z,k,u} > 0$ and $\varepsilon _{{\mathrm{MA}}}^{Z,1,u} > 0$. Here, we define $S_{Z,Z,k_2,u,{\mathrm{det}}}^ - : = S_{Z,Z,k_2,{\mathrm{det}}} - N_{{\mathrm{tag}}}$ and the statistical fluctuation term in the Modified Azuma’s inequality (see Sec. III in the Supplemental material) is given by $g_{{\mathrm{MA}}}(\varepsilon ,q,n) = \frac{{\sqrt {{\mathrm{ln}}\varepsilon ({\mathrm{ln}}\varepsilon - 18nq)} - {\mathrm{ln}}\varepsilon }}{3}$.

Second, we present the estimation result of the number of phase errors N_{ph,Z,Z,1,u,det} for the untagged single-photon emission events in ${\boldsymbol{\kappa }}_{A}^{{\mathrm{sift}}}$. Before describing its expression, we first review briefly the main idea for deriving the number of phase errors. Our analysis is based on the security proofs^26,31,36 of the loss-tolerant protocol. These methods^26,31,36 require to estimate the number of single-photon detection events that Bob would have obtained if he had measured some virtual states in a basis (the X basis) complementary to the key generation basis (namely, the Z basis). Importantly, it turns out that the number of single-photon detection events can be written as a linear combination of those $\{ S_{c,n = 1,u,{\mathrm{det}},y,X}\} _{c\, \in \,{\cal C},y\, \in \,\{ 0,1\} }$, which will be defined soon, of the actual states sent by Alice. To obtain the numbers of these detection events, we use the detection events $\{ {\cal S}_{c,k,{\mathrm{det}},y,b=X}\} _{c\, \in \,{\cal C},k\, \in \,{\cal K},y\, \in \,\{ 0,1\} }$ including basis mismatched events (i.e., the detection events where Alice and Bob’s basis choices are different). By employing these observed number of detection events, we can estimate the number of single-photon detection events of the virtual states (and therefore the number of phase errors).

In the main text, for simplicity of its expression, we only describe N_{ph,Z,Z,1,u,det} with the following restricted phase intervals (with 0 ≤ θ < π/6):

$$R_{{\mathrm{ph}}}^{0_Z} = [ - \theta ,\theta ], R_{{\mathrm{ph}}}^{1_Z} = [\pi - \theta ,\pi + \theta ], R_{{\mathrm{ph}}}^{0_X} = \left[ {\frac{\pi }{2} - \theta ,\frac{\pi }{2} + \theta } \right].$$

(23)

Note that the expression of N_{ph,Z,Z,1,u,det} with the general phase intervals in Eq. (10) should be referred to Sec. V B in the Supplemental material. Under the assumption of Eq. (23), $N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}$ can be written as a linear combination of the parameters $S_{c,1,u,{\mathrm{det}},y,X}^\prime$, which are bounds on the cardinality of the sets ${\cal S}_{c,1,u,{\mathrm{det}},y,X} = \left\{ {\left. {i|c^i = c,n^i = 1,t^i = u, b^i = X, y^i = y} \right)} \right\}$, as

$$\begin{array}{*{20}{l}} {N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}} \hfill & = \hfill & {\frac{{p_Z^Ap_Z^B(1 \,+\, {\mathrm{sin}}\theta )}}{2}\mathop {\sum}\limits_{y = 0}^1 \mathop {\sum}\limits_{c\, \in \,{\cal C}} {\mathrm{\Gamma }}_{y,c}^{\mathrm{U}}} \hfill \\ {} \hfill & {} \hfill & {\frac{{S_{c,1,u,{\mathrm{det}},y \oplus 1,X}^\prime \,+\, {\mathrm{sgn}}({\mathrm{\Gamma }}_{y,c}^{\mathrm{U}})g_{\mathrm{A}}(N_{{\mathrm{det}}},\varepsilon _{\mathrm{A}}^{c,1,u,y,X})}}{{p(c)p_X^B}} + g_{\mathrm{A}}\left( {N_{{\mathrm{det}}},\varepsilon _{\mathrm{A}}^{{\mathrm{ph}},Z,1,u}} \right).} \hfill \end{array}$$

(24)

Here, we define the statistical fluctuation term of the Azuma’s inequality⁴⁸ as $g_{\mathrm{A}}(x,y): = \sqrt {2x\,{\mathrm{ln}}\,1/y}$ and the functions $\{ \Gamma _{y,c}^{\mathrm{U}}\} _{y,c}$³¹ as ${\mathrm{\Gamma }}_{0,0_Z}^{\mathrm{U}} = \frac{{{\mathrm{sin}}\theta }}{{{\mathrm{sin}}\theta + {\mathrm{cos}}\frac{3}{2}\theta }}$ $(0 \le {\mathrm{\Gamma }}_{0,0_Z}^{\mathrm{U}} < \sqrt 2 - 1)$, ${\mathrm{\Gamma }}_{0,1_Z}^{\mathrm{U}} = {\mathrm{\Gamma }}_{0,0_Z}^{\mathrm{U}}$, ${\mathrm{\Gamma }}_{0,0_X}^{\mathrm{U}} = \frac{{1 - {\mathrm{sin}}\theta }}{{{\mathrm{cos}}2\theta - {\mathrm{sin}}\theta }}$ $\left( {1 \le {\mathrm{\Gamma }}_{0,0_X}^{\mathrm{U}} < \infty } \right)$, ${\mathrm{\Gamma }}_{1,0_Z}^{\mathrm{U}} = \frac{{{\mathrm{cos}}\theta }}{{{\mathrm{cos}}\theta - {\mathrm{sin}}\frac{3}{2}\theta }}$ $\left( {1 \le {\mathrm{\Gamma }}_{1,0_Z}^{\mathrm{U}} < 3 + \sqrt 6 } \right)$, ${\mathrm{\Gamma }}_{1,1_Z}^{\mathrm{U}} = {\mathrm{\Gamma }}_{1,0_Z}^{\mathrm{U}}$ and ${\mathrm{\Gamma }}_{1,0_X}^{\mathrm{U}} = - \frac{{1 - {\mathrm{sin}}\theta }}{{1 + {\mathrm{sin}}\theta }}$ $( - 1 \le \Gamma _{1,0_X}^{\mathrm{U}} < - 1/3)$. Regarding $S_{c,1,u,{\mathrm{det}},y,X}^\prime$, we take the following upper or lower bounds on $S_{c,1,u,{\mathrm{det}},y,X}: = |{\cal S}_{c,1,u,{\mathrm{det}},y,X}|$, depending on the sign of ${\mathrm{\Gamma }}_{y,c}^{\mathrm{U}}$, such that N_{ph,Z,Z,1,u,det} takes its upper bound:

$$S_{c,1,u,{\mathrm{det}},y,X}^\prime = \left\{ {\begin{array}{*{20}{l}} {S_{c,1,u,{\mathrm{det}},y,X}^{\mathrm{U}}} \hfill & {{\mathrm{if}}} \hfill & {{\mathrm{\Gamma }}_{y,c}^{\mathrm{U}} > 0,} \hfill \\ {S_{c,1,u,{\mathrm{det}},y,X}^{\mathrm{L}}} \hfill & {{\mathrm{if}}} \hfill & {{\mathrm{\Gamma }}_{y,c}^{\mathrm{U}} \le 0,} \hfill \end{array}} \right.$$

(25)

with

$$\begin{array}{*{20}{l}} {S_{c,1,u,{\mathrm{det}},y,X}^{\mathrm{U}}:} \hfill & = \hfill & {\frac{{{\textstyle{{\left[ {S_{c,k_2,{\mathrm{det}},y,X} \,+\, g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{c,k_2,u,y,X},p_X^B,N_{{\mathrm{det}}}} \right)} \right]e^{ - \mu _{k_3}^ - }} \over {p_{k_2}}}} - {\textstyle{{\left[ {S_{c,k_3,u,{\mathrm{det}},y,X}^ - \,-\, g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{c,k_3,u,y,X},p_X^B,N_{{\mathrm{det}}}} \right)} \right]e^{ - \mu _{k_2}^ + }} \over {p_{k_3}}}}}}{{e^{ - \mu _{k_2}^ - - \mu _{k_3}^ - }\mu _{k_2}^ - \,-\, e^{ - \mu _{k_2}^ + - \mu _{k_3}^ + }\mu _{k_3}^ + }}} \hfill \\ {} \hfill & {} \hfill & { \times \mathop {\sum}\limits_{k \in {\cal K}} {\kern 1pt} p_k\mu _k^ + e^{ - \mu _k^ + } + g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{c,1,u,y,X},p_X^B,N_{{\mathrm{det}}}} \right)} \hfill \end{array}$$

(26)

and

$$\begin{array}{*{20}{l}} {S_{c,1,u,{\mathrm{det}},y,X}^{\mathrm{L}}:} \hfill & = \hfill & {\frac{{\mu _{k_1}^ - \mathop {\sum}\limits_{k \in {\cal K}} p_k\mu _k^ - e^{ - \mu _k^ - }}}{{\left( {\mu _{k_2}^ + \,-\, \mu _{k_3}^ - } \right)\left( {\mu _{k_1}^ - \,-\, \mu _{k_2}^ + \,-\, \mu _{k_3}^ - } \right)}}\left\{ {\frac{{e^{\mu _{k_2}^ - }\left[ {S_{c,k_2,u,{\mathrm{det,}}y,X}^ - \,-\, g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{c,k_2,u,y,X},p_X^B,N_{{\mathrm{det}}}} \right)} \right]}}{{p_{k_2}}}} \right.} \hfill \\ {} \hfill & {} \hfill & { - \frac{{e^{\mu _{k_3}^ + }\left[ {S_{c,k_3,{\mathrm{det}},y,X} \,+\, g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{c,k_3,u,y,X},p_X^B,N_{{\mathrm{det}}}} \right)} \right]}}{{p_{k_3}}}} \hfill \\ {} \hfill & {} \hfill & {\left. { - \frac{{\left( {\mu _{k_2}^ + } \right)^2 \,-\, \left( {\mu _{k_3}^ - } \right)^2}}{{\left( {\mu _{k_1}^ - } \right)^2}}\left( {\frac{{e^{\mu _{k_1}^ + }\left[ {S_{c,k_1,{\mathrm{det}},y,X} \,+\, g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{c,k_1,u,y,X},p_X^B,N_{{\mathrm{det}}}} \right)} \right]}}{{p_{k_1}}}} \right)} \right\} + g_{{\mathrm{MA}}}\left( {\varepsilon _{{\mathrm{MA}}}^{c,1,u,y,X},p_X^B,N_{{\mathrm{det}}}} \right),} \hfill \end{array}$$

(27)

where $S_{c,k,u,{\mathrm{det}},y,X}^ {-} : = S_{c,k,{\mathrm{det}},y,X} - N_{{\mathrm{tag}}}$. Finally, we calculate the failure probability ε_PH associated to the estimation of $N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}$ in Eq. (18), as $\varepsilon _{{\mathrm{PH}}} = \varepsilon _{{\mathrm{PH}}}^{1} + \varepsilon _{{\mathrm{PH}}}^{2}$, and we define $\varepsilon _{{\mathrm{PH}}}^{1}: = \mathop {\sum}\nolimits_{y = 0}^{1} \mathop {\sum}\nolimits_{c \in {\cal C}} \varepsilon _{\mathrm{A}}^{c,1,u,y,X} + \varepsilon _{\mathrm{A}}^{{\mathrm{ph}},Z,1,u}$ for any $\varepsilon _{\mathrm{A}}^{c,1,u,y,X} > 0$ and $\varepsilon _{\mathrm{A}}^{{\mathrm{ph}},Z,1,u} > 0$. $\varepsilon _{{\mathrm{PH}}}^{2}$, on the other hand, is composed of the failure probabilities associated to the estimation of $\{ S_{c,1,u,{\mathrm{det}},y,X}\} _{y\in\{ 0,1\},c\, \in \,{\cal C}}$, and $\varepsilon _{{\mathrm{PH}}}^{2}$ has the form $\varepsilon _{{\mathrm{PH}}}^{2} = \mathop {\sum}\nolimits_{y = 0,1} \mathop {\sum}\nolimits_{c \in {\cal C}} \varepsilon ^{c,1,u,y,X}$ with $\varepsilon ^{c,1,u,y,X} = \mathop {\sum}\nolimits_{k = k_2,k_3} \varepsilon _{{\mathrm{MA}}}^{c,k,u,y,X} + \varepsilon _{{\mathrm{MA}}}^{c,1,u,y,X}$ or $\varepsilon ^{c,1,u,y,X} = \mathop {\sum}\nolimits_{k\, \in \,{\cal C}} \varepsilon _{{\mathrm{MA}}}^{c,k,u,y,X} + \varepsilon _{{\mathrm{MA}}}^{c,1,u,y,X}$ depending on whether we use the upper bound given by Eq. (26) or the lower bound given by Eq. (27).

Simulation of the key rate

We show the numerical simulation results of the key rate for a fibre-based QKD system. In the simulation, we assume that Bob uses a measurement setup with two single-photon detectors with detection efficiency η_det = 10% and dark count probability per pulse p_dark = 10⁻⁵. These parameters are set to be the same as those in ref. ⁴⁹. The attenuation coefficient of the optical fibre is 0.2 dB/km and its transmittance is η_ch = 10^−0.2l/10 with l denoting the fibre length. We denote the channel transmission rate including detection efficiency by η: = η_chη_det. The overall misalignment error of the measurement system is fixed to be e_mis = 1%. In addition, we assume an error correction cost equals to $\lambda _{{\mathrm{EC}}}(\varepsilon _{\mathrm{c}}) = 1.05\, \times \,|{\boldsymbol{\kappa }}_A^{{\mathrm{sift}}}|h(e_{{\mathrm{bit}}}) + \mathrm{log}_2(1/\varepsilon _{\mathrm{c}})$, where e_bit is the bit error rate of the sifted key $({\boldsymbol{\kappa }}_A^{{\mathrm{sift}}},{\boldsymbol{\kappa }}_B^{{\mathrm{sift}}})$. Moreover, we suppose that the intervals of the intensity fluctuation in Eq. (11) are given by $R_{{\mathrm{int}}}^k = [\mu _k(1 - r_k),\mu _k(1 + r_k)]$ for k∈{k₁, k₂} and $R_{{\mathrm{int}}}^{k_3} = [0,10^{ - 3}]$ with μ_k denoting the expected intensity (we suppose that $\mu _{k_3} = 0$) and where r_k represents the deviation of the actual intensity from the expected value. For the intervals of the phase fluctuation $R_{{\mathrm{ph}}}^{c^i}$ in Eq. (23), we take the experimental value of phase modulation error from ref. ³² and we set θ = 0.03 rad. Note that the phase fluctuation ±0.03 rad is the largest experimental value observed in ref. ³² in a protocol that uses the three states {0, π/2, 3π/2} (see table III in ref. ³²). Note also that the authors of ref. ³² measured a different quantity from the one we need here. More precisely, ref. ³² assumes that each sending pulse is IID and measured the fixed deviation due to imperfect encoding. In contrast, we allow each pulse to be different (non-IID case) and we are interested in the deviation of each pulse from the mean. In our simulation, we simply assume that the result in ref. ³² gives us some reasonable estimation on the deviation θ. In Fig. 4, we consider the three cases: (I) N_tag = 0 and p_fail = 0, (II) N_tag = N_sent × 10⁻⁷ in the upper figure and (III) N_tag = N_sent × 10⁻⁶ in the lower figure and p_fail = 0. The case (I) means that all the phases and the intensities lie in their intervals, and the case (II) [the case (III)] means that the number of tagged events is upper bounded by N_sent × 10⁻⁷ in the upper figure [N_tag = N_sent × 10⁻⁶ in the lower figure].

Fig. 4

The key rate (per pulse) in logarithmic scale versus fibre length for the case with the phase fluctuation of ±0.03 rad [namely, θ = 0.03 in Eq. (23)] for any choice of $c^i \in {\cal C}$ and the intensity fluctuation of ±3% for the choice of kⁱ ∈ {k₁, k₂} and $R_{{\mathrm{int}}}^{k_3} = [0,10^{ - 3}]$ for the weakest decoy setting kⁱ = k₃. In solid lines, we assume (I) N_tag = 0 and p_fail = 0, and in the dashed lines, we assume (II) N_tag = N_sent × 10⁻⁷ in the upper figure and (III) N_tag = N_sent × 10⁻⁶ in the lower figure and p_fail = 0. The secrecy and correctness parameters are ε_s = ε_c = 10⁻¹⁰ and for each set of solid and dashed lines, the total number of signals sent by Alice is N_sent ∈ {10¹⁰, 10^10.5, 10¹¹, 10^11.5, 10¹²} from left to right. The rightmost solid and dashed lines respectively correspond to the asymptotic key rate of the cases (I)-(III) where no statistical flucuation terms in $N_{{\mathrm{ph}},Z,Z,1,u,{\mathrm{det}}}^{\mathrm{U}}$ and $S_{Z,Z,1,u,{\mathrm{det}}}^{\mathrm{L}}$ are taken into account. The experimental parameters are described in the main text

Regarding the numbers of detection events S_Z,Z,k,det and S_c,k,det,y,b, we generate these quantities by assuming the following specific setup. In particular, for the i^th trial, we consider that Alice sends Bob pairs of coherent states through the fibre of the form $\left| {e^{{\mathrm{i}}(\delta + \theta _c)}\sqrt {\mu _k/2} } \right\rangle _{S^i}\left| {e^{{\mathrm{i}}\delta }\sqrt {\mu _k/2} } \right\rangle _{R^i}$ with $\theta _{0_Z} = 0$, $\theta _{1_Z} = \pi$ and $\theta _{0_X} = \pi /2$ according to the choices of $k^i = k \in {\cal K}$ and $c^i = c \in {\cal C}$. Note that this assumption is used just to simulate the experimentally observed numbers (namely, S_Z,Z,k,det and S_c,k,det,y,b), and we do not require this assumption in the actual experiments. Bob measures the incoming signals using a Mach-Zehnder interferometer with two 50:50 BSs and a phase modulator as shown in Fig. 3. More precisely, he uses the first 50:50 BS to split the received pulses into two beams, and after that he applies a phase shift 0 or π/2 to one of them according to his basis choice of bⁱ = Z or bⁱ = X, respectively, and finally he lets the resulting pulses interfere with the second 50:50 BS. In this setup, we obtain the following probabilities: $p(y^i = y|c^i = y_Z,k^i = k,b^i = Z) = p(y^i = 0|c^i = 0_X,k^i = k,b^i = X) = \left[ {1 - e^{ - \frac{{\eta \mu _k}}{2}}(1 - p_d)} \right]\left( {1 - \frac{{p_d}}{2}} \right)$, $p(y^i = y \oplus 1|c^i = y_Z,k^i = k,b^i = Z) = p(y^i = 1|c^i = 0_X,k^i = k,b^i = X) = \frac{{p_d\left[ {1 + e^{ - \frac{{\eta \mu _k}}{2}}(1 - p_d)} \right]}}{2}$ for y∈{0,1}, and $p(y^i = y|c^i = x_Z,k^i = k,b^i = X) = p(y^i = y|c^i = 0_X,k^i = k,b^i = Z) = \frac{{1 - (1 - p_{\mathrm{d}})^2e^{ - \frac{{\eta \mu _k}}{2}}}}{2}$ for y, x ∈ {0,1}. Moreover, we assume that the bit error rate e_bit is given by $e_{{\mathrm{bit}}} = \mathop {\sum}\nolimits_{y = 0,1} p(y^i = y \oplus 1|c^i = y_Z,k^i = k_1,b^i = Z)/\mathop {\sum}\nolimits_{x,y = 0,1} p(y^i = y|c^i = x_Z,k^i = k_1,b^i = Z) + e_{{\mathrm{mis}}}$. With these probabilities, we suppose that the experimentally observed numbers satisfy $S_{Z,Z,k,{\mathrm{det}}} = N_{{\mathrm{sent}}}\mathop {\sum}\nolimits_{x,y = 0,1} \frac{{p_Z^A}}{2}p_Z^Bp_k \times p(y^i = y|c^i = x_Z,k^i = k,b^i = Z)$ and $S_{c,k,{\mathrm{det}},y,b} = N_{{\mathrm{sent}}}p(c)p_b^Bp_k \times p(y^i = y|c^i = c,k^i = k,b^i = b)$.

With the above parameters, we simulate the key rate $\ell _{{\mathrm{SCIC}}}/N_{{\mathrm{sent}}}$ for a fixed value of the correctness and secrecy parameters ε_c = ε_s = 10⁻¹⁰ and we set ε_Z = 1/2 × 10⁻¹⁰, ε_PA = ε_PH = 1/16 × 10⁻²⁰, and $\varepsilon _{{\mathrm{MA}}}^{Z,k,u} = \varepsilon _{{\mathrm{MA}}}^{Z,1,u} = \varepsilon _Z/4 = 1/8 \times 10^{ - 10}$. We also assume that each failure probability which is contained in the expression of $\varepsilon _{{\mathrm{PH}}}^1$ and $\varepsilon _{{\mathrm{PH}}}^2$ takes the value $\varepsilon _{\mathrm{A}}^{c,1,u,y,X} = \varepsilon _{\mathrm{A}}^{{\mathrm{ph}},Z,1,u} = 1/26\, \times \,\varepsilon _{{\mathrm{PH}}}$ and $\varepsilon _{{\mathrm{MA}}}^{c,k,u,y,X} = \varepsilon _{{\mathrm{MA}}}^{c,1,u,y,X} = 1/26\, \times \,\varepsilon _{{\mathrm{PH}}}$, respectively, and we set $p_Z^A = p_Z^B = p_{k_1} = 0.8$ and $p_{k_2} = 0.1$. In the simulation, we perform a numerical optimisation of the key rate $\ell _{{\mathrm{SCIC}}}/N_{{\mathrm{sent}}}$ over the two free parameters $\mu _{k_1}$ and $\mu _{k_2}$. In the solid and dashed lines in Fig. 4, we respectively plot the key rate of the cases (I), (II) and (III) for the finite-case when N_sent ∈ {10¹⁰, 10^10.5, 10¹¹, 10^11.5, 10¹²} (from left to right). For comparison, the rightmost solid and dashed lines respectively correspond to the asymptotic key rate of the cases (I), (II) and (III), where no statistical fluctuation terms in Eqs. (21) and (24) are taken into account. Our simulation results show the feasibility of secure key distribution within a reasonable time by employing practical devices that satisfy our device assumptions. For instance, if Alice uses a laser diode operating at 1 GHz repetition rate and she sends N_sent = 10¹² signals, then we find that it is possible to distribute a 1-Mb secret key over a 75-km fibre link in <0.3 h. This scenario corresponds to the solid blue line (the fifth solid line from the left) shown in Fig. 4.

Discussion

In summary, we have provided an information-theoretic security proof for the loss-tolerant QKD protocol which accommodates the setting-choice-independent correlation (SCIC) in the finite key regime. Within the framework of SCIC, the relative phases and intensities of the sending coherent states fluctuate over time. Once realistic intervals for these fluctuations (such as for instance ±0.03 rad and ±3%, respectively) are guaranteed, our numerical simulations have shown that secure quantum communication is feasible with a reasonable number of signal transmissions such as for example N_sent = 10¹². Therefore, our results constitute a significant step towards realising secure quantum communication with practical source devices. On a more general outlook, we leave three open questions for the future works.

• 1. It is an important future work to devise a rigorous experimental method for characterising the source parameters described in Eqs. (10)–(13). Once such a method is established, characterisations could be conducted on-line or it would be repeated many times off-line in which we assume that the property of the source parameters is unchanged after the characterisation.

• 2. Another important future work is to prove the security of MDI-QKD based on our source model of the SCIC framework. The original proposal of the loss-tolerant protocol³⁶ can also be applied to MDI-QKD, and the analysis presented in this paper is an extension of the proof of ref. ³⁶. Therefore, it should be straightforward to apply our proof to MDI-QKD.

• 3. In our analysis, in order to take into account setting-choice-independent correlations, we use the Azuma’s inequality. One possibility to improve the key rate would be to employ the improved decoy state analysis developed in ref. ⁵⁰, which is known to result in a higher key rate than all the existing analyses for the decoy state. However, the analysis in ref. ⁵⁰ assumes that there are no correlations among sending pulses, which is a striking difference from our source model, and it is not clear whether we can apply their analysis to our source.