Introduction

Analog quantum simulations, where engineered systems emulate the behaviour of other, less accessible quantum systems in a controllable and measurable way,1 show significant promise for improving our understanding of complex quantum phenomena without the need for a full fault-tolerant quantum computer.2,3,4,5 In this paradigm, the versatility of the simulator is determined by the range of interaction types and complexity accessible to the emulating quantum system. Promising avenues for pushing beyond what can be simulated with a classical machine include the study of highly interacting many-body systems.6,7,8,9,10 Superconducting circuit quantum electrodynamics (QED) is a very attractive platform for analog quantum simulation because of site-specific control and readout, and because of the flexible and engineerable system designs, which have led to the study of many interesting effects.11,12,13,14,15,16,17,18,19,20,21,22 Adding new components to the circuit QED design toolbox such as novel types of interactions can dramatically increase the range of phenomena that can be simulated.23,24,25 For example, for exploring exotic effects, like quantum phase transitions in systems of strongly correlated particles, it is important to be able to access and rapidly tune between different many-body interaction regimes.

In situ tuneable couplers have been successfully realised in a variety of circuit QED architectures,26,27,28,29,30,31,32,33,34,35 in particular using the more coherent transmon design.36,37,38,39 In recent experiments, transmon arrays with tuneable exchange-type hopping interactions, have been employed to study many-body localisation phenomena of Bose-Hubbard and spin-1/2 XY models.19,20 However, moving beyond linear couplings to incorporate additional nonlinear interactions would enable the emulation of far more complex Hamiltonians. For example, nonlocal cross-Kerr interactions, present in extended Bose-Hubbard models,40,41 introduce much richer many-body phase diagrams, leading to intriguing phenomena such as crystalline and supersolid phases of light as the ratio of the hopping and cross-Kerr coupling strengths is varied.23,24 In the qubit context, nonlinear cross-Kerr coupling, sometimes referred to as longitudinal coupling, is essential for engineering plaquette interactions in lattice gauge theories25 and gives access to a large class of quantum-dimer and XYZ spin-model Hamiltonians.

Here, we demonstrate tuneable hopping and cross-Kerr interactions in a highly coherent two-transmon unit cell. Specifically, using a large capacitor in parallel with a tuneable non-linear inductor as a coupling element, we are able to tune the ratio of the two coupling strengths, even suppressing hopping completely while maintaining a non-zero cross Kerr coupling, giving access to different interaction regimes. We comprehensively characterise the energy landscape of this building block using different spectroscopic techniques. We show excellent agreement with a full theoretical model we have developed to describe the underlying circuit Hamiltonian including higher transmon excitation manifolds. Finally, we have thoroughly studied the qubit coherence as a function of the coupler bias, showing high relaxation times of 15–40 μs, and dephasing times reaching up to 40 μs at flux-insensitive operating points. Our work outlines a new recipe for building scalable analog quantum simulators of complex Hamiltonians using coupled transmon arrays, and our theoretical model provides an invaluable tool for designing and realising larger scale implementations.

Results

Implementing nonlinear couplings

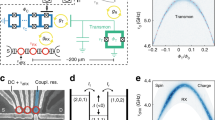
The working principle of the coupler is similar to that of a band-stop LC filter, relying on the fact that its impedance Z(ω) = \({\textstyle{{ - i\omega } \over {C\left( {\omega ^2 - \omega _{{\mathrm{LC}}}^2} \right)}}}\) is infinite on resonance, as currents through the capacitor and the inductor interfere destructively. We implement a nonlinear analog of this circuit by using a nonlinear superconducting quantum interference device (SQUID) as the inductor, realising tuneable cross-Kerr and nearest-neighbour hopping interactions (Fig. 1a). The Josephson nonlinearity of the SQUID gives rise to tuneable higher-order nonlocal terms,40 including cross-Kerr interactions, which are equivalent to longitudinal \(\hat \sigma _z\hat \sigma _z\) coupling in the qubit subspace. By contrast, the linear single-excitation hopping between the two sites is mediated by both the capacitor Cc at a constant rate JC, and by the inductor at a tuneable rate −JL. Because of interference between these two processes, the hopping strength tunes in a different way from the cross-Kerr coupling, making different many-body interaction regimes accessible. In particular, at the point where the hopping rates cancel (JC = JL), we can access a purely nonlinear regime with zero linear interaction.

Fig. 1
figure 1

Working principle and experimental device. a A nonlinear coupler introducing hopping and cross-Kerr interactions between transmons (circles) on a circuit QED lattice. Photon hopping, mediated by the capacitor and the inductor (Josephson junction), can be coherently suppressed at the filtering condition (JL = JC), in analogy with the working principle of an LC filter. Tuning the nonlinear inductance can enable interesting regimes where cross-Kerr and photon-pair tunnelling dynamics are equivalent or even dominant over photon hopping processes. b Optical micrograph of the experimental device with added false-colour on the transmon-coupler superconducting islands. Qubit readout and microwave control is performed via dedicated resonators R1,2 that are coupled to a common feedline. Dedicated drive lines provide additional microwave control to each transmon. On-chip flux bias lines are used to tune the qubit frequencies and their mutual coupling. The scale bar corresponds to 200 μm. c Circuit diagram of the implemented building block. The coupler (dark blue) is realised using a capacitor Cc in parallel with a tuneable nonlinear inductor (SQUID) that is galvanically connected with the two transmon qubits (light blue).

Full size image

The nonlinear coupler is implemented in a circuit QED device of two superconducting transmon qubits, the basic building block required for future lattice implementations (Fig. 1a). The optical micrograph along with a circuit diagram of the device are shown in Fig. 1b, c, respectively. Each transmon, consisting of two superconducting islands connected by an interdigitated capacitor C and a tuneable SQUID inductance, resonates at a plasma frequency ω ≃ \(\left( {\sqrt {8E_{\mathrm{J}}E_{\mathrm{C}}} - E_{\mathrm{C}}} \right){\mathrm{/}}\hbar\), with Josephson energy EJ and charging energy EC = \({\textstyle{{e^2} \over {2\tilde C}}}\), where \(\tilde C\) is the effective transmon capacitance (see Supplementary Eq. (S12)). Transmon frequencies can be independently tuned using on-chip flux lines (Φ1,2), and spectroscopy is performed through dispersively coupled readout resonators (R1,2) measured via a common microwave feedline (see Supplementary Sec. S2 and Fig. S5 for the full measurement setup and Fig. S6 for qubit spectroscopy vs Φ1,2). Microwave drives are applied via either the resonators or dedicated drivelines. The coupler capacitance Cc and flux-tuneable SQUID (Φ3) connect galvanically to the two transmons.

The physics of the two-transmon building block is, to a good approximation, well described by an extended Bose-Hubbard model, which is a Heisenberg XXZ spin model in the qubit regime. To achieve this, we need to operate the qubits detuned from coupler resonances, so that coupler excitations do not participate directly in the system dynamics. Under this condition, the system can be described by a simplified two-transmon Hamiltonian:

$$\begin{array}{*{20}{l}} {\hat {\cal H}{\mathrm{/}}\hbar } \hfill & = \hfill & {\omega _{\mathrm{1}}{\kern 1pt} \hat a^\dagger \hat a - U{\kern 1pt} \hat a^\dagger \hat a^\dagger \hat a\hat a} \hfill \cr {} \hfill & {} \hfill & { + \omega _{\mathrm{2}}{\kern 1pt} \hat b^\dagger \hat b - U{\kern 1pt} \hat b^\dagger \hat b^\dagger \hat b\hat b} \hfill \cr {} \hfill & {} \hfill & { + J\left( {\hat a^\dagger \hat b + \hat b^\dagger \hat a} \right)} \hfill \cr {} \hfill & {} \hfill & { + V{\kern 1pt} \hat a^\dagger \hat a\hat b^\dagger \hat b,} \hfill \end{array}$$
(1)

where \(\hat a^{(\dagger )},\hat b^{(\dagger )}\) are bosonic annihilation (creation) operators for each transmon in the uncoupled basis, with on-site nonlinearity U = \({\textstyle{{E_{\mathrm{C}}} \over {2\hbar }}}\). The interaction between the two sites can be described by hopping of single excitations at a rate

$$J = J_{\mathrm{C}} - J_{\mathrm{L}} = \frac{{\sqrt {8E_{\mathrm{J}}E_{\mathrm{C}}} }}{{2\hbar }}\left( {\frac{{C_{\mathrm{c}}}}{{4C_{{\mathrm{eff}}}}} - \frac{{E_{\mathrm{J}}^{\mathrm{c}}}}{{4E_{\mathrm{J}}}}} \right),$$
(2)

and a cross-Kerr coupling strength

$$V = - \frac{{E_{\mathrm{J}}^{\mathrm{c}}E_{\mathrm{C}}}}{{8\hbar E_{\mathrm{J}}}}.$$
(3)

The capacitive coupling JC is fixed and determined by the ratio of the coupling capacitor Cc to an effective capacitance Ceff, which depends on the circuit network (see Supplementary Eq. (S27)). The interaction strengths JL and V are determined by tuning the Josephson energy of the coupling SQUID, \(E_{\mathrm{J}}^{\mathrm{c}} = E_{\mathrm{J}}^{{\mathrm{c}}{\kern 1pt} {\mathrm{(max)}}}\) cos(πΦ3/Φ0).

Importantly, the cross-Kerr coupling V is different from the diagonal coupling that can be observed in linearly coupled transmon architectures, where the self-Kerr nonlinearity of each transmon leads to an effective cross-Kerr coupling between the normal modes of the system. Such effective diagonal coupling scales with the hopping interaction strength and vanishes at J = 0,42 making it impossible to tune the ratio J/V independently. In our design, however, the cross-Kerr interaction results directly from the nonlinearity of the coupling junction and tunes to zero at a different coupler bias from the linear hopping interaction, giving access to different interaction regimes. As Φ3 is tuned towards the filtering condition (JL ~ JC), the linear hopping term is suppressed more rapidly than the nonlinear cross-Kerr coupling, allowing access to the \(J \ll V\) regime. By contrast, when Φ3 ~ 0.5Φ0, the cross-Kerr coupling is suppressed (V = JL = 0) and the dynamics are dominated by single-photon hopping at a rate JC.

In the full treatment of the quantum circuit, the nonlinear inductance also gives rise to correlated hopping and two-photon tunnelling correction terms, which play a role in the higher-excitation manifold. These terms may also lead to interesting physical phenomena, which we return to in the discussion section. We derive the full quantum model in Supplementary Sec. S1, along with a classical normal-mode analysis providing supporting intuition for the full system behaviour.

Tuneable single-photon hopping

We demonstrate our ability to tune the linear single-photon hopping interaction between the two transmons, by measuring qubit-qubit avoided crossings, in Fig. 2. The top panels show example crossings, as qubit 1 is tuned on resonance with the other at ~6.6 GHz, in three different coupling scenarios, JL > JC in Fig. 2a, J = 0 (JL = JC) in Fig. 2b, and the JC-dominated regime in Fig. 2c. The measurements in Fig. 2a, c are performed via readout resonator R2, while in the zero coupling case (Fig. 2b) we measure via R1. The range of typical coupling strengths that can be achieved with this device is illustrated in Fig. 2d, where we plot \(\left| J \right|\)/2π vs calibrated coupler bias Φ3. We note that we have measured larger coupling strengths, up to 140 MHz, when operating at different qubit frequencies ~5.4 GHz (see Supplementary Fig. S3). The linear coupling is suppressed when the qubit frequencies are equal to the filter frequency \(1{\mathrm{/}}\sqrt {L_{\mathrm{c}}C_{\mathrm{c}}}\), which here takes place around Φ3 ~ 0.3 Φ0. Note that a higher transition of a lower-frequency sloshing mode of the circuit, crossing with the qubits around this point, limits the observed on-off ratio in this device to ~10 (see Supplementary Fig. S3). This low-frequency mode, hybridising with the qubits, is associated with currents flowing only through the coupling inductor (see Supplementary Figs. S1 and S2), and could be avoided with slightly different design parameters (shown in Supplementary Fig. S4). Additional avoided crossing measurements in the regime where the linear coupling gets suppressed and reverses sign are plotted in Supplementary Fig. S9, with spectroscopy on both qubits.

Fig. 2
figure 2

Tuneable linear coupling and single-photon hopping suppression. Top: Avoided crossings for a inductive, b zero and c capacitive coupling regimes. In all three cases, the frequency of qubit 2 is set around 6.6 GHz (Φ2 = 0), while we tune qubit 1 through resonance. Qubit spectroscopy is performed via readout resonator R2 in a, c, and via R1 in b. The coupling elements that participate more strongly to the qubit–qubit interaction are indicated in the insets. d Linear coupling strength \(\left| J \right|\) obtained from a series of fitted avoided crossings, at different values of calibrated coupler flux bias Φ3. e Eigenspectrum of the coupled qubit system on resonance vs Φ3, fitted with a simplified circuit theory model (the fitting parameters are listed in Table 1). The normal-mode splitting gets suppressed at the crossover between inductively and capacitively dominated coupler regimes (Φ3/Φ0 ≃ 0.3). Cross-talk effects between the different flux channels have been calibrated out experimentally.

Full size image

For a more complete characterisation of the tuneable hopping interaction, we fit the experimentally measured coupled-qubit spectrum with our theoretical model of the quantum circuit. More specifically, in Fig. 2e, we fix the qubits on resonance and plot the normal-mode splitting between the dressed states \(\left| + \right\rangle\) = \({\textstyle{{\left| {01} \right\rangle + \left| {10} \right\rangle } \over {\sqrt 2 }}}\) and \(\left| - \right\rangle\) = \({\textstyle{{\left| {01} \right\rangle - \left| {10} \right\rangle } \over {\sqrt 2 }}}\), as we tune the calibrated coupler flux bias. The blue and red curves are theory fits of the single-excitation qubit manifold to the quantum circuit Hamiltonian (Eq. (S11) in the Supplementary), showing excellent agreement with the experimentally obtained spectrum. The parameters obtained from this fit, which neglects higher-order couplings of each transmon to the low-frequency sloshing mode, are listed in Table 1. Note that the antisymmetric mode frequency ω−/2π is unaffected by coupler tuning, which reflects the fact that this mode is only associated with charge oscillations across the qubit junctions (see Supplementary Fig. S2).

Table 1 Table of device parameters
Full size table

Tuneable nonlinear cross-Kerr coupling

As already discussed, a key feature of our implementation which differentiates it from previous tuneable couplers, is the nonlinear cross-Kerr interaction which can be tuned into different coupling regimes relative to the hopping strength and does not zero when J does. This cross-Kerr coupling, which in different contexts is referred to as σzσz, longitudinal,43 or dispersive,44 does not involve excitation hopping processes. Its presence, however, does influence the dynamics as the occupation at one site can alter the energy level spectrum of a neighbouring site, in a process analogous to photon scattering.23

In a coupled two-qubit system, the effect of cross-Kerr interaction can be seen as a shift of the energy level of the \(\left| {11} \right\rangle\) state and can be determined spectroscopically from the transition energies relative to the ground state ω11 − ω− − ω+. For weakly anharmonic systems, such as the transmon, this picture becomes more complicated in the presence of linear hopping (Fig. 3a). A three-state analysis at the two-excitation manifold reveals that \(\left| {11} \right\rangle\), \(\left| {02} \right\rangle\) and \(\left| {20} \right\rangle\) also couple to each other, resulting in an effective upwards repulsion of the \(\left| {11} \right\rangle\) state,45 which scales as ~J2/EC.42 Because the direction of this effect competes with the negative cross-Kerr shift, when the effects are similar in size, it can hinder the observation of cross-Kerr coupling in an individual spectroscopy measurement. To separate the two effects, it is therefore necessary to measure the shift for different coupling levels.

Fig. 3
figure 3

Observation of nonlinear cross-Kerr coupling in spectroscopy. a Level schematic of two coupled transmons up to the two-excitation manifold. At the single-photon level, the linear coupling J results in an avoided crossing between the dressed states \(\left| + \right\rangle\) = \({\textstyle{{\left| {01} \right\rangle + \left| {10} \right\rangle } \over {\sqrt 2 }}}\) and \(\left| - \right\rangle\) = \({\textstyle{{\left| {01} \right\rangle - \left| {10} \right\rangle } \over {\sqrt 2 }}}\). As J becomes comparable to the transmon anharmonicity, the \(\left| {02} \right\rangle\), \(\left| {20} \right\rangle\) and \(\left| {11} \right\rangle\) levels mix with each other, resulting in an effective repulsion of \(\left| {11} \right\rangle\). On the other hand, a qubit–qubit interaction with negative cross-Kerr coupling results in lowering the energy of \(\left| {11} \right\rangle\). b Combined two-tone spectroscopy data (black dots) showing \({\textstyle{{\omega _{11} - \omega _ - - \omega _ + } \over J}}\) vs J. The red curve is theory prediction assuming only hopping interaction between two transmons (V = 0), while the blue one shows simulation results obtained by taking into account also the higher-order nonlinear contributions, \({\textstyle{{V} \over 4}}\left( {a + a^\dagger } \right)^2\left( {b + b^\dagger } \right)^2\), which include the dominant cross-Kerr term. The parameters used are listed in Table 1.

Full size image

We experimentally demonstrate the presence of cross-Kerr interaction between the two transmons, by measuring transitions in the two-excitation manifold of the coupled system. More specifically, we extract the frequency shift of \(\left| {11} \right\rangle\) at different couplings from a series of two-tone spectroscopy measurements (see Supplementary Sec. S3 and Fig. S7), focusing on the inductively dominated regime 0 ⩽ Φ3/Φ0 ⩽ 0.25. In order to distinguish between the negative cross-Kerr shift and the positive shift from linear coupling J, we plot \({\textstyle{{\omega _{11} - \omega _ - - \omega _ + } \over J}}\) as a function of J, in Fig. 3b. The red curve is theoretical prediction assuming only hopping interaction (V = 0) between the two transmons. The blue curve shows numerical results after diagonalising the transmon–transmon Hamiltonian with the full nonlinear coupling terms \({\textstyle{V \over 4}}\left( {a + a^\dagger } \right)^2\left( {b + b^\dagger } \right)^2\), which includes the dominant cross-Kerr interaction. We use the parameters listed in the second column of Table 1, which differ slightly from the fitted parameters of Fig. 2e to accommodate the effects of extra higher-order terms (see later in Fig. 5). At J = 0 (Φ3 ~ 0.3 Φ0) the cross-Kerr coupling \(\left| V \right|\)/2π is around 4 MHz, and it reaches a maximum of 10 MHz at Φ3 = 0. We were unable to explore the region J/2π < 20 MHz in this device, due to a higher transition of the lower-frequency sloshing mode hybridising with the qubits (see Supplementary Fig. S3).

Qubit coherence

Maintaining high coherence for all interaction strengths is an essential requirement for future implementations based on our building block device. In Fig. 4, we investigate the individual qubit properties as a function of the coupler bias, with the transmons far detuned from each other by ~1.8 GHz, at their flux-insensitive top and bottom sweetspots (Φ1 = 0, Φ2/Φ0 = 0.5). In Fig. 4a, b, we demonstrate high relaxation times T1 (15–40 μs) over the entire coupling range. We also report a systematic study of dephasing times in our device, obtained from spin-echo measurements (Fig. 4c, d). \(T_2^{{\mathrm{Echo}}}\) times are large overall, reaching up to 40 μs, except for the points where the qubits hybridise with the lower-frequency sloshing mode (at Φ3/Φ0 ~ 0.28 and Φ3/Φ0 ~ 0.38 as shown in Fig. 4e, f). Note that the qubit frequency shifts of ~200 MHz in Fig. 4e, f are due to inherent changes to the Josephson energy of each transmon as \(E_{\mathrm{J}}^{\mathrm{c}}\) is varied (see Supplementary Eq. (S20)). Repeated long Ramsey measurements were performed at Φ3 = 0, showing a beating pattern consistent with charge dispersion in the transmon regime.36,46 A measurement analysis with fits to the double sinusoidal decay pattern reveals qubit dephasing times \(T_2^ \ast\) of 10–30 μs for qubit 1 and 25–40 μs for qubit 2, around the flux-insensitive points.

Fig. 4
figure 4

Observation of high qubit coherence vs coupler flux bias. a, b T1 measurements showing high energy-relaxation times (15–40 μs) for the whole range of coupler bias, with the qubits detuned at their top and bottom sweetspots. c, d Respective measurements of \(T_2^{{\mathrm{Echo}}}\) decay times vs Φ3/Φ0. High coherence is observed except for the points where a lower sloshing circuit mode crosses the qubits (see text for details). e, f Respective spectroscopy of both qubits vs Φ3/Φ0. As the inductance of the coupler is varied the qubit frequencies change as expected from theory. The 0–3 transition of the lower circuit sloshing mode crossing both qubits at Φ3/Φ0 ~ 0.28 and Φ3/Φ0 ~ 0.38 is also clearly seen.

Full size image

Discussion

Our work demonstrates a key building block for circuit QED devices capable of exploring a rich vein of many-body physics in extended Hubbard models. In the context of driven nonlinear arrays, a chemical potential term, μ = ωq − ωd, could be straightforwardly implemented by coherently driving the transmons through the drive lines at a frequency ωd, which would enable the study of rich many-body phase diagrams with all J, V, μ tuneable.23,24 It may also be possible to implement topological pumping of interacting photons, by modulating the frequency of each transmon, to study bosonic transport of Fock states in a nonlinear array configuration.47 In realisations where higher-excitation manifolds might be explored, additional higher-order terms arising from the junction nonlinearity should be considered. For example, in our implementation, the nonlinearity of the medium leads to correlated hopping terms,

$$\frac{V}{6}\left( {\hat a^\dagger \hat n_a\hat b + \hat a\hat n_a\hat b^\dagger + \hat b^\dagger \hat n_b\hat a + \hat b\hat n_b\hat a^\dagger } \right),$$
(4)

such that a photon can hop between sites, on the condition that another photon is present. Additional contributions at higher excitation manifolds involve photon-pair tunnelling processes

$$\frac{V}{4}\left( {\hat a^\dagger \hat a^\dagger \hat b\hat b + \hat a\hat a\hat b^\dagger \hat b^\dagger } \right),$$
(5)

which might lead to exotic phenomena such as fractional Bloch oscillations.48 These contributions are explicitly derived in Supplementary Sec. S1, following a full quantum mechanical treatment of our circuit. In Fig. 5, we plot the coupled system eigenspectrum up to the two-excitation manifold, based on our full theoretical model including all next-to-leading order terms, which is found to be in excellent agreement with our data obtained at high powers.

Fig. 5
figure 5

Full theoretical model of the higher excitation manifold of the device. Measurement of the coupled system eigenspectrum (as Fig. 2e) at higher powers. Dots show theoretical calculations using the full quantum circuit Hamiltonian including all next-to-leading order transmon–transmon coupling terms and the sloshing mode contributions, for the parameters listed in Table 1. Simulations are performed using a Hilbert space dimension of N = 153.

Full size image

Our circuit can also be used to study many-body effects in spin models. When the transmon anharmonicity is much larger than the coupling strength \(\left( {E_{\mathrm{C}} \gg J} \right)\), a truncation to the qubit subspace is justified, and the transmon–transmon interaction is described by a Heisenberg XXZ Hamiltonian

$$2J\left( {\hat \sigma _x\hat \sigma _x + \hat \sigma _y\hat \sigma _y} \right) + V\hat \sigma _z\hat \sigma _z.$$
(6)

The coupling strengths available in this device are J/2π ~ 8–140 MHz, V/2π ~ 0–10 MHz, with orders of magnitude lower qubit decay rates (3–15 kHz). In a slightly different design, with a larger coupling capacitor Cc, it would also be possible to further explore the \(J \ll V\) regime (see Supplementary Fig. S4). One could then simulate an Ising \(\hat \sigma _z\hat \sigma _z\) interaction Hamiltonian (J = 0), with antiferromagnetic couplings of ~10 MHz. Additionally, time modulated magnetic fluxes threaded through the coupler SQUID can enable a large set of spin–spin interactions (e.g., pure \(\hat \sigma _x\hat \sigma _x\) or \(\hat \sigma _y\hat \sigma _y\)),49 therefore, giving access to emulating the dynamics of almost any spin model and exploring their phase diagrams. Connecting the coupler to four transmons on a lattice could enable simulating models with topological order such as the famous toric code.49 Our circuit could also be employed to engineer plaquette terms in lattice gauge theories or ring-exchange interactions in dimer models, where a longitudinal coupling much larger than the hopping term is required in order to emulate effective fields on the lattice.25 Moreover, a similar architecture, featuring \(\hat \sigma _z\hat \sigma _z\) coupling between transmons has been proposed theoretically for the realisation of a microwave single-photon transistor.50

In order to scale this circuit to larger lattice sizes, future experiments could take an approach where each transmon is connected to couplers via the same superconducting island, with the other island used for drive control and readout. Using a two-island transmon design has the advantages of reducing or eliminating the number of possible current loops involving current flow across qubit junctions, as well as allowing spurious flux cross-talk to be eliminated by linear compensation techniques (see 'Methods'). Our coherence measurements (Fig. 4) suggest that this coupler design can be realised without significantly limiting qubit coherence times, showing promise for scaling up to larger lattice sizes.

In conclusion, the implemented circuit increases the range of available interactions and phenomena that can be explored with circuit QED analog quantum simulators. We have demonstrated hopping and cross-Kerr interactions with in situ tuneability between two transmon qubits in a flexible and scalable superconducting circuit. The observed decay rates are orders of magnitude lower than the coupling strengths, making this a viable platform for analog quantum simulation experiments. Moreover, our full theoretical model of the quantum circuit is in excellent agreement with the measurements, providing a powerful tool for designing future larger scale implementations.

Methods

Chip fabrication

The capacitive network of superconducting islands and ground plane, together with readout and control lines are defined on a thin NbTiN film51 on top of a high resistivity Si substrate. The film is patterned using e-beam lithography on ARN7700 resist and etched with SF6/O2 plasma reactive-ion etching. Josephson junctions are then fabricated on each SQUID using Al-AlOx-Al shadow evaporation following e-beam lithography patterning on a PMGI/PMMA lift-off mask and HF dip to remove surface oxides on the NbTiN contact pads. Finally, after an e-beam patterning and reflowing PMGI step, followed by a second e-beam patterning of a MAA/PMMA resist stack, we evaporate Al airbridges which are used as cross-overs above all lines in order to ensure a uniform ground plane.

On-chip flux cross-talk calibration

Due to the compact geometry of our device, on-chip cross-talk between all flux channels is quite significant and extra care is required in order to decouple them. This requirement is vital for independent control, especially for larger scale implementations where such effects could become a major experimental challenge. We employ a systematic calibration procedure (see Supplementary Fig. S8) which is enabled by the fact that the frequency of the lower circuit sloshing mode (3.2 GHz at flux-insensitive point) is directly associated with tuning the coupling strength via Φ3. There is therefore one circuit degree of freedom corresponding to each bias channel. We track spectroscopically the frequency of each degree of freedom (e.g., qubit 1) around its flux-insensitive point (top sweetspot) and determine the flux offset as we vary the other two channels (2 and 3). Repeating this for all three degrees of freedom and flux channels we were able to measure and calibrate all cross-talk effects, making all flux bias channels Φ1,2,3 orthogonal. Note that the calibration method employed here allows us to distinguish between the on-chip flux cross-talk effects from the intrinsic qubit frequency shifts that are expected by varying the coupling inductance. The latter are deliberately not calibrated out in order to be able to fit the measurement data in Figs. 2e and 5 with the full circuit theory Hamiltonian, however we could straightforwardly compensate for them if required.

Device parameters

The device parameters are presented in Table 1. In the first column, we list the circuit parameters obtained by fitting the resonantly coupled transmon–transmon spectrum in the single-excitation manifold (Fig. 2e) with a simplified circuit model that neglects any higher-order couplings to the sloshing mode. The parameters in the second column are used in our full numerical model that includes all next-to-leading order terms in the circuit Hamiltonian (Supplementary Eq. (S11)), to describe the obtained data at higher excitation manifolds (Fig. 5).

Data availability

The experimental data and numerical code are available by the corresponding author upon reasonable request.