Abstract
The speed at which two remote parties can exchange secret keys in continuous-variable quantum key distribution (CV-QKD) is currently limited by the computational complexity of key reconciliation. Multi-dimensional reconciliation using multi-edge low-density parity-check (LDPC) codes with low code rates and long block lengths has been shown to improve error-correction performance and extend the maximum reconciliation distance. We introduce a quasi-cyclic code construction for multi-edge codes that is highly suitable for hardware-accelerated decoding on a graphics processing unit (GPU). When combined with an 8-dimensional reconciliation scheme, our LDPC decoder achieves an information throughput of 7.16 Kbit/s on a single NVIDIA GeForce GTX 1080 GPU, at a maximum distance of 142 km with a secret key rate of 6.64 × 10−8 bits/pulse for a rate 0.02 code with block length of 106 bits. The LDPC codes presented in this work can be used to extend the previous maximum CV-QKD distance of 100 km to 142 km, while delivering up to 3.50× higher information throughput over the tight upper bound on secret key rate for a lossy channel.
Similar content being viewed by others
Introduction
Quantum key distribution (QKD), also referred to as quantum cryptography, offers unconditional security between two remote parties that employ one-time pad encryption to encrypt and decrypt messages using a symmetric secret key, even in the presence of an eavesdropper with infinite computing power and mathematical genius.1,2,3,4 The security of QKD stems from the no-cloning theorem of quantum mechanics.5,6,7 Unlike classical cryptography, quantum cryptography allows the two remote parties, Alice and Bob, to detect the presence of an eavesdropper, Eve, while also providing security against brute force, key distillation attacks that may be enabled through quantum computing.8 Today’s public key exchange schemes such as Diffie-Hellman and encryption algorithms like RSA, respectively, rely on the computational hardness of solving the discrete log problem and prime factorization.9,10 Both of these problems, however, can be solved in polynomial time by applying Shor’s algorithm on a quantum computer.11,12,13 Future threats may also arise from the discovery of a new classical algorithm capable of solving such cryptography problems in polynomial time on a classical Turing machine.
While such threats remain speculative, QKD systems have already been realized in several commercial and research settings worldwide.14,15,16,17 There are two protocols for generating a symmetric key over a quantum channel: (1) discrete-variable QKD (DV-QKD) where Alice encodes her information in the polarization of single-photon states that she sends to Bob, and (2) continuous-variable QKD (CV-QKD) where Alice encodes her information in the amplitude and phase quadratures of coherent states.4,18 In DV-QKD, Bob uses a single-photon detector to measure each received quantum state, while in CV-QKD, Bob uses homodyne or heterodyne detection techniques to measure the quadratures of light.4,19,20,21 While DV-QKD has been experimentally demonstrated up to 404 km,22 cryogenic temperatures are required for single-photon detection at such distances.4 CV-QKD systems can be implemented using cost-effective detectors that are routinely deployed in classical telecommunications equipment that operates at room temperature.4,18 Recently, the unidimensional CV-QKD protocol was experimentally demonstrated up to 50 km,23 where Alice modulates only one quadrature (e.g., amplitude) instead of two, to reduce cost and complexity, with the trade-off of lower secret key rate and higher sensitivity to channel excess noise.24 Both CV-QKD and DV-QKD protocols are comprised of four steps: (1) quantum transmission over a private quantum channel, (2) sifting of measured quantum states, (3) reconciliation over an authenticated classical public channel that is assumed to be noiseless, and (4) privacy amplification via hashing.2,5,6 The majority of QKD research focuses on applications over optical fiber, since quantum signals for both CV-QKD and DV-QKD can be multiplexed over classical telecommunications traffic in existing fiber optical networks.25,26
The motivation of this work is to address the two key challenges that remain in the practical implementation of CV-QKD over optical fiber: (1) to extend the distance of secure communication beyond 100 km with protection against collective Gaussian attacks,27,28,29,30 and (2) to increase the computational throughput of the key reconciliation (error correction) algorithm in the post-processing step such that the maximum achievable secret key rate remains limited only by the fundamental physical parameters of the optical equipment at long distances.6,7,31,32 There are two limitations to the speed of key reconciliation. The first is the secret key rate, which is fundamentally limited by the transmittance and excess noise on the lossy optical channel, and is measured in bits/pulse.33 The second is the rate of computational throughput from the hardware implementation, measured in bits/second.31 To compare the two rates, we normalize the secret key rate to bits/second by choosing a realistic CV-QKD pulse sampling rate of frep = 1 MHz.7,34 While secure QKD networks can be built using intermediate trusted nodes, or through measurement-device-independent QKD (MDI-QKD) with untrusted relay nodes,35,36,37 the long-distance reconciliation problem is motivated by the following two reasons: (1) each intermediate node introduces additional vulnerability, and (2) implementing efficient quantum repeaters remains a challenge.3,4,22 Jouguet and Kunz-Jacques showed that Megabit/s one-way forward error correction using multi-edge low-density parity-check (LDPC) codes is achievable for distances up to 80 km,31 while Huang et al. showed that the distance could be extended to 100 km by controlling excess noise.38 Two-way interactive error-correction protocols such as Cascade or Winnow are not practical for long-distance QKD due to their large latency and communication overhead.39,40,41,42 Here we explore high-speed LDPC decoding for one-way reconciliation in CV-QKD beyond 100 km.
A particular challenge in designing error-correcting codes for such long distances is the low signal-to-noise ratio (SNR) of the optical quantum channel, which typically operates below −15 dB. At such low SNR, high-efficiency key reconciliation can be achieved only using low-rate block codes with large block lengths on the order of 106 bits,43,44,45,46 where approximately 98% of the bits are redundant parity bits that must be discarded after error-correction decoding. The reconciliation efficiency is defined as β = Rcode/C(s), where \(C(s)\) = \(0.5 {\mathrm{log}}_2(1 + s)\) is the Shannon limit at a particular SNR s, and Rcode = k/n is the code rate of a linear block code where (n − k) redundant parity bits are concatenated with k information bits to form an encoded block of n bits.47,48,49 In order to maximize the secret key rate and reconciliation distance, the error-correcting code must achieve a high β-efficiency and high error-correction performance with low frame error rate (FER). The direction of reconciliation between Alice and Bob also impacts the maximum secret key rate and reconciliation distance. In direct reconciliation, the direction of communication in both the quantum and classical channel is from Alice to Bob. However, the distance with direct reconciliation is limited to about 15 km.50,51,52 The reverse reconciliation scheme achieves a higher secret key rate at longer distances by reversing the direction of communication in the classical channel from Bob to Alice.7,44,53
Jouguet et al. previously explored multi-edge LDPC codes for long-distance reverse reconciliation due to their high efficiency and near-Shannon limit performance with low-rate codes. However, such codes require hundreds of LDPC decoding iterations to achieve asymptotic error-correction performance.7,31,53,54 This is in contrast to LDPC codes employed in the IEEE 802.11ac (Wi-Fi) standard, where the SNR is above 0 dB, the block length is 648 bits, and the LDPC decoder typically operates at 10 iterations to deliver Gigabit/s decoding throughput.55,56,57 At low SNR, a CV-QKD system with a Gaussian input and Gaussian channel can be approximated as a Binary Input Additive White Gaussian Noise Channel (BIAWGNC), where binary LDPC codes can be used in conjunction with multi-dimensional reconciliation schemes to further improve error-correction performance and increase distance.7,44,45,48,53 However, the computational complexity and latency of decoding random LDPC parity-check matrices with block lengths on the order of 106 bits remains a challenge.
We introduce a quasi-cyclic code construction for multi-edge LDPC codes with block lengths of 106 bits to simplify decoder design and increase throughput.54,58 Computational acceleration is achieved through an optimized LDPC decoder design implemented on a state-of-the-art graphics processing unit (GPU), which provides floating-point computational precision and high-bandwidth on-chip memory. GPUs are a low-cost platform that is highly suitable for high-throughput decoding of long block-length codes, as opposed to application-specific integrated circuits (ASICs) or field-programmable gate arrays (FPGAs), which suffer from limited memory, fixed-point computational precision, highly complex routing, and silicon area constraints.59,60,61 The LDPC codes presented in this work can be used to extend the previous maximum CV-QKD distance of 100 km to 142 km, while delivering up to 3.50× higher decoded information throughput over the tight upper bound on the secret key rate for a lossy channel.33 Here we show that LDPC decoding is no longer the computational bottleneck in long-distance CV-QKD, and that the secret key rate remains limited only by the physical parameters of the quantum channel.
Results
Quasi-cyclic multi-edge LDPC codes
We extend the design of low-rate, multi-edge LDPC codes by applying a quasi-cyclic (QC) construction technique.58,62 QC codes impose a highly-regular parity-check matrix structure with a sufficient degree of randomness in order to achieve near-Shannon limit error-correction performance, while reducing decoder implementation complexity.58 QC codes are defined by a parity-check matrix constructed from an array of q × q cyclically-shifted identity matrices or q × q zero matrices.58 The tilings evenly divide the (n − k) × n parity-check matrix into n/q QC macro-columns and (n − k)/q QC macro-rows. The expansion factor q in a QC matrix determines the trade-off between decoder implementation complexity and error-correction performance. Our goal is to construct QC codes that achieve comparable FER performance to a random code with the same degree distribution, but with lower decoding latency to maximize throughput.
We constructed five QC-LDPC codes with expansion factors q ∈ {21, 50, 100, 500, 1000} based on the Rcode = 0.02 multi-edge degree distribution previously designed by Jouguet et al. for CV-QKD reverse reconciliation on the BIAWGNC.7,53 For performance comparison, we also constructed a non-QC multi-edge random code with the same degree distribution. Under Sum–Product decoding, the error-correction performance of the q ∈ {100, 500, 1000} QC codes was significantly worse than the random code. Thus, only the q = 21 and q = 50 QC codes are presented here. Table 1 summarizes the code parameters. In order to maintain the same degree distributions, the block length of the q = 21 QC code was adjusted to n = 1.008 × 106 bits, and the code rate of the q = 50 QC code was adjusted to Rcode = 0.01995.
Our multi-edge LDPC codes achieve similar error-correction performance on the BIAWGNC compared to those developed by Jouguet et al. with multi-dimensional reconciliation.53 Figure 1 presents the FER versus SNR error-correction performance under soft-decision Sum–Product decoding for the d = 1 and d = 8 reconciliation dimensions.63 Both QC codes outperform the random code in the high β-efficiency region at low SNR. The q = 50 QC code achieves the best overall FER performance over d = 1, 2, 4, 8 dimensions, due to its slightly lower code rate. The q = 21 QC code also performs better than the random code over all dimensions, due to its longer block length. With d = 8 dimensional reconciliation, at SNR = 0.0283, which corresponds to a reconciliation efficiency of β = 0.99, the q = 21 and q = 50 QC codes achieve 1.92% and 6.57% lower FER than the non-QC random code, respectively.
The error-correction performance beyond the waterfall region is not of practical interest for long-distance CV-QKD since the codes are intended to operate with a high FER at low SNR with high β-efficiency in order to maximize the secret key rate and distance. While not shown in Fig. 1, the d = 2 and d = 4 reconciliation schemes achieve approximately 0.04 dB and 0.08 dB coding gain, respectively, over the d = 1 scheme in the waterfall region for all three codes. Thus, higher reconciliation schemes extend code performance to lower SNR where the FER > 0 and β → 1.
Secret key rate and distance
Accounting for finite-size effects, the secret key rate for a CV-QKD system with one-way reverse reconciliation is given by
where Nprivacy bits comprise the privacy amplification block, Nquantum is the number of sifted symbols after quantum transmission and measurement, Pe is the reconciliation FER, IAB is the mutual information between Alice and Bob, χBE is the Holevo bound on the information leaked to Eve, and Δ(Nprivacy) is the finite-size offset factor.6,64
For each fixed-rate LDPC code, there exists a unique FER-β pair, where each β corresponds to a particular SNR operating point in each FER-SNR curve shown in Fig. 1. The FER and efficiency β are positively correlated, such that there exists an optimal trade-off between β and FER where Kfinite is maximized for a fixed transmission distance. To achieve key reconciliation at long distances, the operating point must be chosen in the waterfall region of the FER-SNR curve where β is high, despite the high FER where P e → 1.
Key reconciliation for a particular β-efficiency is only achievable over a limited range of distances where Kfinite > 0. When β is high, the FER Pe → 1, and thus Kfinite → 0 as erroneous frames are discarded after decoding. As a result, the maximum reconciliation distance is limited by the error-correction performance of the LDPC code. In general, for a single FER-β pair, LDPC decoding can achieve either (1) a high secret key rate at short distance, or (2) a low secret key rate at long distance. For long-distance CV-QKD beyond 100 km, key reconciliation is only achievable with high β-efficiency at the expense of low secret key rate.
Figures 2 and 3 present the finite secret key rate results for the three LDPC codes over the distance range of interest with Nprivacy = 1012 bits based on the d = 1 and d = 8 reconciliation dimensions, respectively. The quantum channel was characterized using previously published experimental results and parameters.7,38,64 Here we assume the standard loss of a single-mode fiber optical cable to be α = 0.2 dB/km, with a transmittance of \(T = 10^{ - \alpha \ell /10}\), where the distance \(\ell\) is expressed in kilometers. The excess channel noise (measured in shot noise units) is chosen to be constant \(\epsilon\) = 0.01 for 0 ≤ \(\ell\) ≤ 100 km, and monotonically increasing as \(\epsilon\) = 0.01 + 0.001\((\ell - 100)\) for 100 km < \(\ell\) ≤ 170 km.38 Bob’s homodyne detector efficiency is chosen to be η = 0.606, with an added electronic noise of Vel = 0.041 (measured in shot noise units).7 In Eq. (1), we arbitrarily choose Nquantum = 2Nprivacy and a conservative security parameter of 10−10 for Δ(Nprivacy).64 For each curve in Figures 2 and 3, Alice’s modulation variance VA (measured in shot noise units) is calculated at each distance point \(\ell\), assuming a fixed code rate Rcode, such that the β efficiency, SNR, and FER remain constant over the entire distance range where Kfinite > 0. Here, \(V_{\mathrm{A}}(\ell ,\beta )\) = \(s(\beta )(1 + \chi _{\mathrm{total}}(\ell ))\), where the SNR is given by \(s(\beta )\) = \(2^{2R_{{\mathrm{code}}}{\mathrm{/}}\beta } - 1\), and χtotal\((\ell )\) is the total noise added between Alice and Bob.6
The three LDPC codes achieve similar finite secret key rates and reconciliation distances with both d = 1 and d = 8 schemes for β ≤ 0.92, since the codes are operating close to their respective error floors. However, for β > 0.92, the FER becomes a limiting factor to achieving a non-zero secret key rate. The d = 1 scheme achieves a maximum efficiency of β = 0.96, where the maximum distance is limited to 122 km. For β > 0.96, the FER Pe = 1, thus Kfinite = 0. The d = 8 scheme operates up to β = 0.99 efficiency, with a maximum distance of 142 km. The d = 8 scheme achieves higher secret key rates for all three LDPC codes at β = 0.95 and β = 0.96 in comparison to the d = 1 scheme since the code FER performance is higher. The d = 2 and d = 4 schemes both achieve a maximum efficiency of β = 0.97 at 127 km. While not shown here, the maximum reconciliation distance with Nprivacy = 1010 bits is only 128 km for β = 0.99 under d = 8 dimensional reconciliation. Thus, the reconciliation distance is also largely dependent on the privacy amplification block size.
GPU-Accelerated Decoding
We implemented a multi-threaded Sum–Product LDPC decoder on a single NVIDIA GeForce GTX 1080 GPU using the NVIDIA CUDA C++ application programming interface. The operations of the Sum–Product algorithm were re-ordered to avoid uncoalesced memory writes and to maximize the amount of thread-level parallelism for arithmetic computations.
A quasi-cyclic matrix structure reduces data permutation and memory access complexity by eliminating random, unordered memory access patterns. QC codes require fewer memory lookups for message passing since the parity-check matrix can be described with approximately q-times fewer terms, where q is the expansion factor of the QC parity-check matrix, in comparison to a random matrix for the same block length. Table 2 presents the latency of one decoding iteration for the three codes, and also highlights their respective error-correction performance and GPU throughput at the maximum β = 0.99 efficiency with d = 8 reconciliation. The raw GPU throughput (including parity bits) is given by
and the average information throughput of the GPU decoder is given by
The latency per iteration depends on the LDPC code structure and the number of memory lookups, while the FER is bound by the maximum number of iterations.
Table 3 compares the performance of the random and QC codes at the maximum achievable distance for each reconciliation dimension. The QC codes achieve approximately 3× higher raw decoding throughput \(K_{{\mathrm{GPU}}}^{{\mathrm{raw}}}\) over the random code with d = 1, 2, 4, 8 dimensional reconciliation at the maximum distance point for each β-efficiency. When scaled by the FER and code rate, the QC codes achieve between 1.6× and 12.8× higher information throughput \(K_{{\mathrm{GPU}}}^\prime\) over the random code.
Pirandola et al. recently showed that there exists a tight upper bound on the secret key rate for a lossy channel.33 For a fiber-optic channel, this limit is determined by the transmittance T and is given by
The upper bound versus distance is plotted in Fig. 4, along with the GPU-decoded information throughput for the q = 21 QC code under d = 8 dimensional reconciliation. Figure 4 illustrates that the decoded information throughput \(K_{{\mathrm{GPU}}}^\prime\) of the reconciliation algorithm is higher than the upper bound on secret key rate \(K_{{\mathrm{lim}}}^\prime\) on a lossy channel with a 1 MHz source at each maximum distance point from β = 0.8 to β = 0.99. Table 3 presents the finite secret key rate \(K_{{\mathrm{finite}}}^\prime\) and the upper bound on secret key rate \(K_{{\mathrm{lim}}}^\prime\) for a lossy channel for each maximum distance point. Both Klim and Kfinite are scaled by the light source repetition rate frep, such that \(K_{{\mathrm{lim}}}^\prime\) = frepKlim and \(K_{{\mathrm{finite}}}^\prime\) = frepKfinite, where a realistic CV-QKD repetition rate of frep = 1 MHz is assumed.7,34,51
GPU information throughput \(K_{{\mathrm{GPU}}}^\prime\) of the q = 21 QC-LDPC code with d = 8 dimensional reconciliation up to the maximum distance point for β ∈ {0.80, 0.88, 0.92, 0.96, 0.98, 0.99}, and upper bound on secret key rate for a lossy channel \(K_{{\mathrm{lim}}}^\prime\) vs. distance. Here we show that the GPU information throughput \(K_{{\mathrm{GPU}}}^\prime\) is higher than the tight upper bound on secret key rate at the maximum distance point for each β-efficiency using a single NVIDIA GeForce GTX 1080 GPU. Thus, the speed of key reconciliation in the post-processing step is no longer a bottleneck in CV-QKD
The rightmost column in Table 3 (\(K_{{\mathrm{GPU}}}^\prime {\mathrm{/}}K_{{\mathrm{lim}}}^\prime\)) presents the two key results of this work. First, it shows that the GPU decoder can achieve between 2.05× and 3.50× higher information throughput \(K_{{\mathrm{GPU}}}^\prime\) over the upper bound on secret key rate \(K_{{\mathrm{lim}}}^\prime\) with a 1 MHz source using QC-LDPC codes with d = 8 dimensional reconciliation only. This maximum 3.50× speedup is highlighted in Fig. 4 at 142 km with β = 0.99. The second result is that d = 1, d = 2, and d = 4 dimensional reconciliation schemes are not well-suited for long-distance CV-QKD since the \(K_{{\mathrm{GPU}}}^\prime\) speedup over \(K_{{\mathrm{lim}}}^\prime\) is less than 1×. In general, Table 3 shows that QC codes achieve lower decoding latency than the random code at long distances, thereby making them more suitable for reverse reconciliation at high β efficiencies. Since the decoder delivers an information throughput higher than the upper bound on secret key rate, we conclude that LDPC decoding is no longer the post-processing bottleneck in CV-QKD, and thus, the secret key rate remains limited only by the physical parameters of the quantum channel.
The results presented in Table 3 and Fig. 4 assumed a light source repetition rate of frep = 1 MHz. While a higher source repetition rate such as frep = 100 MHz would raise the upper bound on secret key rate \(K_{{\mathrm{lim}}}^\prime\) above the maximum GPU decoder throughput \(K_{{\mathrm{GPU}}}^\prime\), it would still not introduce a post-processing bottleneck for CV-QKD. The GPU decoder currently delivers an information throughput \(K_{{\mathrm{GPU}}}^\prime\) between 5286× and 135,000× higher than the finite secret key rate \(K_{{\mathrm{finite}}}^\prime\) with a 1 MHz light source at the maximum distance points for d = 1, 2, 4, 8 dimensional reconciliation schemes. Even with a source repetition rate of frep = 1 GHz, the GPU information throughput \(K_{{\mathrm{GPU}}}^\prime\) would still exceed the operating secret key rate \(K_{{\mathrm{finite}}}^\prime\) between 5.3× and 13.5× for distances beyond 122 km, assuming the same quantum channel parameters. Further computational speedup can be achieved by concurrently decoding multiple frames using multiple GPUs.
Figure 5 compares the LDPC decoding throughput versus distance for several GPU-based CV-QKD and DV-QKD implementations, illustrating that high-throughput reconciliation at long distances is achievable only using large block-length codes that approach the Shannon limit with >90% efficiency for CV-QKD or <10% quantum bit error rate (QBER) for DV-QKD. This work achieves the longest reconciliation distance compared to the previously published works.
Raw throughput \(K_{{\mathrm{GPU}}}^{{\mathrm{raw}}}\) vs. distance of GPU-based LDPC decoders for CV- and DV-QKD. For CV-QKD implementations,31,32,85 the annotated values indicate the LDPC code code block length n, code rate R, reconciliation efficiency β, and SNR of the quantum channel. For DV-QKD implementations, the annotated values indicate the block length n, code rate R, and QBER.15,65,86 Our LDPC decoder throughput result is obtained using a single NVIDIA GeForce GTX 1080 GPU
At the time of writing, there has not been any reported investigation of the construction of QC codes for multi-edge LDPC codes targeting low-SNR channels below −15 dB for long-distance CV-QKD. Previous DV-QKD implementations used QC-LDPC codes with block lengths of 103 bits from the IEEE 802.11ac (Wi-Fi) standard,55 however, these works did not achieve reconciliation beyond 50 km.65,66 Bai et al. recently showed that rate Rcode = 0.12 QC codes with block lengths of 106 bits can be constructed using progressive edge growth techniques, or by applying a QC extension to random LDPC codes with block lengths of 105 bits, however, the reported QC codes target an SNR of only −1 dB,67 and are thus not suitable for long-distance CV-QKD beyond 100 km.
At the time of writing, there is only one reported decoder implementation designed to operate in the low-SNR regime for long-distance CV-QKD reconciliation.31 Jouguet and Kunz-Jacques reported a GPU-based LDPC decoder that achieves 7.1 Mb/s throughput at SNR = 0.161 (β = 0.93) on the BIAWGNC,31 for a random multi-edge LDPC code with a block length of 220 bits and Rcode = 1/10.54 For throughput comparison purposes, we designed two additional multi-edge codes with the same code rate, block length, and SNR threshold:54 a random code and a q = 512 QC code.
Table 4 presents a performance comparison between our two designed Rcode = 1/10 codes and the result achieved by Jouguet and Kunz-Jacques.31 Our q = 512 QC code achieves 1.29× higher throughput than the 7.1 Mb/s reported by Jouguet and Kunz-Jacques,31 further demonstrating that the QC code structure offers computational speedup benefits for multi-edge codes operating in the high β-efficiency region at low SNR. Both GPU models have a similar memory bus width, which is the primary constraint that limits the latency per iteration. Here, GPU decoder performance is bound by the memory access rate, and not the floating-point operations per second (FLOPS). A wider GPU memory allows for a higher memory access rate, which reduces decoding latency.
GPUs continue to deliver higher computational performance with each successive architecture generation. We present here the potential LDPC decoding speedup improvement using the latest NVIDIA TITAN V GPU (released in December 2017), in comparison to our results achieved on a NVIDIA GeForce GTX 1080 GPU (released in May 2016). The NVIDIA TITAN V delivers 110 TeraFLOPS with 5210 cores and a 652 GB/s memory bandwidth, which is a 2× improvement in both the number of computational cores and memory bandwidth over our NVIDIA GeForce GTX 1080. Since our GPU-based decoder is memory bound, we ignore the improvement in FLOPS, and consider only the increase in memory bandwidth and number of cores. We estimate that our LDPC decoder would achieve 4× higher throughput on the latest NVIDIA TIVAN V GPU. At the maximum distance of 142 km with β = 0.99 and d = 8 reconciliation, using our q = 21 QC-LDPC code on an NVIDIA TITAN V GPU, we estimate that our decoder would achieve a raw throughput \(K_{{\mathrm{GPU}}}^{{\mathrm{raw}}}\) of 6.90 Mb/s, and an information throughput \(K_{{\mathrm{GPU}}}^\prime\) of 28.6 Kb/s, which is 14× higher than the tight upper bound on the secret key rate with a 1 MHz light source.
Discussion
We introduced quasi-cyclic multi-edge LDPC codes to accelerate long-distance reconciliation in CV-QKD by means of a GPU-based decoder implementation and multi-dimensional reconciliation schemes. Other error-correcting codes have also been studied for the low-SNR regime of CV-QKD, including polar codes, repeat-accumulate codes, and Raptor codes.31,68,69 However, at the time of writing, there are no hardware implementations of such codes for long-distance CV-QKD beyond 100 km. In addition to extending information theoretic security to general attacks for finite key sizes,30,70,71,72 a major remaining hurdle to extending the distance in CV-QKD is reducing excess noise in the optical channel.38 Future work might also investigate the security of CV-QKD and LDPC decoding performance with non-Gaussian noise. GPU-based decoder implementations with QC codes would provide a suitable platform for such investigations. Furthermore, QC codes and GPU decoding can also be applied in DV-QKD, where reconciliation is performed on the binary symmetric channel.
In this work, we showed that the first post-processing step (reconciliation) can achieve 3.50× higher information throughput than the upper bound on secret key rate up to 142 km at a speed of 7.16 Kb/s, using rate Rcode = 0.02 LDPC codes with block lengths of n = 106 bits. To achieve this 142 km distance with security against finite-size effects, we assumed that the second post-processing step (privacy amplification) is performed using a block length of Nprivacy = 1012 bits. While the speed of privacy amplification has recently been demonstrated up to 100 Mb/s for a block length of Nprivacy = 108 bits,73 the maximum achievable distance with Nprivacy = 108 bits is limited to 88 km with β = 0.99 and d = 8 reconciliation (assuming the same channel parameters as in this work). For CV-QKD beyond 100 km, privacy amplification block lengths of Nprivacy ≥ 1010 bits are required. Toeplitz hashing methods can be employed to achieve high computational parallelism for block lengths on the order of Nprivacy = 1012 bits.74 Such implementations should achieve a minimum throughput on the order of 10 Kb/s such that the complete post-processing chain (reconciliation and privacy amplification) maintains a higher throughput than the upper bound on secret key rate.
The LDPC codes and reconciliation techniques presented in this work can be applied to two areas that show promise for QKD: (1) free-space QKD using low-Earth orbit satellites to extend the distance of secure communication beyond 200 km without fiber-optic infrastructure,75,76 and (2) fully-integrated monolithic QKD chip implementations that combine optical and post-processing circuits.4,77,78 While GPUs integrate seamlessly into post-processing computer systems and provide a low-cost platform for design exploration, their high power consumption (on the order of 200 W per card) may present QKD system scaling limitations. A single-chip solution would accelerate the adoption of QKD in modern network infrastructure with lower cost, power, and integration complexity.
Methods
Multi-dimensional reverse reconciliation
Following the quantum transmission and sifting steps, Alice and Bob, respectively, share correlated Gaussian sequences, X and Y, of length n, where n is equivalent to the LDPC code block length and n ≤ Nprivacy ≤ Nquantum.5,6,7 The BIAWGNC is induced from the physical parameters of the quantum channel, and is assumed to have zero mean and noise variance \(\sigma _Z^2\), \(Z \sim {\cal N}\left( {0,\sigma _Z^2} \right)\).53 At each distance \(\ell\), the SNR is given by \(s = 1{\mathrm{/}}\sigma _Z^2\) = \(V_{\mathrm{A}}(\ell )\)/\((1 + \chi _{{\mathrm{total}}}(\ell ))\). It follows then that \(X \sim {\cal N}(0,1)\), \(Y \sim {\cal N}\left( {0,1 + \sigma _Z^2} \right)\), and Y = X + Z.53
In reverse reconciliation, Bob generates a uniformly-distributed random binary sequence S of length k, and performs a computationally inexpensive LDPC encoding operation to generate a codeword C of length n, where C i ∈ {0, 1}, based on a binary LDPC parity-check matrix H that is also known to Alice. Bob then transmits his classical message M to Alice, where \(M_i = ( - 1)^{C_i}Y_i\) for i = 1, 2, …, n.6
Long-distance reverse reconciliation can be achieved with multi-dimensional reconciliation schemes where the multiplication and division operators are defined.44,45 Normed division is only defined for four finite-dimensional algebras: the real numbers \({\Bbb R}\) \(\left( {{\Bbb R}^{d = 1}} \right)\), the complex numbers \({\Bbb C}\) \(\left( {{\Bbb R}^{d = 2}} \right)\), the quaternions \({\Bbb H}\) \(\left( {{\Bbb R}^{d = 4}} \right)\), and the octonions \({\Bbb O}\) \(\left( {{\Bbb R}^{d = 8}} \right)\).79 Hence, here we consider only the d = 1, 2, 4, 8 dimensions. Assuming error-free transmission of M over the classical channel, Alice attempts to recover Bob’s codeword C using her sequence X as follows:
Here, R, M, U, X, Y, and Z are d-dimensional vectors. Alice observes a BIAWGNC described by R = U + N, where U is comprised of \(( - 1)^{C_i}\) components, and the multi-dimensional noise is given by N = (UZX*)/\(\left\| {\bf{X}} \right\|^2\).53 For d = 1, Alice observes a channel with binary input \(U_i = ( - 1)^{C_i}\) and additive noise \(N_i = ( - 1)^{C_i}Z_i{\mathrm{/}}X_i\). For d = 2, U = \(\left[ {( - 1)^{C_{2i}},( - 1)^{C_{2i - 1}}} \right]\), and for d = 4, U = \(\left[ {( - 1)^{C_{4i - 3}},( - 1)^{C_{4i - 2}}} \right.\), \(\left. {( - 1)^{C_{4i - 1}},( - 1)^{C_{4i}}} \right]\). The Cayley-Dickson construction can be applied to derive the multi-dimensional noise N for d = 2, 4, 8.80 Since the noise is identically distributed in each dimension, C can be assumed to be the all-zero codeword, i.e., C i = 0 for all i = 1, 2, …, n to simplify the derivation.
For d-dimensional reconciliation, each consecutive group of d quantum coherent-state transmissions has the same channel noise variance. For d = 1, each R i has a unique channel noise variance defined by \(\sigma _{Ni}^2 = \sigma _Z^2{\mathrm{/}}\left| {X_i} \right|^2\) for i = 1, 2, …, n. For d = 2, reconciliation is performed over successive (R2i−1, R2i) pairs: (R1, R2),(R3, R4), …, (Rn−1, R n ), which are constructed from the quadrature transmission of successive (M2i−1, M2i) pairs for i = 1, 2, …, n/2. Here, R2i−1 = \(( - 1)^{C_{2i - 1}} + N_{2i - 1}\) and R2i = \(( - 1)^{C_{2i}} + N_{2i}\) for i = 1, 2, …, n/2. While the real and imaginary noise components, \(N_{2i - 1}\) and N2i, are not equal, the variance of the channel noise is uniform over both dimensions, such that \(\sigma _{N(2i - 1)}^2\) = \(\sigma _{N(2i)}^2\) for each (R2i−1, R2i) pair. For d = 4 and d = 8, each d-tuple of successive R i values has a unique channel noise for each dimensional component, but the channel noise variance remains uniform over all d dimensions.
Alice performs LDPC decoding using the shared parity-check matrix H, and her computed soft-decision value R i and channel noise variance \(\sigma _{Ni}^2\) for each i = 1, 2, …, n via the computationally expensive Sum–Product algorithm to build an estimate \(\widehat {\bf{S}}\) of Bob’s sequence S. LDPC decoding is successful if \(\widehat {\bf{S}} = {\bf{S}}\), whereas a frame error is said to have occurred when \(\widehat {\bf{S}} \ne {\bf{S}}\).
Frame error rate with undetected errors
The number of possible codewords for any binary linear block code is \(2^k = 2^{nR_{{\mathrm{code}}}}\). Here, with n = 106 bits and Rcode = 0.02, the number of possible valid codewords is approximately 4 × 106020. As such, it is possible for the decoder to converge to a valid codeword where the decoded message is incorrect, i.e., the parity check passes but \(\widehat {\bf{S}} \ne {\bf{S}}\). In coding theory, this is referred to as an undetected error. To detect such errors, a cyclic redundancy check (CRC) of Bob’s original message S can be transmitted as part of the frame, and then verified against the computed CRC of Alice’s decoded message \(\widehat {\bf{S}}\). If the CRC results of S and \(\widehat {\bf{S}}\) are equal, the decoding is successful and \(\widehat {\bf{S}}\) can be used to distill a secret key. The probability of detecting an error is given by Pdetected error = P(Parity Fail) + P(Parity Pass ∩ CRC Fail). A truly undetected error occurs when both the parity check and CRC pass, but \(\widehat {\bf{S}} \ne {\bf{S}}\). Both detected and undetected errors contribute to the FER, hence the probability of frame error is defined as Pe = Pdetected error + Pundetected error. We found that a 32-bit CRC code was sufficient to detect all invalid decoded messages without sacrificing information throughput. Thus, the FER is reduced to P e = Pdetected error since Pundetected error = 0.
Constructing quasi-cyclic multi-edge LDPC codes
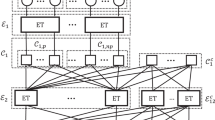
An equivalent definition of a code’s binary parity-check matrix H is given by its Tanner graph \({\cal G}\), which contains two independent vertex sets known as check nodes (CNs) and variable nodes (VNs) that correspond to the rows and columns of H, respectively.81 An edge between CN c i and VN v j belongs to \({\cal G}\) if H(i, j) = 1. An LDPC code of length n can be specified by the number of variable and check nodes, and their respective degree distributions. The number of edges connected to a vertex in \({\cal G}\) is called the degree of the vertex. The degree distribution of \({\cal G}\) is a pair of polynomials \(\omega (x) = \mathop {\sum}\nolimits_i {\kern 1pt} \omega _ix^i\) and \(\psi (x) = \mathop {\sum}\nolimits_i {\kern 1pt} \psi _ix^i\), which, respectively, denote the number of variable and check nodes of degree i in \({\cal G}\). As n → ∞, the error-correction performance of Tanner graphs with the same degree distribution is nearly identical.82 Hence, the variable and check node degree distributions can be normalized to Ω(x) = \(\mathop {\sum}\nolimits_i {\kern 1pt} (\omega _i{\mathrm{/}}n)x^i\) and Ψ(x) = \(\mathop {\sum}\nolimits_i {\kern 1pt} (\psi _i{\mathrm{/}}(n - k))x^i\), respectively. To design a binary LDPC code, first find the normalized degree distribution pair (Ω(x), Ψ(x)) of rate Rcode with the best performance. Then, if n is large, randomly sample a Tanner graph \({\cal G}\) that satisfies the degree distribution defined by ω(x) and ψ(x) (up to rounding error) to construct H.
In a standard LDPC code, the degree distributions are limited to a single edge type, such that all variable and check nodes are statistically interchangeable. Multi-edge codes extend the degree distributions to multiple edge types with an additional edge-type matching condition.54 The design and construction of multi-edge LDPC codes is described by Richardson and Urbanke.54
The Rcode = 0.02 multi-edge LDPC codes in this work have the following normalized degree distribution:
This distribution was designed by Jouguet et al. by modifying a rate 1/10 multi-edge degree structure.53,54 We generated random parity-check matrices by randomly sampling Tanner graphs that satisfied the multi-edge degree distribution defined by ω(x) and ψ(x), and the edge-type matching condition. The random sampling technique does not degrade code performance since the target FER is known to be high (Pe ≈ 10−1), and the error floor is not a concern.83
To design a quasi-cyclic multi-edge code, repeat the random sampling process using n/q as the block length instead of n to obtain a base Tanner graph \({\cal G}_B\). The base matrix H B is obtained from \({\cal G}_B\) by populating each non-zero entry by a random element of the set {1, 2, …, q}. Let I i be the circulant permutation submatrix obtained by cyclically shifting each row of the q × q identity matrix to the right by i − 1. The QC matrix H is obtained from H B by replacing each non-zero entry of value i by I i , and each zero entry by the q × q all-zeros submatrix.
Quantum channel capacity vs. channel coding capacity
Here we examine two definitions of channel capacity in the context of CV-QKD: (1) the capacity of the quantum channel, and (2) the capacity of the channel coding problem. The first capacity is related to the complete QKD system, which has an AWGN channel characterized by the optical quantum losses and modulation variance. The second capacity is related to the reconciliation step, i.e., the channel coding problem presented in Eq. (5). In this paper, we considered the key reconciliation problem as a single problem, however, for clarity, it should be decomposed into two related problems: (1) distilling a common message from correlated random sequences X and Y, and (2) channel coding for a binary input fast fading channel with channel state information available only at the decoder. The first problem is an information theory problem, and is independent of the second channel coding problem.
The information theoretic problem attempts to distill the correlated Gaussian sequence Y, in the presence of the quantum channel noise Z, as given by Y = X + Z. This problem is more formally known as “secret key agreement by public discussion from common information”.84 The efficiency β = Rcode/C(s) and channel capacity \(C(s)\) = \(0.5{\kern 1pt} {\mathrm{log}}_2(1 + s)\) are the efficiency and capacity related to solving the information theoretic problem, where s represents the SNR on the optical quantum channel. For clarity, let us redefine the overall QKD system efficiency as βAWGN and the capacity as CAWGN.
In the channel coding problem, Alice attempts to recover an encoded codeword C via error-correction decoding. In Eq. (5), the noise represents a fading channel where each ith symbol has a unique channel noise variance. Thus, the coding (fading) channel has an ergodic capacity, which can be expressed as Ccoding = \({\Bbb E}\left[ {\frac{1}{2}{\mathrm{log}}_2\left( {1 + \frac{1}{{\sigma _{Ni}^2}}} \right)} \right]\). The ergodic capacity Ccoding can be computed by averaging the SNR given by \(1{\mathrm{/}}\sigma _{Ni}^2\) for i = 1, 2, …, n. It follows then that the channel coding efficiency is given by βcoding = Rcode/Ccoding.
The overall QKD system efficiency can then be expressed independent of the code rate as follows:
The ergodic capacity of multi-dimensional reconciliation schemes d = 2, 4, 8 can be determined by applying the same expression for Ccoding. In this paper, we consider only the overall QKD system efficiency βAWGN, which we denote herein more simply as β.
Data availability
The authors declare that the data supporting the findings of this study are available within the article.
References
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 560, Part 1, 7–11 (2014).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Alléaume, R. et al. Using quantum key distribution for cryptographic purposes: A survey. Theor. Comput. Sci. 560, Part 1, 62–81 (2014).
Diamanti, E., Lo, H.-K., Qi, B. & Yuan, Z. Practical challenges in quantum key distribution. NPJ Quantum Inf. 2, 16025–1–16025–12 (2016).
Grosshans, F. & Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88, 057902–1–057902–4 (2002).
Lodewyck, J. et al. Quantum key distribution over 25 km with an all-fiber continuous-variable system. Phys. Rev. A. 76, 042305–1–042305–10 (2007).
Jouguet, P., Kunz-Jacques, S., Leverrier, A., Grangier, P. & Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 7, 378–381 (2013).
Morris, J. D., Grimaila, M. R., Hodson, D. D., Jacques, D. & Baumgartner, G. Emerging Trends in ICT Security. In Chapter 9 - A Survey of Quantum Key Distribution (QKD) Technologies (eds. Akhgar, B. & Arabnia, H. R.) 141–152 (Morgan Kaufmann, Boston, 2014)..
Rivest, R. L., Shamir, A. & Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21, 120–126 (1978).
Kollmitzer, C. & Pivk, M. Applied Quantum Cryptography, vol. 797 (Springer, Berlin, Heidelberg, 2010).
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26, 1484–1509 (1997).
Adrian, D. et al. Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice. Proc. 22nd ACM SIGSAC Conference on Computer and Communications Security 5–17 (ACM, Denver, 2015).
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nat. Photonics 8, 595–604 (2014).
Peev, M. et al. The SECOQC quantum key distribution network in Vienna. N J. Phys. 11, 075001–1–075001–37 (2009).
Sasaki, M. et al. Field test of quantum key distribution in the Tokyo QKD Network. Opt. Express 19, 10387–10409 (2011).
Jouguet, P. et al. Field test of classical symmetric encryption with continuous variables quantum key distribution. Opt. Express 20, 14030–14041 (2012).
Wang, S. et al. Field and long-term demonstration of a wide area quantum key distribution network. Opt. Express 22, 21739–21756 (2014).
Li, Y.-M. et al. Continuous variable quantum key distribution. Chin. Phys. B 26, 040303 (2017).
Weedbrook, C. et al. Quantum cryptography without switching. Phys. Rev. Lett. 93, 170504 (2004).
Pirandola, S., Mancini, S., Lloyd, S. & Braunstein, S. L. Continuous-variable quantum cryptography using two-way quantum communication. Nat. Phys. 4, 726–730 (2008).
Usenko, V. C. & Filip, R. Feasibility of continuous-variable quantum key distribution with noisy coherent states. Phys. Rev. A 81, 022318 (2010).
Yin, H.-L. et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 117, 190501–1–190501–5 (2016).
Wang, X., Liu, W., Wang, P. & Li, Y. Experimental study on all-fiber-based unidimensional continuous-variable quantum key distribution. Phys. Rev. A 95, 062330 (2017).
Usenko, V. C. & Grosshans, F. Unidimensional continuous-variable quantum key distribution. Phys. Rev. A 92, 062337 (2015).
Patel, K. A. et al. Coexistence of high-bit-rate quantum key distribution and data on optical fiber. Phys. Rev. X 2, 041010–1–041010–8 (2012).
Kumar, R., Qin, H. & Allaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. N. J. Phys. 17, 043027–1–043027–4 (2015).
Garca-Patrón, R. & Cerf, N. J. Unconditional optimality of gaussian attacks against continuous-variable quantum key distribution. Phys. Rev. Lett. 97, 190503 (2006).
Pirandola, S., Braunstein, S. L. & Lloyd, S. Characterization of collective gaussian attacks and security of coherent-state quantum cryptography. Phys. Rev. Lett. 101, 200504 (2008).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Leverrier, A. Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 114, 070501–1–070501–5 (2015).
Jouguet, P. & Kunz-Jacques, S. High performance error correction for quantum key distribution using polar codes. Quant. Inform. Comp. 14, 329–338 (2014).
Huang, D. et al. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 23, 17511–17519 (2015).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043–1–15043–15 (2017).
Huang, D. et al. Continuous-variable quantum key distribution based on a plug-and-play dual-phase-modulated coherent-states protocol. Phys. Rev. A 94, 032305–1–032305–11 (2016).
Braunstein, S. L. & Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 108, 130502 (2012).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503–1–130503–5 (2012).
Pirandola, S. et al. High-rate measurement-device-independent quantum cryptography. Nat. Photonics 9, 397–402 (2015).
Huang, D., Huang, P., Lin, D. & Zeng, G. Long-distance continuous-variable quantum key distribution by controlling excess noise. Sci. Rep. 6, 19201–1–19201–6 (2016).
Grosshans, F. et al. Quantum key distribution using Gaussian-modulated coherent states. Nature 421, 238–241 (2003).
Yan, H.et al. Efficiency of winnow protocol in secret key reconciliation. in 2009 WRI World Congress on Computer Science and Information Engineering 3, 238–242 (2009).
Elkouss, D., Martinez, J., Lancho, D. & Martin, V. Rate compatible protocol for information reconciliation: an application to QKD. IEEE Inform. Theory Workshop Inform. Theory 1–5 (2010).
Benletaief, N., Rezig, H. & Bouallegue, A. Toward efficient quantum key distribution reconciliation. J. Quantum Inf. Sci. 4, 117–128 (2014).
Chung, S.-Y., Forney, J. G. D., Richardson, T. & Urbanke, R. On the design of low-density parity-check codes within 0.0045 dB of the Shannon limit. IEEE Commun. Lett. 5, 58–60 (2001).
Leverrier, A., Alléaume, R., Boutros, J., Zémor, G. & Grangier, P. Multidimensional reconciliation for a continuous-variable quantum key distribution. Phys. Rev. A 77, 042325–1–042325–8 (2008).
Leverrier, A. & Grangier, P. Unconditional security proof of long-distance continuous-variable quantum key distribution with discrete modulation. Phys. Rev. Lett. 102, 180504–1–180504–4 (2009).
Becir, A. & Ridza Wahiddin, M. Phase coherent states for enhancing the performance of continuous variable quantum key distribution. J. Phys. Soc. Jpn. 81, 034005–1–034005–9 (2012).
Fossorier, M., Mihaljevic, M. & Imai, H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation. IEEE Trans. Commun. 47, 673–680 (1999).
Richardson, T., Shokrollahi, M. & Urbanke, R. Design of capacity-approaching irregular low-density parity-check codes. IEEE Trans. Inform. Theory 47, 619–637 (2001).
Bloch, M., Thangaraj, A., McLaughlin, S. W. & Merolla, J. M. LDPC-based secret key agreement over the Gaussian wiretap channel. IEEE Int. Symp. Inform. Theory 1179–1183 (2006).
Weedbrook, C., Pirandola, S., Lloyd, S. & Ralph, T. C. Quantum cryptography approaching the classical limit. Phys. Rev. Lett. 105, 110501–1–110501–4 (2010).
Jouguet, P., Elkouss, D. & Kunz-Jacques, S. High-bit-rate continuous-variable quantum key distribution. Phys. Rev. A 90, 042329–1–042329–8 (2014).
Gehring, T. et al. Implementation of continuous-variable quantum key distribution with composable and one-sided-device-independent security against coherent attacks. Nat. Commun. 6, 8795–1–8795–7 (2015).
Jouguet, P., Kunz-Jacques, S. & Leverrier, A. Long-distance continuous-variable quantum key distribution with a Gaussian modulation. Phys. Rev. A 84, 062317–1–062317–7 (2011).
Richardson, T. et al. Multi-edge type LDPC codes. Workshop honoring Prof. Bob McEliece on his 60th birthday, California Institute of Technology, Pasadena, California 24–25 (2002).
IEEE Standard for Information technology– Telecommunications and information exchange between systemsLocal and metropolitan area networks– Specific requirements–Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications–Amendment 4: Enhancements for Very High Throughput for Operation in Bands below 6 GHz. IEEE Std 802.11ac-2013 1–425 (2013).
Zhang, K., Huang, X. & Wang, Z. High-throughput layered decoder implementation for quasi-cyclic LDPC codes. IEEE J. Sel. Areas Commun. 27, 985–994 (2009).
Park, Y. S., Blaauw, D., Sylvester, D. & Zhang, Z. Low-power high-throughput LDPC decoder using non-refresh embedded DRAM. IEEE J. Solid State Circ. 49, 783–794 (2014).
Fossorier, M. Quasicyclic low-density parity-check codes from circulant permutation matrices. IEEE Trans. Inform. Theory 50, 1788–1793 (2004).
Mohsenin, T., Truong, D. & Baas, B. A low-complexity message-passing algorithm for reduced routing congestion in LDPC decoders. IEEE Trans. Circuits Syst. I 57, 1048–1061 (2010).
Kim, S., Sobelman, G. E. & Lee, H. A reduced-complexity architecture for LDPC layered decoding schemes. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 19, 1099–1103 (2011).
Gal, B. L., Jego, C. & Crenne, J. A high throughput efficient approach for decoding LDPC codes onto GPU devices. IEEE Embed. Syst. Lett. 6, 29–32 (2014).
Mansour, M. & Shanbhag, N. High-throughput LDPC decoders. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 11, 976–996 (2003).
Kschischang, F. R., Frey, B. J. & Loeliger, H. A. Factor graphs and the sum-product algorithm. IEEE Trans. Inform. Theory 47, 498–519 (2001).
Leverrier, A., Grosshans, F. & Grangier, P. Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 81, 062343–1–062343–11 (2010).
Martinez-Mateo, J., Elkouss, D. & Martin, V. Key reconciliation for high performance quantum key distribution. Sci. Rep. 3, 1576–1–1576–6 (2013).
Walenta, N. et al. A fast and versatile quantum key distribution system with hardware key distillation and wavelength multiplexing. N. J. Phys. 16, 013047–1–013047–20 (2014).
Bai, Z., Yang, S. & Li, Y. High-efficiency reconciliation for continuous variable quantum key distribution. Jpn. J. Appl. Phys. 56, 044401–1–044401–4 (2017).
Johnson, S. J., Chandrasetty, V. A. & Lance, A. M. Repeat-accumulate codes for reconciliation in continuous variable quantum key distribution. 2016 Australian Communications Theory Workshop (AusCTW) 18–23 (IEEE, Melbourne, 2016).
Shirvanimoghaddam, M., Johnson, S. J. & Lance, A. M. Design of Raptor codes in the low SNR regime with applications in quantum key distribution. 2016 IEEE International Conference on Communications (ICC) 1–6 (IEEE, Kuala Lumpur, 2016).
Curty, M. et al. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 5, 3732 (2014).
Diamanti, E. & Leverrier, A. Distributing secret keys with quantum continuous variables: principle, security and implementations. Entropy 17, 6072–6092 (2015).
Usenko, V. C. & Filip, R. Trusted noise in continuous-variable quantum key distribution: a threat and a defense. Entropy 18, 20 (2016).
Takahashi, R., Tanizawa, Y. & Dixon, A. High-speed implementation of privacy amplification in quantum key distribution (2016). Poster at QCrypt 2016
Xu, F. et al. Experimental quantum fingerprinting with weak coherent pulses. Nat. Commun. 6, 8735 (2015).
Bourgoin, J.-P. et al. Experimental quantum key distribution with simulated ground-to-satellite photon losses and processing limitations. Phys. Rev. A 92, 052339–1–052339–12 (2015).
Vallone, G. et al. Experimental satellite quantum communications. Phys. Rev. Lett. 115, 040502–1–040502–5 (2015).
Ma, C. et al. Silicon photonic transmitter for polarization-encoded quantum key distribution. Optica 3, 1274–1278 (2016).
Sibson, P. et al. Integrated silicon photonics for high-speed quantum key distribution. Optica 4, 172–177 (2017).
Hurwitz, A. Ueber die Composition der quadratischen Formen von belibig vielen Variablen. Nachr. Von. der Ges. Wiss. zu Gttingen, Math. Phys. Kl. 1898, 309–316 (1898).
Baez, J. C. The octonions. Bull. Am. Math. Soc. 39, 145–205 (2001).
Tanner, R. A. A recursive approach to low complexity codes. IEEE Transactions on Information Theory 27, 533–547 (1981).
Richardson, T. & Urbanke, R. The capacity of low-density parity-check codes under message-passing decoding. IEEE Transactions on Information Theory 47, 599–618 (2001).
Richardson, T. J. Error floors of LDPC codes. Proc. Annu. Allerton Conf. Commun. Control Comput. 41, 1426–1435 (2003).
Maurer, U. M. Secret key agreement by public discussion from common information. IEEE Trans. Inform. Theory 39, 733–742 (1993).
Wang, C. et al. 25 MHz clock continuous-variable quantum key distribution system over 50 km fiber channel. Sci. Rep. 5, 14607–1–14607–8 (2015).
Dixon, A. & Sato, H. High speed and adaptable error correction for Megabit/s rate quantum key distribution. Sci. Rep. 4, 7275–1–7275–4 (2014).
Acknowledgements
The authors would like to thank the Natural Sciences and Engineering Research Council of Canada (NSERC) for supporting this research through the NSERC Discovery Grant Program, Dr. Christian Weedbrook and Dr. Xingxing Xing for their technical guidance related to CV-QKD, Dr. Alhassan Khedr for his guidance on GPU parallel programming, Professor Hoi-Kwong Lo at the University of Toronto for his insights on state-of-the-art implementations, Professor Stefano Pirandola at the University of York for introducing us to the upper bound on secret key rate for lossy channels, Dr. Christoph Pacher at the Austrian Institute of Technology for his clarifications on finite-size effects, Professor Frank Kschischang at the University of Toronto for his insights on quantum vs. coding channel capacity, and Professors Jason Anderson and Stark Draper at the University of Toronto for our discussions on GPU implementations and multi-edge codes.
Author information
Authors and Affiliations
Contributions
M.M. and C.F. developed the mathematical preliminaries for multi-dimensional reverse reconciliation. L.Z. constructed the random and quasi-cyclic multi-edge LDPC codes. M.M. developed the GPU-based decoder, performed the simulations, and extracted the results. P.G. supervised this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Milicevic, M., Feng, C., Zhang, L.M. et al. Quasi-cyclic multi-edge LDPC codes for long-distance quantum cryptography. npj Quantum Inf 4, 21 (2018). https://doi.org/10.1038/s41534-018-0070-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-018-0070-6
This article is cited by
-
Evaluation of adaptive reconciliation protocols for CV-QKD using systematic polar codes
Quantum Information Processing (2024)
-
Practical continuous-variable quantum key distribution with feasible optimization parameters
Science China Information Sciences (2023)
-
Hardware design and implementation of high-speed multidimensional reconciliation sender module in continuous-variable quantum key distribution
Quantum Information Processing (2023)
-
Rate-compatible multi-edge type low-density parity-check code ensembles for continuous-variable quantum key distribution systems
npj Quantum Information (2022)
-
An efficient hybrid hash based privacy amplification algorithm for quantum key distribution
Quantum Information Processing (2022)