Rate-compatible multi-edge type low-density parity-check code ensembles for continuous-variable quantum key distribution systems

Abstract

In this paper, we propose a design rule of rate-compatible punctured multi-edge type low-density parity-check (MET-LDPC) code ensembles with degree-one variable nodes for the information reconciliation (IR) of continuous-variable quantum key distribution (CV-QKD) systems. In addition to the rate compatibility, the design rule effectively resolves the high error-floor issue which has been known as a technical challenge of MET-LDPC codes at low rates. Thus, the proposed design rule allows one to implement rate-compatible MET-LDPC codes with good performances both in the threshold and low-error-rate regions. The rate compatibility and the improved error-rate performances significantly enhance the efficiency of IR for CV-QKD systems. The performance improvements are confirmed by comparing complexities and secret key rates of IR schemes with MET-LDPC codes whose ensembles are optimized with the proposed and existing design rules. In particular, the SNR range of positive secrecy rate increases by 1.44 times, and the maximum secret key rate improves by 2.10 times as compared to the existing design rules. The comparisons clearly show that an IR scheme can achieve drastic performance improvements in terms of both the complexity and secret key rate by employing rate-compatible MET-LDPC codes constructed with code ensembles optimized with the proposed design rule.

Introduction

Quantum key distribution (QKD) systems allow two remote parties to share secret keys by utilizing quantum mechanics¹, which is known to provide unconditional security^2,3. In QKD systems, the secret keys are established by performing the following two phases: (1) exchanging quantum states through a quantum channel and (2) post-processing through an authenticated classical channel⁴. QKD systems are usually categorized into discrete-variable QKD (DV-QKD)^1,2,4, and continuous-variable QKD (CV-QKD) systems^5,6,7, according to their modulation techniques adopted in the quantum state exchanges. In the DV-QKD systems, the polarization of the single-photon is modulated by the information while both the amplitude and phase quadrature of coherent state are modulated in the CV-QKD systems. Recently, there have been extensive studies on practical CV-QKD system developments^8,9,10 since CV-QKD systems can be readily deployed in the existing optical communication infrastructure¹¹ and also overcome limitations of applicability of DV-QKD systems, e.g., the requirement of a sophisticated single-photon detector¹².

To achieve a higher key rate and longer operation range, it is important to increase the efficiency of information reconciliation (IR). In particular, CV-QKD systems operate in the very low signal-to-noise ratio (SNR) region where error-correcting codes (ECCs) for the IR must be designed at extremely low rates. It is technically challenging to design strong ECCs tailored for such a low SNR region, and there have been extensive efforts^13,14,15 to improve the efficiency of IR by designing stronger ECCs of low rates. For instance, Raptor codes are designed at low rates for the IR in refs. ^14,15,16,17 where Raptor codes have capacity-approaching performances. In addition, the rateless feature of Raptor codes enables the IR to maintain high efficiencies across a range of SNRs. However, Raptor codes require a high decoding complexity as compared to other types of ECCs, e.g., multi-edge-type low-density parity-check (MET-LDPC) codes, due to high check node degrees, which leads to excessively long decoding latency.

Meanwhile, MET-LDPC codes at low rates, e.g., 1/50, are employed in the IR for CV-QKD systems due to their good error-correcting performances and more amenable decoding complexity^18,19,20. In ref. ¹⁸, the authors demonstrated high-speed error correction for MET-LDPC codes utilizing a graphic processing unit (GPU). In ref. ¹⁹, it was shown that a quasi-cyclic code construction of MET-LDPC codes is suitable for hardware-accelerated decoding. In the studies^18,19,20, MET-LDPC codes are implemented based on degree distributions simply taken from an open literature¹³, and the authors focus on the demonstrations of practical decoder implementation for MET-LDPC codes. In this work, we are instead interested in designing strong MET-LDPC codes.

There have been studies on MET-LDPC code design^13,21,22 which pay their attention only to the optimization of the threshold performance. Thus, the designed MET-LDPC codes suffer from high error floors which limit the efficiency of the IR^18,19. In particular, the error floors are mainly due to an anomaly called the decoder errors, i.e., decoding into wrong codewords, which requires QKD systems to employ additional error-detection codes such as cyclic redundancy check (CRC) codes to confirm whether the decoded codeword is the transmitted one. In the case that a decoder-error event happens, the QKD system may discard the shared randomness obtained via the first phase, i.e., exchanging quantum state over the quantum channel. It is also possible that the QKD system performs additional communications through a classical public channel to resolve the problem, which however leads to extra information leakage and eventually degrades the secret key rate in the key distillation. In addition, the CRC codes increase the hardware complexity. Thus, it is highly desirable to design MET-LDPC codes without suffering from the error-rate performance loss due to the high error floors caused by the decoder errors.

It was shown²³ that small-weight codewords of MET-LDPC codes mainly induce the decoder errors, and thus the design of MET-LDPC code ensembles must be carried out to avoid small-weight codewords. Then, MET-LDPC codes without error floors can be implemented with ensembles that have diminishing average numbers of small-weight codewords with the growing code length. It is known that if an MET-LDPC code ensemble satisfy a certain condition so called, the t-value condition, it has exponentially few codewords of small weight²⁴. Recently, the t-value condition is further extended²³ to MET-LDPC code ensembles with degree-one variable nodes which are essential for code ensembles of low rates to have good threshold performances²⁵.

The efficiency of IR depends on the code rate of ECC, namely the amount parity bits, which is determined by the quality of the quantum channel. It is often observed that the quality of the quantum channel varies in time due to various factors such as the number of photons affected by the attacker, noise variations, the thermally induced length fluctuations, the timing jitter, etc. Thus, to maximize the IR efficiency, the code rate must be adapted to the variation of quantum channel quality, which can be realized with multiple encoder and decoder pairs of different rates. While the scheme with multiple encoder/decoder pairs seems conceptually straightforward, it is not a pragmatic solution due to the growing complexity as the number of pairs increases. In addition, when the decoding is not successful, the transmitted codeword must be discarded, and a new codeword of a lower rate will be requested, which leads to a loss of IR efficiency.

In this work, we instead consider an IR scheme with a rate-adaptive punctured ECCs which are derived by puncturing the parity bits of a code, called mother code. The puncturing provides a sequence of codes whose rates increase from that of the mother code depending on the number of punctured parity bits. In addition, the puncturing is carried out in the rate-compatible fashion²⁶ where a code of higher rate is embedded in codes of lower rates. That is, punctured bits in a code of a rate must also be punctured in codes of higher rates than the rate. The beauty of rate-compatible punctured ECCs is that only one encoder/decoder pair is needed for the entire range of rates given the puncturing locations are a priori known to the receiver, which conveniently resolves the complexity issue in the scheme using multiple encoder/decoder pairs. More importantly, when the decoding fails, the scheme with rate-compatible punctured ECCs simply transmits some punctured parity bits which will be combined with the already received codeword resulting in a new codeword of a lower rate. The transmission of punctured parity bits can be repeated until the receiver successfully decodes the transmitted codeword. Thus, the scheme with rate-compatible punctured ECCs is an efficient solution to maximize the IR efficiency at reduced complexity. Recently, an IR scheme with punctured MET-LDPC codes was studied in ref. ²⁰ where MET-LDPC codes are randomly punctured to adapt their rates. However, the recent work²⁰ takes degree distributions of MET-LDPC codes from ref. ¹³ which will be shown to have poor error-floor performances. In addition, the random puncturing in ref. ²⁰ results in such poor error-floor performances at all the rates derived from the mother code.

In this work, by utilizing the recent result²³ for designing MET-LDPC codes with both good threshold and error-floor performances, this work proposes an IR scheme using optimized rate-compatible punctured MET-LDPC codes. Since we consider the rate-compatible puncturing to realize the rate adaptability in this work, we simply call rate-adaptive punctured MET-LDPC codes as rate-compatible MET-LDPC codes. The improvements of MET-LDPC codes in the threshold and error-floor regions allow the IR scheme to achieve higher key rates and/or longer distances of CV-QKD systems. The improved error-floor performances enable one to design CV-QKD systems without resorting to certain error-detection codes, which not only improves the efficiency of CV-QKD systems but also reduces the complexity of an IR scheme. In particular, we propose a design of MET-LDPC code ensembles with degree-one variable nodes which have exponentially few small-weight codewords. The designed ensembles allow one to implement MET-LDPC codes with better performances in both the threshold and error-floor regions at a reduced decoding complexity as compared to the ensembles based on the existing design rules^18,19,25. In addition, we will show how to design rate-compatible MET-LDPC codes while holding the t-value condition over a range of code rates that the rate-compatible MET-LDPC codes support. The rate-compatible MET-LDPC codes can be utilized for implementing efficient IR schemes for CV-QKD systems. The details of CV-QKD system and the IR scheme considered in this work will be introduced in “Methods”. We will conduct performance comparisons among IR schemes with rate-compatible MET-LDPC codes and a fixed-rate MET-LDPC code. For implementing the MET-LDPC codes, their code ensembles are optimized with the proposed design rule and existing design rules. The performance comparisons clearly show that significant performance improvements are achievable by employing the rate-compatible MET-LDPC codes using ensembles with the proposed design rule.

Results

The t-value condition for MET-LDPC codes

In this work, we consider a Tanner graph of MET-LDPC code ensemble with degree-one variable nodes shown in Fig. 1 where the entire set of variable node classes, denoted by ${{{\mathcal{V}}}}$, is partitioned into the subsets, ${{{{\mathcal{V}}}}}_{1}$, ${{{{\mathcal{V}}}}}_{2}$, and ${{{{\mathcal{V}}}}}_{12}^{c}$, and ${{{{\mathcal{V}}}}}_{12}^{c}$ is the complement of the set ${{{{\mathcal{V}}}}}_{12}={{{{\mathcal{V}}}}}_{1}\cup {{{{\mathcal{V}}}}}_{2}$. Note that the variable node class ${{{{\mathcal{V}}}}}_{1}$ consists of two sub-classes denoted by ${{{{\mathcal{V}}}}}_{1,p}$ and ${{{{\mathcal{V}}}}}_{1,np}$ which represent punctured and unpunctured variable nodes of degree-one, respectively. Similarly, the check node class ${{{{\mathcal{C}}}}}_{1}$ consists of two sub-classes denoted by ${{{{\mathcal{C}}}}}_{1,p}$ and ${{{{\mathcal{C}}}}}_{1,np}$ which represent check nodes connected to the punctured and unpunctured variable nodes of degree-one, respectively. In this section, it is assumed that the all variable nodes of degree-one are unpunctured, and later in “Results”, we modify the result in ref. ²³ to include the MET-LDPC codes with punctured variable nodes of degree-one.

Fig. 1: Tanner graph of MET-LDPC code ensemble with degree-one variable nodes.

The block denoted by ET are uniform interleaver each of which permutes edges of a type.

In a similar manner, the entire sets of check node classes and edge types in Fig. 1, denoted by ${{{\mathcal{C}}}}$ and ${{{\mathcal{E}}}}$, respectively, are partitioned into ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{1}^{c}$, and ${{{{\mathcal{E}}}}}_{1}$, ${{{{\mathcal{E}}}}}_{2}$, and ${{{{\mathcal{E}}}}}_{12}^{c}$, respectively, where ${{{{\mathcal{E}}}}}_{12}^{c}$ is the complement of ${{{{\mathcal{E}}}}}_{12}={{{{\mathcal{E}}}}}_{1}\cup {{{{\mathcal{E}}}}}_{2}$, and ${{{{\mathcal{C}}}}}_{1}^{c}={{{\mathcal{C}}}}\setminus {{{{\mathcal{C}}}}}_{1}$. The blocks denoted by ET in Fig. 1 are uniform interleavers each of which permutes edges of a type. In particular, ${{{{\mathcal{V}}}}}_{1}$ is the set all variable node classes of degree-one, i.e., ∑_jd_i,j = 1 for $i\in {{{{\mathcal{V}}}}}_{1}$, and ${{{{\mathcal{E}}}}}_{1}=\{j| {d}_{i,j}=1,\ \forall \ i\in {{{{\mathcal{V}}}}}_{1}\}$. Note that ${{{{\mathcal{E}}}}}_{1}$ is the set of edge types corresponding to the variable nodes classes in ${{{{\mathcal{V}}}}}_{1}$. Meanwhile, ${{{{\mathcal{C}}}}}_{1}$ is the set of all check node classes which have check nodes incident with edges of types in ${{{{\mathcal{E}}}}}_{1}$, i.e., for every $i\in {{{{\mathcal{C}}}}}_{1}$, $\exists \ j\in {{{{\mathcal{E}}}}}_{1}$ such that g_i,j = 1. Note that the threshold of MET-LDPC code ensemble will not be defined if a check node is incident with more than one edge of a type in ${{{{\mathcal{E}}}}}_{1}$. Thus, each check node of a class in ${{{{\mathcal{C}}}}}_{1}$ has a single edge of a type in ${{{{\mathcal{E}}}}}_{1}$. Then, ${{{{\mathcal{E}}}}}_{2}$ is the set of all edge types for the edges incident to the check node of classes in ${{{{\mathcal{C}}}}}_{1}$ except for the ones of types in ${{{{\mathcal{E}}}}}_{1}$, i.e., for every $j\in {{{{\mathcal{E}}}}}_{2}$, $\exists \ i\in {{{{\mathcal{C}}}}}_{1}$ such that g_i,j > 0. The set ${{{{\mathcal{V}}}}}_{2}$ contains all variable node classes which have variable nodes incident with edges of types in ${{{{\mathcal{E}}}}}_{2}$, i.e., for every $i\in {{{{\mathcal{V}}}}}_{2}$, $\exists \ j\in {{{{\mathcal{E}}}}}_{2}$ such that d_i,j > 0. It is assumed that for each edge type of $j\in {{{{\mathcal{E}}}}}_{12}^{c}$, there exists a check node of class $i\in {{{{\mathcal{C}}}}}_{1}^{c}$ such that g_i,j ≥2, which is also considered in ref. ²⁴.

An MET-LDPC code ensemble can also be described with a pair of multinomials, and the pair of multinomials for the MET-LDPC code ensemble in Fig. 1 are given by

$$\begin{array}{ll}\nu ({{{\bf{x}}}})=&\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{1}}\atop {{d}_{i,j}=1}}}{\nu }_{i}r{x}_{j}^{1}+{\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{2}}}{\nu }_{i}r\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{2}}{x}_{j}^{{d}_{i,j}}\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{12}^{c}}{x}_{j}^{{d}_{i,j}}\\ &+ {\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{12}^{c}}}{\nu }_{i}r\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{12}^{c}}{x}_{j}^{{d}_{i,j}},\\ \mu ({{{\bf{x}}}})=&\mathop{\sum}\limits_{{{i\in {{{{\mathcal{C}}}}}_{1}}\atop {{g}_{i,j}=1}}}{\mu }_{i}{x}_{j}^{1}\mathop{\prod}\limits_{k\in {{{{\mathcal{E}}}}}_{2}}{x}_{k}^{{g}_{i,k}}+\mathop{\sum}\limits_{i\in {{{{\mathcal{C}}}}}_{1}^{c}}{\mu }_{i}\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{1}^{c}}{x}_{j}^{{g}_{i,j}},\end{array}$$

(1)

where the variable node classes in ${{{{\mathcal{V}}}}}_{1}$, ${{{{\mathcal{V}}}}}_{2}$, and ${{{{\mathcal{V}}}}}_{12}^{c}$ correspond to the first, second and third terms in ν(x), respectively, and the check nodes classes in ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{1}^{c}$ are represented by the first and second terms in μ(x), respectively. The code rate of MET-LDPC code ensemble²⁷ is given by

$$R=1-\frac{{\sum }_{i\in {{{\mathcal{C}}}}}{\mu }_{i}}{{\sum }_{i\in {{{\mathcal{V}}}}}{\nu }_{i}}.$$

(2)

For an MET-LDPC code ensemble, the average number of codewords of weight ℓ is expressed by the asymptotic exponential growth rate defined in Definition 1.

Definition 1 (the asymptotic exponential growth rate)

$$\gamma (w)=\mathop{\lim }\limits_{n\to \infty }\frac{1}{n}{{\mathrm{log}}}\,A(\lfloor nw\rfloor ),$$

(3)

where A (ℓ) is the average number of codewords of weight ℓ, and w is the normalized weight.

Meanwhile, for small-weight codewords, i.e., w ≪ 1, Theorem 1 tells the asymptotic exponential growth rate, i.e., γ(w) in Definition 1.

Theorem 1 Ref. ²². For t ≠ 0, we have

$$\gamma (w)=\mathop{\sup }\limits_{t\in {\mathfrak{T}}}-{{\mathrm{log}}}\,(t)w+O({w}^{2}),$$

(4)

where ${\mathfrak{T}}$ is the set of all t values such that

$${\mathrm{det}} (I-t{{\Lambda }}^{\prime} (t)P^{\prime} )=0$$

(5)

where $\tilde{u}=({\tilde{u}}_{1},{\tilde{u}}_{2},\ldots ,{\tilde{u}}_{| {{{{\mathcal{E}}}}}_{12}^{c}| })$ (resp. $\tilde{s}=({\tilde{s}}_{1},{\tilde{s}}_{2},\ldots ,{\tilde{s}}_{| {{{{\mathcal{E}}}}}_{12}^{c}| })$) is a vector whose elements, ${\tilde{u}}_{i}$’s (resp. ${\tilde{s}}_{i}$’s) are given by ${u}_{f({j}_{i})}$’s (resp. ${s}_{f({j}_{i})}$’s) for $1\le i\le | {{{{\mathcal{E}}}}}_{12}^{c}|$ and a bijective mapping $f:{{{{\mathcal{E}}}}}_{12}^{c}\to \{1,2,\ldots ,| {{{{\mathcal{E}}}}}_{12}^{c}| \}$, and ${{\Lambda }}^{\prime} (t)$ is a square matrix whose elements are given by

$${{\Lambda }}^{\prime}_{f(j),f(k)} (t)=\frac{{\left.\frac{{\partial }^{2}\nu ({{{\bf{x}}}})}{\partial {x}_{j}\partial {x}_{k}}\right|}_{{{{\bf{x}}}} = \tilde{{{{\bf{0}}}}}}}{{\mu }_{{x}_{j}}({{{\bf{1}}}})},$$

(6)

$P^{\prime}$ is a square matrix whose elements are given by

$$P^{\prime}_{f(j),f(k)} =\frac{{\left.\frac{{\partial }^{2}\mu ({{{\bf{x}}}})}{\partial {x}_{j}\partial {x}_{k}}\right|}_{{{{\bf{x}}}} = {{{\bf{1}}}}}}{{\mu }_{{x}_{j}}({{{\bf{1}}}})},$$

(7)

$\tilde{{{{\bf{0}}}}}=({o}_{1},{o}_{2},\ldots ,{o}_{{n}_{e}})$ is a vector of length n_e, ${o}_{m}=t\frac{{\sum }_{i\in {{{{\mathcal{C}}}}}_{1}}{\mu }_{i}{g}_{i,m}}{{\mu }_{{x}_{m}}({{{\bf{1}}}})}$ for $m\in {{{{\mathcal{E}}}}}_{2}$ and zeros for the other elements.

It is shown in Theorem 1 that an MET-LDPC code ensemble with degree-one variable nodes has exponentially few codewords of small weights when the infimum of the solution set for the equation in Eq. (5) is larger than one, which is the t-value condition and summarized in Definition 2.

Definition 2 (t-value condition) For an MET-LDPC code ensemble, the infimum of ${\mathfrak{T}}$ is larger than unity. The infimum of ${\mathfrak{T}}$ will be called the t-value of the ensemble.

Rate-compatible MET-LDPC codes for CV-QKD systems

We will show that it is possible to design rate-compatible MET-LDPC codes with good error-rate performances in both the threshold and error-floor regions, which is carried out by proving that there exists a sequence of punctured MET-LDPC code ensembles of rates with exponentially few codewords of small weights. To this end, we utilize the design rule in ref. ²³ to optimize an MET-LDPC code ensemble with degree-one variable nodes for the threshold performance with the constraint of the t-value condition. It was shown in ref. ²³ that MET-LDPC codes based on the ensemble have good error-rate performances both in the threshold and error-floor regions. The designed MET-LDPC code ensemble is called the mother code ensemble from which MET-LDPC code ensembles of higher rates are derived by puncturing parity bits of the mother code ensemble. Then, it will be shown that the punctured MET-LDPC code ensembles derived from the mother code ensemble also satisfy the t-value condition regardless of the number of punctured parity bits if the mother code ensemble has a certain structure. In the next section, we will show that rate-compatible MET-LDPC codes with good error-floor performances can be implemented using the punctured MET-LDPC code ensembles.

In the design of punctured MET-LDPC code ensembles, we puncture only degree-one variable nodes due to a few practical reasons. The Tanner graph in Fig. 1 shows that each degree-one variable node is incident to a different check node whose neighboring variable nodes are all unpunctured except for the degree-one variable node. Thus, the punctured degree-one variable nodes are one-step-recoverable (1-SR)²⁸, i.e., recoverable in the first iteration of the belief-propagation (BP) decoding. It was demonstrated in ref. ²⁸ that punctured LDPC codes have good threshold performances when only 1-SR variable nodes are punctured. In addition, the generation of coded bits for the punctured variable nodes can be performed with a linear complexity, which reduces the complexity of progressive parity bit generation and transmission.

For an MET-LDPC code ensemble with the degree distribution pair in Eq. (1), the degree distribution of the punctured MET-LDPC code ensemble becomes

$$\begin{array}{ll}\nu ^{\prime} ({\bf{x}})=&{\mathop{\sum}\limits_{{i\in {{\mathcal{V}}}_{1,p}}\atop{{d}_{i,j}=1}}{\nu }_{i}{r}_{0}{x}_{j}^{1}}+{\mathop{\sum}\limits_{{i\in {{{{\mathcal{V}}}}}_{1,np}}\atop{{d}_{i,j}=1}}}{\nu }_{i}{r}_{1}{x}_{j}^{1}\\ &+{\mathop{\sum}\limits_{i\in {\mathcal{V}}_{2}}} {\nu }_{i}{r}_{1}\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{2}}{x}_{j}^{{d}_{i,j}}\mathop{\prod}\limits_{j\in {\mathcal{E}}_{12}^{c}}{x}_{j}^{{d}_{i,j}}+{\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{12}^{c}}}{\nu }_{i}{r}_{1}\mathop{\prod}\limits_{j\in {\mathcal{E}}_{12}^{c}}{x}_{j}^{{d}_{i,j}},\\ \mu ^{\prime} ({{{\bf{x}}}})=&{\mathop{\sum}\limits_{{{i\in {{{{\mathcal{C}}}}}_{1,p}}\atop{{g}_{i,j}=1}}}}{\mu }_{i}{x}_{j}^{1}\mathop{\prod}\limits_{k\in {\mathcal{E}}_{2}}{x}_{k}^{{g}_{i,k}}+{\mathop{\sum}\limits_{{{i\in {\mathcal{C}}_{1,np}}\atop{{g}_{i,j}=1}}}}{\mu }_{i}{x}_{j}^{1}\mathop{\prod}\limits_{k\in {\mathcal{E}}_{2}}{x}_{k}^{{g}_{i,k}}\\ &+\mathop{\sum}\limits_{i\in {\mathcal{C}}_{1}^{c}}{\mu }_{i}\mathop{\prod}\limits_{j\in {\mathcal{E}}_{1}^{c}}{x}_{j}^{{g}_{i,j}},\end{array}$$

(8)

where ${{{{\mathcal{V}}}}}_{1}={{{{\mathcal{V}}}}}_{1,p}\cup {{{{\mathcal{V}}}}}_{1,np}$, ${{{{\mathcal{V}}}}}_{1,p}$, and ${{{{\mathcal{V}}}}}_{1,np}$ indicate the sets of punctured and unpunctured degree-one variable node classes, respectively, and r₀ and r₁ represent the channels for the punctured the unpunctured variable nodes, respectively. The code rate of the punctured MET-LDPC code ensemble becomes

$$\begin{array}{lll}{R}_{\pi }&=&1-\frac{{\sum }_{i\in {{{\mathcal{C}}}}/{{{{\mathcal{C}}}}}_{1,p}}{\mu }_{i}}{{\sum }_{i\in {{{\mathcal{V}}}}/{V}_{1,p}}{\nu }_{i}}=1-\frac{{\sum }_{i\in {{{\mathcal{V}}}}}{\mu }_{i}-\pi {\sum }_{i\in {{{\mathcal{V}}}}}{\nu }_{i}}{{\sum }_{i\in {{{\mathcal{V}}}}}{\nu }_{i}(1-\pi )}\\ &=&\frac{{\sum }_{i\in {{{\mathcal{V}}}}}{\nu }_{i}(1-\pi )-{\sum }_{i\in {{{\mathcal{C}}}}}{\mu }_{i}\,+\,\pi {\sum }_{i\in {{{\mathcal{V}}}}}{\nu }_{i}}{{\sum }_{i\in {{{\mathcal{V}}}}}{\nu }_{i}(1-\pi )}\\ &=&\frac{R}{1-\pi },\end{array}$$

(9)

where π is the fraction of punctured degree-one variable nodes.

It should be noted that in the belief-propagation (BP) decoding, the punctured degree-one variable nodes in ${{{{\mathcal{V}}}}}_{1,p}$ output their messages of zero log-likelihood ratio (LLR) value regardless of decoding iterations. In addition, for the check nodes incident to punctured variable nodes, the messages to unpunctured neighboring variable nodes are bounded by the LLR value of zero. Thus, the punctured degree-one variable nodes and their incident check nodes do not participate in the BP decoding, which allows us to exclude the punctured nodes from the ensemble. That is, the MET-LDPC code ensemble with punctured degree-one variable nodes can be expressed with an equivalent degree distribution pair that has only unpunctured variable nodes. Then, the equivalent MET-LDPC code ensemble is given by

$$\begin{array}{ll}\nu ^{\prime} ({{{\bf{x}}}})=&\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{1,np}}\atop{{d}_{i,j}=1}}}{\nu}_{i}{r}_{1}{x}_{j}^{1}+\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{2}}{\nu }_{i}{r}_{1}\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{2}}{x}_{j}^{d^{\prime}_{i,j}}\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{12}^{c}}{x}_{j}^{{d}_{i,j}}\\ &+\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{12}^{c}}{\nu }_{i}{r}_{1}\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{12}^{c}}{x}_{j}^{{d}_{i,j}},\\ \mu ^{\prime} ({{{\bf{x}}}})=&\mathop{\sum}\limits_{{{i\in {{{{\mathcal{C}}}}}_{1,np}}\atop{{g}_{i,j}=1}}}{\mu}_{i}{x}_{j}^{1}\mathop{\prod}\limits_{k\in {{{{\mathcal{E}}}}}_{2}}{x}_{k}^{{g}_{i,k}}+\mathop{\sum}\limits_{i\in {{{{\mathcal{C}}}}}_{1}^{c}}{\mu}_{i}\mathop{\prod}\limits_{j\in {{{{\mathcal{E}}}}}_{1}^{c}}{x}_{j}^{{g}_{i,j}},\end{array}$$

(10)

where ${d}_{i,j}^{\prime}$ is the degree of the variable node class $i\in {{{{\mathcal{V}}}}}_{2}$ for $j\in {{{{\mathcal{E}}}}}_{2}$. Note that the removal of punctured variable nodes deletes some edges in ${{{{\mathcal{E}}}}}_{2}$ and check nodes of ${{{{\mathcal{C}}}}}_{1}$, which makes the degree ${d}_{i,j}^{\prime}$ less than or equal to d_i,j. i.e., ${d}_{i,j}^{\prime}\le {d}_{i,j}$. The degree ${d}_{i,j}^{\prime}$ is decided in such a way that the numbers of edges in ${{{{\mathcal{E}}}}}_{2}$ from variable nodes and check nodes are the same after removing the punctured variable nodes and their incident check nodes, which is so called the socket count equality²³.

For the equivalent code ensemble in Eq. (10), we have to test the t-value condition²³ to confirm that the punctured MET-LDPC code ensemble has exponentially few codewords of small weight. It is also especially important to know the maximum proportion of punctured bits below which the t-value condition of the mother MET-LDPC code ensemble holds. In Theorem 2, we will prove that the t-value condition of a mother code ensemble holds regardless of the proportion of punctured bits when the mother code ensemble has a certain structure. While the theorem is limited to MET-LDPC codes with the structure, it will be shown that some good mother MET-LDPC code ensembles can be readily designed even if the structural limit is imposed.

Theorem 2 For the MET-LDPC code ensemble of three edge types of ${{{{\mathcal{E}}}}}_{1}=\{1\}$, ${{{{\mathcal{E}}}}}_{2}=\{2\}$, and ${{{{\mathcal{E}}}}}_{12}^{c}=\{3\}$ with g_i,2 = 0 for all $i\in {{{{\mathcal{C}}}}}_{1}^{c}$, the following arguments are true:

• 1. If a mother code ensemble satisfies the t-value condition, punctured MET-LDPC code ensembles also satisfy the t-value condition regardless of the amount of punctured bits.

• 2. If a mother code ensemble does not satisfy the t-value condition, none of punctured MET-LDPC code ensembles satisfies the t-value condition.

Proof For an MET-LDPC code ensemble of three edge types of ${{{{\mathcal{E}}}}}_{1}=\{1\}$, ${{{{\mathcal{E}}}}}_{2}=\{2\}$, and ${{{{\mathcal{E}}}}}_{12}^{c}=\{3\}$ with g_i,2 = 0 for all $i\in {C}_{1}^{c}$, the ensemble in Eq. (1) can be rewritten as

$$\begin{array}{ll}\nu ({{{\bf{x}}}})=&\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{1}}\atop{{d}_{i,1}=1}}}{\nu }_{i}r{x}_{1}^{1}+\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{2}}{\nu }_{i}r{x}_{2}^{{d}_{i,2}}{x}_{3}^{{d}_{i,3}}+\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{12}^{c}}{\nu }_{i}r{x}_{3}^{{d}_{i,3}},\\ \mu ({{{\bf{x}}}})=&\mathop{\sum}\limits_{{{i\in {{{{\mathcal{C}}}}}_{1}}\atop{{g}_{i,1}=1}}}{\mu }_{i}{x}_{1}^{1}{x}_{2}^{{g}_{i,2}}+\mathop{\sum}\limits_{i\in {{{{\mathcal{C}}}}}_{1}^{c}}{\mu }_{i}{x}_{3}^{{g}_{i,3}}.\end{array}$$

(11)

For the ensemble in Eq. (11), the equality in Eq. (5) can be expressed as

$$\begin{array}{ll}\frac{2}{{\mu }_{{x}_{3}}({{{\bf{1}}}})}\cdot \left\{\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{2}}\atop{{d}_{i,3}=2}}}{\nu }_{i}{t}^{{d}_{i,2}+1}+\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{12}^{c}}\atop {{d}_{i,3}=2}}}{\nu }_{i}t\right\}\\\qquad\qquad \times\,\frac{{\sum }_{i\in {{{{\mathcal{C}}}}}_{1}^{c}}{\mu }_{i}{g}_{i,3}({g}_{i,3}-1)}{{\mu }_{{x}_{3}}({{{\bf{1}}}})}=1.\end{array}$$

(12)

Suppose that there exists a solution t ≤1 satisfying the equality in EQ. (12), which implies

$$\left\{\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{2}}\atop{{d}_{i,3}=2}}}{\nu }_{i}+\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{12}^{c}}\atop{{d}_{i,3}=2}}}{\nu }_{i}\right\}\times \frac{2{\sum }_{i\in {{{{\mathcal{C}}}}}_{1}^{c}}{\mu }_{i}{g}_{i,3}({g}_{i,3}-1)}{{\mu }_{{x}_{3}}{({{{\bf{1}}}})}^{2}}\ge 1,$$

(13)

where the lefthand side in Eq. (13) is obtained by replacing t in Eq. (12) with unity and is larger than or equal to the lefthand side in Eq. (12). Thus, when the inequality in Eq. (13) does not hold, the solutions of the equality in Eq. (12) must be larger than unity, i.e., $\inf {\mathfrak{T}} \,>\, 1$. That is, the t-value condition, i.e., $\inf {\mathfrak{T}} \,>\, 1$, can be equivalently expressed as

$$\left\{\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{2}}\atop{{d}_{i,3}=2}}}{\nu }_{i}+\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{12}^{c}}\atop{{d}_{i,3}=2}}}{\nu }_{i}\right\}\times \frac{2{\sum }_{i\in {{{{\mathcal{C}}}}}_{1}^{c}}{\mu }_{i}{g}_{i,3}({g}_{i,3}-1)}{{\mu }_{{x}_{3}}{({{{\bf{1}}}})}^{2}} < 1.$$

(14)

If degree-one variable nodes in the ensemble of Eq. (11) are punctured with a fraction of π, the punctured ensemble can be represented as

$$\begin{array}{ll}\nu ^{\prime} ({{{\bf{x}}}})&=\mathop{\sum}\limits_{{{i\in {{{{\mathcal{V}}}}}_{1,np}}\atop{{d}_{i,1}=1}}}{\nu }_{i}r{x}_{1}^{1}+\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{2}}{\nu }_{i}r{x}_{2}^{d^{\prime}_{i,2} }{x}_{3}^{{d}_{i,3}}+\mathop{\sum}\limits_{i\in {{{{\mathcal{V}}}}}_{12}^{c}}{\nu }_{i}r{x}_{3}^{{d}_{i,3}},\\ \mu ^{\prime} ({{{\bf{x}}}})&=\mathop{\sum}\limits_{{{i\in {{{{\mathcal{C}}}}}_{1,np}}\atop{{g}_{i,1}=1}}}{\mu }_{i}{x}_{1}^{1}{x}_{2}^{{g}_{i,2}}+\mathop{\sum}\limits_{i\in {{{{\mathcal{C}}}}}_{1}^{c}}{\mu }_{i}{x}_{3}^{{g}_{i,3}}.\end{array}$$

(15)

For the degree distribution pair in Eq. (15), the equality in Eq. (5) can be expressed as exactly the same as the one in Eq. (12) except that d_i,2 is changed to ${d}_{i,2}^{\prime}$, which however does not affect the inequality in Eq. (14). Thus, if the t-value condition holds for the mother code, so does for all punctured code ensembles.◻

For arbitrary MET-LDPC code ensembles shown in Fig. 1, it is mathematically intractable to express in a closed-form the maximum proportion of punctured parity bits below which the t-value condition holds. However, it is sufficient to numerically test whether the punctured MET-LDPC code ensemble of the highest rate satisfy the t-value condition since the ones of lower rates have additional parity bits, which does not induce smaller weight codewords.

Performance evaluations

In this section, we compare error-rate performances and efficiencies of IR schemes that have rate-compatible MET-LDPC codes and fixed-rate MET-LDPC codes implemented using code ensembles with/without satisfying the t-value condition. Refer to “Methods” for the CV-QKD system in which the IR schemes are employed. We consider the multidimensional reconciliation with a dimension of 8. It is known in ref. ²⁹ that the channel can safely be assumed to be a binary-input additive-white-Gaussian-noise (BI-AWGN) channel. For decoding MET-LDPC codes, we employ the sum-product algorithm in which the maximum number of iteration is set to 1000. The iterative decoding terminates when all the parity checks are satisfied even before the iteration reaches the preset maximum number of iterations. The error-rate performances are measured in terms of both bit-error rate (BER) and word-error rate (WER) which are evaluated at each SNR value by transmitting codewords until a hundred failed codewords are observed. In addition, the practicality of the MET-LDPC codes is compared in terms of three different metrics, i.e., the maximum variable node degree ${d}_{\max }$, the maximum check node degree ${g}_{\max }$, and a normalized edge density in ref. ³⁰ which is defined as the average number of edges per message bit, i.e., $| {{{\mathcal{E}}}}| /(R\cdot n)$ where $| {{{\mathcal{E}}}}|$, R, and n are the total number of edges, code rate and code length, respectively. The maximum degrees are often used as a measure of decoding latency³¹ while the normalized edge density is adopted to measure the decoding complexity in ref. ³⁰.

First, we design a mother MET-LDPC code ensemble by optimizing the ensemble for the threshold performance²² with the constraint of the t-value condition²³. The MET-LDPC code ensemble is optimized at a code rate of 0.02 for the BI-AWGN channel, and is denoted by ${{{{\mathcal{C}}}}}_{1}$ in Table 1. For comparisons, we take a code ensemble in ref. ¹⁹, and denote it by ${{{{\mathcal{C}}}}}_{2}$ in Table 1. Note that ${{{{\mathcal{C}}}}}_{1}$ has its t-value of 1.0078 > 1 and thus satisfies the t-value condition. Whereas ${{{{\mathcal{C}}}}}_{2}$ has its t-value of 0.9743 < 1 and does not meet the t-value condition. The t-value condition tells when the number of small-weight codewords diminishes, which is obtained by a balance of degree-one and degree-two of edge types at nodes. In the design of ${{{{\mathcal{C}}}}}_{2}$, the code optimization is carried out only for a good threshold performance, which more weighs the degree-one nodes and thus results in poor error-floor performances. Based on the degree distributions of ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{2}$, two MET-LDPC codes of length 10⁶ are implemented with random parity-check matrices, and they are denoted by ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$, respectively. In this work, MET-LDPC codes are denoted by bold symbols, e.g., ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$, while their ensembles are represented by script symbols, e.g., ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{2}$, respectively. Their BER and WER performances on the BI-AWGN channel are compared in Fig. 2 where it is witnessed that ${{\mathbb{C}}}_{2}$ has a high error-floor. The high error-floor associated with ${{{{\mathcal{C}}}}}_{2}$ is mainly due to the decoder errors, i.e., decoding into wrong codewords, caused by small-weight codewords as predicted by the test of the t-value condition. To substantiate the claim, we depict the decoder-error rate (DER) in Fig. 2 where the DER and WER overlap each other in the error-floor region. It should also be noted that the WER and BER of ${{\mathbb{C}}}_{2}$ have a wide gap, which is due to the fact that the decoder-error events are caused by small-weight codewords²³. On the contrary, for the competing code, i.e., ${{\mathbb{C}}}_{1}$, we do not observe any decoder-error event until its WER and BER reach 10⁻⁴ and 10⁻⁵, respectively, and thus no error-floor appears in Fig. 2.

Table 1 Code parameters; the thresholds are measured in terms of SNR in dB.

Fig. 2: BER and WER comparison between existing MET-LDPC code and optimized MET-LDPC code.

Based on the degree distributions of ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{2}$, two MET-LDPC codes of length 10⁶ are implemented with random parity-check matrices, and they are denoted by ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$, respectively.

Now, based on the two mother code ensembles, i.e., ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{2}$ in Table 1, we design rate-compatible MET-LDPC code ensembles which have their code rates between 0.02 and 0.025, equivalently, π ∈ [0, 0.2]. The equivalent degree distributions for the rate-compatible MET-LDPC codes at the highest code rate, i.e., 0.025, are described in Table 1, where the ones based on the code ensembles ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{2}$ are denoted by ${{{{\mathcal{C}}}}}_{1}^{\pi }$ and ${{{{\mathcal{C}}}}}_{2}^{\pi }$, respectively. Note that both the ensembles ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{2}$ are not designed for puncturing. It is possible to investigate into a design rule which also takes the puncturing into account, while it is beyond the scope of this work. Since the puncturing is carried out in the rate-compatible fashion²⁶, it enables one to progressively transmit additional parity bits when a decoding failure happens or an error-detection code finds out a decoder-error event. Note that the rate-compatible MET-LDPC code using ${{{{\mathcal{C}}}}}_{1}$, i.e., ${{{{\mathcal{C}}}}}_{1}^{\pi }$ in Table 1, also satisfies the t-value condition which is tested with the equivalent degree distribution pair in the ${{{{\mathcal{C}}}}}_{1}^{\pi }$ row of Table 1. It should be noted that the ensemble of the mother code, ${{{{\mathcal{C}}}}}_{1}$, has the structure discussed in Theorem 2, and thus the t-value condition is always satisfied regardless of the amount of punctured parity bits. Meanwhile, it is shown in Table 1, the code ensemble using ${{{{\mathcal{C}}}}}_{2}$ does not satisfy the t-value condition. It is also noticed in Table 1 that the thresholds of ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{1}^{\pi }$ are better than those of ${{{{\mathcal{C}}}}}_{2}$ and ${{{{\mathcal{C}}}}}_{2}^{\pi }$ while both ${{{{\mathcal{C}}}}}_{1}$ and ${{{{\mathcal{C}}}}}_{1}^{\pi }$ have lower complexities in terms of all the complexity measures, i.e., edge density, maximum variable node, and check node degrees. Thus, the rate-compatible MET-LDPC codes constructed with ensembles using the proposed design rule not only outperform the rate-compatible MET-LDPC codes using the existing design rule but also have practical advantages.

By puncturing the MET-LDPC codes, i.e., ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$ in Fig. 2, two rate-compatible MET-LDPC codes of rate 0.025 (equivalently, π = 0.2) are implemented and evaluated in terms of BER and WER on the BI-AWGN channel in Fig. 3 where the rate-compatible MET-LDPC codes are denoted by ${{\mathbb{C}}}_{1}^{\pi }$ and ${{\mathbb{C}}}_{2}^{\pi }$. Note that while the rate-compatible MET-LDPC codes ${{\mathbb{C}}}_{1}^{\pi }$ and ${{\mathbb{C}}}_{2}^{\pi }$ are obtained by puncturing their mother codes ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$, the asymptotic behaviors of ${{\mathbb{C}}}_{1}^{\pi }$ and ${{\mathbb{C}}}_{2}^{\pi }$, e.g., thresholds and t-value conditions, are given by the degree distributions in the ${{{{\mathcal{C}}}}}_{1}^{\pi }$ and ${{{{\mathcal{C}}}}}_{2}^{\pi }$ rows of Table 1, respectively. As predicted by Theorem 2, the rate-compatible MET-LDPC code, ${{\mathbb{C}}}_{2}^{\pi }$ suffers from the error floors as its mother code, i.e., ${{\mathbb{C}}}_{2}$ in Fig. 2, does. Whereas the error-floor does not appear in the error rates of ${{\mathbb{C}}}_{1}^{\pi }$ as predicted by the test of the t-value condition for the equivalent degree distribution pair. The comparison of error-rate performances in Fig. 3 confirms the results in “Results”.

Fig. 3: BER and WER comparison between the punctured code of existing MET-LDPC code and optimized MET-LDPC code.

By puncturing the MET-LDPC codes, i.e., ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$ in Fig. 2, two rate-compatible MET-LDPC codes of rate 0.025 (equivalently, π = 0.2) are implemented and evaluated in terms of BER and WER on the BI-AWGN channel. The rate-compatible MET-LDPC codes based on ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$ are denoted by ${{\mathbb{C}}}_{1}^{\pi }$ and ${{\mathbb{C}}}_{2}^{\pi }$, respectively.

The key rate of CV-QKD systems is often^9,19 assumed as

$$K=(1-{{{\rm{WER}}}})(\beta {I}_{{{{\rm{AB}}}}}-{\chi }_{{{{\rm{BE}}}}}).$$

(16)

However, a recent work¹⁶ shows that the key rate formula in Eq. (16) does not reconcile with the results of quantum information theory in some situations. In particular, the issue can happen when the error rates of ECCs are relatively high, which is frequently encountered in long-distance CV-QKD systems. Thus, instead of the key rate in Eq. (16), as suggested in ref. ¹⁶, we use a bound on the key rate which is given by

$$K=(1-{{{\rm{WER}}}})(\beta {I}_{{{{\rm{AB}}}}})-{\chi }_{{{{\rm{BE}}}}},$$

(17)

where β is the IR efficiency defined as R_π/I_AB, R_π is the code rate, π is the maximum fraction of punctured bits when the IR succeeds, I_AB is the mutual information of the virtual Gaussian channel, and χ_BE is the Holevo bound on the information leaked to the eavesdropper, Eve¹¹. The secret key rate depends on various physical parameters such as the length and standard loss of fiber and homodyne detector efficiency, etc. In this work, we take the physical parameters from ref. ¹⁹ where the noise in the quantum channel denoted by χ_tot modeled as the sum of noises from the fiber and detector denoted by χ_line and ${\chi }_{\det }$, respectively. Then, the noise due to fiber of length ℓ with a transmittance T = 10^αℓ/10 is given by χ_line = 1/T − 1 + ε where α = 0.2dB/Km is the standard loss of a single-mode fiber, and the excess channel noise (measured in shot noise units) is ε = 0.01 for 0 Km ≤ ℓ ≤100 Km, and ε = 0.01 + 0.001 × (ℓ − 100) for 100 Km ≤ ℓ ≤170 Km. Meanwhile, the noise in the homodyne detector is given by ${\chi }_{\det }=(1+{V}_{{{{\rm{el}}}}})/\eta -1$ where η and V_el represent the homodyne detector efficiency and additive electronic noise, respectively, and it is assumed that η = 0.606 and V_el = 0.041. Then, the total noise in the quantum channel follows as ${\chi }_{{{{\rm{tot}}}}}={\chi }_{{{{\rm{line}}}}}+{\chi }_{\det }/T$. In addition, the SNR of the virtual Gaussian channel is expressed as V_A/(1 + χ_tot) where V_A is a modulation variance of Alice and has to be optimized to achieve the highest key rate¹³.

We define (1 − WER) × β in Eq. (17) as an effective efficiency which depends on both the WER and the efficiency of ECC, i.e., the maximum code rate at which the IR is successfully performed. We consider IR schemes with rate-compatible MET-LDPC codes by puncturing ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$ in Fig. 2 as their mother codes. In addition, an IR scheme with the MET-LDPC code at a fixed rate of 0.02 denoted by ${{\mathbb{C}}}_{2}$ in Fig. 2. The effective efficiencies of three schemes are compared in Fig. 4 where R-C ${{\mathbb{C}}}_{1}$ and R-C ${{\mathbb{C}}}_{2}$ indicate the IR schemes with the rate-compatible MET-LDPC codes using ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$, respectively. Meanwhile, the IR scheme with the fixed-rate MET-LDPC code of ${{\mathbb{C}}}_{2}$ is denoted by ${{\mathbb{C}}}_{2}$ in Fig. 4. The performance comparison in Fig. 4 is carried out over a range of SNR values over which the maximum effective efficiencies of three schemes are observed. In practice, the SNR values are adjusted by controlling the modulation variance, V_A at a given length of fiber, ℓ. In Fig. 4, the efficiencies of the three schemes are depicted with the curves in blue, red, and black, respectively. In the IR scheme with ${{\mathbb{C}}}_{2}$, the shared randomness obtained via the quantum channel will be discarded when the decoding for ECC fails. Meanwhile, the IR schemes with R-C ${{\mathbb{C}}}_{1}$ and R-C ${{\mathbb{C}}}_{2}$ transmit additional parities when Alice requests on the decoding failure, which results in significant improvements of efficiency. However, the scheme with R-C ${{\mathbb{C}}}_{2}$ suffers from decoder-error events, which requires additional parity bits for the CRC code. In the case that the decoding for CRC code detects a decoder-error event, i.e., $u^{\prime} \ne u$, the scheme discards the shared randomness obtained via the communication over the quantum channel. On the contrary, the scheme with R-C ${{\mathbb{C}}}_{1}$ has no decoder-error event as the consequences of Theorem 2 promise. The comparisons in Fig. 4 quantitively demonstrate the performance improvements obtained by employing the rate-compatible MET-LDPC codes based on the ensemble satisfying the t-value condition. That is, the scheme with R-C ${{\mathbb{C}}}_{1}$ has a clear performance advantage over a wide range of SNR values as compared to the other two schemes, i.e., R-C ${{\mathbb{C}}}_{2}$ and ${{\mathbb{C}}}_{2}$.

Fig. 4: Comparisons of effective efficiency.

We compare the effective efficiencies, i.e., (1 − WER) × β of the IR schemes with three different error-correcting codes denoted by R-C ${{\mathbb{C}}}_{1}$, R-C ${{\mathbb{C}}}_{2}$, and ${{\mathbb{C}}}_{2}$ in which R-C ${{\mathbb{C}}}_{1}$ and R-C ${{\mathbb{C}}}_{2}$ indicate the IR schemes with the rate-compatible MET-LDPC codes using ${{\mathbb{C}}}_{1}$ and ${{\mathbb{C}}}_{2}$, respectively. Meanwhile, the IR scheme with the fixed-rate MET-LDPC code of ${{\mathbb{C}}}_{2}$ is denoted by ${{\mathbb{C}}}_{2}$.

It should be mentioned that the comparison between the schemes with ${{\mathbb{C}}}_{2}$ and R-C ${{\mathbb{C}}}_{2}$ has a crossover at the SNR of −15dB. In the region of SNR less than −15dB, the variation of efficiency, β is relatively small while the WER of ${{\mathbb{C}}}_{2}$ drastically improves with the growing SNR value since the threshold of error rate for ${{\mathbb{C}}}_{2}$ starts at around −15.3dB as shown in Fig. 2. Meanwhile, the improvement of WER for R-C ${{\mathbb{C}}}_{2}$ is limited since the retransmissions of parity bits lead to decoder-error events. This is why the scheme with ${{\mathbb{C}}}_{2}$ has better effective efficiency in the region of SNR less than −15dB. Note that efficiency is defined as the ratio of code rate and channel capacity. Thus, the efficiency β of the scheme with ${{\mathbb{C}}}_{2}$ sharply decreases as the SNR value further increases passing the crossover point, i.e., −15dB, considering that the capacity grows while the rate is fixed. On the contrary, it is not serious for the scheme with R-C ${{\mathbb{C}}}_{2}$ due to the rate adaptability, i.e., the code rate adapts to the channel quality. It is noticed in Fig. 4 that the scheme with R-C ${{\mathbb{C}}}_{2}$ outperforms the one with ${{\mathbb{C}}}_{2}$. As compared to the two schemes with ${{\mathbb{C}}}_{2}$ and R-C ${{\mathbb{C}}}_{2}$, the scheme with ${{\mathbb{C}}}_{1}$ does not suffer from the decoder-error events while taking the advantage of rate adaptability, which provides the performance superiority over the range of SNR values over the competing IR schemes, i.e., the ones with ${{\mathbb{C}}}_{2}$ and R-C ${{\mathbb{C}}}_{2}$.

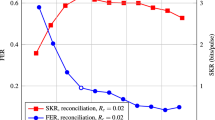
The key rate in Eq. (17) is evaluated in terms of bits per pulse for the three IR schemes in Fig. 5 where the length of fiber is assumed to be ℓ = 90 Km. It is clearly witnessed that the IR scheme with R-C ${{\mathbb{C}}}_{1}$ outperforms the other two schemes over a wider range of SNR values. In addition, Fig. 6 shows that the IR scheme with R-C ${{\mathbb{C}}}_{1}$ consistently performs better than the other schemes at different lengths of fiber of ℓ = 80 Km and 85 Km. In practice, the modulation variance V_A is determined to make the CV-QKD system operate at a certain SNR value of the virtual Gaussian channel. The adjustment of V_A requires a precise channel estimation of the quantum channel, which is hard to achieve in practice. Thus, the SNR value has some variations, and the IR scheme must be designed robust to the SNR variation. In this sense, the IR scheme with R-C ${{\mathbb{C}}}_{1}$ has clear advantages of both performance and practicality.

Fig. 5: Comparisons of key rates.

The key rate is evaluated in terms of bits per pulse for the three IR schemes denoted by R-C ${{\mathbb{C}}}_{1}$, R-C ${{\mathbb{C}}}_{2}$, and ${{\mathbb{C}}}_{2}$ when the length of fiber is assumed to be ℓ = 90 Km.

Fig. 6: Comparisons of key rates.

a The key rate is evaluated in terms of bits per pulse for the three IR schemes denoted by R-C ${{\mathbb{C}}}_{1}$, R-C ${{\mathbb{C}}}_{2}$, and ${{\mathbb{C}}}_{2}$ when the length of fiber is assumed to be ℓ = 80 Km. b The key rate is evaluated when the length of fiber is assumed to be ℓ = 85 Km.

Discussion

In this paper, we proposed a design rule of multi-edge type low-density parity-check code ensembles with degree-one variable nodes. It was shown that the design rule allows one to implement rate-compatible MET-LDPC codes with good performances both in the threshold and low-error-rate regions. It is also demonstrated that the rate-compatible MET-LDPC codes can improve the efficiency of information reconciliation for CV-QKD systems.

Methods

Information reconciliation of QKD system

In this work, we consider the IR scheme for CV-QKD systems introduced in ref. ¹⁵ where the scheme employs rate-compatible error-correcting codes, i.e., rate-compatible MET-LDPC codes in this work. The IR scheme is depicted in Fig. 7 where Alice transmits Gaussian random variables ${x}_{i} \sim {{{\mathcal{N}}}}(0,{\sigma }_{A}^{2})$ for i = 1, 2, …, d over the quantum channel, and for each Gaussian random variable x_i, Bob receives a noisy observation y_i = x_i + n_i from the quantum channel where ${n}_{i} \sim {{{\mathcal{N}}}}(0,{\sigma }_{n}^{2})$ and ${\sigma }_{n}^{2}$ indicates the noise power. Then, Alice and Bob have the correlated random vectors x = (x₁, x₂, …, x_d) and y = (y₁, y₂, …, y_d), respectively, which are normalized to $x^{\prime} =x/| | x| |$ and $y^{\prime} =y/| | y| |$ where ∣∣x∣∣ and ∣∣y∣∣ are the Euclidean norms of the vectors x and y, respectively, and d is called the dimension of multidimensional reconciliation²⁹.

Fig. 7: Block diagram of reverse-reconciliation CV-QKD systems.

The quantum channel is modeled as a virtual BI-AWGN channel, and a rate-compatible MET-LDPC code is assumed as the ECC whose rate is set to the maximum value or the capacity of the virtual BI-AWGN channel by puncturing parity bits.

In the reverse reconciliation³², Bob generates a uniformly random binary sequence u from the quantum random number generator (QRNG), and encodes the sequence u into a codeword ξ, i.e., a codeword of MET-LDPC code in this work. Then, Bob divides ξ into sub-groups of coded bits of length d. Suppose that one of the sub-groups is denoted by c = (c₁, c₂, …c_d) which is converted to a spherical codes $c^{\prime}$ as follows:

$$({c}_{1},{c}_{2},\ldots ,{c}_{d})\to c^{\prime} =\left(\frac{{(-1)}^{{c}_{1}}}{\sqrt{d}},\frac{{(-1)}^{{c}_{2}}}{\sqrt{d}},\ldots ,\frac{{(-1)}^{{c}_{d}}}{\sqrt{d}}\right).$$

(18)

Note that $c^{\prime}$ is uniformly distributed on the unit sphere in the d dimensional Euclidean vector space. For a pair of vectors, $c^{\prime}$ and $y^{\prime}$, Bob calculates the linear mapping $M(y^{\prime} ,c^{\prime} )$ in ref. ²⁹ such that

$$M(y^{\prime} ,c^{\prime} )\cdot y^{\prime} =c^{\prime} .$$

(19)

The mapping $M(y^{\prime} ,c^{\prime} )$ is transmitted to Alice over the classical channel. When Alice receives the mapping $M(y^{\prime} ,c^{\prime} )$, she performs $M(y^{\prime} ,c^{\prime} )\cdot x^{\prime} =c^{\prime} +e$ where e follows a Gaussian distribution with zero mean²⁹. According to ref. ²⁹, as the dimension denoted by d grows, the d consecutive instances of the physical Gaussian channel, i.e., the quantum channel, are reformulated to d copies of a virtual BI-AWGN channel²⁹. Since this work focuses on the benefit of rate-compatible MET-LDPC codes, it is assumed for simplicity that the dimension is fixed to d = 8 at which the quantum channel can be modeled as a BI-AWGN channel as shown in Fig. 7. Since the gain in key rate is mainly due to the proposed coding scheme, the gain is also achievable with different dimensions. The transmission of sub-group c is repeated until the entire codeword ξ is transmitted. Then, in practical systems, the received signal $c^{\prime} +e$ is often represented as a log-likelihood ratio (LLR) vector denoted by L in Fig. 7, and the LLR vector L is fed to the ECC decoder as its input.

In this work, a rate-compatible MET-LDPC code is assumed as the ECC in Fig. 7, and the rate of ECC is set to the maximum value or the capacity of the virtual BI-AWGN channel by puncturing parity bits. If the decoding at the Alice side fails, she requests for additional parity bits. Upon the request, Bob transmits additional parity bits by sending a sequence of mappings corresponding to the punctured parity bits to be transmitted. The request and transmission will be continued until Alice successfully obtains her estimate of the message $u^{\prime}$. In some cases, the estimate $u^{\prime}$ is different from the true message u, which can be detected by employing an additional error-detection code such as a CRC code. In Fig. 7, the parity bits for CRC code is denoted by r. Note that the transmission of parity bits for the CRC code degrades performance of the IR scheme, which can be avoided by carefully designing the ECC. More details of the IR of CV-QKD can be found in refs. ^15,19.