New diffusive interface model for pitting corrosion

Abstract

In this paper, a diffusive interface model for pitting corrosion is proposed, which can be used to simulate diffusion- and activation-controlled pitting corrosion with the pit morphologies and the distribution of metal cation concentration. The diffusive interface equation is derived from the general interface advection-like equation coupled with the description of the normal velocity of the moving pitting boundary from the sharp interface model. The corrosion rate is expressed in an explicit way through the diffusion field in the diffusion-controlled regime, and the activation-controlled corrosion is expressed by introducing the interface kinetic parameter, which greatly simplifies the model. The curvature effect can be subtracted back out directly by introducing a counter term. Predicted results from numerical simulations are compared with the analytical solution to determine numerical parameter in one-dimensional pencil electrode test. The effect of local curvature on simulated semicircle corrosion is discussed. Then, the application scenarios of the model including electropolishing, single and multiple corrosion, corrosion with composite materials are presented.

Introduction

Corrosion is a destructive electrochemical interaction between a sensitive metal and its environment, resulting in the degradation of the integrity and durability of the material^1,2,3. Although some quality engineering materials such as stainless steel and aluminum alloy can prevent corrosive attack by forming a passive, protective oxide layer on their surface, pitting corrosion, an extremely localized form of corrosion, occurs when the passive oxide layer is broken down due to aggressive anions such as chlorides⁴. Since corrosion pits and crevices can cause stress concentration and promote the nucleation of fatigue cracks, pitting corrosion can accelerate material degradation and may result in sudden structural failure^5,6,7. Therefore, pitting corrosion is seen as a seriously threat to the durability of the industrial systems, and there is considerable interest in understanding of the formation and evolution of the pitting corrosion. Numerical simulation is an efficient tool to quantitatively predict the evolution of corrosion pits for developing strategies of the reliable design and health monitoring of metal structures in corrosive environment, and hence modeling of metal corrosion has always been an active research field.

Several numerical models have been proposed for predicting the process of the pitting corrosion^8,9,10. However, these models assume that the pitting interface motion is negligible, which is only effective when the corrosion rate is small enough. Subsequently, a moving boundary model based on finite element method has been proposed to simulate the evolution of pit morphology in metal pitting corrosion^{11,12,13,14,15,16,17}. Since the interface velocity is considered as the boundary condition in the sharp interface model, it is necessary to build a finite element mesh with time dependence on the pitted interface¹⁸. In addition, the Lagrangian–Eulerian method^13,19 and the level set method^14,20 have also been used to track interface position and local mesh evolution. Nevertheless, since each time step requires repartitioning the grid on the phase boundary, these methods not only lead to complex boundary conditions and large computational cost, but also result in a source of error at each time step because of violating the law of conservation of mass. Moreover, Scheiner and his coworkers^21,22 adopted finite volume method to simulate pitting corrosion. This approach eliminates the difficulties associated with creating a consistent mesh by determining the position of the pit interface as a function of the ion concentration in each volume cell. However, the finite volume method has to face challenges in accurately tracking interface positions and predicting pitting in complex material structures.

As a typical a mesoscale numerical method, the diffusive interface model, especially the phase-field method, becomes a widely accepted approach that has received significant attention for predicting complex interfacial morphological evolution due to no need for interfacial tracking^{23,24,25,26,27,28,29,30,31,32,33,34,35,36}. Although the diffusive interface model has been widely applied for dealing with complex moving boundary problems, it has not been implemented to corrosion until a few years ago^23,24. Starting from the free energy functional, Mai et al.²⁵ introduced the auxiliary phase-field variables to establish a phase-field model for metal pitting corrosion. This model can implicitly track the propagation of the diffusion interface and achieve an accurate approximation of the complex interface. By associating the interfacial dynamics parameters with the stress, they obtained a new phase-field model to simulate the phenomenon of stress corrosion cracking (SCC) in metal materials²⁶. Furthermore, they relate the anode current density to the interface dynamics parameters²⁷. In order to improve computational efficiency and reduce complexity, Gao et al.³⁴ proposed a new partial differential equation solving algorithm based on Mai’s model²⁵, which successfully enhances computational efficiency. Additionally, Ansari³⁰ and Xiao³¹ developed a thermodynamically consistent phase-field model to study the pitting kinetics and the corrosion-related properties of different metal potentials. Then a phase-field model for studying stress metal corrosion³² and a multiphase field model for studying intergranular corrosion³⁵ are proposed. Beyond that, the phase-field model with activation-controlled metal pitting has been established²⁸.

To our best knowledge, all of the existing diffusive interface models for pitting corrosion strongly depend on the free energy functional in the thermodynamic system of pitting corrosion with respect to the order parameters and concentration fields. For examples, parabolic functions were used to approximate the free energy density of each phase by Mai et al.^25,26,27; classical potential energy density was used by Lin et al.³³. From the point view of the practice, the normal velocity of the metal-electrolyte interface in the sharp interface is the only basis in the moving boundary. But it is not explicit in existing diffusive interface model. In order to match numerical results from diffusive interface model to the sharp interface model, the coefficient of the diffusion term for the order parameter is of the order O (10⁻⁶) while the coefficient of the driving force term is of the order O (10⁸), where $O$ stands for the infinitesimal of the same order. Consequently, a very small time step is needed in the beginning stage of numerical simulations, resulting in large computational cost and complex algorithm³⁴. Moreover, the interface curvature effect is inevitably introduced to the diffusive interface model due to the existence of the gradient energy density for a unique solution for a stationary front profile for the order parameter. However, the interface curvature has no effect on the interface moving during pitting corrosion according to the sharp interface model. Hence, the elimination of the contribution of the curvature effect in the diffusive model is required meanwhile a unique solution for a stationary front profile for the order parameter is still reserved. Sun et al.³⁷ proposed a general interface tracking method based on the phase-field solution. In their model, the inverse term is used to cancel out the effect of the curvature term. Numerical results show that the fourth-order Convex Essentially Non-Oscillatory (CENO) scheme commonly used in the level set method provides an effective numerical approximation of the flat flux in the dynamic equation for the interface motion driven by an arbitrary outflow field.

In the present study, we proposed a diffusive interface model for pitting corrosion, which can be used to predict diffusion- and activation-controlled pitting corrosion with pit morphologies and distribution of metal cation concentration. The significance of this model is that the curvature effect that is not involved in the sharp interface model for pitting corrosion is eliminated by introducing a counter term. In the “Result” section, predicted results from diffusive interface simulations are compared with the analytical solution to determine numerical parameters in one-dimensional pencil electrode test. The effect of curvature action term on the pitting corrosion also is discussed. Moreover, applications of this diffusive interface model including electropolishing, single and multiple pitting corrosion, corrosion with composite materials are presented. In the “Discussion” section, conclusions and outlooks of this work are presented. In the “Method” section, a diffusion interface model for pitting corrosion is derived from the explicit description of the interface velocity, and the curvature term is subtracted back out directly by introducing a counter term.

Result

Corrosion process

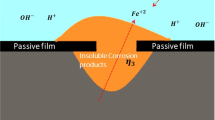
As illustrated in Fig. 1, the stable pitting corrosion usually consists of the following components: (a) solid metal, (b) pit solution, (c) passive oxide film, and (d) bulk solution. In the stable pitting corrosion, corrosion is prevented by the existence of passive oxide film between solid metal and pit solution. When the passive oxide film is mechanically damaged, the solid metal is exposed to the solution and corroded. As the solution gradually corrodes the metal, the solid phase metal is converted into metal cations and enters the solution through the boundary between the solid and liquid. Meanwhile, the solution is divided into two parts: pit solution and bulk solution. Pit solution exists in the damaged passive oxide film and consequently the space is very limited while the bulk solution exists outside it and the far end can be regarded as infinite for pit. There is a saturation concentration of metal cations ${c}_{1}^{{\rm{sat}}}$ in the pit solution, which only exists on the liquid side of the metal-electrolyte interface.

Fig. 1

Schematic of the typical stable pitting corrosion.

Validation and verification studies

Firstly, we implement the diffusive interface model to simulate the corrosion evolution of pencil electrode and compare predicted results with analytical solution to determine the dynamic parameter $\varepsilon$, i.e., the proportionality constant $A$, and the pseudo liquid concentration in the solid ${c}_{\text{l}}^{\text{solid}}$, which is actually a complete model parameter without physical meaning. Here, all physical properties are assumed constants. Note that $\varepsilon$ is nothing but the coupling constant between the dynamic equation of the solid-electrolyte interface and the metal cation concentration, which is similar to that in the phase-field model for alloys solidification. Therefore, it is clear that a variation of the interface thickness actually corresponds to a change in $\varepsilon$. In this numerical simulation, as shown in Fig. 2a, a wire is installed in an epoxy coating, leaving only one section of the wire exposed to the electrolyte. This process can be modeled as a one-dimensional diffusion-controlled corrosion due to the very fast electrochemical reaction resulting in a saturated salt film on the metal surface and driven by a unidirectional flat interface. For one-dimensional pitting corrosion problem, the sharp interface model is the fundamental standard model. Therefore, the predicted results from the diffusive interface simulations are usually validated by comparing with the analytical solution from the sharp interface model, which is given by Eqs. (28)–(31).

Fig. 2: Model validation and variable determination.

a A schematic illustration of the pencil electrode test with boundary conditions; b distribution of cation concentration in the electrode corrosion process at and at ; c comparison of predicted evolution of the interface position from diffusive interface simulations with the analytical solution for various ${\varepsilon }^{* }$ at a fixed $\Delta {c}_{\text{l}}=0.78$; d comparison of predicted evolution of the interface position from diffusive interface simulations with analytical solution for various $\Delta {c}_{\text{l}}$ at a fixed ${\varepsilon }^{* }=5$. e Comparison of present numerical results with experimental results³⁸ and previous numerical results²⁵.

Because the interface is planar, i.e., κ = 0, there is no capillary effect and we can select ${b}^{* }=1$. The schematic illustration of the pencil electrode test with boundary conditions is presented in Fig. 2a, and a typical example of the distribution of cation concentration in the electrode corrosion process for ε^*$=5$. at $t=1\text{s}$. and at $t=5\text{s}$. are shown in Fig. 2b. Figure 2c illustrates the evolution of the interface position $R$ with $\sqrt{t}$ for various ε^* ranging from 0.005 to 50 for L = 1. Note that ε^* can be regarded as a parameter that is inversely proportional to the interface thickness in the diffusive interface model. Therefore, predicted results gradually converge to the analytical solution with the increase of ε^*. Note that the pseudo liquid concentration in the solid phase ${c}_{\text{l}}^{\text{solid}}$ or $\Delta {c}_{\text{l}}=\left({c}_{\text{l}}^{\text{solid}}-{c}_{\text{l}}^{\text{sat}}\right)$ is a free numerical parameter introduced in the diffusive interface model because the metal ion concentration c_l must be continuous everywhere. Here, we discuss the effect of Δc_l on the numerical prediction results on the numerical prediction results given ε* = 1 for L = 1, which are presented in Fig. 2c. As Δc_l drops from 0.9 to 0.5, the slope of the graph rises gradually, and the predicted results agree well with the analytical solution when Δc_l = 0.78. Furthermore, we found that numerical results for Δc_l = 0.78 and ε* = 1 agree well with the experimental results³⁸ and previous numerical results²⁵, as shown in Fig. 2e. This means that in this case, the model can effectively predict pitting corrosion of homogeneous materials such as austenitic SS. Therefore, Δc_l = 0.78 is utilized in the following simulations without otherwise. Similar to the phase-field model of Mai et al. ²⁵, varying the interface kinetic parameter $L$ as a function of the overpotential can predict the transition from the activation-controlled to the diffusion-controlled pitting corrosion. Figure 3 shows that the transition from the activation-controlled (linear kinetics) to the diffusion-controlled (parabolic kinetics) pitting corrosion as $L$ increasing from 0.001 to 0.05.

Fig. 3

Evolution of the interface position for various ${\boldsymbol{L}}$ on one-dimensional electrode corrosion.

Let us turn to the effect of curvature term in the diffusive interface model. The terms ∇² φ + ∂g/∂φ (g is a double-well potential function) determine the interface energy in previous diffusive interface models²⁵ and the contribution of the curvature effect to the corrosion dynamics is inevitable. Again, the pitting corrosion is indeed independent of the local curvature of the interface according to the sharp interface model (Eqs. (7) to (9)). A numerical method for no curvature-driven interface motion is used in our diffusive interface model (see Eq. (23)). The parameter b* is a purely numerical parameter for smoothing the interface singularities since curvature-driven interface motion is not considered. In order to study the curvature term and the influence of parameter b* in numerical simulations, we firstly carried out numerical simulations of the evolution of a dumbbell-like object over time for various b*. The dynamic equation is given by Eq. (32), and the dumbbell-like object is obtained through the arbitrary structure import method based on image recognition processing, given in the “Method” section. Numerical results are shown in Fig. 4. In the case of curvature-driven interface motion with b* = 1, as shown in Fig. 4a, starting from the connecting rod, the dumbbell shrinks rapidly and it completely disappears ultimately. In the case of no curvature-driven interface motion with b* = 1, as shown in Fig. 4b, the pinch-off of the two handles still occurs although the shrinkage is negligible. Figure 4c shows that the dumbbell shape remains unchanged in the case of no curvature-driven interface motion with b* = 0.1, which indicates that the influence of the curvature term is removed without additional effects.

Fig. 4: Evolution of dumbbell morphology with time.

a curvature-driven interface motion with ${b}^{* }=1$; b no curvature-driven interface motion with ${b}^{* }=1$; c no curvature-driven interface motion with ${b}^{*}=0.1$.

In order to investigate the effect of the curvature term, we consider a computational domain with a size of 200 μm × 400 μm, in which a corrosion pit with a radius of 20 μm is initialized and Dirichlet boundary conditions for both metal and electrolyte regions is adopted. Then the diffusive interface model is employed to predict the evolution of the semicircular pitting corrosion depicted in Fig. 5a, where the left part and right part are curvature-driven interface motion and no curvature-driven interface motion, respectively. Figure 5b shows the evolution of corrosion pit radius over time in both cases. It can be seen that the corrosion pit grows faster in the no curvature-driven interface motion case, which indicates that the curvature affects the normal growth of the corrosion pit.

Fig. 5: Comparison of the evolution of semicircular pits for curvature-driven interface motion and no curvature-driven interface motion.

a interfacial motion contrast (curvature-driven interface motion on the left, and no curvature-driven interface motion on the right); b evolution of pit radius over time.

Application problems

In order to explain the application scenarios and advantages of the model established in this paper, the diffusive interface model for pitting corrosion is used to simulate several complex corrosion problems: (a) electropolishing; (b) single and multiple pitting corrosion; (c) corrosion of composite materials. It should be noted that both applications (a) and (c) involve importing complex structures. To solve this problem, we propose a complex structure import method based on image recognition processing. The basic principle is to analyze and screen the color gamut value of the original image with complex structure after single-channel processing, and finally derive the logical data with the value of 0 or 1, which is in line with the value of $\varphi$. Details of the method is presented in the “Method” section.

Electropolishing

Electropolishing technology can be widely used in surface treatment and deburring of metal objects of any shape³⁹. It is often used in industry to reduce the surface roughness of workpiece. The metal workpiece to be electropolished is placed in an electrolyte and an anode potential large enough is applied to it to form a diffusion-controlled corrosion. In order to verify the predictive simulation ability of our corrosion model for this problem, we established a 400 μm × 400 μm computing domain to import the electropolished local workpiece surfaces into the model by any of the structure import methods mentioned in the “Method” section. Here, the metal region is represented by ${c}_{\text{l}}={c}_{\text{l}}^{\text{solid}}$, φ = 1, the electrolyte region is represented by c_l = 0, φ = 0, and the passive film at the electrolyte-metal interface is removed for free corrosion of the entire surface.

Figure 6 shows the surface morphologies of the metal workpiece undergoing electropolishing at different times with the distribution of metal cation in the electrolyte, illustrating how the rough surface of the workpiece transforms into a relatively smooth surface.

Fig. 6

Evolution of surface morphology of metal workpiece with distribution of metal cation concentration in electrolyte at different time during electropolishing.

Single and multiple pitting corrosion

Single pitting corrosion and multiple pitting corrosion are often encountered in engineering practice, especially multiple pitting corrosion, where multiple pits interact with each other to form complex boundaries. In this numerical experiment, we initialize one or more corrosion pits with a radius of 20 μm. There is a passive film (∂c_l/∂n = 0, ∂φ/∂n = 0) at the electrolyte-metal interface except the corrosion pit, and Dirichlet boundary conditions are set for both the metal region and the electrolyte region. In addition, in order to ensure that the cations in the electrolyte can be fully diffused, we deliberately set three quarters of the 400 μm × 400 μm calculation domain to the electrolyte region.

As shown in Fig. 7, the evolution of single pitting corrosion morphology over time and the distribution of metal cations in electrolyte solution during corrosion are plotted. With the increase of time, the corrosion pit gradually grows under the undamaged salt film. However, due to the limitation of salt film, its growth rate is significantly lower than that of semicircle corrosion in Fig. 3. This is because metal cations blocked by the salt film accumulate in the corrosion pit, resulting in the decrease of the corrosion rate.

Fig. 7

Single pitting corrosion morphology and metal cation concentration distribution.

Figure 8 illustrates the interactions between pits at different pit spacing ($d$ ranges from 30 μm to 80 μm) in corrosion and provides the distribution of metal cation concentrations at different times. Obviously, with the growth of corrosion pits, it will fuse with each other, and the corrosion rate will also decrease, which is caused by local metal cation enrichment during the fusion process.

Fig. 8: Pit interactions and the evolution of metal cation concentrations over time.

a model representation, b corrosion results under different pit spacing.

Pitting corrosion of composite materials

In order to improve the mechanical properties of structural materials, some non-metallic materials are sometimes included into the metal in the production practice. These non-metallic materials in the structural materials as the strengthening phase are usually difficult to corrode, for example, ceramic particles embedded in a softer aluminum substrate. However, with the gradual corrosion of structural materials, the non-metallic parts will be removed from the structural materials and its mechanical properties will be reduced. Therefore, it is significant to study the pitting behavior of structural materials with non-metallic composites. This numerical experiment takes aluminum alloy composite ceramic material as an example, establishes a calculation domain with a size of 400 μm × 400 μm, and initializes a corrosion pit with a radius of 20 μm in the composite material. In this experiment, the interface outside the corrosion pit is covered by passive film, and Dirichlet boundary conditions are applied to the composite material and electrolyte. Non-corrosive ceramic particles (L = 0) were imported using the method mentioned in the “Method” section, and the predicted results are shown in Fig. 9.

Fig. 9: Pitting corrosion of aluminum alloys with ceramic particles.

a model representation, b corrosion pit concentration field evolution.

Discussion

In this paper, we derived a diffusive interface model for pitting corrosion based on the general interface advection equation and the description of the normal velocity of the moving pitting boundary by the sharp interface model. We determined the corrosion rate in an explicit way through the diffusion field in the diffusion-controlled regime while the activation-controlled corrosion is expressed by introducing the interface kinetic parameter. Because the pitting corrosion is independent of the local curvature of the electrolyte-metal interface according to the sharp interface of the diffusion-controlled corrosion and the existence of the curvature-driven interface motion may result in artificial shrinkage of the curved interface, the curvature effect can be subtracted back out directly by introducing a counter term. Using the diffusive intermodal, we simulate the corrosion evolution of pencil electrode to compare predicted results with analytical solution to determine the numerical parameters. The curvature effect on the pitting corrosion is studied. Finally, we demonstrate some application scenarios of the model including electropolishing, single and multiple pits corrosion, corrosion of composite materials.

Thus, in this paper, we provide a general method to establish a diffusive interface model for Stefan-like problem based on the analysis of the normal velocity of the interface because the normal velocity of the interface in the sharp interface is the only basis in the moving boundary from the point view of the practice. Similar models can be developed for numerical simulations of the structure formation of hydrogen-induced pitting corrosion, physical vapor deposition, electrochemical deposition, and soon. Moreover, the inevitable curvature effect in diffusive interface model has been eliminated through introducing a counter term. This method avoids large computational cost and complex algorithm, while allowing our numerical results to be directly compared with analytical solution.

It should be noted that the present diffusive interface model for pitting corrosion is established according to the sharp interface model of diffusion-controlled pitting corrosion, but it may not fully reflect the practical pitting problem. In many cases that are practically important, the electromigration of both cation and anion needs to be involved in numerical simulations. In future work, electrostatic field, electromigration, electrochemical reaction, and the pH of electrolyte solutions will be introduced into the diffusive interface model for further predicting the practical corrosion behaviors.

Methods

Shape interface model of pitting corrosion

As discussed by Isaacs⁴⁰, pitting corrosion process can be distinguished as three basic stages, i.e., nucleation, metastable growth and stable pitting growth. In the stable pitting growth stage, the electrolyte-metal interface that separates the solid metal phase from the electrolyte phase moves as a sharp electrode boundary, and hence the pitting corrosion can be classified as a Stefan problem⁴¹, i.e., the free boundary problem, such as the melting of ice, the growth of snowflakes, etc. The stable pitting growth stage involves activation-controlled regime and diffusion-controlled regime. In the activation-controlled regime, the driving force is interface overpotential $\eta$, and when the driving force is very small, the corrosion rate increases exponentially with $\eta$, which is given by the Tafel equation⁴² (Table 1).

$${i}_{\text{a}}={i}_{0}\exp \left(\frac{\eta }{{b}_{\text{a}}}\right),$$

(1)

where i₀ is the exchange current density, i_a the corrosion current density, and b_a the Tafel slope. The relationship between the pitting boundary velocity and i_a can be expressed by Faraday’s second law as

$$v_{\rm{n}}=\frac{i_{0}}{nFc_{\rm{s}}},$$

(2)

where v_n is the normal velocity of the moving pitting boundary, $F$ the Faraday constant, and $n$ the mean charge number, c_s the metal atom concentration in solid.

Table 1 The symbols in this paper and their meanings.

It is worth mentioning that for typical commercial stainless steel, whose mass is mainly derived from the ${Fe}$, ${Cr}$ and ${Ni}$^43,44,45, the molar mass M_Fe, M_Cr and M_Ni is basically the same as that of the corresponding ion, Fe²⁺, Cr²⁺ and Ni²⁺. The apparent mass density ρ_i of each metal is

$${\rho }_{\text{i}}={M}_{\text{i}}{c}_{\text{i}},\text{i}=\text{Fe},\text{Cr},\text{Ni}.$$

(3)

Then, we use a single concentration value to refer to the mixing concentration of each element in the stainless steel alloy, there is

$${\rho }_{\text{steel}}=\mathop{\sum }\limits_{\text{i}=\text{Fe},\text{Cr},\text{Ni}}{\rho }_{\text{i}}=\mathop{\sum }\limits_{\text{i}=\text{Fe},\text{Cr},\text{Ni}}{M}_{\text{i}}{c}_{\text{i}}={c}_{\text{s}}\mathop{\sum }\limits_{\text{i}=\text{Fe},\text{Cr},\text{Ni}}{M}_{\text{i}}{f}_{\text{i}}={c}_{\text{s}}\bar{M},$$

(4)

with $\bar{M}$ as the average molar mass reading as

$$\bar{M}=\mathop{\sum }\limits_{\text{i}=\text{Fe},\text{Cr},\text{Ni}}{M}_{\text{i}}{f}_{\text{i}},$$

(5)

where f_i the molar fraction. And from Eqs. (3)–(5), we know the concentration in solid phase can be expressed as

$${c}_{\text{s}}\equiv \frac{{\rho }_{\text{steel}}}{\bar{M}},$$

(6)

With the pitting corrosion, the concentration at the electrolyte-metal interface reaches saturation, at which time anion in the electrolyte will combine with metal ions and form a salt film on the surface, and consequently limiting the continuous increase of the surface concentration. Meanwhile, the pitting form is changed to diffusion control, and the driving force is related to the concentration of metal cations in the electrolyte, yielding

$$\frac{\partial {c}_{\text{l}}}{\partial t}={D}_{\text{l}}{\nabla }^{2}{c}_{\text{l}},0\le \vec{r}\,<\, \vec{R}\left(t\right),{\rm{in}}\;{\rm{the}}\;{\rm{electrolyte}}\;{\rm{phase}},$$

(7)

$${v}_{\text{n}}=-\frac{{D}_{\text{l}}\nabla {c}_{\text{l}}}{{c}_{\text{s}}-{c}_{\text{l}}^{\text{sat}}},{\rm{in\; the\; electrolyte}}-{\rm{metal\; interface}}$$

(8)

With

$${c}_{\text{l}}\left(\vec{r}\to \vec{R}\left(t\right)\right)={c}_{\text{l}}^{\text{sat}}\,{\rm{and}}\,{c}_{\text{l}}\left(\vec{r}\to 0\right)=0,$$

(9)

where ${c}_{\text{l}}\equiv {c}_{\text{l}}\left(\vec{r},t\right)$ denotes metal ion concentration, D_l the ion diffusion coefficient, $R(t)$ the interface position. The subscript “l” and “s” refer to the electrolyte phase and solid phase, respectively, and the superscript “sat” refer to saturation. It should be noted that Eq. (8) is nothing but the Rankine–Hugoniot condition²¹, i.e., the equilibrium between the dissolved metal ions flux and the velocity of the moving the electrolyte-metal interface.

Diffusive interface model of pitting corrosion

In this paper, we developed a diffusive interface model for the Stefan problem of pitting corrosion in the manner as in the level set given by Osher⁴⁶ and in the phase-field frame for the sharp interface tracking given by Sun and Beckermann³⁷. Here, we derived the diffusive interface equation starting from the general interface advection-like equation, yielding

$$\frac{\partial \varphi }{\partial t}+{\bf{u}}\cdot \nabla \varphi =0,$$

(10)

where the non-conserved order parameter or the auxiliary field variable $\varphi$, which evolves without global conservation with time, is utilized to distinguish phases and describes the motion of the interface, and it has constant values in the bulk phases ($\varphi \,=\,0$ and $\varphi \,=\,1$ correspond to the electrolyte and metal, respectively) and smoothly varies from 0 to 1 in the interface region similar to the previous phase-field model²⁵, and ${\bf{u}}$ is the velocity of the interface motion. Following Osher⁴⁶ and Beckermann et al. ³⁷, the velocity can be expressed as

$${\bf{u}}={u}_{\text{n}}{\bf{n}}+{{\bf{u}}}_{{\bf{e}}},$$

(11)

Where u_n is the normal interface velocity, u_e is the external moving velocity, ${\bf{n}}=\nabla \varphi /{\vert}\nabla \varphi {\vert}$ is the unit vector normal to the interface. Following the work by Sun and Beckermann³⁷, we separate the normal interface velocity into two parts, i.e., the local curvature dependent velocity and the velocity that is independent of the local curvature. It yields

$${u}_{{\rm{n}}}=a-b\kappa ,$$

(12)

where κ is the local curvature of the interface, $a$ and $b$ having the units of m∕s and m²/s are two coefficients related to velocity and diffusion coefficient, respectively. In the process of the pitting corrosion, u_e can be ignored. The local curvature of the electrolyte-metal interface can be written as

$$\kappa =\nabla \cdot {\bf{n}}=\nabla \left(\frac{\nabla {\upvarphi}}{\left|\nabla {\upvarphi}\right|}\right)=\frac{1}{\left|\nabla {\upvarphi}\right|}\left({\nabla }^{2}{\rm{\varphi }}-\frac{\left(\nabla {\upvarphi}\cdot \nabla \right)\left|\nabla {\upvarphi}\right|}{\left|\nabla {\upvarphi}\right|}\right).$$

(13)

Hence, Eq. (10) can be rewritten as

$$\frac{\partial {\upvarphi}}{\partial \textit{t}}=\textit{b}{\kappa}{\vert}\nabla {\upvarphi}{\vert}-\textit{a}{\vert}\nabla {\upvarphi}{\vert}=\textit{b}\left({\nabla }^{2}{\upvarphi}-\frac{\left(\nabla {\upvarphi}\cdot \nabla \right)\left|\nabla {\upvarphi}\right|}{\left|\nabla {\upvarphi}\right|}\right)-\textit{a}{\vert}\nabla {\upvarphi}{\vert}.$$

(14)

Following the derivation by Beckermann et al. ⁴⁷, a unique solution for a stationary front profile for the non-conserved order parameter $\varphi$ can be given by

$$\varphi =\frac{1}{2}\left(1-\tanh \left(\frac{n}{2W}\right)\right),$$

(15)

where $W$ is a measure of the width of the diffusive interface, and n is the normal coordinates of the interface. It should be noted that the profile for $\varphi$ is physically motivated by the analytical solution of the thermodynamically derived phase-field models with well-known double-well potential⁴⁷.

Combining Eq. (14) and Eq. (15), Eq. (14) can be rewritten as

$$\frac{\partial \varphi }{\partial t}=b\left[{\nabla }^{2}\varphi -\frac{\varphi (1-2\varphi )(1-\varphi )}{{W}^{2}}\right]-a\frac{\varphi (1-\varphi )}{W}.$$

(16)

For numerical stability, the term of φ(1 − φ) can be replaced by a higher-order interpolation function φ²(1 − φ)², and hence Eq. (16) can be rewritten as

$$\frac{\partial {\upvarphi}}{\partial \textit{t}}={\it{b}}\left[{\nabla }^{2}{\upvarphi}-\frac{{\upvarphi}(1-2{\upvarphi})(1-{\upvarphi})}{{\textit{W}}^{2}}\right]-\textit{a}\frac{{{\upvarphi}}^{2}{(1-{\upvarphi})}^{2}}{\textit{W}}.$$

(17)

Note that the terms in the square bracket ${\nabla }^{2}\varphi -\varphi (1-2\varphi )(1-\varphi )/{W}^{2}$ determines the interface energy of the diffusive interface model even in the absence of interface curvature, and the stationary solution of ${\nabla }^{2}\varphi -\varphi (1-2\varphi )(1-\varphi )/{W}^{2}=0$ is the hyperbolic tangent profile for $\varphi$ (Eq. (7)). However, according to the sharp interface of the diffusion-controlled corrosion (Eqs. (7)–(9)), the pitting corrosion is independent of the local curvature of the electrolyte-metal interface, i.e., the case of no curvature-driven interface motion. The existence of the curvature-driven interface motion may result in artificial shrinkage of the curved interface. By introducing a counter term, Folch et al.⁴⁸ originally established a numerical method to solve no curvature-driven interface motion, and this method is successfully utilized in the sharp interface tracking based on the phase-field model by Sun and Beckermann³⁷. The curvature term can be subtracted back out directly by

$$\frac{\partial {\upvarphi}}{\partial \textit{t}} = \textit{b}\left[{\nabla }^{2}{\upvarphi}+\frac{{\upvarphi}(1-2{\upvarphi})(1-{\upvarphi})}{{\textit{W}}^{2}}-{\kappa}\left|\nabla {\upvarphi}\right|\right]-\textit{a}\frac{{{\upvarphi}}^{2}{(1-{\upvarphi})}^{2}}{\textit{W}}.$$

(18)

Note that the terms in the square bracket on the right-hand side of Eq. (18) not only cancel out the original curvature effect in the diffusive interface model, but also yield the hyperbolic tangent $\varphi$ profile as stationary analytical solution. This is different from simply setting $b\,= 0$. A rigorous mathematical analysis of the counter term can be found in³⁷. Following Mai et al. ²⁵, the interface kinetics parameter $L$ is introduced to the diffusive interface model to predict both the activation and diffusion-controlled corrosion phenomena, hence Eq. (18) can then be evaluated as

$$\frac{1}{{\textit{L}}^{* }}\frac{\partial {\upvarphi}}{\partial \textit{t}}\,=\,{\textit{b}}^{{\prime}}\left[{\nabla }^{2}{\upvarphi}+\frac{{\upvarphi}(1-2{\upvarphi})(1-{\upvarphi})}{{\textit{W}}^{2}}-{\kappa}\left|\nabla {\upvarphi}\right|\right]-{\textit{a}}^{{\prime}}\frac{{{\upvarphi}}^{2}{(1-{\upvarphi})}^{2}}{\textit{W}},$$

(19)

where ${{L}^{* }}={i}_{\text{a}}/{i}_{0}$ is a dimensionless parameter related to exchange current density ${i}_{0}$ and corrosion current density ${i}_{\text{a}}$, ${a}^{ \prime }=a/{L}^{* }$ and ${b}^{ \prime }=b/{L}^{* }$. The parameter ${a}^{ \prime }$ can be related to the normal velocity of the interface by the explicit relation ${a}^{ \prime }\,={v}_{\text{n}}$ (Eq. (8)), i.e., the velocity is proportional to the metal ion concentration gradient on the electrolyte phase side of the interface. In the diffuse interface model, the concentration varies continuously and smoothly across the interface, and hence the difference in the metal ion concentration gradients at the interface can be approximated as $\nabla {c}_{\text{l}}\cdot {\bf{n}}\,\sim \left({c}_{\text{l}}^{\text{sat}}-{c}_{\text{l}}\right)/W$. It should be noted that $W$, as before, is a measure of the width of the diffusive interface. Therefore, we can obtain that

$$\nabla {c}_{\text{l}}\cdot {\bf{n}}=\,\frac{\left({c}_{\text{l}}^{\text{sat}}-{c}_{\text{l}}\right)}{{AW}},$$

(20)

where $A$ is a constant of proportionality. According to the sharp interface model of the diffusion-controlled corrosion process, the corrosion rate is proportional to the gradient of the metal cation concentration, but is independent of metal atom concentration in the solid. Unlike the phase-field model by Mai et al. ²⁵, we only focus on the metal cation concentration diffusion in the electrolyte according to the sharp interface model for diffusion-controlled pitting corrosion (Eqs. (7) and (8)), and the steep variation of the metal atom concentration across the interface can also be avoided. It should be noted that the metal ion concentration ${c}_{\text{l}}$ has no physical meaning in the solid phase. However, this method is not impeccable because the continuous field variables in the diffusive interface model must be satisfied. Therefore, we set ${c}_{\text{l}}\,\equiv {\,c}_{\text{l}}^{\text{solid}}$ in the solid, where ${\,c}_{\text{l}}^{\text{solid}}$ is a pseudo liquid concentration in the solid phase. Actually, it means that a free numerical parameter is introduced into the diffusive interface model, and it needs to be determined through comparing numerical results with the analytical solution. After introducing the pseudo liquid concentration in the solid phase ${\,c}_{\text{l}}^{\text{solid}}$, Eq. (20) can be further written as

$$\left({c}_{\text{l}}^{\text{sat}}-{c}_{\text{l}}\right)\,=\,({c}_{\text{l}}-({c}_{\text{l}}^{\text{solid}}-{c}_{\text{l}}^{\text{sat}})h(\varphi )-{c}_{\text{l}}^{\text{sat}})$$

(21)

according to the framework of the diffusive interface model of Mai et al. ²⁵.

Substituting Eq. (21), Eq. (20) becomes

$$\begin{array}{l}{a}^{{\prime}}\,=\,-\frac{{D}_{\text{l}}}{{AW}\left({c}_{\text{l}}\,{-\,c}_{\text{l}}^{\text{sat}}\right)}({c}_{\text{l}}-({c}_{\text{l}}^{\text{solid}}-{c}_{\text{l}}^{\text{sat}})h(\varphi )-{c}_{\text{l}}^{\text{sat}})\\\quad\, =-\varepsilon \left({c}_{\text{l}}-\Delta {c}_{\text{l}}h\left(\varphi \right)-{c}_{\text{l}}^{\text{sat}}\right),\end{array}$$

(22)

where $\varepsilon \,=\,{D}_{\text{l}}/({c}_{\text{l}}{-c}_{\text{l}}^{\text{sat}})\,$, $\Delta {c}_{\text{l}}\,=\,({c}_{\text{l}}^{\text{solid}}-{c}_{\text{l}}^{\text{sat}})$. Therefore, the dynamic equation, Eq. (19), can be written as

$$\begin{array}{l}\frac{1}{\textit{L}}\frac{\partial {\upvarphi}}{\partial \textit{t}}\,=\,{\textit{b}}^{{\prime}}\left[{\nabla }^{2}{\upvarphi}+\frac{{\upvarphi}(1-2{\upvarphi})(1-{\upvarphi})}{{\textit{W}}^{2}}-{\kappa}\left|\nabla {\upvarphi}\right|\right]\\\qquad\qquad\qquad\,+\,{\upvarepsilon}({\textit{c}}_{\text{l}}-\Delta {\textit{c}}_{\text{l}}\textit{h}({\upvarphi})-{\textit{c}}_{\text{l}}^{\text{sat}})\frac{{{\upvarphi}}^{2}{(1-{\upvarphi})}^{2}}{\textit{W}}.\end{array}$$

(23)

The evolution equation of the metal cation concentration is

$$\frac{\partial {c}_{\text{l}}}{\partial t}=-\nabla \cdot {\bf{J}},$$

(24)

where ${\bf{J}}$ is cation flux. Taking the diffusive interface into account, it yields

$${\bf{J}}=\,-{D}_{\text{l}}\nabla \left[{c}_{\text{l}}-\Delta {c}_{\text{l}}h(\varphi )-{c}_{\text{l}}^{\text{sat}}\right].$$

(25)

The metal cation concentration equation in our diffusive interface model is similar to that in the phase-field model by Mai et al.²⁵ except the definition of the concentration.

Unless stated otherwise, values of parameters in the following numerical simulations are presented in Table 2.

Table 2 Values of the parameters used in numerical simulations of the 304 stainless steel.

Equations(23) and (24) can be non-dimensionalized by ${\nabla }^{* }\,=\,W\nabla$, ${{\kappa}}^{* }\,=\,{\kappa}W$, ${t}^{* }=\,{D}_{\text{l}}t/{W}^{2}$, ${b}^{* }=\,{b}^{{\prime}}/{D}_{\text{l}}\,$ and ${{\upvarepsilon}}^{* }\,=\,\varepsilon W/{D}_{\text{l}}\,=\,1/\text{A}({c}_{\text{l}}{-c}_{\text{l}}^{\text{sat}})$. Then, Eq. (23) and Eq. (24) can be rewritten as

$$\begin{array}{l}\frac{1}{\textit{L}}\frac{\partial {\upvarphi}}{\partial {\textit{t}}^{* }}\,=\,{\textit{b}}^{* }\left[{{\nabla }^{* }}^{2}{\upvarphi}+{\upvarphi}(1-2{\upvarphi})(1-{\upvarphi})-{{\kappa}}^{* }\left|{\nabla }^{* }{\upvarphi}\right|\right]\\ \qquad\qquad\qquad\,\,+\,{{\upvarepsilon}}^{* }({\textit{c}}_{\text{l}}-\Delta {\textit{c}}_{\text{l}}\textit{h}({\upvarphi})-{\textit{c}}_{\text{l}}^{\text{sat}}){{\upvarphi}}^{2}{(1-{\upvarphi})}^{2},\end{array}$$

(26)

$$\frac{\partial {\textit{c}}_{\text{l}}}{\partial {\textit{t}}^{* }}={{\nabla }^{* }}^{2}\left[({\textit{c}}_{\text{l}}-\Delta {\textit{c}}_{\text{l}}\textit{h}({\upvarphi})-{\textit{c}}_{\text{l}}^{\text{sat}})\right].$$

(27)

Analytical solution of sharp interface model

According to the sharp interface model of the diffusion-controlled corrosion process, Eqs. (7) and (8), the analytical solution in a planar solid-electrolyte can be described by the interface motion driven by diffusion. The general solution for concentration is

$${c}_{\text{l}}\left({r}^{* },{t}^{* }\right)=A+B\text{erf}\left(\frac{{r}^{* }}{\sqrt{4{t}^{* }}}\right),\text{erf}\left(u\right)={\int }_{u}^{{\infty}}{\text{e}}^{-{v}^{2}}\text{d}v,$$

(28)

where $A$ and $B$ are constant related to boundary condition, $\text{erf}\left(u\right)$ the Error function, ${r}^{* }\,=\,r/W$. With the condition of ${c}_{\text{l}}({r}^{* }\to {R}^{* }\left(t\right))\,=\,{c}_{\text{l}}^{\text{sat}}$ and ${c}_{\text{l}}({r}^{* }\to 0)\,=\,0$, Eq. (28) becomes

$${\textit{c}}_{\text{l}}\left({\textit{r}}^{* },{\textit{t}}^{*}\right)=\frac{{\textit{c}}_{\text{l}}^{\text{sat}}}{\text{erfc}\left({\it{K}}\right)}\text{erfc}\left(\frac{{\textit{r}}^{* }}{\sqrt{4{\textit{t}}^{* }}}\right),$$

(29)

where $\text{erfc}\left(u\right)\,=\,1-\text{erf}(u)$ is the Inverse error function, Κ is a constant that derived from Eq. (31). Substitute Eq. (29) into Eq. (8), we obtain

$${c}_{\text{l}}^{\text{sat}}{\text{e}}^{{-K}^{2}}-K\sqrt{{\uppi}}({c}_{\text{s}}-{c}_{\text{l}}^{\text{sat}})\text{erf}(K)\,=\,0.$$

(30)

This form of concentration distribution means that the interface moves in a parabola

$${\textit{R}}^{* }\left(\textit{t}\right)\,=\,K\sqrt{4{\textit{t}}^{* }}.$$

(31)

Curvature action and parameter influence

In order to explore the effects of curvature action and related parameters on numerical results, the velocity term and interface dynamics parameters in Eq. (26) were eliminated, and the dynamic equation obtained is

$$\frac{\partial {\upvarphi}}{\partial {\textit{t}}^{* }}\,=\,{\textit{b}}^{* }\left[{{\nabla }^{* }}^{2}{\upvarphi}+{\upvarphi}(1-2{\upvarphi})(1-{\upvarphi})-{{\kappa}}^{* }\left|{\nabla }^{* }{\upvarphi}\right|\right].$$

(32)

Import method of arbitrary structure

In the process of computational simulation, it is often necessary to introduce structures with complex boundaries (such as metal workpiece surfaces and intermetallic inclusions in this paper) in order to fit with actual conditions. This type of structure is often difficult to be introduced into the computational model. We present a method to introduce arbitrary structure using image processing. Next, we take the importing method of ceramic particle in this paper as an example (illustrated in Fig. 10) to introduce the importing method of arbitrary interface structure.

Fig. 10 : Introduction of ceramic particle structure.

a original image of ceramic particle; b ceramic particles in the model.

First, we draw an image of the ceramic particle structure, where the black area represents ceramic particles and the white area represents no ceramic particles. Then, the image processing technology is used to convert the existing image in RGB three-channel format into a single-channel format, which is conducive to our next step of image processing and conversion. After that, we filter out the ceramic particle region by the difference of the black and white single-channel values, and set the value of the ceramic region to 0, and the value of other regions to 1 (corresponding to the value of $L$ in the calculation domain). It is worth mentioning that this method can be extended to 3D computation and has wide application space.