Plastic injection molding dies using hybrid additively manufactured 420/CX stainless steels: electrochemical considerations

Abstract

This research focused on the corrosion resistance and microstructure of hybrid additively manufactured (HAM) samples of AISI 420/CX (420/CX SS) stainless steels. Potentiodynamic polarization, electrochemical impedance spectroscopy (EIS), and Mott–Schottky analyses as well as the electrochemical noise (EN) technique were used to evaluate the electrochemical behavior of the as-built and heat-treated HAM parts in NaCl solution. The results showed a more protective passive layer formed on the CX SS side. The distribution of Cr-rich M₂₃C₆ carbides in matrix of 420 SS side resulted in a lower corrosion resistance compared to the CX SS side. The noise data analysis confirmed an increase in the galvanic currents of the HAM parts after heat treatment. The stochastic analysis revealed the interface in the heat-treated condition increases pit growth more than the as-built one due to the evolution of nano-sized intermetallic compounds of Al-N/ (Cr, Nb) (N, C) at the heat-treated interface area.

Introduction

A growing demand in the global market for polymer-based components in food, medical, transportation, packaging, and electronic industries made it ever more critical to access low-cost, yet high-performance materials for manufacturing of plastic injection molding (PIM) systems^1,2,3. Heat is more effectively absorbed from the mold using cooling liquids (water, for instance), which is circulated in additively manufactured conformal cooling channels resulting in an improvement of the quality and productivity of the part⁴. A significant remaining challenge in the development of PIM products is the water quality used in the cooling pathways. The safely managed bacteria-free water is commonly treated with chlorine agents that cause pitting corrosion in the microstructure of the dies’ cooling channels³. Pit growth leads to early die fractures under dynamic loadings, i.e., fatigue-corrosion, within the continuous operation. Furthermore, untreated water bears an additional risk of bacterial corrosion of coolant pathways⁵.

Stainless steel, especially AISI 420 steel defined as martensitic stainless steel with the 13 wt.% Cr (main alloying element), is widely utilized as a corrosion-resistant solution in PIM production^2,5. However, the sensitivity of such martensitic stainless steels of Cr-type to pitting as a localized defect, which is induced by the corrosion in an aqueous environment contaminated by chloride ions, raised important concerns and posed as an impediment to be widely adopted as the proper materials for the PIM market⁶. Chloride ions as depolarizer agents attack the passive film formed on stainless-steels’ surfaces. Consequently, the passive layer breaks, and the bare metallic surface would be exposed to the corrosive media. These sequent incidents result in considerable solubility of metal and corrosion damages, which reduce the working life of the molds and impose a high cost for repairing or replacing dies in the industrial sector⁷. Therefore, developing methods to increase the anti-corrosion properties of mold steels became increasingly important.

An effective solution that addresses the concerns pertaining to working life and costs in the PIM is to replace AISI 420 stainless steel parts in cooling channels with an additively manufactured (AM) stainless steel, a CX stainless steel that proves superior corrosion resistance characteristics^8,9. Due to the complex geometries of cooling channels inside the PIM dies, the AM technology can be applied without raising the economic cost of manufacturing¹⁰. A more attractive alternative is to deploy a hybridization manufacturing method in which the CX steel cooling channels fabricated via an AM process is integrated to the AISI 420 steel base fabricated conventionally. This method has the potential to increase the speed of cycling in injection molds by up to 50% and an improvement higher than 30% in PIM die life¹¹. A further incentive to migrate to hybrid additive manufacturing (HAM) techniques for manufacturing PIM parts is the elimination of some metallurgical defects formed within the heating-cooling cycles of the joining of dissimilar materials by conventional welding processes such as the formation of hard and brittle intermetallic compounds¹².

Prior studies provide a comprehensive overview of the HAM processes developed during the last decade and the successful productions of joining two or more materials^12,13. Generally, HAM processes are either categorized based upon the secondary process to provide surface enhancements or integration with bulk-forming, sheet forming and joining by forming processes^12,13. Although the microstructural characteristics and the mechanical performance of the fabricated dissimilar metal parts are explored in the literature^14,15,16, the corrosion performance of the HAM components remained largely understudied, in particular when dealing with dissimilar joints of different types of stainless steels.

Several challenges are attributed to the welding process of dissimilar surfaces whereby the mixing of metals results in a dissimilar joint, which its chemical composition and microstructure is significantly different from the base metal. Similarly, the differences in chemical composition and microstructural features induced within the HAM process could lead to severe galvanic corrosion resulting in accelerating corrosion damages. The presence of pores, cracks, and intermetallic compounds such as inclusions and precipitates reduce the corrosion performance and localizes the corrosion attacks at the interface resulting in a higher corrosion susceptibility in a joint¹⁷. Furthermore, the dissimilar joining of stainless steels by AM processes increases local sensitized zones and degrades the respective corrosion resistance of the joints. The formation of Cr-carbides, which are localized enrichment of Cr would form Cr-depleted zones, promoting the development of the sensitized zones¹⁸. Therefore, investigating the corrosion mechanism of dissimilar joints fabricated by HAM techniques is necessary for an in-depth evaluation of their performance in corrosive environments.

In the previous work of our group, we investigated the microstructure and mechanical performance of hybrid 420/CX SS parts¹⁹. Accordingly, AISI 420 steel was used as a base, and CX SS as martensitic precipitation hardening stainless steel was deposited by laser powder bed fusion (L-PBF) on top of it. Our prior findings suggested that the hybridization of AISI 420 SS and CX SS evolves into a reliable-high-strength interface, that could be applicable in the fabrication of PIMs with geometrically complicated geometries¹⁹.

The electrochemical noise (EN) technique is compared to common electrochemical techniques to obtain in-situ information of the corrosion progress and determine the mechanism of corrosion attacks²⁰. An important novelty of this study is to employ the EN method to assess the corrosion mechanism dominant in corrosion attacks on the HAM components of 420/CX SS, a method and topic that to the best of our knowledge has not been explored by prior electrochemical studies^20,21,22.

This research complements existing studies that employed the EN technique in that it provides additional valuable insights into the behavior of HAM components in the aqueous solutions. The current and potential noise records provide substantial information about the type and mechanism of corrosion. In this regard, we assess the localized corrosion and galvanic corrosion behavior of hybrid components using common electrochemical tests alongside the EN technique.

Results and discussion

Characterization of hybrid additively manufactured 420/CX stainless steel

The morphologies of the microstructural features formed in 420 SS and CX SS samples in both states (as-built and heat-treated) are presented by the SEM and the image quality (IQ) maps in Fig. 1. For the 420 SS sample in the heat-treated condition and CX SS samples in as-built and heat-treated conditions, the martensitic microstructure consists of blocks and laths as the most common phase can be observed. However, unlike other samples, the microscopic morphology in the as-received 420 SS samples is not martensitic laths as shown in SEM image and IQ map. The granular morphology of grains in the as-received 420 SS samples could be related to α- Ferrite phase formed as the matrix (Fig. 1a: IQ map). In addition to these, round or elongated particles are observed from the SEM images related to the as-received and heat-treated 420 SS samples (marked with yellow arrows in Fig. 1a: SEM images). These particles could be Cr-rich carbides, which forms during the annealing process in the ferritic matrix of the as-received samples or formed during the tempering process in the matrix of the heat-treated 420 SS specimen. However, the SEM images do not show any trace of the precipitates formed in CX samples in both as-built and heat-treated conditions. Moreover, a pseudobinary section of the Fe-Cr-C system at a constant 13 wt.% Cr is shown in Fig. 1c. According to this diagram, at temperatures below 800 °C, the precipitation of Cr-rich M₂₃ C₆ carbides is possible in the 420 SS’s matrix containing about 0.25 wt.% C, while a negligible amount of the carbides could be precipitated in the matrix of CX SS samples.

Fig. 1: Microstructural characterization images including SEM, and IQ maps of the martensitic stainless steels before and after heat-treatment related.

a 420 SS sample, and b L-PBF CX SS sample, c Fe-13Cr pseudobinary diagram with the nominal carbon content of CX SS and 420 SS samples superimposed.

Furthermore, the studied stainless steels' X-ray diffraction (XRD) patterns revealed diffraction peaks of the BCC structural α phase which is presented in Fig. 2. Although the martensite and ferrite show a similar axial ratio and it is hard to distinguish these two phases in the conducted XRD analysis, the surface hardness measurements performed in our previous study indicated the hardness value of the as-received 420 SS samples is about 25 HRC. This is significantly lower than the rest of the samples (>35 HRC)¹⁹. Accordingly, the α phase relieved in the XRD patterns related to the as-received 420 SS sample could be indexed as the ferrite phase and as the martensite for other samples. In addition, the XRD and hardness results also are in agreement with the morphological observations of the microstructures (Fig. 1a, b).

Fig. 2: XRD patterns of samples.

a 420 SS samples, and b CX SS samples.

In addition to ferrite and martensite peaks detected from the XRD patterns, the weak peaks within the range of 55° to 75° related to Cr-rich carbides of M₂₃C₆ were determined for the as-received and heat-treated 420 SS samples (Fig. 2a). The peaks of austenite (γ) were also observed for the as-built and heat-treated L-PBF CX SS samples (Fig. 2b) indicating the formation of retained/reverted austenite during the L-PBF and heat-treated processes.

The variation of average grain size after the heat-treatment process is also shown in Fig. 1. As expected, the average grain size of the as-built CX samples (about 1.7 μm) was increased after the solution annealing and aging treatment (about 4.6 μm), while the 420 SS samples showed a reduction in the average size of grains after solution annealing and tempering. The average size of grains for 420 SS sample reduces to about 2.9 μm after the heat-treatment process. This reduction could be attributed to the partial dissolution of carbides in the austenitizing temperature applied within the heat-treatment process in which the presence of some undissolved carbides affects the grain growth of austenite by pinning the grain boundaries, resulting in the evolution of a finer structure after subsequent quenching²³. It was previously shown that as-built CX samples composed of a hierarchical structure including a honeycomb cellular/columnar structure of sub-grains (Fig. 1b: SEM image) confined by the larger micrograins^8,19. Moreover, it is stated that microsegregation of alloying elements and the entangled dislocations could accumulate in sub-grain boundaries formed during the L-PBF solidification process^24,25. Therefore, the grain growth of the L-PBF CX SS sample after the post-heat treatment process could result from reaching a thermally stable structure by annihilating segregation and dislocations leading to recovery/recrystallization and grain growth^24,25.

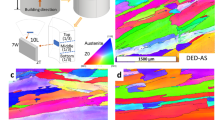
The inverse pole figure (IPF) maps taken from the area including interface and the corresponding grain boundary maps in as-built state and heat-treated condition are displayed in Fig. 3a, b, c, and d, respectively. The interface is marked with a black dashed rectangle in grain boundary maps. The variation of grain size and grain orientation spread (GOS) distributions of the interface in both as-built state and heat-treated condition are also illustrated in Fig. 3e, f, respectively. In these plots, the interface is noted as IHB₁ and IHB₂.

Fig. 3: EBSD measurements (IPF maps and relevant grain boundary distributions) of hybrid samples’ interface area.

(Color code: red VLABs, green LAGBs and blue- HAGBs). a, b as-built condition, and c, d heat-treated condition, e grains size distribution of both as-built state and heat-treated condition from the interface (marked with black dashed rectangle in b and d), and f corresponding GOS maps of the interface. (IHB₁: the interface of hybrid sample in as-built state, IHB₂: the interface of heat-treated hybrid sample).

The IPF maps taken from the interface and adjacent area in the as-built condition showed the presence of a typical lath martensitic microstructure developed from the CX SS side and a more equiaxed granular ferritic structure formed from the 420 SS side (Fig. 3a). Also, the interface region developed from the deposition of the melt-pools formed during the L-PBF process on the 420 SS substrate shows a fine grain structure, while a significant grain growth is observed after the solution annealing and aging/tempering process (Fig. 3c). Accordingly, the average grain size of the as-built and heat-treated samples in the interfaces was calculated to be about 1.4 μm and 2.8 μm, respectively. The grain size in the interface region increased about two times after the heat-treatment process.

It could be postulated that the fine grains detected from the interface are developed below the earlier melt-pool boundaries formed during the L-PBF process. Through subsequent depositions, small grains may be created in the heat-affected zone (HAZ) formed by substance that has already solidified and the 420 SS substrate. Furthermore, temperature excursions above the HAZ's eutectoid point can result in recrystallization and/or local transformation of materials as well²⁶. An increase in grain size of the interface sample after austenization and aging/tempering treatment could also be explained based on the thermodynamical tendency to eliminate sub-grains developed within the L-PBF process. In other words, the segregation of the alloying elements and the accumulation of dislocation in the cell walls of the microstructure developed during the L-PBF process provides a high tendency to recrystallization and grain growth within the heat-treatment process²⁷.

The corresponding grain boundary maps of the interface and its adjacent regions in the as-built state and heat-treated conditions are also displayed in Fig. 3b and d, respectively. The microstructure is characterized by three different types of grain boundaries: LAGBs denotes as the low angle grain boundaries, HAGBs as the high angle grain boundaries, and VLABs which is very (extremely) low angle grain boundaries²⁸. In the present study, the fraction of VLABs and LAGBs of the identified area (boundaries less than 15°) in the as-built state and heat-treated condition are almost the same, while the fraction of HAGBs decreased at the heat-treated condition in comparison with those of the as-built state.

A comparison between the GOS distributions of the interface in both the as-built state and heat-treated condition indicated the average GOS value in the as-built condition (about 1.96°) is a little lower than that in the heat-treating state (around 2.61°). A grain's GOS is the relative orientation of each scan point within a grain measured by comparing its average grain orientation to each scan point's orientation. Also, an increased fraction value of GOS obtained by the number fraction could be attributed to grains including a higher percentage of dislocations²⁹. A higher value of HAGBs in the as-built condition compared to those in the heat-treated condition agrees with the average grain size calculated in both states. Accordingly, finer grains observed in the as-built condition result in a higher fraction of HAGBS than those of the heat-treated state. In addition, the heat-treatment process converted the duplex ferritic/martensitic structure observed in the as-built state to an almost fully lath-type martensitic structure. This conversion results in the evolution of a higher density of the dislocations in the lath martensitic structure increasing average misorientation values, especially GOS.

The TEM and corresponding EDS maps of the interface area in the as-built state and heat-treated condition are illustrated in Fig. 4. It can be found that the main phase at the interface in both conditions is martensite with high density of dislocations (Fig. 4a, c). Moreover, traces of microsegregation of Cr and Ni elements at the interface (marked with red dashed lines in Fig. 4a) and the CX SS side near the interface in the as-built condition are also observed (Fig. 4b).

Fig. 4: Bright-field TEM images and corresponding EDS maps of hybrid samples’ interface area.

a, b as-built condition, and c, d heat-treated condition.

The Cr and Ni segregations observed in the interface, which are extended to the CX SS side in the as-built condition are a result of the L-PBF solidification process. The microsegregation and distinct element distributions can be explained by the particle accumulation structures (PAS) mechanism that occurs during the solidification resulting in the rejection of Cr and Ni from the solid/liquid interface to the instability layer^24,25. As it was mentioned in Fig. 1, the microstructure of the 420 SS side of the hybrid samples in the as-received condition also contain carbide particles with an average size of about 0.5 μm, the EDS maps of the 420 SS side in the as-received condition (Fig. 4b) also showed a population of fine particles dispersed as chains enriched in Cr and C, suggesting the fine particles are likely carbides that precipitate out within the annealing process applied to as-received 420 SS samples.

Figure 4c, d show the bright field TEM images and relevant EDS maps of alloying elements’ distribution in the interface after the heat treatment. The rectangular-shaped particles mainly rich in Al, N, and low amounts of Cr, Ni, and Nb segregations are indicated from the EDS maps in the heat-treated condition. The Cr, Ni, and Nb segregations are somewhat finer and lower than those in the as-built microstructure, which could be related to the partial elimination of microsegregation after the heat-treating process. The precipitation of Al-N particles with a size of about 50–160 nm after austenization and aging/tempering process could also be explained by the higher nitrogen affinity of Al compared to other alloying elements at a temperature lower than 950 °C along austenite prior grain boundaries³⁰. In our previous study, microsegregation of C was also revealed from EDS maps with segregations of Al and N and Nb¹⁹. Therefore, the microsegregation of Cr, Nb, and C near N could also be related to the precipitation of (Cr, Nb)(N, C) particles located immediately near the Al-N particles, forming particle clusters^9,30.

Polarization plots

Figure 5 shows the representative potentiodynamic polarization plots of CX SS, 420 SS, and samples taken from the interface area of the hybrid parts in both as-built and heat-treated conditions named HB₁ and HB₂, respectively. As shown in Fig. 5, except for 420 SS samples in the as-received state and heat-treated condition, S₁ and H₁, respectively, there is a distinct passive region that occurs spontaneously followed by pitting at potential (E_pit) marked by the black dashed arrows in potentiodynamic curves for all samples. The variations of pitting potential (E_pit) values as well as the corrosion potential (E_Corr) and current (i_Corr) are also inset into Fig. 5.

Fig. 5: Potentiodynamic polarization plots of the examined stainless steels in 2000 ppm NaCl at room temperature (about 25 °C).

a the interface area of the hybrid samples in as-built state and heat-treated condition, b as-built samples of CX and 420 SS, c heat-treated CX and 420 SS samples, and d variation of E_pit, E_Corr, and i_Corr of each sample.

Furthermore, Fig. 5a illustrates transient currents (gray dashed arrows) developed at the passive area of the polarization plots for HB₁ and HB₂ indicating a metastable pitting phenomenon. Frequently the generation of current peaks and subsequent repassivation at the passive zone is commonly indexed to the formation of metastable pits³¹. Accordingly, a significant increase in the current density exceeds the passive region suggesting the formation of stable pits at the pitting potential, which is a specific potential at the anodic branch of the polarization curves. Since the pitting corrosion is a probabilistic process³², statistical methods have frequently been used to investigate this phenomenon. In this study, pitting corrosion is also examined by electrochemical noise and statistical methods, which are discussed in the relevant section.

A comparison between the potentiodynamic curves of the as-built CX sample (S₂) and heat-treated CX sample (H₂) showed both samples have almost the same corrosion behavior. Accordingly, E_pit, E_Corr, and i_Corr of CX samples in the as-built and heat-treated conditions are almost identical. The values of E_pit related to the interface area samples (HB₁ and HB₂) is lower than those of the other samples. The value of E_pit for the interface area sample in the heat-treated condition (HB₂) is a little lower than that of the interface area sample in the as-built condition (HB₁ sample). Also, a rapid increase in the current density was detected for the as-received 420 SS sample (S₁) and heat-treated sample of the 420 SS (H₁) as their polarization potential is greater than the corrosion potential (E_Corr), indicating active corrosion with passivation loss.

A comparison between the E_pit, E_Corr, and i_Corr values also indicated a slight difference between the polarization behavior of the as-built and heat-treated CX samples. The 420 SS samples showed a deteriorated corrosion resistance compared to the CX SS samples in both conditions. The loss of passivation and active corrosion behavior of the as-received and heat-treated 420 SS samples could be attributed to the microstructural features, especially the evolution of Cr-rich carbides in their matrixes. The carbides that are enriched with Cr, induce the depleted zones of chromium elements in the matrix/carbide boundaries in the microstructure of the as-built and heat-treated 420 SS samples creating the preferential zones for pitting. Consequently, if the Cr-depleted zones surrounding the carbides are closer together and have a higher density, the formation of protective passive films on 420 SS samples may be hampered³³. In addition to this, the role of grain size and the presence of the reverted/retained austenite could be considered as the other factors affecting the corrosion resistance of the martensitic samples. However, the samples showed a slight difference in the grain size and amount of reverted/reversed austenite. The grain size of 420 SS samples was slightly higher than that of the CX SS samples in both as-received and heat-treated conditions. Therefore, the role of grain size is considered one of the reasons for decreasing the corrosion resistance of the 420 SS samples in comparison with the CX SS samples. It is also suggested that for alloys with an active-passive behavior, grain refinement can decrease the localized corrosion rate because the formation of a higher grain boundaries results in the evolution of a thicker and faster passive layer^34,35.

Also, the presence of reversed/retained austenite in the microstructure of CX SS samples could affect the resistance to pitting. It was reported that the existence of reversed austenite increases the pitting resistance due to the low extent of Cr depletion around the carbides³⁶.

EIS measurements

The EIS measurements were conducted on the 420 SS, CX SS and the samples taken from the interface area of the hybrid parts in both as-built state and heat-treated conditions in 2000 ppm NaCl solution and at open circuit potential (OCP). The Nyquist and Bode plots of all samples are shown in Figs. 6–8, respectively. The Nyquist spectra of all samples shown in Fig. 6 implicate the capacitive arc characteristics, composed of medium-high frequency capacitance arc related to the passive film capacitance (CPE_film) and low-frequency region on behalf of the specimen surface and the solution associated to electric double layer (CPE_dl). In stainless steels, chromium oxide forms the passive films, which are referred to as Cr-rich dual layers³⁷. The constant phase element (CPE) is used to show the passive film and double layer’s capacitances on a heterogeneous surface.

Fig. 6: Nyquist plots of the examined samples in 2000 ppm NaCl aqueous solution at room temperature at OCP.

a the interface area of hybrid samples in both states (as-built and heat-treated), b as-received and heat-treated 420 SS specimens, c CX SS samples in both states including as-built state and heat-treated condition. The equivalent circuit used for fitting the plots is inserted in Fig. 6.

Fig. 7: Bode plots (log |Z| (magnitude) versus log f (frequency)) of the EIS measurements of all samples in 2000 ppm NaCl aqueous solution at room temperature at OCP.

a interface area of hybrid samples in as-built and heat-treated conditions; b as-received and heat-treated 420 SS samples, and c as-built and heat-treated CX SS samples.

Fig. 8: Phase angle φ versus log f of the EIS measurements of all samples in 2000 ppm NaCl aqueous solution at room temperature at OCP.

a interface area of hybrid samples in as-built and heat-treated conditions; b as-received and heat-treated 420 SS samples, and c as-built and heat-treated CX SS samples.

As displayed in Fig. 6, the arc sizes in Nyquist plots of the HB₁, S₂, and H₂ samples are much higher than those of the HB₂, S₁, and H₁ samples. Meanwhile, after the heat-treatment process, the arc diameters of the interface area sample reduced in comparison with those of the same specimen in the as-built state (Fig. 6a–c). However, the arc diameters observed from the Nyquist curves of the as-built state and heat-treated CX SS specimens show a slight difference. In addition to this, the arc diameters of HB₂, S_1, and H₁ samples are much smaller than the others.

Regarding Bode plots, a linear correlation between |Z| and f in logarithmic form was observed over a broad frequency range for all samples shown in Fig. 7 confirming the presence of the capacitive behavior attributed to the double layer and film of passive formed between the surface of specimens and the solution. However, the difference between the time constants of the double-layer and the layer formed on the samples’ surfaces affects the range of frequency in which a straight line with a slope of approximately −1 is widened³⁸. In the low-frequency area, the value of the impedance modules (frequency of 10⁻²) of HB₁, S₂, and H₂ samples were much higher (about 10⁶ Ω cm²) than those of the HB₂, S₁, and H₁ samples (about 10⁴ Ω cm²), which are consistent with the arc diameters observed from their Nyquist curves indicating the greater resistance to the charge transfer and the higher the corrosion resistance³⁸. The maximum phase angles (-θ) observed from the Bode phase curves (Fig. 8) exhibit the same tendency for the HB₁, S₂, and H₂ samples in comparison with those of the HB₂, S₁, and H₁ samples. The maximum phase angle for the HB₁, S₂, and H₂ samples is about 80°, which is much higher than those of the HB₂ (about 62°), and S₁ (about 68°) samples. Finally, the maximum phase angle of the H₁ (72°) sample is slightly higher than the S₁ sample but still lower than those of the HB₁, S₂, and H₂ samples.

The maximum phase angles approached 80° suggesting that a stable film was formed on HB₁, S₂, H₂ samples; however, the lower values of the maximum phase angle detected for the HB₂, S₁ and H₁ samples could be an indication of the deteriorated passive film³⁹.

For fitting the EIS data, an equivalent electrical circuit (EEC) inset in Fig. 6 was employed, which consisted of the solution resistance (R_s) conducted to two R-constant phase element (CPE) elements in series and two-time constants in parallel R_film [CPE_film//(R_ct//CPE_dl)]. In this EEC model, R_film and R_ct show the passive film’s resistance and the charge transfer resistance, respectively. The ions, which are charging agents in the solution would have access to the bare surface of the samples via the formation of pits (showed in EEC superimposed on a scheme of the surface condition of the martensitic samples immersed in the NaCl solution). Also, the capacitances of the passive film and double layer are represented by the CPE_film and CPE_dl, respectively. The results obtained from fitting the EIS data are presented in Fig. 8 with each respective deviation. Generally, the polarization resistance R_p = R_film + R_ct, which is an index of the corrosion resistance, was shown in Fig. 8. The impedance of the CPE can be calculated using Eq. (1)³⁸ written as follows:

$${{{\mathrm{Z}}}}_{{{{\mathrm{CPE}}}}} = \frac{1}{{{{{\mathrm{Q}}}}\left( {\omega {{{\mathrm{j}}}}} \right)^{{{\mathrm{n}}}}}}$$

(1)

where Q denotes the CPE parameters, j denotees $\sqrt { - 1}$, ω is the angular frequency, and $0 \,<\, {{{\mathrm{n}}}} \,<\, 1$ denotes the dispersion coefficient associated with the deviation of the pure capacitance³⁸. In the fitting parameters presented in Fig. 9, n₁, n₂ are the dispersion coefficients of the CPE_film and CPE_dl, respectively.

Fig. 9: The fitted electrochemical parameters.

The parameters obtained for impedance spectra of all experimental samples in 2000 ppm NaCl solution at room temperature.

According to Fig. 9, the dispersion coefficient (n₁) of the passive layers formed on the specimens’ surface is between 0.83 to 0.98, while the dispersion coefficient of the double layers (n₂) for S₁, H₁, and HB₂ (about 0.2 to 0.6) show a higher deviation of pure capacitance in comparison with those of S₂, H₂, and HB₁ (about 0.89 to 0.97) samples. Accordingly, the lower values of the dispersion coefficient of the double layers related to S₁, H₁, and HB₂ samples implicate the presence of a higher surface heterogeneity than those of other samples⁴⁰.

The association between the CPE parameters and the interfacial capacitance has been studied by some researchers. Accordingly, the Q can indicate film thickness, and an increase in film thickness results in a decrease of Q⁴¹. In the present work, the Q_film and Q_dl values of the CX samples in the as-built state and heat-treated condition (S₂ and H₂), and the interface area specimen in the as-built state (HB₁) are lower, and the values of R_p, which is the sum of R_ct and R_film, are larger than those values of the as-built, heat-treated 420 SS (S₁ and H₁) and heat-treated interface sample (HB₂), revealing that more protective passive films deposited on the L-PBF CX samples in both conditions as well as the as-built interface area sample of hybrid parts in comparison with those of the other samples. It is also noticed that, the passive films’ quality would be significantly deteriorated for 420 SS and the interface area samples after tempered/aged at 530 °C as well as the as-received 420 SS sample. As mentioned, the passive layer's deterioration on 420 SS samples could be explained due to the presence of Cr-rich particles formed in their matrix. In addition, the microstructural analyses of the interface area sample showed the evolution of inclusions and particles ((Cr, Nb)(N, C) and Al-N particles) after the heat-treatment process in its matrix as a crucial parameter that affects its resistance to corrosion and the passive layer’s formation on its surface.

Mott-Schottky analysis

To achieve an estimation of the defect densities formed in the passive layer as an indication of the quality of the passive films, the Mott-Schottky analysis was performed on different specimens. The Mott-Schottky theory is explained in³⁸. According to Mott-Schottky's theory, the space charge capacitance of passive films (C) can be calculated, and this value has a linear relationship with the defect densities formed in the passive layer, including donor and acceptor densities³⁸. The donor and acceptor densities of the passive film would be calculated by the slope of the C⁻² vs. E (potential) linear plots. Accordingly, the positive linear slope of the plots is related to forming an n-type semiconductor. Oxygen vacancies and/or cation interstitials as the donors are the major defects in an n-type passive. In contrast, a negative slope of the C⁻² vs. E exhibits a p-type semiconductor where cation vacancies are the major defects of the acceptors³⁸.

According to the potentiodynamic polarization and EIS results, S₁ and H₁ samples indicated a deteriorated passive layer; the Mott-Schottky analysis was conducted on S₂, H₂, and interface area samples in both conditions (HB₁, HB₂). The electrode capacitance is plotted as a function of the applied potential for the different specimens in Fig. 10a–d. It is seen that the plots of the S₂, H_2, and HB₁ samples display a positive slope related to the formation of an n-type passive layer in the potential range, while the relevant plot to the HB₂ sample exhibits the presence of both n-type and p-type semiconductive behavior of passive layer. In consequence, the donor density of defects was calculated for the S₂, H₂, and HB₁ samples indicated in Fig. 10e. In addition, the donor and acceptor density were also estimated for the HB₂ samples (Fig. 10e). The defect density of the as-built CX sample was found to be lower than that of the heat-treated CX sample, and the sum of defects (donor and acceptors) densities shows a higher value in the HB₂ sample than that of the HB₁ sample. Consistent with the EIS and potentiodynamic polarization results, the Mott-Schottky analyses implicate the evolution of a more stable - protective passive film on the as-built sample of CX and the as-built interface area in compassion with their counterparts in the heat-teared conditions indicating a higher corrosion resistance specifically to pitting corrosion attacks.

Fig. 10: Mott-Schottky curves of the examined stainless-steel specimens in 2000 ppm NaCl after the formation of the passive film.

a S₂, b H₂, c HB₁, d HB₂, and e donor and acceptor density of passive layers formed on the experimented samples.

EN measurement and transient analysis

The hybrid additive manufacturing process-induced modifications in the microstructural features were developed in the interface of the 420 SS/CX SS hybrid samples. In addition, the heat-treatment procedure used for the samples after the fabrication process resulted in changes in microstructural features. It is noted that, the formation of different microstructural features in the interface area of the hybrid samples generate dissimilarities in these samples between the base part (420 SS) and the other parts, which could result in the formation of a galvanic pair when the hybrid parts are exposed to the corrosive environment. Therefore, the EN tests in a ZRA mode were designed to analyze the possible galvanic corrosion of the base part/interface area pairs and the formation of metastable pits. The signals of the potential and current for the galvanic couples in both as-built state and heat-treated condition are displayed in Fig. 11.

Fig. 11: The current and potential signals of the galvanic couples formed between the base part/ interface area of the hybrid specimens.

a as-built condition, and b the state of heat-treating.

It is observed from Fig. 11a that the current of the as-built galvanic couples of the interface area increases gradually during the first hour (about 2000 s) followed by an almost stable current for about 4000 s and after that a gradually decrease. However, this decrease is followed by an increasing trend again until the end of the test. Also, the potential fluctuations, Fig. 11a, are consistent with the corresponding currents. The potential noise also showed a reduction trend followed by a stable state. After that, an increase was followed by a reduction trend to the end of the test. The partial dissolution and repassivation of the passive layer that occurred for the galvanic coupling samples in the as-built state might be attributed to the decreasing/increasing trend of the potential together with the increasing/decreasing trend of the current. Figure 11b also shows the EN signals of the heat-treated galvanic couples composed of the interface area of the hybrid samples after the heat-treatment process. The current noise baseline for the heat-treated galvanic pair sample gradually becomes stable, while the potential noise steadily diminishes. Similar to the as-built condition (Fig. 11a), the specimen showed anodic current transients and an overall reduction trend of the potential related to a dissolution of the passive film occurred partially. In addition, it is noticeable that the galvanic current transients showed a positive trend without any negative values, indicating that in both the as-built state and heat-treated condition, the base parts (420 SS) were corroded in comparison with the other parts of the sample. It was also observed that, the average of the galvanic current density values of the as-built sample (about 2.87 nA cm⁻²) is lower than that of the sample in the heat-treated condition (about 24 nA cm⁻²). This fact confirms the heat-treatment process increased the galvanic current density generated between the cathodic part of the interface area and its anodic part. The galvanic couple samples of the interface area are composed of three different zones as follows:

• (1) CX part, which is formed by the L-PBF process and named as the melting zone (MZ).

• (2) 420 part, which is the substrate for the hybrid manufacturing process and named base zone (BZ).

• (3) An interface that formed from the intermixing of the base part (420 SS) and melting pools produced within the L-PBF process of the CX part and is noted as a transition zone (TZ).

Figure 12 presents micrograph images of the interface area, including three different sections and the anodic-cathodic parts of the area. The results of the potentiodynamic polarization and EIS tests showed the corrosion resistance of the as-built and heat-treated CX parts of the hybrid samples is much higher than those of the 420 SS parts in both conditions. Accordingly, the joining of these dissimilar parts resulted in the formation of galvanic couples between them in which a current of electrons would be transported between the anodic section and the cathodic area. Moreover, the transition zones formed between two main parts (MZ and BZ) of the interface area showed different microstructural features resulting in different electrochemical behaviors. EBSD and TEM analyses indicated that the TZ area in the as-built condition composed of the finer grain misconstrue without any traces of the intermetallic compounds; however, the TZ area after the heat-treatment process undergoes a coarser grain structure accompanied with the nano-sized intermetallic compounds of the Cr-rich particles in the form of either (Cr, Nb) (N, C) or M₂₃C₆ particles located immediately adjacent to the Al-N particles. It is ascertained that the TZ area in the as-built condition is similar to the MZ (CX SS part), while this area after the heat-treatment process shows more similarity in terms of the intermetallic phases with the BZ (420 SS side) resulting in the formation of a bigger anodic area in the heat-treated conditions. Furthermore, corrosion resistance reduces as the proportion of anode regions increases⁴². Consequently, the interface area in the heat-treated condition shows inferior corrosion resistance and a higher galvanic current density than that of the as-built state. Moreover, some current transients of the as-built galvanic couples were with an amplitude of about 16 nA, while the heat-treated galvanic couples showed an amplitude of about 200 nA (Fig. 11a, b).

Fig. 12: SEM images of the interface area composed of three sections.

Different sections include MZ (CX SS), TZ (interface), and BS (420 SS) in the as-built and heat-treated conditions. The cathodic and anodic areas are noted on the images.

The analysis of the EN transients' shape, lifespan, number, and amplitude could provide more information about the mechanism of localized corrosion attacks, particularly pitting behavior⁴³. Current transients obtained from the galvanic couples of the interface area samples (HB₁ and HB₂) are plotted in Fig. 13a, b). The characteristics of current transients within the nucleation of pit, as well as metastable and stable pitting, were discussed by several researchers^32,44. The current transients with an amplitude of about 1 pA to 1 nA and lifetime of about 0.5 s are reported to be indicative of the pit nucleation⁴⁵, while the growth of metastable pits is accompanied by a much higher current density⁴⁶. Figure 13 presents two different types of the current transients of the HB₁ and HB₂ samples depending on the ratio of the ascent time, which starts from baseline to the peak (t_R) and the time of drop from peak to baseline (t_D). The t_R is defined as the time for the growth of the metastable pit, and t_D is associated with the repassivation time of the metastable pit.

Fig. 13: Shapes of current transient for the interface area samples (galvanic couples) in 2000 ppm NaCl solution.

Within the period of 12,000 s in a state of as-built (HB₁), and b condition of heat-treated (HB₂).

The two different types of the current transients observed from Fig. 13 could be related to different rates of pitting and repassivation in the interface area samples (HB₁ and HB₂). Accordingly, the first type of current transient is related to the as-built galvanic couple sample (HB₁) and is observed from Fig. 13a. According to Fig. 13a, there is a fast rise of current transient (lower value of t_R) related to the growth of metastable pits and slow drop of the current (higher value of t_D) associated with the repassivation in a low transient amplitude. The second type of current transient is observed for the heat-treated galvanic couple (HB₂). The current transient of the HB₂ sample displayed almost the same t_R and t_D (Fig. 13b) suggesting an equal rate of pitting and repassivation. Soltis et al.⁴⁷ proposed different shapes of current transients, which are related to pitting attacks of the metallic parts, have a close correlation with the type of material. Accordingly, different material microstructures could affect the pitting initiation and the shape of corresponding current transients. Therefore, the pitting initiation mechanism of the hybrid samples in the interface area is because of the different microstructural features developed in them. The existence of a finer grain size in the microstructure of the HB₁ sample compared with that of HB₂ could lead to a higher resistance to localized corrosive attacks³⁴. In addition, the dissolution of non-metallic particles scattered in the matrix of the interface area could cause pitting transients. In the case of the HB₁ samples, Cr-rich carbides with an average size of about 0.5 μm were detected from the 420 SS side, which could trigger the formation of metastable pits. In the heat-treated interface area sample (HB₂), nano-sized precipitates of Cr-rich carbides with an average size of about 150 nm and (Cr, Nb) (N, C)/Al-N intermetallic compounds with 50–160 nm size revealed in the 420 SS side and TZ area, respectively. Therefore, it can be stated that the size of non-metallic particles as the preferential zones to pitting attacks affects the repassivation time resulting in a higher repassivation time (t_D) for the HB₁ sample as compared to the time spent for the repassivation of the pits on the HB₂ sample; however, smaller pits could form on the HB₁ sample with a lower time of growth (t_R) and current amplitude observed from Fig. 13a.

Standard deviation of current, potential and noise resistance

Standard deviations of the current (σ_I) and potential (σ_v) are among the sequence-independent statistical analyses regarding the EN data. The σ_I and σ_v describe the amplitude of a noise signal and correlate with the noise resistance and corrosion rate²¹. According to Eqs. (2), (3), and (4), the σ_I and σ_v, and noise resistance (R_N) at the interval of 1000 s for both HB₁ and HB₂ samples were calculated and plotted as a function of time shown in Fig. 14. The overall trend of the σ_I for the HB₁ sample is lower than that of the HB₂ (Fig. 14a), while the general trend of σ_v shows a higher magnitude for the HB₁ sample as compared to the HB₂ (Fig. 14b). Accordingly, the relevant noise resistance (the ratio of the potential standard devotion to current standard deviation (Eq. (4)) for the HB₁ samples would be higher than that of HB₂. Figure 14c displayed the value of $\frac{1}{{R_N}}$ as a function of time for both samples. The overall trend for HB₁ is lower than that of HB₂ indicating a higher noise resistance in HB₁ than HB₂. Furthermore, according to Eq. (5), there is a relationship between the corrosion current and noise resistance. Assuming the equivalent of R_N and polarization resistance (R_p) and using the Stern-Geary coefficients, the average value of corrosion current obtained from Eq. (5) for HB₁ sample would be lower than that of HB₂.

Fig. 14: Statistical parameters of the EN data.

a standard deviation of current noise, b standard deviation of potential noise, and c reciprocal noise resistance (1/RN) as a function of time in 2000 ppm NaCl solution at room temperature.

The results obtained from the standard deviation and noise resistance calculations are consistent with the current and potential fluctuations detected from the current and potential transients presented in Fig. 11. Somewhat higher σ_I and lower σ_v are observed in Fig. 14a, b as well as the lower reciprocal noise resistance (R_N), could be explained by the passive film’s partial dissolution on galvanic couple samples (HB₁ and HB₂)⁴⁸.

PSD and shot noise analysis

Spectral methods are the sequence-dependent statistical analysis in which the noise data are converted from time into the frequency domain. Accordingly, PSD is defined as the power or energy in a signal as a function of frequencies⁴⁸. It should be noted that, the PSD values correlate with the variance (the standard deviation’s square) and also q and f_n values as the shot noise parameters, which are shown in Eqs. (6) and (7). In this study, the process of converting all data of the potential and current noise obtained in the time domain into the frequency domain, which is known as spectral estimation, was performed via a fast Fourier transform (FFT) process. There is a close relationship between the power spectral of current noise (PSD_I) and corrosion activity, as is shown in Eq. (9). Therefore, the PSD_I is also indicative of the corrosion activity for stainless steel, especially pitting attacks. The corrosion attacks on stainless steel occurred mainly as pitting in the solutions containing chloride ions. The cumulative probability plots of PSD_I of both samples were calculated and indicated in Fig. 15a to show the corrosion activity differences between the two galvanic couple samples. It was noted that, HB₁ samples showed a lower PSD_I value in the same cumulative probability values compared to the HB₂ samples resulting in a higher pitting resistance in the as-built interface area (HB₁) samples than that of the heat-treated interface area sample (HB₂). In addition to PSD calculations, the shot noise parameters, including charge, q, and f_n (characteristic frequency), were calculated for both samples in the interval of 1000 s and are shown in Fig. 15b.

Fig. 15: Cumulative probability and shot noise plots.

a Cumulative probability plots of PSDI for the HB1 and HB2 samples, b corresponding plots of shot-noise parameters including charge (q) vs. fn.

The shot noise theory's q and f_n provide detailed information regarding the nature of corrosion processes²¹. The q indicates the mass of the metal lost in an event, while the rate of corrosion events could be estimated by f_n as defined in Eq. (8)⁴⁹. For the passive samples, it is expected to have a low charge, but the frequency depends on the processes taking place on the passive film⁵⁰. In addition, f_n could be an indicator to study the localized corrosion’s tendency based on the shot noise theory⁴⁹. It has been stated that, the smaller value of f_n results in easier corrosion in a localized type⁴⁹; however, the f_n of the two samples in our study were dispersed throughout a wide range of frequency confirming that the EN signals have stochastic features. A comparison between the plots of q vs. f_n shows the charge values of the HB₁ sample as an indication of loss of metal within the corrosion process are much lower than those of the HB₂ samples in the same range of frequency demonstrating that after the heat-treatment process, the interface area sample has a higher risk of pitting corrosion. Therefore, the results obtained from the potentiodynamic and impedance tests are confirmed by the statistical parameters obtained from EN data.

Estimation of pit radius distribution

As mentioned in the extreme value analysis of the pit growth (presented in the Extreme value analysis for pit growth in the Methods section), Eqs. (12) and (13) could be used to calculate the pit radius, and then the largest pit size of every segment of the ECN signals, which is divided into 12 segments, could be estimated. Also, the Gumbel probability curves named the reduced variant (Y) versus the ordered maximum sizes of pits are shown in Fig. 16a. The reduced variant plots indicate the presence of single slope linear regions, indicating the metastable pitting behavior in both samples. Accordingly, the Gumbel parameters, which are the α and μ related to the linear region of metastable pitting, were estimated using the slope and intercept of the line fitted to the reduced variant (Y) versus pit radii plots. Furthermore, the metastable pit sizes’ probability distribution is calculated using Eq. (14) and shown in Fig. 16b. The pits’ number per m² per second is the probability unit and the pit sizes are calculated in μm. According to Fig. 16b, the probability of growing metastable pits on the HB₂ sample is slightly higher than that of the HB₁ sample. Therefore, it is implied that, the as-built interface area samples are more resistant to the growth of the nucleated pits formed than the heat-treated interface area sample. Accordingly, the growth of a nucleated pit on the HB₁ sample to a size of about 15 μm takes a time of about 194 s, while reaching the same size of the pit on the HB₂ sample needs a shorter time of about 90 s.

Fig. 16: Estimations of pit radius distribution.

a reduced variant versus pit radius, and b the metastable pit sizes' probability distribution in as-built and heat-treated interface area samples taken from hybrid parts.

In addition, the observations of the surface morphology of the interface area specimens (HB₁ and HB₂) after corrosion tests are presented in Fig. 17. The HB₂ sample showed a greater pit size and distribution than those of the HB₁ sample. Also, the feature of pores on the heat-treated interface area sample (HB₂) is diverse, which indicates the continual initiation of pits concurrently with the growth of the existing pits.

Fig. 17: Optical micrographs after corrosion.

Showing the exposed surface of interface area samples after potentiodynamic polarization tests: a HB₂ sample and b HB₁ sample.

Remarks on the manufacturing and post processing processes

Hybrid additive manufacturing (HAB) is currently one of the most attractive manufacturing techniques to join dissimilar materials or hybrid parts in a cost-effective manner. The Fabrication of plastic injection molds (PIM) using AISI 420 and CX stainless steels in a hybrid design promotes their efficiency, strength, and fatigue life. In our case study, the fabrication of AISI 420/ CX HAM parts with a sound interface was one of the important aims. Mechanical strength in terms of ultimate tensile strength, hardness, and toughness as well as fatigue properties and creep resistance of the HAM parts are important measure of success for HAM products to further adopt in the industry. In addition to the mechanical properties, the corrosion resistance of the HAM parts in a corrosive environment, in our case, AISI 420/CX HAM parts is one of the concerns in the PIM industry. Applying suitable post-processing procedures including heat-treatment or machining is critical to achieve comparable mechanical and electrochemical properties of the HAM parts with their conventional manufactured counterparts. Very few reports are available on the effect of different heat-treatment processes on the mechanical properties and corrosion resistance of additively manufactured stainless steel parts. Accordingly, the previous studies showed that there is a competition between the optimum mechanical properties and high corrosion performance of the engineering stainless steel structures. The formation of some microstructural features could be proper for the mechanical properties, while they deteriorate the corrosion properties^51,52,53. Reaching a balance between the mechanical properties and corrosion resistance in a real condition needs a comprehensive investigation using designing different heat treatment procedures.

In our study, the heat-treated AISI 420/CX HAM parts, especially the heat-treated interface area, showed an inferior corrosion performance in comparison with the as-built condition. However, the mechanical properties of the heat-treated hybrid parts, specifically across the interface, qualified for application in PIM dies¹⁹. Therefore, as a gap of knowledge, it is necessary to design different heat-treatment processes regarding the microstructure evolutions in the interface to reach an optimum mechanical strength and corrosion resistance in the hybrid samples and across the interface area. This requires the understanding of the microstructural features formed during different heat-treatment processes and their subsequent effects on both mechanical and corrosion properties.

Methods

Specimens, hybrid additive manufacturing technique, heat treatment, and microstructure

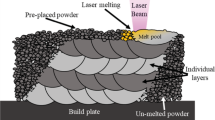
AISI 420 stainless steel (a commercial stainless steel from Uddeholm company) as a conventual material for the plastic injection molding was used as the substrate for the hybrid additive manufacturing process. CX stainless steel (CX SS) layers were deposited on top of the AISI 420 stainless steel (420 SS) using the L-PBF technique. These were cylindrically shaped components of CX stainless steel with dimensions of ɸ12 × 120 mm was deposited vertically on a rod-shaped AISI 420 substrate as shown in Fig. 18. The CX SS powder’s chemical composition and the chemical composition of the Uddeholm 420 SS are presented in¹⁹. 12.48 wt.% Cr, 8.40 wt.% Ni and 1.32 wt.% Al are three main alloying elements of CX SS powder that contain lower than 0.05 wt.% C. In addition, Uddeholm 420 SS contains 12.72 wt.% Cr, 1.26 wt.% Ni and about 0.25 wt.% C. In addition, Mo, Mn, Si, Al, and V with a lower than 0.5 wt.% content were detected in 420 SS samples. The value content of Mo was about 1. 46 wt.% in CX SS powders, and the content of other alloying elements was lower than 0.5 wt.%, similar to those detected in the 420 SS sample.

Fig. 18: Schematic representation of samples and heat-treated process.

a fabricated hybrid 420/CX SS samples, and b heat-treatment process applied after fabrication.

The L-PBF process was carried out using an EOS M290 system under an argon atmosphere. Using the EOS machine, CX SS cylinder parts with 12 mm diameter and 120 mm length were printed on the top of AISI 420 rods. The printing was conducted by a laser power of 258.7 W, and scanning speed of 1066.7 mm/s. The hatching distance, and layer thickness of powders were 100 μm and 30 μm, respectively. A 67° rotation of laser beam was perfumed between successive layers within the process. To reduce the residual stresses within the L-PBF process, the temperature of platform was kept at 80 °C. Moreover, a hybrid heat treatment process regarding the typical austenization and aging/tempering process for martensitic stainless steels was designed to optimize mechanical properties and the compatibility between 420 SS and CX SS¹⁹. Figure 18 shows a schematic of the heat treatment process, which was designed for the hybrid components.

Furthermore, the microstructural characterizations were performed on the specimens sectioned along building direction from the middle part of the hybrid samples, including the interface region (the red section shown in Fig. 18a). The microstructural features were studied by conducting transmission electron microscopy (TEM) and electron backscattered diffraction (EBSD) technique. Specimens were mechanically grinded and polished using colloidal solution of silica for the EBSD analyses. An EBSD (Hikari electron backscatter diffraction) system with TSL-OIM software embedded in a FEG-SEM was used to achieve the EBSD maps at ×2000 magnification with step sizes of 70 and 100 nm. The specimens were further prepared for TEM investigations using focused ion beam (FIB) milling. TEM observations were performed by an FEI Tecnai Osiris TEM and a EDS system by super-X energy-dispersive. In addition, XRD analysis was performed using a Bruker D8 diffractometer with Co-Kα radiation.

Electrochemical measurements

Samples for the electrochemical experiments were prepared from as-built and heat-treated hybrid components. To have a comparative estimation of electrochemical behavior, samples were also cut from CX SS part, 420 SS section, and the interface area of the hybrid components along the building direction at both the as-built and heat-treating states as presented in Fig. 19. The detailed naming of the samples is presented in Table 1.

Fig. 19: Specimens’ locations.

The location of samples cut from hybrid components for the electrochemical tests.

Table 1 Naming of the samples cut from different parts of the hybrid components.

An epoxy resin was used to mount samples with an exposed area from about 0.319 to 1 cm². Before any test, the samples were polished to have a fine surface and ultrasonically cleaned in ethanol. The electrochemical measurement was conducted using a typical three-electrodes cell of a Gamry potentiostat/galvanostat model reference 600+ at room temperature and at 2000 ppm NaCl solution. The reference electrode is a saturated silver chloride electrode (Ag/AgCl), a rod of graphite serves as the auxiliary electrode, and the samples’ surfaces serve as the working electrode in a cell with three-electrodes system. Before the electrochemical tests, open circuit potential (OCP) measurements were taken for each sample about 1 h to obtain stable OCPs. After reaching a stable OCP, potentiodynamic polarization experiments were performed at a scanning rate of 0.166 mV/s from 500 mV (versus. OCP) to maximum to around 1500 mV (vs. OCP). In addition, the Mott-Schottky plots were analyzed in a range potential from 1 V to 0 V (vs. Ag/AgCl) using a potential scan rate of 25 mV. For Mott-Schottky analyses a biased AC potential with 10 mV amplitude and 1 kHz frequency was applied.

EIS experiments were conducted using a perturbation with amplitude of ±10 mV (VS. OCP) and a span of frequency of 0.01 Hz–100 kHz. The fitting of the electrochemical models was performed by Z-view software on experimental results. The electrochemical results' reproducibility was tested at least three experiments after an immersion time of 48 h.

Electrochemical noise (EN) analyses

EN measurements in a zero-resistance ammeter (ZRA) mode were performed to evaluate simultaneously both current and voltage noise. To achieve an assessment of the possible galvanic coupling formed between the areas, including the interface of HAM components and the base part (420 SS), EN measurements were conducted so that two samples of the same surface area were taken, wherein one sample was a galvanic couple (sample taken from the area including the interface of the HAM component, shown in Fig. 18) and the other one was 420 SS sample with the same surface finish. The EN measurements were also performed by the Gamry Framework^TM software at the OCP condition. The EN samples were prepared similar to the other electrochemical tests conducted in this study. The total samples’ surface areas in contact with the solution was around 0.8 cm² in both states.

The electrochemical cell for the ZRA mode of EN measurements was composed of the interface area sample of the HAM component (HB samples) and 420 SS (S₁/H₁ samples) as the two working electrodes (WEs: WE₁ and WE₂) in both states and the saturated silver electrode (Ag/AgCl) as the reference electrode. Accordingly, the measurement of the Nosie potential was performed between the WEs and the reference electrode, and coupling noise current was recorded with a zero-resistance ammeter (ZRA) between the two WEs. In the ZRA mode, the WE connection was held at ground potential by the potentiostat conducting this experiment. If one WE is directly linked to the ground and the second WE is attached to the cable of the working electrode, two WEs are short-circuited together. Therefore, the potential was measured between the WEs and the reference electrode. Since WEs were shorted together, both of them are at the same potential. Figure 20 shows a real set-up as well as a schematic of the three-electrode method of EN measurement in ZRA mode. The data of EN were collected continuously in a 2000 ppm NaCl solution for 4 h at room temperature and at a sampling frequency of 4 Hz. In addition, a fast Fourier transform (FFT) method was applied to transform the time domine data of noise to the frequency domain.

Fig. 20: Measuring set-up for the electrochemical noise.

a real set-up, and b a scheme of the electrochemical noise set-up.

Data Analytics

The fluctuations were measured as electrochemical noise (EN) were generated by the electrochemical reactions occurred during the corrosion process without any external influence. Analyzing the EN data provides much information about the corrosion process. Many attempts were performed to achieve useful information from EN data²¹. Having obtained electrochemical potential noise (EPN), electrochemical current noise (ECN) versus time records with a large class of statistical methods analyzing the EN data can be used²¹.

The shape of transients of the ECN and EPN as the important aspects of the noise analysis are considered here. The electrochemical current and potential during the corrosion process are caused by electrochemical processes, which have a pure stochastic and chaotic character. Accordingly, the EPN and ECN transients are created due to a competition between releasing electrodes from the anodic process and consuming electrons from the cathodic reactions and the charge/discharge interaction of the electrode's surface interfacial capacitance^54,55. Current fluctuations referred to as the noise could be generated due to many electrochemical processes. The alloy surface's inhomogeneity could induce the formation of preferential zones to corrosion attacks resulting in local dissolutions or re-passivation after a short time. Consequently, a current transient is generated due to the release of additional free electrons from the metal surface, which is corroding within a short time. Also, the partial currents produced from the anodic and cathodic reactions lead to the current transients⁵⁶.

Metastable pitting and crevice corrosion can also display as potential and current transients. The current transients could be produced on each of the working electrodes and their directions could be in positive or negative directions depending on which electrode is affected by pitting if the true reference electrode is utilized for the noise measurements. However, due to the pit's anodic transient, which can polarize the two working electrodes' cathodic reaction, potential transient can always be towards the negative direction. Also, a matching should be established between every current transient and potential transient²¹.

The statistical analysis of the EN data could also provide useful information on the type of corrosion occurring. Statistical analysis could be performed by considering the position of the potential and current values or without their positions in the sequence of readings²¹.

The current and potential standard deviations (σ_v and σ_I) (the square root of the variance) are direct indications of the fluctuation’s amplitude related to the noise. They are by far the most common parameters used as the first step of the EN analysis for corrosion monitoring. Standard deviation is calculated by the following Eqs. (2) and (3)²¹:

$$\scriptsize\sigma _{I} = \sqrt {\mathop {\sum}\limits_{{{{\mathrm{n}}}} = 1}^{{{\mathrm{N}}}} {\frac{{\left( {{{{\mathrm{I}}}}\left( {{{\mathrm{n}}}} \right) - {{{\bar{\mathrm I}}}}} \right)^2}}{{{{{\mathrm{N}}}} - 1}}}}$$

(2)

$$\scriptsize \sigma _V = \sqrt {\mathop {\sum}\limits_{{{{\mathrm{n}}}} = 1}^{{{\mathrm{N}}}} {\frac{{\left( {{{{\mathrm{E}}}}\left( {{{\mathrm{n}}}} \right) - {{\bar{\mathrm{E}}}}} \right)^2}}{{{{{\mathrm{N}}}} - 1}}} }$$

(3)

where I(n) and E(n) are the n^th measurement of current and potential, respectively. ${{{\bar{\mathrm I}}}}$ and ${{{\bar{\mathrm E}}}}$ are the mean of current and potential measurements within the EN test, respectively, and N is the number of measurements.

The current standard deviation is divided by the potential standard deviation times the surface area of the specimen to obtain the electrochemical noise resistance, R_n⁵⁷:

$${{{\mathrm{R}}}}_{{{\mathrm{n}}}} = \frac{{\sigma_{V}\;{{{\mathrm{A}}}}}}{{\sigma_{I}}}$$

(4)

where σ_V and σ_I are potential and current’s standard deviations, respectively, and A is the sample's surface area. R_n and linear polarization resistance, R_p considered to be comparable in many studies. This may be described theoretically as well, with R_p being supposed to be the metal-solution interface’s response to the current of noise. Considering the equivalence of R_p and R_n, the relationship between the corrosion current density and R_n could be calculated by the Stern–Geary formula as follows²¹:

$${{{\mathrm{I}}}}_{{{{\mathrm{corr}}}}} = \frac{\beta }{{{{{\mathrm{R}}}}_{{{\mathrm{n}}}}}}$$

(5)

where I_corr is the corrosion current density and is β the Stern–Geary coefficient²¹.

Signals are formed up by data packets that deviate from a baseline in shot noise theory⁴⁹. As a result, current signals are made up of separate charge packets with short lifetimes, according to the shot noise theory⁴⁹. In the shot noise hypothesis, the number of charge carriers travelling through a given site is also a random variable. Each event in a stochastic process is assumed to be independent of the others. As a result, shot noise analysis is only useful for single events⁴⁹. Analysis of EN data by the shot noise theory results in obtaining three parameters as follows:

Q as the characteristic charge in each event, f_n as the frequency of these occurrences, and I_corr as the average of corrosion rate. The parameters are associated with each other as follows⁵⁸:

$$\begin{array}{*{20}{c}} {{{{\mathrm{q}}}} = \frac{{\sigma _{{{\mathrm{I}}}}\sigma _{{{\mathrm{V}}}}}}{{\beta {{{\mathrm{b}}}}}}} & {{{{\mathrm{q}}}} = \frac{{\sqrt {{{{\mathrm{PSD}}}}_I\,{{{\mathrm{PSD}}}}_V} }}{\beta }} \end{array}$$

(6)

$$\begin{array}{*{20}{c}} {{{{\mathrm{f}}}}_{{{\mathrm{n}}}} = \frac{{\beta ^2{{{\mathrm{b}}}}}}{{{{{\mathrm{\sigma }}}}_V^2}}} & {{{{\mathrm{f}}}}_{{{\mathrm{n}}}} = \frac{{\beta ^2}}{{{{{\mathrm{PSD}}}}_V{{{\mathrm{A}}}}}}} \end{array}$$

(7)

PSD_V and PSD_I denotes the values of the power spectral density (PSD) at low frequency associated to potential and current noise, respectively, in Eqs. (6) and (7). σ_I and σ_v are the current and potential standard deviations, β serves as the Stern-Geary coefficient, b is the measurement bandwidth, and the sample’s area surface is A. β value was taken from the Tafel slopes related to the anodic and cathodic reactions during the potentiodynamic polarization tests.

The working electrodes are also undergoing an anodic process with relatively big bursts of charge that are independent of each other and of short duration, based on the shot noise assumption. In these cases, the current on each working electrode follows a Poisson pattern²¹. By understanding the link between q (charge) and I_corr (current), it is also feasible to find the relationship between the average frequency of corrosion events, f_n (also known as the characteristic frequency), q, I_corr, and PSD_I^59,60. These relations are calculated by the Eqs. (8) and (9).

$${{{\mathrm{f}}}}_{{{\mathrm{n}}}} = \frac{{{{{\mathrm{I}}}}_{{{{\mathrm{corr}}}}}}}{{{{\mathrm{q}}}}}$$

(8)

$${{{\mathrm{PSD}}}}_I = 2{{{\mathrm{qI}}}}_{{{{\mathrm{corr}}}}} = 2{{{\mathrm{f}}}}_{{{\mathrm{n}}}}{{{\mathrm{q}}}}^2$$

(9)

The estimation of corrosion pitting could also be done using the parameter PSD_I. As a result, all PSD_I data were sorted from small to large, and the n / (N + 1) was used to calculate the cumulative probability, where n is the sorted list position and N is the total number of positions in the list⁴⁹. The extent of the pitting was established using f_n, and q for the specimens.

Extreme value analysis for pit growth

Gumbel, Aziz, and Shibata^61,62,63 used the extreme value analysis theory for having an estimation of the maximum depth of pit in a material. It was shown that the perdition of the deepest pitting attacks could be calculated using this method. As a result, the Gumbel distribution for maxima shows the depth of pit according to the extreme values^63,64. Therefore, the Gumbel distribution function in the present study is used to estimate the distribution of pit radius. F₁(x), which is the cumulative distribution function, could be represented by Eq. (10). If a random variable’s probability (variable considers as x) shows a maximum value distribution that is a doubly exponential and can be written as follows:

$${{{\mathrm{F}}}}_1\left( {{{\mathrm{x}}}} \right) = \exp \left( { - \exp \left( { - \frac{{\left( {{{{\mathrm{x}}}} - \mu } \right)}}{\alpha }} \right)} \right)$$

(10)

where μ (location parameter) denotes the mean and α (scale parameter) denotes the random variable’s standard deviation. These parameters describe the center and form of the probability distribution of the maximum metastable pit sizes, respectively^64,65.

This study used 12 sets of EN current data (each of them includes 1000 data points) recorded throughout 4 h of exposure to a corrosive environment. For estimation of charge, which passed within each current transient, the integral of the current signal with time was calculated for each set of data. This charge is linked to a single metastable pit's growth, and the physical volume of the pit (V_pit) may be estimated using Faraday's equation written as follows:

$${{{\mathrm{V}}}}_{{{{\mathrm{pit}}}}}\left( {{{{\mathrm{cm}}}}^3} \right) = \frac{{{{{\mathrm{Q}}}}\,{{{\mathrm{M}}}}_{{{\mathrm{m}}}}}}{{F{{{\mathrm{nD}}}}}}$$

(11)

where Q denotes the charge transmitted, M_m denotes the alloy's molecular mass, F denotes the Faraday constant, n denotes the number of electrons released in each anodic reaction, D denotes the alloy's density, and Vpit is the pit volume (cm³). Assuming hemispherical pits, the pit radius is estimated using the Eq. (12).

$${{{\mathrm{Radius}}}}_{{{{\mathrm{pit}}}}}\left( {{{{\mathrm{\mu m}}}}} \right) = \left( {\root {3} \of {{\frac{{3{{{\mathrm{V}}}}_{{{{\mathrm{pit}}}}}}}{{2{{{\mathrm{\pi }}}}}}}}} \right) \times 10^4$$

(12)

The integrated charges related to the biggest transient of current detected in every set of 1000 data were considered to compute the pit radius. The estimated pit radius extreme values were organized in a descending order. The cumulative probability, which is shown by F(Y), was approximated as the formula of 1− [M/(N+1)]. In the 1− [M/(N+1)], M shows the order of pit radius, which was ranked by extreme values, and the total number of the order of pit radius is shown as N. The reduced variant (Y) was estimated by the method Y = −ln{−ln[F(Y)]}^58,64,65. Finally, Eq. (13) was used to calculate the greatest predicted pit size (Pit_max)⁶⁶.

$${{{\mathrm{Pit}}}}_{\max } = \mu + \alpha {{{\mathrm{Ln}}}}\left( {{{\mathrm{J}}}} \right)$$

(13)

The exposed area is J, μ is the location and α is the scale parameters for the largest metastable pits’ distribution.

In the present study, J was considered to be 1. Then, for a given pit size (R_pit), the probability (P) is estimated as follows⁶⁶:

$${{{\mathrm{P}}}} = \exp \left( { - \exp \left( { - \left( {\frac{{{{{\mathrm{R}}}}_{{{{\mathrm{pit}}}}} - \left( {\mu + \alpha {{{\mathrm{Ln}}}}\left( {{{\mathrm{J}}}} \right)} \right)}}{\alpha }} \right)} \right)} \right)$$

(14)