Abstract
Most metals naturally corrode in an engineering environment and form corrosion products. The corrosion products can be either soluble or insoluble in the aqueous solution. The insoluble corrosion products (ICP) could have profound effects on the corrosion kinetics of the concerned metal. In this study, a multi-phase-field formulation is proposed to investigate the effects of ICP formation on pitting corrosion kinetics. The Gibbs free energy of the metal-electrolyte-insoluble corrosion product system consists of chemical, gradient, and electromigration free energy. The model is validated with experimental results and several representative cases are presented, including the effect of the porosity of ICP, under-deposit corrosion, corrosion of sensitized alloys, and microstructure-dependent pitting corrosion. It is observed that corrosion rate and pit morphology significantly depend on ICP and its porosity for the same applied potential.
Similar content being viewed by others
Introduction
Corrosion is a material degradation process that is difficult to avoid because most metallic materials have practical applications in corrosive environments. Most alloys, such as stainless steel and aluminum alloys, have a passive/protective film on their surface that protects them from corrosion. When this passive film is damaged, the metal is exposed to corrosive environments, which results in localized corrosion. Localized corrosion is one of the most dangerous forms of corrosion because of its difficulty of prediction and detection. In developed countries such as the USA and China, corrosion accounts for 3.4%1 and 3.34%,2 respectively, of the gross domestic product, which is much more than the cost of all natural disasters combined. To reduce this high cost, it is necessary to study corrosion behavior so that high strength materials can be designed to withstand extreme corrosive environments. Due to its significant impact on the economy, corrosion has been extensively studied, both experimentally and theoretically, in the past few decades. Pitting corrosion of a metal is usually considered to go through three major stages: pit nucleation, pit growth, and re-passivation through formation of insoluble corrosion products (ICPs). In this work, a multi-phase-field (MPF) model is developed for the prediction of pitting corrosion kinetics with ICP formation.
Several steady-state3,4,5,6,7 and transient-state8,9,10,11 numerical models have been developed over the years. In a notable early effort, Sharland and Taskeer5 presented a one-dimensional (1-D) steady-state numerical model based on the Nernst–Planck equations, in which they neglected the interfacial movement at the corrosion front. Later, with the development of numerical tools, several sharp-interface 2- and 3-D transient-state numerical models have been developed, which incorporate the interfacial movement. Some recent notable efforts that ignore the electromigration effect are Scheiner and Hellmich’s11,12 finite volume method (FVM) models, Duddu’s13 extended finite element method (XFEM), the Mai et al.14 phase field model, and Chen and Bobaru’s15 peridynamic modeling method. Here, it is worth mentioning that metal corrosion can be reaction-, migration- or diffusion-controlled depending on the applied potential and the chemistry of the electrolyte. Because these models ignore the effect of electromigration, they cannot capture a smooth transition from reaction- to diffusion-controlled regimes. Some notable numerical models that do incorporate the effects of electromigration are Laycock and White’s16 FEM model, the Sun et al.17 Arbitrary Lagrangian-Eulerian (ALE) model, and Duddu’s18 XFEM model. More recently, diffuse interface models, namely phase field (PF) models, for localized corrosion have been proposed, which incorporate the electromigration effect and thus have the ability to capture reaction-, migration-, and diffusion-controlled regimes. Xiao et al.19 proposed a PF model that shows good agreement with a so-called sharp-interface model. The major drawback of this model is its limitation to 1-D geometry problems, while PF models, in principle, should naturally extend to 2- and 3-D geometries without any changes in the formulation. Ansari et al.20 overcame this problem and proposed a PF model that showed good agreement with the experimental results in both 1- and 2-D cases. They also presented a set of examples to show the ability of their model to capture the effects of complex microstructures. More recently, Mai and Soghrati21 and Chadwick et al.22 proposed a similar PF models showing good agreement with experimental findings and have the ability to simulate complex microstructures. Tsuyuki et al.23 proposed a PF model that incorporates the pH effect on corrosion rate by considering pH-dependent interface mobility, where pH is approximated for each case by Corrosion Analyzer software. Their model qualitatively describes the overall phenomenon quite well but lacks any validation with experimental results, as identified by the authors.
Most of the numerical models ignore ICP formation completely or consider its effect implicitly.11,13,16,20,24 Experimental findings indicate the importance of ICPs and their effect on corrosion rate and the morphology of the pits.25 Some sharp-interface numerical models based on the ALE method have been presented, which do consider ICP formation.17,26,27 Yin et al.27 studied the formation of corrosion products and their effects on corrosion rate and corroding surface morphology using the ALE method. In a later study, wang et al.26 extended their previous ALE-based formulation and studied the steric hindrance effect of corrosion product on corrosion kinetics. They found that corrosion rate significantly decreases with the formation of corrosion product on corroding surface by limiting the flow of ions through this new phase. ALE uses a moving mesh technique, which not only increases the computation cost and implementation complexity for non-uniform evolving geometries but also introduces additional errors due to the need of adjusting the conforming mesh at each time step. As described by the authors,17 even for a 2-D geometry the mesh quality decreases with time and each simulation needs to be paused multiple times (based on mesh quality criteria) followed by an approximate re-drawing of the domain (and re-meshing) based on the geometry obtained in the previous time step. PF models introduce a diffusive interface rather than using a sharp one, which makes the mathematical functions continuous at the interface. The diffusive interface is represented by dimensionless monotonously varying time-dependent variables which evolve due to the free energy minimization of the system. Therefore, there is no need to track the interface explicitly at each time step. This makes PF models numerically more stable and hence can easily be used to simulate complex 3-D evolving geometries. To the best of our knowledge, no PF model in the literature explicitly considers the formation of ICP as a new phase, or studies its effects on corrosion. Here we present an MPF model that considers ICP formation explicitly.
The remainder of this paper is as follows. In the Results and discussion section, the electrochemical reactions and schematics of the process are described. The proposed MPF model is solved numerically for 1-D, 2-D, and 3-D cases. The results are compared with experimental findings and discussed in detail. Several examples are also presented to demonstrate the corrosion kinetics for different complex corrosion processes. In the Method section, the MPF model derivation is detailed for the metal–electrolyte–ICP system by defining the Gibbs free energy of the system, which consists of chemical, migration, and gradient free energy. The evolution of the order parameters is derived from rate theory. The evolution of ionic concentration is governed by the Nernst–Planck equation, which consists of diffusion, migration, and reaction terms, while the electrostatic potential distribution is governed by the Poisson equation.
Results and discussion
Electrochemical reactions
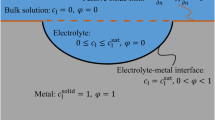
The system studied consists of iron in dilute salt water (Fig. 1). In this work, the following electrochemical reactions and kinetics are considered. During metal corrosion, the metal acts as anode and is oxidized, thus lose electrons.
Another mechanism, proposed by Bockris et al.,28 is widely adopted in the literature to describe metal oxidation in aqueous environments. This metal oxidation mechanism incorporates the effect of OH− and H+ ions (pH variation) on the corrosion rate and pit morphology. The mechanism is as follows:
where subscripts (s), (aq) and (ads) represent solid, aqueous and adsorbed phases, respectively. In this mechanism, iron atoms react with hydroxide ions and form adsorbed iron hydroxide, which then oxidizes to form iron ions (Fe+2) through a one-electron transfer step. In this work, reactions (2 to 4) are considered for metal oxidation. During pitting corrosion, several corrosion products may form such as FeCl2, Fe(OH)2 and Fe(OH)3.
where subscript (ppt) in the above reactions represents precipitate. According to the Pourbaix diagram of iron, among these corrosion products only Fe(OH)3 is a stable compound for an electrolyte having a pH value in the range (2–14). Its stability also depends on the applied potential and is usually more stable at higher potentials. In this study, Fe(OH)3 is considered as a stable ICP that limits the flow of ions diffusing from the metal surface into the electrolyte and in turn slows down the metal corrosion. It is also possible to add cathodic reactions when cathode becomes rate-limiting electrode. This addition is straightforward and has been detailed in the Appendix C of our previous work.29 The MPF model formulation is detailed in the Methods section. To numerically solve the MPF model, the boundary conditions and initial values for all 1-D, 2-D, and 3-D geometries are given in the Supplementary Note 2 and Fig. S1.
One-dimensional MPF model
First, the proposed MPF model is compared with experimental results.30 ICP formation is not considered for this case. The experimental data30 were obtained from trials conducted at Swansea Public Wharf (SPW) for mild steel. The parameters given in the experimental report,30 specifically temperature, pH, salinity, and electrolyte conductivity, are 18.7 °C, 8.2, 32 g/kg (0.55 mol/L NaCl), and 4.7 S/m, respectively. An applied potential of −200 mV vs saturated calomel electrode (SCE) is used in this case. Figure 2a shows that overall the simulation results agree well with the experimental results. It seems that the initial corrosion rate predicted by the 1-D MPF model is slightly lower than the experimental values, but later the two slopes meet (after 12 days of corrosion) and then the MPF model tends to overestimate the corrosion rate. Because the molar concentration of metal ions close to the interface is well below the saturation limit, as shown in Fig. 2b, the process is far away from diffusion- or migration-controlled kinetics. The linear relation in Fig. 2a shows that the process is reaction-controlled. The gradual decrease in the slope in the experiments might be due to the formation of ICPs, which usually limit the flow of ions and make the process diffusion-controlled. This phenomenon can be better described by incorporating ICP formation in the model. Because the thickness of the corrosion product on the corroding surface and the metal ion concentration are not available in the experimental data, it is difficult to quantitatively compare the experimental results with our 1-D MPF model while incorporating ICP formation. It should also be noted that non-uniform corrosion rate in the experiment may also have been due to several other factors, namely electrolyte flow and the small amounts of sulfate, nitrate, ammonia, phosphorus, and calcium in the sea water of SPW, which are assumed in the model to have no effect on the corrosion rate, an assumption that might not be true in general. The effect of variation in the applied potential in 1-D model with ICP is studied in the following section. The applied potential variation effect on corrosion without ICP formation is not studied in this work. Readers are referred to our previous PF work where the effect of the variation of applied potential is studied in detail including a comparison with the experimental results.20 In this work, we focus on the evolution of ICP and its role in corrosion kinetics.
a Corrosion loss (μm) of mild steel in SPW experiments30 (blue diamonds) and results of 1-D MPF model (black) against time (days). b Metal ion concentration (mol/L) at the metal–electrolyte interface plotted with phase fractions
Now, the 1-D MPF model is used to simulate an ICP phase between the electrolyte and the metal. Figure 3a shows that the corroded length increases linearly with time at low applied potentials (−100 and −50 mV vs SCE) over the range examined in this study. The linear relation suggests that the process is reaction-controlled at these two low potentials, even in the presence of a small ICP phase between metal and electrolyte. This linear relation can be understood through inspection of Fig. 3c, which shows that the metal ion concentration at the metal–ICP interface is still significantly smaller than the saturation value. From this information, one can safely deduce that the electrochemical reaction at these two low applied potentials is slower than the diffusion process and hence the process is reaction-controlled. As the applied potential is increased further, the relation between corroded length and time becomes non-linear at 0 mV and 50 mV vs SCE. Because both migration- and diffusion-controlled kinetics are non-linear, we must inspect the metal ion concentration at the metal–ICP interface to interpret whether the process is migration- or diffusion-controlled. For the case of 0 mV vs SCE, Fig. 3c shows that the metal ion concentration at the interface is very high, but still less than the saturation concentration. Therefore, the process is migration-controlled throughout the given simulation time, although it might become diffusion-controlled later. For 50 mV vs SCE, the metal ion concentration reaches the saturation value at the metal–ICP interface very quickly and hence the process becomes diffusion-controlled.
If the applied potential is increased further, assuming all other conditions and parameters are kept the same, the plot of corroded length versus time will remain similar to that at 50 mV vs SCE because the process has already become diffusion-controlled. Note that the results in Fig. 3a–c are obtained for a porosity (εp) of 0.05, as given in Table S1. This value corresponds to a diffusion coefficient of 1.12 × 10−11 m2/s inside the ICP, obtained by solving Eq. (28). Together with the applied potential, the porosity is one of the key parameters that control the corrosion process. To better understand the role of these two parameters, the porosity is varied for a fixed applied potential of 50 mV vs SCE. This applied potential is chosen because for a porosity value of 0.05, the process is already diffusion-controlled. Four cases are investigated for porosity values of 0.05, 0.1, 0.2, and 0.3, respectively. Note that the increase in porosity results in an increase in diffusion coefficient in the ICP, as can be seen in Fig. 4d. The corroded length shows a non-linear relation versus time for a porosity value of 0.05, indicating a diffusion-controlled corrosion process. However, as the porosity is increased this relation approaches linearity and eventually becomes linear at a porosity of 0.3, as shown in Fig. 4a. This suggests that the process becomes reaction-controlled for an applied potential of 50 mV vs SCE if the ICP phase is sufficiently porous (εp = 0.3). The corroded length at 50 mV vs SCE differs significantly between the porosity values of 0.05 and 0.3, signifying the importance of the porosity of ICPs in corrosion rate estimation. Figure 4c shows that with the increase in porosity of ICP, the metal ion concentration at the metal–ICP interface decreases from the saturation value at a porosity of 0.05, which also suggests the transition from diffusion- to reaction-controlled corrosion. The process can be either reaction- or diffusion-controlled for the same value of applied potential depending on the porosity of the ICP medium. Note that the ICP thickness increase significantly with the increase in porosity value. This suggests that the effective volume of the more porous ICP (εp = 0.3) is significantly higher than the other cases. It is also possible to develop correlations based on the corrosion kinetics for each case. If the metal corrosion does not slowdown with time, then the corrosion process is controlled by reaction and is known as linear kinetics.31 The corroded length in that case can be approximated by a linear relation, \({\rm{corroded}}\,{\mathrm{length}} = K_{\mathrm{L}} \times {\mathrm{time}}\), where KL is the linearity factor. The simulation results of Fig. 4a show that the corrosion length has a linear relationship with time for εp = 0.3 and KL = 0.11. When metal corrosion slows down with time, then the process is considered as transport controlled. In transport controlled processes, if the controlling mechanism is by diffusion, the corrosion length and time can be approximated by a parabolic relation of the form, \(({\mathrm{corroded}}\,{\mathrm{length}})^2 = K_{\mathrm{p}} \times {\mathrm{time}}\)31 where Kp is the parabolic rate constant. It seems that the corrosion process is diffusion controlled for εp = 0.05. This case follows parabolic kinetics with Kp = 0.30. This effect will be studied in more detail later for a 2-D geometry.
Two-dimensional MPF model
In this section, a 2-D geometry is simulated for two different cases: metal corrosion with and without ICP formation. First, the MPF model is used to study metal corrosion without ICP formation. Figure 5a shows the geometry of the 2-D case under study, where the metal surface is largely covered by a passive film (black) with a narrow opening of 4 μm at the metal surface. The simulations are carried out at an applied potential of 0 mV vs SCE. Because the corrosion process is symmetric about the center of the pit along the vertical axis, only half of the geometry is simulated to save computation time. Figure 5b shows that the initial flat metal surface exposed to the electrolyte eventually evolves into a pit. This pit morphology reflects the fact that the ions can only diffuse through the narrow opening, which results in the corrosion rate being highest along the opening. The diffusion pathway is constrained by the protective effect of the passive film, which results in a significantly higher metal ion concentration (mol/L) inside the pit than outside the pit, as shown in Fig. 5c. The value of the corresponding electrostatic potential (mV) in the electrolyte is shown in Fig. 5d. Note that if the surface of the metal have no passive film, it would keep its flat shape during corrosion.
2-D simulation of pitting corrosion at an applied potential of 0 mV vs SCE (a) the initial geometry of the simulation, (b) the evolution of the dimensionless order parameter (η1). c shows the corresponding molar concentration (mol/L) distribution of metal ions (Fe+2). d shows the electrostatic potential (mV) distribution, where gray color shows the metal part
To understand the role of ICPs in corrosion kinetics, we next study the case of corrosion with ICP formation. Figure 6b, c shows the evolution of the dimensionless order parameter η1 over time. It can be seen that the pit is significantly shallower in the presence of ICP as compared to that obtained in Fig. 5b. This decrease in pit depth, which indicates a lower corrosion rate, as shown in Fig S2, occurs because the metal ions have to diffuse through the ICP, which has a far lower diffusivity than the electrolyte. Figure 6d–f shows the evolution of the ICP over time, while Fig. 6j–l shows the pH of the solution at different times. The pH is low inside the ICP and gradually increases away from the ICP to achieve the pH value of 6 in the bulk electrolyte. This low pH (or high H+ ion concentration) is due to the formation of H+ ions as a result of Eq. (7). Such low pH values are usually an indicator of active pits, buried under the ICPs, and have also been reported in experimental studies.25 Figure 6m–o shows the evolution of the electrostatic potential in the electrolyte. It can be seen that the electrostatic potential is relatively high inside the ICP and gradually decreases in the bulk solution. The high electrostatic potential is due to slow ionic diffusion through the ICP, which results in the accumulation of metal ions close to the surface of the pit. Note that this study does not consider the microstructural effects of the ICP phase, which may result in non-uniform morphology of the corroded metal. It should also be noted that a tiny initial ICP seed is simply placed at the interface between metal and electrolyte in this work. It is possible to include the nucleation of ICP in the model but it requires special treatment. Nucleation of new phases in PF models has been dealt with using different methods. For example, one method is based on thermal fluctuation of the system, in which a Langivin random noise term is added in the dynamic equations for long range order parameters (for example, the dynamic equation for η3 in this work). This noise term satisfies the Gaussian distribution and meets the requirement of the fluctuation-dissipation theorem.32 We have used this technique in modeling hydride nucleation in zirconium alloys.33 In this work, our main effort is to develop multi-phase-field modal for ICP evolution. In addition, the location for new phase nucleation is very limited within a small interface area where passive film is damaged.
2-D MPF model results of pitting with insoluble corrosion product (ICP) formation at an applied potential of 0 mV vs SCE. a Initial geometry of the problem under study. b, c show the evolution of metal atom distribution. d–f show the evolution of ICP. g–i show the metal ion concentration (mol/L). j–l show the pH variation in the electrolyte and ICP. m–o show the corresponding electrostatic potential (mV)
The effects of porosity of ICP on pitting corrosion and ICP morphology are studied using 2-D geometry. The geometry of the problem under study is shown in Fig. 7a. The initial thickness of ICP medium is 3 μm. Two cases of porosity values 0.05 and 0.3 are studied to observe the difference in ICP morphology. The applied potential is kept at 50 mV vs SCE for both cases. Figure 7b, c shows that the morphology of ICP phase after a simulation time of 50 s is significantly different for the two cases. The size of ICP phase for a porosity of 0.3 is much higher than the case of 0.05 due to two reasons. First, more metal is corroded which results in higher ICP formation. The second reason is the increase in effective molar volume of ICP phase with the increase in porosity. The relation of porosity with effective volume variation is described in Supplementary Note 3. A video (M1) comparing these two cases for a total simulation time of 50 s is also available in Supplementary Material, showing the evolution of all three phases (metal, electrolyte, and ICP) for two different porosity values as labeled in the video.
Corrosion in sensitized alloys
The sensitization of alloys is the increase in sensitivity of the grain boundaries after heat treatment for a specific period of time. Sensitized alloys such as stainless steel34 and aluminum alloys35 are more vulnerable than un-sensitized samples to corrosion along the grain boundaries at relatively low potentials. This phenomenon is known as intergranular corrosion (IGC) and has been studied for several decades.34,35,36 The degree of sensitization (DOS) for a steel alloy depends on the carbon content, time, and temperature of heat treatment. The DOS can be approximated from the time–temperature–transformation (TTT) curve for each alloy. In sensitized stainless steel (SS316), IGC is believed to result from the depletion of chromium element content along the grain boundaries, which can be reduced from 18% in the grains to just 11% along the grain boundaries, when heat-treated for 300 h at 700 °C.34 Experimental findings show that the corrosion potential in sensitized alloys along the grain boundaries can be 200–250 mV lower than inside the grains.35 In sensitized alloys the grain boundaries act as anodes; therefore, the alloy corrodes along the grain boundaries when exposed to a corrosive environment.
To study this process in detail, the MPF model is used to simulate IGC in 3-D. As shown in Fig. 8a, the grains, sensitized grain boundaries, and electrolyte in the 3-D geometry are represented in red, gray, and blue, respectively. Figure 8c is an optical micrograph of the etched surface of sensitized SS304. The sample was sensitized along the grain boundaries by a 10-h heat treatment at 850 °C. This heat-treated SS304 was then etched in strong acidic electrolyte. A small rectangular area marked in Fig. 8c is sketched and extruded in 3-D, as shown in Fig. 8b. The grains and sensitized grain boundaries are represented by two different order parameters, ηg and ηgb, respectively. These order parameters follow the reaction kinetics described in Eq. (20), with different ψa. ψa is a function of EΘ, and is considered to be 200 mV lower along sensitized grain boundaries, on the basis of experimental findings.35 For the sake of simplicity, it is assumed that no ICP will form during this process. Figure 8d–f shows the evolution of ηg (red), η2 (blue), and ηgb (gray) in each case at different times. Similarly, Fig. 8g–i shows the evolution of the grains and sensitized grain boundaries with time. The electrolyte is hidden from Fig. 8g–i to better illustrate the evolution of the corroding surface, which is not visible in Fig. 8d–f. It can be seen that the grain boundary phase corrodes much faster than the grain phase. In fact, the grain shows almost no corrosion during this short time, consistent with the etching experiment. Animations of these two cases, M2 and M3, are also available as Supplementary Material to better visualize the evolution of the grains and sensitized grain boundaries in a corrosive electrolyte. It should be noted that the grains in these simulations are not considered as cathodic or inert (non-corrodible), but instead are anodic, and corrode at a relatively slower rate. In reality, grains do corrode when the applied potential is above the corrosion potential, but at a significantly lower rate than the sensitized grain boundaries. In open circuit situation, the sensitized grain boundary and grain interior can form galvanic corrosion cells, with sensitized grain boundary region as the anode and grain interior as the cathode. In this case, both anodic reactions and cathodic reactions can be included in the current model using the method given in Appendix C of our published work.29
3-D MPF model simulations of IGC in a sensitized alloy at an applied potential of −150 mV vs SCE. a shows the geometry of the model with three distinct phases, grain matrix (red), sensitized zone (gray), and electrolyte (blue). b shows the corroding surface morphology (without electrolyte). c Optical micrograph of sensitized SS304 with an etched surface. d–f show the evolution of all phases (grain, grain boundaries, and electrolyte) in transparent mode at 3, 6, and 9, respectively. g–i show the evolution of grains (red) and grain boundaries (gray) at 3, 6, and 9 s, respectively
Under-deposit corrosion
Sometimes, active pits are buried under the deposits and stay undetected for longer periods, leading to catastrophic failures. These deposits may consist of corrosion products (metal oxide/hydroxide) or can be a combination of corrosion products, carbonates, bi-carbonates, and/or sea sand.37 Such deposits are usually found in pipe lines in the oil industry, where insufficient flow of electrolyte leads to deposition of these materials over the active pits. The real problem is that the pits can stay active below these deposits, usually with lower corrosion rates, which makes them difficult to identify with normal inspection procedures. Several studies, both experimental and numerical, have been reported over the years, unmasking some key factors of this phenomenon.37,38,39 To the best of our knowledge, there is still no PF model that can explicitly study the role of deposits in corrosion. To address this, we use our MPF model to illustrate this phenomenon numerically.
The geometry of the problem simulated in this case is shown in Fig. 9a. The metal is buried under a quarter-circular ICP with a radius of 6 μm. In this case, we assume that the deposit layer consists only of Fe(OH)3 and will follow the reaction kinetics of Eq. (7). The results in Fig. 9b, c show that the metal corrodes under the deposit at a significantly slower rate than shown in Fig. 5b. The metal corrosion is limited by the slow diffusion of metal ions through the deposit. This effect can also be seen in Fig. 9g–i where the metal ion concentration is much higher at the metal–deposit interface than in the bulk electrolyte or even at the deposit–electrolyte interface. This also illustrates that the corrosion becomes diffusion-controlled in the presence of a deposit layer. Figure 9j–l shows the pH value at 0, 100, and 300 s, respectively. It can be seen that the pH of the solution is very high at the metal–deposit interface and gradually decreases away from the interface. Note that the pH within the deposit layer is below zero, indicating that the pit under the deposit layer is still active. Such low values of pH are often reported in experimental studies of active pits under a deposit layer.25 Indeed, pH measurement is one criterion used in industry to determine if a pit is still active under a rust or deposit layer.
2-D MPF model results for under-deposit corrosion kinetics at an applied potential of 0 mV vs SCE. a Schematics of the problem under study. b, c show the evolution of metal atom concentration at 100 and 200 s, respectively. d–f show the evolution of the deposit. g–i show the metal ion concentration (mol/L). j–l show the pH of the system
Microstructure-dependent corrosion
Experimental studies show that pit initiation and growth strongly depend on microstructural features such as grain shapes, secondary phase particles, inclusions, flaws, dislocations, mechanical damage, and crystallographic orientations.40 It is important to study these features in detail to understand the reasons for the formation of pits with irregular shapes. The MPF formulation provides the opportunity to study microstructural and electrolyte effects together. Note that all of the above microstructural effects can be included in the MPF model if the relevant reaction kinetics are known. In the following example, for the sake of simplicity we only consider the effect of crystallographic orientations on corrosion. Most alloys, such as stainless steel, aluminum alloys, and even pure iron, show crystallographic orientation-dependent corrosion.41,42 Several studies suggest that the corrosion rate along the three principal orientations in stainless steel varies in the order of [111] < [110] < [100].41 In the extreme cases, the corrosion potential can vary by 5–10% between the [111] and [100] planes.43 In our example, the MPF model is used to study crystallographic orientation-dependent corrosion. Three principal planes, [111], [110], and [100], are represented by three different order parameters, ηa, ηb, and ηc, respectively. The phase evolution of all three order parameters is governed by Eq. (20), where ψa is a function of crystallographic orientation. Relative to the [111] plane, the corrosion potential is assumed to be 5% lower for [110] and 10% lower for [100]. A lower corrosion potential corresponds to an increase in corrosion rate, given that the applied potential is unchanged. The labels in Fig. 10a schematically show the crystal plane in each grain that is assumed to face the electrolyte. The evolution of the pit over time is shown in Fig. 10b–d. It can be seen that the pit loses its semi-circular shape when the electrolyte approaches the [100] plane and corrodes faster on this plane. The difference in corrosion rate for different orientations results in a non-uniform pit shape. This example illustrates the ability of the MPF model to handle complex phenomena. The MPF model developed in this work provides a generalized formulation in which various effects, each with their own reaction kinetics, can be explicitly incorporated as a new phase or order parameter, enabling us to study the role of multiple effects together and to identify the dominant effect.
Methods
Multi-phase-field formulation
A MPF model for corrosion is formulated in this section. Most PF models introduce two dimensionless parameters, also known as order parameters, which vary from non-zero values to zero within a finite interface, to describe two different physical states (e.g. metal–electrolyte). Because ICP formation is also considered explicitly in this work, three order parameters, η1, η2, and η3, are introduced which represent metal, electrolyte, and ICP, respectively. The binary interphases involved in the process are outlined in Fig. 11. The temporal evolution of the order parameters describes the evolution of metal–electrolyte, metal–ICP, and ICP–electrolyte binary interfaces during the process. The molar concentration of species i is expressed by Ci (i = Fe, Fe(OH)3, Fe+2, Cl−, Na+, OH−, H+, and FeOH+). Note that the normalized molar concentrations of Fe atoms and the Fe(OH)3 product are represented in the Results and discussion section by the order parameters η1 = CFe/CFe,o and η3 = CFe(OH)3/C Fe(OH)3,o, where CFe,o and CFe(OH)3,o are the molar concentrations of Fe and Fe(OH)3, respectively, in their bulk phases. The ionic molar concentrations are also normalized as ci = Ci/CFe,o, where ci is the normalized molar concentration for ionic species i.
The driving force for metal corrosion and ICP formation is the minimization of the Gibbs free energy of the system. The Gibbs free energy is a summation of chemical, gradient (interfacial), and electrostatic free energy and is expressed as
The first term in Eq. (8) is the chemical free energy density and Ci is the concentration of the ionic species i in the electrolyte. This chemical free energy density is given by
where f0 is a fourth order Landau polynomial of the order parameters (ηk) and is given by44
where N is the number of order parameters. The PF parameters m and γk,j are related to the surface energy σk and width of the diffuse interface l. The second term in Eq. (9) is the free energy of the electrolyte, where R and T are the gas constant and absolute temperature, respectively. The last term in Eq. (9) is the free energy of the system at the reference state, where \(\mu _i^\Theta\) is the chemical potential. The second term in Eq. (8) corresponds to the gradient energy density
where κ(η) is the gradient energy coefficient related to the interface surface energy. The last term in Eq. (8)
corresponds to the electrostatic free energy density, where φ is the electrostatic potential and ρe is the electric charge density,
where F is Faraday’s constant and zi is the valence of the ionic species.
The net rate (Rnet) of any chemical reaction is the difference of the forward and backward reactions. Rnet, which describes the reaction kinetics while satisfying the detailed balance of the system, can be expressed as45
where the first and second term on the right side of Eq. (14) are the forward and backward reactions, respectively. \(\mu _{\mathrm {TS}}^{\mathrm {ex}}\) is the excess chemical potential at the transition state while μ1 and μ2 are the chemical potential at the initial and final state, respectively. The equilibrium constants for the forward \(\left( {r_0^ \to } \right)\) and backward \(\left( {r_0^ \leftarrow } \right)\) reaction are equal \(\left( {r_0 = r_0^ \to = r_0^ \leftarrow } \right)\) for appropriately defined μ.45 We consider the order parameters to evolve according to the electrochemical reaction rate (Rnet) following the work of Chen et al.46 The readers are referred to the original article for more details.46 The above relation Eq. (14) can be described in terms of thermodynamic driving force (Δμ = μ2 − μ1) as
where α is the charge transfer coefficient (or symmetry factor) and Δμk is the thermodynamic force, given by
where ψk is the total overpotential, which is given by ψk = ψa,k + ψc,k. Here, ψa,k and ψc,k represent the activation and concentration overpotential, respectively. The activation potential can be defined as
where E is the applied potential on the electrode, EΘ is the standard electrode potential. The reaction affinity ai of a species is given by45
where
is the mixing free energy density relative to the reference state.45 The derivation of the evolution of order parameters is detailed in Supplementary Note 1. Here, we provide the derived temporal evolution equations for the order parameters η1 (metal atom evolution) and η3 (ICP formation),
where Lσ, Lψ1, and Lψ3 are the kinetic interface constants. ai, \(i = \left\{ {{\mathrm {Fe}^{ + 2},\mathrm {H}^ {+} ,\mathrm {OH}^ {-}} } \right\}\), is the activity of the ionic species i and can be expressed as \(a_i = \chi _ic_i\), where χi is the activity coefficient. Because the electrochemical reactions are localized on the binary interfaces, the second terms in Eqs. (20) and (21) are multiplied by λ1 and λ3, respectively. In classical PF formulations, a polynomial function of the form 6η−6η2 is used, which is non-zero only at the interface. This polynomial function is limited to two-phase PF models and hence cannot be used in our formulation. Here, λ1 and λ3 are given by
where Hk (k = 1, 2, 3) represents the phase fraction, which is a function of the order parameters ηk. The phase fractions are given by44
where N is the number of phases. Metal dissolution increases the metal ion concentration at the corroding surface. When the metal ion concentration reaches the saturation value at the corroding surface, corrosion cannot continue unless the saturated metal ions at the interface diffuse into the bulk electrolyte. In order to limit the reaction rate at saturation concentration, a simple criterion is devised. \(S_c = 1 - c_{\mathrm {Fe}^{ + 2}}/c_{\mathrm {sat,Fe}^{ + 2}}\), the saturation factor, is multiplied by the second term in Eq. (20), where csat,Fe+2 is the normalized saturation concentration of Fe+2 in salt water. Similar non-linear kinetic formulations have been adopted in a number of non-linear PF models (but not multi-phase models) for electrodeposition processes.46,47,48 The numerical examples presented in the Results and discussion section show that this MPF model produces good quantitative agreement with the experimental findings.
Evolution of ionic concentration
The time-dependent evolution of the molar concentration distribution of ionic species in the electrolyte is governed by the classical Nernst–Planck equation. It comprise the diffusion of ions due to the concentration gradient, migration of ions due to the electrostatic force, and source/sink terms.
where i = [Fe+2, Cl−, Na+, OH−, H+, and FeOH+], Dieff is the effective diffusion coefficient of species i, which is given by
where superscript m, e, and ICP on Di represent metal, electrolyte, and ICP phases, respectively. The diffusivity of all of the ionic species in the metal phase is assumed to be zero. The ICP phase is considered as porous. Therefore, the diffusion coefficient of ionic species in the ICP phase is assumed to follow the Bruggeman relation.39,49
where εp is the porosity of the corrosion product. Note that the Bruggeman relation has limited validity when structural effects of the porous material are important. However, because this work does not take into account the structural effects of the ICP, the Bruggeman relation can be safely used.49 Ri in Eq. (26) is the rate of consumption/production of species i in the electrolyte. The production of Fe2+ as a result of metal corrosion in Eqs. (2–4) and its consumption as a result of ICP formation in Eq. (7) is given by
where Rprod and Rcons are given by \(- \partial \eta _1/\partial t\) and \(\left( {C_{{\mathrm{Fe}}\left( {{\mathrm{OH}}} \right)_3,{\mathrm o}}/C_{\mathrm {Fe,o}}} \right)\partial \eta _3/\partial t\), respectively. Bulk molarity of ICP \(C_{{\mathrm{Fe}}\left( {{\mathrm{OH}}} \right)_3,{\mathrm {o}}}\)is a function of porosity and this relation is detailed in Supplementary Note 3. Similarly, H+ ion production as a result of (7) is given by
The molar concentration distribution of the remaining ionic species in the electrolyte is considered to vary according to the electrostatic potential to keep the solution neutral. The electrostatic potential distribution in the electrolyte and ICP is governed by the Poisson relation,
where σeff is the effective electronic conductivity, which depends on the phase fractions and is expressed as \(\sigma ^{\mathrm {eff}} = \sigma _{\mathrm e}{\mathrm H_2} + \sigma _{{\mathrm {ICP}}}{\mathrm H_3}\) . σe and σICP are the conductivities in electrolyte and ICP phase, respectively. IR is the current density, related to the reaction rate by
where n1 = 2 and n2 = 1 are the number of electrons transferred as a result of metal corrosion and ICP formation reactions. Note that these source current density terms are non-zero only at the binary interfaces; thus, it is an implied flux boundary condition incorporated in the governing equation at the diffuse interfaces.
The governing Eqs. (20–22), (26) and (31) are solved by a finite element method. The standard Galerkin50 formulation is used to discretize the space, and the backward differentiation formula (BDF) method,51 due to its inherent stability, is used for the time integration of the governing equations. Uniform grid points are used in the 1-D models, while in the 2-D and 3-D cases, triangular and tetrahedral Lagrangian mesh elements, respectively, are used to discretize the space.
Data availability
All data generated or analyzed during this study are included in this article (and its Supplementary Information Files).
References
Koch, G. et al. International measures of prevention, application, and economics of corrosion technologies study. NACE International IMPACT Report (NACE International, Houston, Texas, USA, 2016).
Hou, B. et al. The cost of corrosion in China. npj Mater. Degrad. 1, 4 (2017).
Galvele, J. R. Transport processes and the mechanism of pitting of metals J. Electrochem. Soc. 123, 464–474 (1976).
Galvele, J. Transport processes in passivity breakdown—II. Full hydrolysis of the metal ions. Corros. Sci. 21, 551–579 (1981).
Sharland, S. M. & Tasker, P. W. A mathematical model of crevice and pitting corrosion—I. The physical model. Corros. Sci. 28, 603–620 (1988).
Walton, J. C. Mathematical modeling of mass transport and chemical reaction in crevice and pitting corrosion. Corros. Sci. 30, 915–928 (1990).
Abodi, L. et al. Modeling localized aluminum alloy corrosion in chloride solutions under non-equilibrium conditions: steps toward understanding pitting initiation. Electrochim. Acta 63, 169–178 (2012).
Oldfield, J. W. & Sutton, W. H. Crevice corrosion of stainless steels: I. A mathematical model. Br. Corros. J. 13, 13–22 (1978).
Watson, M. K. & Postlethwaite, J. Numerical simulation of crevice corrosion: the effect of the crevice gap profile. Corros. Sci. 32, 1253–1262 (1991).
Friedly, J. C. & Rubin, J. Solute transport with multiple equilibrium-controlled or kinetically controlled chemical reactions. Water Resour. Res. 28, 1935–1953 (1992).
Scheiner, S. & Hellmich, C. Stable pitting corrosion of stainless steel as diffusion-controlled dissolution process with a sharp moving electrode boundary. Corros. Sci. 49, 319–346 (2007).
Scheiner, S. & Hellmich, C. Finite Volume model for diffusion- and activation-controlled pitting corrosion of stainless steel. Comput. Methods Appl. Mech. Eng. 198, 2898–2910 (2009).
Duddu, R. Numerical modeling of corrosion pit propagation using the combined extended finite element and level set method. Comput. Mech. 54, 613–627 (2014).
Mai, W., Soghrati, S. & Buchheit, R. G. A phase field model for simulating the pitting corrosion. Corros. Sci. 110, 157–166 (2016).
Chen, Z. & Bobaru, F. Peridynamic modeling of pitting corrosion damage. J. Mech. Phys. Solids 78, 352–381 (2015).
Laycock, N. & White, S. Computer simulation of single pit propagation in stainless steel under potentiostatic control. J. Electrochem. Soc. 148, B264–B275 (2001).
Sun, W., Wang, L., Wu, T. & Liu, G. An arbitrary Lagrangian–Eulerian model for modelling the time-dependent evolution of crevice corrosion. Corros. Sci. 78, 233–243 (2014).
Duddu, R., Kota, N. & Qidwai, S. M. An extended finite element method based approach for modeling crevice and pitting corrosion. J. Appl. Mech. 83, 081003 (2016).
Xiao, Z., Hu, S., Luo, J., Shi, S. & Henager, C. A quantitative phase-field model for crevice corrosion. Comput. Mater. Sci. 149, 37–48 (2018).
Ansari, T. Q. et al. Phase-field model of pitting corrosion kinetics in metallic materials. npj Comput. Mater. 4, 38 (2018).
Mai, W. & Soghrati, S. New phase field model for simulating galvanic and pitting corrosion processes. Electrochim. Acta 260, 290–304 (2018).
Chadwick, A. F., Stewart, J. A., Enrique, R. A., Du, S. & Thornton, K. Numerical modeling of localized corrosion using phase-field and smoothed boundary methods. J. Electrochem. Soc. 165, C633–C646 (2018).
Tsuyuki, C., Yamanaka, A. & Ogimoto, Y. Phase-field modeling for pH-dependent general and pitting corrosion of iron. Sci. Rep. 8, 12777 (2018).
Sharland, S. M. A review of the theoretical modelling of crevice and pitting corrosion. Corros. Sci. 27, 289–323 (1987).
Beck, T. R. Salt film formation during corrosion of aluminum. Electrochim. Acta 29, 485–491 (1984).
Wang, Y., Yin, L., Jin, Y., Pan, J. & Leygraf, C. Numerical simulation of micro-galvanic corrosion in al alloys: steric hindrance effect of corrosion product. J. Electrochem. Soc. 164, C1035–C1043 (2017).
Yin, L., Jin, Y., Leygraf, C. & Pan, J. A FEM model for investigation of micro-galvanic corrosion of Al alloys and effects of deposition of corrosion products. Electrochim. Acta 192, 310–318 (2016).
JO’M, B., Drazic, D. & Despic, A. The electrode kinetics of the deposition and dissolution of iron. Electrochim. Acta 4, 325–361 (1961).
Lin, C., Ruan, H. & Shi, S. Q. Phase field study of mechanico-electrochemical corrosion. Electrochim. Acta 310, 240–255 (2019).
Melchers, R. E. & Jeffrey, R. Early corrosion of mild steel in seawater. Corros. Sci. 47, 1678–1693 (2005).
Bradford, S. A. & Bringas, J. E. Corrosion Control. Vol. 115 (Springer, Boston, MA, 1993).
Pitaevskii, L. & Lifshitz, E. Statistical Physics. (Pergamon press ltd., England, 1980).
Xiao, Z., Hao, M., Guo, X., Tang, G. & Shi, S.-Q. A quantitative phase field model for hydride precipitation in zirconium alloys: Part II. Modeling of temperature dependent hydride precipitation. J. Nucl. Mater. 459, 330–338 (2015).
Hall, E. L. & Briant, C. L. Chromium depletion in the vicinity of carbides in sensitized austenitic stainless steels. Metall. Trans. A 15, 793–811 (1984).
Jain, S., Lim, M., Hudson, J. & Scully, J. Spreading of intergranular corrosion on the surface of sensitized Al-4.4 Mg alloys: a general finding. Corros. Sci. 59, 136–147 (2012).
Bruemmer, S., Arey, B. & Charlot, L. Influence of chromium depletion on intergranular stress corrosion cracking of 304 stainless steel. Corrosion 48, 42–49 (1992).
Tan, Y., Fwu, Y. & Bhardwaj, K. Electrochemical evaluation of under-deposit corrosion and its inhibition using the wire beam electrode method. Corros. Sci. 53, 1254–1261 (2011).
Durnie, W., Gough, M. & De Reus, H. in CORROSION 2005. 3–7 (NACE International, Houston, Texas, 2005).
Chang, Y.-C., Woollam, R. & Orazem, M. E. Mathematical models for under-deposit corrosion I. aerated media. J. Electrochem. Soc. 161, C321–C329 (2014).
Sedriks, A. J. Corrosion of Stainless Steel, 2nd edn. (Wiley, United States, 1996).
Shahryari, A., Szpunar, J. A. & Omanovic, S. The influence of crystallographic orientation distribution on 316LVM stainless steel pitting behavior. Corros. Sci. 51, 677–682 (2009).
Lindell, D. & Pettersson, R. Crystallographic effects in corrosion of austenitic stainless steel 316L. Mater. Corros. 66, 727–732 (2015).
Brewick, P. T. et al. Microstructure-sensitive modeling of pitting corrosion: effect of the crystallographic orientation. Corros. Sci. 129, 54–69 (2017).
Moelans, N. A quantitative and thermodynamically consistent phase-field interpolation function for multi-phase systems. Acta Mater. 59, 1077–1086 (2011).
Bazant, M. Z. Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics. Acc. Chem. Res. 46, 1144–1160 (2013).
Chen, L. et al. Modulation of dendritic patterns during electrodeposition: a nonlinear phase-field model. J. Power Sources 300, 376–385 (2015).
Liang, L. et al. Nonlinear phase-field model for electrode-electrolyte interface evolution. Phys. Rev. E 86, 051609 (2012).
Liang, L. & Chen, L.-Q. Nonlinear phase field model for electrodeposition in electrochemical systems. Appl. Phys. Lett. 105, 263903 (2014).
Tjaden, B., Cooper, S. J., Brett, D. J., Kramer, D. & Shearing, P. R. On the origin and application of the Bruggeman correlation for analysing transport phenomena in electrochemical systems. Curr. Opin. Chem. Eng. 12, 44–51 (2016).
Fairweather, G. Finite Element Galerkin Methods for Differential Equations (M. Dekker, New York, 1978).
Ascher, U. M. & Petzold, L. R. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. Vol. 61 (Society For Industrial Applied Mathematics (SIAM), Philadelphia, U.S., 1998).
Acknowledgements
This work was supported by Research Grants Council of Hong Kong (PolyU 152140/14E) and funds from the Hong Kong Polytechnic University (RUTS and 4-88Y2).
Author information
Authors and Affiliations
Contributions
S.-Q.S. and T.Q.A. conceived the idea. T.Q.A. developed the model, performed simulations, and wrote the manuscript. S.Q.S. and J-L.L. provided critical comments and contributed to revisions of the manuscript. S.Q.S. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ansari, T.Q., Luo, JL. & Shi, SQ. Modeling the effect of insoluble corrosion products on pitting corrosion kinetics of metals. npj Mater Degrad 3, 28 (2019). https://doi.org/10.1038/s41529-019-0090-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41529-019-0090-5