Abstract
In the last decade, stretchable electronics evolved as a class of novel systems that have electronic performances equal to established semiconductor technologies, but can be stretched, compressed, and twisted like a rubber band. The compliance and stretchability of these electronics allow them to conform and mount to soft, elastic biological organs and tissues, thereby providing attractive opportunities in health care and bio-sensing. Majority of stretchable electronic systems use an elastomeric substrate to carry an ultrathin circuit mesh that consists of sparsely distributed stiff, thin-film electronic components interconnected by various forms of stretchable metal strips or low-dimension materials. During the fabrication processes and application of stretchable electronics, the thin-film components or nanomaterials undergo different kinds of in-plane deformation that often leads to out-of-plane or lateral buckling, in-surface buckling, or a combination of all. A lot of creative concepts and ideas have been developed to control and harness buckling behaviors, commonly regarded as pervasive occurrences in structural designs, to facilitate fabrication of stretchable structures, or to enhance stretchability. This paper provides a brief review of recent progresses on buckling analysis in stretchable electronics. Detailed buckling mechanics reveals important correlations between the geometric/material properties and system performance (e.g., mechanical robustness, deformability, structural architecture, and control). These mechanics models and analysis provide insights to design and optimize stretchable electronics for a wide range of important applications.
Similar content being viewed by others
Introduction
In the last decade, stretchable electronics evolved as a class of novel systems that have electronic performances equal to established semiconductor technologies, but can be stretched, compressed, and twisted like a rubber band. The compliance and stretchability of these electronics allow them to conform and mount to soft, elastic biological organs and tissues, therefore providing attractive opportunities in health care,1,2,3,4 portable batteries5, 6 and photovoltaics7, soft robotics8, and bio-sensing9. Success of stretchable electronics depends on mechanical designs in electronic materials and structures that allow them to be significantly bent, stretched, twisted, and compressed. Majority of stretchable electronic systems use an elastomeric substrate to carry an ultrathin circuit mesh that consists of sparsely distributed stiff, thin-film electronic components interconnected by various forms of stretchable metal strips. During the fabrication processes and application of stretchable electronics, the thin-film components undergo different kinds of in-plane deformation that often leads to out-of-plane or lateral buckling,10, 11 or a combination of both. A lot of creative concepts and ideas have been developed to control and harness buckling behaviors, commonly regarded as pervasive occurrences in structural designs, to facilitate fabrication of stretchable structures, or to enhance stretchability. This paper provides a brief review of recent progresses on buckling analysis in stretchable electronics. Detailed buckling mechanics reveals important correlations between the geometric/material properties and system performance (e.g., mechanical robustness, deformability, and structural architecture control). These mechanics models and analysis provide insights to design and optimize stretchable electronics for a wide range of important applications. Here, we briefly summarize the fundamental buckling analyses in these studies in the next several sections.
Buckling of compressed thin-film structures
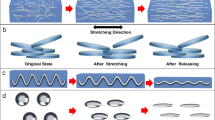
Khang et al.12 started the ground breaking work in stretchable electronics by demonstrating the concept of stretchable silicon films. The processes (Fig. 1) start with fabrication of thin (20 ~ 320 nm) silicon ribbons by lithographic processing, followed by etching of the silicon and SiO2 layers of a silicon on insulator (SOI) wafer (Fig. 1, top). A pre-strained elastomer (made of poly-dimethylsiloxane, or PDMS) is then used to transfer the silicon ribbons from the SOI wafer to the surface of the elastomer (Fig. 1, middle). Releasing the pre-strain relaxes the elastomer back to its unstrained state, leading to the formation of periodic wavy structures that enable stretchability (Fig. 1, bottom).
Schematic illustration of the process for fabricating stretchable single-crystal Si devices on elastomeric substrates. (reprinted with permission from ref. 12.)
Khang et al.12 and Huang et al.13 analyzed the behavior in this well-controlled wavy configuration and found it to be consistent with the initial buckled geometry in a uniform, thin, high-modulus layer (silicon ribbons in this case) on a semi-infinite low-modulus support (PDMS substrate).13, 14 The wavelength λ 0 and amplitude A 0 of the wavy structure is found to be:
where h is the thickness of the stiff thin film (silicon), ε pre is the pre-strain of the PDMS, and
is the critical buckling strain given in terms of the plane-strain moduli \({\bar E_{\boldsymbol{S}}}\) and \({\bar E_{\boldsymbol{f}}}\) of the substrate and film, respectively. This controlled buckling configuration allows silicon ribbons of 100 nm thickness to be stretched by nearly 30%, which is a very significant improvement from the 1% tensile limit of single-crystal silicon.
Equations (1) and (2) agree very well with experimental observations when the pre-strain is small, but it was found out that larger pre-strain has significantly influenced the wavelength and amplitude. Song et al.15 obtained the wavelength and amplitude for finite deformation as
where \(\xi = 5{\varepsilon _{{\rm{pre}}}}\left( {1 + {\varepsilon _{{\rm{pre}}}}} \right){\rm{/}}32\). Equations (3), also plotted in Fig. 2, agrees very well with the experimental data and finite element analysis.
a Wavelength and b amplitude of buckled structure of Si (100 nm thickness) on PDMS as a function of the pre-strain. The finite-deformation buckling theory yields wavelengths and amplitudes that agree well with experiments and finite element analysis. Results from previous mechanics models (i.e., small deformation limit) are also shown. (Reprinted with permission from ref. 15)
These analyses (referred to as local buckling here) work very well for the case when the substrate is much thicker than the silicon ribbons. However, in cases where the silicon covers a large area and the substrate is relatively thin, another undesirable global buckling mode has been observed in experiments, as shown in the inset of Fig. 3. The single-wave warping type of global buckling does not offer much stretchability. Wang et al.16 analytically obtained the critical condition for global buckling mode as
where \(\bar E \, \bar A = {\bar E_{{ s}}}{h_{{ s}}} + {\bar E_{{ f}}}{h_f}\) is the effective tensile rigidity of the composite beam, \(F_{{\rm{cr}}}^0 = \frac{{4{\rm{\pi }}\bar E\bar I}}{{{L^2}}}\) is the critical buckling load neglecting the effect of shear, and \(\begin{array}{ccccc}\\ \bar E\bar I = \left[ {{{\left( {{{\bar E}_{{ f}}}h_f^2 - {{\bar E}_{{ s}}}h_s^2} \right)}^2} + 4{{\bar E}_{{s}}}{h_s}{{\bar E}_{{ f}}}{h_{{ f}}}{{\left( {{h_{{ s}}} + {h_{{ f}}}} \right)}^2}} \right] \,/\left[ {12\left( {{{\bar E}_s}{h_{{ s}}} + {{\bar E}_{{ f}}}{h_{{ f}}}} \right)} \right]\\ \end{array}\) is the effective bending rigidity. \(\bar G\) is the effective shear modulus of the composite beam, which is approximately the shear modulus \({G_s}\) of the substrate since the film is very stiff (\({\bar E_{{ f}}} >> {\bar E_s}\)) and thin \({h_{{ f}}} < < {h_{{ s}}}\). Figure 3 shows the critical strain for local (blue curve) and global buckling (red curve) vs. the substrate thickness. For small substrate thickness where \(\varepsilon _{\rm{c}}^{{\rm{global}}} < \varepsilon _{\rm{c}}^{{\rm{local}}}\), global buckling occurs. Local buckling prevails once the substrate thickness exceeds a critical value (the intersection between the red and blue curves). Similar criteria are established by Wang et al.16 for differentiating the local and global buckling in two-dimensional thin membrane on PDMS substrate subjected to equibiaxial compression. These analyses provide criteria for achieving locally buckled wavy thin-film structures for enhanced stretchability.
Critical strains of local and global buckling vs. substrate thickness h s for Si/PDMS structures. (Reprinted with permission from ref. 16)
To further enhance stretchability and the overall strength of this type of integrated electronics, Cheng et al.17 adopted a bi-layer PDMS substrate in which a top softer layer carries the silicon films and facilitates buckling, and the relatively stiff layer at the bottom significantly enhance the strength of the system. By minimization of energy, Cheng et al.17analytically obtained the buckled geometry when the system is subjected to pre-strain
where \({\eta _0} = 4\left( {1 + {\varepsilon _{{\rm{pre}}}}} \right)\sqrt {\varepsilon _{{\rm{critical}}}^{{\rm{local}}}} \left( {{h_{{ s}}}/{h_{{ f}}}} \right)\), and \(r = {\bar E_{s1}}/{\bar E_{{{s2}}}}\) is the ratio of Young’s moduli of the top to bottom substrate layers. This analysis provides an analytical tool for designing the materials and the geometries of the bi-layer substrate to achieve optimum stretchability.
The concept of compressing silicon films to form wavy, stretchable structures is further exploited by Zhang et al.,18 who presented a systematic study on the buckling physics of stretchable serpentine microstructures (metal, consists of semicircle segments connected by straight segments, Fig. 4b, c). Zhang et al.19 obtained the criterion for localized wrinkling in serpentine interconnects as:
where l 2 is the straight segment of the serpentine and λ is the buckling wavelength of the serpentine interconnect, which is obtained analytically as:
where \({\bar E_{{{PI}}}}\) and \({t_{PI}}\) are the Young’s modulus and thickness of polyimide, respectively, \({\bar E_S}\) is the Young’s modulus of the Ecoflex substrate, \({\bar E_{metal}}\) and \({t_{{{metal}}}}\) are the Young’s modulus and thickness of metal layer, respectively. Equations (6) and (7), plotted in Fig. 4a, show that metal serpentine wires thinner than 0.9 μm form localized wrinkles under compression, while thicker wires do not show wrinkling behavior. The three-dimensional (3D) configurations of the deformed serpentine interconnect from FEA and experiments are shown in Fig. 4b, c, which agree very well. This analysis allows design of pre-strained serpentine wires that form locally wrinkled waves and that can be repeatedly stretched up to 189%.
a Wrinkling wavelength vs. metal thickness of the serpentine; b numerical results and c 3D XCT scanning images of the deformed configurations for the three buckling modes. (Reprinted with permission from ref. 19)
Applying two-dimensional (2D) pre-stain during the fabrication of similar structures results in wavy configurations that can expand the stretchability in multiple directions. Choi et al.20 introduced a biaxially stretchable structure that consists of silicon nanomembranes buckled periodically in two in-plane directions on the surface of a carrying elastomeric substrate. Lim et al.21 reported fabrication process for a biaxially stretchable array of microsuper capacitors on a deformable substrate, designed to minimize the strain applied to the active region of the device. By biaxially compressing a bilayer polymeric structure, Kim et al.22 observed a repetitive wrinkle-to-fold transition that creates periodic folds. Li23applied equal-biaxial compression to a monolayer graphene supported by a soft substrate to form a wrinkled graphene that can be stretched up to 50%, which demonstrates a feasible route to use graphene and other 2D materials in future designs of stretchable electronics.
Bonding thin-film electronics onto the surface of a pre-strained elastomer is exploited as an effective method to compress thin-film materials in one or two directions. The compression induces local buckling of the thin films into wavy configurations that can then be stretched without breaking the brittle materials. Buckling analysis on these structures enables stretchable forms of brittle materials such as silicon, metal, and dielectrics. It will be further discussed in Section 5 where these brittle electronic materials and structures are mapped into complex 3D geometries.
Buckling of one-dimensional materials
One-dimensional materials such as nanowires and nanotubes represent attractive options for stretchable electronics because of their small size (1 ~ 100 nm in at least one of the dimensions), high strength, and high flexibility, as well as other attractive electronic properties.24 Xiao et al.11 exploited the pre-strain method used in silicon thin films and transferred various one-dimensional materials, such as silicon nanowires, single-walled carbon nanotubes, multiwalled carbon nanotubes, and carbon nanotube bundles, on a pre-strained PDMS substrate. Upon release of the pre-strain, these nanomaterials do not buckle out-of-plane like the 2D silicon thin films, but rather form in-surface buckling patterns on the surface of the soft substrate. Xiao et al.11 established a continuum mechanics theory for this in-surface buckling of one-dimensional nanomaterials on compliant substrates and obtained the analytical expressions for the buckling wavelength, amplitude, and critical buckling strain as
where \({\varepsilon _{{ c}}} = \left\{ {EI{k^4} + {\rm{\pi }}{{\bar E}_{{ s}}}{{\left[ {\left( {3 - {\nu _{{ S}}}} \right){{\left( {1 - {\nu _S}} \right)}^{ - 1}} - 2\gamma - 2\ln \left( {k\omega } \right)} \right]}^{ - 1}}} \right\}/\left( {EA{k^2}} \right)\) is the critical buckling strain of a stiff beam on a compliant substrate, \({\varepsilon _{pre}}\) is the pre-strain, \(EI\) and \(EA\) are the bending and tension stiffness of a stiff beam on the surface of a compliant substrate, \({\bar E_{{ s}}} = {E_{{ s}}}{\rm{/}}\left( {1 - \nu _{{ S}}^2} \right)\) is the plane-strain modulus of the substrate, \({E_{{ s}}}\) and \({\nu _{{ S}}}\) are the Young’s modulus and Poisson’s ratio of the compliant substrate, respectively, \(k\) is the wave number related to the wavelength \(\lambda\) by k = 2π/λ, ω is the half width of the contact region with the substrate, and γ is the Euler’s constant. Plugging material and geometric properties for various types of nanomaterials into the above Eq. (8), Xiao et al.11 obtained analytically the buckling configurations for various nanomaterials. In addition, by comparing the total potential energies, it was found that the energy for in-surface buckling is lower than that for normal (out-of-surface) buckling, and is therefore energetically favorable. A few other research groups also studied the buckling of one-dimensional materials on elastomeric substrates. Duan et al.25 used electrospinning to deposit polyvinylidene fluoride micro/nanowires directly onto a pre-strained PDMS substrate and studied the buckling behaviors. They found that both out-of-plane and in-surface buckling modes are possible, and the material properties of the nanomaterials have large influence on the critical buckling strain. However, as the material properties of the nanomaterials and the elastomeric substrate differ by four to five orders of magnitude, they have negligible effect on the buckling mode. The buckling mode with smaller critical buckling strain is energetically favorable, and it is mainly determined by the micro/nanowires’ cross-section morphology. Recently, there are research findings on the effect of surface stress on the critical buckling strains of stretchable electronics. Park26and Gao et al.27 quantified the impact of nanoscale surface stresses on the critical buckling strains of silicon nanowires, and found that the buckling strains of nanowires are controlled by the initial state from which they are tested, where the initial state is strongly influenced by surface stress effects. They derived the critical strain for the out-of-surface buckling of nanowire as:
where \({\tau ^0}\) is the residual surface stress and EI, EA, and b are the tensile stiffness, bending stiffness, and width of the nanowire, respectively. k is the wavevector related to the wavelength λ by k = 2π/λ, ω is the half width of the contact region with the substrate, and γ is the Euler’s constant.
One-dimensional materials are extremely attractive options for stretchable electronics because of their inherently flexible nature. Materials and fabrication processes remain challenging, but with future technological advances, these materials offer many opportunities that cannot be achieved by thin-film or other electronic formats.
Mapping electronics/structures into 3D, complex shapes
Integration of stretchable electronic devices with soft, curvy, and elastic biological tissues and organs (e.g., human body parts) provides powerful diagnostic and therapeutic capabilities. Besides being soft, flexible, and stretchable, electronics will also need to be mapped from the as-fabricated planar form onto complex, curvilinear, 3D shapes. Representative examples also include bio-mimicking smart devices such as the electronic eye-ball camera,3 electronics that conform to the surface of the heart28, 29 or the skins,30 and also the more complex compound-eye31, 32 and focus-tunable cameras.33
Ko et al.34 introduced a strategy to map electronic circuit mesh from a planar layout onto complex curvilinear shapes. The process starts with mold-casting an elastomeric transfer element that has the shape of the target geometry, then radially stretch the transfer element to a flat drumhead shape, onto which electronics are transfer-printed. Releasing the radial stretch causes the transfer element to shrink back to, approximately, its original shape, carrying the electronics to the target geometry. During this process, the electronic circuit mesh is largely compressed when the transfer element shrinks, which causes the interconnections in the circuits to buckle. These interconnects undergo different levels of compression depending on their positions on the transfer element (obviously the rim of the element deforms much more than the radial origin of it), and exhibits a few different buckling modes—namely, global, local, and no buckling (Fig. 5, insets). Wang et al.35 presented systematic mechanics analysis for these different buckling modes, and analytically obtained the buckling critical conditions. The results showed that the buckling modes are governed by the levels of pre-strain \(\left| {{\varepsilon _{pre}}} \right|\) (level of stretch during the radial stretching) and the various works of adhesion γ between the interconnects and the transfer element. These analytical conditions separating the three buckling modes are plotted as a non-dimensional deformation map in Fig. 5, where \({\varepsilon _{{ c}}} = \frac{{{{\rm{\pi }}^2}{h^2}}}{{3{L^2}}}\), and \(E\), \(h\) , and \(L\) are Young’s modulus, the thickness, and the length of the interconnect, respectively. Figure 5 clearly shows that for weak adhesion such that \(\gamma \le 8Eh\varepsilon _{{ c}}^{{2}}\), local buckling does not exist and the interconnects form local buckling pattern for small strain and global buckling for larger strain; for strong adhesion such that \(\gamma >8Eh\varepsilon _{{ c}}^2\), the buckling modes transit from no buckling for small strain, to local buckling for intermediate strain, and eventually to global buckling for large strain. Figure 5 provides a useful tool to predict the buckling modes of interconnect bridges over different parts of curvilinear substrates (of arbitrary shapes).
Deformation map for different buckling modes (normalized strain vs. work of adhesion). (Reprinted with permission from Ref. 35)
Wang et al.36 presented a more detailed mechanics model by considering the transition from no buckling, to multiwave wrinkling (without delamination), to partial delamination, and eventually to total delamination (Fig. 6a–d). Depending on the relative stiffness of the interconnect to the elastomeric transfer element \({e_{{ w}}} = {\left( {3{E_{\rm{s}}}/{E_{{ f}}}} \right)^{2/3}}{\rm{/}}\left( {4{\varepsilon _{{ c}}}} \right)\), the results were summarized into four cases plotted in Fig. 6e.
The four buckling modes a flat, b wrinkling, c partial delamination, and d total delamination. e Deformation maps that separate the four buckling modes for various values of e w and γ. (Reprinted with permission from ref. 36)
The curves of Fig. 6e were obtained from Eqs. (6)~(12) from ref. 36 These analytical solutions agree very well with the results obtained numerically, and can be used to predict the buckling modes for any material under any adhesion conditions. They also provide an analytical tool to predict the maximum strains in these buckled structures, and to control the buckling pattern of the electronics.
Complex 3D structures in biology (e.g., cytoskeletal webs, neural circuits, and vasculature networks) provide essential functions in many basic forms of life. Compelling opportunities exist for analogous 3D architectures in human-made devices. Complex 3D buckling patterns, such as helical, spring-like, and so on, are feasible by compressing thin film or nanofibers on a soft substrate, which can be used to fabricate micro/nanostructures in extremely complex geometries.37 Chen et al.38, 39 studied the transition from the in-plane buckling to the helical buckling for the SiNW on the PDMS substrate (Fig. 7a, b). This study provided insights on configuring one-dimensional materials into complex 3D nanostructures and stretchable forms of electronics. Yan et al.40 exploited controlled buckling and origami-inspired ideas to assemble complex 3D structures for various materials across a wide range of length scales (Fig. 7c). Xu et al.41 developed nanofabrication and design strategies for forming complex 3D mesostructures by controlled buckling of a planar structure (Fig. 7d), which is bonded to a pre-strained elastomer at designated locations. Relaxing pre-strain in the elastomer causes compression in the patterned thin-film structure that then buckle to a well-controlled and pre-defined 3D shape. This strategy can be used to construct advanced materials (e.g., device-grade silicon) into designated complex 3D configurations. The authors demonstrated a great variety of geometries from helices (Fig. 7d, top), array of tents, trilayer flower, and mixed array of tents and tables (Fig. 7d, bottom) etc., to name just a few from a collection of more than 40 representative structures.
a, b FEM simulations and experiment of the typical configurations of the helical buckling of a SiNW on PDMS substrate (reprinted with permission from ref. 39); c complex “windmill” mesostructure (bilayer of silcon and SU8; reprinted with permission from ref. 40). d Distributed 3D mesoscale networks comprising interconnected collections of the 3D structures. (Reprinted with permission from ref. 41)
Suppressing buckling behaviors with thick interconnects for ultralarge stretchability
Recently, Su et al.42 introduced a different route to stretchable structures, where thick bar geometries replace thin ribbon layouts, to yield scissor-like deformations instead of in-plane or out-of-plane buckling modes. In their systematic theoretical, numerical, and experimental studies, it was observed that three different buckling modes exist for serpentine interconnects consisting of both straight and curved segments, as the thickness of interconnects increases from tens of nanometers to ~100 μm. The three buckling modes were referred to as wrinkling (localized, multiwave, out-of-plane buckling, Fig. 8a), buckling (coupled out-of-plane buckling and twisting, Fig. 8b, d), and scissoring (purely in-plane bending deformation, Fig. 8c). The scissoring structure significantly enhanced the level of stretchability from 20% for thin, wrinkling structures to ~100% for thick, scissoring structures. Suppressing buckling behavior in this type of serpentine interconnect is found to be beneficial for stretchability. With optimum designs, the scissoring mechanism can be exploited to increase elastic stretchability (defined as maximum cyclic stretching level that does not cause fracture) to ~350%, which represents a sixfold enhancement than previously reported values (about 60%).43 Su et al.42 analyzed the three buckling modes from the energy perspectives, and obtained analytically the criteria to separate the three different buckling modes:
where \({\bar E_{{\rm{sub}}}}\) and \({\bar E_{\rm{m}}}\) are the plane-strain modulus of the substrate and metal, respectively, and \({t_{\rm{m}}}\), \({w_{\rm{m}}}\), and L are the thickness, width, and length of the straight segment of the serpentine interconnect, respectively. This analytical criterion shows that the scissoring mode prevails for serpentine interconnects with the thickness greater than their widths, thereby providing a simple and very important design guideline for achieving thick, scissoring structure to suppress buckling behaviors in interconnects and to realize large stretchability. It was also found that the scissoring physics depends only on the thickness/width aspect ratio (Eq. (10)), and the stretchability is reversely proportional to the width. Because of the large thickness and therefore large cross-section area, scissoring designs also provide low electrical resistance and efficient heat dissipation in interconnect structures due to their thick geometries. The findings demonstrated that scissor-like mechanics represents an important, design approach in stretchable electronics, where high elastic stretchability, high areal coverages of active devices, and high electric performance can be achieved simultaneously. The mechanics and technical approaches are distinct from those traditionally exploited in stretchable electronics, thereby providing some important, additional design options and technical capabilities.
Scanning electron microscopy image results associated with these regimes, illustrated at thicknesses a 1 μm, b 12.5 μm, and c 80 μm, each stretched to the corresponding limit of elastic stretchability. d Experimental measurement and FEA study of the dependence of the elastic stretchability on the thickness of Cu interconnects, from 50 nm to 80 μm. Three regimes of deformation occur in this range: wrinkling, buckling, and scissoring. (Reprinted with permission from ref. 42)
Conclusion
This paper briefly reviewed the buckling behaviors in various types of stretchable electronics. Thin-film and low-dimension materials are bonded to pre-stretched substrate, and relaxation of the pre-strain leads to compression that causes various forms of buckling in the stiff materials. The buckling analysis of these structures provides analytical tools for predicting buckling configurations, maximum strains in critical locations, as well as the complex 3D geometries. Compared with experimental trial and error approaches, these analytical/numerical design tools provide criteria to avoid or promote certain buckling modes, or even to suppress instability behaviors, and therefore is very useful in aiding materials/geometric designs. We list here a few review papers by others for readers who are interested in exploring more details of the mechanics: Khang et al.44 discussed the mechanics of buckling, the thin-film metrology based on buckling phenomena, and the buckling application of the stretchable electronics. Song et al. reviewed mechanics of stretchable electronics in wavy designs and island-bridge designs,45 as well as the thermal management of stretchable inorganic electronics.46 Wang et al.47 and also Hong and Chen48 presented the typical design concepts and mechanics theories of stretchable electronic systems.
References
Liu, Y. et al. Epidermal mechano-acoustic sensing electronics for cardiovascular diagnostics and human-machine interfaces. Sci. Adv. 2, doi:10.1126/sciadv.1601185 (2016).
Kang, S.-K. et al. Bioresorbable silicon electronic sensors for the brain. Nature 530, 71–76 (2016).
Ko, H. C. et al. A hemispherical electronic eye camera based on compressible silicon optoelectronics. Nature 454, 748–753 (2008).
Song, Y. M. et al. Digital cameras with designs inspired by the arthropod eye. Nature. 497, 95–99 (2013).
Xu, S. et al. Stretchable batteries with self-similar serpentine interconnects and integrated wireless recharging systems. Nat. Commun. 4, 1543 (2013).
Zhang, Y., Huang, Y. & Rogers, J. A. Mechanics of stretchable batteries and supercapacitors. Curr. Opin. Solid State Mater. Sci. 19, 190–199 (2015).
Yoon, J. et al. Ultrathin silicon solar microcells for semitransparent, mechanically flexible and microconcentrator module designs. Nat. Mater. 7, 907–915(2008).
Lu, N. & Kim, D.-H. Flexible and stretchable electronics paving the way for soft robotics. Soft Robot. 1, 53–62 (2013).
Kim, D.-H., Ghaffari, R., Lu, N. & Rogers, J. A. Flexible and stretchable electronics for biointegrated devices. Annu. Rev. Biomed. Eng. 14, 113–128 (2012).
Ryu, S. Y. et al. Lateral buckling mechanics in silicon nanowires on elastomeric substrates. Nano. Lett. 9, 3214–3219 (2009).
Xiao, J. et al. Mechanics of nanowire/nanotube in-surface buckling on elastomeric substrates. Nanotechnology 21, 085708 (2010).
Khang, D.-Y., Jiang, H., Huang, Y. & Rogers, J. A. A stretchable form of single-crystal silicon for high-performance electronics on rubber substrates. Science 311, 208–212 (2006).
Huang, Z. Y., Hong, W. & Suo, Z. Nonlinear analyses of wrinkles in a film bonded to a compliant substrate. J. Mech. Phys. Solids 53, 2101–2118 (2005).
Chen, X. & Hutchinson, J. W. Herringbone buckling patterns of compressed thin films on compliant substrates. J. Appl. Mech. 71, 597–603 (2004).
Song, J. et al. Buckling of a stiff thin film on a compliant substrate in large deformation. Int. J. Solids Struct. 45, 3107–3121 (2008).
Wang, S., Song, J., Kim, D.-H., Huang, Y. & Rogers, J. A. Local versus global buckling of thin films on elastomeric substrates. Appl. Phys. Lett. 93, 023126 (2008).
Cheng, H., Zhang, Y., Hwang, K.-C., Rogers, J. A. & Huang, Y. Buckling of a stiff thin film on a pre-strained bi-layer substrate. Int. J. Solids Struct. 51, 3113–3118 (2014).
Zhang, Y. et al. Buckling in serpentine microstructures and applications in elastomer-supported ultra-stretchable electronics with high areal coverage. Soft Matter 9, 8062–8070 (2013).
Zhang, Y. et al. Experimental and theoretical studies of serpentine microstructures bonded to prestrained elastomers for stretchable electronics. Adv. Funct. Mater. 24, 2028–2037 (2014).
Choi, W. M. et al. Biaxially stretchable “Wavy” silicon nanomembranes. Nano. Lett. 7, 1655–1663 (2007).
Lim, Y. et al. Biaxially stretchable, integrated array of high performance microsupercapacitors. ACS Nano 8, 11639–11650 (2014).
Kim, P., Abkarian, M. & Stone, H. A. Hierarchical folding of elastic membranes under biaxial compressive stress. Nat. Mater. 10, 952–957 (2011).
Li, Y. Reversible wrinkles of monolayer graphene on a polymer substrate: toward stretchable and flexible electronics. Soft Matter 12, 3202–3213 (2016).
Xia, Y. et al. One-dimensional nanostructures: synthesis, characterization, and applications. Adv. Mater. 15, 353–389 (2003).
YongQing, D., YongAn, H. & ZhouPing, Y. Competing buckling of micro/nanowires on compliant substrates. J. Phys. D. Appl. Phys. 48, 045302 (2015).
Park, H. S. Surface stress effects on the critical buckling strains of silicon nanowires. Comput. Mater. Sci. 51, 396–401 (2012).
Gao, F., Cheng, Q. & Luo, J. Mechanics of nanowire buckling on elastomeric substrates with consideration of surface stress effects. Phys. E 64, 72–77 (2014).
Kim, D.-H. et al. Electronic sensor and actuator webs for large-area complex geometry cardiac mapping and therapy. Proc. Natl Acad. Sci. 109, 19910–19915 (2012).
Xu, L. et al. 3D multifunctional integumentary membranes for spatiotemporal cardiac measurements and stimulation across the entire epicardium. Nat. Commun. 5, 3329 (2014).
Kim, D.-H. et al. Epidermal electronics. Science 333, 838–843 (2011).
Xiao, J. et al. Bio-inspired hemispherical compound eye camera. Proc. SPIE 8958, Bioinspired, Biointegrated, Bioengineered Photonic Devices II, 89580A, doi: 10.1117/12.2041112 (2014).
Marefat, F., Partovi, A. & Mousavinia, A. A hemispherical omni-directional bio inspired optical sensor, In 20th Iranian Conference on Electrical Engineering. 668–672 (ICEE, 2012).
Jung, I. et al. Dynamically tunable hemispherical electronic eye camera system with adjustable zoom capability. Proc. Natl Acad. Sci. USA 108, 1788–1793 (2011).
Ko, H. C. et al. Curvilinear electronics formed using silicon membrane circuits and elastomeric transfer elements. Small 5, 2703–2709 (2009).
Wang, S. et al. Mechanics of curvilinear electronics. Soft Matter 6, 5757–5763 (2010).
Wang, B. & Wang, S. Adhesion-governed buckling of thin-film electronics on soft tissues. Theor. Appl. Mech. Lett. 6, 6–10 (2016).
Chen, X. & Yin, J. Buckling patterns of thin films on curved compliant substrates with applications to morphogenesis and three-dimensional micro-fabrication. Soft Matter 6, 5667–5680 (2010).
Chen, Y., Zhu, Y., Chen, X. & Liu, Y. Mechanism of the transition from in-plane buckling to helical buckling for a Stiff Nanowire on an elastomeric substrate. J. Appl. Mech. 83, 041011 (2016).
Chen, Y., Liu, Y., Yan, Y., Zhu, Y. & Chen, X. Helical coil buckling mechanism for a stiff nanowire on an elastomeric substrate. J. Mech. Phys. Solids 95, 25–43 (2016).
Yan, Z. et al. Controlled mechanical buckling for origami-inspired construction of 3D microstructures in advanced materials. Adv. Funct. Mater. 26, 2629–2639 (2016).
Xu, S. et al. Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science 347, 154–159 (2015).
Su, Y. et al. In-plane deformation mechanics for highly stretchable electronics. Adv. Mater. 29, 1604989 (2016).
Fan, J. A. et al. Fractal design concepts for stretchable electronics. Nat. Commun. 5, 3266 (2014).
Khang, D.-Y., Rogers, J. A. & Lee, H. H. Mechanical buckling: mechanics, metrology, and stretchable electronics. Adv. Funct. Mater. 19, 1526–1536 (2009).
Song, J. Mechanics of stretchable electronics. Curr. Opin. Solid State Mater. Sci. 19, 160–170 (2015).
Song, J., Feng, X. & Huang, Y. Mechanics and thermal management of stretchable inorganic electronics. Natl Sci. Rev. 3, 128–143 (2015).
Wang, S., Huang, Y. & Rogers, J. A. Mechanical designs for inorganic stretchable circuits in soft electronics. IEEE Trans. Compon. Packag. Manuf. Technol. 5, 1201–1218 (2015).
Hocheng, H. & Chen, C.-M. Design, fabrication and failure analysis of stretchable electrical routings. Sensors 14, 11855 (2014).
Author information
Authors and Affiliations
Contributions
B.W., S.B., S.V., and P.G. studied the literatures. B.W. and S.W. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, B., Bao, S., Vinnikova, S. et al. Buckling analysis in stretchable electronics. npj Flex Electron 1, 5 (2017). https://doi.org/10.1038/s41528-017-0004-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41528-017-0004-y
This article is cited by
-
Vertical serpentine interconnect-enabled stretchable and curved electronics
Microsystems & Nanoengineering (2023)
-
Realizing high stretch ratio of flexible wavy circuit via laser carving
Scientific Reports (2022)
-
Instabilities of Thin Films on a Compliant Substrate: Direct Numerical Simulations from Surface Wrinkling to Global Buckling
Scientific Reports (2020)
-
Local Wrinkle Patterning with Controlled Morphologies on a Membrane
International Journal of Precision Engineering and Manufacturing (2019)
-
Reversible conductivity recovery of highly sensitive flexible devices by water vapor
npj Flexible Electronics (2018)