Abstract
The surface tension of dispersions presents many types of behaviours. Although some models, based on classical surface thermodynamics, allow partial interpretation, fundamental understanding is still lacking. This work develops a single analytical physics-based formulation experimentally validated for the surface tension of various pure nanoparticle dispersions, explaining the underlying mechanisms. Against common belief, surface tension increase of dispersions appears not to occur at low but rather at intermediate surface coverage, owed by the relatively large size of nanoparticles with respect to the fluid molecules. Surprisingly, the closed-form model shows that the main responsible mechanism for the various surface tension behaviours is not the surface chemical potential of adsorbed nanoparticles, but rather that of non-occupied sites, triggered and delicately controlled by the nanoparticles ‘at a distance’, introducing the concept of the ‘non-occupancy’ effect. The model finally invites reconsidering surface thermodynamics of dispersions and provides for criteria that allow in a succinct manner to quantitatively classify the various surface tension behaviours.
Similar content being viewed by others
Introduction
Fluid dynamics of complex fluids represent a field of study that concerns a series of energetic, medical and industrial engineering applications. Since these applications concern, in many cases, fluids wherein dispersions are used for material printing or separation processes at the surface level, it is important to control the behaviour of surface-related mechanisms1. Stability requirements during the dispersion processing and the printing process depend on the physical properties, such as the viscosity, and its deposition quality depends on controlling the fluid dynamics of the deposited fluids and the underlying mechanisms2,3. Moreover, the wettability is a relevant physical property for processes where droplet impingement, thin film flows, microfluidics, surface speciation and heat transfer are implied4,5.
In order to focus on surface-related mechanisms of complex fluid dynamics, microgravity experiments are useful, cancelling thereby the interference of buoyancy. A sounding rocket experiment took place under the framework of the Advanced Research on Liquid Evaporation in Space (ARLES) experiment supported by the European Space Agency (ESA). ARLES was part of the payload in a SubOrbital Express rocket (MASER 14) and aims at studying the evaporation of pure and complex sessile droplets. It also serves as a preparation of an experiment to be performed in the near future at the European Drawer Rack 2 on board the International Space Station. The evaporation of the complex droplets resulted into pattern depositions of nanoparticles, interesting for future printing applications. These experiments allowed studying the depositions, but not how fluid dynamics, surface effects and particle–fluid interactions controlled those depositions. Another sounding rocket experiment is planned to be performed in the near future, where one of the focuses will be to monitor the fluid dynamics of the complex droplets. In order to prepare the flight scenario, a numerical model has been developed. The condition expressing the tangential stress balance, including surface-tension-induced convection, i.e. Marangoni convection, at the interface is given by
where σg and σl are the stress tensors at the interface on the gas and liquid sides, respectively, n the normal vector on the interface, γ the surface tension, (∇∙n)Σ stands for the curvature of the interface, ∇Σ = ∇ − nn ∙ ∇ for the surface gradient, T and φ stand for the temperature and nanoparticle volume fraction at the interface, respectively, whereas γT defines the surface tension derivative with respect to the temperature and γφ the surface tension derivative with respect to the volume fraction. Generally, γT is readily available and reasonably approximated to be constant. However, the behaviour of γφ is not so clear. Since at microgravity, convection responsible for fluid patterns is of the surface-tension type, it is crucial to not only have a physics-based analytical expression for the surface tension of nanoparticle-laden fluids but also to understand the underlying mechanisms that govern the surface tension of such complex fluids.
It appears from several experimental studies that apparently contradictory tendencies of the surface tension as a function of nanoparticle content are observed: the surface tension is observed to increase, decrease or pass through a minimum as a function of the nanoparticle content in the dispersions6,7,8,9,10,11,12,13,14,15. Even for the same nanoparticle, e.g. SiO2, a constant and increasing trend is observed9,13, while for Al2O3 both decreasing and increasing trends, in two separate cases, are observed7. Due to the diversity of nanodispersions, there is no universal relation yet that could comprehend and clarify quantitatively such observed trends. Fitted correlations or empiric relations may give good comparison to experimental values, but are specific to experiment conditions, do not explain physically why certain surface tension phenomena occur and lack often generality7,10. One may find some explanations, but mostly based on a qualitative assessment of the Gibbs free energy or on mere intuition. Some works have explained surface tension behaviour by an energy variation upon nanoparticle transfer to the interface16, attractive van der Waals or attractive capillary forces6,17 or even by analogy with electrolyte solutions18. Interestingly, it is just the presence of nanoparticles at the surface that is given as reason for surface tension increase in ref. 11, while the nanoparticle adsorption is suggested to cause a decrease in the surface tension elsewhere17. Others explain surface tension decrease by a high ionic strength of the base fluid countering the otherwise repulsive force between the nanoparticles and the liquid–gas interface18. This, however, does not explain the decrease of surface tension of nanoparticle-laden fluids with low ionic strength, such as nanoparticle dispersions in distilled water19 nor for surface tension minima. The initial decrease of the surface tension is suggested to be due to the large spacing between the nanoparticles, favouring electrostatic forces between the nanoparticles6 or to initial adsorption of nanoparticles at the liquid–gas interface17.
The apparently contradictory explanations for surface tension behaviour are often intuitively provided and many existing models, useful as they might be, only predict part of the tendencies, which is a consequence of universal underlying mechanisms still remaining unelucidated. This work develops an analytical model proposing a new insight in surface thermodynamics, surface energy and, more particularly, in the interaction between the dispersed phase and the liquid–gas interface. The model mainly aims at elucidating the underlying mechanisms of the surface tension of nanoparticle dispersions, both correctly predicting and explaining thereby the different experimentally observed tendencies. We start by formulating the framework within which the liquid-gas interface is defined. This will also allow introducing definitions of nanoparticle (excess) surface concentrations based on geometrical and size considerations. The nanoparticles are modelled as being incompressible, non-stretchable and the only material that can be adsorbed on the liquid–gas interface. Then, an analytical expression for the surface tension of nanoparticles will be calculated and compared to several experimental data of different nanoparticle dispersions. The model will be used to explain the different observed phenomena. Finally, it will be shown that two parameters can predict the type of surface tension behaviour for all the considered material systems.
Methods
Representation of an interfacial layer on a dividing surface
The surface energy of a nanoparticle dispersion can commonly be described by Gibbs adsorption isotherm \({{{\mathrm{d}}}}\gamma = - {{{\mathrm{{\Gamma}}}}}_{{{\mathrm{p}}}}{{{\mathrm{d}}}}\eta _{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}} - {{{\mathrm{{\Gamma}}}}}_{{{\mathrm{f}}}}{{{\mathrm{d}}}}\eta _{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}}\), an exact differential. Here, \(\eta _{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\) and \(\eta _f^{{{\mathrm{{\Sigma}}}}}\) are the surface chemical potentials induced by nanoparticle and fluid surface coverage, respectively, whereas Γp and Γf stand, respectively, for the excess surface concentrations of the nanoparticles and the base fluid. Choosing the Gibbs dividing surface to be there where the excess surface concentration of the liquid equals zero, we set Γf ≡ 0. This leaves us with \({{{\mathrm{d}}}}\gamma = - {\Gamma}_{{{\mathrm{p}}}}{{{\mathrm{d}}}}\eta _{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\). We will start discussing the excess surface concentration first. This inherently entails the definition of a framework that explains how to deal with the representation of a three-dimensional interfacial layer, whilst Gibbs adsorption isotherm imposes to work with a two-dimensional one, i.e. the Gibbs dividing surface. As excess surface concentrations of nanoparticles Γp are not widely documented, such a framework will allow us to propose analytical expressions for Γp. The excess surface concentration is composed out of a surface equivalent of the bulk concentration, discussed later, and an actual surface concentration. Let us begin with the latter. The surface concentration of the nanoparticles ΓpΣ is defined by the surface coverage θp times the maximum surface concentration \({{{\mathrm{{\Gamma}}}}}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}}\):
the surface coverage θp stems from principles concerning thermodynamic equilibrium and adsorption kinetics and it is more appropriate to discuss it later in a proper context. For now, we will focus on the framework of the dividing surface and how the surface concentration is represented within its context.
In Eq. (2), \({\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}}\) is the maximum surface concentration of the nanoparticles, assumed to be determined by the principle of maximum stacking via a maximum coverage fraction f∞20,21,22. Other geometrical considerations of particle adsorption have been treated in refs. 21,22, but we only need here their results for maximum coverage. In the presence of nanoparticles, the liquid–gas layer can be defined as the layer where the nanoparticles go gradually from a bulk concentration cp to a purely surface concentration ΓpΣ. The surface concentration is then usually obtained by integrating the concentration profile over the thickness of that layer. It has therefore, generally, a thickness that is larger than the size of the nanoparticles, a thickness that is defined by the difference between the dividing surface and an imaginary parallel surface, beyond which the bulk concentration is attained. The degree of strength of the interaction energy between the fluid molecules and the nanoparticles in that layer will determine the amount of nanoparticles that are ‘trapped’, i.e. adsorbed, or allowed to disperse in the bulk. Each nanoparticle that adsorbs will push away fluid molecules. In analogy to the bulk, according to the lattice model, (where each lattice fits a liquid molecule), we can define that the surface area that is occupied by a fluid molecule harbours a possible adsorption site. As such, the adsorption sites are geometrically equivalent to the fluid molecules in the interfacial layer. In order to represent this framework in a manner that fits Gibbs’ isotherm, we have defined a dividing surface. Speaking of the maximum surface concentration, this also necessitates to project the real maximum concentration in the interfacial layer onto the dividing surface (that has zero thickness). This projection method is depicted in Fig. 1a, while Fig. 1b focusses on the projection of an adsorbing nanoparticle with the corresponding parameters that will be used in the model. Figure 1c shows the surface that is deemed to participate to the adsorption. In fact, upon adsorption, it can be imagined that not the whole surface of the nanoparticles participates in the process. It is quite difficult to assess the portion of surface that participates to this process and not much is known about this. In this work, we will heuristically assume that only half of a nanoparticle’s surface, i.e. the half that faces the dividing surface, participates in its adsorption. The reason for this will be discussed later. We will call this the participating surface. Later in ‘Three counter-intuitive effects of Kp on surface tension’, a verification will be discussed to show that such an assumption appears to be quite reasonable.
a Principle of projecting nanoparticles on dividing surface at maximum coverage. Note that at a coverage below the maximum one, the principle is the same. b Projection of nanoparticles (with volume VP and surface AP) on a two-dimensional surface. The projected circles are oval because they are drawn in perspective, but they should be seen as circular for the spherical and disk nanoparticles, and as a square for the cubic nanoparticles. The fluid molecules (with volume VP and surface AP) at the surface Σ, on which a nanoparticle adsorbs, also participate to the adsorption and are illustrated as fluid molecules that become projected (on the dividing surface) as two-dimensional adsorption sites, depicted for simplicity as a flat plane Σ at exactly the dividing surface. c Illustration of the surfaces that come into play in the volume-to-surface ratio for the spherical, cubical and disk nanoparticles. The images are not in scale.
Let us, at maximum coverage, order the nanoparticles into several layers that are parallel to the dividing surface. As we are in maximum coverage, each layer contains the same amount of nanoparticles. Let us then project, in each such layer, the participating surface of the nanoparticles (as if a nanoparticle was a balloon that is cut in half, of which one half is spread over the surface) on the dividing surface (for the first layer at the dividing surface) and on subsequent imaginary layers parallel to the dividing surface. This gives in each layer the same maximum surface concentration per unit surface, so that considering only the layer adjacent to the dividing surface is sufficient to determine the maximum surface concentration per unit surface, as Fig. 1a shows.
This will result in a molar concentration of nanoparticles per unit surface on the dividing surface that would be equivalent to the corresponding real molar concentration in a realistic adsorption layer, through scaling by a certain defined characteristic length, so-defined as \({{{\mathcal{L}}}}_{{{\mathrm{p}}}}\). As Fig. 1b shows, the projected maximum surface concentration per unit surface times the characteristic length gives the same volume as that of the nanoparticle. It follows then that that characteristic length must be a volume-to-surface ratio.
We define this volume-to-surface ratio by the total volume divided by half of the total surface (the participating surface, as is shown in Fig. 1c). The fluid particles that surround this participating surface of a nanoparticle in a real interfacial layer are fully projected on the dividing surface as they represent geometrically the adsorption sites on that surface (see the schematic representation in Fig. 1b). The characteristic length of these fluid particles, or adsorption sites, is calculated by a standard volume-to-surface ratio.
The projected surfaces depend on the size of the nanoparticles and the fluid molecules (geometrically equivalent to that of the adsorption sites). This means that the difference in sizes between the nanoparticles and the adsorption sites can be expected to have a great impact on the adsorption process. Each adsorbed nanoparticle will induce a change in the possible entropic configurations of a great number of adsorption sites. As these sites are not occupied, yet have a large influence on the entropy, they are named as non-occupied sites, because their non-occupancy matters entropically. We can say that the total area of these non-occupied sites (denoted by subscript NO) per total surface area is given by
where \(m_{{{\mathrm{i}}}}^{{{\mathrm{{\Sigma}}}}}\) and ςi are, respectively, the number of particles of a constituent per unit interface surface and the specific surface area per particle of that constituent, whilst the superscript Σ indicates that it concerns a surface property. The specific surface area of a constituent is given by \(\varsigma _{{{\mathrm{i}}}} \equiv \frac{{M_{{{\mathrm{i}}}}}}{{\rho _{{{\mathrm{i}}}}{{{\mathcal{L}}}}_{{{\mathrm{i}}}}N_{{{\mathrm{A}}}}}}\), with i = NO, f, p, standing for non-occupied sites, the fluid and nanoparticles, respectively. Equivalently, the specific surface area of a constituent may conveniently also be given per mole, i.e. \(\varsigma _{{{\mathrm{i}}}} \equiv \frac{{M_{{{\mathrm{i}}}}}}{{\rho _{{{\mathrm{i}}}}{{{\mathcal{L}}}}_{{{\mathrm{i}}}}}}\). In that case, \(m_{{{\mathrm{i}}}}^{{{\mathrm{{\Sigma}}}}}\) would simply be the number of mole of a constituent per unit surface via scaling by NA and Eq. (3) remains valid. Expressions for the characteristic length \({{{\mathcal{L}}}}_{{{\mathrm{i}}}}\) will be developed later (with \({{{\mathcal{L}}}}_{{{{\mathrm{NO}}}}} = {{{\mathcal{L}}}}_{{{\mathrm{f}}}}\) as geometrically the adsorption sites are equivalent to the fluid molecules). It is important to notice here that ςi introduces a size effect, i.e. the number densities depend on the size of the nanoparticles and the surface fluid particles.
We have now defined the framework for calculating the surface concentrations and may proceed with proposing a formula that allows calculating these concentrations. The maximum surface concentration is given by the maximum number of nanoparticle moles, \(\frac{{m_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}}}{{N_{{{\mathrm{A}}}}}}\), divided by a unit surface, i.e. \({\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}} = \frac{1}{{N_{{{\mathrm{A}}}}}}\frac{{m_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}}}{{A_{{{\mathrm{t}}}}}}\), where At is a total (arbitrary portion of unit) surface. This can conveniently be rewritten as \({\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}} = \frac{{V_{{{\mathrm{p}}}}}}{{A_{{{\mathrm{p}}}}/2}}\frac{{m_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}A_{{{\mathrm{p}}}}/2}}{{A_{{{\mathrm{t}}}}}}\frac{1}{{N_{{{\mathrm{A}}}}V_{{{\mathrm{p}}}}}}\), where Ap and Vp are the surface and volume per nanoparticle, respectively. It can be noted that \(\frac{{V_{{{\mathrm{p}}}}}}{{A_{{{\mathrm{p}}}}/2}}\) is nothing else than two times the nanoparticle’s volume to surface ratio, defined as \({{{\mathcal{L}}}}_{{{\mathrm{p}}}}\) (see Fig. 1). Moreover, \(\frac{1}{{N_{{{\mathrm{A}}}}V_{{{\mathrm{p}}}}}}\) is the mole of nanoparticles per unit volume, also given by \(\frac{{\rho _{{{\mathrm{p}}}}}}{{M_{{{\mathrm{p}}}}}}\), where ρp and Mp are the nanoparticle’s density and molar mass, respectively. Also \(\frac{{m_{{{{\mathrm{p,max}}}}}A_{{{\mathrm{p}}}}/2}}{{A_{{{\mathrm{t}}}}}}\) is simply the maximum geometric coverage fraction f∞, being f∞ ≈ 0.547 for spherical non-overlapping hard particles on a two-dimensional surface21,22. This value is obtained by considering random packing of spheres after their projection on the interface. It is therefore not the same as the random packing of circles as the latter would neglect the purpose of the projection method, where it is sought to obtain expressions on a 2D surface whilst preserving the information from realistic 3D interfaces as Fig. 1 shows. For cubic nanoparticles, it is reasonable to expect that the maximum coverage will be close to unity, to that we take f∞ ≈ 1 for cubic nanoparticles21,22. For disk-like nanoparticles, of which the circular part faces the dividing surface, we take a maximum coverage that corresponds to maximum standard hexagonal stacking of circles on a surface, i.e. \(f_\infty = \frac{{\pi \sqrt 3 }}{6} \approx 0.907\) for disk nanoparticles. This leads to
It should be noted that when nanoparticles are coated or surface treated, the maximum coverage might be less due to possible repulsive forces or more if the nanoparticles have a soft compressible coating with interparticle attractive forces. Note that similar expressions have been proposed in refs. 20,23. Nanoparticles may come in various shapes, the main ones kibeing often of spherical, cubical or disk shape. We will, for the demonstration, limit ourselves to such undeformable shapes. The volume and participating surface, i.e. \(\left( {V_{{{\mathrm{p}}}},\;\frac{{A_{{{\mathrm{p}}}}}}{2}} \right)\), as defined in Fig. 1c, would then be \(\left( {\frac{{4\pi }}{3}a_{{{\mathrm{p}}}}^3,\;2\pi a_{{{\mathrm{p}}}}^2} \right)\), \(\left( {8a_{{{\mathrm{p}}}}^3,\;12a_{{{\mathrm{p}}}}^2} \right)\) and \(\left( {\pi a_{{{\mathrm{p}}}}^2h_{{{\mathrm{p}}}},\;\pi a_{{{\mathrm{p}}}}^2 + \pi a_{{{\mathrm{p}}}}h_{{{\mathrm{p}}}}} \right)\) for a spherical, cubical and disk nanoparticle, respectively. The volume-to-surface ratio \({{{\mathcal{L}}}}_{{{\mathrm{p}}}}\) can then be calculated. For a spherical nanoparticle, \({{{\mathcal{L}}}}_{{{\mathrm{p}}}} = \frac{{2a_{{{\mathrm{p}}}}}}{3}\) (with radius ap), for a square-like nanoparticle, \({{{\mathcal{L}}}}_{{{\mathrm{p}}}} = \frac{{2a_{{{\mathrm{p}}}}}}{3}\) (with 2ap the side of the cube) and for a disk-like nanoparticle, \({{{\mathcal{L}}}}_{{{\mathrm{p}}}} = \frac{{a_{{{\mathrm{p}}}}h_{{{\mathrm{p}}}}}}{{a_{{{\mathrm{p}}}}\, + \,h_{{{\mathrm{p}}}}}}\) (with radius ap and thickness hp). Note that it is not straightforward to define a molar mass of a nanoparticle, since it is not a molecule nor an atom. We will approximate the molar mass of a nanoparticle, in analogy with that of a polymer constituted by many monomers, as an ensemble of atoms or molecules chemically connected to one another. The molar mass of a nanoparticle equals then \(M_{{{\mathrm{p}}}} = M_{{{{\mathrm{p}}}}^\prime }f_{{{\mathrm{p}}}}\frac{{V_{{{\mathrm{p}}}}}}{{V_{{{{\mathrm{p}}}}^\prime }}}\), where fp represents the maximum stacking factor of spheres in a three-dimensional setting, assumed here to be \(f_{{{\mathrm{p}}}} = \frac{{\uppi }}{{3\sqrt 2 }}\) (that of an fcc or hcp structure), Mp′ the molar mass of one atom or molecule, Vp the volume of one nanoparticle and \(V_{{{{\mathrm{p}}}}^\prime } = \frac{{4{\uppi}}}{3}\ell _{{{\mathrm{p}}}}^3\) the volume of one atom or molecule, assumed to be of spherical form, with \(\ell _{{{\mathrm{p}}}}\) the radius of that atom or molecule \(\ell _{{{\mathrm{p}}}} = \root {3} \of {{\frac{{M_{{{{\mathrm{p}}}}^\prime }}}{{\rho _{{{\mathrm{p}}}}N_{{{\mathrm{A}}}}}}\frac{3}{{4{\uppi}}}}}\). The effective radius of a fluid molecule, assuming sphericity, can be calculated in the same manner as \(\ell _{{{\mathrm{f}}}} = \root {3} \of {{\frac{{M_{{{\mathrm{f}}}}}}{{\rho _{{{\mathrm{f}}}}N_{{{\mathrm{A}}}}}}\frac{3}{{4{\uppi}}}}}\), where ρf and Mf are the fluid’s density and molar mass, respectively. With \(V_{{{\mathrm{f}}}} = \frac{{4\pi }}{3}\ell _{{{\mathrm{f}}}}^3\) and \(A_{{{\mathrm{f}}}} = 4\pi \ell _{{{\mathrm{f}}}}^2\), the volume-to-surface ratio for a fluid particle is given by \({{{\mathcal{L}}}}_{{{\mathrm{f}}}} = \frac{{\ell _{{{\mathrm{f}}}}}}{3}\). With these definitions, the geometric definition of the maximum surface concentration ΓpΣ can be calculated from material properties and size values.
The difference between the excess surface concentration Γp and the surface concentration ΓpΣ is usually defined as
where cp is the nanoparticle concentration in the bulk layer, and λb = zb − z0, with z0 the position at which Γf = 0 and zb at which we can consider conceptually to have a bulk concentration. In order to determine λb, let us make a preliminary remark. The maximum surface concentration has been obtained by projecting a layer of adsorbed nanoparticles on a two-dimensional surface at the dividing surface, which we defined as Γf = 0. When doing this, it has been explained that the characteristic length of nanoparticle projection equals \({{{\mathcal{L}}}}_{{{\mathrm{p}}}}\). For consistency, we should do the same here. In the definition of the excess surface concentration, the term \(\left( { - {\int}_{z_0}^{z_{{{\mathrm{b}}}}} {c_{{{\mathrm{p}}}}{{{\mathrm{d}}}}z} } \right)\) denotes a deduction from the surface concentration of an imaginary extrapolation of the bulk concentration, integrated over the interfacial thickness λb. So, it should rather be seen as an imaginary surface-equivalent of the bulk concentration, \({\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{b}}}}} \equiv {\int}_{z_0}^{z_{{{\mathrm{b}}}}} {c_{{{\mathrm{p}}}}{{{\mathrm{d}}}}z = c_{{{\mathrm{p}}}}\lambda _{{{\mathrm{b}}}}}\), defined at an imaginary surface at z = zb. This also means that it is analogous to the projection of the bulk nanoparticle concentration on the dividing surface, named here Γp*, so that Γp* ≡ Γp,b. It remains to find Γp*. Imagine at the dividing surface Γf = 0 a slab \({{{\mathcal{V}}}}_{{{\mathrm{p}}}}\) of thickness \({{{\mathcal{L}}}}_{{{\mathrm{p}}}}\), of which the contents are projected on that surface. If the projected nanoparticle surface concentration is given by Γp*, then the corresponding nanoparticle concentration in \({{{\mathcal{V}}}}_{{{\mathrm{p}}}}\) would be \(\frac{{{\Gamma}_{{{{\mathrm{p}}}} \ast }}}{{{{{\mathcal{L}}}}_{{{\mathrm{p}}}}}}\) as defined by the projection procedure in Fig. 1. If the projected specific surface area per mole of nanoparticles is given by ςp, then the corresponding volume per mole of nanoparticles in \({{{\mathcal{V}}}}_{{{\mathrm{p}}}}\) would be \(\varsigma _{{{\mathrm{p}}}}{{{\mathcal{L}}}}_{{{\mathrm{p}}}}\). The same could be done for the fluid particles, so that the volume fraction φ in that slab would be described by \(\frac{\varphi }{{1 - \varphi }} = \frac{{\varsigma _{{{\mathrm{p}}}}{\Gamma}_{{{{\mathrm{p}}}} \ast }}}{{\varsigma _{{{\mathrm{f}}}}{\Gamma}_{{{{\mathrm{f}}}} \ast }}}\). Within the slab \({{{\mathcal{V}}}}_{{{\mathrm{p}}}}\), the projected surface concentration for the fluid particles Γf* would simply be equal to the bulk concentration cf times the thickness of \({{{\mathcal{V}}}}_{{{\mathrm{p}}}}\), i.e. \({\Gamma}_{{{{\mathrm{f}}}} \ast } = c_{{{\mathrm{f}}}}{{{\mathcal{L}}}}_{{{\mathrm{p}}}}\). We then have \({\Gamma}_{{{{\mathrm{p}}}} \ast } = c_{{{\mathrm{f}}}}{{{\mathcal{L}}}}_{{{\mathrm{p}}}}\frac{{\varsigma _{{{\mathrm{f}}}}}}{{\varsigma _{{{\mathrm{p}}}}}}\frac{\varphi }{{1 - \varphi }}\). Note that \(c_{{{\mathrm{f}}}} = \left( {1 - \varphi } \right)\frac{{\rho _{{{\mathrm{f}}}}}}{{M_{{{\mathrm{f}}}}}}\). Filling in the definitions of ςp and ςf leads to \({\Gamma}_{{{{\mathrm{p}}}} \ast } = \frac{{\rho _{{{\mathrm{f}}}}}}{{M_{{{\mathrm{f}}}}}}{{{\mathcal{L}}}}_{{{\mathrm{p}}}}\frac{{M_{{{\mathrm{f}}}}}}{{\rho _{{{\mathrm{f}}}}{{{\mathcal{L}}}}_{{{\mathrm{f}}}}}}\left( {\frac{{M_{{{\mathrm{p}}}}}}{{\rho _{{{\mathrm{p}}}}{{{\mathcal{L}}}}_{{{\mathrm{p}}}}}}} \right)^{ - 1}\varphi = \frac{{\rho _{{{\mathrm{p}}}}}}{{M_{{{\mathrm{p}}}}}}\frac{{{{{\mathcal{L}}}}_{{{\mathrm{p}}}}^2}}{{{{{\mathcal{L}}}}_{{{\mathrm{f}}}}}}\varphi\). Figure 2 illustrates the analogy that we have discussed here.
As \(c_{{{\mathrm{p}}}} = \varphi \frac{{\rho _{{{\mathrm{p}}}}}}{{M_{{{\mathrm{p}}}}}}\), it follows that \(\lambda _{{{\mathrm{b}}}} = \frac{{{{{\mathcal{L}}}}_{{{\mathrm{p}}}}^2}}{{{{{\mathcal{L}}}}_{{{\mathrm{f}}}}}}\). Filling this in (5) gives, with Eq. (2), for the excess surface concentration
with
where \({\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}}\) is given by Eq. (4) and φΓbΣ is the surface equivalent of the bulk concentration and KΣ a constant that measures the potential of the nanoparticles to rather adsorb at the interface than stay dispersed in the bulk. As will be seen later, KΣ is a function of nanoparticle size, maximum packing and fluid molecule size. The surface coverage θp in Eq. (6) will be treated in the context of surface kinetics, but we will first deduce the surface chemical potentials and surface adsorption.
Surface chemical potential
If we have \(m_{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}}\) number densities of adsorption sites, containing \(m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}}\) number densities of non-occupied sites and \(m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\) number densities of adsorbed nanoparticles, the total number of microstates would equal \(W = \frac{{\left( {m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}} \right)!}}{{m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}!m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}}!}}\). Boltzmann’s equation of entropy would give \(S_{{{\mathrm{d}}}} = k_{{{\mathrm{B}}}}ln\left( W \right) = k_{{{\mathrm{B}}}}ln\left( {\frac{{\left( {m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}} \right)!}}{{m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}!m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}}!}}} \right)\). For a pure fluid, only one undistinguishable combination exists, i.e. Sf = kBln(1) = 0. The corresponding surface fraction is given by \(y_{{{\mathrm{p}}}} = \frac{{m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}}{{m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}}\). The surface coverage is defined to be equal to the surface fraction, θi ≡ yi, so that θp + θNO = 1. Defining the configurational entropy of dispersing, due to nanoparticle coverage and non-occupied sites, as ∆sd = SdNA − SfNA, and using Stirling’s approximation for the logarithm of factorials, gives
where kB and NA are, respectively, Boltzmann’s constant and Avogadro’s number. In dilute conditions, the enthalpy of dispersing can be neglected. It should be noted that this enthalpy results from heat liberated or absorbed due to new interactions that stem from the mixing process, while it is not the same as the enthalpy of adsorption, which plays a role in the equilibrium adsorption constant. In such conditions, we deal with an ideal dispersion, being consistent with the Langmuir’s adsorption isotherm, of which a detailed deduction is presented in the next section. The Gibbs surface free energy of dispersing is then given by \({\Delta}g_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}} = - T{\Delta}s_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}}\) resulting into
We define \(\omega _{{{\mathrm{p}}}} \equiv \frac{{\varsigma _{{{\mathrm{p}}}}}}{{\varsigma _{{{{\mathrm{NO}}}}}}}\) and \(\omega _{{{\mathrm{f}}}} \equiv \frac{{\varsigma _{{{\mathrm{f}}}}}}{{\varsigma _{{{{\mathrm{NO}}}}}}}\). The chemical potentials of a component i are defined by
with i = p, f and j = p, f. The number ωp can also be understood as the number of adsorption sites per nanoparticle. We then use the aforementioned definition \(\theta _{{{\mathrm{i}}}} = \frac{{m_{{{\mathrm{i}}}}^{{{\mathrm{{\Sigma}}}}}}}{{m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}}\), fill this in in Eq. (10), apply Eq. (11) and rewrite the result back in terms of θi. This finally gives \(\eta _{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}} = k_{{{\mathrm{B}}}}TN_{{{\mathrm{A}}}}\omega _{{{\mathrm{f}}}}ln\left( {1 - \theta _{{{\mathrm{p}}}}} \right)\) and
where \(\omega _{{{\mathrm{p}}}} \equiv \frac{{\varsigma _{{{\mathrm{p}}}}}}{{\varsigma _{{{{\mathrm{NO}}}}}}} \equiv \frac{{\varsigma _{{{\mathrm{p}}}}}}{{\varsigma _{{{\mathrm{f}}}}}}\) (as \(\omega _{{{\mathrm{f}}}} \equiv \frac{{\varsigma _{{{\mathrm{f}}}}}}{{\varsigma _{{{{\mathrm{NO}}}}}}}\) and ωf ≡ 1 because the adsorption sites are within the present framework geometrically equivalent to the projected liquid molecules, see Fig. 1b and corresponding discussion) is given by
Surface adsorption isotherm
Equilibrium of the adsorption process is described by a net zero change of the total Gibbs free energy of the system: \({{{\mathrm{d}}}}{\Delta}G_{{{\mathrm{a}}}} = d{\Delta}G_{{{{\mathrm{ad}}}}}^{{{\mathrm{{\Sigma}}}}} + d{\Delta}G_{{{{\mathrm{ad}}}}}^{{{\mathrm{b}}}} + d{\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}} + d{\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{b}}}} \equiv 0\), where the subscripts ‘ad’ and ‘d’ denote the adsorption (due to translational or confinement effects, or effects related to particle surface energies, dipole-dipole and coulomb interactions24, for instance) and the dispersion (mixing) free energies, respectively, and ‘Σ’ and ‘b’ the surface and bulk phases, respectively. We focus first on the dispersing. We can then define \({\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}} = A\frac{{m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}}{{N_{{{\mathrm{A}}}}}}{\Delta}g_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}}\) and \({\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{b}}}} = V\frac{{m_{{{\mathrm{l}}}}^{{{\mathrm{b}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{b}}}}}}{{N_{{{\mathrm{A}}}}}}{\Delta}g_{{{\mathrm{d}}}}^{{{\mathrm{b}}}}\), where \(m_{{{\mathrm{l}}}}^{{{\mathrm{b}}}}\) and \(m_{{{\mathrm{p}}}}^{{{\mathrm{b}}}}\) are the number of bulk fluid particles and nanoparticles per unit volume of the dispersion, whereas A and V are an arbitrary unit surface and volume, respectively. Note here that \(\frac{{m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}}{{N_{{{\mathrm{A}}}}}}\) has unit moles per unit surface and \(\frac{{m_{{{\mathrm{l}}}}^{{{\mathrm{b}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{b}}}}}}{{N_{{{\mathrm{A}}}}}}\) unit moles per unit volume. Note also that we can define a mole fraction of nanoparticles in the bulk as \(x_{{{\mathrm{p}}}} = \frac{{m_{{{\mathrm{p}}}}^{{{\mathrm{b}}}}}}{{m_{{{\mathrm{l}}}}^{{{\mathrm{b}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{b}}}}}}\). Neglecting the enthalpy of dispersing as mentioned before, an addition of nanoparticles to the surface would result into a change \({{{\mathrm{d}}}}{\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}}\left( {m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}},m_{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}}} \right)\), which can mathematically be written as \({{{\mathrm{d}}}}{\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}} = N_{{{\mathrm{A}}}}\frac{\partial }{{\partial m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}}\left( {A\frac{{m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}}{{N_{{{\mathrm{A}}}}}}{\Delta}g_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}}} \right)_{T,p,m_{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}}}{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}} + N_{{{\mathrm{A}}}}\frac{\partial }{{\partial m_{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}}}}\left( {A\frac{{m_{{{{\mathrm{NO}}}}}^{{{\mathrm{{\Sigma}}}}} + m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}}{{N_{{{\mathrm{A}}}}}}{\Delta}g_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}}} \right)_{T,p,m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}}{{{\mathrm{d}}}}m_{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}} = A\left( {\eta _{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}} + \eta _{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}}{{{\mathrm{d}}}}m_{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}}} \right)\). From (3) and the total number density, it can be derived that \({{{\mathrm{d}}}}m_{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}} = \left( {\omega _{{{\mathrm{p}}}} - 1} \right){{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\). With the definitions for \(\eta _{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\) and \(\eta _{{{\mathrm{f}}}}^{{{\mathrm{{\Sigma}}}}}\) (see Eq. (12) and text above), this leads with ωf = 1 to \({{{\mathrm{d}}}}{\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}} = k_{{{\mathrm{B}}}}TN_{{{\mathrm{A}}}}ln\left( {\frac{{\theta _{{{\mathrm{p}}}}}}{{1 - \theta _{{{\mathrm{p}}}}}}} \right)A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\). An equivalent procedure can be performed for the bulk phase leading, under the approximation of diluted dispersion, to the relation \({{{\mathrm{d}}}}{\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{b}}}} = k_{{{\mathrm{B}}}}TN_{{{\mathrm{A}}}}ln\left( {x_{{{\mathrm{p}}}}} \right)V\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{b}}}}\). Mass conservation stipulates that the net mass change is zero, i.e. \(A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}} + V\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{b}}}} = 0\). This leads to \({{{\mathrm{d}}}}{\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{{\Sigma}}}}} + {{{\mathrm{d}}}}{\Delta}G_{{{\mathrm{d}}}}^{{{\mathrm{b}}}} = k_{{{\mathrm{B}}}}TN_{{{\mathrm{A}}}}( {ln( {\frac{{\theta _{{{\mathrm{p}}}}}}{{1 - \theta _{{{\mathrm{p}}}}}}} ) - ln( {x_{{{\mathrm{p}}}}})} )A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\).
A change in the nanoparticles number in both phases upon adsorption also induces a change in the free energy of the adsorption, which can be symbolically (as an already existing thermodynamic relation for the free energy of adsorption will be used, there is no need to enter into details as we did for the free energy of dispersion earlier) written as \({{{\mathrm{d}}}}{\Delta}G_{{{{\mathrm{ad}}}}}^{\Sigma}\left( {A\,m_{{{\mathrm{p}}}}^{\Sigma}} \right) + {{{\mathrm{d}}}}{\Delta}G_{{{{\mathrm{ad}}}}}^{{{\mathrm{b}}}}\left( {V\,m_{{{\mathrm{p}}}}^b} \right) = {\Delta}g_{{{{\mathrm{ad}}}}}^{\Sigma}A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{\Sigma} + {\Delta}g_{{{{\mathrm{ad}}}}}^{{{\mathrm{b}}}}V\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^b\). We can use the mass conservation principle \(A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{\Sigma} + V\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{{{\mathrm{b}}}} = 0\) and write \({{{\mathrm{d}}}}{\Delta}G_{{{{\mathrm{ad}}}}}^{\Sigma} + {{{\mathrm{d}}}}{\Delta}G_{{{{\mathrm{ad}}}}}^{{{\mathrm{b}}}} = \left( {{\Delta}g_{{{{\mathrm{ad}}}}}^{{{\mathrm{{\Sigma}}}}} - {\Delta}g_{{{{\mathrm{ad}}}}}^{{{\mathrm{b}}}}} \right)A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{\Sigma} \equiv {\Delta}g_{{{{\mathrm{ad}}}}}A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{\Sigma}\), where ∆gad stands for the net difference of the free energy of adsorption per mole of adsorbed nanoparticles. At equilibrium, ∆gad is related to the thermodynamic equilibrium constant Ke via Van‘t Hoff’s equation for adsorption ∆gad = −RTln(Ke) with Ke the thermodynamic equilibrium constant of adsorption. The total Gibbs free energy of the system d∆Ga becomes finally \({{{\mathrm{d}}}}{\Delta}G_{{{\mathrm{a}}}} = k_{{{\mathrm{B}}}}TN_{{{\mathrm{A}}}}( {ln( {\frac{{\theta _{{{\mathrm{p}}}}}}{{1 - \theta _{{{\mathrm{p}}}}}}} ) - ln( {x_{{{\mathrm{p}}}}})} )A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{\Sigma} - RTln( {K_{{{\mathrm{e}}}}} )A\,{{{\mathrm{d}}}}m_{{{\mathrm{p}}}}^{\Sigma} \equiv 0\) at equilibrium. This leads finally to \(- lnK_{{{\mathrm{e}}}} + ln\left( {\frac{{\theta _{{{\mathrm{p}}}}}}{{1 - \theta _{{{\mathrm{p}}}}}}} \right) - ln\left( {x_{{{\mathrm{p}}}}} \right) = 0\), which is known as an adsorption isotherm for ideal dispersions or solutions. The equilibrium constant Ke is for ideal cases related to the dimensional Langmuir equilibrium constant \(K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}}\), which can be traditionally described by the equilibrium adsorption reaction: cp + [*] ⇆ [P − *], where cp is the nanoparticle molar bulk concentration, [*] the surface molar concentration of empty adsorption sites and [P − *] the surface molar concentration of adsorbed nanoparticles, respectively. If we define \({\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}}\) as the maximum surface concentration, we can write \(\left[ \ast \right] + \left[ {P - \ast } \right] = {\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}}\), which is equivalent to defining the surface coverage as \(\theta _{{{\mathrm{p}}}} = \frac{{\left[ {P - \ast } \right]}}{{{\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}}}}\) and therefore \(\frac{{\left[ \ast \right]}}{{{\Gamma}_{{{{\mathrm{p}}}},{{{\mathrm{max}}}}}^{{{\mathrm{{\Sigma}}}}}}} \equiv 1 - \theta _{{{\mathrm{p}}}}\). Note that later, we will use the notation ΓpΣ for [P − *]. Thermodynamically, \(K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}} = \frac{{\left[ {P - \ast } \right]}}{{c_{{{\mathrm{p}}}}\left[ \ast \right]}} = \frac{{\theta _{{{\mathrm{p}}}}}}{{c_{{{\mathrm{p}}}}\left( {1 - \theta _{{{\mathrm{p}}}}} \right)}}\). As cp has unity moles per unit volume, \(K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}}\) has unity volume per mole. Furthermore, as Ke is dimensionless, this means that we can define \(K_{{{\mathrm{e}}}} = c_{{{\mathrm{t}}}}K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}}\), where ct must have unity moles per volume. Similar discussions on the various definitions of Ke and \(K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}}\) have been performed in the literature, indicating that Ke in Van’t Hoff’s equation is dimensionless and that \(K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}}\) in the Langmuir’s adsorption equation has a dimension depending on the concentrations, confirming this analysis25,26. We can also deduce (in dilute systems, cf ≈ ct, with cf and ct the molar concentrations of the base fluid and the bulk phase, respectively) that ct can be represented by the molar concentration of the bulk phase25,26. Filling this in the adsorption isotherm gives finally \(- ln\left( {c_{{{\mathrm{t}}}}K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}}} \right) + ln\left( {\frac{{\theta _{{{\mathrm{p}}}}}}{{1 - \theta _{{{\mathrm{p}}}}}}} \right) - ln\left( {x_{{{\mathrm{p}}}}} \right) = 0\), which (keeping in mind that xpct = cp) simplifies to \(\frac{{\theta _{{{\mathrm{p}}}}}}{{1 - \theta _{{{\mathrm{p}}}}}} = K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}}c_{{{\mathrm{p}}}}\), which is the well-known Langmuir’s adsorption isotherm, subject to further discussion in the next section. This can be rearranged into
The equilibrium adsorption constant Ke could be calculated thermodynamically via Van’t Hoff’s relation. However, experimental values for the molar adsorption enthalpies and entropies are not readily available for the studied nanoparticle dispersions and especially not for various concentrations. Other expressions and methods make use of more available surface energies and surface tensions. However, even if one may perform such measurements, such a procedure would not allow an analytical physics-based analysis of the behaviour of the surface tension and would not offer the understanding of the underlying mechanisms for the various surface tension behaviours. Therefore, it would not align with the purposes of this work. In order to obtain theoretical parameters, independent of the experimental surface tension data, experimental regression procedures or any fitting methods, one of the often-used ways is to use a kinetic model. Adsorption and desorption are often described kinetically. Material properties for kinetic models are readily available for solid–liquid interfaces and the methods are widely used and understood. As less data are available for liquid–fluid interfaces, it is the question whether similar kinetic models would be applicable. One can argue that the adsorption of surface-charged nanoparticles (an important method to obtain stable dispersions) on liquid-fluid interfaces (often charged with the same sign) can be approximated by adsorption on solid–liquid interfaces. Although subject to more investigation, it has already been applied successfully for liquid–fluid interfaces24. This motivates that within such a reasonable assumption the equilibrium adsorption constant for the nanoparticle dispersions can be obtained without fitting. The interpretation of underlying mechanisms would benefit from such a physics-based approach.
Surface kinetics
It remains to find the equilibrium adsorption constant \(K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}}\) or for later convenience, a dimensionless version Kp thereof. ‘Surface adsorption isotherm’ presented the thermodynamic theory behind the Langmuir adsorption isotherm. It was mentioned that unavailable experimental data for the nanoparticle dispersions studied here and the aim to provide for a physics-based model encourage the use of another way. Commonly, the equilibrium adsorption constant is determined kinetically, where material properties necessary for the model are readily available. The kinetic model is based on an equilibrium between standard adsorption and desorption kinetics and is treated in details in the literature27,28,29,30. We mention the main points here. Note that desorption becomes relevant when the energy of particle trapping is of the order of the thermal energy. Adsorption (with standard rate ka) depends on the bulk concentration cp and the available adsorption sites (1 − θp). Desorption (with standard rate kd) depends on the adsorbed nanoparticles θp per specific surface area of adsorbed nanoparticles ςp. This writes as
From kinetic considerations, it can be stated that nanoparticle accumulation, through a flux balance equation, at the interface is given by \(\frac{1}{{\varsigma _{{{\mathrm{p}}}}}}\frac{{\partial \theta _{{{\mathrm{p}}}}}}{{\partial t}} = j_{{{\mathrm{a}}}} - j_{{{\mathrm{d}}}}\), where we remind that here ςp is the specific surface area per mole of nanoparticles. At quasi-stationarity, i.e. \(\frac{{\partial \theta _{{{\mathrm{p}}}}}}{{\partial t}} = 0\), we have from Eqs. (15) and (16) that
Comparison with (14) learns that \(K_{{{\mathrm{p}}}}^{{{\mathrm{d}}}} = \frac{{k_{{{\mathrm{a}}}}}}{{k_{{{\mathrm{d}}}}}}\varsigma _{{{\mathrm{p}}}}\). As the molar concentration can also be expressed into the volume fraction φ by \(c_{{{\mathrm{p}}}} \equiv \frac{{\rho _{{{\mathrm{p}}}}}}{{M_{{{\mathrm{p}}}}}}\varphi\), we can rewrite (17) as
This allows defining a dimensionless Langmuir’s equilibrium constant \(K_{{{\mathrm{p}}}} \equiv \frac{{k_{{{\mathrm{a}}}}}}{{k_{{{\mathrm{d}}}}}}\frac{{\rho _{{{\mathrm{p}}}}}}{{M_{{{\mathrm{p}}}}}}\varsigma _{{{\mathrm{p}}}} = \frac{{k_{{{\mathrm{a}}}}}}{{k_{{{\mathrm{d}}}}}}\frac{1}{{{{{\mathcal{L}}}}_{{{\mathrm{p}}}}}}\), and relating the surface coverage with the bulk volume fraction as
If we assume that particle transport occurs under a quasi-linear and stationary diffusional regime (this is a valid approximation because of the very small relaxation time), it has been shown that general analytical solutions for the adsorption and desorption constants can be obtained27,28,29,30, i.e. \(\frac{{k_a}}{{k_d}} = \delta _m\sqrt {\frac{{\pi k_BT}}{{\left| {{\Phi}_m} \right|}}} e^{ - \frac{{{\Phi}_m}}{{k_BT}}}\), which finally leads to
where Φm is the total potential energy, Φt, at a distance z = δm, i.e. \({{{\mathrm{{\Phi}}}}}_{{{\mathrm{m}}}} = \left. {{{{\mathrm{{\Phi}}}}}_t} \right|_{z = {\updelta}_{{{\mathrm{m}}}}}\). The total potential energy stands here for the potential energy between a particle and the liquid-air interface, being composed of many mechanisms. The DLVO theory mentions that the most important interactions are the electrostatic \(\left( {{{{\mathrm{{\Phi}}}}}_{{{{\mathrm{p}}}} - {{{\mathrm{{\Sigma}}}}}}^{{{{\mathrm{EDL}}}}}} \right)\) and van der Waals \(\left( {{{{\mathrm{{\Phi}}}}}_{{{{\mathrm{p}}}} - {{{\mathrm{{\Sigma}}}}}}^{{{{\mathrm{vdW}}}}}} \right)\) interaction energies24,31,32,33. Image charge effects in the form of a repulsive particle-image \(\left( {{{{\mathrm{{\Phi}}}}}_{{{{\mathrm{p}}}} - {{{\mathrm{p}}}}\prime }^{{{{\mathrm{EDL}}}}}} \right)\) potential energy are esteemed to be of importance, the reason being that in cases of particles being oppositely charged to the interface, repulsion was still observed24,34. Non-DLVO interaction energies \(\left( {{{{\mathrm{{\Phi}}}}}_{{{{\mathrm{p}}}} - {{{\mathrm{{\Sigma}}}}}}^{{{{\mathrm{Hy}}}}}} \right)\), suggested to be of the Lewis acid-base type, also appear to be of great importance, such as hydrophilic repulsive interactions and hydrophobic attraction energies35,36,37,38. The electrostatic double layer interaction potential between a nanoparticle and a flat fluid–air interface is given by32
where εr, ε0, ee, ζp, ζΣ, and λD, are, respectively, the relative permittivity, the absolute permittivity, the elementary charge, the zeta potential of the nanoparticles, the zeta potential of the liquid–air interface and Debye length. Debye’s length is given by \(\lambda _{{{\mathrm{D}}}} = \sqrt {\frac{{\varepsilon _{{{\mathrm{r}}}}\varepsilon _0k_{{{\mathrm{B}}}}T}}{{2N_{{{\mathrm{A}}}}e_{{{\mathrm{e}}}}^2I}}}\), where I stands for the ionic strength of the base fluid. The potential energy between a particle, p, and its image, p′, in the phase at the other side of the fluid-air interface is given by refs. 24,34
where ζp′ stands for the zeta potential of the image particle, given by \(\zeta _{{{{\mathrm{p}}}}^\prime } = \frac{{2k_{{{\mathrm{B}}}}T}}{{e_{{{\mathrm{e}}}}}}{{{\mathrm{ArcSinh}}}}( {\frac{{\varepsilon _{{{\mathrm{r}}}} - \varepsilon _{{{{\mathrm{r}}}}^\prime }}}{{\varepsilon _{{{\mathrm{r}}}} + \varepsilon _{{{{\mathrm{r}}}}^\prime }}}{{{\mathrm{Sinh}}}}( {\frac{{\zeta _{{{\mathrm{p}}}}e_{{{\mathrm{e}}}}}}{{2k_{{{\mathrm{B}}}}T}}} )} )\)33. Here, εr′ is the relative permittivity of the phase at the opposite side of the interface opposed to the relative permittivity of the phase where the nanoparticles are dispersed, εr. The van der Waals potential energy between the nanoparticle and the interface is given by
where Ap−Σ is the non-retarded Hamaker constant for the particle–interface interaction, where the particle (p) interaction with air (a) through the base fluid (f) is assessed. This constant is derived by the theory of London-dispersion forces and is often approximated by the combining relation \(A_{{{{\mathrm{p}}}} - {{{\mathrm{{\Sigma}}}}}} = A_{{{{\mathrm{pfa}}}}} = \left( {\sqrt {A_{{{{\mathrm{pp}}}}}} - \sqrt {A_{{{{\mathrm{ff}}}}}} } \right)\left( {\sqrt {A_{{{{\mathrm{aa}}}}}} - \sqrt {A_{{{{\mathrm{ff}}}}}} } \right)\)39,40. Non-DLVO interaction energies may be considered as one potential energy, being either repulsive or attractive depending on the solid–water contact angle36. In another work, a Hydra parameter, depending on the hydrophobicity of the surface, was introduced in one expression, being either negative or positive, defining, respectively, a hydrophilic repulsive or hydrophobic attractive potential energy. The Hydra potential energy is given by refs. 36,37,41,42
where λ0 is a decay length, ϑ the radial liquid–solid static contact angle and z0 a constant of the value of 0.16 nm41,42. The total potential energy is given by \({\Phi}_t = {\Phi}_{p - {\Sigma}}^{EDL} + {\Phi}_{p - p\prime }^{EDL} + {\Phi}_{p - {\Sigma}}^{vdW} + {\Phi}_{p - {\Sigma}}^{Hy}\).
Material properties
Table 1 shows the material properties of the used nanodispersions at ambient temperature. Effect of temperature on solid properties is neglected. For the base fluids, only the densities are adapted for temperatures different than ambient. Since these values are well tabulated, not more attention is given. Some data are reported in the literature as a function of the mass fraction. If ξ is the nanoparticle mass fraction, ρp the nanoparticle density and ρf the fluid density, then the nanoparticle volume fraction φ can be calculated as \(\varphi = \frac{\xi }{{\rho _{{{\mathrm{p}}}}}}\left( {\frac{\xi }{{\rho _{{{\mathrm{p}}}}}} + \frac{{1 - \xi }}{{\rho _{{{\mathrm{f}}}}}}} \right)^{ - 1}\). Table 1 also shows general physical constants used in the model.
Equations (20)–(24) allow calculating the equilibrium constant Kp. Several data are needed for this calculation. These data are collected from the literature and tabulated in Table 2. A summary of the variables and their meaning is given in Table 3.
It should be noted that it is difficult to obtain precise values for the parameters ϑ, δm, ζint, I, λ0, and ζp, which need some discussion. Reasonable values can be obtained from experimental data for ϑ, δm, ζint, I. The minimum thickness between the nanoparticle and the interface at adsorption, δm, is often assumed to be of the order of δm = 0.5 nm27,43. For the interface zeta potential, ζint, the approximated mean value of ζint = −40 mV is taken for water44,45. For ethanol, tri-ethylene glycol, ethylene glycol and glycerol the same value is assumed, while n-decane, n-dodecane and n-hexadecane are considered to be an oily liquid as hexane and a value of ζint = −10 mV is taken44. The ionic strength of a fluid is somewhat an unknown. However, works have indicated that for deionized water, typical ionic strength values are measured of the order of I = 1 mol/m346. This value is assumed for all the fluids used. The values for λ0 and ζp depend strongly on the experimental conditions and only ranges can be indicated. Decay lengths, λ0, of values up to 2.2 nm are reported for several systems20,37,41. The zeta-potentials ζp of nanodispersions were typically found to be approximately between −75 and −25 mV20,34,43. Educated guesses, not affecting the analysis in this work, for these two parameters within these indicated ranges are implemented in Table 4 for the calculation of the equilibrium constant. The obtained equilibrium constants for the nanoparticle dispersions are shown later in Table 5.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Results and discussion
Comparison of model with experimental data
Gibbs adsorption isotherm \({{{\mathrm{d}}}}\gamma = - {\Gamma}_{{{\mathrm{p}}}}{{{\mathrm{d}}}}\eta _{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\) can now be integrated. We use Eq. (6) for Γp (with (19) for θp) and Eq. (12) for \(\eta _{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}}\). The surface tension of nanoparticle dispersions is finally given by
where γf is the surface tension of the base fluid, Rg the universal gas constant, T the temperature, KΣ given by (8), Kp given by (20), ωp given by (13) and φ the nanoparticle volume fraction. The equilibrium constant is a kinetic parameter obtained by models from the literature, summarised in ‘Surface kinetics’. The other parameters are developed in this work using geometric principles and characteristic length scales, which would, for clarity, benefit from a summary in Table 4.
Table 5 shows the nanoparticle dispersions that we consider in this work. For completeness, the calculated numerical parameters that are necessary for determining the surface tension as a function of the volume fraction, i.e. γf, KΣ, ωp and \({\Gamma}_{{{\mathrm{b}}}}^{{{\mathrm{{\Sigma}}}}}\), are given in Table 5 for these nanoparticle dispersions.
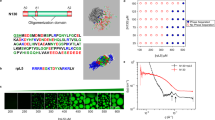
Different kinds of behaviours for the surface tension of nanoparticle dispersions are represented by several experimental case studies, representing different materials (for both the nanoparticles and liquids) with different sizes6,9,10,11,19,38,47,48. The surface tension is calculated from Eq. (25) for these nanoparticle dispersions and compared to the experimental data in Fig. 3a–f. The experimental data in Fig. 3 show different types of behaviours and the present model has an overall good agreement with those data. This motivates to use the model to explain these observations.
a Al2O3-W ( ,
,  ), Al2O3-Ws (
), Al2O3-Ws ( ,
,  ), Laponite-W (
), Laponite-W ( ,
,  ) and ZnO-EG (
) and ZnO-EG ( ,
, ), b Al2O3-D (
), b Al2O3-D ( ,
,  ), Al-D (
), Al-D ( ,
,  ) and B-D (
) and B-D ( ,
,  ), c Al2O3-E (
), c Al2O3-E ( ,
,  ), Al-E (
), Al-E ( ,
,  ) and B-E (
) and B-E ( ,
,  ), d Al2O3-TEG (
), d Al2O3-TEG (
 ,*) and MgO-TEG (
,*) and MgO-TEG ( ,
, ), e SiO2-W (
), e SiO2-W ( ,
,  ), Ag-W (
), Ag-W (
 ,
,  ), (dl)Au-D (
), (dl)Au-D ( ,
,  ), (dl)Au-DD (
), (dl)Au-DD ( ,
,  ) and (dl)Au-HD (
) and (dl)Au-HD ( ,
,  ), the inset being a zoom of the (dl)Au-D system concentrating at the region of smaller φ-values, f a magnification of the systems (dl)Au-D (
), the inset being a zoom of the (dl)Au-D system concentrating at the region of smaller φ-values, f a magnification of the systems (dl)Au-D ( ,
,  ), (dl)Au-DD (
), (dl)Au-DD ( ,
,  ) and (dl)Au-HD (
) and (dl)Au-HD ( ,
,  ). The studied systems are indicated in the form “nanoparticle-fluid”. The model values are indicated by lines, while the experimental data are given by markers in the form (line,marker).
). The studied systems are indicated in the form “nanoparticle-fluid”. The model values are indicated by lines, while the experimental data are given by markers in the form (line,marker).
Non-occupancy contribution
We can divide the surface chemical potential, \(\eta _{{{\mathrm{p}}}}^{{{\mathrm{{\Sigma}}}}} \equiv \eta _{{{\mathrm{p}}}} + \eta _{{{{\mathrm{NO}}}}}\), in a part that stands for the contribution by non-occupied sites ηNO ≡ −ωpRgTln(1 − θp) and a part that represents the contribution of the adsorbed nanoparticles ηp ≡ RgTln(θp). We can also split the surface tension change into two parts as γ − γf = ∆γp + ∆γNO, where
Equations (26) and (27) show the multiplication of two terms in the integral. The term \(( { - {\Gamma}_{{{\mathrm{b}}}}^{{{\mathrm{{\Sigma}}}}}\frac{{\partial \eta _{{{{\mathrm{NO}}}}}}}{{\partial \varphi }}} )\) in Eq. (27) stands physically for the change in the surface chemical potential of non-occupied adsorption sites per unit surface upon a change in the nanoparticle bulk concentration. It is worthy to note that this emphasises the influence that non-adsorbed bulk nanoparticles have on the surface chemical potential of non-occupied sites, called here the non-occupancy effect. For later use, we assign for this term the following symbol
A larger absolute value of \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) means a greater non-occupancy effect, i.e. one bulk nanoparticle will have more impact on the surface energy (and thus the surface chemical potential) of the non-occupied sites. Note that an equivalent analysis can be made for the adsorbed nanoparticles contribution (see Eq. (26)) through the term \(( { - {\Gamma}_{{{\mathrm{b}}}}^{{{\mathrm{{\Sigma}}}}}\frac{{\partial \eta _{{{\mathrm{p}}}}}}{{\partial \varphi }}} ) = {{{\mathcal{H}}}}_{{{\mathrm{p}}}}\), called the occupancy effect. The term \(( {\frac{{{\Gamma}_{{{\mathrm{p}}}}}}{{{\Gamma}_{{{\mathrm{b}}}}^{{{\mathrm{{\Sigma}}}}}}}} )\) stands for the excess surface concentration normalised by the surface-equivalent of the bulk concentration. We will assign the following symbol to it
A positive value of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) means a high degree of adsorption of nanoparticles (decreasing the surface energy), while a negative value indicates a preference of nanoparticles to remain dispersed in the bulk. In summary, the sign of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) indicates whether the surface tension will increase or decrease and the value of \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) with what amplitude. As both depend on φ, it is easy to understand that the magnitude and variation of the surface tension might be different as a function of φ, generating the different observed trends. More interestingly, Table 5 shows that the several nanoparticle dispersions considered here have quite different values for the nanoparticle equilibrium adsorption constant Kp. This implies that this property plays an important role in determining the behaviour of the surface tension. Note that the parameters \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) and \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) also depend on the surface coverage θp, which is linked to φ through Kp. This encourages to consider φ and the property Kp as suitable parameters for the present analysis.
We should define a certain reference system that represents a nanoparticle dispersion of which we can change freely the parameters φ and Kp and monitor their influence on the behaviour of \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) and therefore on that of the surface tension. To perform numeric demonstrations, allowing the quantification of our analysis, we may choose data from any dispersion. Only because the B-D system is an example of an interesting decrease-increase behaviour, its data are used for the present demonstration. As the discussion should be followed in a general sense, and we only use the physical properties of this dispersion but changing freely Kp, it is appropriate to name it differently: the reference system R1.
Figure 4a shows the surface tension of the R1 system as a function of φ for various imposed Kp values and two different nanoparticle sizes.
a γ of the R1 system vs φ for theoretically imposed Kp values ( =~0,
=~0,  = 10,
= 10,  = 102,
= 102,  = 103,
= 103,  = 5*103 for 2ap = 46 and 5 nm. b \(\frac{{{\Delta}\gamma _{{{\mathrm{i}}}}}}{{R_{{{\mathrm{g}}}}T}}\) with i = p,NO vs φ of the R1 system, where thin and thick lines stand for Kp = 10 and 5 * 103, respectively, and dashed and solid lines stand for i = p and i = NO, respectively, for 2ap = 46 and 5 nm. Note that all the dashed lines are significantly horizontal. c \(\frac{{{\Delta}\gamma _{{{{\mathrm{p}}}},{{{\mathrm{NO}}}}}}}{{R_{{{\mathrm{g}}}}T}}\) of the R1 system vs Kp for φ = 0.001 (dashed line) and φ = 0.025 (solid line) and 2ap = 46 with three specific values of Kp based on the value from Table 5 (Kp* = 416): \(\frac{{K_{{{{\mathrm{p}}}} \ast }}}{{1000}}\) (
= 5*103 for 2ap = 46 and 5 nm. b \(\frac{{{\Delta}\gamma _{{{\mathrm{i}}}}}}{{R_{{{\mathrm{g}}}}T}}\) with i = p,NO vs φ of the R1 system, where thin and thick lines stand for Kp = 10 and 5 * 103, respectively, and dashed and solid lines stand for i = p and i = NO, respectively, for 2ap = 46 and 5 nm. Note that all the dashed lines are significantly horizontal. c \(\frac{{{\Delta}\gamma _{{{{\mathrm{p}}}},{{{\mathrm{NO}}}}}}}{{R_{{{\mathrm{g}}}}T}}\) of the R1 system vs Kp for φ = 0.001 (dashed line) and φ = 0.025 (solid line) and 2ap = 46 with three specific values of Kp based on the value from Table 5 (Kp* = 416): \(\frac{{K_{{{{\mathrm{p}}}} \ast }}}{{1000}}\) ( for φ = 0.001 and
for φ = 0.001 and  for φ = 0.025), Kp* (
for φ = 0.025), Kp* ( for φ = 0.001 and
for φ = 0.001 and  for φ = 0.025) and 100Kp* (
for φ = 0.025) and 100Kp* ( for φ = 0.001 and
for φ = 0.001 and  for φ = 0.025). On the second axis, Γp of the reference system vs Kp for φ = 0.001 (dashed line) and φ = 0.025 (solid line) and 2ap = 46, d \(\frac{{{\Delta}\gamma _{{{{\mathrm{p}}}},{{{\mathrm{NO}}}}}}}{{R_{{{\mathrm{g}}}}T}}\) of the R2 system vs Kp for φ = 0.001 (dashed line) and φ = 0.025 (solid line) and 2ap = 100. On the second axis, Γp of the R2 system vs Kp for φ = 0.001 (dashed line) and φ = 0.025 (solid line) and 2ap = 100, e \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) vs φ, and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) vs φ, for three specific values of Kp: \(\frac{{K_{{{{\mathrm{p}}}} \ast }}}{{1000}}\) (dotted line), Kp* (solid line) and 100Kp* (dashed line) for the R1 system, f \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) vs φ for three specific values of Kp: \(\frac{{K_{{{{\mathrm{p}}}} \ast }}}{{1000}}\) (dotted line), Kp* (solid line) and 100Kp* (dashed line) for the reference system and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) for Kp = Kp* (dotdashed line) for the Ag-W system.
for φ = 0.025). On the second axis, Γp of the reference system vs Kp for φ = 0.001 (dashed line) and φ = 0.025 (solid line) and 2ap = 46, d \(\frac{{{\Delta}\gamma _{{{{\mathrm{p}}}},{{{\mathrm{NO}}}}}}}{{R_{{{\mathrm{g}}}}T}}\) of the R2 system vs Kp for φ = 0.001 (dashed line) and φ = 0.025 (solid line) and 2ap = 100. On the second axis, Γp of the R2 system vs Kp for φ = 0.001 (dashed line) and φ = 0.025 (solid line) and 2ap = 100, e \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) vs φ, and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) vs φ, for three specific values of Kp: \(\frac{{K_{{{{\mathrm{p}}}} \ast }}}{{1000}}\) (dotted line), Kp* (solid line) and 100Kp* (dashed line) for the R1 system, f \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) vs φ for three specific values of Kp: \(\frac{{K_{{{{\mathrm{p}}}} \ast }}}{{1000}}\) (dotted line), Kp* (solid line) and 100Kp* (dashed line) for the reference system and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) for Kp = Kp* (dotdashed line) for the Ag-W system.
Note that for small Kp values, the surface tension remains significantly constant. As this is counter intuitive (usually non-adsorption should lead to an increase in the surface tension as this entails that Γp < 0), special attention will be given to the small Kp-case later. Figure 4a shows that, as Kp increases, γ(φ), for a given φ, first increases and then starts to decrease for small φ, followed by an overall decrease in the depicted φ -range. This first increase is also counter intuitive (usually more adsorption should lead to a decrease of the surface tension), a second point given special attention later. As Kp continues to increase, even a minimum in γ(φ) as a function of φ is observed, a third point discussed later as well. For even higher Kp, the surface tension shows a decreasing trend, which is what one would expect. Figure 4a also shows that a smaller nanoparticle size tends to favour a decrease in the surface tension. The latter effect can be understood by noticing that smaller nanoparticles will increase, for the same φ, the number of nanoparticles and therefore also the number of adsorbed nanoparticles, which leads eventually (for sufficiently small nanoparticles) to a decrease in the surface tension.
Let us, before entering into such an analysis, first determine what contribution to the surface tension is more important, ∆γp or ∆γNO. Figure 4b shows, through ∆γi (i = p,NO) scaled by RgT, that the contribution of the non-occupied sites (i = NO, the solid lines) is the main one, especially at larger Kp-values. The main reason for this is size-related. The nanoparticles are much larger than the fluid molecules, which constitute the adsorption sites. This means that the number of fluid molecules involved in the adsorption of a nanoparticle is quite large, expressed in large ωp-values, i.e. ωp ≫ 1, as Table 5 shows. So, it is now evident that the non-occupied site contribution of the surface chemical potential will be a key part in the following discussions.
Three counter-intuitive effects of K p on surface tension
Figure 4c shows ∆γNO and Γp for two volume fractions for the R1 system as a function of Kp. To facilitate the discussion three markers have been introduced for ∆γNO: one corresponding to the Kp from Table 5 for the B-D system (≡Kp*), a smaller \(\frac{{K_{{{{\mathrm{p}}}} \ast }}}{{1000}}\) one and a larger 100Kp* one. Figure 4d represents ∆γNO and Γp for two volume fractions as a function of Kp for a so-called R2 system, where we use the data from the Ag-W system, merely to illustrate that Kp has the same type of effect on the surface tension for whatever nanoparticle dispersion’s physical properties. Figure 4e shows \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\), \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) (combined contribution of the latter two) versus φ for three Kp values for the R1 system.
For small \(K_{{{\mathrm{p}}}}( { = \frac{{K_{{{{\mathrm{p}}}} \ast }}}{{1000}}} )\), Fig. 4e shows that \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) is significantly negative over the whole volume fraction range. Figure 4e shows that at small Kp there is a negligible contribution of the absolute value (being, by the way, always negative) of \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) (dotted blue line), it is significantly constant over the φ range. Although \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) is clearly negative (dotted red line in Fig. 4e), which stands for a negative surface excess concentration and would conventionally imply an increase in the surface tension, the resulting surface tension remains significantly constant as shown by Fig. 4a (straight solid lines). To understand why this is, we take the limit of Eq. (25) for Kp → 0, which gives
Filling in Eq. (30) the data for the R1 system reveals that \(\gamma _{K_{{{\mathrm{p}}}} \to 0} - \gamma _{{{\mathrm{f}}}} = O(10^{ - 5} - 10^{ - 4})\varphi\). This explains the seemingly (in reality, very weakly increasing) constant value of the surface tension. The reason behind the seemingly constant value of the surface tension at Kp → 0 lies in the value of ΓbΣ. From Table 4 one may easily deduce that \({\Gamma}_{{{\mathrm{b}}}}^{{{\mathrm{{\Sigma}}}}} \propto \frac{1}{{a_{{{\mathrm{p}}}}\ell _{{{\mathrm{f}}}}}}\). Nanoparticles have generally a larger size than fluid molecules and apparently large enough for ΓbΣ to be sufficiently small and hence a seemingly constant behaviour of the surface tension can be predicted. This explains the first counter-intuitive observation.
At Kp = Kp*, Fig. 4e shows that for a small range of φ we have \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\, > \,0\) (equivalent to Γp > 0, let us recall), while \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\) becomes bigger than for the previous case (see solid line in Fig. 4e as opposed to the dotted line). As \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}} < 0\) (always), this leads to \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\, < \,0\) (solid line in Fig. 4f). As we increase φ, Fig. 4e shows that \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) changes sign, i.e. \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\, < \,0\), with \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\) still being significantly larger than zero, resulting into \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\, > \,0\). As the surface tension depends on the integration of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) from 0 to φ, the surface tension will decrease as long as \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\, < \,0\) and increases as long as \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\, > \,0\), passing thus through a minimum. This analysis implies that the sign of the integrated surface of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) as a function of φ will determine the existence and positioning of a surface tension minimum. It is then logical to elaborate further on the dependence of \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) on φ. From Eqs. (6) and (19), we have that
and from Eqs. (19) and (28) that
The analysis of Eqs. (31) and (32) needs some mathematical considerations. From Eq. (31), we can easily deduce that \({{{\mathcal{D}}}}_{{{\mathrm{p}}}} = 0\) when \(\varphi = \frac{{K_{{{\mathrm{p}}}}K_{{{\mathrm{{\Sigma}}}}} - 1}}{{K_{{{\mathrm{p}}}}}}\) or φ = 0, but the latter is a trivial solution not considered further. The sign of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) depends on the values of Kp and KΣ. With respect to this, two cases can be considered: \(K_{{{\mathrm{p}}}} \le \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\) and \(K_{{{\mathrm{p}}}} > \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\). These cases will depend on the parameter KΣ. From Table 4, we can deduce that \(K_{{{\mathrm{{\Sigma}}}}} \propto f_\infty \frac{{\ell _{{{\mathrm{f}}}}}}{{a_{{{\mathrm{p}}}}}}\). The values of parameter f∞ (see Table 4) are constant for a certain shape and KΣ will depend on the ratio \(\frac{{\ell _{{{\mathrm{f}}}}}}{{a_{{{\mathrm{p}}}}}}\) much more than on f∞. Therefore, for the discussion of Eq. (31) we will only take into consideration \(K_{{{\mathrm{{\Sigma}}}}} \propto \frac{{\ell _{{{\mathrm{f}}}}}}{{a_{{{\mathrm{p}}}}}}\)
We treat the case \(K_{{{\mathrm{p}}}} \le \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\). When \(K_{{{\mathrm{p}}}} \le \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\), we have \(\frac{{K_{{{\mathrm{p}}}}K_{{{\mathrm{{\Sigma}}}}} - 1}}{{K_{{{\mathrm{p}}}}}} \le 0\) and it can be verified that this means that for all φ > 0 we have \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\, < \,0\). As \({{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) is always negative, the result is a strictly increasing surface tension. Depending on the amplitude of \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\), this increase will be significantly measurable or not. Focussing mainly on the value of Kp (the value of which may vary orders of magnitude more than ωp and ΓbΣ, see Table 5), two cases are thus possible: vanishing Kp values (Kp → 0) and non-vanishing Kp values (\(O(0) \ll K_{{{\mathrm{p}}}} \le \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\), where O(0) stands for a value that is so low that considering it zero would reflect a measured reality).
Equation (32) shows that for small Kp (e.g. Kp → 0), we have \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right| \to 0\), so that the surface tension increase is not noticeable. This has been discussed previously around Eq. (30) for small Kp values and a real example for this is the SiO2-W system (see Fig. 3e Table 5 where indeed \(K_{{{\mathrm{p}}}} \ll \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\)).
When Kp is significantly non-zero but not too large, i.e. \(O(0) \ll K_{{{\mathrm{p}}}} \le \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\) (defined as the lower-intermediary region), so that it can be verified that \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\) has a significant value, the increase of the surface tension will be measurable. A real example for this is the Ag-W system, where Table 5 shows that Kp ≫ O(0) and \(K_{{{\mathrm{p}}}} < \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\). Moreover, Fig. 4f illustrates this as well by a continuously increasing \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) (brown dot-dashed line). Departing from a fully desorbed case (Kp → 0), we can say that upon enhancement (Kp ≫ O(0)) of the surface adsorption kinetics (up to the limit \(K_{{{\mathrm{p}}}} \le \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\)), the surface tension behaviour becomes a strictly increasing one due to the combination of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}} < 0\) and a significant value of \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\). So, initially, a higher adsorption appears not to lead to a lower but rather to a higher surface tension. As \(\frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}} \propto \frac{{a_{{{\mathrm{p}}}}}}{{\ell _{{{\mathrm{f}}}}}}\), nanoparticles (having much higher size than the fluid molecules) allow for a much larger limit for Kp for which \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) remains negative. So, within this limit, upon increasing Kp, the strength of the non-occupancy effect \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\) becomes significant, whilst the excess surface concentration remains \({{{\mathcal{D}}}}_{{{\mathrm{p}}}} < 0\), resulting into a surface tension increase and not decrease. This explains the second counter-intuitive observation.
We treat the case \(K_{{{\mathrm{p}}}} > \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\). When \(K_{{{\mathrm{p}}}} > \frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\), we have a particular situation where \({{{\mathcal{D}}}}_{{{\mathrm{p}}}} > 0\) (and therefore a decreasing surface tension) for \(0\, < \,\varphi\, < \,\frac{{K_{{{\mathrm{p}}}}K_{\Sigma} - 1}}{{K_{{{\mathrm{p}}}}}}\) and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\, < \,0\) (increasing surface tension) for \(\varphi\, > \,\frac{{K_{{{\mathrm{p}}}}K_{\Sigma} - 1}}{{K_{{{\mathrm{p}}}}}}\), where we limit φ to a certain maximum value φmax, considered reasonable for typical nanoparticle dispersions (as discussed later). It can be verified that the surface tension is strictly decreasing if \(\frac{{K_{{{\mathrm{p}}}}K_{\Sigma} - 1}}{{K_{{{\mathrm{p}}}}}} \ge 1\), which means for \(K_{\Sigma} \ge 1 + \frac{1}{{K_{{{\mathrm{p}}}}}}\). This gives two regions, the one given by the latter condition and \(K_{\Sigma} < 1 + \frac{1}{{K_{{{\mathrm{p}}}}}}\).
The values given in Table 5 show that for nanoparticle dispersions typically KΣ ≪ 1. This means that Kp ≫ 1. The smaller \(\frac{{K_{{{\mathrm{p}}}}K_{\Sigma} - 1}}{{K_{{{\mathrm{p}}}}}}\) (due to larger nanoparticles as \(K_{\Sigma} \propto \frac{{\ell _{{{\mathrm{f}}}}}}{{a_{{{\mathrm{p}}}}}}\) or due to lower Kp) is, the closer the value of φ for which \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) changes sign will be to zero. As a consequence, this fits within the typical operating φ-ranges (φ < φmax), resulting into an observable minimum for the surface tension. This is the case for e.g. the B-D, Al-D, Al2O3-D systems (see Fig. 3b and Table 5 for the values). As, however, \(\frac{{K_{{{\mathrm{p}}}}K_{\Sigma} - 1}}{{K_{{{\mathrm{p}}}}}}\) becomes somewhat larger (smaller nanoparticles or higher Kp) the φ for which \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) changes sign will increase and may fall out of the aforementioned typical operating φ-ranges (φ > φmax). This results into a minimum that is no longer observed (mathematically still present, but experimentally not observed within typical φ-ranges) and the surface tension is virtually decreasing. This can also be numerically verified in Table 5 and visually in Fig. 3a for e.g. the Lap-W system. For systems with even higher Kp, Eq. (32) shows that \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\) as well as the negative part of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) become more important, confirmed by the 100Kp* case for the R1 system in Fig. 4(e) and (f) (dashed lines). The (dl)Au dispersions (see again Table 5 and also Fig. 3(e) and (f)) illustrate this situation by presenting surface tensions that decrease quickly for very low volume fractions. In summary, this means that an observable surface tension minimum is the result of a delicate balance between a sufficiently large, but not too small, nanoparticle (through \(K_{\Sigma} \propto \frac{{\ell _{{{\mathrm{f}}}}}}{{a_{{{\mathrm{p}}}}}}\)) and a sufficient amount of adsorption (through \(K_{{{\mathrm{p}}}} > \frac{1}{{K_{\Sigma}}}\)). This effect is therefore not an external one but stems from the same parameters that cause strictly increasing or decreasing behaviours, merely because the conditions are right. This explains the third counter-intuitive observation.
Mathematically speaking, a strict decrease (over the whole range 0 < φ < 1) in the surface tension would occur if, next to \(K_{{{\mathrm{p}}}} > \frac{1}{{K_{\Sigma}}}\), we have \(K_{\Sigma} \ge 1 + \frac{1}{{K_{{{\mathrm{p}}}}}}\). We have mentioned earlier that typically Kp ≫ 1. This means that, as approximation, we are practically dealing here with the condition KΣ ≥ 1, which entails that \(a_{{{\mathrm{p}}}} \le O(\ell _{{{\mathrm{f}}}})\). This would besides possibly quantum dots or surfactants, be rather untypical for nanoparticle dispersions. Therefore, this case can be disregarded as well for nanoparticle dispersions in general.
Trends and comments
In fine, it seems that the right combination between adsorption strength (Kp) and nanoparticle size (ap of which the main effect is represented by the parameter KΣ) is responsible for the different behaviours. Table 6 shows a summary of the different surface tension behaviours as a function of the parameters Kp and KΣ, in the form of the product KpKΣ.
Table 6 shows that as one goes from left to right, the value of KpKΣ increases by several orders of magnitude. This is by either increasing Kp, KΣ or both. Table 5 shows that KΣ for all the nanoparticle dispersions is of the order of 10−2−10−3. This means that when KpKΣ increases several orders of magnitude, this is mainly due to Kp. Nevertheless, for quantitative assessments, it is more convenient to mention KpKΣ.
In order to put the results in perspective, some additional comments are in place here. In the case \(K_{{{\mathrm{p}}}}\, > \,\frac{1}{{K_{{{\mathrm{{\Sigma}}}}}}}\) and \(K_{\Sigma}\, < \,1 + \frac{1}{{K_{{{\mathrm{p}}}}}}\), we have made a distinction for the surface tension behaviour between three ranges of orders of magnitude for KpKΣ. Mathematically, these three cases represent all a minimum in the surface tension somewhere in the range 0 < φ < 1. The reason for making the three distinctions is on a conceptual level, involving measured data and a defined framework. As Fig. 3 shows, most of nanoparticle dispersions that are used for engineering purposes (one might also think of medical ones as well, for that matter) present operating conditions that involve φ values that are often limited by a value φmax that is of the order of φmax ≈ O(10−2) or slightly higher, but still φmax < O(10−1). In Table 6, φmax is schematically indicated for the case \(K_{{{\mathrm{p}}}}\, > \,\frac{1}{{K_{\Sigma}}}\) and \(K_{\Sigma} < 1 + \frac{1}{{K_{{{\mathrm{p}}}}}}\) by blue vertical dotted lines, set to a same hypothetical value for the three images in question. It shows that as KpKΣ increases the minimum of the surface tension becomes less pronounced and shifts towards higher φ values (not on scale), falling out of the range limited by φmax. At φ values beyond φmax it is the question whether we can still speak of dispersions and we then might have to deal with another type of “fluid” with additional phenomena at the surface. When working with nanoparticle dispersions, we have limited the analysis within the range 0 < φ < φmax (named the “operating range”). As such, depending on the value of KpKΣ, the mathematical minimum of the surface tension may well be out of that range and therefore not observed nor experimentally measured. Then, it is justified to indicate conditions (that is, within the range 0 < φ < φmax), where we can observe a minimum in the surface tension (for KpKΣ ≈ O(100−101)) and where we observe a virtual decrease. Even for the virtual decrease of the surface tension, we have made a distinction between a “soft” decrease (KpKΣ ≈ O(102−103)) and a “steep” decrease (KpKΣ ≈ O(104−106), the upper limit 106 being indicative with respect to the observed experiments, but may conceptually be even higher). The soft decrease is defined as the surface tension having a steady decrease over the whole operating range, such as the Lap-W case. The steep decrease is characterised by a strong decrease of the surface tension for φ ≪ O(φmax) with a seemingly constant value afterwards, such as the dl(Au) dispersions.
For the parameter KΣ, we have mentioned that for nanoparticles we have \(K_{\Sigma} \propto \frac{{\ell _{{{\mathrm{f}}}}}}{{a_{{{\mathrm{p}}}}}}\), not considering f∞ in the discussions. There are, however, cases where this parameter may play a role. When strong repulsive forces are present or when the nanoparticle surfaces (because of their nature or their functionalization) are such that we cannot consider them as hard spheres, the maximum coverage may, respectively, decrease or increase, whereas the shape may also be altered by the stretching or compressing of the adsorbed nanoparticles. In such cases, additional considerations should be made in order to include these forces between nanoparticles49. One may say that these forces will be effective there where the nanoparticles are present at the interface, so that the surface tension of particle-laden interfaces is argued to be an effective magnitude49. In some cases, the nanoparticles are grafted with polymers, which may cause additional effects on the surface tension due to the dangling chains of the polymers50. When ions are present (one may think of electrolytes or charged organic molecules) strong coulomb interactions may also influence the maximum coverage.
The effect of the nanoparticle size has been mainly expressed through the parameter KΣ. It should be recalled that the nanoparticle size also figures in the parameter ωp. The parameter ωp (standing for the number of adsorption sites) can also quantitatively interfere with the magnitude of the surface tension change through its linear relation with the non-occupancy effect Eq. (32). Moreover, the parameter ωp, when much larger than unity, is responsible for the non-occupancy effect to outnumber the occupancy effect through the surface chemical potential (see Eq. (12)). Should it be around unity, the free energy contribution of the adsorbed nanoparticles would also be important for the chemical potential and our discussion would be different. Nevertheless, once it is established that for nanoparticles generally ωp ≫ 1, and that the variation of Kp is, as mentioned earlier, of far more importance for the non-occupancy effect, the variation of the parameter ωp is not given more attention in our analysis.
The size of the nanoparticles also matters from another point of view. The projection method necessitates that the radius of curvature (reciprocal of the curvature) should be much larger than the nanoparticle radius. In other words, the interface should be “flat” with respect to the size of the nanoparticles. If the pressure difference over the interface is negligible, Young’s equation (where the pressure difference is related to the surface tension and the interface curvature) predicts that such an assumption would be realistic.
In ‘Representation of an interfacial layer on a dividing surface’, we mentioned that we used half the surface to calculate the volume-to-surface ratio. A heuristic reason was employed for this, assuming that only half the surface facing the dividing surface would matter in the adsorption process for particles that are much larger than the fluid molecules that constitute the adsorption sites. As a verification, we performed surface tension calculations using cases with a fourth, a sixth and the whole particle’s surface to calculate the volume-to-surface ratio. It appeared that the heuristic choice we have made for the calculation of the volume-to-surface ratio, i.e. using half the nanoparticle’s surface, was the most appropriate one with respect to the experimental data. It would be interesting to investigate the degree of this participating surface experimentally. However, for this work, the heuristic choice we have made appeared to be sufficient.
It should be noted that the way Kp has been calculated assumes that it is enough to take into account the wettability of the nanoparticles in the potential energy. The DLVO theory is known to be used for adsorption on solid-liquid interfaces. In refs. 24,51 as well as in the present work, it is assumed that the DLVO theory, albeit extended, is applicable for liquid-fluid interfaces as well. Although already used by others24,51, such a kinetic model should be studied in more details. In addition, it would be encouraged to provide benchmark studies with experimental data on the adsorption coefficients of various nanoparticle adsorption on liquid–air (fluid) interfaces.
Finally, the present model considers the adsorption of nanoparticles alone in order to focus on this phenomenon. It would be interesting to generalise or adapt Eq. (3) for the inclusion of the adsorption of molecular species, which could generalise the model for the application of studying the surface tension of solutions containing surfactants or other (in)organic molecules. Should multiple adsorption occur, the thermodynamic model presented in this work lends itself to be extended starting, most importantly, from an adaptation of Eq. (3).
Mapping of the surface tension behaviour
The previous analysis has shown a general dependence of the surface tension behaviour on KpKΣ, where KΣ and Kp stand for the effect of nanoparticle size and adsorption strength, respectively. In order to quantify this dependence and map these behaviours, we choose four representative systems, having, respectively, seemingly constant, strictly increasing, minimum containing and virtually decreasing behaviours for the surface tension. Figure 5a shows the values of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\), \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\) and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) for these four nanoparticle dispersions, at two volume fractions, that have distinct behaviours with low to high KpKΣ in the following order: SiO2-W < Al2O3-W < B-D < Lap-W. Figure 5a shows that, although SiO2-W and Al2O3-W have comparable negative \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) values, \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) is only significant for Al2O3-W due to a much higher \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\), confirming the analysis in the previous section, which means a non-measurable increasing surface tension for SiO2-W and a measurable one for Al2O3-W. As KpKΣ increases, i.e. for B-D, we can see a positive \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) for φ = 0.005 and a negative one for φ = 0.01. As the value \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\) is significant enough, this results into a visibly negative \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) for φ = 0.005 and a positive one for φ = 0.01, meaning first a decrease and then an increase in the surface tension. For even larger KpKΣ, i.e. for Lap-W, we can see a positive \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) for both φ’s. With a large \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\), \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) is considerably negative for both φ’s, corresponding to a virtually decreasing surface tension behaviour that was observed for Lap-W.
a Competition of key parameters \(\left| {{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}} \right|\), \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) for the nanoparticle dispersions SiO2-W (1), Al2O3-W (2), B-D (3) and Lap-W (4) for two volume fractions: φ = 0.005, φ = 0.01. Note that for a better visualisation both the values of \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}\) and \({{{\mathcal{D}}}}_{{{\mathrm{p}}}}{{{\mathcal{H}}}}_{{{{\mathrm{NO}}}}}\) for only the Lap-W system have been divided by 5 and 2 for the cases φ = 0.005, φ = 0.01, respectively. b All the considered nanoparticle dispersion systems are resumed in a Kp − KΣ map, representing five observed γ-vs-φ behaviours: “significantly constant” where the change (proven to be mathematically an increase) in γ is not observable (less than 1%) on the 1 mN/m range, “strictly increasing” where ∂φγ > 0 over any φ-range, “distinct minimum” where a clear minimum is visible at operating φ ranges, “virtually decreasing” where ∂φγ < 0 at operating φ ranges and “stronger decrease” where ∂φγ decreases distinctly steeper than the previous case. It is to be reminded that the latter three cases are distinguished within the φ-range under which typical nanoparticle dispersions are used. Moreover, the latter two cases are conceptually the same but are distinguished for application or engineering purposes: much higher adsorption kinetics and/or smaller nanoparticles induce (although theoretically having the same tendency) for the observer a decrease that is much steeper and occurs at much lower nanoparticle concentrations, which justifies to make a distinction between them. The colours indicate qualitatively the transition from one region to another, whereas the model gives two mathematical limits: the limit KpKΣ = 1 (red dashed line) designates formally the crossover from ∂φγ|∀φ > 0 to ∂φγ|φ→0 < 0, while the limit \(K_{\Sigma} = 1 + \frac{1}{{K_{{{\mathrm{p}}}}}}\) (blue dashed line) stands for the crossover from ∂φγ|φ→0 < 0 to ∂φγ|∀φ < 0. Interestingly, b shows that the dispersions seem to correspond to sets of simultaneously increasing Kp and KΣ, indicated by the left-to-right diagonally up-going set of points. This confirms the link between KpKΣ and the behaviour of the surface tension.
In the present study, we aimed at proposing a framework, model and explanation dealing with the different behaviours of the surface tension of nanoparticle dispersions. We have seen that the adsorption strength (KpKΣ) and the nanoparticle size (through KΣ) collaborate or compete in determining these different tendencies. It is then interesting to map the surface tension behaviours of all the nanoparticle dispersions that were presented in Fig. 3 as a function of Kp and KΣ. Such a mapping is presented in Fig. 5b and gives the opportunity to tailor nanoparticle dispersions, e.g. through size (affecting KΣ) and surface properties (affecting Kp, since the surface of the nanoparticles have a direct influence on their adsorption strengths), for the envisioned effect of the surface tension.
Data availability
The data in this study are available upon reasonable request.
Code availability
The commercial software Mathematica has been used to analyse the results.
References
Akshai, A., Abdul Raouf, A. & Chaudhuri, R. G. Importance of interfacial and rheological properties in the suppression of uniform deposition to coffee ring pattern of zinc oxide nanofluids in the presence of anionic surfactants. Colloid Polym. Sci. 298, 587–594 (2020).
Machrafi, H. Universal relation between the density and the viscosity of dispersions of nanoparticles and stabilized emulsions. Nanoscale 12, 15081–15101 (2020).
Yamada, T. et al. Nanoparticle chemisorption printing technique for conductive silver patterning with submicron resolution. Nat. Commun. 7, 11402 (2016).
Carrillo-Berdugo, I. et al. Interface-inspired formulation and molecular-level perspectives on heat conduction and energy storage of nanofluids. Sci. Rep. 9, 7595 (2019).
Matin, N. S., Steckel, J. A., Thompson, J., Sarma, M. & Liu, K. Application of surface tension model for prediction of interfacial speciation of CO2‑loaded aqueous solutions of monoethanolamine. Ind. Eng. Chem. Res. 56, 5747–5755 (2017).
Tanvir, S. & Qiao, L. Surface tension of nanofluid-type fuels containing suspended nanomaterials. Nanoscale Res. Lett. 7, 226 (2012).
Khaleduzzaman, S. S., Mahbubul, I. M., Shahrul, I. M. & Saidur, R. Effect of particle concentration, temperature and surfactant on surface tension of nanofluids. Int. J. Heat. Mass Transf. 49, 110–114 (2013).
Pantzali, M. N., Kanaris, A. G., Antoniadis, K. D., Mouza, A. A. & Paras, S. V. Effect of nanofluids on the performance of a miniature plate heat exchanger with modulated surface. Int. J. Heat. Fluid Flow. 30, 691–699 (2009).
Kim, S. J., Bang, I. C., Buongiorno, J. & Hu, L. W. Surface wettability change during pool boiling of nanofluids and its effect on critical heat flux. Int. J. Heat. Mass Transf. 50, 4105–4116 (2007).
Ranjbar, H., Khosravi-Nikou, M. R. K., Safiri, A., Bovard, S. & Khazaei, A. Experimental and theoretical investigation on nano-fluid surface tension. J. Nat. Gas. Sci. Eng. 27, 1806–1813 (2015).
Moosavi, M., Goharshadi, E. K. & Youssefi, A. Fabrication, characterization, and measurement of some physicochemical properties of ZnO nanofluids. Int. J. Heat. Fluid Flow. 31, 599–605 (2010).
Bell, C. G., Breward, C. J. W., Howell, P. D., Penfold, J. & Thomas, R. K. Macroscopic modeling of the surface tension of polymer−surfactant systems. Langmuir 23, 6042–6052 (2007).
Ravera, F., Santini, E., Loglio, G., Ferrari, M. & Liggieri, L. Effect of nanoparticles on the interfacial properties of liquid/liquid and liquid/air surface layers. J. Phys. Chem. B 110, 19543–19551 (2006).
Wang, H., Gong, Y., Lu, W. & Chen, B. Influence of nano-SiO2 on dilational viscoelasticity of liquid/air interface of cetyltrimethyl ammonium bromide. Appl. Surf. Sci. 254, 3380–3384 (2008).
Hua, X., Bevan, M. A. & Frechette, J. Competitive adsorption between nanoparticles and surface active ions for the oil−water interface. Langmuir 34, 4830–4842 (2018).
Llamas, S., Torres, A. P., Liggieri, L., Santini, E. & Ravera, F. Surface properties of binary TiO2-SiO2 nanoparticle dispersions relevant for foams stabilization. Colloids Surf. A 575, 299–309 (2019).
Dong, L. & Johnson, D. T. The study of the surface tension of charge-stabilized colloidal dispersions. J. Dispers. Sci. Technol. 25, 575–583 (2004).
Olayiwola, S. O. & Dejam, M. Mathematical modelling of surface tension of nanoparticles in electrolyte solutions. Chem. Eng. Sci. 197, 345–356 (2019).
Chen, R. H., Phuoc, T. X. & Martello, D. Surface tension of evaporating nanofluid droplets. Int. J. Heat. Mass Transf. 54, 2459–2466 (2011).
Kubiak, K., Adamczyk, Z. & Ocwieja, M. Kinetics of silver nanoparticle deposition at PAH monolayers: reference QCM results. Langmuir 31, 2988–2996 (2015).
Hinrichsen, E. L., Feder, J. & Jossang, T. Geometry of random sequential adsorption. J. Stat. Phys. 44, 793–827 (1986).
Evans, J. W. Random and cooperative sequential adsorption. Rev. Mod. Phys. 65, 1281–1329 (1993).
Yazhgur, P. A. et al. Dynamic properties of mixed nanoparticle/surfactant adsorption layers. Soft Matter 9, 3305–3314 (2013).
Dugyala, V. R., Muthukuru, J. S., Mani, E. & Basavaraj, M. G. Role of electrostatic interactions in the adsorption kinetics of nanoparticles at fluid–fluid interfaces. Phys. Chem. Chem. Phys. 18, 5499 (2016).
Zhou, X. & Zhou, X. The unit problem in the thermodynamic calculation of adsorption using the Langmuir equation. Chem. Eng. Commun. 201, 1459–1467 (2014).
Liu, Y. Is the free energy change of adsorption. Correctly calculated? J. Chem. Eng. Data 54, 1981–1985 (2009).
Morga, M., Adamczyk, Z. & Kosior, D. Silica nanoparticle monolayers on a macroion modified surface: formation mechanism and stability. Phys. Chem. Chem. Phys. 19, 22721 (2017).
Adamczyk, Z. Particle adsorption and deposition: role of electrostatic interactions. Adv. Colloid Interface Sci. 100-102, 267–347 (2003).
Adamczyk, Z. Kinetics of diffusion-controlled adsorption of colloid particles and proteins. J. Colloid Interface Sci. 229, 477–489 (2000).
Ranke, W. & Joseph, Y. Determination of adsorption energies and kinetic parameters by isosteric methods. Phys. Chem. Chem. Phys. 4, 2483–2498 (2002).
Garbin, V., Crocker, J. C. & Stebe, K. J. Nanoparticles at fluid interfaces: exploiting capping ligands to control adsorption, stability and dynamics. J. Colloid Interface Sci. 387, 1–11 (2012).
Lin, S. & Wiesner, M. R. Exact analytical expressions for the potential of electrical double layer interactions for a sphere-plate system. Langmuir 26, 16638–16641 (2010).
Tantra, R., Schulze, P. & Quincey, P. Effect of nanoparticle concentration on zeta-potential measurement results and reproducibility. Particuology 8, 279–285 (2010).
Wang, H., Singh, V. & Behrens, S. H. Image charge effects on the formation of pickering emulsions. J. Phys. Chem. Lett. 3, 2986–2990 (2012).
van Oss, C. J. Long-range and short-range mechanisms of hydrophobic attraction and hydrophilic repulsion in specific and aspecific interactions. J. Mol. Recognit. 16, 177–190 (2003).
Borden, M. A. & Song, K. H. Reverse engineering the ultrasound contrast agent. Adv. Colloid Interface Sci. 262, 39–49 (2018).
Zeng, H. et al. Recent experimental advances on hydrophobic interactions at solid/water and fluid/water interfaces. Biointerphases 11, 018903 (2016).
Matsubara, H., Otsuka, J. & Law, B. M. Finite-size and solvent dependent line tension effects for nanoparticle at the air-liquid surface. Langmuir 34, 331–340 (2018).
Eichenlaub, S., Chan, C. & Beaudoin, S. P. Hamaker constants in integrated circuit metalization. J. Colloid Interface Sci. 248, 389–397 (2002).
Lefèvre, G. & Jolivet, A. Calculation of Hamaker constants applied to the deposition of metallic oxide particles at high temperature. Proc. Int. Conf. Heat. Exch. Fouling Clean. 8, 120–124 (2009).
Nguyen, A. V. Drelich, J., Colic, M., Nalaskowski, J., Miller, J. D. Bubbles: interaction with solid surfaces. In: Somasundaran P. (ed.) Encyclopedia of Surface and Colloid Science, London, 1, 1–29, (Taylor and Francis, 2006).
Yao, J., Han, H., Hou, Y., Gong, E., Yin, W. A method of calculating the interaction energy between particles in minerals flotation. Math. Probl. Eng., 2016, 8430745, (2016).
Varade, S. R. & Ghosh, P. Foaming in aqueous solutions of zwitterionic surfactant: effects of oil and salts. J. Disp. Sci. Technol. 38, 1770–1784 (2017).
Chaplin, M. Theory vs experiment: what is the surface charge of water? Water 1, 1–28 (2009).
Wenfa, N. G. Methodology Development for Environmental Microbiology: Medium Formulation and Surface Charge Analysis. MSc thesis, National University of Singapore, (2012).
Ishida, N. & Craig, V. S. J. Direct measurement of interaction forces between surfaces in liquids using atomic force microscopy. KONA Powder Part. J. 36, 187–200 (2019).
Wi, H. S., Cingarapu, S., Klabunde, K. J. & Law, B. M. Nanoparticle adsorption at liquid-vapor surfaces: influence of nanoparticle thermodynamics, wettability, and line tension. Langmuir 27, 9979–9984 (2011).
Das, S. K., Putra, N. & Roetzel, W. Pool boiling characteristics of nano-fluids. Int. J. Heat. Mass Transf. 46, 851–862 (2003).
Guzman, E. et al. Particle-laden fluid/fluid interfaces: physico-chemical foundations. J. Phys. Condens. Matter 33, 333001 (2021).
Alvarez, N. J., Anna, S. L., Saigal, T., Tilton, R. D. & Walker, L. M. Interfacial dynamics and rheology of polymer-grafted nanoparticles at air-water and xylene-water interfaces. Langmuir 28, 8052–8063 (2012).
Bizmark, N., Ioannidis, M. A. & Henneke, D. E. Irreversible adsorption-driven assembly of nanoparticles at fluid interfaces revealed by a dynamic surface tension probe. Langmuir 30, 710–717 (2014).
Médout-Marère, V. A simple experimental way of measuring the hamaker constant A11 of divided solids by immersion calorimetry in apolar liquids. J. Coll. Interf. Sci. 228, 434–437 (2000).
Takagishi, H., Masuda, T., Shimoda, T., Maezono, R. & Hongo, K. Method for the calculation of the Hamaker constants of organic materials by the Lifshitz macroscopic approach with DFT. J. Phys. Chem. A 123, 8726–8733 (2019).
Banachowicz, E. & Danielewicz-Ferchmin, I. Static permittivity of water in electric field higher than 108 V m−1 and pressure varying from 0.1 to 600 MPa at room temperature. Phys. Chem. Liq. 44, 95–105 (2006).
Leese, H., Bhurtun, V., Lee, K. P. & Mattia, D. Wetting behaviour of hydrophilic and hydrophobic nanostructured porous anodic alumina. Colloids Surf. A 420, 53–58 (2013).
Farrokhbin, M. et al. Surfactant mediated particle aggregation in nonpolar solvent. Phys. Chem. Chem. Phys. 21, 18866–18876 (2019).
Fini, M. N., Soroush, S. & Montazer-Rahmati, M. M. Synthesis and optimization of chitosan ceramic-supported membranes in pervaporation ethanol dehydration. Membranes 8, 119 (2018).
Masliyah, J.H., Bhattacharjee, S. Electrokinetic and Colloid Transport Phenomena, (John Wiley & Sons, 2006).
Rodrigues, S. P. Development of Hybrid Surface Treatments for Controlling Wettability and Improving Tribological Performance, PhD thesis, University of Coimbra, (2019).
Petong, P., Pottel, R. & Kaatze, U. Dielectric relaxation of H-bonded liquids. Mixtures of ethanol and n-hexanol at different compositions and temperatures. J. Phys. Chem. A 103, 6114–6121 (1999).
Chen, Z. et al. Halloysite nanotube-based electrospun mat: a novel support for zeolite membranes. R. Soc. Open Sci. 3, 160552 (2016).
Ahmadi, L. et al. Influence of an Al2O3 surface coating on the response of polymeric waveguide sensors. Opt. Express 25, 21 (2017).
Kang, X. et al. New insights for phase‐change immersion cooling enhancement of solar cells under high concentration ratios. Int. J. Energy Res. 42, 466–476 (2018).
Diana, A., Castillo, M., Brutin, D. & Steinberg, T. Sessile drop wettability in normal and reduced gravity. Microgravity Sci. Technol. 24, 195–202 (2012).
Liu, X., Wazne, M., Christodoulatos, C. & Jasinkiewicz, K. L. Aggregation and deposition behavior of boron nanoparticles in porous media. J. Coll. Interf. Sci. 330, 90–96 (2009).
Hudge, P. G., Pawar, R. N., Watode, B. D. & Kumbharkhane, A. C. Dielectric relaxation behavior of triethylene glycol [TEG]+water mixture as a function of composition and temperature using TDR technique. Ind. J. Pure Appl. Phys. 56, 269–275 (2018).
Borodinova, T. I., Styopkin, V. I., Kutsenko, V. E., Vasko, A. A. & Marchenko, O. A. Formation of gold nanoprisms on atomically flat mica surface. J. Mater. Sci. Nanotechnol. 5, 105 (2017).
Bergström, L. Hamaker constants of inorganic materials. Adv. Coll. Interf. Sci. 70, 125–169 (1997).
Bryk, P. et al. What is the value of water contact angle on silicon? Materials 13, 1554 (2020).
Tseng, H. Y. Using Novel Printing Techniques. PhD University of California, (2011).
Chiu, T. L., Mandal, H., Zhang, M., Yang, S. P. & Chuang, Y. T. Effects of anodic buffer layer in top-illuminated organic solar cell with silver electrodes.Int. J. Photoenergy 2013, (2013).
Shahin, A. & Joshi, Y. M. Physicochemical effects in aging aqueous laponite supsensions. Langmuir 28, 15674–15686 (2012).
Shang, J., Flury, M., Harsh, J. B. & Zollars, R. L. Contact angles of aluminosilicate clays as affected by relative humidity and exchangeable cations. Colloids Surf. A 353, 1–9 (2010).
Li, W. et al. Oil-in-water emulsions stabilized by Laponite particles modified with short-chain aliphatic amines. Colloids Surf. A 400, 44–51 (2012).
Sengwa, R. J., Kaur, K. & Chaudhary, R. Dielectric properties of low molecular weight poly(ethylene glycol)s. Polym. Int. 49, 599–608 (2000).
Pradhan, S., Mishra, S. & Acharya, L. Ethylene glycol as entrainer in 1-propanol dehydration: scrutiny of physicochemical properties of ethylene glycol+1-propanol binary mixture at different temperature. Int. J. Inn. Technol. Expl. Eng. 8, 12S (2019).
Patel, K. H. & Rawal, S. K. Contact angle hysteresis, wettability and optical studies of sputtered zinc oxide nanostructured thin films. Ind. J. Eng. 24, 469–476 (2017).
Acknowledgements
Financial support from BelSPo and the MAP Evaporation programme from ESA is acknowledged.
Author information
Authors and Affiliations
Contributions
H.M. developed the model, performed the calculations and comparison with experimental data, analysed the results, wrote and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Machrafi, H. Surface tension of nanoparticle dispersions unravelled by size-dependent non-occupied sites free energy versus adsorption kinetics. npj Microgravity 8, 47 (2022). https://doi.org/10.1038/s41526-022-00234-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41526-022-00234-3