Abstract
We have developed a strong-coupling perturbation scheme for a general doped Hubbard model around a particle-hole-symmetric reference system, which is free from the fermionic sign problem. Our approach is based on the lattice determinantal Quantum Monte Carlo (QMC) method in both continuous and discrete time versions for large periodic clusters in a fermionic bath. By considering the first-order perturbation in the shift of the chemical potential and the second-neighbor hopping, we are able to obtain an accurate electronic spectral function for a range of parameters that correspond to optimally doped cuprate systems at temperatures of up to T = 0.1t, which are challenging to access using straightforward lattice QMC calculations. We also discuss the formation of the pseudogap and the nodal-antinodal dichotomy for a doped Hubbard system with the interaction parameter U equal to the bandwidth and the optimal value of the next-nearest-neighbor hopping parameter \({t}^{{\prime} }\) for high-temperature superconducting cuprates.
Similar content being viewed by others
Introduction
Search for a numerically exact solution of the \(t-{t}^{{\prime} }-U\) Hubbard model in thermodynamic limit at arbitrary interaction strength, long-range hoppings and doping δ or, equivalently, chemical potential μ at low temperature T = 1/β is tremendously difficult. Modern computational approaches, based on the lattice determinantal Quantum Monte Carlo (QMC) methods have seen incredible progress in the half-filled case without \({t}^{{\prime} }\)1, but face an unacceptable fermionic sign problem for a general case related to cuprate high-temperature superconductivity (HTSC) problem, which is the main factor restricting the accuracy of QMC calculations for interacting fermions2,3,4,5. A very important and largely unresolved problem is related to the next-nearest-neighbor hopping \({t}^{{\prime} }\) in the Hubbard model and its role in the tendency towards superconductivity6,7,8,9,10,11,12. There are two recent successful attempts to resolve this long-standing problem using zero-temperature variational QMC scheme for realistic HTSC systems13 in combination with the DMRG scheme for the \(t-{t}^{{\prime} }-U\) Hubbard model for a large ribbon geometry14.
On the other hand, the new class of diagrammatic Monte Carlo scheme15 is claimed to have a “sign blessing” property which helps to reduce the effects of high-order diagrams. The state-of-the-art diagrammatic Monte Carlo scheme in the connected determinant mode (C-DET)16 based on efficient Continuous Time Quantum Monte Carlo(CT-QMC) scheme in the weak coupling technique(CT-INT)17 gives unprecedented accuracy for the doped Hubbard model18,19. It becomes possible to study the formation of the pseudogap already at the beginning of a strong coupling case with U/t = 618. Nevertheless, exponential convergence of the C-DET scheme for weak interactions20,21, turns to a divergence at large U values due to poles in the complex U-plane19. This means that calculations for interactions close to the bandwidth U/t ≈ 8 and temperature T/t ≈ 0.1 are still within a prohibited area in the phase diagram19.
There is a recent interesting attempt to use a dynamical variational QMC scheme for the doped Hubbard model22,23 which gives a very reasonable description of the spectral function. The existence of the pseudogap can be explained in the simple model of electron fractionalization and appearing of “dark” fermion which is supported by 2 × 2 cluster Dynamical Mean Field Theory (C-DMFT)10,24. Moreover, the experimental RIXS spectrum25 of doped cuprate materials can be interpreted in such a theoretical model of the pseudogap formation. Also, the general spectral function of doped Hubbard model can be obtained in such 4 × 4 dynamical cluster approximation26,27 the detailed k-dependent spectral function is beyond the scope of such small cluster DMFT. The larger cluster in the C-DMFT scheme for the doped case has an unacceptable fermionic sign problem within the QMC scheme. Recently, the importance of vertex corrections for pseudogap physics was discussed in the parquet formalism for dual fermions for large lattice model28.
In this paper, we discuss a different route to tackle the “sign problem” in the determinantal lattice QMC scheme and design a strong-coupling perturbative solution for a general Hubbard model. The starting point is related to the “reference system” idea29 which is basically quite simple and straightforward. The conventional choice of the noninteracting Hamiltonian as the reference system for the perturbation30 is justified by Wick’s theorem which allows to calculate exactly any many-particle Green’s functions: they are all expressed in terms of single-particle Green’s functions. The choice of single-site approximation like dynamical mean-field theory31 as the reference system leads to the dual fermion technique29,32. Actually, the reference system can be arbitrary assuming that we can calculate its Green’s functions of arbitrary order. Of course, in practice this is hardly doable.
At the same time, sometimes even taking into account the simplest, first-order diagram, seems to be quite successful. In the conventional weak-coupling expansion it is equivalent to the famous Hartree-Fock approximation33 which is able to catch a lot of important many-body physics including e.g. superconductivity within the BCS model. It can be shown34,35,36 that the unrestricted Hartree-Fock trial wave function is optimal within a very broad class of variational ground-state wave functions for different physical systems. It is worthwhile to mention here the very successful Peierls-Feynman-Bogoliubov variational principle37,38,39 which can be formulated in the path-integral scheme. In this case, a good variational estimate of the system’s free energy F with the Hamiltonian H1 is achieved on an optimal reference system with the Hamiltonian H0, namely \({F}_{1}\le {F}_{0}+{\langle {H}_{1}-{H}_{0}\rangle }_{0}\). One can hope therefore that even first-order corrections to the properly chosen reference system will already give a rich and adequate enough physical picture. At least, this is definitely an assumption worth checking.
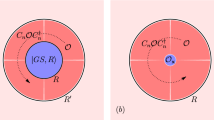
Here our reference system corresponds to the half-filled (μ = 0) particle-hole symmetric (\({t}^{{\prime} }=0\)) case (Fig. 1) where lattice Monte Carlo has no sign problem and the numerically exact solution for any practical value of U is possible within a broad range of temperatures40. Then we apply the lattice dual fermion perturbation theory29,32,41 to find the first-order perturbative corrections in μ and \({t}^{{\prime} }\). To this aim, it is sufficient to calculate the two-particle Green’s function, or, equivalently, four-leg vertex, which can be done accurately enough within the continuous time Quantum Monte Carlo. This approach can be considered as a far-going generalization of the Hartree-Fock approximation to the case of a dynamical effective interaction. Our reference system already has the main correlation effects in the lattice and shows characteristic “four-peak” structure with high-energy Hubbard bands around ± U/2 and antiferromagnetic Slater bands close to the insulating gap (which can be seen in the density of states in Fig. 1, left panel). After the dual fermion perturbation scheme the correlated metallic states with the DMFT-like “three peak” structure appear together with a pseudogap-like feature at a high temperature (the density of states in Fig. 1, right panel). The results for the strong-coupling case (U = W = 8t) with practically interesting values of the chemical potential and next-nearest-neighbor hoppings corresponding to cuprate superconductors have shown formation of a pseudogap and nodal-antinodal dichotomy (that is, well-defined quasiparticles in the nodal part of the Fermi surface and strong quasiparticle damping for the antinodal part) which makes this approximation a perspective for practical applications.
Results
Spectral function
We have calculated the Green’s function for the doped two-dimensional Hubbard model for a periodic 8 × 8 system with U/t = 8, \({t}^{{\prime} }/t=-0.3\) and μ = − 2.0 in units of t for β = 10 (in units 1/t) using a CT-INT version of the CT-QMC scheme17. Note that for the non-interacting Green’s function, we used the infinite-lattice limit with periodic boundary conditions for the calculated 8 × 8 system (see Section METHODS). This scheme reduces the cluster-size dependence for the bare Green’s function: in particular, the local one does not depend at all on the choice of the “simulation box”. On the other hand, it may underestimate the effect of U-interactions, since it appears only in the calculated cluster. This may explain a small gap in the half-filled reference system compared to a standard lattice determinantal QMC scheme42.
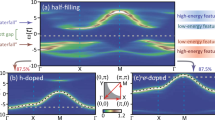
The results for the first-order dual-fermion perturbation from the half-filled system indicate the formation of correlated pseudogap electronic structure. Figure 2 shows the color map of the spectral function along the irreducible path (Γ−X−M−Γ) in the square Brillouin zone. For analytical continuation, the newly developed scheme43 was used.
Several characteristic features of the correlated metallic phase in generic cuprate systems can be detected: formation of an extended pseudogap region around the X-point towards the M-point, a shadow antiferromagnetic band at energy −2t near the M-point, a strongly renormalized metallic band near the nodal point around ΓM/2. Overall, the spectral function for U = W clearly shows strong correlation features of the electronic structure far beyond a simple renormalized-band paradigm.
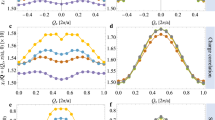
In order to see more clearly the pseudogap and nodal-antinodal dichotomy we plot the energy dependence of two spectral functions at the X- and ΓM/2-points in the Brillouin zone (Fig. 3). While at the X = (π, 0)-point there is a reasonably deep pseudogap formation already at β = 10, the nodal spectral function at (π/2, π/2) has correlated metallic behavior. A more unusual feature of the strong-coupling spectral function in Fig. 2 is related to a “shark mouth” pseudogap dip starting at X in the direction of M until the half way. One can see from the energy dependence of the spectral function in the direction of X−M (Fig. 4, middle panel) that the pseudogap splitting of the sharp quasiparticle peak at zero for the XM/4 point is even larger than at the X-point. The same feature was observed for a self-energy in the diagrammatic Monte Carlo (C-DET) investigation of the doped Hubbard model at U/t = 618. We would like to point out that all these effects are not simply an artifact of the analytical continuation with the MaxEnt scheme and can be detected by inspection of the original complex Matsubara Green’s function from DF-QMC calculations (Fig. 5). If we compare the X = (π, 0) and XM/4 = (π, π/4) points then both quasiparticle peaks located almost at the Fermi energy (the real part of G(k, ωn) is close to zero, but the pseudogap or upturn of the imaginary part of G(k, ωn) for the first Matsubara frequencies are more pronounced at the (π, π/4)-point. We have also checked this characteristic feature for the Hirsch-Fye QMC scheme44 and different MaxEnt implementations. The general structure of this spectral function is similar to recent results of dynamical variational Monte Carlo schemes22,23.
Fermi surface
We plot a broadened Fermi surface using the momentum-dependent spectral function for the first Matsubara frequency (Fig. 6). Comparison with the non-interacting tight-binding Fermi surface for the same doping shows a large region of the pseudogap around the X-point and formation of Fermi arcs near the nodal point. Moreover, one can understand that the pseudogap is more pronounced a bit away from the X-point towards the M-point, where the non-interacting Fermi surface crosses the Brillouin zone. We also compare the Fermi surface plot for smaller values of U/t = 5.6, which was investigated in the diagrammatic Monte Carlo technique45,46; this value is related to a plaquette degenerate point12. While the Fermi surface for small U/t = 5.6 agrees well with the results of the diagrammatic Monte Carlo approach46 and resembles the tight-binding one with only large broadening around the X-point, the U/t = 8 results show already a formation of the pseudogap and Fermi arcs, that is, a nodal-antinodal dichotomy.
Fermi surface of the square-lattice Hubbard model or k-dependent spectral function at the first Matsubara frequency \(-\frac{1}{\pi }G({{{\bf{k}}}},{\omega }_{0})\) for dual fermion QMC (CT-INT) with \({t}^{{\prime} }/t=-0.3\), β = 10 and U/t = 8, μ = − 2.0 (a) U/t = 5.6, μ = − 0.9 (b). The non-interacting Fermi surface with the same doping is shown for comparisson as a white contour.
Discussion
We developed, for Hubbard-like correlated lattice models, the first-order strong-coupling dual fermion expansion in the shift of the chemical potential (doping) and in the second-neighbor hoppings (\({t}^{{\prime} }\)). The starting reference point corresponds to the half-filled particle-hole symmetric system which can be calculated numerically exactly, without the fermionic sign problem. For a physically interesting parameter range of cuprate-like systems (around 10% doping and \({t}^{{\prime} }/t=-0.3\)0 we can obtain a reasonable Green’s function for a periodic 8 × 8 lattice for the temperature T = 0.1t. The formation of the pseudogap around the antinodal X-point and the nodal-antinodal dichotomy are clearly seen in the present approach.
We would like to point out a few main reasons why such a “super-perturbation” scheme works: first of all, the reference system already contains the main correlation effects which result in the four-peak structure of the density of states for the half-filled lattice Monte-Carlo calculations42; second, the first-order strong-coupling perturbation relies on the lattice four-point vertex γ1234 (Eq. (7)) which is obtained numerically exactly and has all the information about the spin and charge susceptibilities of the lattice; and third, if the dual perturbation Green’s function \({\tilde{G}}_{12}^{0}\) (Eq. (6)) is relatively small, results will be reasonable. The complicated question of convergence for such a dual-fermion perturbation can be checked numerically by calculating the second-order contribution in \({\widetilde{\Sigma }}_{12}\). For this term, one needs to calculate in the lattice QMC a six-point vertex γ(6) which will be also a direction of future developments. In principle, one can also discuss an instability towards antiferromagnetism or d-wave superconductivity, introducing symmetry-breaking fields8, which we also plan to investigate.
It is worthwhile to mention that for the starting reference system, we can choose not only the half-filled case, but any doped case where the sign problem is mild, so we can use a QMC calculation to expand this numerically exact solution to “Terra incognita” regions where the sign problem is unacceptable for direct QMC calculations. Recently, the new interesting class of a “sign-free”47 or “mild-sign”48,49 lattice models related to the spin-fermions problems or the magic-angle twisted bilayer graphene for integer feeling were discovered. One can use such new “reference systems” together with the proposed dual-fermion QMC scheme for general non-integer doping or more complicated interacting lattice systems.
Methods
We start with the general version of the cluster dual fermion scheme32,50 for \(t-{t}^{{\prime} }-U\) square lattice Hubbard model. The general strategy of the dual fermion approach as a strong coupling theory is related to formally exact expansion around an arbitrary reference system29.
Hamiltonian
The simplest model describing interacting fermions on a lattice is the single-band Hubbard model, defined by the Hamiltonian
where tij is the hopping matrix elements including the chemical potential μ in the diagonal elements.
where \({n}_{i\sigma }={c}_{i\sigma }^{{\dagger} }{c}_{i\sigma }^{}\). We introduce a “scailing” parameter α = (0, 1), which defined a reference system H0 for α = 0 which corresponds to the half-filled Hubbard model (μ0 = 0) with only nearest neighbors hoppings (\({t}_{0}^{{\prime} }=0\)) and final system H1 for α = 1 for given μ and \({t}^{{\prime} }\). Notes, that long-range hoping parameters can be trivially included similar to \({t}^{{\prime} }\).
Real space scheme
For the super-perturbation in the lattice Monte-Carlo scheme, we use a general dual-fermion expansion around arbitrary reference system within the path-integral formalism29,32 similar to a strong coupling expansion51. In this case our N × N lattice and corresponding reference systems represent N × N-part which we cut from infinite lattice and periodize the bare Green’s function \({{{{\mathcal{G}}}}}_{\alpha }\) (see Supplementary Note 1). The general lattice action for discretise N × N × L space-time lattice (for CT-INT scheme imaginary time space τ is continuous in the [0, β) interval) with Hamiltonian Eq. (1) reads
In order to keep the notation simple, it is useful to introduce the combined index \(\left\vert 1\right\rangle \equiv \left\vert i,\tau ,\sigma \right\rangle\) (i being the site index suppressed above) while assuming summation over repeated indices. For a bare antisymmetric interaction vertex we use the more general four-indices form U1234.
To calculate the bare propagators \({({{{{\mathcal{G}}}}}_{\alpha })}_{12}\) we start from the N × N cluster from infinite lattice and then force translation symmetry and periodic boundary condition. This procedure is easy to realize in the k-space, by doing first a double Fourier transform of the bare Green’s function for non-periodic N × N cluster \({{{{\mathcal{G}}}}}_{{{{\bf{k}}}},{{{{\bf{k}}}}}^{{\prime} }}^{\alpha }\) and then keep only periodic part, \({{{{\mathcal{G}}}}}_{{{{\bf{k}}}}}^{\alpha }{\delta }_{{{{\bf{k}}}},{{{{\bf{k}}}}}^{{\prime} }}\).
A perturbation matrix corresponds to a difference of one-electron part of the action from Eq. (3):
The transformed dual action29,32 in a paramagnetic state reads
where the bare dual Green’s function has the following matrix form:
with g being an exact Green’s matrix of the interacting reference system.
We used the following definition of the connected four-point vertex:
The first order dual self-energy is given by the diagram shown in Fig. 7
Here the density vertex reads
and the final Green’s function for original fermions reads32:
Within the determinant DQMC with Ising-fields {s} or inside the CT-INT with a stochastic sampling of interaction order expansion {s} for the two-particle correlators, we can use the Wick-theorem:
For a small system of 2 × 2 cluster we can calculate the matrix of Green’s function from Eq. (10) directly in the real space formalism and check convergence of dual perturbations. In this case, we do not need any additional periodization since 2 × 2 cluster is “self-periodic”. Since there is almost no sign problem in the DQMC method for the doped 2 × 2 cluster in the bath, we can compare the first-order dual-fermion perturbation with numerical exact DQMC results. All three non-equivalent Green’s functions for 2 × 2 system are shown in Fig. 8 using first-order DF-correction within Hirsch-Fye QMC formalism. For small perturbation Δμ = − 0.3 and \(\Delta {t}^{{\prime} }=0\) a comparison with exact DQMC results (point on Fig. 8) is perfect. For a large perturbation Δμ = − 1.5 and \(\Delta {t}^{{\prime} }=0.15\) one can already see a small difference from the exact DQMC Green’s function. Nevertheless, the results of DF-QMC with only first-order corrections for the dual self-energy are very satisfactory. Note that for square lattice one need to compare the perturbation in Δμ with \(4\Delta {t}^{{\prime} }\), also dispersion of \({t}^{{\prime} }\) tight-binding contributions and a relative sign of these terms made such a simple estimation questionable.
Three non-equivalent real-space components of the Green’s functions for 2 × 2 system as a function of imaginary time for U = 5.56, β = 5 and μ = − 0.3, \({t}^{{\prime} }/t=0\) (a) and μ = − 1.3, \({t}^{{\prime} }/t=-0.15\) (b) with DF-QMC (full lines) and exact DQMC (points). Note that in Hirsch-Fay DQMC we use definition with positive local Green’s function.
K space scheme
For large systems (N ≥ 4) it is much faster to calculate the dual self-energy in the K-space within the QMC Markov chain. The dual action in K-space reads
Using the short notation k ≡ (k, νn) and νn = (2n + 1)π/β, with \(n\in {\mathbb{Z}}\), the dual Green’s function is equal to
Since the bare dual Green’s function was calculated in the independent QMC run for the reference system, it is fully translationally invariant \({\tilde{G}}_{43}^{0}\equiv {\tilde{G}}^{0}(3-4)\) and we used the Fourier transform to calculate the K-space dual Green’s function \({\tilde{G}}_{k}^{0}\). Within the QMC Markov chain the lattice auxiliary Green’s function is not translationally invariant therefore \({g}_{12}^{s}=-{\langle {c}_{1}{c}_{2}^{* }\rangle }_{s}\) and we use double Fourier transform to calculate \({g}_{k{k}^{{\prime} }}^{s}\). To take into account a “disconnected part” of the vertex in equation Eq. (7) we just subtract exact Green’s function from the first QMC run of the reference system as follows:
In the K-space scheme due to the periodicity of the reference system, these subtractions have the following form
For the representation of the vertex \({\gamma }_{1234}^{d}\) in Eq. (9) within the QMC step we take into account that indices (3, 4) are “diagonal” in K-space due to multiplication by translationally invariant dual Green’s function \({\tilde{G}}_{34}^{0}\) which transforms as \({\tilde{G}}_{k}^{0}{\delta }_{k{k}^{{\prime} }}\) and indices (1, 2) become translationally invariant after QMC-summation, which finally leads us to the following equation for the spin-up components of the first order dual self-energy \({\tilde{\Sigma }}_{k}\)
Here Nk = N2 is number of k-popints for the N × N lattice and one factor of \(\frac{1}{\beta {N}_{k}}\) comes from the double Fourier transform of \({\tilde{g}}_{{k}^{{\prime} }{k}^{{\prime} }}\). Additional normalization factor \(\frac{1}{\beta {N}_{k}}\) comes from the momentum \({{{{\bf{k}}}}}^{{\prime} }\) sum for the N × N lattice and summation over the Matsubara frequencies, namely \(\frac{1}{\beta }{\sum }_{{\nu }^{{\prime} }}(...)\). For paramagnetic calculations, we average over two spin projections.
Corresponding lattice Green’s function reads:
Finally, we note, that if we neglect the dual self-energy, \({\tilde{\Sigma }}_{k}=0\), this approximation is equivalent to so-called cluster-perturbation theory (CPT) for N × N lattice52.
As the test for convergence of the present scheme as a function of temperature, we present results for the 4 × 4 system in Fig. 9 using the CT-INT method. This system is also quite small, plus the external fermionic bath results in a mild sign problem, which made an exact QMC test still possible. The interacting U, hopping \({t}^{{\prime} }\) and μ parameters correspond to anomalous point with the strongest pseudogap effects45. For all six non-equivalent k points the dual-fermion QMC scheme can reproduce the strong temperature dependence of the self-energy for lattice models. The strongest deviation for the lowest temperature Green’s function appears to be at (π, 0) point with dispersion located close to the Fermi level. One can use this information in order to discuss possible instability in the electronic spectrum within first-order perturbation. For larger system 8 × 8 there is already unacceptably strong sign problem. We still can check convergence of the DF-QMC results as function of lattice size. In Fig. 10 we compare results of 8 × 8 and 10 × 10 systems for Matsubara Green’s function at three main k points in the Brillouin zone, which shows a very good convergence with respect to the lattice size. Note that for large 10 × 10 system we can do the CT-INT Monte Carlo calculations only for relatively high temperature T = 0.2t. The overall numerical complexity scales with average order expansion M and system size N as \(O({N}^{2}{M}^{2}\log (M))\). For the 8 × 8 system at β = 10 the average expansion order M ~ 700. Each CT-QMC simulation at this regime requires around 50,000 CPU hours to achieve acceptable stochastic error. The tests for different system sizes (see Supplementary Notes 2 and 3) show reasonable convergence of the first-order DF-QMC approximation for reasonably small perturbations.
Matsubara Green’s functions Re G(k, ωn) (left) and Im G(k, ωn) (right) for dual fermion CT-INT QMC (Dual) in comparison with exact CT-INT results (Reference) for all 6 nonequivalent k-points on (4 × 4) lattice with U/t = 5.6, \({t}^{{\prime} }/t=-0.3\) and μ/t = − 0.9 and different inverse temperature: β = 5 (a, b), β = 10 (c, d), β = 10 (e, f).
Data availability
The data that support the findings of this study are available in Zenodo with the identifier https://doi.org/10.5281/zenodo.10557124.
Code availability
The codes in this study are available from the corresponding author upon reasonable request.
References
Schäfer, T. et al. Tracking the footprints of spin fluctuations: a multimethod, multimessenger study of the two-dimensional Hubbard model. Phys. Rev. X 11, 011058 (2021).
De Raedt, H. & Lagendijk, A. Monte Carlo simulation of quantum statistical lattice models. Phys. Rep. 127, 233–307 (1985).
Loh, E. Y. et al. Sign problem in the numerical simulation of many-electron systems. Phys. Rev. B 41, 9301–9307 (1990).
Troyer, M. & Wiese, U.-J. Computational complexity and fundamental limitations to fermionic quantum Monte Carlo simulations. Phys. Rev. Lett. 94, 170201 (2005).
Mondaini, R., Tarat, S. & Scalettar, R. T. Quantum critical points and the sign problem. Science 375, 418–424 (2022).
Jiang, H.-C. & Devereaux, T. P. Superconductivity in the doped Hubbard model and its interplay with next-nearest hopping t’. Science 365, 1424–1428 (2019).
Jiang, Y.-F., Zaanen, J., Devereaux, T. P. & Jiang, H.-C. Ground state phase diagram of the doped Hubbard model on the four-leg cylinder. Phys. Rev. Res. 2, 033073 (2020).
Chung, C.-M., Qin, M., Zhang, S., Schollwöck, U. & White, S. R. Plaquette versus ordinary d-wave pairing in the \({t}^{{\prime} }\)-Hubbard model on a width-4 cylinder. Phys. Rev. B 102, 041106 (2020).
Qin, M. et al. Absence of superconductivity in the pure two-dimensional Hubbard model. Phys. Rev. X 10, 031016 (2020).
Harland, M., Katsnelson, M. I. & Lichtenstein, A. I. Plaquette valence bond theory of high-temperature superconductivity. Phys. Rev. B 94, 125133 (2016).
Harland, M., Brener, S., Katsnelson, M. I. & Lichtenstein, A. I. Exactly solvable model of strongly correlated d-wave superconductivity. Phys. Rev. B 101, 045119 (2020).
Danilov, M. et al. Degenerate plaquette physics as key ingredient of high-temperature superconductivity in cuprates. npj Quant. Mater. 7, 50 (2022).
Schmid, M. T., Morée, J.-B., Kaneko, R., Yamaji, Y. & Imada, M. Superconductivity studied by solving ab initio low-energy effective Hamiltonians for carrier doped cacuo2, bi2sr2cuo6, bi2sr2cacu2o8, and hgba2cuo4. Phys. Rev. X 13, 041036 (2023).
Xu, H. et al. Coexistence of superconductivity with partially filled stripes in the Hubbard model. Preprint at https://arxiv.org/abs/2303.08376 (2023).
Prokof’ev, N. & Svistunov, B. Bold diagrammatic Monte Carlo technique: When the sign problem is welcome. Phys. Rev. Lett. 99, 250201 (2007).
Rossi, R. Determinant diagrammatic Monte Carlo algorithm in the thermodynamic limit. Phys. Rev. Lett. 119, 045701 (2017).
Rubtsov, A. N., Savkin, V. V. & Lichtenstein, A. I. Continuous-time quantum Monte Carlo method for fermions. Phys. Rev. B 72, 035122 (2005).
Šimkovic, F., Rossi, R., Georges, A. & Ferrero, M. Origin and fate of the pseudogap in the doped Hubbard model. Preprint at http://arxiv.org/abs/2209.09237 (2022).
Šimkovic, F., Rossi, R. & Ferrero, M. Two-dimensional Hubbard model at finite temperature: weak, strong, and long correlation regimes. Phys. Rev. Res. 4, 043201 (2022).
Rossi, R., Prokof’ev, N., Svistunov, B., Houcke, K. V. & Werner, F. Polynomial complexity despite the fermionic sign. Europhys. Lett. 118, 10004 (2017).
Kim, A. J., Prokof’ev, N. V., Svistunov, B. V. & Kozik, E. Homotopic action: a pathway to convergent diagrammatic theories. Phys. Rev. Lett. 126, 257001 (2021).
Charlebois, M. & Imada, M. Single-particle spectral function formulated and calculated by variational Monte Carlo method with application to d-wave superconducting state. Phys. Rev. X 10, 041023 (2020).
Rosenberg, P., Sénéchal, D., Tremblay, A.-M. S. & Charlebois, M. Fermi arcs from dynamical variational Monte Carlo. Phys. Rev. B 106, 245132 (2022).
Sakai, S., Civelli, M. & Imada, M. Hidden fermionic excitation boosting high-temperature superconductivity in cuprates. Phys. Rev. Lett. 116, 057003 (2016).
Singh, A. et al. Unconventional exciton evolution from the pseudogap to superconducting phases in cuprates. Nat. Commun. 13, 7906 (2022).
Vidhyadhiraja, N. S., Macridin, A., Şen, C., Jarrell, M. & Ma, M. Quantum critical point at finite doping in the 2d Hubbard model: A dynamical cluster quantum Monte Carlo study. Phys. Rev. Lett. 102, 206407 (2009).
Chen, K.-S., Meng, Z. Y., Pruschke, T., Moreno, J. & Jarrell, M. Lifshitz transition in the two-dimensional Hubbard model. Phys. Rev. B 86, 165136 (2012).
Krien, F., Worm, P., Chalupa-Gantner, P., Toschi, A. & Held, K. Explaining the pseudogap through damping and antidamping on the fermi surface by imaginary spin scattering. Commun. Phys. 5, 336 (2022).
Brener, S., Stepanov, E. A., Rubtsov, A. N., Katsnelson, M. I. & Lichtenstein, A. I. Dual fermion method as a prototype of generic reference-system approach for correlated fermions. Annal. Phys. 422, 168310 (2020).
Abrikosov, A. A., Gorkov, L. P. & Dzyaloshinski, I. E. Methods of Quantum Field Theory in Statistical Physics. (Dover, New York, NY, 1975).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Rubtsov, A. N., Katsnelson, M. I. & Lichtenstein, A. I. Dual fermion approach to nonlocal correlations in the Hubbard model. Phys. Rev. B 77, 033101 (2008).
Bethe, H. A & Jackiw, R. W. Intermediate Quantum Mechanics 3rd edn. (Taylor and Francis, 1986).
Katsnelson, M. I. & Irkhin, V. Y. Metal-insulator transition and antiferromagnetism in the ground state of the Hubbard model. J. Phys. C 17, 4291–4308 (1984).
Irkhin, V. Y. & Katsnelson, M. I. On the ground state wave function of a superconductor in the BCS model. Phys. Lett. A 104, 163–165 (1984).
Irkhin, V. Y. & Katsnelson, M. I. Theory of intermediate-valence semiconductors. Sov. Phys. JETP 63, 631–636 (1986).
Peierls, R. On a minimum property of the free energy. Phys. Rev. 54, 918–919 (1938).
Feynman, R. P. Statistical Mechanics: A Set of Lectures (Benjamin/Cummings, 1972).
Bogolyubov, N. N. On a variational principle in the many-body problem. Sov. Phys. Dokl. 3, 292–294 (1958).
Scalettar, R. T., Noack, R. M. & Singh, R. R. P. Ergodicity at large couplings with the determinant Monte Carlo algorithm. Phys. Rev. B 44, 10502–10507 (1991).
Rohringer, G. et al. Diagrammatic routes to nonlocal correlations beyond dynamical mean field theory. Rev. Mod. Phys. 90, 025003 (2018).
Rost, D., Gorelik, E. V., Assaad, F. & Blümer, N. Momentum-dependent pseudogaps in the half-filled two-dimensional Hubbard model. Phys. Rev. B 86, 155109 (2012).
Fei, J., Yeh, C.-N., Zgid, D. & Gull, E. Analytical continuation of matrix-valued functions: Carathéodory formalism. Phys. Rev. B 104, 165111 (2021).
Hirsch, J. E. & Fye, R. M. Monte Carlo method for magnetic impurities in metals. Phys. Rev. Lett. 56, 2521–2524 (1986).
Wu, W., Ferrero, M., Georges, A. & Kozik, E. Controlling Feynman diagrammatic expansions: physical nature of the pseudogap in the two-dimensional Hubbard model. Phys. Rev. B 96, 041105 (2017).
Rossi, R., Šimkovic, F. & Ferrero, M. Renormalized perturbation theory at large expansion orders. Europhys. Lett. 132, 11001 (2020).
Grossman, O. & Berg, E. Robust fermi-liquid instabilities in sign problem-free models. Phys. Rev. Lett. 131, 056501 (2023).
Zhang, X., Pan, G., Xu, X. Y. & Meng, Z. Y. Fermion sign bounds theory in quantum Monte Carlo simulation. Phys. Rev. B 106, 035121 (2022).
Zhang, X. et al. Polynomial sign problem and topological mott insulator in twisted bilayer graphene. Phys. Rev. B 107, L241105 (2023).
Hafermann, H., Brener, S., Rubtsov, A. N., Katsnelson, M. I. & Lichtenstein, A. I. Cluster dual fermion approach to nonlocal correlations. JETP Lett. 86, 677–682 (2008).
Pairault, S., Sénéchal, D. & Tremblay, A.-M. S. Strong-coupling expansion for the Hubbard model. Phys. Rev. Lett. 80, 5389–5392 (1998).
Gros, C. & Valentí, R. Cluster expansion for the self-energy: a simple many-body method for interpreting the photoemission spectra of correlated fermi systems. Phys. Rev. B 48, 418–425 (1993).
Acknowledgements
The authors thank Alexei Rubtsov, Evgeny Stepanov, Igor Krivenko, Sergey Brener, Jörg Schmalian, Richard Scalettar, Emanuel Gull, Fedor Šimkovic IV, Riccardo Rossi and Antoine Georges for valuable comments on the work. This work was partially supported by the Cluster of Excellence “Advanced Imaging of Matter” of the Deutsche Forschungsgemeinschaft (DFG) - EXC 2056 - Project No. ID390715994 and through the research unit QUAST, FOR 5249 - project No. ID449872909, by European Research Council via Synergy Grant 854843 - FASTCORR. SI is supported by the Simons Foundation via the Simons Collaboration on the Many Electron Problem. The part of simulations were performed on the national supercomputer HPE Apollo Hawk at the High Performance Computing Center Stuttgart (HLRS) under the grant number QMCdynCOR/44167. This work used Expanse at SDSC through allocation DMR130036 from the Extreme Science and Engineering Discovery Environment (XSEDE), which was supported by National Science Foundation grant number 1548562. This work was partially supported by the Cluster of Excellence “Advanced Imaging of Matter” of the Deutsche Forschungsgemeinschaft (DFG) - EXC 2056 - Project No. ID390715994 and through the research unit QUAST, FOR 5249 - project No. ID449872909, by European Research Council via Synergy Grant 854843 - FASTCORR. SI is supported by the Simons Foundation via the Simons Collaboration on the Many Electron Problem. The part of simulations were performed on the national supercomputer HPE Apollo Hawk at the High Performance Computing Center Stuttgart (HLRS) under the grant number QMCdynCOR/44167. This work used Expanse at SDSC through allocation DMR130036 from the Extreme Science and Engineering Discovery Environment (XSEDE), which was supported by National Science Foundation grant number 1548562.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
The idea of the method was developed by AIL and MIK. Practical implementation in CT-INT lattice scheme by SI and in Hirsch-Fye QMC by AIL. The computations were performed by SI and AIL. AIl authors discussed the results and contributed to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iskakov, S., Katsnelson, M.I. & Lichtenstein, A.I. Perturbative solution of fermionic sign problem in quantum Monte Carlo computations. npj Comput Mater 10, 36 (2024). https://doi.org/10.1038/s41524-024-01221-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-024-01221-w