Abstract
Optimization of experimental materials synthesis and characterization through active learning methods has been growing over the last decade, with examples ranging from measurements of diffraction on combinatorial alloys at synchrotrons, to searches through chemical space with automated synthesis robots for perovskites. In virtually all cases, the target property of interest for optimization is defined a priori with the ability to shift the trajectory of the optimization based on human-identified findings during the experiment is lacking. Thus, to highlight the best of both human operators and AI-driven experiments, here we present the development of a human–AI collaborated experimental workflow, via a Bayesian optimized active recommender system (BOARS), to shape targets on the fly with human real-time feedback. Here, the human guidance overpowers AI at early iteration when prior knowledge (uncertainty) is minimal (higher), while the AI overpowers the human during later iterations to accelerate the process with the human-assessed goal. We showcase examples of this framework applied to pre-acquired piezoresponse force spectroscopy of a ferroelectric thin film, and in real-time on an atomic force microscope, with human assessment to find symmetric hysteresis loops. It is found that such features appear more affected by subsurface defects than the local domain structure. This work shows the utility of human–AI approaches for curiosity driven exploration of systems across experimental domains.
Similar content being viewed by others
Introduction
The achievable progress in the field of automated and autonomous experiments, and the idea of ‘self-driving’ laboratories more generally, hinges on the ability of probabilistic machine learning models to be used to rapidly identify areas of the parameter space that have a high (modeled) likelihood of optimizing target properties of interest1,2,3,4,5. Recent examples include explorations of chemical space6 in the synthesis of nanoparticles7 and thin films for photovoltaic applications8,9. Additionally, numerous examples exist of autonomous microscopes that can be used to identify structure–property relationships in both electron4 and scanning probe spectroscopies10,11, as well as scattering measurements at the beamline, for e.g., efficient capture of diffraction patterns for phase mapping or for strain imaging12,13,14,15. Such work seeks to improve not only the efficiency at which the target property of interest can be found and/or maximized but also to improve our understanding of how composition and structure impact functionality, ideally unearthing them in real-time.
In nearly all cases of active learning within experiments, the target property of interest is defined a priori. This target can be a human-designed behavior of interest, for example, some measured property, or feature of a spectrum that is captured such as area, peak position, peak ratio, etc. In these cases, the objective of the experiment is to efficiently probe the parameter space to maximize the selected target. Alternatively, an information-theory approach can be used where the goal is instead to minimize the uncertainty of a developed surrogate model. In both cases, however, the human is generally kept out of the loop after the target is selected and a sampling policy is initiated. Indeed, a celebrated review of Bayesian optimization is titled ‘Taking Humans out of the Loop: A Review of Bayesian Optimization’16. In traditional active learning methods for autonomous experiments such as Bayesian optimization, we need to preselect a target or goal and the BO guides the experiment autonomously to accelerate the learning towards the goal.
However, this may not always be ideal. During the course of the experiments (especially when the search space is minimally explored as in the early stage of autonomous experiments), we are likely to find completely different target structures which would be more interesting to explore. Thus, in some situations, experimentalists would prefer to observe a few of the spectra prior to target formulation, to obtain a sense of the potential importance of the regions that could be probed. A recent Nature article reports that leveraging human expertise within the optimization process can greatly improve recipes for materials processing17. Additionally, with little prior knowledge, it may also be challenging to design a suitable scalarizer that captures the essence of the target. Moreover, it is possible that the human may prefer one target to seeing some spectra, and then observe something more interesting in subsequent points and decide that is more worthwhile exploring. The ability to shift the trajectory of the optimization based on human-identified findings during the experiment is lacking in a fully AI-driven experiment. Thus, a method is needed to engender the best of both human operators as well as AI-driven experiments. We attempt to fill this void with the development of a human-guided AI system that steers microscope experiments based on real-time assessments, enabling types of experiments to be performed on the microscope that could likely be previously out of reach. In other words, human guidance overpowers AI at the early stage of optimization when prior knowledge is minimal and uncertainty is high, while the AI overpowers the human during the later stage to speed the overall process of learning with the human-assessed definite goal. This dynamic setting and changing of targets, which need to be inferred by the algorithm, is a problem that is well encountered in other fields such as social media and has been solved via recommendation engines, which are built from user voting (‘likes’) to populate the feeds with content agreeable with the user18,19,20.
Here we present the development of a method of an automated experiment that employs a human-in-the-loop experimental workflow, which we term the Bayesian optimized active recommender system (BOARS). We develop and apply it to the case of finding spectra encountered during piezoresponse force spectroscopy measurements, first trialing the method on pre-acquired data to gauge the effectiveness, and then implementing it in real-time on an operating instrument. The framework allows the human operator to vote for a certain number of spectra to construct a target and then proceeds to explore the search space optimally in view of retrieving spectra that bear a strong structural similarity to the target, and in the process, unearth key structure–property relationships present autonomously. In this manner, we bypass the need for a pre-defined target and add flexibility to a standard automated experiment, where rather than fixing a target prior to the start of the experiment, the human operator retains the ability to dynamically adjust the target via real-time result assessments. It is to be noted that the framework is purposefully developed to overcome the experimental scenarios when a definite goal to explore cannot be confirmed due to inadequate prior domain knowledge or the complexity of having several unknown key features of the system to explore when a pre-defined goal for a fully automated experiment is not possible. It is evident if the experimentalist prefers to set a definite goal and confirm it during the experiment, as it is when the material system is fairly known, then human collaboration with AI is not required (out of the scope of the proposed paper). In other words, the utility of the BOARS in the paper is when the above assumption is not true, as it is for several cases in the exploration and discovery of materials.
The overall framework has two major architectural components - an active recommender system (ARS) and Bayesian Optimization (BO) engine. The ARS is developed as a dynamic, human-augmented computational framework where, given a location in the search area of the material samples, the microscope performs a spectroscopic measurement at the location in real-time. This spectrum provides knowledge about various key features (e.g., it can be energy loss, nucleation barriers, degree of crystallinity, etc.). The ARS system allows the user to upvote and downvote spectra according to the features of their own interest, and this method is free from any generalized objective functions. Previously, human-augmented recommender systems have been developed in microscopy in accelerating meaningful discoveries in different fields of applications such as rapid validation of thousands of biological objects or specimen tracking results21, and rapid material discovery of lithium-ion conducting oxides through synthesis of unknown chemically relevant compositions22.
The second part of the architecture is the BO engine, which guides the path to locate the regions of interest with maximum structural similarity to the human-upvoted spectra, through sequential updating with a computationally cheap surrogate model and enables an efficient trade-off between exploration and exploitation of the unknown search area. Bayesian optimization (BO) or (multi-objective) BO16,23,24,25,26,27, has been originally developed as a low computationally cost global optimization tool for design problems having expensive black-box objective functions. BO has been extensively applied for rapid exploration of large material28,29,30,31,32,33,34,35 and chemical36,37 control parameters and/or functional properties space exploration to enable optimization towards desired device applications. Here, the BO replicates the expensive function evaluations with a cheap (scalable) surrogate model and then utilizes an adaptive sampling technique through maximizing an acquisition function to learn or update the knowledge of the parameter space towards finding the optimal region. Over the years, the development of BO has been extended for various complex problems. Biswas and Hoyle extended the application of BO over discontinuous design space by remodeling it into a domain knowledge-driven continuous space38. BO has been extended in discrete space such as in consumer modeling problems where the responses are in terms of user preference discrete39,40,41,42. Here, Thurstone40 and Mosteller41 transform the user preference discrete response function into continuous latent functions using the Binomial-Probit model for binary choices, whereas Holmes42 uses a polychotomous regression model to be applicable for more than two discrete choices. For practical implementation of BO over high-dimensional input space, some examples like Dhamala et al.43 Valleti et al.44 and Wang et al.45 attempted the approach of random embedding in a low-dimensional space; Grosnit et al.46 and Biswas et al.47 attempted the approach to project into a low-dimensional latent space with variational autoencoder; and Oh et al.48, Wilson et al.49 and Ziatdinov et al.50 tackles with implementing special kernel functions.
A Gaussian Process Model (GPM)51 is generally integrated into BO as the surrogate model, which also provides the measure of uncertainty of the estimated expensive functions over the parameter space such that the uncertainty is minimal at explored regions and increases towards the unexplored regions. Alternatively, random forest regression has also been proposed as an expressive and flexible surrogate model in the context of sequential model-based algorithm configuration52. The detailed workflow of BO and mathematical representation of GPM is provided in Supplementary Method. Once a cheap surrogate model is fitted in a BO iteration with the sampled data, the next task is to find the next best locations for sampling through maximizing the acquisition function (AF). The latter defines the likelihood of finding the region of interest or better objective function values. Several acquisition functions, such as Probability of Improvement (PI), Expected Improvement (EI), Confidence Bound criteria (CB) have been developed with different trade-offs between exploration and exploitations23,53,54,55.
In all the stated BO applications where the target is required to be set prior to the optimization, in this paper, the proposed approach bypasses that requirement by introducing a human-in-the-loop architecture, thus adding flexibility to the automated experimental workflow. We additionally explore the effect of local structures encoded in image patches and different kernel functions on the performance of the optimization trajectory. Therefore, here the major contribution of the paper is the development of BOARS model. In the traditional setting, this flexibility of on-the-fly experimental steering is lacking with such a rigid defined target, which we have filled the gap with an active recommender system design. The other main contribution of this work is to implement the BOARS model for a test case of a microscope with a human in the loop voting for spectral target generation. We further explore the role of the kernel in the utility of our BOARS workflow.
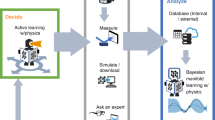
Figure 1 shows the overall high-level structure of the BOARS system with the detailed flow-chart of the algorithm provided in Supplementary Fig. 1. The workflow can be stated as follows: Given a material sample, we run the microscope to scan a high-resolution image, which is the parameter space for the exploration. Next, we segment the image space into several image patches of set window size, \(w\). We define these local image patches as the input for Bayesian optimization. Next, we initialize BO and capture spectra from microscope measurements at a few randomly generated locations. Next, we introduce the steps for human-operation which is the major contribution of this work. Given a spectrum, the user (human) visualizes the spectra and provide subjective vote on its quality. The workflow for the computation of the human visual assessment based on the fly target structure generation and thereafter the human-guided objective function can be described as follows. As we start the experiment by visualizing the first characterized spectrum (\({\rm{i}}=1),\) consider the case where the user either skipped the voting or downvoted it: the target is still not defined, as \({{\bf{T}}}_{i=1}=\varnothing\). If the user votes after visualizing the second spectrum (\({\rm{i}}=2\)), a target is defined as \({{\bf{T}}}_{i=2}={{\bf{S}}}_{i=2}\) where \({{\bf{S}}}_{i}\) is the \({{i}}{{\rm{th}}}\) spectrum. Let us assume the user again downvoted the third spectrum (\({\rm{i}}=3\)), then \({{\bf{T}}}_{i=3}={{\bf{T}}}_{2}={{\bf{S}}}_{2}\). If the next spectrum is upvoted (\({\rm{i}}=4)\), the target is accordingly updated as per Eq. (1) below. Once the voting is complete for the first few randomly selected j spectra, a human-guided objective function is calculated as per Eq. (2).
where \({{\bf{T}}}_{i}\) is the target after \({{i}}{{\rm{th}}}\) spectra assessment given the user upvoted the spectra, \({p}_{i}\) is the user preference (0–1 with 1 being highest) of adding features of new spectra to the current target, \({v}_{i}\) is the user vote of the \({{i}}{{\rm{th}}}\) spectra, \({Y}_{i}\) is the objective function value for the \({{i}}{{\rm{th}}}\) spectra, \({{\bf{T}}}_{j}\) is the target after voting all the \({\rm{j}}\) spectra, \(R\) is the reward on voting.
In this AE workflow, the step under the orange region is the contribution in this paper where we introduce a human-operator active recommender system to vote and build a target spectral through visual inspection and define a reward-based structural similarity-based objective function. The steps under green and yellow regions are traditional Bayesian optimization (BO) workflow and instrument (microscope) operations to scan an image of the sample and capture spectra at BO-guided locations over the image space. Additionally, the red highlighted arrow between the yellow and orange region is another contribution of the paper which builds the connection of the workflow between human-operated tasks (recommender system) and the microscope operations for real-time implementations of this overall human-in-the-loop AE architecture. The other red highlighted arrows signify the coupling between different environments of the framework: between microscope and traditional BO workflow and vice-versa, and between human-in-the-loop part and traditional BO workflow.
The objective function is the voting augmented structural similarity index function where \(\psi\) is the structural similarity function, computed from the function structural_similarity in skimage.metrics Python library56. Then, given the dataset with input local image patches and output objective function value, we run the BO—fitted with a Gaussian process model, and maximizing the acquisition function derived from the GP estimations. The acquisition function suggests the next best location to capture spectra. Next, microscopic measurement is carried out to retrieve the spectrum at the stated location and similar human assessment is carried out on the new spectrum. Given whether the user upvoted or downvoted the new spectrum, the target is either updated following Eq. (1) or remains the same, and the objective function is calculated iteratively following Eq. (2). This iterative GP training with new data, undertaking microscope measurements at new locations, and the introduced human-in-the-loop process to evaluate the spectra, update the target and calculate the objective function continues until the user is satisfied with the current target, which can be provided in a ‘Yes/No’ popup message after every iteration. Then, the remaining iterations are carried out until BO convergence without any further human interaction, with the objective function value modified to Eq. (3).
where \({Y}_{j+k}\) is the objective function for \({{k}}{{\rm{th}}}\) iteration of BO, after randomly sampling \({j}\) spectra. As seen, we removed the human-voting part as now the target \({\bf{T}}\) is fixed and the task is to identify the spectra maximizing the structural similarity with the target. Thus, in the proposed design, within the loop of BO, here we define and refine the target (spectral structure) through human assessment, and simultaneously optimize either the human-augmented objective function or the fully automated objective function, following Eqs. (2) or (3) respectively, given the state of decision-making in updating the target. The detailed mathematical algorithm of the methodology is provided later in the “Methods” section for additional information.
Results and discussion
We first begin by testing the BOARS system on pre-acquired data (i.e., data where the ground truth is known, and not on the active microscope) to determine the applicability of the method and to note the effects of hyperparameters. To this aim, we explored data from two PbTiO3 (PTO) thin film samples. The samples are both 200 nm-thick PbTiO3 thin films grown on (110) SrTiO3 via pulsed laser deposition, with ‘designer’ grain boundaries fabricated by a process outlined in ref. 57. In this instance, our measurements are not in the vicinity of the grain boundary; however, the domain structure of the PTO sample is dependent on the strain imparted by the thickness of the underlying substrate, and this leads to different domain structures for the part of the sample rotated with respect to the underlying (110) STO, as the underlying substrate is a rotated (110) STO membrane of limited (~10 nm) thickness. As such, both samples imaged display different domain patterns enabling us to test the BOARS on samples with different domain features. For this paper, we refer to PTO sample 1 as the sample where the domains imaged are on the original (110) oriented STO crystal (thickness 500 µm), and PTO sample 2 as the sample where we image the region of the sample where the sample is rotated (~2°) with respect to the substrate and has a much lower thickness of the STO (and thus likely to be much less strained).
Case study: BOARS analysis on existing PTO data
To demonstrate the method, and before implementing it on the real-time microscope, we began with a full ground truth dataset where we measured the spectral data for all the grid locations (2500 grid points on a 50 × 50 grid).
To study the performance, we first considered the BOARS architecture with a simple benchmarked surrogate model such as the Gaussian process model with a standard periodic kernel function. It is to be noted we tested with other inbuilt kernel functions like radial basis, and matern kernel, but periodic kernel provided superior exploration. The hyper-parameter of the kernel function is optimized with Adam optimizer58 with learning rate = 0.1. We started with 10 initial samples, \(j=10\) and 200 BO iterations, \(M=200\), a total of 210 evaluations. In regard to incorporating the local image patches as an additional channel for structure-spectra learning, we considered the image patch of window size, \(w=4\,{\rm {{px}}}.\) Thus, the dimension of each input, \({{\bf{X}}}_{1},\) is an array of 16 elements. For a comparative study, we upvoted spectra that appeared (by eye) to possess roughly symmetrical hysteresis loops in terms of amplitude, i.e., similar remanent piezoresponse for positive and negative bias. For both PTO samples, we utilized voting (target learning) of the first 10 spectra and then fixed the target for the remaining iterations. The detailed user voting of the spectra used to set the final target for both PTO samples is provided in Supplementary Figs. 2 and 3. The detailed analysis of the BOARS system with a standard surrogate model has been provided in Supplementary Figs. 4 and 5, for the first and second PTO samples, respectively.
The analysis shows the traditional kernel function could be unstable depending on the complexity of the parameter space and the degree of correlation between the prior knowledge (embedded in local structural image patches) and the posterior knowledge on structural similarity with the human-assessed target. This could be due to the inefficient learning of traditional kernel functions over high dimensional inputs59. Our prior work60 has shown that in such instances, it may be advantageous to utilize deep kernels in a scheme termed deep kernel learning (dKL)49. dKL is built on the framework on a fully connected neural network (NN) where the high-dimensional input image patch is first embedded into low dimensional kernel space (in this case set as 2), and then a standard GP kernel operates, such that the parameters of GP and weights of NN are learned jointly. This dKL technique has been implemented for better exploration through active learning in experimental environments4,50,61,62,63. Here, we utilized a DKL implementation from an open-source AtomAI software package60.
The overall BOARS structure remains the same, but we simply replace the standard GP with a dKL-based approach. All other parameters were kept constant. The detailed user voting of the spectra to set the final target for both oxide samples is similar in Supplementary Figs. 2 and 3. Figures 2 and 3 are the detailed analysis of the estimated spectral similarity maps, after adaptive learning with BOARS system, for the first and second PTO samples, respectively. Firstly, it can be clearly seen comparing the scanned images of the PTO samples (Figs. 2a and 3a) with the respective structural similarity (ground truth) images (Figs. 2d and 3d) that these are not highly correlated, particularly for Fig. 3. That is, there is minimal correlation between the initial PFM scan and the structural similarity map. This is expected in cases where the features targeted in the spectral domain, here, symmetric remnant response, is not significantly dependent on the surface domain structure image and is likely to be more heavily determined more by sub-surface defects that are not manifest in the image. The objective for the appropriate model, which the standard kernels fail to do in this case, would be to balance between prior (local domain correlation) knowledge from scanned images and the posterior objective function knowledge through sequential learning, such that it tends towards efficient estimation of the structural similarity map at the explored and unexplored regions (predicting the unknown ground truth with sparse adaptively selected samples).
a Downsampled PFM amplitude image of the PTO film, with exploration points for the spectral locations where the user voted only, b final learned target spectral structure after voting through explored spectra in (a, c). Plot of a with all the explored spectral locations overlaid d ground truth image, i.e., the structural similarity map as in Eq. (3), given the user-voted target spectral. e estimated structural similarity map (as represented by the colorbar in the right with the light region being higher values and the dark region being lower values) from the surrogate model, with all the explored spectral locations, f map (as represented by the colorbar in the right) of the model’s associated uncertainty. The samples color coding represents (red being higher values and blue being lower values) the color of the explored locations with the human-augmented objective function values in (a), automated objective function values in (c, e), and the objective ground truth image in (d). Within sub-figure (c), (i)–(iv) are the visualization of the spectra at some of the BO explored locations. The scale bar in (a) is 200 nm.
a Downsampled PFM amplitude image of the PTO film, with exploration points for the spectral locations where the user voted only, b final learned target spectral structure after voting through explored spectra in (a, c). Plot of (a) with all the explored spectral locations overlaid (d) ground truth image, i.e., the structural similarity map as in Eq. (3), given the user-voted target spectral. e estimated structural similarity map from the surrogate model, with all the explored spectral locations, f map of the model’s associated uncertainty. The explanation of the colorbars can be referred to as stated in Fig. 2. Within sub-figure (c), (i)–(iv) are the visualization of the spectra at some of the BO explored locations. The scale bar in (a) is 200 nm.
Observing both Figs. 2 and 3, it can be seen that the dKL method serves to better capture the correlations between the local image patches and the objective function, ultimately in adaptive learning of the estimated GP spectral similarity maps (see Figs. 2e and 3e). We also observe an overall better trade-off with regards to BO exploration and exploitation, with more scattered sampling to look for potential regions of interest, particularly in Fig. 3 when the local structure–spectral correlation is minimal, ultimately to provide a better structural similarity map. For example, unlike in Supplementary Fig. 4, the estimated uncertainty map Fig. 2f within the white region has relatively lower variance, with a comparatively significant reduction of variances throughout the image space. Additionally, as in Supplementary Fig. 5, BOARS with dKL (Fig. 3c) still explores more near the phase boundary (dark channels) of the scanned image due to the input of the image patches; however, unlike the BOARS with traditional kernel, the dKL also adjusts the knowledge through posterior exploration and yields a majority of regions with high-valued targets (light region), as we know from the ground truth, providing a significant reduction of uncertainty as well. Thus, with the comparative analysis, we see an overall stability and enhancement of BOARS system, with efficient learning of user-desired spectra with incorporating local image patches of the system and rapid discovery of the changes in the structural similarity map through experimental evaluations, provided that the kernel is intelligently learned from the sparse data as by dKL.
To support our interpretation and validate the models, we provide the squared error map between the ground truth and the GP estimated spectral map in Fig. 4 for all the discussed case studies and the relative mean squared errors (MSE) over the entire image space. For both the samples, we see an overall low MSE which shows a goodness of fit of the general BOARS architecture. For PTO sample 1, we see the MSEs are comparatively similar between the BOARS with periodic and dKL functions, with slightly better performance with dKL. However, as expected, we see a significant improvement (much lower MSE) in the performance of BOARS with dKL for PTO sample 2. Furthermore, we see similar MSE values under BOARS with dKL for both the case studies which gives better stability or insensitiveness to the complexity of the problem and the efficiency of the prior knowledge (given in the form of the image patch). To summarize, the purpose of testing our proposed BOARS model with samples 1 and 2 is to test on different domain structures. Again, the purpose of doing so is to ensure the model works appropriately without underfitting or overfitting by checking how well it learns the unknown ground truth. For that case, we considered two samples: PTO sample 1—where we have seen the degree of correlation between the known input PFM amplitude image and the unknown ground truth image is relatively higher, and PTO sample 2—where the degree of correlation between the known input PFM amplitude image and the unknown ground truth image is minimal. We wanted to test how the kernel will perform in such two cases. It is evident to mention that the objective is not to find what kind of imaging techniques will provide more correlation with ground truth, but the goal is that given a structure image how well the BOARS model can perform to provide a better structure–property relationship (align to better representation of ground truth), irrespective of any degree of actual correlation between structure image and unknown ground truth (good or poor prior knowledge from structure image). In the actual experimental setting, there is no such guarantee the input structure image will always have a high correlation with the objective we are looking for and therefore the added focus on appropriate implementation of kernel function for deployment.
a Oxide sample 1: BOARS with periodic kernel, b Oxide sample 1: BOARS with deep kernel (dKL), c Oxide sample 2: BOARS with periodic kernel, d Oxide sample 2: BOARS with deep kernel (dKL). The respective mean square errors (MSE) over the entire image space are 0.059, 0.058, 0.066, and 0.05. Note: c error map has been scaled during plotting for comparison with (d).
Case study: BOARS real-time implementation on atomic force microscopy (AFM)
Given that the model once developed needs to be implemented on an operational microscope where the cost of experiments is actually high and we do not know the ground truth, we need to ensure the proposed BOARS model (like any AI-driven model) aligns with the human-identified targets and provide meaningful information. After investigations on pre-acquired data, it is clear that the implementation on the real microscope will require the use of deep kernel learning. As such we proceeded to apply the BOARS system with dkl kernel in real-time automated experiments on the microscope. Considering PTO sample 2, we considered the high-resolution image (128 × 128) with an input image patch of window size, \(w=4\,{\rm {{px}}}.\) We started with 10 initial samples, \(j=10\) and 100 BO iterations.
Here also, we considered the goal to obtain a symmetrical loop, however, the voting sequences to set the target were different from our earlier analysis. This is done intentionally to understand the sensitivity of the result with different voting or targets but considering similar user-desired features (as common in a subjective assessment between two users but with similar goals). The purpose of analyzing the structure-property relationship over aiming to autonomously learning the potential defect-free areas (good regions) in the material domain space due to imaging and the potential defected areas (bad regions) as represented by higher non-symmetrical loops. Figure 5 shows the iterative learning of the spectral structural similarity map with the BOARS system. We can see the estimated spectral similarity map (see Fig. 7g) shows similar trends as to what we observed in Fig. 5, with a more refined map due to a higher-resolution parameter space. As in Fig. 5, we see the domain walls in the scanned image are highlighted as the potentially interesting regions of user-desired spectra, and therefore the relative estimated structural similarity map has high values at the domain walls. However, as we also see from earlier analysis, the overall space is highly valued virtually throughout, and here also we see such a trend (the estimated map in Fig. 7g has very minimal dark regions). Regarding the computational cost, the total runtime of this AE analysis took less than 1 h, whereas the computational cost to run the experiment exhaustively for all grid points (in 128 by 128-pixel image) can take about 15–24 h.
a–f GP estimated structural similarity map (left) and respective uncertainty map (right) for stated BO iterations. In the figures, the green dots are the explored locations while the red dots are the new locations to be explored on the next iteration. g analysis after BO convergence with 100 iterations. (left) high-resolution (128 × 128) PFM amplitude image of the PTO film, with all the explored spectral locations till BO convergence, (middle) GP prediction of structural similarity, and (right) associated uncertainty map. Scale bar in g is 200 nm. The sample color coding represents (red being higher values and blue being lower values) the color of the explored locations with the objective function values (100 BO iterations) in (g).
These results highlight two key points. One is that the degree of symmetry of the amplitude response to hysteresis loops in standard ferroelectrics like PbTiO3 can be more affected by features that are not correlated with the surface domain structure, such as sub-surface defects that cannot be imaged by PFM and serve to suppress or enhance polarization. This opens the possibility to deliberately find spectral features that are not correlated with the original PFM image, and therefore, to identify notable sub-surface defect regions (for example, as in ref. 64). It should be noted that it is possible that sub-surface defects may show signatures in either electrostatic force microscopy or Kelvin probe force microscopy measurements if they significantly affect the local surface potential65. As such, one can imagine attempting to find spectra that are similar to those predicted from particular types of defects, enable the algorithm to find the locations in the sample where these spectra are located, and then use these as sites for further chemical and electronic characterization with other AFM and chemical imaging modalities. Secondly, the fact that the dKL method is able to learn the appropriate correlations between the local image patches and the local spectra is a key distinguishing feature. Standard kernels appear to struggle to ‘ignore’ the domain structure, whereas the learned kernel appears better at this task. This suggests that kernel choice is important not only for feature learning but for minimizing the impact of spurious correlations in active learning regimes.
Case study: Edge case scenarios of early human assessment of spectral structures
Finally, though the BOARS architecture is designed based on the assumption that the operator is a domain expert (i.e., assumed to make knowledgeable decisions and upgrade learning of suitable targets on the fly), we looked at two edge case scenarios where the assessment is not done with expert knowledge. We attempt to test the edge case scenarios to learn how the assessment can change the shape of the target and thereby change the ground truth map. We refer to these edge cases as EC1 and EC2. EC1 is defined as a random assessment of initially randomly generated 30 samples. EC2 is defined as assessing the quality of three highly different (hard to find in the image space) spectra as ‘good’.
Figures 6 and 7 show the detailed analysis for PTO samples 1 and 2, respectively. We refer to the target with expert assessment as shown in Figs. 2 and 3 as the actual target and the respective generated ground truth as the actual ground truth. That is, let us assume that the goal in this experiment was to find spectra close to that found by the domain expert in sample 2, but here, a different operator is chosen who has significantly less experience and decides to either randomly assign ratings, or chooses to upvote spectral features that are very rare in the dataset. We attempt to quantify how these would be different from the actual ground truth and explore how these edge cases will play out with this algorithm.
a final learned target spectral structure after assessment by the domain expert (reproduced from Fig. 2b). b Actual ground truth image for target (a) (reproduced from Fig. 2d). The colorbar represents the red region with the spectrum having high structural similarity with the target, and blue region with the spectrum having low structural similarity with the target. c Final learned target spectral structure for EC1 (red) and mean spectral structure (black). d Difference in structural similarity map between actual ground truth and ground truth generated for EC1. e Final learned target spectrum for EC2. d Difference in structural similarity map between actual ground truth and ground truth generated for EC2. The colorbar for figs (d, f) represents the red region with spectral having higher structural similarity with the actual target, and the blue region with spectral having higher structural similarity with the edge case generated targets.
a Final learned target spectral structure after assessment by the domain expert (reproduced from Fig. 3b). b Actual ground truth image for target (a) (reproduced from Fig. 3d). The colorbar represents the red region with spectral having high structural similarity with the target, and blue region with spectral having low structural similarity with the target. c Final learned target spectral structure for EC1 (red) and mean spectral structure (black). d Difference in structural similarity map between actual ground truth and ground truth generated for EC1. e Final learned target spectral structure for EC2. d Difference in structural similarity map between actual ground truth and ground truth generated for EC2. The colorbar for figs. d, f represents the red region with spectral having higher structural similarity with the actual target, and blue region with spectral having higher structural similarity with the edge case generated targets.
The results are shown in Fig. 6 for this type of analysis. First, we start with a reproduction of the target in Fig. 2a, which is shown in Fig. 6a. We compute the structural similarity score of every spectrum in the dataset, against this target, and the results are plotted in Fig. 6b. Next, we generate targets by strategy EC1, i.e., random voting of 30 samples. The resultant target is shown in Fig. 6c. It is evident that randomly voting for spectra tends to generate a target spectrum that is close to the mean in the dataset, as is expected from intuition (see the mean spectral response in Fig. 6c). The structural similarity map is shown in Supplementary Fig. 6. To gain an idea as to what areas are now focused on, we plot the difference between the structural similarity map for this target, subtracted from the structural similarity map from Fig. 6b. If this resultant difference map was close to zero, then it effectively means that the resultant BO would be almost identical. As can be seen, there are some differences in the structural similarity map, but many regions where there is little difference. This suggests that the original voting by the domain expert was not too far from a common ‘mean’ hysteresis loop, so the result of random voting is also not likely to result in very different behavior through the BO process.
At the other end of the spectrum, it is possible that the operator chooses to find and upvote spectra that are comparatively rare in the dataset, i.e. edge case 2. In EC2, the target is formed after upvoting 3 quite rare spectra, and the resultant target is shown in Fig. 6e. It can be seen in the associated difference map of the structural similarity in Fig. 6f, that there are not many overlapping regions (i.e., regions where the difference is close to 0).
This analysis suggests that providing a few incorrect assessments based on the level of expertise of the operator will be less likely to have an effect on the potential region of interest, which is learned autonomously with BO (sampling <5% over whole image space). However, if there are very few spectra that are rated, then this becomes more problematic as individual outliers can begin to shape the target in undesired ways.
Summary
In summary, we developed a dynamic, human-augmented Bayesian optimized active recommender system (BOARS) for curiosity-driven exploration of systems across experimental domains, where the target properties are not priorly known. The ARS system provides a framework for human-in-the-loop automated experiments and leverages user voting as well, and a BO architecture to provide an efficient adaptive exploration towards rapid spectral learning and maximize the structural similarity of the captured spectra. We explore the effect of different kernel functions towards providing a flexible framework in a balanced learning between prior structural knowledge of local scanned image patches and the captured spectra. This partially combined human-in-the-loop—AI workflow enables types of experiments to be performed on the microscope that have been previously out of reach.
Currently, the model has three ratings (one downvote option and two different upvote options). Also, the number of assessments required to shape the target is up to the operators, based on the trade-off between the cost of assessment (time the operators need) and the satisfaction of the target shaping (which the operator aims to explore). In our case (shaping for symmetrical loop structure), we have considered 10 assessments for pre-acquired data and 10 for real analysis, before switching off the human input. From the BOARS architectural point of view, there is no constraint applied on the minimum number of downvoted assessed spectra and the need for at least one upvoted assessed spectra. In other words, as long as any spectra are upvoted and a target is generated, the operator can switch to the fully autonomous approach (see Step 6 in the “Methods” section). The model also performs based on the assumption that the decision-maker, to shape the target spectral structure, is a domain expert and does not provide the visual assessment randomly.
It is evident to mention this assumption also holds for configuring any pre-defined targets in the fully autonomous BO approach as well. In other words, it is reasonable to assume the experimentalist or the microscope operator is aware of the physics to define the target in order to learn over the unknown image space, and a traditional BO drives the characterization autonomously based on the pre-defined targets. Our BOARS model fills the gap when the experimentalist does not have prior knowledge of what would be the best spectral structure (target) to learn for the material. In our use of the BOARS model, we found that shaping of the target is robust to a few incorrect assessments as the number of assessments progresses (say after 10–20), due to formulating on the weighted (preference-based) average from all the assessed spectra. However, the BOARS model is limited to incorporating uncertainty propagation based on the differences in the assessment from multiple domain expert operators to attain a similar goal. Moreover, the limitation of this method occurs when different spectra are upvoted that have competing mechanisms, i.e., when usually trying to find one type of structure will be anti-correlated with finding another type of structure. This problem needs to be handled through multi-objective means, and such work will be considered in future scope.
Methods
Detail algorithm of Bayesian optimized active recommender system
Here, we provide the detailed algorithm of the BOARS system. Here we provided two objective functions formulation, based on whether the user input is satisfied or not with the current target. It is to be noted the algorithm is the major contribution, specifically the human-operated process in steps 2 and 6, and therefore is the pivotal element to the paper. We described the workflow and mathematical approaches taken in steps 2 and 6 to define/update the targets and the objective functions and their connections with standard BO steps.
-
1.
Segmentation of local image patches as additional channel for structure-spectra learning:
-
a.
Choose a material sample. Set the control parameters of the microscope.
-
b.
Run microscope. Scan a high-resolution (e.g. 128 × 128 grid points) image of the sample.
-
c.
Segment the image into several square patches with window size, \(w\). The image patches are considered as input for BO, which provides the local physical information (eg. correlation) of the input location.
-
a.
-
2.
Initialization for BO: State maximum BO iteration, \(M\). Randomly select \(j\) samples (image patches), \({\bf{X}}\). We highlight this step as the contribution in this paper in introducing human operations in the proposed AE workflow.
-
a.
For sample \(i\) in \(j\), pass \({{\bf{X}}}_{i}\) into microscope. Run microscope and generate spectral data, \({{\bf{S}}}_{i}.\)
-
b.
Human-augmented process: User votes \({{\bf{S}}}_{i}\) with voting options, \({v}_{i}\): Bad(0), Good(1) and Very Good(2). Next follow either (c) or (d).
-
c.
Generate target: If the user voted good/very good for first time, then target, \({{\bf{T}}}_{i}={{\bf{S}}}_{i}\). Normalize \({{\bf{T}}}_{i}\).
-
d.
Update target: If \({{\bf{T}}}_{i}\ne \varnothing\), user select preference, \({p}_{i}\) (0–1 with 1 being highest) of adding features of new spectral to the current target. Calculate \({{\bf{T}}}_{i}\) as per Eq. (4). Normalize \({{\bf{T}}}_{i}\).
$${{\bf{T}}}_{i}=\left(\left(1-{p}_{i}\right)* \mathop{\sum }\limits_{{ii}=1}^{i-1}{v}_{{ii}}* {{\bf{T}}}_{i-1}\right)+({p}_{i}* {v}_{i}* {{\bf{S}}}_{i})/\left(\left(1-{p}_{i}\right)* \mathop{\sum }\limits_{{ii}=1}^{i-1}{v}_{{ii}}\right)+({p}_{i}* {v}_{i})$$(4) -
e.
Calculate human-augmented objective function: For sample \(i\) in \(j,\) calculate the voting augmented structural similarity index function as per Eq. (5). \(\psi\) is the structural similarity function; \({{\bf{T}}}_{j}\) is the current target following step c, d, after user voted \(j\) samples; \(R\) is the reward parameter. \(\psi\) is computed from the function structural_similarity in skimage.metrics library.
$${Y}_{i}=\psi \left({{\bf{T}}}_{j},{{\bf{S}}}_{i}\right)+{v}_{i}* R$$(5) -
f.
Build dataset, \({{\bf{D}}}_{j}\,{\boldsymbol{=}}\,{\boldsymbol{\{}}{\bf{X}}{\boldsymbol{,}}{\bf{Y}}{\boldsymbol{\}}}\) with \({\bf{X}}\) is a matrix with shape \((j,w* w)\) and \({\bf{Y}}\) is an array with shape \((j)\)
-
a.
Start BO. Set \(k=1\). For \(k\le M\)
-
3.
Surrogate modeling: Develop or update GPM models, given the training data, as \({\boldsymbol{\triangle }}{\boldsymbol{(}}{{\bf{D}}}_{j+k-1}{\boldsymbol{)}}\).
-
a.
Optimize the hyper-parameters of kernel functions of the surrogate models.
-
4.
Posterior predictions: Given the surrogate model, compute posterior means and variances for the unexplored locations, \(\overline{\overline{{{\bf {X}}}_{{k}}}}\), over the parameter space as \({\boldsymbol{\pi }}\left(\right.{\bf{Y}}(\overline{\overline{{{\bf{X}}}_{k}}})|{\Delta}\) and \({\boldsymbol{\sigma}}^{{\bf{2}}}\left(\right.{\bf{Y}}(\overline{\overline{{{\bf{X}}}_{k}}})|{\Delta}\), respectively.
-
5.
Acquisition function: Compute and maximize acquisition function, \(\mathop{\max }\nolimits_{X}U(.|{{\triangle }})\) to select next best location, \({{\bf{X}}}_{j+k}\) for evaluations.
-
6.
Expensive Black-box evaluations:
We highlight this step as the contribution in this paper in introducing the human operations in the proposed AE workflow.
-
a.
User interaction for target update: User gets a prompt message if the user is satisfied with the current target. User has option to choose, Yes or No. Mathematically, we can represent as \({\upsilon }_{k}=\left\{\begin{array}{c}0\,({No})\\ 1\,({Yes})\end{array}\right.\)
-
b.
Human-augmented process: Given \({\upsilon }_{k}=0\), follow steps 2(b)–(e) for sample patch \({{\boldsymbol{X}}}_{{\boldsymbol{j}}{\boldsymbol{+}}{\boldsymbol{k}}}\). Equations (4) and (5) can be simply modified to Eqs. (6) and (7) respectively.
-
a.
-
a.
Automated process: This step is included to speed up the search process to avoid redundant user interaction in case the user is satisfied with learning of the target spectral and therefore the goal changes to learn the spectral similarity map towards achieving the converged target. Therefore, Given \({\upsilon }_{k}=1\), \({{\bf{T}}}_{j+k}\,{\boldsymbol{=}}\,{\bf{T}}\,{\boldsymbol{=}}\,{{\bf{T}}}_{j+k-1}\). Calculate the structural similarity index function as per Eq. (8). It is to be noted that we recalculate the objective function once the user switches from a human-augmented to an automated process since the function changes. However, since we already have stored the previous spectral data for the explored image patches, the recalculation cost is negligible. Also, the architecture is currently set up where the switch from human-augmented to automated process is irreversible to avoid prompting the user repeatedly in Step 6(a).
-
7.
Augmentation: Augment data, \({{\bf{D}}}_{j+k}=[{{\bf{D}}}_{j+k-1};\{{{\bf{X}}}_{j+k},{Y}_{j+k}\}\).
Data availability
The analysis reported here is summarized in Colab Notebook for the purpose of tutorial and application to other data and can be found in https://github.com/arpanbiswas52/varTBO.
Code availability
The code is summarized in Colab Notebook for the purposeof tutorial and application to other data and can be found in https://github.com/arpanbiswas52/varTBO.
References
Kalinin, S. V. et al. Automated and autonomous experiments in electron and scanning probe microscopy. ACS Nano 15, 12604–12627 (2021).
Stach, E. et al. Autonomous experimentation systems for materials development: a community perspective. Matter 4, 2702–2726 (2021).
Stein, H. S. & Gregoire, J. M. Progress and prospects for accelerating materials science with automated and autonomous workflows. Chem. Sci. 10, 9640–9649 (2019).
Roccapriore, K. M., Kalinin, S. V. & Ziatdinov, M. Physics discovery in nanoplasmonic systems via autonomous experiments in scanning transmission electron microscopy. Adv. Sci. 9, 2203422 (2022).
Abolhasani, M. & Kumacheva, E. The rise of self-driving labs in chemical and materials sciences. Nat. Synth. 1–10 https://doi.org/10.1038/s44160-022-00231-0 (2023).
Shirasawa, R., Takemura, I., Hattori, S. & Nagata, Y. A semi-automated material exploration scheme to predict the solubilities of tetraphenylporphyrin derivatives. Commun. Chem. 5, 1–12 (2022).
Soldatov, M. A. et al. Self-driving laboratories for development of new functional materials and optimizing known reactions. Nanomaterials 11, 619 (2021).
Ahmadi, M., Ziatdinov, M., Zhou, Y., Lass, E. A. & Kalinin, S. V. Machine learning for high-throughput experimental exploration of metal halide perovskites. Joule 5, 2797–2822 (2021).
Reinhardt, E., Salaheldin, A. M., Distaso, M., Segets, D. & Peukert, W. Rapid characterization and parameter space exploration of perovskites using an automated routine. ACS Comb. Sci. 22, 6–17 (2020).
Thomas, J. C. et al. Autonomous scanning probe microscopy investigations over WS2 and Au{111}. Npj Comput. Mater. 8, 1–7 (2022).
Krull, A., Hirsch, P., Rother, C., Schiffrin, A. & Krull, C. Artificial-intelligence-driven scanning probe microscopy. Commun. Phys. 3, 1–8 (2020).
Rauch, E. F. et al. New features in crystal orientation and phase mapping for transmission electron microscopy. Symmetry 13, 1675 (2021).
Rauch, E. F. et al. Correction: Rauch et al. New features in crystal orientation and phase mapping for transmission electron microscopy. Symmetry 2021, 13, 1675. Symmetry 13, 2339 (2021).
Munshi, J. et al. Disentangling multiple scattering with deep learning: application to strain mapping from electron diffraction patterns. Npj Comput. Mater. 8, 1–15 (2022).
Shi, C. et al. Uncovering material deformations via machine learning combined with four-dimensional scanning transmission electron microscopy. Npj Comput. Mater. 8, 1–9 (2022).
Shahriari, B., Swersky, K., Wang, Z., Adams, R. P. & de Freitas, N. Taking the human out of the loop: a review of Bayesian optimization. Proc. IEEE 104, 148–175 (2016).
Kanarik, K. J. et al. Human–machine collaboration for improving semiconductor process development. Nature 616, 707–711 (2023).
Jiang, L., Liu, L., Yao, J. & Shi, L. A hybrid recommendation model in social media based on deep emotion analysis and multi-source view fusion. J. Cloud Comput. 9, 57 (2020).
Santos, F. P., Lelkes, Y. & Levin, S. A. Link recommendation algorithms and dynamics of polarization in online social networks. Proc. Natl Acad. Sci. USA 118, e2102141118 (2021).
Kranthi, G. N. P. S. & Ram Kumar, B. V. Online social voting techniques in social networks used for distinctive feedback in recommendation systems. Int. J. Sci. Eng. Adv. Technol. 6, 263–268 (2018).
Li, M. & Yin, Z. Debugging object tracking by a recommender system with correction propagation. IEEE Trans. Big Data 3, 429–442 (2017).
Suzuki, K. et al. Fast material search of lithium ion conducting oxides using a recommender system. J. Mater. Chem. A 8, 11582–11588 (2020).
Brochu, E., Cora, V. M. & de Freitas, N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. Preprint at https://doi.org/10.48550/arXiv.1012.2599 (2010).
Jones, D. R., Schonlau, M. & Welch, W. J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 13, 455–492 (1998).
Biswas, A., Fuentes, C. & Hoyle, C. A Mo-Bayesian optimization approach using the weighted Tchebycheff method. ASME. J. Mech. Des. 144, 011703 (2022).
Biswas, A., Fuentes, C. & Hoyle, C. A nested weighted Tchebycheff multi-objective Bayesian optimization approach for flexibility of unknown Utopia estimation in expensive black-box design problems. ASME. J. Comput. Inf. Sci. Eng. 23, 014501 (2023).
Tran, A., Eldred, M., McCann, S. & Wang, Y. SrMO-BO-3GP: a sequential regularized multi-objective constrained Bayesian optimization for design applications. Am. Soc. Mech. Eng. Digit. Collect. https://doi.org/10.1115/DETC2020-22184 (2020).
Morozovska, A. N., Eliseev, E. A., Biswas, A., Morozovsky, N. V. & Kalinin, S. V. Phys. Rev. Appl. 16, 044053 (2021).
Biswas, A., Morozovska, A. N., Ziatdinov, M., Eliseev, E. A. & Kalinin, S. V. Multi-Objective Bayesian optimization of ferroelectric materials with interfacial control for memory and energy storage applications. J. Appl. Phys. 130, 204102 (2021).
Greenhill, S., Rana, S., Gupta, S., Vellanki, P. & Venkatesh, S. Bayesian optimization for adaptive experimental design: a review. IEEE Access 8, 13937–13948 (2020).
Ueno, T., Rhone, T. D., Hou, Z., Mizoguchi, T. & Tsuda, K. COMBO: an efficient Bayesian optimization library for materials science. Mater. Discov. 4, 18–21 (2016).
Solomou, A. et al. Multi-objective Bayesian materials discovery: application on the discovery of precipitation strengthened NiTi shape memory alloys through micromechanical modeling. Mater. Des. 160, 810–827 (2018).
Kotthoff, L., Wahab, H. & Johnson, P. Bayesian optimization in materials science: a survey. Preprint at https://doi.org/10.48550/arXiv.2108.00002 (2021).
Kalinin, S. V., Ziatdinov, M. & Vasudevan, R. K. Guided search for desired functional responses via Bayesian optimization of generative model: hysteresis loop shape engineering in ferroelectrics. J. Appl. Phys. 128, 024102 (2020).
Gopakumar, A. M., Balachandran, P. V., Xue, D., Gubernatis, J. E. & Lookman, T. Multi-objective optimization for materials discovery via adaptive design. Sci. Rep. 8, 3738 (2018).
Griffiths, R.-R. & Hernández-Lobato, J. M. Constrained Bayesian optimization for automatic chemical design. Chem. Sci. 11, 577–586 (2020).
Morozovska, A. N. et al. Chemical control of polarization in thin strained films of a multiaxial ferroelectric: phase diagrams and polarization rotation. Phys. Rev. B 105, 094112 (2022).
Biswas, A. & Hoyle, C. An approach to Bayesian optimization for design feasibility check on discontinuous black-box functions. J. Mech. Des. 143, (2021).
Chu, W. & Ghahramani, Z. Extensions of Gaussian processes for ranking: semisupervised and active learning. Learn. Rank 29, 1–6 (2005).
Thurstone, L. L. A law of comparative judgment. Psychol. Rev. 34, 273–286 (1927).
Mosteller, F. Remarks on the method of paired comparisons: I. The least squares solution assuming equal standard deviations and equal correlations. In Selected papers of Frederick Mosteller. Springer Series in Statistics (eds Fienberg, S. E. & Hoaglin, D. C.) (Springer, New York, NY, 2006).
Holmes, C. C. & Held, L. Bayesian auxiliary variable models for binary and multinomial regression. Bayesian Anal. 1, 145–168 (2006).
Dhamala, J. et al. Embedding high-dimensional Bayesian optimization via generative modeling: parameter personalization of cardiac electrophysiological models. Med. Image Anal. 62, 101670 (2020).
Valleti, M., Vasudevan, R. K., Ziatdinov, M. A. & Kalinin, S. V. Bayesian optimization in continuous spaces via virtual process embeddings. Digit. Discov. 1, 910–925 (2022).
Wang, Z., Hutter, F., Zoghi, M., Matheson, D. & De Freitas, N. Bayesian optimization in a billion dimensions via random embeddings. J. Artif. Intell. Res. 55, 361–387 (2016).
Grosnit, A. et al. High-dimensional Bayesian optimisation with variational autoencoders and deep metric learning. Preprint at https://doi.org/10.48550/arXiv.2106.03609 (2021).
Biswas, A., Vasudevan, R., Ziatdinov, M. & Kalinin, S. V. Optimizing training trajectories in variational autoencoders via latent Bayesian optimization approach*. Mach. Learn. Sci. Technol. 4, 015011 (2023).
Oh, C., Gavves, E. & Welling, M. BOCK: Bayesian Optimization with Cylindrical Kernels. In Lawrence, N. (ed) Proc. 35th International Conference on Machine Learning (PMLR) Vol. 80 3868–3877 (Proceedings of Machine Learning Research (PMLR), 2018).
Wilson, A. G., Hu, Z., Salakhutdinov, R. & Xing, E. P. Deep Kernel Learning. In Lawrence, N. (ed) Proc. 19th International Conference on Artificial Intelligence and Statistics (PMLR) Vol. 51, 370–378 (Proceedings of Machine Learning Research (PMLR), 2016).
Ziatdinov, M., Liu, Y. & Kalinin, S. V. Active learning in open experimental environments: selecting the right information channel(s) based on predictability in deep kernel learning. Preprint at https://doi.org/10.48550/arXiv.2203.10181 (2022).
Frean, M. & Boyle, P. Using Gaussian processes to optimize expensive functions. In AI 2008: Advances in Artificial Intelligence (eds Wobcke, W. & Zhang, M.) Lecture Notes in Computer Science 258–267 (Springer, Berlin, Heidelberg, 2008).
Hutter, F., Hoos, H. H. & Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Learning and Intelligent Optimization; (ed. Coello, C. A. C.) Lecture Notes in Computer Science 507–523 (Springer, Berlin, Heidelberg, 2011).
Jones, D. R. A taxonomy of global optimization methods based on response surfaces. J. Glob. Optim. 21, 345–383 (2001).
Kushner, H. J. A new method of locating the maximum point of an arbitrary multipeak curve in the presence of noise. J. Basic Eng. 86, 97–106 (1964).
Cox, D. D. & John, S. A statistical method for global optimization. In Proc. 1992 IEEE International Conference on Systems, Man, and Cybernetics Vol. 2, 1241–1246 (IEEE, 1992).
van der Walt, S. et al. Scikit-Image: image processing in Python. PeerJ 2, e453 (2014).
Wu, P.-C. et al. Twisted oxide lateral homostructures with conjunction tunability. Nat. Commun. 13, 2565 (2022).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at https://doi.org/10.48550/arXiv.1412.6980 (2017).
Binois, M. & Wycoff, N. A survey on high-dimensional Gaussian process modeling with application to Bayesian optimization. ACM Trans. Evol. Learn. Optim. 2, 8:1–8:26 (2022).
Ziatdinov, M., Ghosh, A., Wong, C. Y. & Kalinin, S. V. AtomAI framework for deep learning analysis of image and spectroscopy data in electron and scanning probe microscopy. Nat. Mach. Intell. 4, 1101–1112 (2022). (Tommy).
Liu, Y. et al. Automated experiments of local non-linear behavior in ferroelectric materials. Small 18, 2204130 (2022).
Liu, Y. et al. Experimental discovery of structure–property relationships in ferroelectric materials via active learning. Nat. Mach. Intell. 4, 341–350 (2022).
Liu, Y. et al. Learning the right channel in multimodal imaging: automated experiment in piezoresponse force microscopy. Preprint at https://doi.org/10.48550/arXiv.2207.03039 (2023).
Kalinin, S. V. et al. Probing the role of single defects on the thermodynamics of electric-field induced phase transitions. Phys. Rev. Lett. 100, 155703 (2008).
Hong, S. Single frequency vertical piezoresponse force microscopy. J. Appl. Phys. 129, 051101 (2021).
Acknowledgements
The experiments, autonomous workflows, and deep kernel learning were supported by the Center for Nanophase Materials Sciences (CNMS), which is a US Department of Energy, Office of Science User Facility at Oak Ridge National Laboratory. Algorithmic development was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, MLExchange Project, award number 107514; and supported by the center for 3D Ferroelectric Microelectronics (3DFeM), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences under Award Number DE-SC0021118. J.-C.Y. and Y.-C.L. acknowledge support from the National Science and Technology Council (NSTC), Taiwan, under grant no. NSTC-111-2628-M-006-005.
Author information
Authors and Affiliations
Contributions
A.B. designed the algorithm, wrote the codes for implementation and analysis, analyzed data and wrote the paper. N.C. wrote codes for the spectral voting system. Y.L. assisted with experimental setup and code integration. Y.-C.L. and J.-C.Y. grew the samples used. S.J. wrote the acquisition software for python-controlled spectral acquisition. S.V.K. assisted with analysis of results and paper writing. M.A.Z. assisted with code development in the dKL framework. R.K.V. supervised the project, conceived of the idea, performed AFM experiments, and co-wrote the paper. All authors commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Biswas, A., Liu, Y., Creange, N. et al. A dynamic Bayesian optimized active recommender system for curiosity-driven partially Human-in-the-loop automated experiments. npj Comput Mater 10, 29 (2024). https://doi.org/10.1038/s41524-023-01191-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-023-01191-5