Abstract
Nonvolatile electrical control of spin polarization in two-dimensional (2D) magnetic semiconductors is greatly appealing toward future low-dissipation spintronic nanodevices. Here, we report a 2D material VSeF, which is an intrinsic bipolar magnetic semiconductor (BMS) featured with opposite spin-polarized valence and conduction band edges. We then propose a general nonvolatile strategy to manipulate both spin-polarized orientations in BMS materials by introducing a ferroelectric gate with proper band alignment. The spin-up/spin-down polarization of VSeF is successfully controlled by the electric dipole of ferroelectric bilayer Al2Se3, verifying the feasibility of the design strategy. The interfacial doping effect from ferroelectric gate also plays a role in enhancing the Curie temperature of the VSeF layer. Two types of spin field effect transistors, namely multiferroic memory and spin filter, are further achieved in VSeF/Al2Se3 and VSeF/Al2Se3/Al2Se3 multiferroic heterostructures, respectively. This work will stimulate the application of 2D BMS materials in future spintronic nanodevices.
Similar content being viewed by others
Introduction
Two-dimensional (2D) magnetic materials, showing great potential in information storage, transmission and processing by utilizing the spin degree of freedom1,2,3, have attracted extensive interests since the experimental discovery of atom-thick magnetic materials CrI34, Cr2Ge2Te65, and Fe3GeTe26. Meanwhile, the sheer openness of 2D magnetic materials makes them possess gate tunability and integrated flexibility6,7, which is appealing for next-generation nanoscale spintronic devices. In order to develop high-performance 2D spintronic nanodevices, the flexible manipulation of carriers’ spin polarization is highly desirable. As compared with the traditional external magnetic field control of spin orientation in materials, electric field control is an extremely exciting research area, both in fundamental science and technology application8,9,10, such as exploring multiferroic physics and exploiting the magnetoelectric coupling in ultrafast magnetic memories11,12,13,14. Recently, magnetic anisotropy15,16,17, magnetic conductivity18,19,20, magnetic configuration21,22,23 and magnetic moment24 have been reported to be tuned by the ferroelectric polarization via interfacial magnetoelectric effects.
Bipolar magnetic semiconductors (BMSs), whose valence band maximum (VBM) and conduction band minimum (CBM) are derived from opposite spin channels, offer an ideal platform to achieve the electrical manipulation of both spin orientation around Fermi energy25,26. Till now, only a few intrinsic 2D BMSs have been theoretically predicted27,28,29,30,31,32, where the origins of bipolar semiconducting character are complicated and remain to be further explored. On the other hand, the state-of-the-art proposed way to manipulate carriers’ spin-polarized orientation in BMS materials requires persistent electrical control which is volatile and achieved by applying a gate voltage19,26,33. Thus, designing 2D BMSs, exploring the formation mechanism of the bipolar semiconducting properties, and realizing nonvolatile control of the carriers’ spin polarization are crucial for 2D BMSs’ application. That will stimulate and accelerate the future development of 2D BMS materials in 2D spintronics.
In this work, we first report an intrinsic 2D BMS VSeF with a strongly correlated charge-transfer-type electronic band structure, where the hole effective mass is far less than the electron effective mass. Inspired by the ferroelectric (FE) materials with spontaneous electric polarization, we propose a general strategy to achieve nonvolatile manipulation of the carriers’ spin polarization in BMSs by introducing a FE gate with proper band alignment. Using first-principles calculation, our proposal has been achieved in the BMS VSeF monolayer by putting it on 2D FE Al2Se3 layer, considering the lattice mismatch. As stacked on a single-layer FE Al2Se3, monolayer VSeF preserves its BMS character when Al2Se3 (↓) is downward electric polarized, while it transforms into a half-metal upon reversing the electric polarized orientation of Al2Se3 (↑). To induce a larger built-in electric field, we increase the thickness of the FE layer to bilayer Al2Se3. It is found that the VSeF is n-doped with spin-up carriers by the upward electric polarization of bilayer Al2Se3 (↑), while it’s p-doped with spin-down carriers by the downward electric polarization of bilayer Al2Se3 (↓). Due to the interfacial doping effect, the Curie temperature of VSeF can be enhanced from 66 K to 71 K, 76 K and 81 K in VSeF/Al2Se3 (↑), VSeF/biAl2Se3 (↓) (bilayer Al2Se3) and VSeF/biAl2Se3 (↑), respectively. Based on these multiferroic van der Waals (vdW) heterostructures, we further design two types of spin field effect transistors (FETs), namely few-layer multiferroic memory and spin filter, using VSeF/Al2Se3 bilayer heterostructure and VSeF/biAl2Se3 trilayer heterostructure, respectively. We find that the choices of FE gates are abundant. Different FE gates would lead to different carriers’ doping concentrations. Our results pave the way for the realization and application of 2D BMS in future spintronic nanodevices.
Results
Structure and magnetic properties of VSeF monolayer
The crystal structure of the VSeF monolayer, as depicted in Fig. 1a, consists of buckled double VSe layers sandwiched by two F atomic layers. The VSeF monolayer crystallizes in the orthorhombic symmetry group (space group Pmmn), which takes the same structure as the experimentally synthesized 2D magnetic semiconductor CrSBr34. VSeF monolayer is screened from MXY compounds (M = Ti, V, Cr, Mn, Fe, Co, Ni, X = O, S, Se, Te, Y = F, Cl, Br, I), taking CrSBr as prototype structure. The calculated results are summarized in Supplementary Table 1, containing stable nonmagnetic metals, nonmagnetic semiconductors, magnetic metals and magnetic semiconductors. Among them, only VSF and VSeF are dynamically stable 2D bipolar magnetic semiconductors (BMS). Supplementary Fig. 1 presents the electronic band structure and phonon spectrum of VSF, which is similar with that of VSeF. The calculated lattice parameters of VSeF monolayer are listed in Supplementary Table 2. Phonon spectrum calculation was performed. As shown in Fig. 1b, no imaginary frequency is observed in the phonon spectrum, indicating that VSeF monolayer is dynamically stable. The thermal stability of VSeF monolayer is evaluated by performing ab initio molecular dynamical (AIMD) simulations at 300 K and 500 K. The geometric structure of the VSeF monolayer at different temperatures keeps intact (Supplementary Fig. 2), which indicates that VSeF monolayer is thermally stable. The thermodynamical stability of VSeF monolayer is evaluated by performing a global structure optimization for 2D V-Se-F crystal via CALYPSO code35,36, and investigating its energy above convex hull. We didn’t find other structures which have lower formation energies than that of our studied structure after 15-generation optimizations. In addition, the energy above convex hull obtained from the Computational 2D Materials Database (C2DB) is only 0.14 eV/atom, lower than the thermodynamical stability criteria of 0.2 eV/atom in previous literatures37,38. These results thus indicate that VSeF monolayer is thermodynamically stable.
a Top and side views of VSeF monolayer, and a local distorted VSe4F2 octahedron. Red, yellow, and gray balls represent V, Se, and F atoms, respectively. b Phonon spectrum of VSeF monolayer. c The 3d orbital splitting from an ideal octahedron with Oh symmetry to a distorted octahedron with C2v symmetry, and further splitting with a larger energy gap between occupied states and unoccupied states in V3+ 3d2 due to the electronic correlation. d Simulated magnetic moment (black data) and magnetic susceptibility (red data) as functions of temperature for 2D VSeF.
The magnetic property of VSeF monolayer is largely dependent on the local environment of V3+. Each V3+ is surrounded by four Se2- and two F- forming a distorted octahedron VSe4F2 with C2v symmetry. As illustrated in Fig. 1c, under an ideal octahedral crystal field with Oh symmetry, the fivefold degenerate d orbitals split into double degenerate eg orbitals and threefold degenerate t2g orbitals. In VSeF, the distorted octahedral crystal field further lifts double degenerate eg orbitals into two a1 orbitals, and threefold degenerate t2g orbitals into b1, b2, and a2 orbitals. The two V3+ d2 electrons occupy two of three nearly degenerate orbitals (b2 and a2 orbitals), which is different from the situation in CrSBr39. In the case of Cr3+ d3 orbitals, the three nearly degenerate orbitals (b1, b2, and a2 orbitals) are half-filled, which can be described by the nondegenerate single-band Hubbard model. However, the physical picture of the partial occupation of degenerate orbitals needs to be described by a multiband Hubbard model.
The multi-orbital Hamiltonian is given as
where i and j represent the two neighboring magnetic sites, m and m’ are the orbital indexes. The first term describes the nearest-neighbor hopping, the second term describes the on-site orbital energies, the third to fifth terms are the intra- (U) and interorbital (U’) Coulomb interactions and the Hund’s coupling (J), where U’ = U – 2 J40,41. Single-band Hubbard model only contains the first three items of Eq. (1), completely neglecting the interorbital Coulomb interactions. However, when the strongly correlated degenerate orbitals are partially filled, the interorbital repulsion between occupied orbitals and unoccupied orbitals (U’ – J) cannot be neglected, which is crucial to decide the electronic structure (Fig. 1c). Similar cases have been reported in VS242, VI343, VOCl44, TiOCl41, etc. In VI3 (V3+ with d2 electronic configuration), the Hubbard U value shifts up (down) the unoccupied (occupied) orbital levels producing a semiconducting character43.
The two d2 electrons of V3+ in VSeF produce a local magnetic moment of 2 μB, which is in accordance with the results from DFT calculations. To determine the magnetic ground state of VSeF monolayer, we considered five possible magnetic configurations (Supplementary Fig. 3). It is found that the ferromagnetic state is the most stable configuration. And the ferromagnetic ground state of VSeF is robust against the Hubbard U (Supplementary Fig. 5) and spin-orbit coupling (SOC) effect (Supplementary Table 3). The easy axis of magnetization of VSeF monolayer is along the out-of-plane direction, whose energy is lower than that of the in-plane direction (Supplementary Table 4). Based on the classical Heisenberg Hamiltonian,
where J1, J2, and J3 are the nearest, next-nearest and third-nearest-neighbor exchange interaction parameters, respectively. Ax and Ay represent to single-ion anisotropy along the x and y direction, respectively. These parameters can be extracted by comparing the relative energies of different magnetic configurations (Supplementary Table 4). We carried out Monte Carlo simulation to estimate the Curie temperature (Tc) by using a 50 × 50 superlattice. The susceptibility is calculated according to χ = (〈E2〉 − 〈E〉2)/(kBT). The calculated magnetization and susceptibility indicate that the Curie temperature is around 66 K (Fig. 1d), which is higher than that of the experimentally known Tc of 2D magnetic semiconductor CrI3 (45 K).
Electronic structures and the origin of BMS
The electronic band structure of VSeF calculated by the GGA + U (Ueff = 3.25 eV) shows that the VSeF monolayer behaves as a BMS, where the VBM and CBM are derived from different spin channels (Fig. 2a). As the HSE06 functional generally gives more accurate band structures for semiconductors, we also calculated the band structure of VSeF by using an HSE06 functional (Supplementary Fig. 6), which is qualitatively consistent with the result from GGA + U calculation, indicating that the BMS character of VSeF is robust. Since the Se atom is heavy, the spin-orbit coupling (SOC) effect may affect the electronic structure of VSeF, we further calculated the electronic band structure including the SOC effect. The calculated band structure (Supplementary Fig. 7) exhibits bipolar character, which is consistent with that obtained without considering SOC effect. The spin-resolved projected density of states (PDOS) shows that the VBMs of both spin channels are mainly contributed by Se-p orbitals, and the CBMs are mainly contributed by V-d orbitals (Fig. 2a). That is in accordance with the partial charge densities of VBMs and CBMs of both spin channels (Fig. 2b). The charge densities of VBMs of both spin channels (①: spin up channel; ②: spin down channel) are similar, showing the main Se-px orbital feature and partial Se-px and V-dxz bonding feature. The charge densities of CBMs of both spin channels (③: spin up channel; ④: spin down channel) which are mainly localized in V atoms are also similar.
a Spin-resolved band structure where red lines and blue dashed lines represent spin-up and spin-down channels, respectively, element-resolved PDOS of VSeF monolayer and zoom-in PDOS near the Fermi level where blue, magenta, and gray regions represent the PDOS contributed by V, Se, and F atoms, respectively. Fermi level is set to 0 eV, as labeled by horizontal black dashed line. b Partial charge densities of VBMs and CBMs of both spin channels. The marked numbers correspond to band decomposed locations in panel a. The magenta and blue isosurfaces represent the electron densities of VBMs and CBMs, respectively, where the isosurface value is 4 × 10–3 e·bohr-3. c Schematic spin-resolved DOS of VSeF monolayer with the BMS behavior where the red and blue colors represent spin-up and spin-down channel, respectively, and the BMS feature can be described by three energy parameters (Δ1, Δ2, and Δ3). Δ2 is the bipolar bandgap. d The variations of three energy parameters (Δ1, Δ2, and Δ3) as the Ueff = U – J parameter. When Ueff is less than 1.25 eV, VSeF is a metal (Δ2 = 0; the pink region). Once Ueff is larger than 1.25 eV, VSeF is a BMS (the gray region).
The BMS feature of VSeF can be described by three energy gaps (Δ1, Δ2, and Δ3), as shown in Fig. 2c. The Δ2 gap is defined as the spin-flip gap between the VBM and CBM from different spin channels. Δ1 + Δ2 and Δ2 + Δ3 represent the spin-conserved gaps for two spin channels, respectively. Fig 2c depicts the schematic density of states (DOS) of VSeF, where the Se-p orbital bands with broad bandwidth are full-occupied, while the V-d orbital bands are partially occupied and localized. According to the aforementioned multiband Hubbard model, the orbital repulsion between the occupied states and unoccupied states with the same spin orientation is U’ – J, while the orbital repulsion between the occupied states and unoccupied states from different orbitals with different spin orientation is U’. Therefore, we investigated the influence of the effective Hubbard U parameter Ueff on the band structure of VSeF. As shown in Supplementary Fig. 8, the splitting between occupied V-d orbitals and unoccupied V-d orbitals gradually increases with Ueff value, and a transition from metal to BMS happens when Ueff equals 1.25 eV, indicating the strongly correlated characteristic of VSeF. When Ueff equals 0, VSeF is a metal where the d-orbital splitting originated from the distorted crystal field is small. Increasing the Ueff value gradually enhances the interorbital splitting between occupied and unoccupied orbitals, inducing a semiconducting bandgap. The magnitude of the three energy gaps (Δ1, Δ2, and Δ3) as a function of Ueff are summarized in Fig. 2d. In the BMS region, Δ1 and Δ2 gradually increase with Ueff value, while Δ3 is less affected. That’s in accordance with the depicted picture in Fig. 2c.
It is worth noting that VSeF is a charge-transfer semiconductor, where the hole effective mass is smaller than the electron-effective mass45. Therefore, the carrier mobility of VSeF is largely dependent on the carrier type. Here, due to the broken time-reversal symmetry in ferromagnetism, the spin-up channels of valence band (VB) and conduction band (CB) together downward shift, while the spin-down channels upward shift, lifting Kramer’s degeneracy. Therefore, the VBM and CBM of VSeF are derived from the opposite spin channel. Δ1 and Δ3 are the spin exchange splitting gaps of VB and CB, respectively. Due to the partial hybridization between Se-px orbitals and V-dxz orbitals in VBMs, the spin splitting gap Δ1 is moderate. The origin of BMS in VSeF is different from the BMS formation mechanism of other transition metal compounds proposed by Deng et al., where the bipolar bandgap Δ2 is derived from the spin exchange splitting of the same d orbital28,46.
Monolayer Al2Se3 ferroelectric gate
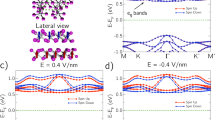
The electronic structure of BMS enables electrical fields to control the carriers’ spin-polarization directions. It’s common to manipulate the spin polarization of BMS materials by applying a gate voltage (Supplementary Fig. 9). The 100% spin-polarized channel currents can be realized by changing the sign of the applied gate voltage. Supplementary Fig. 10 shows the variation of band structure of VSeF with the carrier concentrations. Upon hole (electron) doping, the spin-down (spin-up) carriers dominate the Fermi level. Besides, VSeF monolayer always keeps the ferromagnetic magnetic ground state under different carrier doping concentrations (Supplementary Fig. 11). However, the realization of electrical control of spin polarization by applying a gate voltage in BMS materials remains to be explored in the experiment. And this way to control carriers’ spin polarization is volatile, requiring a persistent external electrical field.
To solve these problems, we proposed that it’s possible to manipulate the spin polarization of BMS materials by applying a ferroelectric gate, as shown in Fig. 3a. Ferroelectric materials exhibit spontaneous polarization which can be maintained even if removing the external electric field. And the ferroelectric polarization can be switched by applying a short-term pulse voltage. Due to the built-in electric field induced by the ferroelectric polarization, the energy band alignment between ferroelectric dielectric layer and BMS channel layer can be altered by switching the direction of ferroelectric polarization. Consequently, the charge transfer between ferroelectric layer and BMS layer is also tunable (Fig. 3a). When the VBM of FE locates within the CBMs of spin-up and spin-down channel of BMS, n-type doping occurs in BMS, and electron carriers possess spin-up orientation. When the CBM of FE locates within the VBMs of spin-up and spin-down channel of BMS, p-type doping occurs in BMS, and hole carriers possess spin-down orientation. Therefore, nonvolatile electrical control of spin polarization is expected to be realized by constructing multiferroic BMS/FE heterostructures. This way can overcome the volatility in traditional electrical control approaches, which is more energy-efficiency.
a Schematic diagram of spin FET based on BMS, the spin orientations in the conducting channel (BMS region, marked in blue) can be controlled by switching the electric polarization of ferroelectric dielectric (FE region, marked in yellow). The bottom panel depicts the desired band alignments between BMS and FE under different ferroelectric polarized states, and associated charge transfers. Here, the solid and dashed lines represent VBM and CBM, respectively. Black arrows denote the electron spin, where electrons fill to the VBMs. The spin-up and spin-down bands of BMS are split, due to the intrinsic magnetism of BMS. b Top and side views of VSeF/Al2Se3 bilayer heterostructures. The red arrow represents the polarization direction of Al2Se3. c Band alignments of VSeF/Al2Se3 (↑) and VSeF/Al2Se3 (↓) with respect to the vacuum level of VSeF. The red and blue bars show the band edges of spin-up and spin-down channels of BMS, respectively, the purple bars show the band edges of FE. d Layer-resolved PDOS of VSeF/Al2Se3 (↑) and VSeF/Al2Se3 (↓), where the orange and purple lines represent the PDOS contributed by VSeF and Al2Se3, respectively. The potential energy decreases along the direction of black dashed line.
To verify the proposal, we first constructed a multiferroic vdW heterostructure for the predicted 2D BMS VSeF by combining a 2D ferroelectric Al2Se3, as shown in Fig. 3b. Single-layer Al2Se3 possesses the same structure as α-In2Se3 monolayer with hexagonal symmetry group47, which is screened from the family of 2D ferroelectric III2-VI3 materials by considering the band alignments and lattice mismatch between VSeF monolayer and 2D III2-VI3 ferroelectrics (Supplementary Fig. 12). The ferroelectric polarization state depends on the movement of the middle Se layer. When the middle Se atom is close to the bottom (upper) Al atom, it’s upward (downward) polarization P ↑ (P ↓ ). Considering the lattice mismatch, the relaxed \(\sqrt 3 \times 3\) -Al2Se3 supercell with orthorhombic lattice is strained by 2.3% (x direction) and -6.8% (y direction) to match the 2 × 2-VSeF. To evaluate the stability of Al2Se3 ferroelectric state under strained, we calculated the entire ferroelectric polarization reversal path of strained Al2Se3 to compare the energy difference between the centrosymmetric phase and ferroelectric phase. As shown in Supplementary Fig. 13, the ferroelectric state of strained Al2Se3 is still more stable than the paraelectric phase. We considered 24 possible stacking mode between VSeF and Al2Se3 by shifting their relative positions in the in-plane direction. As shown in Supplementary Fig. 14, by comparing the total energies of these 24 configurations, the most stable structures are obtained, which are the same for both P ↑ and P ↓ .
In our calculations, we fixed the lattice constant of VSeF and only relaxed the atomic positions in heterostructures for eliminating the strain influences on the BMS properties of VSeF. Due to the built-in electric field, there is a potential drop of 1.73 eV across the two sides of Al2Se3 (Supplementary Fig. 15), which produces different band alignments when VSeF contacts with P ↑ and P ↓ Al2Se3. As illustrated in Fig. 3c, the different band alignments lead to different interfacial charge transfer. When combined with P ↑ Al2Se3, the potential energy of VSeF is lower than that of Al2Se3 (Supplementary Fig. 16a), which makes that the spin-up CBM of VSeF is lower than the VBM of Al2Se3, suggesting that electrons can transfer from Al2Se3 to spin-up channel of VSeF. In contrast, for VSeF/Al2Se3 (↓), the potential energy of Al2Se3 is lower (Supplementary Fig. 16b), but the CBM of Al2Se3 is still slightly higher than the spin-down VBM of VSeF. Therefore, the electrons transfer from VSeF to Al2Se3 is blocked.
The calculated layer-resolved PDOS are consistent with the analysis of band alignments. As indicated in Fig. 3d, in VSeF/Al2Se3 heterostructure, the potential energy decreases along the direction of black dashed arrow, leading to the band relative shift between VSeF and Al2Se3. We found that the half-metallicity with spin-up polarization appears in the VSeF part of VSeF/Al2Se3 (↑) heterostructure, showing n-type doping feature. In contrast, VSeF remains as a semiconductor, when combined with P ↓ Al2Se3. Therefore, the ferromagnetic half-metal/semiconductor switching in VSeF can be controlled by the polarized states of the Al2Se3 monolayer.
Bilayer Al2Se3 ferroelectric gate
To realize nonvolatile electrical control of spin polarization in VSeF, we further tried to stack VSeF on the bilayer Al2Se3 forming a trilayer vdW heterostructure (Fig. 4a), where the bilayer Al2Se3 possesses enhanced ferroelectric polarization47,48. Similar to VSeF/Al2Se3 bilayer heterostructure, we first calculated the band alignments for VSeF/biAl2Se3 (↑) and VSeF/biAl2Se3 (↓). As shown in Fig. 4b, the band alignments between VSeF and neighbor Al2Se3 (FE1) are less affected by the added bottom Al2Se3 (FE2), which are similar to that of VSeF/Al2Se3 bilayer heterostructure. Particularly, due to the built-in electric field, there also exists charge transfer between bilayer Al2Se3. To visualize the charge redistribution in VSeF/biAl2Se3 heterostructure, the charge density difference, plane-averaged charge density difference (Δρ) and the z-direction integral of plane-averaged charge density difference (n) are shown in Fig. 4c, d for VSeF/biAl2Se3 (↑) and VSeF/biAl2Se3 (↓), respectively. The negative Δρ represents the charge depletion and the positive Δρ represents the charge accumulation.
a Side views of VSeF/biAl2Se3 trilayer heterostructures. The red arrow represents the polarization direction of Al2Se3. b Band alignments of VSeF/biAl2Se3 (↑) and VSeF/biAl2Se3 (↓) with respect to the vacuum level of VSeF. The red and blue bars depict the band edges of spin-up and spin-down channel of VSeF, respectively. The purple bars depict the band edges of two layers of FE Al2Se3. c, d Charge density difference, planar-averaged density difference (black line) and the integral (red lines) of planar-averaged density difference along z-direction for VSeF/biAl2Se3 (↑) and VSeF/biAl2Se3 (↓), respectively, where the blue dashed lines indicate the atomic boundary of each layer, and the cyan and magenta isosurfaces represent electronic accumulation and depletion with isovalue of 2.03 × 10–3 e Å−3, respectively. e, f Layer-resolved PDOS of VSeF/biAl2Se3 (↑) and VSeF/biAl2Se3 (↓). The potential energy decreases along the direction of black dashed line. FE1 and FE2 denote the upper Al2Se3 layer and the bottom Al2Se3 layer, respectively. The orange, purple, and pink lines represent the PDOS contributed by VSeF, FE1, and FE2, respectively.
Clearly, the charge transfer not only occurs between VSeF and FE1, but also between FE1 and FE2. The z-direction integral of plane-averaged charge density difference indicates that the total charge depletion and accumulation of each layer mainly occur within VSeF and FE2, and the variation of total charge of FE1 is small. Therefore, it can be equivalently viewed that the charge transfer mainly happens between VSeF and FE2, where the FE1 acts as a bridge. As reflected in the layer-resolved PDOS (Fig. 4e, f), because the effective charge transfer occurs within VSeF and FE2, both VSeF and FE2 exhibit metallicity, while FE1 always remains as a semiconductor. Interestingly, n-doped VSeF with spin-up carriers appears in VSeF/biAl2Se3 (↑) heterostructure, and p-doped VSeF with spin-down carriers appears when reversing the ferroelectric polarization of bilayer Al2Se3. Therefore, nonvolatile electric control of spin polarization is achieved in VSeF/biAl2Se3 trilayer heterostructure. Different spin-orientation channel current in VSeF can be switched by the polarized states of bilayer Al2Se3.
Doping effect on VSeF from FE substrates
It’s worth noting that the VSeF layer always maintains the ferromagnetic ground state and out-of-plane easy magnetization axis in all heterostructures, as shown in Supplementary Table 4, the energies of out-of-plane ferromagnetic configuration are lowest for whichever heterostructure. Due to the interfacial engineering on magnetism49,50, we further explored the influence of FE substrates on the Curie temperature of VSeF. As shown in Figs. 5a, b, the Tc value of VSeF is enhanced to 71 K, 76 K and 81 K in VSeF/Al2Se3 (↑), VSeF/biAl2Se3 (↓) and VSeF/biAl2Se3 (↑) heterostructures, respectively. While for the VSeF/Al2Se3 (↓) heterostructure, the Tc value is slightly decreased to 61 K. Since the lattice constants of VSeF layer are fixed in all heterostructures and the structure variations of VSeF layer are minor (Supplementary Table 5 and Supplementary Fig. 4), the change of Tc value can be primarily attributed to the interfacial charge transfer between VSeF and FE substrates. VSeF layer is n-type doped in VSeF/Al2Se3 (↑) and VSeF/biAl2Se3 (↑) heterostructures, and p-type doped in VSeF/biAl2Se3 (↓) heterostructure, exhibiting ferromagnetic half-metallic property. However, VSeF layer keeps its ferromagnetic semiconducting property in VSeF/Al2Se3 (↓) heterostructure. Generally, due to the existence of itinerant carriers, ferromagnetic metals possess higher Curie temperatures than that of ferromagnetic semiconductors4,5,6.
a, b The variations of magnetic moment and susceptibility as functions of temperature in VSeF/Al2Se3 (↓) (blue line), VSeF/Al2Se3 (↑) (green line), VSeF/biAl2Se3 (↓) (orange line) and VSeF/biAl2Se3 (↑) (magenta line) heterostructures. The black dashed line indicates the Tc value of pristine VSeF monolayer. c The doping concentration of VSeF layer under different FE substrates (bilayer Al2Se3, bilayer Ga2Se3 and bilayer In2Se3) and FE polarized states (upward polarization or downward polarization). The blue and green bars depict the doping concentrations from upward and downward electric polarized FE gates, respectively. The positive and negative doping concentration indicate electron and hole doping, respectively.
By calculated the charge density difference (Fig. 4c, d and Supplementary Fig. 17a, b), we also quantitatively analyzed the doping concentrations of Al2Se3 gates under different layer numbers and FE polarized states. The doping concentrations on VSeF layer are 1.6 × 1013 cm−2, 0 cm−2, 3.1 × 1013 cm−2 and −1.5 × 1013 cm−2 in VSeF/Al2Se3 (↑), VSeF/Al2Se3 (↓), VSeF/biAl2Se3 (↑) and VSeF/biAl2Se3 (↓) heterostructures, respectively. Here, the positive values represent electron doping and negative values represent hole doping. We found that the Curie temperature increases with the carrier doping concentration. And the hole carriers with smaller effective mass are more beneficial for the enhancement of Tc than electron carriers. Therefore, bilayer Al2Se3 FE gates not only can control the carriers’ spin polarization in VSeF channel layer, but also can enhance the Curie temperature of VSeF.
Furthermore, we revealed that such nonvolatile electric control of spin polarization can be applied to other 2D BMS/FE multiferroic heterostructures, where the choices of FE gates and 2D BMS channel materials are abundant. For example, both bilayer Ga2Se3 and In2Se3 FE substrates show reversible interfacial doping effect which results in the manipulation of carriers’ type and spin-polarized direction in VSeF layer by switching the ferroelectric polarized state (Supplementary Fig. 18 and Supplementary Fig. 19). However, since the band alignment between VSeF and different FE substrates is different, the interfacial charge transfer in VSeF/FE heterostructures would be different, which is related to the FE material species and FE polarized states. By calculating the charge density difference in different VSeF/FE heterostructures (Supplementary Fig. 17), we summarized the doping concentration of different FE gates in Fig. 5c. The carrier doping concentrations from different FE gates are all on the order of 1013 cm−2, which is comparable with the traditional gate-voltage applied51. Besides, we verified the nonvolatile control strategy is also achieved in LaBr2/triAl2Te3 (trilayer Al2Te3) multiferroic heterostructure (Supplementary Fig. 20), where LaBr2 has been predicted to be a 2D BMS52. For the other screened BMS VSF, the reversible control of carriers’ spin polarization is also achieved in the VSF/biGa2S3 multiferroic heterostructure (Supplementary Fig. 21). These results indicate the feasibility and generality of our proposed nonvolatile electrical control strategy to BMS materials.
Devices based on VSeF/Al2Se3 and VSeF/biAl2Se3 heterostructures
Nanoscale devices are the inevitable trend of future technology development. Here, we suggested that the VSeF/Al2Se3 bilayer and VSeF/biAl2Se3 trilayer vdW heterostructures are promising structures for designing nanoscale spintronic devices. As shown in Fig. 6a, b, an atom-thick multiferroic memory device can be constructed based on the VSeF/Al2Se3 bilayer heterostructure. Since the electronic properties of the upper VSeF layer, either ferromagnetic half-metallic (100% spin-up polarization) or semiconducting, are controllable by the polarized state of Al2Se3, it serves as a channel material to be selectively conductive. Spin-up electrons can propagate through the VSeF (“on” state) for VSeF/Al2Se3 (↑) (Fig. 6a), while the electron transmission is blocked (“off” state) for VSeF/Al2Se3 (↓) (Fig. 6b). Here, data writing in the memory is realized by switching the ferroelectric polarized states, and data reading is realized by detecting the electrical signals.
a, b Atom-thick multiferroic memory based on the VSeF/Al2Se3 bilayer heterostructure, where the data writing and reading can be achieved by manipulating the ferroelectric polarization states of Al2Se3 monolayer and measuring the conductivity of VSeF channel, respectively. The red and blue arrows represent carriers’ spin-up and spin-down polarized orientations, respectively. c, d spin filter based on the VSeF/biAl2Se3 trilayer heterostructure, where the carriers’ spin-polarized orientation and carriers’ type (electron/hole) in the VSeF channel depend on the ferroelectric polarization states of bilayer FE Al2Se3.
As for VSeF/biAl2Se3 trilayer heterostructure, we designed a spin filter device (Fig. 6c, d). The spin polarization of the upper VSeF layer, either spin-up or spin-down, are controlled by the ferroelectric polarized state of bilayer Al2Se3. For VSeF/biAl2Se3 (↑), n-doped VSeF layer only allows spin-up electron carrier pass (Fig. 6c). When the polarization direction of bilayer Al2Se3 is reversed by an external electric field, the upper VSeF layer is p-type doped, only allowing spin-down hole carrier pass (Fig. 6d). Therefore, the manipulation of spin-polarized current can be achieved in this device.
Discussion
In summary, based on first-principles calculations, we reported an intrinsic 2D BMS VSeF and unveiled the microscopic origin of its BMS feature. The non-negligible interorbital Coulomb repulsion between occupied states and unoccupied states in V3+ ([Ar]3d2) and spin exchange splitting are both responsible for its bipolar character. Furthermore, we proposed a nonvolatile way to manipulate the spin polarization of BMS by introducing the ferroelectric gate. As embodied in the 2D BMS VSeF, the magnetic half-metal/semiconductor switching and spin-up/spin-down polarization switching in VSeF can be realized by manipulating the electric polarization of monolayer FE Al2Se3 and bilayer FE Al2Se3 in VSeF/Al2Se3 bilayer and VSeF/biAl2Se3 trilayer multiferroic heterostructures, respectively. These reversible switching endow VSeF with many promising applications in nanodevices, such as atom-thick multiferroic memory and spin filter. We find that the interfacial doping effect from FE gates also plays a role to enhance the Curie temperature of VSeF layer, which facilitates the utilization of spintronic nanodevices based on VSeF BMS. Finally, it’s worth noting that our proposed nonvolatile way to manipulate spin polarization in BMS materials by introducing FE gates was feasible and general, where the choices of BMS channel materials and FE gates are abundant. Therefore, our work not only reports an intrinsic 2D BMS, but also provides a feasible and general approach to achieve nonvolatile electrical control of 2D BMS.
Methods
All first-principles calculations were performed by using the density functional theory (DFT), as implemented in the Vienna ab initio simulation package (VASP)53. The Perdew-Burke-Ernzerhof generalized gradient approximation (PBE-GGA)54 was employed to deal with the electron exchange-correlation potentials. The projector-augmented-wave (PAW)55 pseudopotentials were applied to describe the electron-ion interaction with a plane-wave cutoff of 520 eV. 3p63d44s1 of V, 4s24p4 of Se, 3s23p4 of S, 2s22p5 of F, 3s23p1 of Al, 4s24p1 of Ga, 5s25p1 of In, 5s25p65d16s2 of La, 4s24p5 of Br and 5s25p4 of Te electronic configurations were treated as valence electrons, respectively. The strong Coulomb interaction between V-3d electrons is corrected by the DFT + U method in the Dudarev form56, where the effective U parameter Ueff = U – J was applied to the d orbitals of V atoms. The hybrid Heyd-Scuseria-Ernzerhof functional (HSE06)57 was also used to obtain the band structure for VSeF monolayer. A 20 Å thickness vacuum layer was introduced along the z-axis in all calculations. Ab initio molecular dynamical simulations (AIMD) were performed under an NVT ensemble. The ferroelectric reversal barrier was calculated using climbing nudged elastic band (CI-NEB) method58,59. The interlayer van der Waals interaction was considered by using the DFT-D3 method of Grimme60 for VSeF/Al2Se3, VSeF/biAl2Se3, VSeF/biGa2Se3, VSeF/biIn2Se3, LaBr2/triAl2Te3 (trilayer Al2Te3) and VSF/biGa2S3 heterostructures. A dipole correction was applied to eliminate spurious dipole-dipole interaction between periodic images. Atomic positions and lattice parameters were fully relaxed until the force acting on each atom was less than 10–3 eV Å−1 for VSeF monolayer, VSF monolayer and LaBr2 monolayer. For VSeF/Al2Se3, VSeF/biAl2Se3, VSeF/biGa2Se3, VSeF/biIn2Se3, LaBr2/triAl2Te3 and VSF/biGa2S3 heterostructures, due to the lattice mismatch, we fixed the lattice constant of VSeF, VSF and LaBr2 ferromagnetic layer and only relaxed the atomic positions with the force convergence criterion of 10–2 eV Å−1. The phonon spectrum was calculated using the finite-displacement method implemented in the PHONOPY code61. The dynamical Monte Carlo (MC) simulation based on the Heisenberg model was performed to estimate the magnetic transition temperature.
Data availability
The data supporting the findings of this paper are available from the corresponding authors upon reasonable request.
Code availability
The central code used in this paper is VASP. Detailed information related to the license and user guide are available at https://www.vasp.at.
References
Han, W., Kawakami, R. K., Gmitra, M. & Fabian, J. Graphene spintronics. Nat. Nanotechnol. 9, 794–807 (2014).
Soumyanarayanan, A., Reyren, N., Fert, A. & Panagopoulos, C. Emergent phenomena induced by spin-orbit coupling at surfaces and interfaces. Nature 539, 509–517 (2016).
Zutic, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Deng, Y. et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 563, 94–99 (2018).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Huang, B. et al. Electrical control of 2D magnetism in bilayer CrI3. Nat. Nanotechnol. 13, 544–548 (2018).
Matsukura, F., Tokura, Y. & Ohno, H. Control of magnetism by electric fields. Nat. Nanotechnol. 10, 209–220 (2015).
Eerenstein, W., Mathur, N. D. & Scott, J. F. Multiferroic and magnetoelectric materials. Nature 442, 759–765 (2006).
Gajek, M. et al. Tunnel junctions with multiferroic barriers. Nat. Mater. 6, 296–302 (2007).
Scott, J. F. Data storage. Multiferroic memories. Nat. Mater. 6, 256–257 (2007).
Fiebig, M., Lottermoser, T., Meier, D. & Trassin, M. The evolution of multiferroics. Nat. Rev. Mater. 1, 16046 (2016).
Khomskii, D. Classifying multiferroics: mechanisms and effects. Physics 2, 20 (2009).
Wang, W. et al. Tunning magnetism and anisotropy by ferroelectric polarization in 2D van der Waals multiferroic heterostructures. Mater. Today Phys. 27, 100803 (2022).
Xue, F., Wang, Z., Hou, Y., Gu, L. & Wu, R. Control of magnetic properties of MnBi2Te4 using a van der Waals ferroelectric III2−VI3 film and biaxial strain. Phys. Rev. B 101, 184426 (2020).
Gong, C., Kim, E. M., Wang, Y., Lee, G. & Zhang, X. Multiferroicity in atomic van der Waals heterostructures. Nat. Commun. 10, 2657 (2019).
Li, Z. & Zhou, B. Theoretical investigation of nonvolatile electrical control behavior by ferroelectric polarization switching in two-dimensional MnCl3/CuInP2S6 van der Waals heterostructures. J. Mater. Chem. C 8, 4534–4541 (2020).
Zhao, Y., Zhang, J. J., Yuan, S. & Chen, Z. Nonvolatile electrical control and heterointerface‐induced half‐metallicity of 2D ferromagnets. Adv. Funct. Mater. 29, 1901420 (2019).
Garcia, V. et al. Ferroelectric control of spin polarization. Science 327, 1106–1110 (2010).
Sun, W. et al. Controlling bimerons as skyrmion analogues by ferroelectric polarization in 2D van der Waals multiferroic heterostructures. Nat. Commun. 11, 5930 (2020).
Cheng, H.-X., Zhou, J., Wang, C., Ji, W. & Zhang, Y.-N. Nonvolatile electric field control of magnetism in bilayer CrI3 on monolayer In2Se3. Phys. Rev. B 104, 064443 (2021).
Lu, Y. et al. Artificial multiferroics and enhanced magnetoelectric effect in van der Waals Heterostructures. ACS Appl. Mater. Interfaces 12, 6243–6249 (2020).
Sun, W., Wang, W., Chen, D., Cheng, Z. & Wang, Y. Valence mediated tunable magnetism and electronic properties by ferroelectric polarization switching in 2D FeI2/In2Se3 van der Waals heterostructures. Nanoscale 11, 9931–9936 (2019).
Li, J., Li, X. & Yang, J. A review of bipolar magnetic semiconductors from theoretical aspects. Fundam. Res. 2, 511–521 (2022).
Li, X., Wu, X., Li, Z., Yang, J. & Hou, J. G. Bipolar magnetic semiconductors: a new class of spintronics materials. Nanoscale 4, 5680–5685 (2012).
Zhang, J., Zhao, B., Ma, C. & Yang, Z. Bipolar ferromagnetic semiconductors and doping-tuned room-temperature half-metallicity in monolayer MoX3 (X=Cl, Br, I): An HSE06 study. Phys. Rev. B 103, 075433 (2021).
Deng, J., Guo, J., Hosono, H., Ying, T. & Chen, X. Two-dimensional bipolar ferromagnetic semiconductors from layered antiferromagnets. Phys. Rev. Mater. 5, 034005 (2021).
Luo, N., Si, C. & Duan, W. Structural and electronic phase transitions in ferromagnetic monolayer VS2 induced by charge doping. Phys. Rev. B 95, 205432 (2017).
Li, X. & Yang, J. Toward Room-Temperature Magnetic Semiconductors in Two-Dimensional Ferrimagnetic Organometallic Lattices. J. Phys. Chem. Lett. 10, 2439–2444 (2019).
Sun, Z. et al. A new phase of the two-dimensional ReS2 sheet with tunable magnetism. J. Mater. Chem. C. 6, 1248–1254 (2018).
Sun, Y., Zhuo, Z. & Wu, X. Bipolar magnetism in a two-dimensional NbS2 semiconductor with high Curie temperature. J. Mater. Chem. C. 6, 11401–11406 (2018).
Li, X. & Yang, J. Bipolar magnetic materials for electrical manipulation of spin-polarization orientation. Phys. Chem. Chem. Phys. 15, 15793–15801 (2013).
Lee, K. et al. Magnetic order and symmetry in the 2D semiconductor CrSBr. Nano Lett. 21, 3511–3517 (2021).
Oganov, A. R. & Glass, C. W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 124, 244704 (2006).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Gjerding, M. N. et al. Recent progress of the computational 2D materials database (C2DB). 2D Mater. 8, 044002 (2021).
Haastrup, S. et al. The Computational 2D Materials Database: high-throughput modeling and discovery of atomically thin crystals. 2D Mater. 5, 042002 (2018).
Wang, H., Qi, J. & Qian, X. Electrically tunable high Curie temperature two-dimensional ferromagnetism in van der Waals layered crystals. Appl. Phys. Lett. 117, 083102 (2020).
Medici, L., Hassan, S. R., Capone, M. & Dai, X. Orbital-selective Mott transition out of band degeneracy lifting. Phys. Rev. Lett. 102, 126401 (2009). de’.
Zhang, Y. Z., Foyevtsova, K., Jeschke, H. O., Schmidt, M. U. & Valenti, R. Can the Mott insulator TiOCl be metallized by doping? A first-principles study. Phys. Rev. Lett. 104, 146402 (2010).
Zhuang, H. L. & Hennig, R. G. Stability and magnetism of strongly correlated single-layer VS2. Phys. Rev. B 93, 054429 (2016).
Nguyen, T. P. T., Yamauchi, K., Oguchi, T., Amoroso, D. & Picozzi, S. Electric-field tuning of the magnetic properties of bilayer VI3: a first-principles study. Phys. Rev. B 104, 014414 (2021).
Glawion, S. et al. Electronic structure of the two-dimensional Heisenberg antiferromagnet VOCl: a multiorbital Mott insulator. Phys. Rev. B 80, 155119 (2009).
Li, Y. et al. Rational design of heteroanionic two-dimensional materials with emerging topological, magnetic, and dielectric properties. J. Phys. Chem. Lett. 13, 3594–3601 (2022).
Deng, J. et al. Screening and design of bipolar magnetic-semiconducting monolayers and heterostructures. ACS Appl. Electron. Mater. 4, 3232–3239 (2022).
Ding, W. et al. Prediction of intrinsic two-dimensional ferroelectrics in In2Se3 and other III2-VI3 van der Waals materials. Nat. Commun. 8, 14956 (2017).
Soleimani, M. & Pourfath, M. Ferroelectricity and phase transitions in In2Se3 van der Waals material. Nanoscale 12, 22688–22697 (2020).
Wang, H. et al. Above room-temperature ferromagnetism in wafer-scale two-dimensional van der Waals Fe3GeTe2 tailored by a topological insulator. ACS Nano 14, 10045–10053 (2020).
Zhu, W. et al. Interface‐enhanced ferromagnetism with long‐distance effect in van der Waals Semiconductor. Adv. Funct. Mater. 32, 2108953 (2021).
Palacios, T. et al. High-performance E-mode AlGaN/GaN HEMTs. IEEE Electron Device Lett. 27, 428–430 (2006).
Zhao, P. et al. Single-layer LaBr2: two-dimensional valleytronic semiconductor with spontaneous spin and valley polarizations. Appl. Phys. Lett. 115, 261605 (2019).
Kresse, G. & Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study. Phys. Rev. B 57, 1505–1509 (1998).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207 (2003).
Zarkevich, N. A. & Johnson, D. D. Nudged-elastic band method with two climbing images: finding transition states in complex energy landscapes. J. Chem. Phys. 142, 024106 (2015).
Henkelman, G., Uberuaga, B. P. & Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Acknowledgements
This work was supported by grants from the National Natural Science Foundation of China (61888102, 52102193, 52272172, 11974045), the Major Program of National Natural Science Foundation of China (92163206), the National Key Research and Development Program of China (2021YFA1201501), and the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB30000000), and the Fundamental Research Funds for the Central Universities. Computational resources were provided by the National Supercomputing Center in Tianjin.
Author information
Authors and Affiliations
Contributions
S.D. and J.P. conceived and supervised the research project. Y.L. performed the first-principles calculations and data analysis. Y.L. wrote the initial manuscript. All authors participated in discussing and editing the manuscripts.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Y., Deng, J., Zhang, YF. et al. Nonvolatile electrical control of spin polarization in the 2D bipolar magnetic semiconductor VSeF. npj Comput Mater 9, 50 (2023). https://doi.org/10.1038/s41524-023-01005-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-023-01005-8