Abstract
The recent discovery of nickel oxide superconductors have highlighted the importance of first-principles simulations for understanding the formation of the bound electrons at the core of superconductivity. Nevertheless, superconductivity in oxides is often ascribed to strong electronic correlation effects that density functional theory (DFT) cannot properly take into account, thereby disqualifying this technique. Being isostructural to nickel oxides, Sr1-xKxBiO3 superconductors form an ideal testbed for unveiling the lowest theory level needed to model complex superconductors and the underlying pairing mechanism yielding superconductivity. Here I show that parameter-free DFT simulations capture all the experimental features and related quantities of Sr1-xKxBiO3 superconductors, encompassing the prediction of an insulating to metal phase transition upon increasing the K doping content and of an electron-phonon coupling constant of 1.22 in sharp agreement with the experimental value of 1.3 ± 0.2. The proximity of a disproportionated phase is further demonstrated to be a prerequisite for superconductivity in bismuthates.
Similar content being viewed by others
Introduction
Superconductivity is a peculiar state of materials characterized by zero resistance to direct current and the expulsion of magnetic flux. It is explained by the formation of bound electrons called Cooper pairs1. To date, the microscopic mechanism behind the Cooper pair formation is yet to be clarified and unified between all known superconductors. In simple elements, it is usually explained by the exchange of phonons. In high-temperature oxides superconductors, the proximity of a magnetic phase transition and/or a charge-ordered state is proposed to explain the formation of bound electrons. The discovery of superconductivity in nickel-based oxides R1-xSrxNiO2 in 20192 arouses the newest interest from solid-state scientists as it offers a new testbed for theories of superconductivity in complex oxides. It also highlights the importance of electronic structure calculations for understanding phenomena associated with superconductivity. In that regard, there is an established consensus that high critical temperature (Tc) reached in the oxide superconductors might be favored by strong correlation effects that have to be accounted for in electronic structure simulations3,4,5,6,7,8,9.
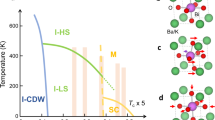
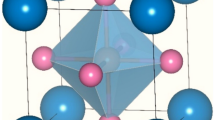
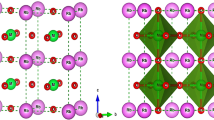
Aiming at understanding the role of electronic correlations and the mechanism behind Cooper pairs formation, Sr1-xKxBiO3 and Ba1-xKxBiO3 sit as ideal compounds for testing our first-principles simulations techniques since these materials (i) host several complexities exhibited by oxides and (ii) belong to the few oxide superconductors adopting the simple ABO3 perovskite structure with SrTiO3-x and Ba1-xKxSbO310,11,12,13,14. In bulk, SrBiO3 and BaBiO3 are insulating with a band gap Eg estimated between 0.2 and 0.8 eV in BaBiO315,16,17. They both adopt a monoclinic P21/n symmetry at low temperature10,18, characterized by the usual a0a0c+ (\(\emptyset _z^ +\), irreps M2+ with A cation sitting at the corner of the primitive Pm-3m cell) and a-a-c0 (\(\emptyset _{{{{\mathrm{xy}}}}}^ -\), irreps R5−) octahedra rotations in Glazer’s notations19 (Fig. 1a, b) induced by the A-to-B cation size mismatch—quantified by a Goldschmidt20 tolerance factor t = 0.88 in SrBiO3. While the two O6 group rotations produce the usual orthorhombic Pbnm symmetry exhibited by most ABO3 perovskites, the P21/n phase is reached by the appearance of a breathing distortion Boc (Fig. 1c)—also called bond disproportionation21—producing a dimerization of the material along the [111] cubic direction. This lattice instability, appearing at the R point of the primitive Pm-3m, undistorted, cubic cell Brillouin zone (i.e., (1/2,1/2,1/2), irreps R2-), results in a rock-salt pattern of large and compressed O6 octahedra, splitting the Bi cations into BiL and BiS, respectively (Fig. 1c)22,23. The breathing mode is associated with disproportionation of the unstable 4+ formal oxidation state (FOS) of Bi4+-6s1 cations to more stable 3 + (6s2) and 5 + (6s0) FOS in the P21/n insulating phase16,21,22,24,25. However, bismuthates fall within the negative charge transfer insulator regime26,27 and the Bi 6s band is localized well below the Fermi level and the O 2p band24,25,28. While the disproportionation should result in the localization of spin-paired electrons and holes on the s states of BiL and BiS cations, respectively, O anions supply electrons to the depleted BiS5+ cations resulting in the localization of two holes on the surrounding O atoms and yielding a BiL–6s2 and BiS–6s2L2 electronic configuration where the notation L stands for a ligand hole21,24,25,28,29.
Upon hole doping by substituting the divalent Sr or Ba cations with the monovalent K ion, Sr1-xKxBiO3 and Ba1-xKxBiO3 show superconductivity for doping contents ranging from x = 0.45–0.6 and 0.3–0.45, respectively, with a critical temperature Tc measured between 5 to 30 K, depending on the doping content as well as on the O stoichiometry of the samples10,11,12. Superconductivity is explained by an electron-phonon coupling (EPC) with a constant λ = 1.3 ± 0.24. It is proposed on the basis of first-principles simulations that λ is enhanced by strong electronic correlations3,4 but also by octahedral rotations30. At moderate hole doping content, these compounds exhibit a semiconducting state, explained by the appearance of localized states in the gap and trapped holes in the lattice (i.e., a hole bipolaronic state)29,31.
Several theoretical studies have tried to address the physics of the bismuthates and their related superconducting phase3,21,22,23,24,25,28,29,30,31,32,33,34,35,36,37. Most of these studies point out that density functional theory (DFT) is unable to account for the insulating character or appearance of the breathing mode Boc in BaBiO3 within the usual Local Density Approximation (LDA) and Generalized Gradient Approximation (GGA) exchange-correlation functionals3,22,23,38 thereby hindering its doping effect study. This is also true for the extraction of superconducting quantities such as electron-phonon matrix elements and coupling strength that are underestimated by LDA or GGA with respect to experiments (λ = 0.343,23 or 0.4830 with LDA and GGA, respectively, instead of 1.3 ± 0.2 with angular resolved photoemission spectroscopy experiments4). Both the band gap and superconducting fundamental quantities can be improved by more sophisticated, but prohibitive, DFT hybrid functional and/or Green Functions and screened Coulomb interaction (GW) calculations3,29,31. Nevertheless, including all degrees of freedom (e.g., structural such as symmetry lowering events and cation disorder appearing in alloys, electronic instabilities lifting degeneracies, local spin formation, and long-range spin orders…) of complex oxides for different doping contents are not affordable for these techniques, that are way too demanding in terms of computational resources since one has to deal with very large supercells—hybrid DFT and GW calculations are usually restricted to very small cell size preventing symmetry lowering events. Thus, affordable but still predictable DFT calculations are required for understanding trends in the doping of complex oxides and superconductors.
Recently, the band gap opening of ABO3 oxides perovskites with a 3d element has been addressed by DFT simulations and revealed to originate from four simple modalities rather than the usual explanation based on strong dynamical correlation effects codified by the Hubbard model:39 (i) the octahedral crystal field splitting the d states and Hund’s rule; (ii) symmetry lowering events such as octahedral rotation further lifting orbital degeneracies; intrinsic electronic instabilities yielding (iii) a Jahn-Teller effect and removing orbital degeneracies, or (iv) disproportionation effects of unstable formal oxidation state (FOS) to more stable FOS and resulting in a double local environment for the B cations. These results have been ratified by using appropriate DFT exchange-correlation functionals properly amending self-interaction errors inherent to the implementation of DFT and by supplying enough flexibility to the simulation (e.g., local motif, symmetry lowering events, spin polarization…)21,27,39,40,41. Furthermore, these conclusions are supported by DFT simulations using the Strongly Constrained and Appropriately Normalized (SCAN)42 exchange-correlation functional, but without any empirical parameter U such as in DFT + U, that properly account for the bulk perovskite oxide properties27,40 and the trends in doping effects of oxide insulators such as rare-earth nickelates43 RNiO3 or copper oxides44 such as La2CuO4. One may thus question “what is the lowest DFT exchange-correlation functional needed for capturing trends in doping effects in complex oxides superconductors”. Furthermore, an open issue in the physics of SrBiO3 (and BaBiO3) is the superconducting transition upon doping, that is up to now largely elusive. Studies have been performed for selected K doping contents in Ba1-xKxBiO3 for instance, but getting a global trend on structural and electronic properties as a function of x remains theoretically ignored.
Here I show that the SCAN functional is sufficient to capture the trends in insulating to the metal character of SrBiO3 upon hole doping and to reveal the mechanism and prerequisites behind the appearance of superconductivity. By mapping the first-principles DFT results on a Landau model involving the relevant lattice distortions, the insulating phase is shown to be reached by disproportionation effects associated with an intrinsic instability of Bi4+ cations to disproportionation to Bi3+/Bi5+ cations in the bulk ground state. This is accompanied by a breathing mode distortion Boc whose amplitude is further enhanced by the octahedra rotations. At weak doping content (x = 0.0625 to 0.125), holes are trapped on the lattice and intermediate states are localized in the band gap, ultimately resulting in a semiconducting behavior. At intermediate doping content (x = 0.1875 to 0.375), a metallic phase is reached but the breathing mode is still present in the ground state due to its coupling with octahedral rotations, despite the fact that the structural distortion alone is not willing to spontaneously pop up in the material. The presence of this mode induces small gaps in the bands dispersing around the Fermi level. No gaps are anymore identified in the band structure at x = 0.4375, a doping content reminiscent of the superconducting phase reported experimentally (x = 0.45–0.6). Around x ≥ 0.4375, the breathing mode is found on the verge of becoming stable in the material due to octahedral rotations and thus its vibration can form spin-paired electrons and holes in the material, i.e., Cooper pairs. These results thus suggest that the proximity of a lattice instability producing spin-paired electrons and holes is a prerequisite for superconductivity in the bismuthates, in sharp agreement with the bounded doping content observed experimentally for the superconducting phase. Within the superconducting phase at x = 0.4375, an electron-phonon coupling constant λ associated with the breathing mode Boc of 1.22 and a Boc frequency of 66 meV are extracted from the simulations, in sharp agreement with the experimental values (λ = 1.3 ± 0.2 and ω = 62 meV, respectively). At larger doping content, the breathing mode frequency becomes harder and the density of states at the Fermi level decreases but a slightly increased reduced electron-phonon matrix element with increasing x preserves a non-zero Tc up to x = 0.625. This study thus (i) validates the use of SCAN-DFT for studying doping effects in complex oxide superconductors and (ii) calls for inspection of disproportionation effects in superconducting nickelates and other oxide superconductors to see if the identified mechanism in bismuthates is also relevant for these newly identified oxide superconductors.
Results
The bulk material
DFT ground states properties
The bulk P21/n structure experimentally observed at low temperatures for SrBiO3 is first relaxed in order to identify the ground state with our DFT functional. Key structural and electronic properties of the bulk material are reported in Table 1. SCAN-DFT predicts that SrBiO3 is an insulator in agreement with experiments, with a band gap amplitude improved with respect to GGA calculations (0.3 eV in ref. 25. instead of 0.48 in the present study). In terms of structural parameters, the computed lattice parameters are in close agreement with experiments10, with less than 1% of an error on the volume of the unit cell. Regarding the key lattice distortion amplitude exhibited by the compound, the optimized structure in DFT is also in agreement with the experimental structure although the amplitude of the breathing mode Boc is underestimated by ~10% with respect to the experiment. This mode produces the rock-salt pattern between the compressed and contracted octahedra (see Fig. 1c). It results in a clear cut of the electronic structure between the two types of Bi cations as inferred by the projected density of states of Fig. 2a. Nevertheless, the Bi-s states are well below the O-p states, the band gap is mostly formed between occupied and unoccupied O-p states (see Fig. 2a) and SrBiO3 falls within the negative charge transfer insulator regime. Using the partial charge density maps of states just above the Fermi level (Fig. 2b), the unoccupied O-p bands have an s-like orbital character centered on Bis site—in agreement with the Wannier functions analysis presented in ref. 25—hinting at the fact that the O anions supply electrons to the depleted BiS cation and bear the two holes that are centered at BiS sites.
a Density of states (in states/eV/f.u) projected on BiS-s (in green), BiL-s (in red), and O-p (in blue) states. b Partial charge density map associated with the states at the bottom of the conduction band indicated by the orange area in panel a. c–e Potential energy surface starting from a perfectly undistorted Pm-3m cubic cell associated with the anti-phase a-a-c0 \(\emptyset _{xy}^ -\) and in-phase a0a0c+ \(\emptyset _z^ +\) octahedral rotations (d), breathing mode Boc (e) and breathing mode Boc at fixed \(\emptyset _z^ +\) and \(\emptyset _{xy}^ -\) octahedral rotations amplitude. The lattice parameter of the cubic cell is chosen so that its volume is identical to the ground state volume. An amplitude of 1 corresponds to the amplitude appearing in the DFT relaxed ground state structure.
The origin of the insulating phase
Figure 2c–e report the potential energy surface associated with the relevant distortion modes identified in the ground state of SrBiO3 when starting from a perfectly undistorted Pm-3m cubic cell (see method). As one can see, octahedral rotations show a double-well potential whose minimum is located at non-zero amplitudes Q of the distortions. It indicates that these modes are unstable and are willing to spontaneously appear in the ground state due to steric effects. The breathing mode Boc also exhibits a double-well potential, albeit with smaller energy gains with respect to octahedral rotations. (Fig. 2d) Thus, the material spontaneously wants to get rid of the unstable 4+ formal oxidation state (FOS) of Bi cations and adopt the more stable 3+/5+ FOS. This is in agreement with previous DFT work on BaBiO3 performed by Tonhauser and Rabe in Ref. 22. Nevertheless, the breathing mode would exhibit only 50% of its amplitude appearing in the P21/n ground state if considered alone.
The importance of octahedral rotations for the stabilization of the breathing mode Boc
Mercy et al. identified in rare-earth nickelates RNiO3 (R = Lu-Pr, Y)45 that the breathing mode Boc amplitude QBoc is directly connected to the octahedra rotation amplitudes \(Q_{\emptyset _{{{{\mathrm{xy}}}}}^ - }\) and \(Q_{\emptyset _{{{\mathrm{Z}}}}^ + }\), respectively, through the lattice mode couplings allowed in the free energy expansion F displayed in Eq. 1:
where a, b, and c are coefficients. It follows that rotations can renormalize the coefficient in front of \(Q_{{{{\mathrm{Boc}}}}}^2\) thereby acting on the possibility to stabilize a finite amplitude of Boc (aeff < 0) or not (aeff > 0) in the material. Figure 2e displays the potential energy surface as a function of the Boc mode amplitude QBoc but at fixed octahedral rotation amplitudes \(Q_{\emptyset _{{{{\mathrm{xy}}}}}^ - }\) and \(Q_{\emptyset _{{{{\mathrm{xy}}}}}^ - }\). The stabilization of the breathing mode is enhanced by the O6 group rotations, increasing the amplitude of the Boc mode appearing in the material and associated energy gain. Obviously, even though the breathing mode Boc alone would not be intrinsically unstable (a > 0 in Eq.1), it can still be forced to appear in the ground state due to its coupling with finite octahedra rotation amplitude yielding aeff < 0 in Eq.1. Thus, neglecting octahedral rotations by using smaller, but more convenient unit cells, is not indicated as it can ultimately act on the presence of Boc and related electronic features.
Polaronic state formation upon hole doping
Intermediate states in the band gap
Following the understanding of the bulk properties, DFT calculations at low hole doping content have been performed in order to check whether or not polaronic states can be trapped on the lattice and yield a semiconducting behavior. To that end, a Sr1-xKxBiO3 solid solution with x = 0.0625 using a 32 f.u. supercell is considered (see method). Then, 2 Sr2+ cations are substituted by 2 K+ cations in the 32 f.u. supercell, yielding the release of two holes in the material. After the structural relaxation, a semiconducting state with a band gap of 0.25 eV is identified in the material. By inspecting the projected density of states presented in Fig. 3a, a split-off band localized in the band gap mostly formed by O-p and BiL-s states, very similar to the character of the valence band maximum, is revealed. An acceptor state is thus created in the material. The charge density maps associated with this intermediate state presented in Fig. 3b confirms that the holes are localized on a BiL cation that is occupied by two spin-paired electrons in the pristine material.
a Projected density of states on O-p (in blue), BiL-s (in red), and BiS-s (green) states. The zero is set at the valence band maximum (VBM). The orange area indicates the intermediate states localized in the band gap. b Partial charge density maps associated with the intermediate states localized in the band gap corresponding to the orange area in panel a.
Existence of a trapped hole bipolaronic state
This is locally accompanied by a modification of the lattice with the average “BiL-O bond length” of 2.16 Å on this hole site while BiL-O bond lengths are roughly 2.30 Å for the other BiL sites in the material. It is in fact very similar to a BiS cation that indeed shows an average BiS-O bond length of 2.15 Å. In conclusion, a hole bipolaronic state is trapped in the material and tends to transform BiL cations into BiS cations, i.e., locally annihilating the breathing distortion mode Boc. This is in sharp agreement with previous DFT predictions in hole-doped BaBiO3 performed with higher DFT.
Trends in insulating-to-metal transition and structural properties upon hole doping
Limited miscibility of K within SrBiO3
Before inspecting the trend in electronic and structural properties with hole doping SrBiO3, the possibility of inserting the K cations within the SrBiO3 P21/n structure has been checked. In bulk, KBiO3 is not willing to adopt a P21/n cell based on corner-sharing octahedra as in SrBiO3, but it prefers to crystallize within an edge-sharing octahedra network with a Pn-3 cell. This symmetry is more stable than the P21/n symmetry by 290 meV/f.u. By inspecting the insertion of Sr within the Pn-3 and P21/n cells starting from KBiO3, the doped Pn-3 cell remains more stable than the doped P21/n cell for x = 0.9–1 in KxSr1-xBiO3 (Fig. 4). However, by comparing the total energy of single phase solution Sr1-xKxBiO3 either adopting the P21/n or the Pn-3 symmetries with that of a biphasic solid solution (i.e., \({{{\mathrm{E}}}}_{{{{\mathrm{biphase}}}}} = {{{\mathrm{E}}}}_{{{{\mathrm{SBO}}}}} + {{{\mathrm{x}}}}({{{\mathrm{E}}}}_{{{{\mathrm{KBO}}}}} - {{{\mathrm{E}}}}_{{{{\mathrm{SBO}}}}})\), one observes that the biphasic solid solution is more stable than any single phase solid solutions for 0.65 ≤ x <1 (Fig. 4). Thus, there is a limited miscibility of K within the SrBiO3 structure. These results are in sharp agreement with the impossibility to synthesize Sr1-xKxBiO3 for x > 0.6 experimentally10. The present study will thus be limited to doping effects up to x = 0.625. Finally, one notices a strong stability of the monophasic solid solution Sr1-xKxBiO3 for 0.4 < x < 0.6.
The insulator to metal transition upon K substitutions
The projected density of states on BiL and BiS-s states as a function of various K doping content x are reported in Fig. 5a. At moderate doping content (x = 0.0625 and x = 0.125), intermediate states are formed in the gap and yield a semiconducting behavior. At x = 0.1875 up to x = 0.375, the material is found metallic but still with a clear asymmetry of electronic structures between BiL and BiS cations. This hints at the fact that parts of disproportionation may still be present in the material. Finally, at x = 0.4375 up to x = 0.625, no asymmetries between BiS and BiL electronic structures are observed suggesting that disproportionation effects have disappeared and the two Bi sites become equivalent in the material.
a Projected density of states on BiS (in green) and BiL (in red) s states as a function of the K doping content x. The Fermi level in semiconducting states (0%, 6.25%, and 12.5 %) is set to the valence band maximum. b Amplitudes of lattice distortions (in Å/f.u) extracted from a symmetry mode analysis for the a-a-c0 (\(\phi _{xy}^ -\)) octahedral rotation (upper panel), a0a0c+ (\(\phi _z^ +\)) octahedral rotation (middle panel) and breathing mode (Boc) (lower panel). c Potential energy surface (in meV/f.u) associated with the Boc mode amplitude (in fractional units) starting from a perfectly cubic cell for different doping content x. d Potential energy surface (in meV/f.u) associated with the Boc mode amplitude (in fractional units) starting from a perfectly cubic cell for different doping content x but at fixed octahedra rotation amplitude appearing in the relaxed ground state. An amplitude of 1 corresponds to the amplitude appearing in the ground state of pristine, undoped, SrBiO3. For each doping content, the cubic cell volume is fixed to the relaxed ground state volume.
Structural distortions upon K substitutions
The amplitude of distortions associated with the octahedral rotations \(\phi _{{{{\mathrm{xy}}}}}^ -\) and \(\phi _{{{\mathrm{z}}}}^ +\) as well as the breathing mode Boc at different doping contents are reported in Fig. 5b. The two octahedral rotations' amplitude decrease with increasing the K doping content, albeit not disappearing at all in the ground state structure. This fact is due to the A-to-B cation size mismatch that are altered by the introduction of K atoms (KBiO3 adopting a cubic Pm-3m cell would have a tolerance factor t = 1.01 that favors a cubic cell). The behavior of the breathing mode Boc as a function of the hole doping content is different with respect to rotations: (i) at moderate doping content (x = 0 to 0.375), the Boc mode amplitude diminishes until (ii) it totally vanishes at x = 0.4375 up to x = 0.625. The absence of the breathing mode for 0.375 ≤ x ≤ 0.625 is in line with the similar electronic structures observed for BiS and BiL cations using the projected density of states presented in Fig. 5a. Thus, Bi cations become all equivalent in the material.
Doping effects suppress the electronic instability toward disproportionation of the formal oxidation state
Potential energy surfaces associated with the breathing mode starting from a perfectly cubic cell for different x values are displayed in Fig. 5c. Whatever x, the Boc mode is associated with a single well potential (a > 0 in Eq. 1). It follows that the instability toward disproportionation of the unstable 4+ FOS of cations to more stable 3+/5+ FOS identified in the pristine compound is suppressed by the introduction of K atoms in the material. Furthermore, one can identify that the curvature of the total energy as a function the Boc mode amplitude becomes steeper signaling that the breathing mode hardens with increasing the Sr substitutions. Thus considered alone, the Boc mode possesses an a coefficient in Eq. 1 that becomes positive and larger when x increases.
Persistence of the breathing mode due to octahedral rotations
The coupling of Boc with the two rotations observed in bulk may still renormalize the effective coefficient aeff in Eq. 1 by supplying sufficiently large and negative b and c coefficient contributions counterbalancing the hardening of the Boc mode alone. This is confirmed by the first-principles calculations of the potential energy surfaces associated with the Boc mode but at fixed O6 group rotation amplitudes presented in Fig. 4d. At x = 0.25 or x = 0.3125, the Boc mode indeed presents a double-well potential (i.e., aeff < 0 in Eq. 1) while at x = 0.4375 or x = 0.5, it is associated with a single well potential whose minimum is at 0 (i.e., aeff > 0). Thus, up to x = 0.375, rotations are sufficiently large to produce a negative effective coefficient aeff. At x ≥ 0.4375, rotation amplitude are not large enough thereby resulting in a positive effective coefficient aeff in front of \(Q_{{{{\mathrm{Boc}}}}}^2\) in Equation 1.
Band structure upon K substitutions and the absence of Peierls instability signatures in the superconducting state
Figure 6a–g displays the unfolded band structures in the primitive high symmetry Pm-3m cubic Brillouin zone of Sr1-xKxBiO3 for the different doping contents x tested in the simulations. Only bands dispersing around the Fermi level are reported. The pristine material is insulating with an indirect band gap of 0.48 eV. One can notice the existence of gaps along a specific path in the Brillouin zone, notably a gap of 1.2 eV halfway through the Γ-R path. The existence of this gap comes from the R-point lattice instability producing a dimerization along the [111] cubic direction and the rock-salt pattern of BiL3+ and BiS3+ cations in the insulating phase. At low doping content (x = 0.0625 and x = 0.125), the band structure is mainly not altered but intermediate states appear in the band gap. For doping contents x ranging from 0.1875 to 0.375, the band structure is altered notably the band gap along the Γ-R path progressively diminishing with increasing x. Although the material is metallic, energy gaps are still present in the band structure and the conduction and valence bands have not yet merged into a single “parabola” centered at the Γ point. This is due to the persistence of the Boc lattice distortion discussed above. At x = 0.4375, no more gaps are visible in the band structure and the initial valence and conduction bands in the pristine material have now totally merged. One is then left with a single parabola centered at the Γ point and dispersing on a bandwidth of roughly 4.4 eV. This feature only appears once any finite Boc mode amplitude has totally vanished in the ground state of the material.
a–g Unfolded band structures in the primitive Pm-3m Brillouin zone exhibited by Sr1-xKxBiO3 as a function of the K doping content x. The size of the dots are associated with the spectral weight of each points. Tiny points are mostly associated with replicas associated with the band folding when supercells have to be used. High symmetry reciprocal points have the following coordinates: Γ (0, 0, 0), X (1/2, 0, 0), M (1/2, 1/2, 0), and R (1/2, 1/2, 1/2). h Gap opening due to the presence of the breathing mode Boc in doped Sr1-xKxBiO3 at x = 0.4375 along the Γ-R path. The breathing mode amplitude is 0.159 Å and the relaxed ground state at x = 0.4375 is considered.
The vicinity of a phase possessing a disproportionation instability is a prerequisite to superconductivity
The extinction of any type of disproportionation signatures (BiL-O and BiS-O bond lengths and BiS and BiL electronic structure asymmetries), as well as the observation of a single parabola centered at Γ and dispersing over a large energy range for doping contents x ranging from x = 0.4375 to x = 0.625 in the simulations, relates closely with the experimental doping content (x = 0.45–0.6) required to reach the superconducting state10—one recalls here that the Boc mode is underestimated by ~10% in the DFT bulk with respect to experiments thereby one may predict a superconducting transition at lower doping content with DFT simulations. It clearly suggests that the breathing mode Boc is the key behind the superconducting phase. The latter is likely reached when the effective coefficient in front \(Q_{{{{\mathrm{Boc}}}}}^2\) in Eq. 1 is nearly zero or slightly positive. Lattice vibrations with the Boc character potentially facilitated by O6 group rotation vibrations may produce spin-paired electrons and holes on the lattice, i.e., Cooper pairs—although the Boc distortion does not stabilize any finite amplitude in the material. One indeed checks in the simulations that the Boc mode at x = 0.4375 is strongly softened when rotation amplitudes are fixed to the pristine value (∅ = 1 in Fig. 5d) with respect to the situation for the ground state at x = 0.4375 (∅ = 0.66 in Fig. 5d).
K doping is mainly related to simple steric effects
Following the proposed mechanism, the role of the K doping for the appearance of superconductivity is rather indirect and related to a simple steric effect: (i) Sr substitutions by K thus increase the t factor of Sr1-xKxBiO3 thereby diminishing the rotations amplitude and (ii) in turn it suppresses the breathing mode stabilization in the material.
The proposed scenario is corroborated by experimental facts in BaBiO3
Ba is larger than Sr atoms and hence the t factor of BaBiO3 is larger (t = 0.92) than the t factor of SrBiO3. Octahedral rotations in BaBiO3 are ultimately smaller than in SrBiO3 and thus the expected K doping needed to suppress the stabilization of the Boc distortion in the ground state is necessarily smaller in BaBiO3 than in SrBiO3 following the identified mechanism. This is verified experimentally:11 the superconducting phase in Ba1-xBixO3 is reached for x ≈ 0.30–0.45 while it is for x = 0.45–0.6 in SrBiO3.
Superconducting properties associated with the breathing distortion
The Boc mode frequency in the superconducting state
In order to assess the frequency of the breathing mode Boc in the superconducting phase, the potential energy surface associated with the Boc mode is computed by freezing some displacements of the distortion in the 32 f.u. ground state structure (i.e., the relaxed DFT cell containing the octahedral rotations) for doping contents x of 0.4375 up to 0.625. By fitting the resulting energy curve (see method), the frequency ωBoc for the breathing mode is computed to 66 meV at x = 0.4375. This value is in sharp agreement with the quantity extracted experimentally in the superconducting phase of BaBiO3 for this mode (ω = 62 meV in ref. 46). As one can see from Fig. 7b, ωBoc linearly hardens upon adding more K in Sr1-xKxBiO3. This is in line with diminishing octahedral rotations induced by Sr substitutions that result in a positive and increasing aeff in Eq. 1.
a Reduced electron-phonon matrix element (D, in eV/Å), b breathing mode frequency ωBoc (in meV), c density of states N(EF) at the Fermi level, d computed electron-phonon coupling constant, and e estimated critical temperature Tc (in K) for a screened Coulomb potential µ* = 0.15 as a function of the doping content x.
The reduced electron-phonon coupling matrix element
In order to extract the quantification of the REPME labeled D (see method), a Boc displacement u is frozen in the ground state structure for x = 0.4375 to x = 0.625. It results in a gap opening of ∆Eg = 1.23 eV along the Γ-R path for x = 0.4375 (Fig. 6h). It yields a reduced electron-phonon matrix element (REPME) D = 11.7 eV/Å (see method). This value is an improvement over classical LDA and GGA quantities (GGA yields D = 7.8 eV/Å) and hybrid DFT using the HSE06 functional (D = 11 eV/Å) and closely matches the REPME computed with quasi-particle Green’s function and screened Coulomb interaction (GW) technic that evaluates D to 13.7 eV/Å in optimally doped BaBiO3 (ref. 3). Amazingly, D linearly increases with the doping content, suggesting that one cannot simply fix the D value obtained at one x for all other doping contents x (Fig. 7a)
The electron-phonon coupling constant and the critical temperature
Using the REPME, the computed frequency of the breathing mode and the density of states N(EF) evaluated for all ground states for x = 0.4375 to x = 0.625 (Fig. 7c)—values in sharp agreement with N(EF) evaluated experimentally to 0.225–0.335 in Ba1-xKxBiO3, see ref. 11—the electron-phonon coupling (EPC) constant λ associated with the breathing mode is evaluated between 1.03 to 1.24 for 0.4375 < x < 0.625 (Fig. 7d). These values are in agreement with the experimental value of λ = 1.3 ± 0.2 obtained in Ba0.51K0.49BiO34 and is an improvement over hybrid DFT calculation of ref. 3. The discrepancy with more sophisticated DFT functionals may originate from the fact that important structural distortions and relevant lattice mode couplings were not considered in the ground state calculations of ref. 3. The importance of octahedral rotations on the EPC was already suggested in ref. 30.
Following the methodology proposed in ref. 3, the logarithmic average frequency is identified by implementing the SCAN-DFT corrections to λ within the ωlog obtained by LDA simulations. Using the Mac Millan equation47 (Eq. 4), the critical temperature is found to be rather constant and between 25–33 K for screened Coulomb potentials μ* of 0.15 (Fig. 7e). This is in very good agreement with the critical temperatures evaluated in potassium doped bismuthates reaching 34 K11. The rather constant Tc computed for 0.4375 < x < 0.625 originates from compensating quantities: the diminishing N(EF) and \(1/\omega _{{{{\mathrm{Boc}}}}}^2\) contributions are counterbalanced by an increasing D factor with increasing the doping content (Fig. 7a–c).
Discussion
The DFT simulations reveal that hole doping has an indirect effect progressively suppressing the charge and bond disproportionation effects through the reduction of the octahedral rotations induced by simple steric effects. Once the disproportionation effects have vanished, no more energy gaps are identified in the band structure and the superconducting phase is reached. In this regime, the bond disproportionation vibration, that can be favored by its coupling with octahedral rotation vibrations, can produce spin-paired electrons and holes on the lattice, i.e., Copper pairs. The computed electron-phonon and related quantities are all in sharp agreement with experimental quantities obtained in these bismuthates. It is thus clear that the proximity of a charge and bond-ordered phase is a prerequisite to superconductivity. Numbers may of course be improved by involving a full electron-phonon calculation implying all phonon modes—this is however not affordable for a 32 f.u with cation disorder. However, the electron-phonon coupling constant and estimated Tc trend are already well captured by the SCAN functional and the simpler model, thereby suggesting that the breathing distortion phonon mode is dominating the superconducting properties of bismuthates. This would possibly be a common factor to several materials prone to exhibit charge orderings14,48,49,50,51,52.
These results being ratified with parameter-free DFT calculations, further shows that DFT is sufficient to capture the physics of complex oxide superconductors, thereby showing that strong correlation effects may not be a universal explanation behind the high critical temperature observed in oxide superconductors. The “constant” Tc computed within the superconducting region finally appears fortuitous due to antagonist effects with increasing D that counterbalances the diminishing N(EF) and \(1/\omega _{{{{\mathrm{Boc}}}}}^2\) factors. It thus suggest that computing the superconducting parameters at a fixed doping content and applying them at other doping content is not indicated as doping can act differently on the important quantities entering the Mac Millian’s equation (Eq. 4). Thus, properly modeling trends in electronic and structural properties versus doping effects may not be circumvented. The search for similar strongly coupled electron-phonon features such as disproportionation signatures, trends in doping effects, and lattice mode couplings between relevant distortions might be a key point for understanding pairing mechanisms in other oxide superconductors.
Method
The choice of the exchange-correlation functional
DFT simulations have been performed with the meta-GGA SCAN42 functional that improves the correction of self-interaction errors inherent to practice DFT over the classical LDA and GGA functionals and yields correct trends in lattice distortions and metal-insulator transitions as a function of A and B cations in bulk ABO3 perovskite oxides40. This functional also has the advantage of being parameter-free and can therefore perfectly adapt to multiple formal oxidation states that an ion can develop in a doped material.
The method to describe doping effects
Hole doping effects are modeled by substituting Sr2+ cations with the monovalent K+ cation. Special Quasi-random Structure (SQS) technique proposed in ref. 53 that allows to extract the cation arrangement maximizing the disorder characteristic of an alloy within a given supercell size are used to determine the best approximant of the cation disorder at each doping content. Thus, all possible local motifs for Bi cations in terms of surrounding Sr and K cations are available at each doping content, reminiscent of the situation in a real alloy. In order to allow enough flexibility for the material to develop the different lattice distortions exhibited by perovskites that can open the band gap39, such as those displayed in Fig. 1, and to stabilize polaronic states, a 32-formula unit supercell that corresponds to a (2√2, 2√2, 4) supercell with respect to the primitive, undistorted, cubic Pm-3m cell is used.
The used crystallographic cell
Only the low-temperature P21/n phase adopted by SrBiO3 is used throughout the study as a starting point.
Potential energy surfaces and relevant phonon frequency calculation
Potential energy surfaces associated with lattice distortions are plotted starting from a perfectly undistorted Pm-3m cubic cell in which finite amplitudes of the different lattice distortions are condensed. In order to determine the frequencies ω of interesting lattice distortions in the ground state structure reached upon doping, a full phonon calculation is not affordable for a 32-formula unit supercell without any symmetry. Instead, some lattice mode amplitudes Q associated with a lattice distortion are frozen in the ground state structure and the associated potential energy surface is computed. Recalling that E = 1/2Mω2 Q2 for a harmonic oscillator with a frequency ω and where M is the mass of the moving atoms, the frequency is identified by fitting the potential energy surface with an expression, of the E = aQ2 + bQ4 where a and b are coefficients representing harmonic and anharmonic effects. One can then identify that \(\omega = \sqrt {\frac{{2a}}{M}}\).
Computing superconducting properties
The reduced electron-phonon coupling matrix element (REPME) associated with the breathing distortion Boc are evaluated by freezing its atomic displacements in the relaxed ground state structure. Using the gap opening amplitude ∆Eg appearing in the band structure due to the frozen phonon displacement, the REPME labeled D is computed by the following formula:
where u is the displacement of one oxygen atom. The electron-phonon coupling constant λ is evaluated by the following equation:
where N(EF) is the density of states at the Fermi level per spin channel per formula unit, M is the mass of the displaced atoms and \(\omega _{{{{\mathrm{Boc}}}}}^2\) is the square of the computed Boc frequency. The critical temperature Tc is computed by using the modified Mac Millan equation:47
where ωlog is average logarithmic frequency and μ* is the screened Coulomb potential with conventional values between 0.1 and 0.15.
Other technical details
DFT simulations are performed with the Vienna Ab initio Simulation package (VASP)54,55. The energy cut-off is set to 650 eV and is accompanied by a 4 × 4 × 3 Gamma-centered kmesh for the 32 f.u. supercell. The kmesh is increased to 5 × 5 × 3 for density of states, potential energy surfaces, and frequency calculations. Projector augmented wave (PAW) potentials56 are used with Bi d states being treated as core states. Geometry relaxations (atomic positions plus lattice parameters) are performed until forces acting on each atom are lower than 0.05 eV/Å. The symmetry of the relaxed structures are extracted with the Findsym application57 and amplitudes of distortions are extracted using a symmetry mode analysis with respect to the primitive Pm-3m cell with the Isodistort tool from the Isotropy applications58,59.
Data availability
All data are available upon reasonable request to the author.
Code availability
VASP DFT code license can be purchased from Vienna University.
References
Cooper, L. N. Bound electron pairs in a degenerate fermi gas. Phys. Rev. 104, 1189 (1956).
Li, D. et al. Superconductivity in an infinite-layer nickelate. Nature 572, 624–627 (2019).
Yin, Z. P., Kutepov, A. & Kotliar, G. Correlation-enhanced electron-phonon coupling: applications of GW and screened hybrid functional to bismuthates, chloronitrides, and other high-Tc superconductors. Phys. Rev. X 3, 021011 (2013).
Wen, C. H. P. et al. Unveiling the superconducting mechanism of Ba0.51K0.49BiO3. Phys. Rev. Lett. 121, 117002 (2018).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Garg, A., Randeria, M. & Trivedi, N. Strong correlations make high-temperature superconductors robust against disorder. Nat. Phys. 4, 762–765 (2008).
Li, H. et al. Coherent organization of electronic correlations as a mechanism to enhance and stabilize high-TC cuprate superconductivity. Nat. Commun. 9, 26 (2018).
Worm, P. et al. Correlations tune the electronic structure of pentalayer nickelates into the superconducting regime. Phys. Rev. Mater. 6, L091801 (2022).
Kitatani, M. et al. Nickelate superconductors—a renaissance of the one-band Hubbard model. npj Quantum Mater. 5, 59 (2020).
Chaillout, C. et al. Discovery of a second family of bismuth-oxide-based superconductors. Nature 390, 148–150 (1997).
Sleight, A. W. Bismuthates: BaBiO3 and related superconducting phases. Phys. C: Supercond. Appl. 514, 152–165 (2015).
Mattheiss, L. F., Gyorgy, E. M. & Johnson, D. W. Superconductivity above 20 K in the Ba-K-Bi-O system. Phys. Rev. B 37, 3745 (1988).
Schooley, J. F., Hosier, W. R. & Cohen, M. L. Superconductivity in semiconducting SrTiO3. Phys. Rev. Lett. 12, 474 (1964).
Kim, M. et al. Superconductivity in (Ba,K)SbO3. Nat. Mater. 21, 627–633 (2022).
Federici, J. F., Greene, B. I., Hartford, E. H. & Hellman, E. S. Optical characterization of excited states in BaBiO3. Phys. Rev. B 42, 923 (1990).
Sarkar, S., Raghunathan, R., Chowdhury, S., Choudhary, R. J. & Phase, D. M. The mystery behind dynamic charge disproportionation in BaBiO3. Nano Lett. 21, 8433–8438 (2021).
Sleight, A. W., Gillson, J. L. & Bierstedt, P. E. High-temperature superconductivity in the BaPb1-xBixO3 system. Solid State Commun. 17, 27 (1975).
Kennedy, B. J., Howard, C. J., Knight, K. S., Zhang, Z. & Zhou, Q. Structures and phase transitions in the ordered double perovskites Ba2BiIIIBiVO6 and Ba2BiIIISbVO6. Acta Crystallogr. B. 62, 537 (2006).
Glazer, A. M. The classification of tilted octahedra in perovskites. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 28, 3384–3392 (1972).
Goldschmidt, V. M. Die Gesetze der krystallochemie. Naturwissenschaften 14, 477–485 (1926).
Dalpian, G. M., Liu, Q., Varignon, J., Bibes, M. & Zunger, A. Bond disproportionation, charge self-regulation, and ligand holes in s-p and in d-electron ABX3 perovskites by density functional theory. Phys. Rev. B 98, 075135 (2018).
Thonhauser, T. & Rabe, K. M. Fcc breathing instability in BaBiO3 from first principles. Phys. Rev. B 73, 212106 (2006).
Meregalli, V. & Savrasov, S. Y. Electron-phonon coupling and properties of doped BaBiO3. J. Supercond. Nov. Magn. 12, 185 (1999).
Foyevtsova, K., Khazraie, A., Elfimov, I. & Sawatzky, G. A. Hybridization effects and bond disproportionation in the bismuth perovskites. Phys. Rev. B 91, 121114 (2015).
Varignon, J., Santamaria, J. & Bibes, M. Electrically switchable and tunable Rashba-type spin splitting in covalent perovskite oxides. Phys. Rev. Lett. 122, 116401 (2019).
Zaanen, J., Sawatzky, A. & Allen, J. W. Band gaps and electronic structure of transition-metal compounds. Phys. Rev. Lett. 55, 418 (1985).
Varignon, J., Malyi, O. I. & Zunger, A. Dependence of band gaps in d -electron perovskite oxides on magnetism. Phys. Rev. B 105, 165111 (2022).
Khazraie, A., Foyevtsova, K., Elfimov, I. & Sawatzky, G. A. Oxygen holes and hybridization in the bismuthates. Phys. Rev. B 97, 075103 (2018).
Franchini, C., Sanna, A., Marsman, M. & Kresse, G. Structural, vibrational, and quasiparticle properties of the Peierls semiconductor BaBiO3: A hybrid functional and self-consistent GW + vertex-corrections study. Phys. Rev. B 81, 085213 (2010).
Bazhirov, T., Coh, S., Louie, S. G. & Cohen, M. L. Importance of oxygen octahedra tilts for the electron-phonon coupling in K-doped BaBiO3. Phys. Rev. B 88, 224509 (2013).
Franchini, C., Kresse, G. & Podloucky, R. Polaronic hole trapping in doped BaBiO3. Phys. Rev. Lett. 102, 256402 (2009).
Benam, M. R., Foyevtsova, K., Khazraie, A., Elfimov, I. & Sawatzky, G. A. Bond versus charge disproportionation and nature of the holes in s−p ABX3 perovskites. Phys. Rev. B 104, 195141 (2021).
Smolyanyuk, A., Boeri, L. & Franchini, C. Ab initio prediction of the high-pressure phase diagram of BaBiO3. Phys. Rev. B 96, 035103 (2017).
Rice, T. M. & Sneddon, L. Real-space and k-space electron pairing in BaPb1-xBix03. Phys. Rev. Lett. 47, 689 (1981).
Varma, C. M. Missing valence states, diamagnetic insulators, and superconductors. Phys. Rev. Lett. 61, 2713 (1988).
Chakraverty, B. K. & Ranninger, J. Bipolarons and superconductivity. Philos. Mag. Part B 52, 669 (1985).
Scalapino, D. J., White, S. R. & Zhang, S. Insulator, metal, or superconductor: the criteria. Phys. Rev. B 47, 7995 (1993).
Zeyher, R. & Kunc, K. Instabilities in cubic BaBiO3 from total-energy calculations. Solid State Commun. 74, 805 (1990).
Varignon, J., Bibes, M. & Zunger, A. Origin of band gaps in 3d perovskite oxides. Nat. Commun. 10, 1658 (2019).
Varignon, J., Bibes, M. & Zunger, A. Mott gapping in 3d ABO3 perovskites without Mott-Hubbard interelectronic repulsion energy U. Phys. Rev. B 100, 035119 (2019).
Varignon, J., Bibes, M. & Zunger, A. Origins Vs. fingerprints of the Jahn-Teller effect in d-electron ABX3 perovskites. Phys. Rev. Res. 1, 033131 (2019).
Sun, J., Ruzsinszky, A. & Perdew, J. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 115, 036402 (2015).
Iglesias, L., Bibes, M. & Varignon, J. First-principles study of electron and hole doping effects in perovskite nickelates. Phys. Rev. B 104, 035123 (2021).
Furness, J. W. et al. An accurate first-principles treatment of doping-dependent electronic structure of high-temperature cuprate superconductors. Commun. Phys. 1, 11 (2018).
Mercy, A., Bieder, J., Íñiguez, J. & Ghosez, P. Structurally triggered metal-insulator transition in rare-earth nickelates. Nat. Commun. 8, 1677 (2017).
Braden, M., Reichardt, W., Ivanov, A. S. & Rumiantsev, A. Y. Anomalous dispersion of LO phonon branches in Ba0.6K0.4BiO3. Europhys. Lett. 34, 531 (1996).
Allen, P. B. & Dynes, R. C. Transition temperature of d-f-band superconductors. Phys. Rev. B 12, 905 (1975).
Zhao, H. et al. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature 599, 216–221 (2021).
Carrasco Álvarez, Á. A. et al. Charge ordering as the driving mechanism for superconductivity in rare-earth nickel oxides. Preprint at arXiv 2211.04870 (2022).
Li, L. et al. Superconducting order from disorder in 2H-TaSe2-xSx. npj Quantum Mater. 2, 11 (2017).
Kusmartseva, A. F., Sipos, B., Berger, H., Forró, L. & Tutiš, E. Pressure induced superconductivity in pristine 1T-TiSe2. Phys. Rev. Lett. 103, 236401 (2009).
Koley, S., Mohanta, N. & Taraphder, A. Charge density wave and superconductivity in transition metal dichalcogenides. Eur. Phys. J. B 93, 77 (2020).
Zunger, A., Wei, S.-H., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures. Phys. Rev. Lett. 65, 353 (1990).
Kresse, G. & Hafner, J. Ab. initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Stokes, H. T. & Hatch, D. M. FINDSYM: program for identifying the space-group symmetry of a crystal. J. Appl. Crystallogr. 38, 237 (2005).
Campbell, B. J., Stokes, H. T., Tanner, D. E. & Hatch, D. M. ISODISPLACE: a web-based tool for exploring structural distortions. J. Appl. Crystallogr. 39, 607–614 (2006).
Stokes, H. T., Hatch, D. M. & Campbell, B. J. ISOTROPY software suite. iso.byu.edu (2022).
Acknowledgements
J.V. acknowledges access granted to HPC resources of Criann through the projects 2020005 and 2007013 and of Cines through the DARI project A0080911453.
Author information
Authors and Affiliations
Contributions
The study was designed by J.V. J.V. performed all calculations and analysis of the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Varignon, J. Origin of superconductivity in hole doped SrBiO3 bismuth oxide perovskite from parameter-free first-principles simulations. npj Comput Mater 9, 30 (2023). https://doi.org/10.1038/s41524-023-00978-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-023-00978-w