Abstract
Magnetism in two-dimensional (2D) van der Waals (vdW) materials has lately attracted considerable attention from the point of view of both fundamental science and device applications. Obviously, establishing a detailed and solid understanding of their magnetism is the key first step toward various applications. Although Fe3GeTe2 is a representative ferromagnetic (FM) metal in this family, many aspects of its magnetic and electronic behaviors still remain elusive. Here, we report our new finding that Fe3GeTe2 is a special type of correlated metal known as “Hund metal”. Furthermore, we demonstrate that Hund metallicity in this material is quite unique by exhibiting remarkable site dependence of Hund correlation strength, hereby dubbed “site-differentiated Hund metal”. Within this new picture, many of the previous experiments can be clearly understood, including the ones that were seemingly contradictory to one another.
Similar content being viewed by others
Introduction
Fe3GeTe2 has been a focus of the recent surge of 2D magnetic material research1,2,3,4,5,6,7,8,9,10,11,12. On the one hand, it displays many fascinating properties such as high critical temperature (Tc ≃ 220 K)6,8, heavy fermion behavior9, and the relative ease of exfoliation5,7. Its great potential has also been highlighted by recent experiments showing that Tc can be increased even up to room temperature10,11 and that the large anomalous Hall current is originated from the unique band topology12. On the other hand, its electronic and magnetic properties are far from being clearly understood. The very basic picture for the magnetic moment is still under debate9,13,14. The measured quasiparticle masses are not consistent with each other and exhibit an order-of-magnitude difference depending on experimental probes9,12,13,14. These puzzles are posing a challenge to the current theory of this material.
In this work, we suggest a new physical picture for Fe3GeTe2. We first provide convincing evidence that Fe3GeTe2 is a “Hund metal”. The term Hund metal was coined to refer to an intriguing type of correlated (not necessarily magnetic) metals15,16,17,18,19 in which Hund coupling JH, rather than Hubbard U, plays the main role in determining the electronic properties19. Hund metals can host various interesting phenomena such as spin freezing20,21, spin-orbital separation22,23,24,25,26, orbital differentiation27,28, and unconventional superconductivity21,29. This concept has been providing a compelling view for many of multiorbital systems15,19,20,21,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44, most prominently for iron-based superconductors15,19,29,30,32,33,37,45, ruthenates20,21,31,36,40, and presumably also for recently discovered nickelate superconductors46,47. Our analysis demonstrates that Fe3GeTe2 is a new member of this family.
Further, we show that Hund metallicity of this material is distinctive from other known Hund metals by exhibiting the remarkable site dependence of correlation strengths; dubbed “site-differentiated” Hund metal (see Fig. 1). This intriguing site dependence is originated from the microscopic details of underlying band structure. The suggested new picture is an important key to understand experiments including the ones that are seemingly contradictory to each other.
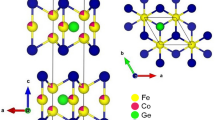
Left panel: A schematic illustration of “site-differentiated Hund metal” physics in Fe3GeTe2. Colored areas highlight different regimes or phases; Mott insulator (dark green; i.e., whose charge gap is opened due to Hubbard U), Mott metal (light green; i.e., whose correlated metallic behavior is governed by U), weakly correlated metal (yellow; electronic correlation is weak enough), and Hund metal (red; i.e., whose correlated metallic behavior is governed by Hund JH). For more details to define each region of the phase diagram, we refer to refs. 35,42,61. While both Fe sites fall into the Hund metal regime, they are clearly differentiated in terms of electron scattering rate Γ, quasiparticle effective mass m*/mb, and Sommerfeld coefficient γ (as depicted along z axis) which are attributed to the electronic structure details (see the schematic DOS). In parentheses shown are the calculated spin-orbital-averaged values of (Γ, m*/mb, γ) taken at T = 100 K. The unit of Γ is meV. The x- and y axis corresponds to JH/U and U/W, respectively. U = 5.0 and J = 0.9 eV (JH/U = 0.18) were used for both Fe-I and Fe-II; see “Methods” for a more detailed discussion. The effective bandwidth WFe-I for Fe-I is found to be smaller than that of Fe-II through the analysis of the hybridization function (see the main text). A rough estimation of their difference based on the integrated DOS yields ~1.6 eV (see the main text). Right panel: Crystal structure of Fe3GeTe2.
Results and discussion
Fe3GeTe2 is a Hund metal
Fe3GeTe2 is a vdW material with a layered Fe3Ge substructure sandwiched by two Te layers. Five Fe-3d levels of both Fe-I and Fe-II are split into three groups, namely \({d}_{{{{\rm{{z}}}^{2}}}},{d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}/{{{\rm{xy}}}}}\) and dxz/yz. More details can be found in Supplementary Note 1 of Supplementary Information (SI).
We firstly demonstrate that all the key features defining Hund metal are well identified in Fe3GeTe2via density functional theory plus dynamical mean-field theory (DFT+DMFT) calculations (see “Methods”). In order to concentrate on the intrinsic nature of correlation (separately from magnetism), we suppress magnetic ordering unless otherwise specified. The result of U = 5 and JH = 0.9 eV will be presented as our main parameter choice. Computation methods, including the parameter dependence and other details, are given in “Methods”.
First, we examine so-called two-faced or “Janus” effect which represents the physics governed by JH distinctively from that of Mott correlation U18,19. The straightforward way is to see the simultaneous increase of both Uc (the critical value of U at which the metal-to-Mott-insulator transition occurs) and “correlation strength” as measured typically by the inverse of quasiparticle weight Z (or equivalently, the quasiparticle scattering rate Γ) as JH increases18,19.
Let us uncover the “first face” of this effect, namely, the Uc increase by JH. To avoid the demanding computations scanning the large parameter space, here we simply examine the atomic gap Δat ≡ EN+1 + EN−1 − 2EN (EN: the atomic ground state energy of N-electron subspace). According to the original Mott–Hubbard picture, the gap opening is associated with Δat > W (W: bandwidth), and the system gets closer to Mott transition as Δat increases. This analysis, albeit simple, is well justified by the observations that the actual DMFT phase diagrams are consistent with the behavior of Δat in the large JH regime19,42. We found that Δat ≈ U − 1.52JH from a five-degenerate-orbital model with 6 electrons, which guarantees that ∂Δat/∂JH < 0 (see the inset of Fig. 2a). Note that JH drives the system away from being a Mott insulator; hereby the Janus' first face is unveiled.
a The JH dependence of quasiparticle scattering rate Γ for each orbital in Fe-I (orange) and Fe-II (blue) at T = 300 K. Inset in (a) shows the JH dependence of Δat for a degenerate five-orbital model with six electrons. b, c Temperature dependence of the susceptibilities (b) kBTχspin/orb and (c) χspin of Fe-I (orange) and Fe-II (blue). The filled and open symbols refer to the spin and orbital susceptibility, respectively. Two arrows in (b) indicate the onset temperature of spin screening below which χspin deviates from the Curie law of free local moment. The inset in (c) is an enlarged view of \({\chi }_{{{{\rm{Fe-II}}}}}^{{{{\rm{spin}}}}}\) in the low-temperature region.
To see its “second face”, the calculated Γ is presented in Fig. 2a. Here, \({\Gamma }_{l}={Z}_{l}{{{\rm{Im}}}}{\Sigma }_{l}({{{\rm{i}}}}{\omega }_{n}){| }_{{\omega }_{n}\to {0}^{+}}\), where Zl is the quasiparticle weight and Σl(iωn) the local self-energy on the imaginary frequency (ωn) axis for a given orbital l (see Supplementary Note 2 of SI for additional discussion). It is clear that the Γ is enhanced as JH increases. Also, the scattering rate is strongly orbital-dependent as depicted by different symbols, and the differences become more pronounced as JH increases. This feature, often called orbital differentiation, has been regarded as one of the key pieces for identifying iron-based superconductors as a Hund metal27,28.
Having evidenced Janus behavior, we now turn to another defining feature of Hund metallicity, namely, spin-orbital separation22,23,24,25,26. As discussed in previous works, the electronic behavior of Hund metals follows the local-atomic and Landau-quasiparticle picture in the high- and low-enough energy region, respectively, due to the gradual development of screenings. Deng et al. suggested that the much higher onset screening temperature for the orbital degree of freedom (\({T}_{{{{\rm{onset}}}}}^{{{{\rm{orb}}}}}\)) than that of spin (\({T}_{{{{\rm{onset}}}}}^{{{{\rm{spin}}}}}\)) is a key signature of Hund metals; i.e., \({T}_{{{{\rm{onset}}}}}^{{{{\rm{orb}}}}}\gg {T}_{{{{\rm{onset}}}}}^{{{{\rm{spin}}}}}\)26. Following the literature, we tracked local susceptibilities up to high enough temperature. Figure 2b shows the calculated local spin and orbital susceptibilities multiplied by kBT (kB: Boltzmann constant). The spin susceptibility with no prefactor kBT is presented in Fig. 2c. The onset screening temperatures for spin (below which kBTχspin starts to deviate from the Curie law) are indicated by the vertical orange arrows; \({T}_{{{{\rm{onset}}}}}^{{{{\rm{spin}}}}}\approx 3000\) K and 9000 K for Fe-I and Fe-II, respectively. Importantly, the onset temperatures for orbital screenings are much higher; \({T}_{{{{\rm{onset}}}}}^{{{{\rm{orb}}}}} > 20000\) K for both Fe-I and Fe-II; see the empty symbols. The well-separated \({T}_{{{{\rm{onset}}}}}^{{{{\rm{spin}}}}}\) and \({T}_{{{{\rm{onset}}}}}^{{{{\rm{orb}}}}}\) provide further evidence that Fe3GeTe2is a Hund metal.
We also investigated the long-time correlators, Cspin/orb(τ = 1/2kBT) (τ: imaginary time); see Supplementary Note 3 of SI for its definition and the related discussion. These quantities were recently used as another useful proxy to measure the degree of spin-orbital separation42. The results also clearly show that Fe3GeTe2is well classified as a Hund metal.
We finally note that the ferromagnetic transition temperature (Tc ≃ 220 K) of Fe3GeTe2 is much lower than the characteristic temperature scales of Tonset for spin and orbital. It indicates that the Hund metal character is developed well above the ferromagnetic transition temperature and the magnetic order itself is not immediately relevant to Hund metallicity.
Site-differentiated Hund metallicity
Hund metallicity in Fe3GeTe2is unique in that its Hund physics is clearly differentiated at two sites. Note that the scattering rate Γ is an order-of-magnitude larger in Fe-I. Γ of Fe-I \({d}_{{{{\rm{{x}}}^{2}-{y}^{2}/xy}}}\) (orange triangles in Fig. 2a) reaches 0.6 at JH = 1.3 eV, whereas that of Fe-II \({d}_{{{{\rm{{z}}}^{2}}}}\) only 0.05 (blue circles) for example. The orbital-dependent correlation is also more pronounced in Fe-I (Fig. 2a).
χspin also shows remarkable site dependence as presented in Fig. 2c: As the temperature is lowered, χspin of Fe-I (orange line) well follows ~1/T behavior in sharp contrast to Fe-II (blue line) which almost saturates at ~100 K (see inset of Fig. 2c). It implies that, below this temperature, the spin moments of Fe-II tend to be itinerant. For Fe-I, on the other hand, we could not find any indication of susceptibility saturation down to the lowest temperature we reached (~100 K), indicative of the persistent local moment character. See also Supplementary Note 3 of SI for further analysis based on long-time correlators.
What is the origin of this site-dependent Hund physics? First of all, we note that the d-orbital occupations are almost the same in both sites; the calculated electron occupancy is 6.431 ± 0.001 at U = 0 and 6.18 ± 0.05 at U = 5 eV (−/+ corresponding to Fe-I/Fe-II). It is largely attributed to the strong covalency in this chalcogenide material. Although the electron number depends on the charge-counting method, this level of coincidence can effectively exclude the possibility of the site-differentiated Hund physics being originated simply from the different charge status or valence. Rather, it indicates the more subtle electronic origins. Second, the calculated density of states (DOS) does not show significant difference between Fe-I and Fe-II other than the more pronounced van Hove singularity (vHS) for Fe-I dx2-y2/xy (see Supplementary Note 4 of SI).
Highly useful insights are obtained from the calculated “one-shot” hybridization function Δ(iωn) for each orbital. For its definition and the related figures, refer to Sec. S4 of SI. \(-{{{\rm{Im}}}}\Delta ({{{\rm{i}}}}{\omega }_{n})\) at high energy (which approximately scales as the square of the bandwidth) is smaller for Fe-I than Fe-II (see Supplementary Fig. 4a in SI). It shows that the effective bandwidth for Fe-I is smaller than Fe-II, indicative of the stronger correlation at Fe-I. This feature of smaller bandwidth for Fe-I is also seen in the integrated DOS analysis (see Supplementary Fig. 4b). It is therefore consistent with the larger Γ (discussed above; see Fig. 2a) and the greater mass of Fe-I (to be discussed below; see Fig. 3d). Also, in the low-frequency regime, \(-{{{\rm{Im}}}}\Delta ({{{\rm{i}}}}{\omega }_{n})\) of Fe-I dx2-y2/xy is smallest and exhibits a downturn as ωn → 0. Note that \(-{{{\rm{Im}}}}\Delta ({{{\rm{i}}}}{\omega }_{n}){| }_{{\omega }_{n}\to 0} \sim 1/\{(\pi D({E}_{{{{\rm{f}}}}}))\}\). Here, D(Ef) is the DOS at the Fermi level Ef. Thus, this downturn of \(-{{{\rm{Im}}}}\Delta ({{{\rm{i}}}}{\omega }_{n})\) is most likely due to the well-developed vHS (i.e., the divergence of DOS), which in turn suppresses the low-energy effective hopping processes31. That is, electron scattering and mass enhancement of Fe-I dx2-y2/xy are further boosted by vHS.
a The momentum-dependent spectral function A(k, ω) calculated from FM phase in comparison with ARPES data. The two figures on the left (expressed with black and white intensity) are the ARPES results measured with differently polarized photons of linear horizontal (LH) and linear vertical (LV) polarization taken from ref. 14. The rightmost figure is the kz-integrated DFT+DMFT result at T = 100 K. It is found that each band has the significantly mixed characters of Fe-I, Fe-II, and other anions. b Fermi surfaces in the kx--ky plane. The two left plots are the ARPES results (black and white)14. The right three plots (colored) show the kz-integrated DFT+DMFT results: FM at T = 100 and 200 K, and paramagnetic at T = 300 K. ARPES data in (a) and (b) are presumably measured below 25 K14. c The calculated Γ/kBT as a function of temperature. A vertical dotted line indicates the experimentally reported incoherence-coherence crossover temperature9,48, and the colored areas highlight the regions for which Γ≤kBT31 (yellow) and T≤Tc (skyblue). The upper- and the lower-filled symbols refer to the values of the majority and minority spin, respectively in the FM phase, and the fully filled symbols represent the values of the paramagnetic phase. d The calculated m*/mb of each orbital at T = 100 K for Fe-I (orange) and Fe-II (blue). The filled and empty stars indicate the values of the majority and minority spin, respectively in the FM phase, and the circles represent the values from paramagnetic phase. The horizontal dash-dotted and dashed line indicates the values from specific heat13 and ARPES experiments12,14, respectively. e The calculated orbital-decomposed Sommerfeld coefficient in FM phase at T = 100 K. Here “total” denotes the sum of all orbital contributions, and “the rest” the contributions from the other states than Fe d-orbitals. The experimentally measured values are represented by horizontal dashed lines6,13,62.
Understanding the experiments
The new picture for Fe3GeTe2 as a “site-differentiated Hund metal” provides useful insights to understand the experiments. Before discussing those features in detail, let us take a look at the spectral function A(k, ω) which can be directly compared with angle-resolved photoemission spectroscopy (ARPES) results, thereby enabling us to check the reliability of our parameter choices for interactions and the correlated electronic structure. Figure 3a shows the excellent agreement between theory and experiment. For example, the pronounced spectral features, namely the bands assigned as γ, ζ and ω in ref. 14 are well identified in our A(k, ω). The near-Fermi-level states are also well reproduced; see, e.g., α, δ and η bands.
The first experimental quantity we want to revisit is the large quasiparticle mass; m*/mb = γ/γb ≃ 13 reported from specific heat measurement13 (i.e., taken from the measured Sommerfeld coefficient γ and its DFT estimate γb). This value remains as a puzzle especially because ARPES data was deemed to be in fair agreement with band calculations m*/mb ≃ 1.612,14. This large discrepancy has been highlighted throughout the literature9,13,14, but the issue remains still unresolved.
Here, we argue that these seemingly contradictory experimental results can be understood as a natural manifestation of the site-differentiated Hund physics. In multiorbital systems, the mass enhancement measured by specific heat is mainly determined by the more correlated orbital27. In fact, our calculation shows m*/mb ≈ 7–23 for the more correlated site Fe-I, which is comparable to the value from specific heat experiment (dash-dotted line in Fig. 3d). It is due to that Sommerfeld coefficient γ extracted from specific heat is a sum of each orbital contribution \({\gamma }_{l} \sim {({m}^{* }/{m}^{{{{\rm{b}}}}})}_{l}\); see Supplementary Note 5 in SI for more details. As discussed in ref. 27, it is comparable to the series resistor in a circuit for which total resistance is given by the direct sum, and the total voltage can be approximated by the one applied to the large resistor. Indeed, the site- and orbital-decomposed values (Fig. 3e) clearly show that the Fe-I contributions dominate the total value γtot, whereas those of Fe-II are much smaller. The sum over all orbitals γtot eventually gives rise to good agreement with experiments.
The ARPES situation is quite different on the other hand. The mass enhancement of a given “band” is a weighted sum of each orbital contribution therein. In fact, the previous study revealed that most bands in this material have both Fe-I and Fe-II characters (see, e.g., Supplementary Fig. 3 of ref. 14). As inferred from m*/mb ≈ 2–4 of Fe-II being comparable to an ARPES estimate (Fig. 3d), we presume that, at least in some bright bands captured by ARPES, the weaker correlated Fe-II d-orbitals as well as the other itinerant Ge and Te states possibly have the larger portion than Fe-I, which can result in the small m*/mb (see Supplementary Note 6 in SI for the related analysis).
Now let us examine the heavy fermion behavior and the incoherence-coherence crossover observed at T ~ 100 K9,48. Figure 3c presents Γ/kBT as a function of temperature for both paramagnetic (fully filled symbols) and FM phases (partially filled). Here, the coherence temperature T* is defined by Γ/kBT* = 1 (see the yellow region in which Γ≤kBT), namely the temperature below which quasiparticle lifetime exceeds the timescale of thermal fluctuation31,42. We note that the sizable site dependence of correlation makes electron scattering very different at two Fe sites: Whereas Γ/kBT of Fe-II remains less than 1 even well above the experimental T*, that of Fe-I is much greater. The larger contribution from Fe-I, particularly \({d}_{{{{\rm{{x}}}^{2}-{y}^{2}/xy}}}\) orbitals, and its significant temperature dependence as T → T* indicate that the experimentally observed incoherence-coherence crossover around T ~ 100 K9,48 is mainly attributed to the corresponding orbitals residing in Fe-I.
For comparison, we also investigate the isostructural material Ni3GeTe2 whose γ ~ 9 mJ/mol ⋅ K2 is much smaller13. Our calculation reasonably well reproduces the experiment and the mass enhancements m*/mb≤1.5 with no appreciable site differentiation (see Supplementary Note 6 in SI for our calculation results). This contrasting behavior, attributed to the absence of vHS and the different valence (see Supplementary Fig 6c in SI), renders Fe3GeTe2 as a unique example of site-differentiated Hund metal.
Finally, another important issue for Fe3GeTe2 is related to the nature of its magnetic moment. While in the early works it was understood or discussed within itinerant Stoner picture9,13, more recent studies emphasized the local nature of spin. For example, Xu et al. observed the nearly unchanged exchange splitting in their ARPES data even up to T > Tc14. The situation is therefore reminiscent of a prototypical FM Hund metal SrRuO3 whose exchange splitting persists above Tc due to the enhanced local spin character whereas the very low-temperature behavior is well described within Stoner theory49,50. Note that, near Tc ≃ 220 K, χspin of Fe-I clearly indicates the local moment behavior (Fig. 2c), and as a consequence, Γ is large. As temperature decreases, on the other hand, Γ gets reduced by the enhanced spin screenings, which eventually result in the long-lived quasiparticles well below T ~ 100 K (Fig. 3c). Therefore, our current study provides a unified picture for Fe3GeTe2 within which its spin moment can be described as being localized above and itinerant well below Tc.
We demonstrated that Fe3GeTe2 is a Hund metal with intriguing site dependence originated from the microscopic details in the underlying band structure. The proposed new picture of “site-differentiated Hund metal” not just makes this representative metallic vdW ferromagnet an even more exciting material platform, but also provides useful insights to understand the previous experiments including the ones that are seemingly contradictory to each other. Our results hopefully stimulate further experimental and theoretical investigations of the related systems. For example, the direct experimental observations of the site- or orbital-selective correlation effects can be an interesting research direction.
Methods
Computation details of DFT+DMFT calculations
The DFT electronic structure of Fe3GeTe2 was obtained by using FLAPWMBPT package51, which is based on the full-potential linearized augmented plane wave plus local orbital method, employing the local density approximation (LDA). We used experimental lattice parameters as reported in ref. 5. On top of this non-spin-polarized DFT band structure, 108 maximally localized Wannier functions were constructed with a wide energy window of [−15:10] eV containing Fe-s, Fe-p, Fe-d, Ge-s, Ge-p, Ge-d, Te-s, Te-p, and Te-d characters, and its tight-binding Hamiltonian was built through the JX interface52. We performed single-site dynamical mean-field theory (DMFT)53,54 calculations for d-orbitals of Fe-I and Fe-II by employing COMCTQMC55 implementation of the hybridization-expansion continuous-time quantum Monte Carlo (CTQMC) algorithm56 as an impurity solver. Namely, we solved two impurity problems, one for Fe-I and one for Fe-II, per DMFT self-consistency loop. Within our DFT+DMFT scheme, electronic self-energy is momentum-independent (i.e., local in space)53, and is assumed to be diagonal in cubic harmonics basis to avoid a sign problem by omitting the off-diagonal elements of hybridization functions whose values are actually small. The self-energy on the real frequency axis was obtained from the analytic continuation of imaginary axis data using the maximum entropy method57. For the magnetically ordered phase of Fe3GeTe2, we used EDMFTF package58 for DFT+DMFT calculations.
For the double counting (DC) self-energy, we adopted the nominal DC scheme which reads \({\Sigma }_{{{{\rm{DC}}}}}({n}_{0})=U({n}_{0}-\frac{1}{2})-\frac{J_{\rm H}}{2}({n}_{0}-1)\)59, where n0 is the nominal charge. We took n0 = 6.0 for both Fe-I and Fe-II, which is close to the d-orbital occupancy obtained from DFT (nDFT ≃ 6.4). Note also that this DC scheme with n0 = 6.0 was used for this material in a previous study13, which yields good agreement of magnetic moment with experimental data. While we mainly present the results obtained from n0 = 6.0, we found that varying n0 in a range of [5.4:6.6] does not lead to any qualitative changes; e.g., see Supplementary Note 7 of SI for spin and orbital susceptibilities obtained from different ΣDC(n0) values.
The Hubbard U and Hund coupling JH of Fe-d were chosen to be U ≡ F0 = 5.0 eV and JH ≡ (F2 + F4)/14 = 0.9 eV for both Fe-I and Fe-II, which were used in a previous study on Fe3GeTe212. These values are also comparable to the theoretically estimated values for iron chalcogenide family60. Here, F0, F2, and F4 are Slater integrals, and the ratio F4/F2 = 0.625 was used for parametrization of on-site Coulomb interaction tensor. For Ni3GeTe2 which will be discussed in Supplementary Note 6 of SI, the same computation scheme was used except for the use of a larger nominal charge (n0 = 8.0) for the DC self-energy and a larger Hubbard U of U ≡ F0 = 6.0 eV, considering its chemical environment on Ni sites. Note also that, for Ni3GeTe2, we did not consider any magnetic order due to its absence even at very low temperatures5,13. We used experimental lattice parameters of Ni3GeTe25.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
All codes used in this work are accessible through their websites.
References
Burch, K. S., Mandrus, D. & Park, J.-G. Magnetism in two-dimensional van der Waals materials. Nature 563, 47–52 (2018).
Gong, C. & Zhang, X. Two-dimensional magnetic crystals and emergent heterostructure devices. Science 363, caav4450 (2019).
Mak, K. F., Shan, J. & Ralph, D. C. Probing and controlling magnetic states in 2D layered magnetic materials. Nat. Rev. Phys. 1, 646–661 (2019).
Gibertini, M., Koperski, M., Morpurgo, A. F. & Novoselov, K. S. Magnetic 2D materials and heterostructures. Nat. Nanotechnol. 14, 408–419 (2019).
Deiseroth, H.-J., Aleksandrov, K., Reiner, C., Kienle, L. & Kremer, R. K. Fe3GeTe2 and Ni3GeTe2—two new layered transition-metal compounds: crystal structures, HRTEM investigations, and magnetic and electrical properties. Eur. J. Inorg. Chem. 2006, 1561–1567 (2006).
Chen, B. et al. Magnetic properties of layered itinerant electron ferromagnet Fe3GeTe2. J. Phys. Soc. Jpn. 82, 124711 (2013).
Fei, Z. et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 17, 778–782 (2018).
Jang, S. W. et al. Origin of ferromagnetism and the effect of doping on Fe3GeTe2. Nanoscale 12, 13501–13506 (2020).
Zhang, Y. et al. Emergence of Kondo lattice behavior in a van der Waals itinerant ferromagnet, Fe3GeTe2. Sci. Adv. 4, eaao6791 (2018).
Deng, Y. et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 563, 94–99 (2018).
Wang, H. et al. Above room-temperature ferromagnetism in wafer-scale two-dimensional van der Waals Fe3GeTe2 tailored by a topological insulator. ACS Nano 14, 10045–10053 (2020).
Kim, K. et al. Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal. Nat. Mater. 17, 794–799 (2018).
Zhu, J.-X. et al. Electronic correlation and magnetism in the ferromagnetic metal Fe3GeTe2. Phys. Rev. B 93, 144404 (2016).
Xu, X. et al. Signature for non-Stoner ferromagnetism in the van der Waals ferromagnet Fe3GeTe2. Phys. Rev. B 101, 201104 (2020).
Haule, K. & Kotliar, G. Coherence-incoherence crossover in the normal state of iron oxypnictides and importance of Hund rule coupling. N. J. Phys. 11, 025021 (2009).
Yin, Z. P., Haule, K. & Kotliar, G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat. Mater. 10, 932–935 (2011).
de’ Medici, L. Hund’s coupling and its key role in tuning multiorbital correlations. Phys. Rev. B 83, 205112 (2011).
de’ Medici, L., Mravlje, J. & Georges, A. Janus-faced influence of Hund’s rule coupling in strongly correlated materials. Phys. Rev. Lett. 107, 256401 (2011).
Georges, A., Medici, L. D. & Mravlje, J. Strong correlations from Hund’s coupling. Annu. Rev. Condens. Matter Phys. 4, 137–178 (2013).
Werner, P., Gull, E., Troyer, M. & Millis, A. J. Spin freezing transition and non-fermi-liquid self-energy in a three-orbital model. Phys. Rev. Lett. 101, 166405 (2008).
Hoshino, S. & Werner, P. Superconductivity from emerging magnetic moments. Phys. Rev. Lett. 115, 247001 (2015).
Okada, I. & Yosida, K. Singlet ground state of the localized d-electrons coupled with conduction electrons in metals. Prog. Theor. Phys. 49, 1483–1502 (1973).
Yin, Z. P., Haule, K. & Kotliar, G. Fractional power-law behavior and its origin in iron-chalcogenide and ruthenate superconductors: insights from first-principles calculations. Phys. Rev. B 86, 195141 (2012).
Stadler, K., Yin, Z., von Delft, J., Kotliar, G. & Weichselbaum, A. Dynamical mean-field theory plus numerical renormalization-group study of spin-orbital separation in a three-band Hund metal. Phys. Rev. Lett. 115, 136401 (2015).
Horvat, A., Žitko, R. & Mravlje, J. Low-energy physics of three-orbital impurity model with Kanamori interaction. Phys. Rev. B 94, 165140 (2016).
Deng, X. et al. Signatures of Mottness and Hundness in archetypal correlated metals. Nat. Commun. 10, 2721 (2019).
de’ Medici, L., Giovannetti, G. & Capone, M. Selective Mott physics as a key to iron superconductors. Phys. Rev. Lett. 112, 177001 (2014).
Kostin, A. et al. Imaging orbital-selective quasiparticles in the Hund’s metal state of FeSe. Nat. Mater. 17, 869–874 (2018).
Lee, T.-H., Chubukov, A., Miao, H. & Kotliar, G. Pairing mechanism in Hund’s metal superconductors and the universality of the superconducting gap to critical temperature ratio. Phys. Rev. Lett. 121, 187003 (2018).
Yin, Z. P., Haule, K. & Kotliar, G. Magnetism and charge dynamics in iron pnictides. Nat. Phys. 7, 294–297 (2011).
Mravlje, J. et al. Coherence-incoherence crossover and the mass-renormalization puzzles in Sr2RuO4. Phys. Rev. Lett. 106, 096401 (2011).
Bascones, E., Valenzuela, B. & Calderón, M. J. Orbital differentiation and the role of orbital ordering in the magnetic state of Fe superconductors. Phys. Rev. B 86, 174508 (2012).
Lanatà, N. et al. Orbital selectivity in Hund’s metals: the iron chalcogenides. Phys. Rev. B 87, 045122 (2013).
Khajetoorians, A. et al. Tuning emergent magnetism in a Hund’s impurity. Nat. Nanotechnol. 10, 958–964 (2015).
Fanfarillo, L. & Bascones, E. Electronic correlations in Hund metals. Phys. Rev. B 92, 075136 (2015).
Mravlje, J. & Georges, A. Thermopower and entropy: lessons from Sr2RuO4. Phys. Rev. Lett. 117, 036401 (2016).
de’ Medici, L. Hund’s induced fermi-liquid instabilities and enhanced quasiparticle interactions. Phys. Rev. Lett. 118, 167003 (2017).
Isidori, A. et al. Charge disproportionation, mixed valence, and Janus effect in multiorbital systems: a tale of two insulators. Phys. Rev. Lett. 122, 186401 (2019).
Ryee, S., Sémon, P., Han, M. J. & Choi, S. Nonlocal Coulomb interaction and spin-freezing crossover as a route to valence-skipping charge order. npj Quantum Mater. 5, 19 (2020).
Kugler, F. B. et al. Strongly correlated materials from a numerical renormalization group perspective: how the fermi-liquid state of Sr2RuO4 emerges. Phys. Rev. Lett. 124, 016401 (2020).
Chen, X. et al. Unconventional Hund metal in a weak itinerant ferromagnet. Nat. Commun. 11, 3076 (2020).
Ryee, S., Han, M. J. & Choi, S. Hund physics landscape of two-orbital systems. Phys. Rev. Lett. 126, 206401 (2021).
Fanfarillo, L., Valli, A. & Capone, M. Synergy between Hund-driven correlations and boson-mediated superconductivity. Phys. Rev. Lett. 125, 177001 (2020).
Karp, J. et al. Sr2MoO4 and Sr2RuO4: disentangling the roles of Hund’s and van Hove physics. Phys. Rev. Lett. 125, 166401 (2020).
Watzenböck, C., Edelmann, M., Springer, D., Sangiovanni, G. & Toschi, A. Characteristic timescales of the local moment dynamics in Hund’s metals. Phys. Rev. Lett. 125, 086402 (2020).
Wang, Y., Kang, C.-J., Miao, H. & Kotliar, G. Hund’s metal physics: from SrNiO2 to NdNiO2. Phys. Rev. B 102, 161118 (2020).
Kang, B. et al. Infinite-layer nickelates as Ni-eg Hund’s metals. Preprint at https://arxiv.org/abs/2007.14610 (2021).
Corasaniti, M. et al. Electronic correlations in the van der Waals ferromagnet Fe3GeTe2 revealed by its charge dynamics. Phys. Rev. B 102, 161109 (2020).
Jeong, D. W. et al. Temperature evolution of itinerant ferromagnetism in SrRuO3 probed by optical spectroscopy. Phys. Rev. Lett. 110, 247202 (2013).
Kim, M. & Min, B. I. Nature of itinerant ferromagnetism of SrRuO3: a DFT+DMFT study. Phys. Rev. B 91, 205116 (2015).
Kutepov, A. L., Oudovenko, V. S. & Kotliar, G. Linearized self-consistent quasiparticle GW method: application to semiconductors and simple metals. Comput. Phys. Commun. 219, 407–414 (2017).
Yoon, H., Kim, T. J., Sim, J.-H. & Han, M. J. Jx: An open-source software for calculating magnetic interactions based on magnetic force theory. Comput. Phys. Commun. 247, 106927 (2020).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Choi, S., Semon, P., Kang, B., Kutepov, A. & Kotliar, G. ComDMFT: a massively parallel computer package for the electronic structure of correlated-electron systems. Comput. Phys. Commun. 244, 277–294 (2019).
Gull, E. et al. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349–404 (2011).
Jarrell, M. & Gubernatis, J. Bayesian inference and the analytic continuation of imaginary-time quantum Monte Carlo data. Phys. Rep. 269, 133–195 (1996).
Haule, K., Yee, C.-H. & Kim, K. Dynamical mean-field theory within the full-potential methods: electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5. Phys. Rev. B 81, 195107 (2010).
Pourovskii, L. V., Amadon, B., Biermann, S. & Georges, A. Self-consistency over the charge density in dynamical mean-field theory: a linear muffin-tin implementation and some physical implications. Phys. Rev. B 76, 235101 (2007).
Miyake, T., Nakamura, K., Arita, R. & Imada, M. Comparison of ab initio low-energy models for LaFePO, LaFeAsO, BaFe2As2, LiFeAs, FeSe, and FeTe: electron correlation and covalency. J. Phys. Soc. Jpn. 79, 044705 (2010).
Strand, H. U. R. Valence-skipping and negative-U in the d-band from repulsive local Coulomb interaction. Phys. Rev. B 90, 155108 (2014).
Liu, Y., Stavitski, E., Attenkofer, K. & Petrovic, C. Anomalous Hall effect in the van der Waals bonded ferromagnet Fe3−xGeTe2. Phys. Rev. B 97, 165415 (2018).
Acknowledgements
T.J.K. thanks Hongkee Yoon for the discussion on Fe3GeTe2 at the initial stage and comments on the use of JX interface for constructing tight-binding Hamiltonians. S.R. is grateful to Sangkook Choi for the fruitful conversation. This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (Grant Nos. 2021R1A2C1009303 and NRF-2018M3D1A1058754), the KAIST Grand Challenge 30 Project (KC30) in 2021 funded by the Ministry of Science and ICT of Korea and KAIST (N11210105), and the National Supercomputing Center with supercomputing resources, including technical support (KSC-2020-CRE-0084).
Author information
Authors and Affiliations
Contributions
T.J.K. performed all the calculations and initiated the project by noticing the site differentiation in Fe3GeTe2. S.R. led the data analysis. M.J.H. supervised the project. All authors participated in the interpretation of the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, T.J., Ryee, S. & Han, M.J. Fe3GeTe2: a site-differentiated Hund metal. npj Comput Mater 8, 245 (2022). https://doi.org/10.1038/s41524-022-00937-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00937-x
This article is cited by
-
Unraveling the electronic structure and magnetic transition evolution across monolayer, bilayer, and multilayer ferromagnetic Fe3GeTe2
npj 2D Materials and Applications (2024)
-
Unraveling effects of electron correlation in two-dimensional FenGeTe2 (n = 3, 4, 5) by dynamical mean field theory
npj Computational Materials (2023)