Abstract
Concrete, as the most widely used construction material, is inextricably connected with human development. Despite conceptual and methodological progress in concrete science, concrete formulation for target properties remains a challenging task due to the ever-increasing complexity of cementitious systems. With the ability to tackle complex tasks autonomously, machine learning (ML) has demonstrated its transformative potential in concrete research. Given the rapid adoption of ML for concrete mixture design, there is a need to understand methodological limitations and formulate best practices in this emerging computational field. Here, we review the areas in which ML has positively impacted concrete science, followed by a comprehensive discussion of the implementation, application, and interpretation of ML algorithms. We conclude by outlining future directions for the concrete community to fully exploit the capabilities of ML models.
Similar content being viewed by others
Introduction
Concrete is the most prevalent human-made material on Earth, and the most consumed commodity after water1. Compared to other engineering materials like steel, plastics, and wood, concrete plays a pivotal role in the construction industry due to its unique combination of strength, affordability, moldability, and durability2. Buildings, roads, bridges, dams, and many common infrastructure elements are primarily made of concrete. The annual consumption of concrete in the world has reached 35 billion tons, which is twice as much as that of all other building materials combined3,4.
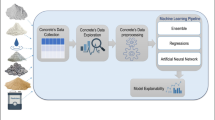
As illustrated in Fig. 1, early concrete research has followed three paradigms of science, namely, empiricism, theory, and computation. The properties and performance of concrete can be tailored to meet design requirements by varying the type and quantity of the mixture constituents (e.g., cement, water, aggregate, and admixtures). Traditional approaches for designing concrete mixtures often rely on trial-and-error, iterative proportioning, processing, and characterization until the target properties are achieved5 (the first paradigm: empirical science; Fig. 1). Although this method has yielded some success, it requires considerable investments in time and resources. For example, it is possible to optimize the compressive strength of concrete mixtures by adjusting the water/cement ratio, total aggregate/cement ratio, and coarse aggregate/total aggregate ratio6. Yet the practical application of this iterative refinement approach is limited by the exponential increase in the number of specimens and experiments when complex concrete mixtures are studied and several compositional parameters are simultaneously considered as combinatorial variables. As a result, materials development in concrete science involves time-consuming validation/development cycles from laboratory trials to field applications. Efforts to accelerate knowledge acquisition and materials design in concrete science are thus of paramount importance.
From left to right, representative examples include: trial-and-error, iterative experiments (proportioning, processing, and characterization); numerical simulations on cement hydration (e.g., hydration, morphology, and structural development model, HYMOSTRUC10); molecular dynamics simulations on cement hydrates (e.g., calcium silicate hydrate gel224); and artificial intelligence and machine learning predictions using experimental and computational data. Figure adapted with permission from ref. 225, CC BY 4.0.
Beginning in the 1980s, the development of microstructural models of cement hydration has enabled a fundamental understanding of microstructure–property relationships in concrete7, which has marked the second paradigm (theoretical science; Fig. 1) by applying basic laws of kinetics, thermodynamics, and mechanics, and providing analytical solutions to cement hydration. Successful demonstrations include the three-dimensional cement hydration and microstructure development model (CEMHYD3D)8,9; the hydration, morphology, and structural development model (HYMOSTRUC)10; the integrated particle kinetics model11; and the microstructural modeling platform (μic)12. These microstructural models simulate the hydration process and microstructure development of cementitious systems (e.g., dissolution and diffusion, chemical reactions, and precipitation of hydration products) by integrating kinetic laws, being a basis for the description of time-dependent material properties, including mechanical and transport properties. In parallel, the application of thermodynamics in cement chemistry has facilitated the systematic investigation of the stability and performance of concrete mixtures13,14,15. However, the complex nature of cement hydration makes it challenging to develop accurate and generalizable models, and these modeling approaches, to varying degrees, rely on thermochemical, physical, and structural data that must be obtained either from accurate experimental observations or from calculations at the atomistic and molecular scales.
In this context, the use of density-functional theory (DFT) and classical molecular dynamics (MD) simulations has been explored in concrete science since the 2000s owing to the ever-growing computing power16. This has given rise to the third paradigm (computational science; Fig. 1), where the first-principle models have been integrated and employed to further describe cementitious materials properties and improve understanding of cement hydration. Related simulation efforts have focused primarily on cementitious phases such as the calcium silicate hydrate (C-S-H) gel, the essential reaction product of cement hydration17,18. Advanced knowledge gained from these simulations elucidates the intrinsic behaviors of concrete at the atomistic and molecular scales, while offering valuable insights (e.g., structural data or kinetic parameters) into microstructure modeling and complementary interpretations of experimental studies; however, these computational techniques require considerable computational resources and thus come with significant challenges, such as their limited time scales and the relatively small number of atoms in a simulated system. In addition, it may be difficult to validate these simulations with experiments, given the small time and length scales and high-fidelity measurements required.
While the previous three paradigms of concrete science have provided valuable contributions and yielded some success, there still exist several challenges, including iterative trial-and-error cycles, significant domain expertise required, and high labor and computational costs. Unlike other materials, concrete is inherently much more complex and heterogeneous, due to the virtually infinite combinatorial space of mixture constituents (including cement, water, aggregate, and admixtures) and the wide variability in physical and chemical properties of these constituents3,19. Thus, understanding the process–structure–property–performance relationships for concrete materials with existing methods remains a difficult task.
As a complementary route, artificial intelligence and machine learning (ML) approaches are establishing the fourth paradigm (data-driven science; Fig. 1) in concrete research and offering fresh perspectives and practical solutions for accelerating innovations in the design and development of cementitious materials. By leveraging existing datasets with data-driven models, ML can automatically learn implicit patterns and extract valuable information while accounting for the inherent complexity of concrete mixtures and their properties5. As such, ML is being exploited as a powerful tool to express process–structure–property–performance relationships, identify cement hydration and concrete degradation mechanisms, and assist concrete materials design and discovery, together with high-throughput experimentation and computation. The use of ML in concrete science has been explored for cement pastes20,21, mortars22,23, as well as various types of concrete, including high performance concrete24,25,26, self-consolidating concrete27,28,29, reinforced concrete30,31,32, pervious concrete33, recycled aggregate concrete34,35,36, lightweight aggregate concrete37,38, alkali-activated concrete39,40, and 3D-printed concrete41,42, to name a few.
As ML models are becoming more accessible to users (an extensive survey of open-source software packages in ML is provided in ref. 43), it is expected that applications of ML will further expand in the concrete field to guide data analysis and enable scientific discovery. Thus, an overview of the current state of ML adoption in concrete science will be helpful in the design and development of cementitious materials. Existing reviews largely depended on manual appraisals, potentially leading to subjective interpretation. Moreover, there exist many challenges in implementing and interpreting ML models, which have seldom been examined in the literature. In order to tackle these limitations, the objectives of this work are to: (1) provide a comprehensive literature survey and an extensive bibliographic analysis of ML studies in concrete science; (2) offer a high-level summary of the most compelling ML applications and main research interests in concrete science; and (3) systematically assess the imminent challenges and opportunities for ML-based concrete research.
Applications
To begin with, we provide a literature survey and a bibliographic analysis of 389 peer-reviewed publications on applications of ML methods to concrete research (criteria of the literature survey are explained in Supplementary Note 1 and compiled data associated with the bibliographic analysis are provided in Supplementary Dataset). A high-level summary of applications of ML in concrete science (Table 1), commonly accessible datasets (Table 2), and current research directions is also presented.
The earliest article identified in connection to concrete and ML was published in 1992 (ref. 44), followed by a second one in 1994 (ref. 45). The number of publications remained relatively low and did not reach double digits until 2009 (Fig. 2a). Since then, there has been rapid growth in the number of ML studies, owing to the emergence of petascale computing centers, publicly accessible data repositories, and ready-for-use ML software libraries. The majority of studies have focused on regression tasks (88.2%), while research on classification (10.5%) has not emerged until recently, when deep learning for computer vision started to garner attention46,47,48.
a–d, Number of publications based on publication year (a, b); algorithm used (overlapped regions in the bar ‘NN’ indicate that publications of interest include both regression and classification tasks or both classification and clustering tasks) (c); and sample size (presented as relative frequency with a fixed bin width of 100 or unequal bin sizes (inset); only for publications with regression tasks; maximum values were selected if more than one dataset was used in a publication) (d). Data source: Web of Science; period: 1990–2020; survey criteria and collected data can be found in Supplementary Note 1 and Supplementary Dataset, respectively. NN neural network, SVM support vector machine, DT decision tree, RF random forest, KNN, k-nearest neighbors.
As can be inferred from Fig. 2b, c, the most commonly applied ML algorithms are neural networks, which have been dominant in concrete science from 1992 and employed for most classification tasks. Other methods such as support vector machines, decision trees, random forests, and k-nearest neighbors algorithms have also entered the concrete field and stimulated remarkable advances after 2010. A representative but not exhaustive list of applications of these ML models in concrete science is provided in Table 1, and commonly encountered ML terms are defined in Supplementary Note 2. While a detailed algorithmic comparison between different ML models is beyond the scope of this paper, the reader is referred to refs. 5,49,50,51,52 for a comprehensive presentation of existing ML techniques.
For publications focusing on regression tasks, the size of the data sample varied from 5 to 262,569, with the median being 174 or 169, before or after data pre-processing, respectively (Fig. 2d). In addition, most regression studies (93.6%) utilized data collected from empirical experiments, whereas few (7.3%) of them used data from computational simulations. Among the experimental studies, 93.8% were based on laboratory tests and 8.4% on field tests. (Note that some studies obtained data from both experiments and simulations, and for experiments, from both laboratory and field tests. Hence, the sums of these percentages are over 100%.)
Facilitated by the availability of open-source ML algorithms (Table 1) and of publicly released datasets (Table 2), the adoption of ML in concrete science has enabled multiple materials innovations. Some of the major research advancements are showcased in Fig. 3 and discussed below:
-
(1)
Property prediction. As seen in Table 1, one of the most common and direct uses of ML in concrete science consists of predicting the performance of concrete materials, such as fresh, hardened, and durability properties, which are of particular interest to the industry. By enabling the accurate prediction of target properties as a function of composition, ML can significantly accelerate the process of concrete mixture design with little to no physical knowledge prerequisite53,54. A representative example is compressive strength prediction of concrete mixtures, where the type and quantity of concrete constituents (e.g., cement, water, aggregate, and admixtures) are related to compressive strength, followed by an optimization procedure to identify mixtures that minimize the cost and the estimated CO2 impact for a given target strength54 (Fig. 3a). This approach offers a solution to the problem of screening optimal mixture proportions that can be further tailored to meet different design specifications, while reducing time and labor intensity in trial-batch testing.
-
(2)
Materials characterization. Characterization technologies with increasing spatial and temporal resolution are producing an immense quantity of experimental data, but are also posing considerable challenges of data curation and data interpretation. In this regard, ML has begun to play a key role in processing and analyzing disparate data. A large number of ML studies have been combined with non-destructive testing approaches, including acoustic methods (e.g., ultrasonic pulse velocity55,56,57, acoustic emission58,59, and impact echo44,60), electromagnetic methods (e.g., ground-penetrating radar55,61 and electrical resistivity55,57), and optical methods (e.g., digital photography62,63,64, laser scanning65,66, and infrared thermography61,67) for concrete properties evaluation and damage detection. Also of interest are the applications of ML in concrete petrographic analyses by flatbed scanning68, scanning electron microscopy32,69, and X-ray computed tomography31,70,71, for automated segmentation of pores, cracks, aggregates, or fibers. These image-based characterization techniques can leverage the power of deep learning to achieve human-level accuracy and beyond. Figure 3b presents a framework for analyzing complex, multi-phase cementitious composites (e.g., fibre-reinforced concretes) by applying deep learning to the automated segmentation of X-ray computed tomography images70. The accurate and efficient segmentation of relevant constitutive phases enables quantification of microstructures in terms of content, size, and orientation, and thus facilitates microstructural reconstructions for coupled experimental-numerical analyses70,71.
-
(3)
Materials simulation. One application of ML in concrete science that has received far less attention is the improvement and acceleration of computational simulations. For example, the combination of ML techniques with kinetic20,72, thermodynamic40, and mechanical73,74 modeling enables determination of parameters that require extensive experimental data, thereby assisting materials design and optimization via high-throughput computational simulations. In addition, molecular simulations that are limited by computational cost can immensely benefit from ML acceleration. By approximating complex quantum-chemistry potential energy surfaces, ML potential has achieved an accuracy comparable to that of the underlying DFT models, allowing a large-scale MD simulation of an idealized nanoporous C-S-H model (with 3,084 atoms for 2 ns), which would be beyond the limit of typical DFT calculations75 (Fig. 3c). ML interatomic potentials thus offer a promising path in executing large-scale MD simulations of realistic cement hydrates by minimizing computational cost while preserving quantum-chemical accuracy.
a Concrete compressive strength prediction (left) followed by mixture design optimization, e.g., strength-cost optimization (middle) and strength-cost-CO2 optimization (right)54. b Automated segmentation of X-ray computed tomography images for multi-phase cementitious composites with pores, aggregates, fibers, and cement matrix70. c Large-scale molecular dynamics (MD) simulation of calcium silicate hydrate (C-S-H) using ML potential75. DFT, density-functional theory; MSD, mean square displacement. Figure adapted with permission from: a, ref. 54, Elsevier; b, ref. 70, Elsevier; and c, ref. 75, Elsevier.
Challenges
A typical ML study consists of six steps: (1) problem definition, (2) data collection, (3) data pre-processing (or data cleaning), (4) model development, (5) model evaluation, and (6) model deployment76,77,78 (Fig. 4). In this section, we present challenges that may arise when applying ML procedures in concrete research, focusing mainly on supervised regression problems (which are the most employed, as shown in the survey presented above)—although many of these challenges are in fact common to a majority of ML problems. Specifically, challenges related to data [corresponding to steps (2, 3)], validation [steps (4, 5)], and interpretability [steps (5, 6)] in ML studies are discussed.
Six steps are typically involved in ML workflows, from (1) problem definition, (2) data collection, and (3) data pre-processing to (4) model development, (5) model evaluation, and (6) model deployment. Developed ML models can be deployed to identify new concrete mixtures with desired properties, which are then validated through empirical or computational experiments, with the outcome appended to the collected datasets and iteratively calibrating the models. Relevant terminology and reporting guidelines can be found in Supplementary Notes 2 and 3, respectively.
Data challenge
ML models require data to learn patterns and relationships, and then generalize these trends to a larger population. The quality of these data (i.e., their representativeness, completeness, and correctness) is of primary importance to the performance and validity of the model. In the following, we discuss the challenges raised by data quality in concrete research.
Data sparsity
The collection and curation of extensive datasets are critical to ML; however, data collection is especially costly and time-consuming in the concrete science domain, where multiple samples are required to be cast and tested after a long curing duration (typically 28 days for engineering applications, and up to several years for durability studies). While hundreds of thousands of concrete mixtures and their corresponding properties have been reported in the literature over the past few decades, it is daunting to collect and organize these experimental data in a systematic manner. Different reporting formats (e.g., as text or in figures, tables, and schematics) and experimental parameters (e.g., type and quantity of individual constituents) are used in the literature and not all the experimental results are reported with the same level of completeness. In the open-access concrete tensile strength dataset79 (Table 2), for example, a considerable portion of the 714 concrete mixtures were reported without information related to cement strength class: 34.6% and 38.0% of the mixtures have missing cement compressive and tensile strengths, respectively. These mixtures may be excluded if cement strengths are of special interest as inputs, unless a proper data imputation procedure is used.
As a result, datasets used in ML-based concrete research tend to be small. Figure 2d shows that the distribution of the sample sizes is indeed strongly skewed to the right (i.e., with a long tail toward large samples). The inset shows that over 55% of studies had sample sizes of less than 200, while only about 11% contained more than 1,000 samples (below which a dataset is often considered insufficient80,81). Failure to assemble a sufficiently large dataset raises the risk of overfitting82 (Fig. 5). A small but potentially complex dataset can prevent ML models from producing accurate and generalizable results. Scarcity of observed data would also lead to high-dimensionality and data-bias problems, as explained in the following sections.
a An illustrative low-dimensional example in concrete science, consisting of 40 real concrete mixtures (from the publicly accessible concrete compressive strength dataset24,112 in Table 2) with one input (water/cement ratio) and one output (compressive strength, MPa). The dataset was divided into a training set and a validation set by an 80/20 split. Three polynomial models with polynomial degrees p = 1, 3, or 10 were fitted to the training data. The polynomial of degree three was identified as the optimal model based on the good prediction performance on the validation set, while those of degrees one and ten were showcased as underfitting (too simple to capture patterns in the data) and overfitting (too complex such that noise was learned), respectively. b Error (root mean square error, MPa) in the prediction of the training and validation sets as a function of model complexity (i.e., polynomial degree herein). Simple statistical models may underfit the data, whereas complex models tend to overfit without extreme caution. The optimal model complexity yields the best generalization performance. As machine learning models are generally much more complex than traditional statistical models, proper implementation and validation are required, especially when dealing with small datasets.
High dimensionality
The generalizability of a given ML model depends not only on the sample size but also on the number of input variables (i.e., dimensionality). Many algorithms work adequately in low dimensions but become intractable as the dimensionality increases (the so-called ‘curse of dimensionality’)83. The number of samples required for model training grows exponentially with the input space to achieve sufficient confidence or certainty84. If the sample size is relatively small (as is generally the case in practical scenarios), the input variables of a dataset can lose their discriminating ability, as all samples in the dataset seem very distinct from each other with high dimensionality85.
This problem has become of increasing importance, especially in concrete research, where fresh and hardened properties of concrete are dependent on a wide range of variables including individual constituent characteristics (e.g., the type, quantity, physical and chemical properties of cementitious materials, aggregates, and admixtures) and spatiotemporal environmental conditions (i.e., temperature and humidity). As a general rule, the ratio of the number of samples to the number of input variables should be of at least one order of magnitude86. Note that this is based on historical statistical models but may be insufficient for some of the most complex ML models. In that case, feature selection and feature engineering can be adopted to reduce the input dimensionality and thus increase the ratio between the number of samples and the number of variables87,88. A thorough review of this subject can be found in refs. 87,89.
Data bias
The effectiveness of ML techniques is critically dependent on whether the collected data are representative of the entire data population. Unfortunately, the representativeness of the sampled data is rarely sufficient in concrete science due to limited sample size, causing data bias that may exist in many types and forms90,91,92. Four common types of data bias in concrete science are discussed below:
-
(1)
Representation bias occurs when the sample underrepresents the population90. Data in many ML studies were collected from published literature, where mean values and standard deviations for the output (e.g., compressive strength) instead of all the measured values were typically reported. Researchers tend to assemble the dataset by collecting these reported mean values, which would produce fewer data for training and add another layer of inaccuracy by not taking the additional uncertainty into account.
-
(2)
Measurement bias happens from the way the variables are selected, collected, and computed90. One possible issue in concrete studies is that the variables of the models are often oversimplified. For example, fly ash can be classified into two types, namely, Class C and Class F, both of which have distinct chemical compositions, reactivities, and thus different suggested dosages93. However, the essential information regarding the type or property of fly ash is often neglected during data collection, and thus the material is treated identically regardless of its classifications, making it less feasible to fully capture the contribution of fly ash in a ML model.
-
(3)
Temporal bias arises when populations or behaviors differ over time92. A telling example can be found in concrete mixture design, where old types of concrete have higher water/cement ratios and lower strengths, whereas modern concretes tend to contain more admixtures and exhibit higher strengths94,95. Additionally, the chemical and physical properties of cementitious materials have been changing over time due to various factors like production technology and raw material supply, which leads to a higher alkali content in modern cements96. As a result, data collected from old literature may fail to adequately represent current compositions.
-
(4)
Deployment bias arises from the mismatch between the problem a model is designed to solve and the way it is actually used in practice90. Extensive studies have demonstrated the ability of ML models to predict properties of laboratory concrete. Despite their vast potential, various challenges hinder their systematic adoption in the construction industry. One key question is whether a model built for laboratory concrete can be used for field concrete, given variable environmental conditions and other operational uncertainties introduced during concrete construction and curing97 (cf. Section ‘Linking laboratory and field data’). As the population of laboratory concrete can be quite different from that of field concrete, there is no guarantee that the estimated performance of the developed model on laboratory concrete will represent actual field performance.
Validation challenge
The ultimate goal of ML is to obtain a model that is generalizable to practical situations. Ensuring this generalizability requires adequate validation methods; however, validation methods may not be systematically used in the concrete literature, especially when the sample size is limited. In the following, we provide a concise discussion of this frequent problem.
Hold-out method
The simplest validation technique is the two-way hold-out method, where available data are randomly partitioned into two subsets, namely, the training and testing sets (Fig. 6a). In this process, some fixed hyper-parameter values have to be defined arbitrarily based on intuition, prior knowledge, or default setting. A model is then built on the training set and evaluated on the testing set. Since the testing set is designed to represent new, unseen data to the model, it should only be used once to avoid data leakage (unintentionally revealing information from the testing set98) and overly optimistic estimates of the generalization performance. This approach is intended for model evaluation, rather than model selection, as no special hyper-parameter tuning should be performed. However, researchers might be tempted to mistakenly reuse the testing set multiple times and modify some aspects of their approaches (e.g., pre-determined model hyper-parameters) in light of the final results, thereby introducing data leakage and overfitting43 (Fig. 5).
a Two-way hold-out method (a single split of the whole dataset into training and testing sets). b Three-way hold-out method (a single split of the whole dataset into training, validation, and testing sets). c k-fold outer cross-validation (CV; on the whole dataset). d k-fold inner CV (a single split of the whole dataset into training and testing sets, followed by CV on the training set). e n × k nested CV with n-fold outer CV loops each containing k-fold inner CV. For illustration purposes, an 80/20 split was showcased in methods (a) and (d) for the training/testing split; a 60/20/20 split was showcased in method (b) for the training/validation/testing split; and both n and k were set as 5 for CV approaches. Note that methods (a) and (c) are merely used for model evaluation, while the remaining methods can be adopted for both model selection and model evaluation.
To avoid reusing testing data while tuning hyperparameters for model selection, a slight modification can be applied to the initial hold-out method: instead of the two-part split, the dataset is randomly divided into three subsets (so-called three-way hold-out method), i.e., training, validation, and testing sets (Fig. 6b). In the three-way hold-out method, multiple models with various combinations of hyper-parameters are trained on the training set; the model with the best combination of hyper-parameters that gives the highest accuracy on the validation set is then chosen as the final model and evaluated on the testing set. This method allows one to keep the testing set independent for model evaluation and thus has been one of the widely used validation techniques in the concrete literature. Nevertheless, both the two-way and three-way hold-out methods only apply a single split to the data, which can be less robust when the size of the dataset becomes smaller. In fact, using these procedures, an issue may arise when concrete datasets are not sufficiently large to be split into two or three statistically representative subsets (cf. Section ‘Data sparsity’), thereby introducing biases and unreliable performance estimates.
Cross-validation
Cross-validation (CV) provides a solution to evaluating generalization performance in the case of scarce sample size99. The most commonly used CV method is the k-fold CV (cf. Supplementary Note 2 for the definition), which includes k splits rather than a single split to achieve multiple iterations for model validation and thus more robust estimations. Similar to the hold-out methods, the k-fold CV can be used for model evaluation or model selection. For model evaluation, a k-fold CV is performed on the whole dataset (Fig. 6c), which we refer to as outer CV to clearly distinguish it from the inner and nested CV methods described below. Compared with the two-way hold-out method, the outer CV results in k different models fitted to distinct yet partially overlapping training sets and evaluated on non-overlapping testing sets, providing more statistically consistent measures when dealing with small datasets.
In practice, k-fold CV is more commonly used for model selection. In this case, the dataset is split into a full training set (including a validation set) and an independent testing set, followed by CV on the full training set (here referred to as inner CV; see Fig. 6d). The inner CV is preferred over the three-way hold-out method since it offers more robustness (i.e., k iterations) for hyper-parameter tuning when the dataset is relatively small89 (which is often the case in concrete science). However, the three-way hold-out method was often used in the early concrete literature as it is computationally cheaper without any iteration, which questions the validity and reliability of the early ML studies with small datasets.
Thanks to recent advances in computational performance, CV has been rapidly adopted in ML studies within the concrete science domain54,100. However, two potential limitations arise in this context. Firstly, the term CV is used loosely in the literature. Hyper-parameter tuning and model selection are typically reported in research papers, but researchers do not always clearly specify whether CV is performed on the training set (Fig. 6d) or mistakenly on the whole dataset (Fig. 6c). The latter case can markedly inflate the accuracy, especially for small and high dimensional datasets, and lead to erroneous overoptimism as well as misleading conclusions. We thus emphasize the importance of providing a detailed description of the CV methods in publications and the need to develop a standard procedure for reporting ML analyses (cf. Section ‘Sharing data and tools’ and Supplementary Note 3). Second, CV for model selection (i.e., inner CV; Fig. 6d) involves a single training/testing split prior to performing CV on the full training set. The accuracy on the testing set can be quite sensitive to how exactly this single split is applied, especially for a small dataset, where the testing set is unlikely to share the same distribution with the training set. A testing set only containing ‘easy’ samples will result in overoptimistic performance estimates. Conversely, a testing set only containing ‘hard’ samples would lead to pessimistically biased estimates. According to the simulations in Vabalas et al.99, the bias introduced by k-fold CV is still substantial even with a sample size of 1000. This questions the suitability of the validation methods currently used in the concrete literature (~89% datasets have a sample size less than 1000, as shown in Fig. 2d).
An alternative to k-fold CV is n × k nested CV, which can produce robust and unbiased performance estimates regardless of the size of datasets99. The n × k nested CV is a nesting of inner and outer CV loops. It consists of n different k-fold inner CV for model selection and n distinct testing sets for model evaluation (Fig. 6e). The average performance on the n testing sets gives almost completely unbiased estimates of the true generalization performance101,102, although the computational cost would be higher.
There are many validation approaches for model selection and model evaluation. As discussed, some of them may be ill-suited for concrete research, given the limited sizes of the typical datasets compiled and used in existing studies. We stress that proper validation methods should be selected depending on research tasks and available data to offer valuable insights into concrete science.
Interpretability challenge
Conventional approaches for the analysis and design of experiments in concrete science are primarily developed from mathematical analysis, mechanistic modeling, and statistical inference5,103, where the formulas or models are explicit and thus often readily understood and accepted by the community. However, the recent shift towards correlation-based ML models due to their promising performance has raised challenges for the practitioner to interpret the models. We herein discuss two critical aspects associated with ML interpretability in concrete science, namely, diagnostics and causality.
Diagnostics
Once a ML model is developed, one simple yet useful way to interpret it is to conduct sensitivity analyses. Sensitivity of a model describes the influence of each input variable on the uncertainty in the prediction of the model104,105,106. Common techniques for such analysis are permutation-based diagnostic methods, including permutation feature importance, partial dependence plots, and individual conditional expectation plots107. These techniques provide global and statistically coherent insights into the model while avoiding tuning parameters and re-training it108. However, these methods can be misleading when correlations exist between input variables107,109.
For instance, permutation feature importance consists of randomly shuffling the values of an input variable while keeping other input variables unchanged; the decrease in the prediction accuracy of the model after permuting is then quantified and reported as a measure of importance110,111. This permutation feature importance measure works well if input variables are independent, but it can produce unrealistic data points if input variables are fully or partially dependent109. Figure 7 shows two examples in concrete strength prediction, where permutation generates unrealistic concrete mixtures. The use of superplasticizers (high-range water-reducing admixtures) is known to reduce the water content by 20 to 30% and increase the flowability2. In the concrete compressive strength dataset24,112 (Table 2) using the absolute volume method, the superplasticizer dosage varies from 0 to 32 kg/m3 and the water content from 122 to 247 kg/m3. The negative relationship between superplasticizer and water seems reasonable and the Pearson correlation coefficient (the most common, straightforward measure of correlation) was calculated as –0.66 (black circles in Fig. 7a). However, some concrete mixtures generated after permutation (red pluses in Fig. 7a) can be meaningless and misleading. Those mixtures located in the upper right corner (high water content and high superplasticizer dosage) may lead to segregation or excessive bleeding; those in the lower-left corner (low water content with no superplasticizer) tend to be sticky. In other words, both fail to meet the workability requirement.
Data were obtained from the concrete compressive strength dataset available in the UC Irvine Machine Learning Repository24,112 (Table 2). a, b The variable for water (a) or cement (b) was randomly shuffled while keeping other variables constant. The black circles refer to the observed mixtures, the red pluses to the generated mixtures after shuffling, and their transparency represents the frequency. SCMs, supplementary cementitious materials.
The same issue can occur among the input variables for cementitious materials, namely, cement and supplementary cementitious materials (SCMs, including fly ash and slag). Since cement is often partially replaced by SCMs for environmental, economic, and durability considerations, the content of cement is expected to decrease with the application of SCMs, as shown in Fig. 7b, where the original mixtures (black circles) have a Pearson correlation coefficient between cement and SCMs as –0.55. Nevertheless, the permutation approach can produce unrealistic concrete mixtures, e.g., high cement and SCM contents (red pluses in the upper right corner) or low cement content with no SCMs (red pluses in the lower-left corner), making the water/cementitious materials ratio too low or too high, respectively, and thus producing unrealistic mixtures in terms of practical applications.
These unrealistic concrete mixtures force the model to probe regions where there is little to no data during training and in reality. This can inflate model uncertainty and greatly bias the estimated feature importance. There is, therefore, a critical need to eliminate these potential outliers before applying permutation-based diagnostic tools. Correlation between input variables needs to be checked during data pre-processing (a detailed discussion of correlation measures is provided in ref. 109) and some of the highly correlated ones should be removed. When the model has to contain correlated variables, which is often the case in practice, additional information about the distribution and correlation among the data should be reported. Alternative methods include conditional permutation or simulation (e.g., accumulated local effects plot), re-evaluation after dropping a variable (yet requiring re-training), and their combination107. Recent advances in interpretable ML have also provided some promising approaches such as SHAP (SHapley Additive exPlanations)108,113,114. As this problem remains an open question in the ML community, robust solutions must still be developed and comprehensive comparisons between existing strategies are still needed. In particular, specialized methods are required in the field of concrete research.
Causality
As causes play a crucial role in the accuracy of a given model, researchers are usually tempted to interpret the result of ML models (which typically show superior accuracy) from a causal perspective109,115. However, it is important to note that ML models are not designed to identify causal relationships but rather association relationships116. Identification of associations between variables is just the first step towards causal inference, followed by prediction of the effect of interventions and evaluation of counterfactual queries117. While ML models are not guaranteed to reflect causality that is of interest in many scientific domains, these models can still be an essential starting point to search for relevant patterns of association and propose novel scientific hypotheses that can be further investigated. However, researchers should refrain from extrapolating conclusions from ML models, especially when working with small and potentially unrepresentative data118.
In the context of concrete research, inappropriate conclusions of causation are exacerbated by the fact that the information provided by the input variables is often insufficient. For example, the knowledge of the amount of individual constituents used for the prediction of concrete properties may not be adequate to describe the underlying physical and chemical interactions between each constituent (cf. Section ‘Data bias’). Hence, a model built from those input variables will fail to offer causal insights, even though some variables may help to reconstruct the unobserved influence on the output. To improve consistency, accuracy, and interpretability of ML studies in concrete science, we provide a list of potentially missing yet crucial variables in currently available datasets and call for a detailed evaluation of their effects on ML models:
-
(1)
Characteristics of aggregate. Porosity, density, shape, surface texture, mineralogical composition, and gradation of aggregates are well-known to affect the behavior of fresh and hardened concrete2.
-
(2)
Properties of cementitious materials. The reactivity of cementitious materials including cement and SCMs relies not only on their quantity but their physical and chemical properties, e.g., shape, fineness, density, chemical composition (especially the contents of CaO, SiO2, and Al2O3), loss on ignition, among other properties. These properties can vary significantly from region to region.
-
(3)
Properties of chemical admixtures. Water-reducing admixtures, for example, contain different types of plasticizing surfactants with varying efficiency, including lignosulfonate, melamine sulfonate, naphthalene sulfonate, and polycarboxylate119. Their chemical composition and solid content depending on manufacturers have a direct impact on their dosage and the effects on the fresh and hardened performance of concrete mixtures.
-
(4)
Curing regimes. Performance of concrete materials can be influenced by various laboratory and field curing regimes. Detailed information regarding temperature and relative humidity as well as any applicable standards is essential and should be provided.
Best practices
In the preceding sections, we presented a critical overview of the applications and challenges of ML in the domain of concrete science. Despite a substantial number of publications on ML applications to cement and concrete research over the past decade, current challenges are hindering the adoption of ML in the construction industry. Here, we provide our perspectives on best practices in ML to foster the development of a robust, data-informed concrete science ecosystem.
Sharing data and tools
ML algorithms enable one to examine extensive, multidimensional datasets and automatically capture complex relationships from these data. However, most ML models in the realm of concrete science were trained and tested on insufficient data due to long experimental duration and inconsistent data formats (cf. Section ‘Data sparsity’). Very few large datasets are publicly accessible to the community to date (Table 2), and as part of the current move towards open science, research efforts to fill this gap should be intensified.
A possible approach for addressing data sparsity is to develop new data repositories and broaden the accessibility to existing data. For example, the UC Irvine Machine Learning Repository112 serves as a platform maintaining a collection of datasets from different scientific domains; the Materials Project120 has built a large and rich materials database to accelerate advanced materials discovery and deployment. Another example is the FHWA InfoMaterials Web portal121, which is being developed and maintained to offer characterization data of pavement concrete materials. Researchers should be encouraged to make their experimental data accessible to the public, either as supplementary materials to published research articles, or as data repositories on data-sharing platforms. Even negative or null results constitute valuable information, especially for training ML models. Although there may be other considerations such as data protection and ownership, we believe these challenges will be overcome as a cultural shift is underway toward improving the accessibility and traceability of research data.
Inconsistency or incompleteness of data across literature studies should also be addressed. Depending on the testing standards adopted or the laboratory conventions, specimen preparation, testing procedure, and measuring timing can be different96. Another problem commonly encountered in the literature pertains to the description of materials and methods122. For example, the categorizations for types of cement and SCMs may differ from country to country, and simple descriptions like Type I cement and Class C fly ash may cause ambiguities. Their physical and chemical properties are often unknown during data collection, although this information could be useful for concrete property prediction (cf. Section ‘Causality’). There is, therefore, a need for the concrete community to develop unambiguous standards for reporting and sharing experimental data with consistent categorization across research studies.
In addition to data dissemination, the sharing of computational methodologies (including proposed models, adopted procedures, and source codes) would lower the barriers to data and model verification. Due to the emerging role of increasingly elaborate ML models, the lack of reproducibility and generalizability of ML studies has become a critical hurdle. External validation of those studies by employing the same tools on the same datasets (for reproducibility) and real-world data (for generalizability) is needed, although it has not been traditionally incentivized in concrete research. Besides, the proposed computational methodologies can serve as baseline for other researchers to further extend the models and develop new ones. Addressing this growing problem requires comprehensive descriptions of the methodological steps, including problem definition, data collection, data pre-processing, model development, and model evaluation. Supplementary Note 3 provides some recommendations for reporting ML analyses in future concrete research.
Linking laboratory and field data
Extensive efforts have been made to develop ML models and predict concrete properties using laboratory concrete datasets (93.8% of ML studies using experimental data were based on laboratory tests, as mentioned in Section ‘Applications’). While these models show adequate prediction performance50, there are hesitations in deploying them to construction projects, because their validity for field-placed concrete has not been assessed.
Laboratory conditions are usually well-controlled but fail to reflect the variability and complexity in actual practice. Variations in materials (e.g., aggregate, cementitious materials, and chemical admixtures) and processes (e.g., mixing, transportation, placement, and curing) can introduce additional noise to field concrete data. For instance, raw material properties (cf. Section ‘Causality’) and environmental conditions (temperature and humidity) are often varying at construction sites depending on material availability and local weather, respectively; there can be tremendous variation in operations between skilled and unskilled construction workers; and additional water is sometimes mistakenly added for various reasons in field practice (e.g., leftover water from washing ready-mix trucks that is unaccounted for in the mixture design). A model built for laboratory concrete is thus likely to underperform when employed for concrete in the field due to deployment bias (cf. Section ‘Data bias’).
It is expected that a model trained on field data can achieve satisfying predictions for field concrete properties54,97, since the sampled data used for model development is an estimation of the population. Unlike laboratory data, however, field data are less straightforward to collect and field concrete mixtures tend to be more common and widely acceptable in the industry. Hence, the development of approaches for accurate prediction of properties of field concrete (i.e., knowledge transformation from laboratory to field, especially for new mixtures proposed in laboratories) is an important research priority.
One possible solution to this challenge is the hybridization of laboratory and field data for training ML models. DeRousseau et al.97 investigated the effect of replacement percentages of field data in the training dataset (i.e., 0%, 10%, 20%, 30%, 40%, and 50%) on field compressive strength prediction using a random forest laboratory model, as shown in Fig. 8, and found that a replacement percentage of 10% significantly improves the prediction performance and reduces the root mean square error by 43% compared with that of 0% (i.e., only laboratory data were used). This result revealed the potential for improving the performance prediction of field-placed concrete even with limited field data. Future research in this area should explore different ML algorithms with the hybridization of laboratory and field data and incorporate other new hybridization strategies (cf. Section ‘Conclusions and outlook’).
Insets show the comparisons between measured and predicted strength values at the replacement percentages of 0%, 10%, 30%, and 50% by field data (transparency of the data points represents their frequency). RMSE, root mean square error. Figure adapted with permission from ref. 97, Elsevier.
Starting with simple models
One advantage of ML models over traditional statistical models lies in their ability to account for complex relationships. However, a common mistake is to implement opaque and complex ML models (e.g., neural networks) when interpretable and simple models (e.g., linear regression models and decision trees) are sufficient, i.e., when the prediction performance of traditional statistical models is only negligibly worse—or even the same or better—than that of ML models. In this case, simpler models with fewer coefficients or assumptions are preferable to complex ones (Occam’s razor)123.
There is also an argument between the prediction accuracy and the data accuracy (i.e., representativeness to the ground-true population): when the collected data have biases and fail to represent the population, it makes little to no sense to increase the model complexity to simply improve the prediction accuracy. This is because the accuracy of a model is measured by the observed data and does not account for the ability to explain the underlying physical processes (which produce the ground-true population)115. As elaborated in Section ‘Data challenge’, data quality in concrete science for ML studies is typically insufficient. In particular, cumulative random errors introduced by experiments (such as variation of raw materials, operators, and apparatuses between laboratories) cannot be ignored. As a result, the prediction error by simple models may not be significant in contrast to the random errors; i.e., the prediction capability from simple models could be comparable or even more reliable to the reproducibility of experiments in different laboratories124. In this case, there may be no need to develop a more complex ML model.
Once the research question is well-defined, a good practice is to start with simple, interpretable models and gradually increase the complexity in a stepwise manner, where the prediction performance is evaluated with caution. Complex models with less interpretability may only be utilized when additional accuracy gain is significant and necessary.
Knowing when to trust a model
Concrete research generally adopts the 2-sigma (p value ≤ 0.05) rule to validate experimental results125,126,127. However, due to a lack of reproducibility, the 2-sigma statistical criterion may not be as reliable as typically assumed128,129,130. Past evidence thus raises challenges regarding the use of arbitrary thresholds to evaluate the performance of a predictive model. As ML models have become ubiquitous in the concrete science domain, a consensus on when to trust the models needs to be reached. Because of major safety concerns, inconsiderate applications of ML models in the construction industry can lead to catastrophic consequences.
Reported performance measures (e.g., accuracy) of ML models should be interpreted with caution. The results of the metrics then call into question whether or not a model with an accuracy level of 90% (and possibly higher complexity) would be more trustworthy compared to that with 70%. First, there can be some inappropriate implementations—during data collection, data pre-processing, model development and evaluation—that lead to overoptimistic performance estimates (cf. Sections ‘Data challenge’ and ‘Validation challenge’). To make the modeling process transparent, detailed descriptions are required when reporting the models and their performance (Supplementary Note 3). Second, the reported accuracy of a model for the testing data may not precisely reflect its performance on real-world data, when there is a substantial mismatch between testing and practical cases. For instance, the performance of a model built for laboratory concrete is not necessarily a good indicator of its performance on field-placed concrete (as discussed in Section ‘Linking laboratory and field data’). This challenge highlights the need for researchers to report the potential sources of uncertainties in evaluating the performance of the model (e.g., the intended use of the proposed model, characteristics of the data served to train and evaluate the model, and detailed metrics that reflect the potential practical impacts of the model), and for users to assess the model in practical scenarios before deploying it131.
Additionally, as ML models become more complex and thus potentially more opaque, the inability to understand how the algorithms work is a central concern, especially when a discrepancy occurs between evaluation and deployment environments with potentially catastrophic consequences for civil infrastructure. Hence, trust in ML models is strongly related to their interpretability, which has thus become a focus of active research in the ML community116,132. Moving forward, ML studies in the concrete science domain should be extended to systematically assess the interpretability of the models, thereby accelerating their practical adoption in the industry.
Conclusions and outlook
The field of data-driven concrete science has recently experienced a surge of interest, and ML models are being applied for accurate property prediction, advanced materials characterization and analysis, and accelerated simulations of increasingly complex cementitious systems. Despite the widespread adoption of ML in concrete studies, their validity and reliability are rarely questioned and examined. In this work, we have highlighted the importance of data preparation, model validation, and model interpretation and discussed critical aspects of their challenges raised by implementing and interpreting ML models without necessary caution. In doing so, we have underscored the critical need for sharing data and methodologies, linking laboratory and field data, starting with simple models, and knowing when to trust a model.
As applications of ML to concrete science are still in their infancy, we propose the following directions of development:
-
(1)
Physics-guided ML. ML models purely built on data are often agnostic of the underlying physical processes (e.g., the process–structure–property–performance relationships), which leads to inability to produce physically consistent results with limited available training data133,134. This further prevents the models from reliable generalization and extrapolation. Hence, the integration of prior physical knowledge into ML-based models has recently been explored135,136,137,138. Specifically, physical laws describing micromechanical responses139, degradation mechanisms104,140, and chemical reactivity141 have been utilized for data pre-processing (e.g., feature selection, feature engineering, and data augmentation) during the development of ML models in concrete research. Other promising yet under-developed physics-ML integration approaches include, but are not limited to, adding physics-based loss function terms, pre-training ML models on data produced by physcis-based models, encoding physical principles into ML architecture design136. Although this research area is still nascent in concrete science, it is expected that transforming data-driven ML models into physics-aware surrogate models would increase their interpretability, make them more robust and generalizable to field-relevant scenarios, and reduce the sample size required for their training and thus their overall computation cost.
-
(2)
Transfer learning. Another powerful approach that can address data sparsity is transfer learning, whereby the knowledge gained from an initial training task is used in a different but related problem142. In the context of concrete materials, there remains a substantial difference in data quantity between different target properties (Table 2), while most examples of ML in concrete science use separate models for each property, resulting in potentially insufficient data for training and an overwhelming number of parameters with few of them shared across models. However, multiple properties (e.g., compressive, flexural, and tensile strengths) of the same mixture are often closely related. Likewise, the nature of the relationship between inputs and output may be interrelated in similar concrete types (e.g., concretes reinforced with different types of fibers32). In this regard, the knowledge shared in interdependent properties of the same material or in the same property of similar concrete types can be transferred to accelerate the training process and improve the accuracy performance of ML models, even with relatively small amounts of available data143,144.
-
(3)
Natural language processing (NLP). Empirical experiments and computational simulations toward concrete mixture design optimization have produced an immense amount of data in the publication and patent literature; however, it is challenging to manually collect and organize these data due to their inconsistent data formats (e.g., text, figures, tables, and schematics; cf. Section ‘Data sparsity’). This offers the opportunity for NLP to extract materials data from millions of documents in an automated and more efficient manner, compared with the manual collection, and thus establish large datasets that can leverage the power of ML techniques134. Another exciting outcome from NLP is to extract the process–structure–property–performance relationships by mining text corpora, which has enabled one to discover new materials145 and identify materials synthesis procedures146, although there have been limited applications of this approach in concrete science.
To conclude, ML has already changed the field of concrete science and facilitated the discovery, design, and deployment of new concrete materials. Although the arguments presented in this paper are not exhaustive, we hope to have initiated a constructive discussion on current practices and encouraged cautious approaches in applying ML techniques to concrete research. With continual improvements in data availability and data-driven models, ML is poised to become an accurate, transparent, and interpretable complement to existing experimental and computational techniques that together will propel concrete science into the 21st century and beyond.
Data availability
Source data for Fig. 2 are available in Supplementary Dataset. Source data for Figs. 5 and 7 are available in the UC Irvine Machine Learning Repository, https://archive.ics.uci.edu/ml/datasets/concrete+compressive+strength. All other data supporting the findings of this work are available from the corresponding author upon reasonable request.
References
Monteiro, P. J., Miller, S. A. & Horvath, A. Towards sustainable concrete. Nat. Mater. 16, 698–699 (2017).
Mehta, P. K. & Monteiro, P. J. M. Concrete: microstructure, properties, and materials (McGraw-Hill Education, 2014).
Van Damme, H. Concrete material science: Past, present, and future innovations. Cem. Concr. Res. 112, 5–24 (2018).
Gagg, C. R. Cement and concrete as an engineering material: An historic appraisal and case study analysis. Eng. Fail. Anal. 40, 114–140 (2014).
DeRousseau, M. A., Kasprzyk, J. R. & Srubar, W. V. Computational design optimization of concrete mixtures: A review. Cem. Concr. Res. 109, 42–53 (2018).
Soudki, K. A., El-Salakawy, E. F. & Elkum, N. B. Full Factorial Optimization of Concrete Mix Design for Hot Climates. J. Mater. Civ. Eng. 13, 427–433 (2001).
Garboczi, E. J., Bentz, D. P. & Frohnsdorff, G. J. The past, present, and future of the computational materials science of concrete. In J. Francis Young Symposium (Materials Science of Concrete Workshop, 2000).
Bentz, D. P. Three-dimensional computer simulation of portland cement hydration and microstructure development. J. Am. Ceram. Soc. 80, 3–21 (1997).
Bentz, D. P. Modelling cement microstructure: Pixels, particles, and property prediction. Mater. Struct. 32, 187–195 (1999).
van Breugel, K. Numerical simulation of hydration and microstructural development in hardening cement-based materials (I) theory. Cem. Concr. Res. 25, 319–331 (1995).
Navi, P. & Pignat, C. Simulation of cement hydration and the connectivity of the capillary pore space. Adv. Cem. Based Mater. 4, 58–67 (1996).
Bishnoi, S. & Scrivener, K. L. μic: A new platform for modelling the hydration of cements. Cem. Concr. Res. 39, 266–274 (2009).
Lothenbach, B. & Winnefeld, F. Thermodynamic modelling of the hydration of Portland cement. Cem. Concr. Res. 36, 209–226 (2006).
Damidot, D., Lothenbach, B., Herfort, D. & Glasser, F. P. Thermodynamics and cement science. Cem. Concr. Res. 41, 679–695 (2011).
Lothenbach, B. & Zajac, M. Application of thermodynamic modelling to hydrated cements. Cem. Concr. Res. 123, 105779 (2019).
Cho, B. H., Chung, W. & Nam, B. H. Molecular dynamics simulation of calcium-silicate-hydrate for nano-engineered cement composites-a review. Nanomaterials 10, 1–25 (2020).
Thomas, J. J. et al. Modeling and simulation of cement hydration kinetics and microstructure development. Cem. Concr. Res. 41, 1257–1278 (2011).
Dolado, J. S. & Van Breugel, K. Recent advances in modeling for cementitious materials. Cem. Concr. Res. 41, 711–726 (2011).
Scrivener, K. L. & Kirkpatrick, R. J. Innovation in use and research on cementitious material. Cem. Concr. Res. 38, 128–136 (2008).
Park, K. B., Noguchi, T. & Plawsky, J. Modeling of hydration reactions using neural networks to predict the average properties of cement paste. Cem. Concr. Res. 35, 1676–1684 (2005).
Ford, E., Kailas, S., Maneparambil, K. & Neithalath, N. Machine learning approaches to predict the micromechanical properties of cementitious hydration phases from microstructural chemical maps. Constr. Build. Mater. 265, 120647 (2020).
Akkurt, S., Tayfur, G. & Can, S. Fuzzy logic model for the prediction of cement compressive strength. Cem. Concr. Res. 34, 1429–1433 (2004).
Koniorczyk, M. & Wojciechowski, M. Influence of salt on desorption isotherm and hygral state of cement mortar - Modelling using neural networks. Constr. Build. Mater. 23, 2988–2996 (2009).
Yeh, I. C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 28, 1797–1808 (1998).
Han, Q., Gui, C., Xu, J. & Lacidogna, G. A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Constr. Build. Mater. 226, 734–742 (2019).
Kaloop, M. R., Kumar, D., Samui, P., Hu, J. W. & Kim, D. Compressive strength prediction of high-performance concrete using gradient tree boosting machine. Constr. Build. Mater. 264, 120198 (2020).
El-Chabib, H. & Nehdi, M. Effect of mixture design parameters on segregation of self-consolidating concrete. ACI Mater. J. 103, 374–383 (2006).
Hendi, A. et al. Mix design of the green self-consolidating concrete: Incorporating the waste glass powder. Constr. Build. Mater. 199, 369–384 (2019).
Ramkumar, K. B., Kannan Rajkumar, P. R., Noor Ahmmad, S. & Jegan, M. A Review on Performance of Self-Compacting Concrete - Use of Mineral Admixtures and Steel Fibres with Artificial Neural Network Application. Constr. Build. Mater. 261, 120215 (2020).
Mu, B., Li, Z. & Peng, J. Short fiber-reinforced cementitious extruded plates with high percentage of slag and different fibers. Cem. Concr. Res. 30, 1277–1282 (2000).
Tong, Z., Gao, J., Wang, Z., Wei, Y. & Dou, H. A new method for CF morphology distribution evaluation and CFRC property prediction using cascade deep learning. Constr. Build. Mater. 222, 829–838 (2019).
Tong, Z., Huo, J. & Wang, Z. High-throughput design of fiber reinforced cement-based composites using deep learning. Cem. Concr. Compos. 113, 103716 (2020).
Zhang, J., Huang, Y., Ma, G., Sun, J. & Nener, B. A metaheuristic-optimized multi-output model for predicting multiple properties of pervious concrete. Constr. Build. Mater. 249, 118803 (2020).
Xu, J. et al. Parametric sensitivity analysis and modelling of mechanical properties of normal- and high-strength recycled aggregate concrete using grey theory, multiple nonlinear regression and artificial neural networks. Constr. Build. Mater. 211, 479–491 (2019).
Han, T., Siddique, A., Khayat, K., Huang, J. & Kumar, A. An ensemble machine learning approach for prediction and optimization of modulus of elasticity of recycled aggregate concrete. Constr. Build. Mater. 244, 118271 (2020).
Nunez, I. & Nehdi, M. L. Machine learning prediction of carbonation depth in recycled aggregate concrete incorporating SCMs. Constr. Build. Mater. 287, 123027 (2021).
Alshihri, M. M., Azmy, A. M. & El-Bisy, M. S. Neural networks for predicting compressive strength of structural light weight concrete. Constr. Build. Mater. 23, 2214–2219 (2009).
Migallón, V., Navarro-González, F., Penadés, J. & Villacampa, Y. Parallel approach of a Galerkin-based methodology for predicting the compressive strength of the lightweight aggregate concrete. Constr. Build. Mater. 219, 56–68 (2019).
Gunasekera, C. et al. Design of Alkali-Activated Slag-Fly Ash Concrete Mixtures Using Machine Learning. ACI Mater. J. 117, 263–278 (2020).
Ke, X. & Duan, Y. Coupling machine learning with thermodynamic modelling to develop a composition-property model for alkali-activated materials. Compos. Part B: Eng. 216, 108801 (2021).
Kazemian, A., Yuan, X., Davtalab, O. & Khoshnevis, B. Computer vision for real-time extrusion quality monitoring and control in robotic construction. Autom. Constr. 101, 92–98 (2019).
Davtalab, O., Kazemian, A., Yuan, X. & Khoshnevis, B. Automated inspection in robotic additive manufacturing using deep learning for layer deformation detection. J. Intell. Manufact. 33, 771–784 (2020).
Morgan, D. & Jacobs, R. Opportunities and Challenges for Machine Learning in Materials Science. Annu. Rev. Mater. Res. 50, 71–103 (2020).
Pratt, D. & Sansalone, M. Impact-echo signal interpretation using artificial intelligence. ACI Mater. J. 89, 178–187 (1992).
Mo, Y. L. & Lin, S. S. Investigation of framed shearwall behaviour with neural networks. Mag. Concr. Res. 46, 289–299 (1994).
Martinez, P., Al-Hussein, M. & Ahmad, R. A scientometric analysis and critical review of computer vision applications for construction. Autom Constr. 107, 102947 (2019).
Li, Z. & Radlińska, A. Artificial intelligence in concrete materials: A scientometric view. In Naser, M. Z. (ed.) Leveraging Artificial Intelligence in Engineering, Management, and Safety of Infrastructure (CRC Press, 2022).
Khallaf, R. & Khallaf, M. Classification and analysis of deep learning applications in construction: A systematic literature review. Autom. Constr. 129, 103760 (2021).
Rafiei, M. H., Khushefati, W. H., Demirboga, R. & Adeli, H. Neural network, machine learning, and evolutionary approaches for concrete material characterization. ACI Mater. J. 113, 781–789 (2016).
Ben Chaabene, W., Flah, M. & Nehdi, M. L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 260, 119889 (2020).
Nunez, I., Marani, A., Flah, M. & Nehdi, M. L. Estimating compressive strength of modern concrete mixtures using computational intelligence: A systematic review. Constr. Build. Mater. 310, 125279 (2021).
Alpaydin, E. Introduction to machine learning (MIT Press, 2020).
Rafiei, M. H., Khushefati, W. H., Demirboga, R. & Adeli, H. Novel approach for concrete mixture design using neural dynamics model and virtual lab concept. ACI Mater. J. 114, 117–127 (2017).
Young, B. A., Hall, A., Pilon, L., Gupta, P. & Sant, G. Can the compressive strength of concrete be estimated from knowledge of the mixture proportions?: New insights from statistical analysis and machine learning methods. Cem. Concr. Res. 115, 379–388 (2019).
Sbartaï, Z. M., Laurens, S., Elachachi, S. M. & Payan, C. Concrete properties evaluation by statistical fusion of NDT techniques. Constr. Build. Mater. 37, 943–950 (2012).
Amini, K., Jalalpour, M. & Delatte, N. Advancing concrete strength prediction using non-destructive testing: Development and verification of a generalizable model. Constr. Build. Mater. 102, 762–768 (2016).
Chun, P. J., Ujike, I., Mishima, K., Kusumoto, M. & Okazaki, S. Random forest-based evaluation technique for internal damage in reinforced concrete featuring multiple nondestructive testing results. Constr. Build. Mater. 253, 119238 (2020).
Farhidzadeh, A., Mpalaskas, A. C., Matikas, T. E., Farhidzadeh, H. & Aggelis, D. G. Fracture mode identification in cementitious materials using supervised pattern recognition of acoustic emission features. Constr. Build. Mater. 67, 129–138 (2014).
Ma, G. & Du, Q. Structural health evaluation of the prestressed concrete using advanced acoustic emission (AE) parameters. Constr. Build. Mater. 250, 118860 (2020).
Dorafshan, S. & Azari, H. Deep learning models for bridge deck evaluation using impact echo. Constr. Build. Mater. 263, 120109 (2020).
Omar, T., Nehdi, M. L. & Zayed, T. Rational Condition Assessment of RC Bridge Decks Subjected to Corrosion-Induced Delamination. J. Mater. Civ. Eng. 30, 04017259 (2018).
Manca, M., Karrech, A., Dight, P. & Ciancio, D. Image Processing and Machine Learning to investigate fibre distribution on fibre-reinforced shotcrete Round Determinate Panels. Constr. Build. Mater. 190, 870–880 (2018).
Liu, Z., Cao, Y., Wang, Y. & Wang, W. Computer vision-based concrete crack detection using U-net fully convolutional networks. Autom. Constr. 104, 129–139 (2019).
Flah, M., Suleiman, A. R. & Nehdi, M. L. Classification and quantification of cracks in concrete structures using deep learning image-based techniques. Cem. Concr. Compos. 114, 103781 (2020).
González-Jorge, H., Gonzalez-Aguilera, D., Rodriguez-Gonzalvez, P. & Arias, P. Monitoring biological crusts in civil engineering structures using intensity data from terrestrial laser scanners. Constr. Build. Mater. 31, 119–128 (2012).
Park, S. E., Eem, S. H. & Jeon, H. Concrete crack detection and quantification using deep learning and structured light. Constr. Build. Mater. 252, 119096 (2020).
Omar, T., Nehdi, M. L. & Zayed, T. Infrared thermography model for automated detection of delamination in RC bridge decks. Constr. Build. Mater. 168, 313–327 (2018).
Song, Y., Huang, Z., Shen, C., Shi, H. & Lange, D. A. Deep learning-based automated image segmentation for concrete petrographic analysis. Cem. Concr. Res. 135, 106118 (2020).
Tong, Z., Guo, H., Gao, J. & Wang, Z. A novel method for multi-scale carbon fiber distribution characterization in cement-based composites. Constr. Build. Mater. 218, 40–52 (2019).
Lorenzoni, R. et al. Semantic segmentation of the micro-structure of strain-hardening cement-based composites (SHCC) by applying deep learning on micro-computed tomography scans. Cem. Concr. Compos. 108, 103551 (2020).
Lorenzoni, R. et al. Combined mechanical and 3D-microstructural analysis of strain-hardening cement-based composites (SHCC) by in-situ X-ray microtomography. Cem. Concr. Res. 136, 106139 (2020).
Park, K. B., Jee, N. Y., Yoon, I. S. & Lee, H. S. Prediction of temperature distribution in high-strength concrete using hydration model. ACI Mater. J. 105, 180–186 (2008).
Yan, Y., Ren, Q., Xia, N., Shen, L. & Gu, J. Artificial neural network approach to predict the fracture parameters of the size effect model for concrete. Fatigue Fract. Eng. Mater. Struct. 38, 1347–1358 (2015).
Alnaggar, M. & Bhanot, N. A machine learning approach for the identification of the Lattice Discrete Particle Model parameters. Eng. Fract. Mech. 197, 160–175 (2018).
Kobayashi, K. et al. Machine learning potentials for tobermorite minerals. Comput. Mater. Sci. 188, 110173 (2021).
Schmidt, J., Marques, M. R., Botti, S. & Marques, M. A. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 5, 83 (2019).
Wang, A. Y. T. et al. Machine Learning for Materials Scientists: An Introductory Guide toward Best Practices. Chem. Mater. 32, 4954–4965 (2020).
Tao, Q., Xu, P., Li, M. & Lu, W. Machine learning for perovskite materials design and discovery. npj Comput. Mater. 7, 1–18 (2021).
Zhao, S. et al. Dataset of tensile strength development of concrete with manufactured sand. Data Brief. 11, 469–472 (2017).
Ng, A. Machine learning yearning: Technical strategy for AI engineers in the era of deep learning (GitHub, 2018). http://www.mlyearning.org.
Teschendorff, A. E. Avoiding common pitfalls in machine learning omic data science. Nat. Mater. 18, 422–427 (2019).
Kassraian-Fard, P., Matthis, C., Balsters, J. H., Maathuis, M. H. & Wenderoth, N. Promises, pitfalls, and basic guidelines for applying machine learning classifiers to psychiatric imaging data, with autism as an example. Front. Psychiatry 7, 177 (2016).
Bellman, R. E. Adaptive control processes: a guided tour (Princeton University Press, 1961).
Scott, D. W. Multivariate density estimation: theory, practice, and visualization (John Wiley & Sons, 2015).
Pestov, V. An axiomatic approach to intrinsic dimension of a dataset. Neural Netw. 21, 204–213 (2008).
Kutner, M. H. et al. Applied linear statistical models (McGraw-Hill Irwin, 2005).
Zheng, A. & Casari, A. Feature engineering for machine learning: principles and techniques for data scientists (O’Reilly Media, 2018).
Kuhn, M. & Johnson, K. Feature engineering and selection: A practical approach for predictive models (CRC Press, 2019).
Müller, A. C. & Guido, S. Introduction to machine learning with Python: a guide for data scientists (O’Reilly Media, 2016).
Suresh, H. & Guttag, J. A Framework for Understanding Sources of Harm throughout the Machine Learning Life Cycle. In Equity and Access in Algorithms, Mechanisms, and Optimization, 1–9 (2021).
Mehrabi, N., Morstatter, F., Saxena, N., Lerman, K. & Galstyan, A. A Survey on Bias and Fairness in Machine Learning. ACM Comput. Surv. 54, 1–35 (2021).
Olteanu, A., Castillo, C., Diaz, F. & Kícíman, E. Social Data: Biases, Methodological Pitfalls, and Ethical Boundaries. Front. Big Data 2, 13 (2019).
ASTM Committee. ASTM C618-19 Standard Specification for Coal Fly Ash and Raw or Calcined Natural Pozzolan for Use (2019).
Bažant, Z. R. & Li, G. H. Unbiased statistical comparison of creep and shrinkage prediction models. ACI Mater. J. 105, 610–621 (2008).
Wendner, R., Hubler, M. H. & Bažant, Z. P. Optimization method, choice of form and uncertainty quantification of Model B4 using laboratory and multi-decade bridge databases. Mater. Struct. 48, 771–796 (2015).
Hubler, M. H., Wendner, R. & Bažant, Z. P. Comprehensive database for concrete creep and shrinkage: Analysis and recommendations for testing and recording. ACI Mater. J. 112, 547–558 (2015).
DeRousseau, M. A., Laftchiev, E., Kasprzyk, J. R., Rajagopalan, B. & Srubar, W. V. A comparison of machine learning methods for predicting the compressive strength of field-placed concrete. Constr. Build. Mater. 228, 116661 (2019).
Kaufman, S., Rosset, S., Perlich, C. & Stitelman, O. Leakage in data mining: Formulation, detection, and avoidance. ACM Trans. Knowl. Discov. Data 6, 1–21 (2012).
Vabalas, A., Gowen, E., Poliakoff, E. & Casson, A. J. Machine learning algorithm validation with a limited sample size. PLoS ONE 14, 1–20 (2019).
Ouyang, B. et al. Predicting concrete’s strength by machine learning: Balance between accuracy and complexity of algorithms. ACI Mater. J. 117, 125–134 (2020).
Varma, S. & Simon, R. Bias in error estimation when using cross-validation for model selection. BMC Bioinforma. 7, 1–8 (2006).
Robinson, M. C., Glen, R. C. & Lee, A. A. Validating the validation: reanalyzing a large-scale comparison of deep learning and machine learning models for bioactivity prediction. J. Computer-Aided Mol. Des. 34, 717–730 (2020).
Ghafari, E., Costa, H. & Júlio, E. Statistical mixture design approach for eco-efficient UHPC. Cem. Concr. Compos. 55, 17–25 (2015).
Allahyari, H., Heidarpour, A., Shayan, A. & Nguyen, V. P. A robust time-dependent model of alkali-silica reaction at different temperatures. Cem. Concr. Compos. 106, 103460 (2020).
Ghorbani, B., Arulrajah, A., Narsilio, G. & Horpibulsuk, S. Experimental investigation and modelling the deformation properties of demolition wastes subjected to freeze-thaw cycles using ANN and SVR. Constr. Build. Mater. 258, 119688 (2020).
Khademi, F., Akbari, M., Jamal, S. M. & Nikoo, M. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Front. Struct. Civ. Eng. 11, 90–99 (2017).
Hooker, G., Mentch, L. & Zhou, S. Unrestricted permutation forces extrapolation: variable importance requires at least one more model, or there is no free variable importance. Stat. Comput. 31, 1–16 (2021).
Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable (Lulu.com, 2019). https://christophm.github.io/interpretable-ml-book.
Molnar, C. et al. General Pitfalls of Model-Agnostic Interpretation Methods for Machine Learning Models. In International Workshop on Extending Explainable AI Beyond Deep Models and Classifiers, 39–68 (2022).
Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).
Fisher, A., Rudin, C. & Dominici, F. All models are wrong, but many are useful: Learning a variable’s importance by studying an entire class of prediction models simultaneously. J. Mach. Learn. Res. 20, 1–81 (2019).
Dua, D. & Graff, C. UCI Machine Learning Repository. http://archive.ics.uci.edu/ml (2019).
Lundberg, S. M. & Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Guyon, I. et al. (eds.) Advances in Neural Information Processing Systems, vol. 30 (Curran Associates, Inc., 2017).
Naser, M. Z. An engineer’ s guide to eXplainable Artificial Intelligence and Interpretable Machine Learning: Navigating causality, forced goodness, and the false perception of inference. Autom. Constr. 129, 103821 (2021).
Li, J., Liu, L., Le, T. D. & Liu, J. Accurate data-driven prediction does not mean high reproducibility. Nat. Mach. Intell. 2, 13–15 (2020).
Lipton, Z. C. The mythos of model interpretability: In machine learning, the concept of interpretability is both important and slippery. Queue 16, 1–28 (2018).
Pearl, J. & Mackenzie, D. The Book of Why: The New Science of Cause and Effect (Basic Books, 2018).
Grollemund, V. et al. Machine learning in amyotrophic lateral sclerosis: Achievements, pitfalls, and future directions. Front. Neurosci. 13, 1–28 (2019).
Chandra, S. & Björnström, J. Influence of cement and superplasticizers type and dosage on the fluidity of cement mortars - Part I. Cem. Concr. Res. 32, 1605–1611 (2002).
Jain, A. et al. Commentary: The materials project: A materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
FHWA. FHWA InfoMaterials. https://infopave.fhwa.dot.gov/InfoMaterials (2021).
ACI Committee 209. 209.2-08 Guide for Modeling and Calculating Shrinkage and Creep in Hardened Concrete (2008).
Witten, I. H., Frank, E., Hall, M. A. & Pal, C. J. Data Mining: Practical Machine Learning Tools and Techniques (Morgan Kaufman, 2017).
Oey, T., Jones, S., Bullard, J. W. & Sant, G. Machine learning can predict setting behavior and strength evolution of hydrating cement systems. J. Am. Ceram. Soc. 103, 480–490 (2020).
Chi, J. M., Huang, R., Yang, C. C. & Chang, J. J. Effect of aggregate properties on the strength and stiffness of lightweight concrete. Cem. Concr. Compos. 25, 197–205 (2003).
Bouziani, T. Assessment of fresh properties and compressive strength of self-compacting concrete made with different sand types by mixture design modelling approach. Constr. Build. Mater. 49, 308–314 (2013).
Song, P. S., Wu, J. C., Hwang, S. & Sheu, B. C. Assessment of statistical variations in impact resistance of high-strength concrete and high-strength steel fiber-reinforced concrete. Cem. Concr. Res. 35, 393–399 (2005).
Nuzzo, R. Scientific method: statistical errors. Nature 506, 150–152 (2014).
Leek, J. et al. Five ways to fix statistics. Nature 551, 557–559 (2017).
Halilaj, E. et al. Machine learning in human movement biomechanics: Best practices, common pitfalls, and new opportunities. J. Biomech. 81, 1–11 (2018).
Yin, M., Vaughan, J. W. & Wallach, H. Understanding the effect of accuracy on trust in machine learning models. In Conference on Human Factors in Computing Systems, 1–12 (2019).
Schmidt, P. & Biessmann, F. Quantifying interpretability and trust in machine learning systems. Preprint at http://arxiv.org/abs/1901.08558 (2019).
Liu, H., Fu, Z., Yang, K., Xu, X. & Bauchy, M. Machine learning for glass science and engineering: A review. J. Non-Cryst. Solids: X. 4, 100036 (2019).
Batra, R., Song, L. & Ramprasad, R. Emerging materials intelligence ecosystems propelled by machine learning. Nat. Rev. Mater 6, 655–678 (2021).
Daw, A., Karpatne, A., Watkins, W., Read, J. & Kumar, V. Physics-guided neural networks (PGNN): An application in lake temperature modeling. Preprint at http://arxiv.org/abs/1710.11431 (2017).
Willard, J., Jia, X., Xu, S., Steinbach, M. & Kumar, V. Integrating scientific knowledge with machine learning for engineering and environmental systems. Preprint at https://arxiv.org/abs/2003.04919v6 (2022).
Vonrueden, L. et al. Informed machine learning - A taxonomy and survey of integrating prior knowledge into learning systems. IEEE Trans. Knowl. Data Eng. 1–20 (2021).
Karniadakis, G. E. et al. Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440 (2021).
Guo, P., Meng, W., Xu, M., Li, V. C. & Bao, Y. Predicting mechanical properties of high-performance fiber-reinforced cementitious composites by integrating micromechanics and machine learning. Materials 14, 3143 (2021).
Liu, J.-c, Huang, L., Tian, Z. & Ye, H. Knowledge-enhanced data-driven models for quantifying the effectiveness of PP fibers in spalling prevention of ultra-high performance concrete. Constr. Build. Mater. 299, 123946 (2021).
Zhang, L. V., Marani, A. & Nehdi, M. L. Chemistry-informed machine learning prediction of compressive strength for alkali-activated materials. Constr. Build. Mater. 316, 126103 (2022).
Pan, S. J. & Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 22, 1345–1359 (2010).
Chen, C., Ye, W., Zuo, Y., Zheng, C. & Ong, S. P. Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 31, 3564–3572 (2019).
Ravinder et al. Artificial intelligence and machine learning in glass science and technology: 21 challenges for the 21st century. Int. J App Glass Sci. 12, 277–292 (2021).
Tshitoyan, V. et al. Unsupervised word embeddings capture latent knowledge from materials science literature. Nature 571, 95–98 (2019).
Huo, H. et al. Semi-supervised machine-learning classification of materials synthesis procedures. npj Comput. Mater. 5, 1–7 (2019).
Nguyen, H., Vu, T., Vo, T. P. & Thai, H. T. Efficient machine learning models for prediction of concrete strengths. Constr. Build. Mater. 266, 120950 (2021).
Nasr, D., Behforouz, B., Borujeni, P. R., Borujeni, S. A. & Zehtab, B. Effect of nano-silica on mechanical properties and durability of self-compacting mortar containing natural zeolite: Experimental investigations and artificial neural network modeling. Constr. Build. Mater. 229, 116888 (2019).
Hossain, K. M., Anwar, M. S. & Samani, S. G. Regression and artificial neural network models for strength properties of engineered cementitious composites. Neural Comput. Appl. 29, 631–645 (2018).
Adhikary, B. B. & Mutsuyoshi, H. Artificial neural networks for the prediction of shear capacity of steel plate strengthened RC beams. Constr. Build. Mater. 18, 409–417 (2004).
Elsanadedy, H. M., Abbas, H., Al-Salloum, Y. A. & Almusallam, T. H. Shear strength prediction of HSC slender beams without web reinforcement. Mater. Struct. 49, 3749–3772 (2016).
Xu, J. et al. Prediction of triaxial behavior of recycled aggregate concrete using multivariable regression and artificial neural network techniques. Constr. Build. Mater. 226, 534–554 (2019).
El-Chabib, H., Nehdi, M. & Sonebi, M. Artificial intelligence model for flowable concrete mixtures used in underwater construction and repair. ACI Mater. J. 100, 165–173 (2003).
Yeh, I. C. Modeling slump flow of concrete using second-order regressions and artificial neural networks. Cem. Concr. Compos. 29, 474–480 (2007).
Elemam, W. E., Abdelraheem, A. H., Mahdy, M. G. & Tahwia, A. M. Optimizing fresh properties and compressive strength of self-consolidating concrete. Constr. Build. Mater. 249, 118781 (2020).
Güneyisi, E., Gesoglu, M. & Özbay, E. Evaluating and forecasting the initial and final setting times of self-compacting concretes containing mineral admixtures by neural network. Mater. Struct. 42, 469–484 (2009).
Basma, A. A., Barakat, S. A. & Al-Oraimi, S. Prediction of cement degree of hydration using artificial neural networks. ACI Mater. J. 96, 167–172 (1999).
Wang, Y., Shao, Y., Matovic, M. D. & Whalen, J. K. Recycling combustion ash for sustainable cement production: A critical review with data-mining and time-series predictive models. Constr. Build. Mater. 123, 673–689 (2016).
Song, Y. et al. Machine Learning Enables Rapid Screening of Reactive Fly Ashes Based on Their Network Topology. ACS Sustain. Chem. Eng. 9, 2639–2650 (2021).
Lyngdoh, G. A., Li, H., Zaki, M., Krishnan, N. M. & Das, S. Elucidating the constitutive relationship of calcium-silicate-hydrate gel using high throughput reactive molecular simulations and machine learning. Sci. Rep. 10, 1–15 (2020).
Vimonsatit, V. et al. Identification of transversely isotropy of calcium silicate hydrate using nanoindentation and finite element analysis. Constr. Build. Mater. 261, 119900 (2020).
Xi, X., Yang, S., Hu, X. & Li, C. Q. Computational determination of interface fracture properties for concrete by inverse analysis. ACI Mater. J. 117, 43–53 (2020).
Xi, X., Yin, Z., Yang, S. & Li, C. Q. Using artificial neural network to predict the fracture properties of the interfacial transition zone of concrete at the meso-scale. Eng. Fract. Mech. 242, 107488 (2021).
Karthikeyan, J., Upadhyay, A. & Bhandari, N. M. Artificial neural network for predicting creep and shrinkage of high performance concrete. J. Adv. Concr. Technol. 6, 135–142 (2008).
Han, B., Xie, H. B., Zhang, D. J. & Ma, X. Sensitivity analysis of creep models considering correlation. Mater. Struct. 49, 4217–4227 (2016).
Li, K., Long, Y., Wang, H. & Wang, Y.-f. Modeling and Sensitivity Analysis of Concrete Creep with Machine Learning Methods. J. Mater. Civ. Eng. 33, 1–13 (2021).
Nehdi, M. L. & Soliman, A. M. Artificial intelligence model for early-age autogenous shrinkage of concrete. ACI Mater. J. 109, 353–362 (2012).
Mermerdaş, K. & Arbili, M. M. Explicit formulation of drying and autogenous shrinkage of concretes with binary and ternary blends of silica fume and fly ash. Constr. Build. Mater. 94, 371–379 (2015).
Bhamare, D. K., Saikia, P., Rathod, M. K., Rakshit, D. & Banerjee, J. A machine learning and deep learning based approach to predict the thermal performance of phase change material integrated building envelope. Build. Environ. 199, 107927 (2021).
Aizawa, T. & Yokoshita, T. Applications of neural network technology to the operation and control of cement plants. ZKG Int. 48, 532–538 (1995).
Schmidt, D. & Schmidt, D. Online prediction of the free lime content in the sintering zone and the use of neural networks for process optimization. ZKG Int. 54, 471–479 (2001).
Oh, J. W., Lee, I. W., Kim, J. T. & Lee, G. W. Application of neural networks for proportioning of concrete mixes. ACI Mater. J. 96, 61–67 (1999).
Ji, T., Yang, Y., Fu, M. Y., Chen, B. C. & Wu, H. C. Optimum design of reactive powder concrete mixture proportion based on artificial neural and harmony search algorithm. ACI Mater. J. 114, 41–47 (2017).
Zhou, S. et al. Quick image analysis of concrete pore structure based on deep learning. Constr. Build. Mater. 208, 144–157 (2019).
Das, A. et al. Influence of Pumping/Extrusion on the Air-Void System of 3D Printed Concrete. In Second RILEM International Conference on Concrete and Digital Fabrication. 28, 417–427 (2020).
Isa, N. A. M. et al. Suitable features selection for the HMLP and MLP networks to identify the shape of aggregate. Constr. Build. Mater. 22, 402–410 (2008).
Al-Batah, M. S., Mat Isa, N. A., Zamli, K. Z., Sani, Z. M. & Azizli, K. A. A novel aggregate classification technique using moment invariants and cascaded multilayered perceptron network. Int. J. Miner. Process. 92, 92–102 (2009).
Choi, H., Venkiteela, G., Gregori, A. & Najm, H. Advanced Quality Control Models for Concrete Admixtures. J. Mater. Civ. Eng. 32, 04019349 (2020).
Najigivi, A., Khaloo, A., Iraji zad, A. & Abdul Rashid, S. An Artificial Neural Networks Model for Predicting Permeability Properties of Nano Silica-Rice Husk Ash Ternary Blended Concrete. Int. J. Concr. Struct. Mater. 7, 225–238 (2013).
Karakoç, M. B., Demirboa, R., Türkmen, I. & Can, I. Modeling with ANN and effect of pumice aggregate and air entrainment on the freeze-thaw durabilities of HSC. Constr. Build. Mater. 25, 4241–4249 (2011).
Taffese, W. Z., Sistonen, E. & Puttonen, J. CaPrM: Carbonation prediction model for reinforced concrete using machine learning methods. Constr. Build. Mater. 100, 70–82 (2015).
Kwon, S. J. & Song, H. W. Analysis of carbonation behavior in concrete using neural network algorithm and carbonation modeling. Cem. Concr. Res. 40, 119–127 (2010).
Lee, H., Lee, H. S. & Suraneni, P. Evaluation of carbonation progress using AIJ model, FEM analysis, and machine learning algorithms. Constr. Build. Mater. 259, 119703 (2020).
Güneyisi, E., Gesoğlu, M., Özturan, T. & Özbay, E. Estimation of chloride permeability of concretes by empirical modeling: Considering effects of cement type, curing condition and age. Constr. Build. Mater. 23, 469–481 (2009).
Asghshahr, M. S., Rahai, A. & Ashrafi, H. Prediction of chloride content in concrete using ANN and CART. Mag. Concr. Res. 68, 1085–1098 (2016).
Güneyisi, E. M., Mermerdaş, K., Güneyisi, E. & Gesoğlu, M. Numerical modeling of time to corrosion induced cover cracking in reinforced concrete using soft-computing based methods. Mater. Struct. 48, 1739–1756 (2015).
Xu, Y. & Jin, R. Measurement of reinforcement corrosion in concrete adopting ultrasonic tests and artificial neural network. Constr. Build. Mater. 177, 125–133 (2018).
Haj-Ali, R. M., Kurtis, K. E. & Sthapit, A. R. Neural network modeling of concrete expansion during long-term sulfate exposure. ACI Mater. J. 98, 36–43 (2001).
Goktepe, A. B., Inan, G., Ramyar, K. & Sezer, A. Estimation of sulfate expansion level of PC mortar using statistical and neural approaches. Constr. Build. Mater. 20, 441–449 (2006).
Chang, C. H. & Yang, C. C. Artificial neural networks in prediction of concrete strength reduction due to high temperature. ACI Mater. J. 103, 68–69 (2006).
Özbay, E. & Lachemi, M. Relative compressive strength of concretes under elevated temperatures. ACI Mater. J. 109, 165–175 (2012).
Huang, Y., Zhang, J., Tze Ann, F. & Ma, G. Intelligent mixture design of steel fibre reinforced concrete using a support vector regression and firefly algorithm based multi-objective optimization model. Constr. Build. Mater. 260, 120457 (2020).
Nguyen-Sy, T. et al. Predicting the compressive strength of concrete from its compositions and age using the extreme gradient boosting method. Constr. Build. Mater. 260, 119757 (2020).
Yazdi, J. S., Kalantary, F. & Yazdi, H. S. Prediction of Elastic Modulus of Concrete Using Support Vector Committee Method. J. Mater. Civ. Eng. 25, 9–20 (2013).
Aydogmus, H. Y. et al. A comparative assessment of bagging ensemble models for modeling concrete slump flow. Comput. Concr. 16, 741–757 (2015).
Ünlü, R. An assessment of machine learning models for slump flow and examining redundant features. Comput. Concr. 25, 565–574 (2020).
Liu, H. et al. Predicting the early-stage creep dynamics of gels from their static structure by machine learning. Acta Mater. 210, 116817 (2021).
Liao, K. W., Chen, C. T., Wu, B. H., Chen, W. L. & Yeh, C. M. Investigation of chloride diffusion in cement mortar via statistical learning theory. Mag. Concr. Res. 68, 237–249 (2016).
Cai, R. et al. Prediction of surface chloride concentration of marine concrete using ensemble machine learning. Cem. Concr. Res. 136, 106164 (2020).
Fan, L., Fan, M., Alhaj, A., Chen, G. & Ma, H. Hyperspectral imaging features for mortar classification and compressive strength assessment. Constr. Build. Mater. 251, 118935 (2020).
Koch, C., Georgieva, K., Kasireddy, V., Akinci, B. & Fieguth, P. A review on computer vision based defect detection and condition assessment of concrete and asphalt civil infrastructure. Adv. Eng. Inform. 29, 196–210 (2015).
Gopalakrishnan, K., Khaitan, S. K., Choudhary, A. & Agrawal, A. Deep Convolutional Neural Networks with transfer learning for computer vision-based data-driven pavement distress detection. Constr. Build. Mater. 157, 322–330 (2017).
Aravind, N., Nagajothi, S. & Elavenil, S. Machine learning model for predicting the crack detection and pattern recognition of geopolymer concrete beams. Constr. Build. Mater. 297, 123785 (2021).
Zhang, M., Li, M., Shen, Y., Ren, Q. & Zhang, J. Multiple mechanical properties prediction of hydraulic concrete in the form of combined damming by experimental data mining. Constr. Build. Mater. 207, 661–671 (2019).
Zhang, J., Li, D. & Wang, Y. Toward intelligent construction: Prediction of mechanical properties of manufactured-sand concrete using tree-based models. J. Clean. Prod. 258, 120665 (2020).
Zhang, J., Huang, Y., Wang, Y. & Ma, G. Multi-objective optimization of concrete mixture proportions using machine learning and metaheuristic algorithms. Constr. Build. Mater. 253, 119208 (2020).
Behnood, A. & Golafshani, E. M. Machine learning study of the mechanical properties of concretes containing waste foundry sand. Constr. Build. Mater. 243, 118152 (2020).
Abbasloo, A. A., Shayanfar, M. A., Pahlavan, H., Barkhordari, M. A. & Hamze-Ziabari, S. M. Prediction of shear strength of FRP-reinforced concrete members using a rule-based method. Mag. Concr. Res. 71, 271–286 (2019).
Chen, D., Montano, V., Huo, L., Fan, S. & Song, G. Detection of subsurface voids in concrete-filled steel tubular (CFST) structure using percussion approach. Constr. Build. Mater. 262, 119761 (2020).
Marani, A. & Nehdi, M. L. Machine learning prediction of compressive strength for phase change materials integrated cementitious composites. Constr. Build. Mater. 265, 120286 (2020).
Cook, R. et al. Machine learning for high-fidelity prediction of cement hydration kinetics in blended systems. Mater. Des. 208, 109920 (2021).
Nilsen, V. et al. Prediction of concrete coefficient of thermal expansion and other properties using machine learning. Constr. Build. Mater. 220, 587–595 (2019).
Pei, L. et al. Pavement aggregate shape classification based on extreme gradient boosting. Constr. Build. Mater. 256, 119356 (2020).
Luo, Q., Ge, B. & Tian, Q. A fast adaptive crack detection algorithm based on a double-edge extraction operator of FSM. Constr. Build. Mater. 204, 244–254 (2019).
Naser, M. Z. & Salehi, H. Machine learning-driven assessment of fire-induced concrete spalling of columns. ACI Mater. J. 117, 7–16 (2020).
Okazaki, Y., Okazaki, S., Asamoto, S. & Chun, P. J. Undersampling strategy for machine-learned deterioration regression model in concrete bridges. J. Adv. Concr. Technol. 18, 753–766 (2020).
Knaack, A. M., Kurama, Y. C. & Kirkner, D. J. Compressive Strength Relationships for Concrete under Elevated Temperatures. ACI Mater. J. 108, 270–280 (2011).
Gandomi, A. H., Sajedi, S., Kiani, B. & Huang, Q. Genetic programming for experimental big data mining: A case study on concrete creep formulation. Autom. Constr. 70, 89–97 (2016).
Özgenel, Ç. F. Concrete Crack Images for Classification. Mendeley Data (2018).
Özgenel, F. & Gönenç Sorguç, A. Performance comparison of pretrained convolutional neural networks on crack detection in buildings. In ISARC 2018 - 35th International Symposium on Automation and Robotics in Construction and International AEC/FM Hackathon: The Future of Building Things (2018).
Dorafshan, S., Thomas, R. J. & Maguire, M. SDNET2018: An annotated image dataset for non-contact concrete crack detection using deep convolutional neural networks. Data Brief. 21, 1664–1668 (2018).
Dorafshan, S., Thomas, R. J. & Maguire, M. Comparison of deep convolutional neural networks and edge detectors for image-based crack detection in concrete. Constr. Build. Mater. 186, 1031–1045 (2018).
Yang, Q., Shi, W., Chen, J. & Lin, W. Deep convolution neural network-based transfer learning method for civil infrastructure crack detection. Autom. Constr. 116, 103199 (2020).
Merlino, S., Bonaccorsi, E. & Armbruster, T. Tobermorites: Their real structure and order-disorder (OD) character. Am. Mineral. 84, 1613–1621 (1999).
Agrawal, A. & Choudhary, A. Perspective: Materials informatics and big data: Realization of the “fourth paradigm" of science in materials science. APL Mater. 4, 053208 (2016).
Acknowledgements
The authors would like to thank Fan Zou and Te Pei (Pennsylvania State University), Dr. Binyang Song (Massachusetts Institute of Technology), and Weichao Ying (University of Hong Kong) for their insightful and inspiring remarks during the planning and development of this work.
Author information
Authors and Affiliations
Contributions
Z.L. and I.D. conceived this work. Z.L. drafted the manuscript. Z.L. and J.Y. conducted the literature survey and collected the data. Z.L., R.Z. and I.D. prepared the visualizations. I.D., R.Z., W.V.S. and J.Y. provided critical feedback on the manuscript. A.R., I.D. and F.R. supervised the work. All authors discussed the results and contributed to the revision of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Z., Yoon, J., Zhang, R. et al. Machine learning in concrete science: applications, challenges, and best practices. npj Comput Mater 8, 127 (2022). https://doi.org/10.1038/s41524-022-00810-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00810-x
This article is cited by
-
Modelling the mechanical properties of concrete produced with polycarbonate waste ash by machine learning
Scientific Reports (2024)
-
A comparative assessment of uncrushed-river concrete mix of Hari-River, and Kamar-Kalaq: the two widely used concrete mix in Herat, Afghanistan
Scientific Reports (2024)
-
Machine learning assisted discovery of high-efficiency self-healing epoxy coating for corrosion protection
npj Materials Degradation (2024)
-
Predicting superconducting transition temperature through advanced machine learning and innovative feature engineering
Scientific Reports (2024)
-
Machine learning models for predicting the compressive strength of agro-waste stabilized bricks for sustainable buildings
Discover Civil Engineering (2024)