Abstract
Recently the alternating twisted trilayer graphene is discovered to exhibit unconventional superconductivity, which motivates us to study the electronic structures and possible correlation effects for this class of alternating twisted multilayer graphene (ATMG) systems. In this work we consider generic ATMG systems with M-L-N stacking configurations, in which the M (L) graphene layers and the L (N) layers are twisted by an angle θ (−θ). Based on analysis from a simplified k⋅p model approach, we derive generic partition rules for the low-energy electronic structures, which exhibit various band dispersions including two pairs of flat bands and flat bands co-existing with various gapless Fermionic excitations. For a mirror-symmetric ATMG system with doubled flat bands, we further find that Coulomb interactions may drive the system into a state with intertwined electric polarization and orbital magnetization orders, which can exhibit an interaction-driven orbital magnetoelectric effect.
Similar content being viewed by others
Introduction
The recent discoveries of some phenomena, such as superconductivity1,2,3,4,5,6,7,8, quantum anomalous Hall effect9,10,11,12,13,14,15, and correlated insulator states4,5,6,7,9,16,17,18,19,20,21 in magic-angle twisted bilayer graphene (TBG) have aroused great interest. In magic-angle TBG22, the interlayer moiré potential generates pseudo magnetic fields, which are coupled with the Dirac fermions from the two layers, leading to topological nontrivial flat bands with eightfold degeneracy with valley, spin, and sublattice degrees of freedom23,24,25,26,27,28. Such degeneracy can be split by strong Coulomb interactions, leading to symmetry-breaking states reminiscent of quantum Hall ferromagnetism. The interplay between nontrivial topology and strong Coulomb interaction gives rise to fruitful physics in magic-angle TBG29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57.
The flat-bands physics is not unique for magic-angle TBG. It has been theoretically proposed and experimentally observed that topologically nontrivial flat bands with strong correlation effects can also exist in twisted multilayer systems such as twisted bilayer-monolayer graphene and twisted double bilayer graphene16,58,59,60,61,62,63,64,65,66,67,68. Moreover, recently unconventional superconductivity has been observed in alternating twist trilayer graphene69,70,71,72, which is a new type of twisted graphene system with topologically nontrivial flat bands co-existing with dispersive Dirac cone around the charge neutrality point (CNP)73,74,75. This motivates us to study the electronic structures and correlation effects of alternating twisted multilayer graphene systems. One would expect that the extra twist may fundamentally change the low-energy electronic structures, and the extra layers may introduce additional degrees of freedom that may give rise to interesting interaction effects76,77,78.
In this work, we theoretically study the alternating twisted multilayer graphene (ATMG): a class of twisted graphene systems consisting of three sequences of graphene multilayers with alternating twist angles. We describe the non-interacting band structures of the ATMG system using extended continuum model Hamiltonians of the Bistritzer-MacDonald type22. The low-energy band dispersions of the ATMG system (for each valley each spin) can be classified into three types, including one pair of flat bands, two pairs of flat bands, as well as flat bands co-existing with E(k) ~ kJ dispersive bands (J is positive integer). Based on an analytic analysis from a simplified k⋅p model approach, we find that the low energy band structures can be described by a generic partition rule. According to the partition rule, there must be double flat bands for mirror-symmetric ATMG with more than one layers in the middle sequence. Lastly, we consider Coulomb interaction effects in a mirror-symmetric ATMG system with two pairs of flat bands for each spin and valley. We have theoretically studied the ground states at each integer filling of the double flat bands based on unrestricted self-consistent Hartree–Fock calculations including the screening effects from the remote bands. At certain fillings, we find that Coulomb interactions may drive the system into a state breaking both time-reversal and mirror symmetries, which can exhibit orbital magnetoelectric effect due to the intertwining of electric polarization and orbital magnetization orders in the symmetry-breaking state.
Results and discussion
Continuum model
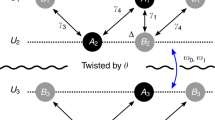
We consider a class of ATMG, which consist of three sets of graphene multilayers with the number of layers denoted by M, L, and N, respectively. The stacking sequence within each set of multilayers can be Bernal (ABA), rhombohedral (ABC), or a mixture of the two. These multilayers are stacked from bottom to up in the M-L-N sequence, where the N (L) layers and the L (M) layers are twisted by an angle θ (−θ) as schematically shown in Fig. 1a. Such a system forms a moiré pattern in real space with the moiré superlattice constant \({L}_{s}\,=\,a/(2\sin \theta /2)\), where a = 2.46 Å is the graphene lattice constant. The corresponding moiré Brillouin zone is shown in Fig. 1b. Similar to twisted bilayer graphene (TBG), the low energy states of the ATMG system are contributed by those from the atomic K and \(K^{\prime}\) valleys, which are approximately decoupled from each other at the non-interacting level for small twist angles. Thus, it is generally assumed that the system preserves valley charge conservation at small twist angles22. Therefore, we generalize the Bistritzer-MacDonald continuum model22 to describe the low-energy states of the ATMG system for each valley and each spin, assuming the states from the K and \(K^{\prime}\) valleys are completely decoupled. The continuum model for valley μ (μ = ∓ for K and \(K^{\prime}\) valleys) is expressed as
where \({H}_{N}^{\mu }\), \({H}_{L}^{\mu }\) and \({H}_{M}^{\mu }\) denote the k⋅p Hamiltonians of the untwisted graphene multilayers, which consist of the Dirac fermions of each monolayer graphene and the interlayer hopping terms. \({{\mathbb{U}}}_{\mu }{e}^{i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}\) stands for the moiré potential term for valley μ, which arises from the mutual twist between two sets of adjacent multilayers. ΔK = (0, 4π/(3Ls)) is a vector characterizing the shift of Dirac points due to the twist.
a Lattice structure of alternating twist multilayer graphene. b Brillouin zones of M, L and N layers and Moiré Brillouin zone with high symmetry points. Band structure of c A-A-A and d A-ABA-A at K valley(solid line) and \({K}^{\prime}\) valley(dashed line) in the chiral limit, considering nearest neighbor interlayer hopping with zero displacement field.
One can obtain various types of low-energy band structures from the Hamiltonian given by Eq. (1). A careful study reveals that the ATMG systems can be roughly divided into three types based on their low-energy band dispersion: for type (i) there is only one pair of flat bands for each valley and spin, which is similar to TBG; for type (ii) there is one pair of flat bands co-existing with some low-energy bands characterized by the dispersion E(k) ~ kJ(J is positive integer); and for type (iii) there are two pairs of flat bands. In Fig. 1c, d we show the band structures of two typical ATMG systems with A-A-A and A-ABA-A stacking, where the solid and dashed lines denote energy bands from the K and \(K^{\prime}\) valleys respectively in chiral limit, i.e., the intrasublattice coupling between twisted layers vanishes. For the A-A-A system, there is one pair of flat bands co-existing with a Dirac cone (per valley per spin), which can be categorized as type (ii) ATMG; while there are two pairs of flat bands for each valley and spin for the A-ABA-A system, which is the simplest example of type (iii) ATMG. In what follows we will explain the origin of such low-energy dispersion and derive partition rules for generic ATMG systems.
Generic partition rules and the simplified k⋅p model
To better illustrate the origin of these low-energy dispersions, we first consider the chiral limit in which all the intrasublattice couplings are turned off. Within the chiral limit, we first analyze the low-energy states of the untwisted multilayers, then discuss the effects of the moiré potentials at the twisted interfaces. It has been proposed that a multilayer graphene with arbitrary stacking sequence and with the total number of layers N can be decomposed into SN chiral segments79, within each of which the stacking chirality is unchanged. Then the low-energy states contributed by the ith chiral segment with the number of layers Ji consists of a chiral doublet described by the following effective Hamiltonian79
where \(\tan {\phi }_{{{{\bf{k}}}}}={k}_{y}/{k}_{x}\), and σx,y denote Pauli matrices in the sublattice space. Then the low-energy Hamiltonian of the untwisted N layers from valley μ can be written as a direct sum of those of the SN chiral segments: \({H}_{N}^{\mu }\approx {H}_{{J}_{1}}^{\mu }\oplus {H}_{{J}_{2}}^{\mu }...\oplus {H}_{{J}_{{S}_{N}}}^{\mu }\). Each segment contributes to a chiral doublet with the dispersion \(E \sim {k}^{{J}_{i}}\) around Kμ point (μ = ± is the valley index). Then we consider the N layers are stacked with the other M layers and are twisted by angle θ. The moiré potential at the interface would couple the topmost chiral segment of the N layers with the bottom-most segment of the M layers, giving rise to a pair of flat bands for each spin and each valley. These flat bands would co-exist with the dispersive chiral doublets contributed by the remaining uncoupled chiral segments (if any) of the two sets of multilayers80. The ATMG system introduces additional complexity due to the additional multilayers (L layers) and the additional twist. It turns out that the situations with the number of middle layers L = 1 and L > 1 need to be treated separately.
To evaluate the difference between ATMG systems with L = 1 and L > 1, we first consider alternating twisted trilayer graphene (TTG), i.e., M = L = N = 1. In TTG, three alternating twisted graphene monolayers are coupled together. The Hamiltonian of TTG can be decoupled into a TBG-like Hamiltonian and a free Dirac-fermion Hamiltonian through a proper unitary transformation. The TBG part and Dirac fermion part are completely decoupled from each other, which contribute to one pair of flat bands co-existing with a Dirac cone as shown in Fig. 1c. For L = 1 but M, N > 1, one can apply the chiral decomposition rule to the M layers and N layers. The topmost chiral segment from the M layers and the bottom-most segment from the N layers are coupled with the L = 1 middle layer through the moiré potentials, contributing to one pair of flat bands co-existing with either a Dirac cone or a pair of quadratic bands. The remaining chiral segments (if any) in the N layers and M layers would contribute to additional E(k) ~ kJ dispersive bands. On the other hand, when L > 1, one needs to apply the chiral decomposition rule to the L multilayers as well, and carefully study how the chiral doublets contributed by the M, L, and N layers are coupled to each other through the moiré potentials at the two twisted interfaces.
After a comprehensive theoretical analysis based on a simplified k⋅p model approach (see Methods and Supplementary Information for more details), we have derived a set of generic partition rules describing the low-energy band structures of ATMG systems in the chiral limit. First, the M, L, and N multilayers are divided into SM, SL, and SN chiral segments, and the number of layers of the ith segment, say, in N multilayer is denoted as JN,i (i = 1, . . . , SN). We also need to keep the chiral segments that are closest to the twisted interfaces to be as long as possible, i.e., we need to make a choice of chiral decomposition to make \({J}_{M,{S}_{M}}\), JL,1, \({J}_{L,{S}_{L}}\) and JN,1 as large as possible. Based on the above choice of chiral segments, we reach the following partition rules for the low-energy dispersion in the chiral limit:
-
(a)
For L = 1: the \({J}_{M,{S}_{M}}\), JL,1 and JN,1 chiral segments are coupled through the moiré potential generated by the alternating twisted structure. When the stacking chirality of \({J}_{M,{S}_{M}}\) and JN,1 are the same, there are one pair of flat bands and one Dirac cone co-existing near Kμ point (per spin per valley); while if \({J}_{M,{S}_{M}}\) and JN,1 have opposite stacking chiralities, there are one pair of flat bands and one pair of quadratic bands co-existing near Kμ point. The remaining chiral segments in the M (N) multilayers would contribute to additional chiral doublets with the dispersion \(E({{{\bf{k}}}})\, \sim \,{k}^{{J}_{M,i}}\) (\(E({{{\bf{k}}}})\, \sim \,{k}^{{J}_{N,i}}\)) near Kμ point.
-
(b)
For L > 1: if the L multilayer can be divided into more than one chiral segments (SL > 1), there are two pairs of flat bands (double flat bands) around CNP; while if the L multilayer is in the chiral (rhombohedral) stacking sequence with SL = 1, there is only one pair of flat bands. When SL > 1, the remaining chiral segment {JL,i, 2 ≤ i ≤ SL − 1} that are decoupled from the M and N multilayers would contribute to dispersive bands \(E({{{\bf{k}}}}) \sim {k}^{{J}_{L,i}}\) around CNP. Similarly, the remaining chiral segments {JM,i, 1 ≤ i ≤ SM − 1} ({JN,i, 2 ≤ i ≤ SN}) from the M (N) multilayer that are not coupled the middle L multilayer would contribute to the low-energy dispersive bands with \(E({{{\bf{k}}}}) \sim {k}^{{J}_{M,i}}\) (\(E({{{\bf{k}}}}) \sim {k}^{{J}_{N,i}}\)).
In Table 1, we illustrate some ATMG systems as typical cases and apply the partition rules described above to these systems to characterize their low energy band structures, where the notation (m, n) means that there are m pairs of bands with dispersion E(k) ~ kn around Ks or \(K^{\prime}_s\) points. For example, for A-A-ABAC system, it can be divided into two parts including the alternating twisted layers A-A-AB and untwisted layers AC. The twisted layers would contribute one pair of flat bands co-existing with a Dirac cone around Kμ point, while the untwisted layers give rise to a pair of quadratic bands(E(k) ~ k2) centered at Kμ point.
The partition rules presented above can be derived using a simplified k⋅p model approach. In this approach, we write a k⋅p model within the moiré Brillouin zone by expanding the flat bands and the Dirac cones around the moiré Ks or \(K^{\prime}_s\) points including the coupling terms between them. In the chiral limit both the flat bands and the Dirac cone can be solved exactly23, then we can analytically construct a greatly simplified k⋅p model on the basis of the zero modes (flat-band wavefunctions) and the Dirac fermions, and solve it exactly. From the analytic solutions of the simplified k⋅p model, we derive the partition rules for generic ATMG systems presented above. Such an approach can capture the essential low-energy physics, while neglecting the irrelevant high-energy bands obtained from a direct numerical diagonalization of the original continuum Hamiltonian. More details and examples about the k⋅p model approach are presented in Methods and Supplementary Information.
It is worthwhile to note that the simplified k⋅p model is constructed in the chiral limit neglecting all the intrasublattice couplings. Consequently, the partition rules derived from the simplified k⋅p model and the above discussions about double flat bands are rigorous only in the chiral limit. In a more realistic situation, one needs to include the intrasublattice component of the moiré potential and the further neighbor interlayer hopping within the untwisted layers (see Supplementary Information), which break chiral symmetry. With these additional coupling terms, the otherwise exactly flat bands at the magic angle may acquire nonzero bandwidths, and the E(k) ~ kJ bands may have slightly modified dispersion. However, despite these perturbative changes, the main conclusions sketched by the partition rules are unchanged.
Symmetry-breaking ground states in mirror-symmetric ATMG system
It follows from the previous arguments that a mirror-symmetric ATMG system with L > 1 must satisfy the condition of SL > 1 (SL denotes the total number of chiral segments within the L multilayer), thus there must be two pairs of flat bands for mirror-symmetric ATMG with L > 1. The double flat bands can be classified by the opposite mirror eigenvalues ± 1 for ATMG with mirror (mz) symmetry74. In Fig. 2a we present the band structures of the A-ABA-A system including the intrasublattice moiré potential and the further neighbor interlayer hopping, where the color-coding indicates the weight projected onto the middle layer. First, we note that compared with the band structures in the chiral limit shown Fig. 1d, in the realistic situation two of the four flat bands become more dispersive with the bandwidth ~25 meV, while the other pair of flat bands remain flat with very small bandwidth ~10 meV. Second, we note that the weight of the middle layer for the pair of flat bands lower in energy with small bandwidth is vanishing, while the upper pair of flat bands with relatively large bandwidth have significant contributions from the middle-layer states. This is because the two flat bands lower/upper in energy have mirror eigenvalues ∓ 1, and the Bloch states with −1 mirror eigenvalue must have zero contribution from the middle layer. In the presence of Coulomb interactions, the mz symmetry could be broken spontaneously at certain filling factors.
The band structure of A-ABA-A for two valleys including intrasublattice moiré potential and the further neighbor interlayer hopping. a The non-interacting band structures with weight projected to the middlemost layer. b The Hartree–Fock band structure for two valleys. c The vertical polarization, and d the valley polarization and the corresponding orbital magnetization of the symmetry-breaking ground state at -3 filling as a function of vertical electrostatic potential drop Ud.
The ubiquitous flat bands in ATMG make these systems strongly susceptible to Coulomb interactions. Moreover, unlike magic-angle TBG, in magic-angle ATMG typically there are flat bands co-existing with other dispersive bands (such as Dirac cone) or double flat bands. The extra low-energy dispersive bands (e.g., Dirac cone) may be coupled with the flat bands under weak displacement fields and display different correlated states from those in magic-angle TBG at certain filling factors77,78. On the other hand, in mirror-symmetric ATMG with double flat bands, e.g., in A-ABA-A system, the extra pair of flat bands marked by opposite mirror eigenvalues introduce additional degrees of freedom. What are the correlated ground states in such double-flat-band systems at different filling factors of the flat bands, how the extra degrees of freedom (mirror eigenvalues) would play a role, and how the correlated states would differ from those of TBG, are all open questions. We try to answer these questions by studying the correlated states at different integer fillings of ATMG with A-ABA-A stacking, the simplest mirror-symmetric ATMG system with double flat bands.
We consider intravalley Coulomb interactions in this work, which are orders of magnitude greater than intervalley Coulomb scatterings at small twist angles. The Coulomb interactions are considered to be screened by single metallic gate (see Methods). We further project the Coulomb interactions onto the double flat bands and perform unrestricted self-consistent Hartree–Fock calculations within the subspace of the double flat bands. Besides, the Coulomb interactions between electrons in the double flat bands can be further screened by virtual particle-hole excitations in the remote energy bands, and such screening effects in our calculation are treated with the constrained random phase approximation(cRPA)40,81. The details of the Hartree–Fock and cRPA methods are presented in Methods and Supplementary Information.
We first calculate the ground states at different integer fillings of the double flat bands using the Hartree–Fock and cRPA methods described above. The filling factor is counted with respect to the CNP, i.e., the filling factor is defined as ν = n − 8 when n out of the 16 flat bands (including valley and spin degeneracy) are filled. Then we calculate the expectation values of the order parameters of the Hartree–Fock ground states at each integer filling, and figure out the dominant ones which are presented in Table 2, where τ, s, and σ denote Pauli matrices defined in valley, spin, and sublattice space respectively. For example, the ground state at filling -3 is a gapped spin-valley polarized state. In order to depict the spontaneous mz symmetry breaking, we also calculate the vertical electric polarization at different filling factors. The vertical electric polarization per moiré supercell pz is defined as: \({p}_{z}\,=\,\mathop{\sum }\nolimits_{l = 1}^{5}\,(l-3)\,{q}_{l}{d}_{0}\), where d0 = 3.35 Å is the interlayer distance of Bernal bilayer graphene, \({q}_{l}=e\left\langle {\tau }_{0}{{{{\rm{s}}}}}_{0}{{\mathbb{L}}}_{l}{\sigma }_{0}\right\rangle\) is the layer resolved charge density, where \({{\mathbb{L}}}_{l}\) is the projection operator onto layer l, a 5 × 5 matrix with the lth diagonal element identity and all other elements being zeros. The unit of the electric polarization is e ⋅ Å per moiré supercell. We also evaluate the orbital magnetization and valley polarization. The valley polarization ξz is defined as: \({\xi }_{z}\,=\,\mathop{\sum }\nolimits_{l = 1}^{5}{\xi }_{z}(l)\,=\,\mathop{\sum }\nolimits_{l = 1}^{5}\left\langle {\tau }_{z}{s}_{0}{{\mathbb{L}}}_{l}{\sigma }_{0}\right\rangle\), where ξz(l) is defined as the valley polarization projected onto layer l. A finite valley polarization would give rise to non-vanishing net orbital magnetization. In Table 2, we present the calculated vertical electric polarization and valley polarization of the spontaneous symmetry-breaking states at different integer filling factors. We find that mz symmetry is spontaneously broken by Coulomb interactions at all integer fillings, which generate small but nonzero electric polarization.
Orbital magnetoelectric effect through intertwined orders
In order to characterize the effects of vertical displacement field, we calculate both the vertical electric polarization and valley polarization of the Hartree−Fock ground states for the A-ABA-A system at filling factor −3 with increasing displacement fields. The displacement field (D) is introduced by applying a homogeneous vertical electrostatic potential difference Ud between the topmost and bottommost layers, i.e., Ud = 4eDd0/ϵBN, where ϵBN ≈ 4 is the dielectric constant of the BN substrate. Our calculations indicate that the dominant order parameters of the ground states at filling −3 are unchanged for 0 ≤ Ud ≤ 0.02 eV, i.e., the system always stays in the spin-valley polarized state with broken mz symmetry, suggesting that no phase transition occurs at least for 0 ≤ Ud ≤ 0.02 eV. However, by virtue of the mz symmetry and the additional layer degrees of freedom, the valley polarization acquires nontrivial layer distributions as shown by the ξz(l) (l = 1, . . . , 5) values in Table 3. We see that ξz(1) and ξz(2) are approximately the same, while ξz(4) and ξz(5) are approximately the same, which are all different from ξz(3). As a result, the layer-resolved valley polarization can be approximately decomposed into three terms:
where
and \({\hat{\xi }}_{z}\) is a 5 × 5 matrix with its lth diagonal element denoting the valley polarization contributed by layer l, i.e., \({\hat{\xi }}_{z,ll}={\xi }_{z}(l)\). \({\xi }_{z}^{s}\) and \({\xi }_{z}^{a}\) denote the layer-symmetric and layer anti-symmetric components of the valley polarization, with \({\xi }_{z}^{s}=\mathop{\sum }\nolimits_{l = 1}^{5}{\xi }_{z}(l)/5\), and \({\xi }_{z}^{a}={\sum }_{l\ne 3}{{{\rm{sgn}}}}[(l-3)]({\xi }_{z}(l)-{\xi }_{z}^{s})/4\). In other words, \({\xi }_{z}^{s}=\langle {\tau }_{z}\otimes {{\mathbb{1}}}_{5\times 5}\rangle /5\) is the layer average of valley polarization (\({{\mathbb{1}}}_{5\times 5}\) denotes identity matrix in layer space), and \({\xi }_{z}^{a}=\langle {\tau }_{z}\otimes ({\hat{P}}_{z}+{\hat{Q}}_{z})\rangle /4\), where \(\langle \hat{O}\rangle\) denotes the expectation value of operator \(\hat{O}\) evaluated with respect to the symmetry-breaking ground state. The layer-symmetric and layer anti-symmetric valley polarization for the ground states at filling − 3 with different Ud are presented in the last two rows of Table 3.
We note that \({\hat{P}}_{z}\) is exactly the vertical electric polarization operator \({\hat{p}}_{z}\,=\,e{d}_{0}{\hat{P}}_{z}\), which couples linearly to external electric field; while the valley polarization operator is proportional to the orbital magnetization operator \({\hat{M}}_{z}\,=\,{g}_{z}{\mu }_{B}{\tau }_{z}\) which couples linearly to external magnetic field, where gz is introduced as an effective g factor and μB is the Bohr magneton. Given the above discussions, we introduce an effective mean-field Hamiltonian to describe how the symmetry-breaking state at filling -3 would respond to external electric and magnetic fields
where Δz0 and Δzz are the “mean fields” that are self consistently generated by Coulomb interactions which are coupled with the \({\tau }_{z}\otimes {{\mathbb{1}}}_{5\times 5}\) operator and \({\tau }_{z}\otimes ({\hat{P}}_{z}+{\hat{Q}}_{z})\) operator respectively, while Bz is the vertical magnetic field and Ud is the vertical electrostatic energy drop. As the electric polarization operator and the valley polarization operator are intertwined together, Eq. (5) implies a tunable electric polarization by magnetic field and conversely a tunable valley polarization (orbital magnetization) by electric field. To be specific, a vertical electric field is coupled to the \({\hat{P}}_{z}\) operator, which is in turn intertwined with the layer anti-symmetric component of the valley polarization operator, thus would change the valley polarization and orbital magnetization of the system. Conversely, a vertical magnetic Bz is coupled to orbital magnetization (valley polarization), and the valley polarization operator is intertwined with the electric polarization operator, which would change electric polarization of the system. It is clearly seen from Table 3 that the layer symmetric valley polarization is larger than the layer anti-symmetric one, implying that the orbital magnetization still has the strongest coupling to magnetic field, but can be tuned by electric field. In Fig. 2c, d, we present the calculated electric polarization and valley polarization of the symmetry-breaking states at filling -3 under different Ud. As Ud increases, clearly the electric polarization is linearly enhanced as shown in Fig. 2c. On the other hand, the valley polarization and the corresponding orbital magnetization are also dramatically enhanced with the increase of Ud as shown by the blue and red dots in Fig. 2d. This indicates orbital magnetoelectric effect driven by Coulomb interactions in mirror-symmetric ATMG system with double flat bands.
We note that structural relaxations are usually significant in moiré graphene systems82,83,84,85,86, which may have substantial effects on the electronic structures. Therefore, we have performed the structural relaxation calculations for the A-ABA-A ATMG system based on a realistic elastic model proposed by Koshino et al.87, and we have further calculated the band structures of the A-ABA-A ATMG system with the fully relaxed lattice structures. The main conclusion is that, depending on the twist angles, the structural relaxations can either enhance or reduce the bandwidth of the double flat bands. In particular, we find θ ≈ 0. 9 ∘ seems to be an “optimal" angle at which the double flat bands have a total bandwidth ~25 meV, and are energetically separated from the remote bands by gaps ~10 meV. In the meanwhile, the topological properties of the double flat bands are unchanged by the structural relaxations. Therefore, it is expected that the intertwined polarization-magnetization orders and the interaction-driven orbital magnetoelectric effect are more likely to be realized at θ ≈ 0. 9∘. On the other hand, in experiments the two twist angles at the interfaces of the ATMG system may not be exactly equal in amplitudes. Thus, we also consider the inequality in the amplitudes of the two twist angles, and find that it has very weak effects on the electronic structure. We refer the readers to Supplementary Material for more details about the structural relaxation calculations and the effects of inequality of the two twist angles.
To summarize, in this work we have theoretically studied the electronic structures and interaction effects of alternating twisted multilayer graphene (ATMG) systems. We find that these ATMG systems exhibit various non-interacting band dispersions including one pair of flat bands, one pair of flat bands co-existing with Dirac cones or more generally E(k) ~ kJ(J is positive integer) dispersion, as well as two pairs of flat bands which may also co-exist with E(k) ~ kJ(J is positive integer)dispersion. Based on an analysis from a simplified k⋅p model approach, we find that the low energy band structures of the ATMG system can be described by a set of generic partition rules. We have also considered Coulomb interaction effects in ATMG with A-ABA-A stacking, the simplest mirror-symmetric ATMG system having two pairs of flat bands. We have studied the symmetry-breaking ground states at different integer filling factors under zero external fields based on unrestricted Hartree–Fock calculations. We find that at certain fillings both time-reversal symmetry and the mirror symmetry can be broken spontaneously by Coulomb interactions, leading to gapped states with intertwined electric polarization and orbital magnetization. As a result of such intertwined ordering, the system can exhibit orbital magnetoelectric effect with the orbital magnetization (electric polarization) being highly tunable by external electric (magnetic) field. Our work is a significant step forward in understanding the electronic structures and correlation effects of alternating twisted graphene systems, and will provide useful guidelines for future experimental and theoretical studies.
Methods
The continuum model for alternating twisted multilayer graphene
We define the atomic structure of ATMG starting from three sets of graphene multilayers, denoted as M, L, and N. These multilayers are stacked from bottom to top, where the N(L) layers and the L(M) layers are twisted by an angle θ(−θ). For small twist angles, the slight mismatch between layers gives rise to a long-period moiré supercell. The lattice vectors of the moiré superlattice are: \({{{{\bf{t}}}}}_{1}=(\sqrt{3}{L}_{s}/2,{L}_{s}/2),{{{{\bf{t}}}}}_{2}=(0,{L}_{s})\), where \({L}_{s}=a/(2\sin (\theta /2))\) is the moiré lattice constant, a is the atomic lattice constant of graphene. Like TBG, we consider corrugation effects in AMTG systems, which would lead to a difference between intrasublattice and intersublattic moiré potential parameters.
The low-energy electronic structure of ATMG can be well described based on the Bistritzer-MacDonald continuum model22. The free Dirac fermions from the atomic K and \({K}^{\prime}\) valleys contribute to the low energy states of ATMG. We may consider the low energy states from two different atomic valleys as decoupled at small twist angle, i.e., the total Hamiltonian is block-diagonalized into the two independent valleys. The continuum model of the μ = ∓ (\(K/K^{\prime}\)) valley is:
where \({H}_{N}^{\mu }\), \({H}_{L}^{\mu }\), and \({H}_{M}^{\mu }\) denote the k⋅p Hamiltonians of the untwisted graphene multilayers, which consist of the Dirac fermions of each monolayer graphene and the interlayer hopping terms. \({{\mathbb{U}}}_{\mu }{e}^{i\mu {{\Delta }}{{{\bf{K}}}}\cdot {{{\bf{r}}}}}\) stands for the moiré potential term for valley μ (μ = ∓ for \(K/K^{\prime}\) valley), which arises from the mutual twist between two sets of adjacent multilayers. ΔK = (0, 4π/(3Ls)) is a vector characterizing the shift of Dirac points due to the twist. The details of the continuum Hamiltonian are presented in Supplementary Information.
The ATMG system introduces additional complexity due to the additional twist. We will show that for TTG, i.e., M = L = N = 1, the continuum Hamiltonian for each valley can be decomposed into a TBG-like Hamiltonian and a free Dirac fermion Hamiltonian. For the sake of convenience, we first apply a gauge transformation to the basic functions of the ATMG system: \({\widetilde{\psi }}_{ls,{{{\bf{k}}}}}^{\mu }({{{\bf{r}}}})={\psi }_{ls,{{{\bf{k}}}}}^{\mu }({{{\bf{r}}}}){e}^{i{{{{\bf{K}}}}}_{l}^{\mu }\cdot {{{\bf{r}}}}}\), where \({{{{\bf{K}}}}}_{l}^{\mu }\) denotes the Dirac point of valley μ and layer l, and s is the sublattice index. Such a gauge transformation would remove the phase factor ei±μΔK⋅r in the moiré potential term, and would move the Dirac points of the different twisted layers to the same origin. Then we apply a unitary transformation to the alternating TTG Hamiltonian, \({\tilde{H}}_{TTG}^{\mu }={W}^{{\dagger} }{H}_{TTG}^{\mu }W\). The Hamiltonian after the unitary transformation \({\tilde{H}}_{TTG}^{K}\) is expressed as
where hμ(k) = − \(\hslash\)Fk⋅σμ, with the Pauli matrices σμ = (μσx, σy) defined in the sublattice space, and the unitary transformation matrix W is expressed as
From Eq. (7) it is immediately seen that the total Hamiltonian of alternating twisted trilayer graphene consists of a TBG-like part with the moiré potential rescaled by \(\sqrt{2}\) and a free Dirac fermion part. Moreover, since the magic angle is determined by the ratio between the intersublattice component of the moiré potential and the Fermi velocity, the re-scaled moiré potential in Eq. (7) implies that the magic angle for the TTG system is rescaled by the same factor, i.e., the new magic angle should be \(\sqrt{2}\times 1.0{5}^{\circ }\approx 1.{5}^{\circ }\).
The simplified k⋅p model
We write a simplified k⋅p model to capture the essential low-energy physics, while neglecting the irrelevant high-energy bands obtained from a direct numerical diagonalization of the original continuum model. To construct such a simplified k⋅p model for a generic ATMG system (in the chiral limit), we should first find proper unitary transformations to the original continuum Hamiltonian to decompose it into a form consisting of a TBG-like continuum Hamiltonian and free Dirac fermions, e.g., as illustrated in Eq. (7). For each of the TBG-like terms, we can obtain the zero-mode solution of magic-angle TBG in the chiral limit. The analytical wave functions for the zero modes in magic-angle TBG in the chiral limit are expressed as23:
where \(l=\bar{\alpha },\bar{\gamma }\) refers to the two mix-layer indices, Ψls,K(r) refers to the s (s = A, B) sublattice component of the zero-mode solution at the Dirac point K23. \({f}_{{{{\bf{k}}}}}(z)={\vartheta }_{{a}_{1},{b}_{1}}(z)/{\vartheta }_{{a}_{2},{b}_{2}}(z)\), where ϑa,b(z) is the theta function defined in the previous work23. For the untwisted layers, we take the k⋅p Hamiltonians of the Dirac fermions and expand them around the Dirac points within the moiré Brillouin zone. The coupling between the zero modes from the twisted layers and the Dirac fermions from the untwisted layers can be evaluated by re-expressing the original interlayer hopping matrix on the basis of the zero-mode wavefunctions and the free Dirac-fermion states. We provide details of the simplified k⋅p model and two examples in Supplementary Information.
Hartree–Fock and constrained random phase approximation
We have performed unrestricted self-consistent Hartree–Fock calculations for the A-ABA-A system within the subspace of the double flat bands.
where \(\mu ,{\mu }^{\prime}=\pm\) are the valley indices, \(\alpha ,\alpha ^{\prime}\) are the layer/sublattice indices, and now the wavevectors ka, \({{{{\bf{k}}}}}_{a}^{\prime}\), and qa are expanded around the Dirac point of valley μ (Kμ), which can decomposed as ka = k + Q, where k is the moiré wavevector in moiré Brillouin zone, and Q is the moiré lattice vector. \({\hat{c}}^{{\dagger} }\) and \(\hat{c}\) operators in the above equation are the electron creation and annihilation operators. A single-gate screened Coulomb interaction V(qa) is adopted in this work,
where ΩM is the area of moiré primitive cell, ds ≈ 40 nm is the distance between the ATMG system and the metallic gate, ϵBN ≈ 4 is the dielectric constant of the BN substrate. The Coulomb interactions are further projected onto the double-flat bands, i.e., we can project the electron creation/annihilation operator on the subspace of the double flat bands: \({\hat{c}}_{{{{{\bf{k}}}}}_{a},\mu \alpha \sigma }={\sum }_{n}{C}_{\mu \alpha {{{\bf{G}}}},n}({{{\bf{k}}}}){\hat{c}}_{\mu \sigma ,n{{{\bf{k}}}}}\), where CμαG,n(k) is the non-interacting wavefunction of the nth Bloch eigenstate at moiré wave vector k from valley μ, and the summation of band index n is restricted to the subspace of the double flat bands. We make Hartree–Fock approximations to Eq. (10) to decompose the two-particle interactions into a superposition of the Hartree and Fock mean-field single-particle Hamiltonians, and find self-consistent solutions. Besides, the Coulomb interactions between electrons in the flat bands can be further screened by virtual particle-hole excitations from the remote energy bands, and such screening effects in our calculation are treated with the constrained random phase approximation(cRPA)40,81, where the cRPA dielectric constant is expressed as: \(\epsilon ({{{\bf{q}}}}+{{{\bf{Q}}}})={\epsilon }_{{{{\rm{BN}}}}}{({\mathbb{1}}+{\hat{\chi }}^{0}({{{\bf{q}}}})\hat{V}({{{\bf{q}}}}))}_{{{{\bf{Q}}}},{{{\bf{Q}}}}}\). Here \({\hat{\chi }}^{0}({{{\bf{q}}}})\) is the zero-frequency bare susceptibility at moiré wavevector q, and \(\hat{V}({{{\bf{q}}}})\) is the Coulomb interaction matrix defined in the space of reciprocal moiré lattice vector Q, with \(\hat{V}{({{{\bf{q}}}})}_{{{{\bf{Q}}}},{{{\bf{Q}}}}}=V({{{\bf{q}}}}+{{{\bf{Q}}}})\). We provide more details of the Hartree–Fock and cRPA methods in Supplementary Information.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The codes for the continuum-model calculations are available from the corresponding author upon reasonable request.
References
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Codecido, E. et al. Correlated insulating and superconducting states in twisted bilayer graphene below the magic angle. Sci. Adv. 5, eaaw9770 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Stepanov, P. et al. Untying the insulating and superconducting orders in magic-angle graphene. Nature 583, 375–378 (2020).
Saito, Y., Ge, J., Watanabe, K., Taniguchi, T. & Young, A. F. Independent superconductors and correlated insulators in twisted bilayer graphene. Nat. Phys. 16, 926–930 (2020).
Liu, X. et al. Tuning electron correlation in magic-angle twisted bilayer graphene using coulomb screening. Science 371, 1261–1265 (2021).
Cao, Y. et al. Nematicity and competing orders in superconducting magic-angle graphene. science 372, 264–271 (2021).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Stepanov, P. et al. Competing zero-field chern insulators in superconducting twisted bilayer graphene. Phys. Rev. Lett. 127, 197701 (2021).
Nuckolls, K. P. et al. Strongly correlated chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).
Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators, van hove singularities and topological flat bands in magic-angle twisted bilayer graphene. Nat. Mater. 20, 488–494 (2021).
Das, I. et al. Symmetry-broken chern insulators and rashba-like landau-level crossings in magic-angle bilayer graphene. Nat. Phys. 17, 710–714 (2021).
Pierce, A. T. et al. Unconventional sequence of correlated chern insulators in magic-angle twisted bilayer graphene. Nat. Phys. 17, 1210–1215 (2021).
Shen, C. et al. Correlated states in twisted double bilayer graphene. Nat. Phys. 16, 520–525 (2020).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95 (2019).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. 108, 12233–12237 (2011).
Tarnopolsky, G., Kruchkov, A. J. & Vishwanath, A. Origin of magic angles in twisted bilayer graphene. Phys. Rev. Lett. 122, 106405 (2019).
Liu, J., Liu, J. & Dai, X. Pseudo landau level representation of twisted bilayer graphene: Band topology and implications on the correlated insulating phase. Phys. Rev. B 99, 155415 (2019).
Song, Z. et al. All magic angles in twisted bilayer graphene are topological. Phys. Rev. Lett. 123, 036401 (2019).
Ahn, J., Park, S. & Yang, B.-J. Failure of Nielsen-Ninomiya theorem and fragile topology in two-dimensional systems with space-time inversion symmetry: application to twisted bilayer graphene at magic angle. Phys. Rev. X 9, 021013 (2019).
Po, H. C., Zou, L., Senthil, T. & Vishwanath, A. Faithful tight-binding models and fragile topology of magic-angle bilayer graphene. Phys. Rev. B 99, 195455 (2019).
Ledwith, P. J., Tarnopolsky, G., Khalaf, E. & Vishwanath, A. Fractional chern insulator states in twisted bilayer graphene: an analytical approach. Phys. Rev. Res. 2, 023237 (2020).
Balents, L., Dean, C. R., Efetov, D. K. & Young, A. F. Superconductivity and strong correlations in moiré flat bands. Nat. Phys. 16, 725–733 (2020).
Andrei, E. Y. et al. The marvels of moiré materials. Nat. Rev. Mater. 6, 201–206 (2021).
Liu, J. & Dai, X. Orbital magnetic states in moiré graphene systems. Nat. Rev. Phys. 3, 367–382 (2021).
Kang, J. & Vafek, O. Strong coupling phases of partially filled twisted bilayer graphene narrow bands. Phys. Rev. Lett. 122, 246401 (2019).
Seo, K., Kotov, V. N. & Uchoa, B. Ferromagnetic mott state in twisted graphene bilayers at the magic angle. Phys. Rev. Lett. 122, 246402 (2019).
Xie, M. & MacDonald, A. H. Nature of the correlated insulator states in twisted bilayer graphene. Phys. Rev. Lett. 124, 097601 (2020).
Wu, F. Topological chiral superconductivity with spontaneous vortices and supercurrent in twisted bilayer graphene. Phys. Rev. B 99, 195114 (2019).
Bultinck, N., Chatterjee, S. & Zaletel, M. P. Mechanism for anomalous hall ferromagnetism in twisted bilayer graphene. Phys. Rev. Lett. 124, 166601 (2020).
Wu, F. & Das Sarma, S. Collective excitations of quantum anomalous hall ferromagnets in twisted bilayer graphene. Phys. Rev. Lett. 124, 046403 (2020).
Bultinck, N. et al. Ground state and hidden symmetry of magic-angle graphene at even integer filling. Phys. Rev. X 10, 031034 (2020).
Liu, J. & Dai, X. Theories for the correlated insulating states and quantum anomalous hall effect phenomena in twisted bilayer graphene. Phys. Rev. B 103, 035427 (2021).
Zhang, S., Lu, X. & Liu, J. Correlated insulators, density wave states, and their nonlinear optical response in magic-angle twisted bilayer graphene. arXiv preprint at arXiv:2109.11441 (2021).
Hejazi, K., Chen, X. & Balents, L. Hybrid wannier chern bands in magic angle twisted bilayer graphene and the quantized anomalous Hall effect. Phys. Rev. Res. 3, 013242 (2021).
Kang, J. & Vafek, O. Non-abelian dirac node braiding and near-degeneracy of correlated phases at odd integer filling in magic-angle twisted bilayer graphene. Phys. Rev. B 102, 035161 (2020).
Chen, B.-B. et al. Realization of topological mott insulator in a twisted bilayer graphene lattice model. Nat. Commun. 12, 5480 (2021).
Lu, C., et al. Chiral so (4) spin-charge density wave and degenerate topological superconductivity in magic-angle-twisted bilayer-graphene. arXiv Preprint arXiv:2003.09513 (2020).
Da Liao, Y. et al. Correlation-induced insulating topological phases at charge neutrality in twisted bilayer graphene. Phys. Rev. X 11, 011014 (2021).
Bernevig, B. A., Song, Z.-D., Regnault, N. & Lian, B. Twisted bilayer graphene. iii. Interacting hamiltonian and exact symmetries. Phys. Rev. B 103, 205413 (2021).
Lian, B. et al. Twisted bilayer graphene. iv. Exact insulator ground states and phase diagram. Phys. Rev. B 103, 205414 (2021).
Xie, F. et al. Twisted bilayer graphene. vi. An exact diagonalization study at nonzero integer filling. Phys. Rev. B 103, 205416 (2021).
Soejima, T., Parker, D. E., Bultinck, N., Hauschild, J. & Zaletel, M. P. Phys. Rev. B 102, 205111 (2020).
Potasz, P., Xie, M. & MacDonald, A. H. Exact diagonalization for magic-angle twisted bilayer graphene. Phys. Rev. Lett. 127, 147203 (2021).
Zhang, X., Pan, G., Zhang, Y., Kang, J. & Meng, Z. Y. Momentum space quantum Monte Carlo on twisted bilayer graphene. Chin. Phys. Lett. 38, 077305 (2021).
Hofmann, J. S., Khalaf, E., Vishwanath, A., Berg, E. & Lee, J. Y. Fermionic Monte Carlo study of a realistic model of twisted bilayer graphene. Phys. Rev. X 12, 011061 (2022).
Parker, D. E., Soejima, T., Hauschild, J., Zaletel, M. P. & Bultinck, N. Strain-induced quantum phase transitions in magic-angle graphene. Phys. Rev. Lett. 127, 027601 (2021).
He, W.-Y., Goldhaber-Gordon, D. & Law, K. T. Giant orbital magnetoelectric effect and current-induced magnetization switching in twisted bilayer graphene. Nat. Commun. 11, 1650 (2020).
Zhu, J., Su, J.-J. & MacDonald, A. H. Voltage-controlled magnetic reversal in orbital chern insulators. Phys. Rev. Lett. 125, 227702 (2020).
Huang, C., Wei, N. & MacDonald, A. H. Current-driven magnetization reversal in orbital chern insulators. Phys. Rev. Lett. 126, 056801 (2021).
Ying, X., Ye, M. & Balents, L. Current switching of valley polarization in twisted bilayer graphene. Phys. Rev. B 103, 115436 (2021).
Liu, J., Ma, Z., Gao, J. & Dai, X. Quantum valley hall effect, orbital magnetism, and anomalous hall effect in twisted multilayer graphene systems. Phys. Rev. X 9, 031021 (2019).
Lee, J. Y. et al. Theory of correlated insulating behaviour and spin-triplet superconductivity in twisted double bilayer graphene. Nat. Commun. 10, 5333 (2019).
Koshino, M. Band structure and topological properties of twisted double bilayer graphene. Phys. Rev. B 99, 235406 (2019).
Liu, X. et al. Tunable spin-polarized correlated states in twisted double bilayer graphene. Nature 583, 221–225 (2020).
Cao, Y. et al. Tunable correlated states and spin-polarized phases in twisted bilayer–bilayer graphene. Nature 583, 215–220 (2020).
Polshyn, H. et al. Electrical switching of magnetic order in an orbital chern insulator. Nature 588, 66–70 (2020).
Chen, S. et al. Electrically tunable correlated and topological states in twisted monolayer–bilayer graphene. Nat. Phys. 17, 374–380 (2021).
He, M. et al. Symmetry breaking in twisted double bilayer graphene. Nat. Phys. 17, 26–30 (2021).
Xu, S. et al. Tunable van hove singularities and correlated states in twisted monolayer–bilayer graphene. Nat. Phys. 17, 619–626 (2021).
Zhang, S., Dai, X. & Liu, J. Spin-polarized nematic order, quantum valley hall states, and field-tunable topological transitions in twisted multilayer graphene systems. Phys. Rev. Lett. 128, 026403 (2022).
Ma, Z. et al. Topological flat bands in twisted trilayer graphene. Sci. Bull. 66, 18–22 (2021).
Kim, H. et al. Spectroscopic signatures of strong correlations and unconventional superconductivity in twisted trilayer graphene. arXiv Preprint at arXiv:2109.12127 (2021).
Cao, Y., Park, J. M., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Pauli-limit violation and re-entrant superconductivity in moiré graphene. Nature 595, 526–531 (2021).
Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Tunable strongly coupled superconductivity in magic-angle twisted trilayer graphene. Nature 590, 249–255 (2021).
Liu, X. et al. Isospin order in superconducting magic-angle twisted trilayer graphene. Nat. Phys. (2022).
Khalaf, E., Kruchkov, A. J., Tarnopolsky, G. & Vishwanath, A. Magic angle hierarchy in twisted graphene multilayers. Phys. Rev. B 100, 085109 (2019).
Li, X., Wu, F. & MacDonald, A. H. Electronic structure of single-twist trilayer graphene. arXiv Preprint at arXiv: 1907.12338 (2019).
Liu, Z., Shi, W., Yang, T. & Zhang, Z. Magic angles and flat chern bands in alternating-twist multilayer graphene system. J. Mater. Sci. Technol. 111, 28–34 (2022).
Christos, M., Sachdev, S. & Scheurer, M. S. Superconductivity, correlated insulators, and Wess-Zumino-Witten terms in twisted bilayer graphene. Proc. Natl Acad. Sci. 117, 29543–29554 (2020).
Xie, F., Regnault, N., Călugăru, D., Bernevig, B. A. & Lian, B. Twisted symmetric trilayer graphene. ii. projected Hartree-Fock study. Phys. Rev. B 104, 115167 (2021).
Călugăru, D. et al. Twisted symmetric trilayer graphene: single-particle and many-body hamiltonians and hidden nonlocal symmetries of trilayer moiré systems with and without displacement field. Phys. Rev. B 103, 195411 (2021).
Min, H. & MacDonald, A. H. Electronic structure of multilayer graphene. Prog. Theor. Phys. Suppl. 176, 227–252 (2008).
Zhang, S., Xie, B., Wu, Q., Liu, J. & Yazyev, O. V. Chiral decomposition of twisted graphene multilayers with arbitrary stacking. arXiv Preprint at arXiv:2012.11964 (2020).
Vanhala, T. I. & Pollet, L. Constrained random phase approximation of the effective Coulomb interaction in lattice models of twisted bilayer graphene. Phys. Rev. B 102, 035154 (2020).
Uchida, K., Furuya, S., Iwata, J.-I. & Oshiyama, A. Atomic corrugation and electron localization due to moiré patterns in twisted bilayer graphenes. Phys. Rev. B 90, 155451 (2014).
Angeli, M. et al. Emergent D6 symmetry in fully relaxed magic-angle twisted bilayer graphene. Phys. Rev. B 98, 235137 (2018).
Nam, N. N. T. & Koshino, M. Lattice relaxation and energy band modulation in twisted bilayer graphene. Phys. Rev. B 96, 075311 (2017).
Cantele, G. et al. Structural relaxation and low-energy properties of twisted bilayer graphene. Phys. Rev. Res. 2, 043127 (2020).
Liu, X., Peng, R., Sun, Z. & Liu, J. Phonons in magic-angle twisted bilayer graphene. arXiv Preprint at arXiv: 2112.13240 (2021).
Koshino, M. & Son, Y.-W. Moiré phonons in twisted bilayer graphene. Phys. Rev. B 100, 075416 (2019).
Acknowledgements
This work is supported by the National Key R & D program of China (grant no. 2020YFA0309601), the National Science Foundation of China (grant no. 12174257), and the start-up grant of ShanghaiTech University. We thank the HPC platform of ShanghaiTech University for providing the computational resource.
Author information
Authors and Affiliations
Contributions
J.P.L. conceived and supervised this project. B.X. performed the continuum-model calculations and k⋅p model analysis. B.X. and S.H.Z. performed the mean-field calculations. B.X. and R.P. performed the structural relaxation calculations. B.X. and J.P.L. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xie, B., Peng, R., Zhang, S. et al. Alternating twisted multilayer graphene: generic partition rules, double flat bands, and orbital magnetoelectric effect. npj Comput Mater 8, 110 (2022). https://doi.org/10.1038/s41524-022-00789-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00789-5
This article is cited by
-
The interlayer twist effectively regulates interlayer excitons in InSe/Sb van der Waals heterostructure
npj Computational Materials (2024)
-
Doubled Moiré flat bands in double-twisted few-layer graphite
Science China Physics, Mechanics & Astronomy (2023)