Abstract
Two-dimensional materials with ferroelectric properties break the size effect of conventional ferroelectric materials and unlock unprecedented potentials of ferroelectric-related application at small length scales. Using first-principles calculations, a sliding-induced ferroelectric-to-antiferroelectric behavior in bilayer group-IV monochalcogenides (MX, with M = Ge, Sn and X = S, Se) is discovered. Upon this mechanism, the top layer exhibits a reversible intralayer ferroelectric switching, leading to a reversible transition between the ferroelectric and antiferroelectric states in the bilayer MXs. Further results show that the interlayer van der Waals interaction, which is usually considered to be weak, can actually generate an in-plane lattice distortion and thus cause the breaking/forming of intralayer covalent bonds in the top layer, leading to the observed anomalous phenomenon. This unique property has advantages for energy harvesting over existing piezoelectric and triboelectric nanogenerators. The interlayer sliding-induced big polarization change (40 μC cm−2) and ultrahigh polarization changing rate generate an open-circuit voltage two orders of magnitude higher than that of MoS2-based nanogenerators. The theoretical prediction of power output for this bilayer MXs at a moderate sliding speed 1 m s−1 is four orders of magnitude higher than the MoS2 nanogenerator, indicating great potentials in energy harvesting applications.
Similar content being viewed by others
Introduction
Ferroelectric (FE) materials possessing stable and switchable spontaneous electric polarization are essential elements in many technology applications, including memories, field-effect transistors, solar cells, sensors, and actuators. Over the past decade, advances in two-dimensional (2D) functional materials have stimulated broad research interest in 2D ferroelectrics1. Compared with traditional FE materials, 2D ferroelectrics are more easily integrated as functional components in miniaturized electronic devices owing to their intrinsic nanoscale size and ferroelectricity without the limitation of the size effect2. Following extensive theoretical predictions of 2D FE materials in the past few years, ferroelectricity has been experimentally observed in some 2D materials with thicknesses as low as several unit cells and even one unit cell2,3,4,5,6. Similar to conventional ferroelectrics, the intrinsic intralayer polarization of 2D materials usually originates from an asymmetric crystal structure caused by atom displacement and/or asymmetric charge redistribution. For example, a distorted SnTe monolayer was experimentally detected, giving rise to a robust in-plane intralayer polarization2. The displacement of Mo atoms breaks the inversion symmetry of 1T-MoS2 and results in an out-of-plane intralayer polarization7,8. A similar atomic displacement and lattice distortion-induced polarization has also been found in CuInP2S63, In2Se39, and elemental group-V monolayer materials10. The intralayer electric polarization of 2D FE materials can be as high as 48 μC cm−2, which is comparable with that of conventional FE materials11.
Moreover, 2D materials offer new artificial designation approaches, e.g., interlayer sliding, to induce non-intrinsic ferroelectricity owing to their unique layered crystal structures. The relatively weak interlayer van der Waals (vdW) interaction allows 2D materials to stack freely without being limited by the directional atomic bonds or lattice mismatch and endows these materials with diverse stacking-dependent properties12,13,14,15. Tuning stacking order can break the centrosymmetric nature of the crystal and induce interlayer charge transfer in bilayers or few-layer 2D materials, such as WTe25, VS2 bilayers16, and BN bilayers17,18,19,20, which then leads to an out-of-plane interlayer electric polarization. Interlayer sliding is predicted to change the interlayer potential and switch the polarization from upward to downward17,21,22. This is an interesting phenomenon since it provides a new way to control the FE polarization in addition to the conventional electric field. Such unique properties could stimulate novel concepts for various applications, such as triboelectric nanogenerators (NGs) for energy harvesting. However, the interlayer charge transfer is weak, and the obtained FE polarization is less than 0.68 μC cm−2, i.e., two orders of magnitude smaller than that of conventional FE BaTiO3 (30 μC cm−2)20,23. The dilemma is the following: while, on one side, the weak interlayer interaction gives rise to interlayer sliding-controlled ferroelectrics, on the other side, it severely limits the polarization magnitude and thus the applications.
In light of the large intralayer FE polarization of some 2D materials11,24,25,26, a natural question arises: is it possible to use interlayer sliding to switch the intralayer polarization and thus solve the dilemma? Intuitively, this sounds very unlikely since the interlayer vdW interaction is very weak, whereas intralayer atom displacement is usually constrained by strong chemical bonds. In this work, using density functional theory (DFT) calculations, we prove this hypothesis for bilayer group-IV monochalcogenides, namely MX (M = Ge, Sn; X = S, Se), thus revealing a huge potential for 2D ferroelectrics. MXs have a distorted puckered structure that generates a considerably large intralayer FE polarization in all predicted 2D ferroelectrics1,27. Our results show that a mechanical interlayer sliding can trigger a direction change of the electric polarization of the top layer, leading to a reversible transition between the FE and antiferroelectric (AFE) states of bilayer MXs. Our in-depth analysis shows that, under different stacking orders of bilayer MXs, the out-of-plane interlayer vdW interaction can induce an in-plane lattice distortion and thus promote intralayer covalent bond breaking/forming in the top layer. This new sliding-induced FE-to-AFE phenomenon shows that the robust intralayer FE polarization in 2D materials can be switched not only by external fields, as is traditionally done28,29,30,31, but also by this unique interlayer sliding mechanism. Under a sliding speed of 1 m s−1, the large polarization switching occurring within the nanoscale atomic lattice leads to an alternating displacement current with ultrahigh frequency. For example, a bilayer MX flake with a length of 10 nm can in principle generate a short-circuit current of 35 nA and a maximum power output of 107 nW, which is four orders of magnitude higher than the state-of-the-art MoS2-based NG32. The superior electrical performance renders bilayer MXs promising candidates for potential application as NGs and energy harvesting devices. Through the recently obtained advances in 2D material tribology, many techniques have been developed to precisely manipulate interlayer sliding33,34,35. Therefore, it is of great relevance to implement these findings in real-world applications.
Results and discussion
Stacking order of bilayer MX and FE/AFE state
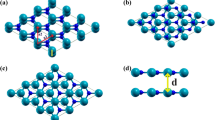
Monolayer group-IV monochalcogenides, namely MX (M = Ge, Sn; X = S, Se), have a hinge-like crystal structure similar to that of black phosphorene36,37. Due to the broken centrosymmetry in the monolayer, a considerable spontaneous electric polarization, ranging from 18 to 48 μC cm−2, exists along the x (armchair) direction (Fig. 1a) and is retained at room temperature26,30,38,39. For bilayer MXs stacked together by two monolayers, as shown in Fig. 1b, there are four high-symmetry stacking orders (8 atoms per unitcell). The AA stacking order refers to the top layer being precisely matched with the bottom layer in the x–y plane. Compared with the AA stacking, the AB stacking corresponds to the top layer being shifted by a half lattice constant along the x-direction, i.e., by 0.5a (where a is the lattice constant in the armchair direction). Shifting the top layer by a half lattice constant 0.5b along the y-direction (where b is the lattice constant in the zigzag direction) yields the AC stacking. Finally, moving the top layer by a half lattice constant along both the x- and y-direction results in the AD stacking. As each monolayer exhibits intrinsic FE polarization, bilayer MX can be constructed with either parallel or anti-parallel polarization coupling between the two layers for a given stacking order. Consequently, a specific stacking order exhibits either an FE state or an AFE state (Fig. 1c).
a Monolayer MX crystal structure with a built-in spontaneous FE polarization along the armchair (x-) direction. b Four high-symmetry stacking orders of bilayer MX. Placing the top layer onto the (0, 0), (0.5, 0), (0, 0.5), and (0.5, 0.5) positions in the x-y plane with respect to the bottom layer leads to the AA, AB, AC, and AD stacking orders, respectively. c The FE polarization of the top and bottom layers can be parallel or anti-parallel, leading to the FE or AFE state, respectively. The total energy differences between the FE and AFE states for bilayer MX are illustrated for the four different stacking orders. For all investigated MX materials, the AA and AC stacking orders prefer the FE state, whereas the AB and AD stacking orders prefer the AFE state.
The energetic orders of these bilayer MXs for these four staking orders and corresponding two electric polarization states were investigated via DFT calculations. In these DFT calculations, the relative position of the two layers was fixed, while the lattice constants and interlayer spacing were allowed to relax. Supplementary Table 1 summarized the results. For bilayer MXs under the FE state, the AC stacking order, here denoted by ACFE, is the most stable. The general energetic order trend is as follows: ACFE < ABFE < AAFE < ADFE. By contrast, for the AFE state, bilayer MXs with the ABAFE stacking order are the most stable, and ACAFE is the second most stable stacking order structure. GeSe, SnS, and SnSe bilayers have AAAFE < ADAFE, which is similar to the FE state. However, the opposite is true for GeS bilayers.
Figure 1c shows the energy difference between the FE and AFE states for each stacking order. For all these bilayer MXs, the AA and AC stacking orders prefer the FE state, but the AB and AD stacking orders prefer the AFE state. Although the bulk allotrope of these four MX materials has an AFE configuration, both the FE and AFE states in 2D nanoscale materials have been successfully fabricated and characterized in experiments29,31,40,41. Based on these results, we speculate that the change of stacking order via mechanical interlayer sliding (in tribology) could lead to the intralayer polarization switching of top layer, thus, for bilayer MXs, corresponding to a phase transition between the FE and AFE states. Such a phase transition and resultant polarization change/switch has not yet been reported.
Interlayer sliding-induced reversible FE-to-AFE transition and polarization switching
Using DFT calculations, the total energies and the polarization variation (in the x-direction) of bilayer MX were examined through a progressive mechanical sliding of the top layer with respect to the bottom layer. The ACFE state was taken as the starting point. Note that, owing to the significant advances obtained in 2D material tribology in the past few years, precise control of mechanical interlayer sliding in various 2D materials has been achieved 33,34,42,43.
Bilayer SnSe is here taken as an example to demonstrate the variation of atomic structure in Fig. 2a and the polarization variation along two sliding pathways that connect two high-symmetry stacking orders: from AC to AD in Fig. 2b and from AC to AB in Fig. 2c. Note that bilayer SnSe exhibits a stable FE state for the AC stacking and a stable AFE state for both AD and AB stackings (Fig. 1c). As the top layer moves toward the AD stacking along the x-direction (Fig. 1b), the horizontal Sn–Se bonds in the top layer break and reconnect with another neighbor. At the same time, the vertical Sn–Se bonds gradually tend to perpendicular with the x–y plane and finally rotate into the opposite direction. Figure 2b shows a gradual reduction of Ps from 40 to ~30 μC cm−2 followed by an abrupt drop to nearly zero at a sliding distance of 0.128a. After careful inspection of the crystal structure (Supplementary Fig. 1), it was found that the top layer had switched the polarization direction via breaking and forming of Sn–Se covalent bonds. The anti-parallel polarization of the two layers forms an AFE state. This AFE state remains unchanged until the top layer continues to slide into the ADAFE state. In the reverse sliding direction (starting from the ADAFE state), bilayer SnSe remains in the AFE state until the relative sliding distance reaches 0.021a. At this critical point, a sharp increase of Ps from zero to ~40 μC cm−2 is observed, indicating a phase transition back to the FE state. Indeed, the analysis of the crystal structures shows that the polarization of the top layer switches back to the initial state during this backward sliding process (Supplementary Fig. 1). Therefore, the observed phase transition between ACFE and ADAFE is reversible and occurs spontaneously. The different critical phase transition points in these two opposite sliding directions result in a hysteresis loop, as shown in Fig. 2b. Similarly, Fig. 2c shows the pathway from AC to AB. Ps decreases slightly to 35 μC cm−2 and then drops abruptly to nearly zero at a sliding distance of 0.115a in the x-direction. Again, via inspection of the atomic structures (Supplementary Fig. 1), a crystal structure change of the top layer similar to that of the AC–AD case is observed, i.e., breaking and subsequent forming of Sn–Se covalent bonds. A backward mechanical sliding results in a sudden increase of Ps to 40 μC cm−2 at 0.06a, indicating a spontaneous reverse phase transition to the FE state.
a The variation of atomic structures in the sliding process. b FE polarization Ps and total energy difference as functions of the sliding distance (along the x-direction) of the top layer from the AC to the AD stacking order for bilayer SnSe. The sudden drop in the increase of Ps at the critical sliding distance of 0.128a or 0.021a indicates the spontaneous FE-to-AFE or AFE-to-FE phase transition, respectively. A hysteresis loop can be observed, which is analogous to that of the traditional FE materials under external electric field stimulus. At the two critical transition points, bilayer SnSe suddenly releases energy and transforms into the more stable phase. The energy crossing point is between the two critical points. c Ps and total energy difference as functions of the sliding distance (along the diagonal direction in the x–y plane) from the AC stacking to the AB stacking. Similar phase transitions and hysteresis loop can be observed. A double-well-like curve due to the metastable AB stacking is shown (different from the unstable AD stacking). d–g Contour plots of Ps as a function of the mechanical sliding distance (leading to different stacking orders) for SnS, SnSe, GeS, and GeSe, respectively. The color bar denotes the Ps magnitude of bilayer MX. The black dotted lines represent the phase boundary between the FE and AFE states. The tribological mechanical sliding of the top layer across the boundary leads to the reversible FE-to-AFE phase transition, i.e., reversible switching of the FE polarization. This new phenomenon is here referred to as tribo induced FE-to-AFE behavior.
Moreover, the relative total energy change versus interlayer sliding was investigated. The bottom plot of Fig. 2b shows the case of the corresponding path from AC to AD. The total energy of ACFE is here taken as reference. Starting from ACFE, the relative energy shows a parabolic-like increase until a sliding distance of 0.128a, at which point the energy suddenly drops, corresponding to the FE-to-AFE phase transition. The energy then increases following another smooth curve till the AD stacking is reached. It should be noted that ADAFE is at the top of the energy curve and is thus mechanically unstable. Once the mechanical sliding constraints applied to the top layer are released, the top layer slides spontaneously in the backward direction. In the backward sliding process, the bilayer SnSe energy follows the second smooth energy curve till 0.021a, at which point the energy drops, corresponding to the AFE-to-FE phase transition in the curve of polarization. These two smooth energy curves clearly correspond to the FE (black) and AFE (red) states, respectively. They have a crossing point at ~0.08a, which separates the stable FE and AFE regions. Note that the two observed spontaneous phase transitions do not take place at this crossing point. This can be attributed to the presence of an energy barrier that will be discussed later. The bottom plot of Fig. 2c shows the variation of the relative total energy along the AC–AB sliding pathway. In contrast to ADAFE in Fig. 2b, ABAFE is a metastable structure with an energy barrier of 18 meV per atom (i.e., 144 meV per cell) that separates it from the ground state ACFE. Upon releasing the sliding constraints, bilayer SnSe remains in the ABAFE stacking order. This phenomenon could be used in information storage applications.
Furthermore, comprehensive DFT calculations were conducted to obtain the variation of the electric polarization and total energy as a function of the interlayer sliding in the whole x–y plane. Fig. 2d, e shows the polarization-sliding map for SnS and SnSe, respectively. Supplementary Fig. 2 shows the total energy landscape. Note that these two maps are obtained by progressively sliding the top layer along various sliding pathways (starting from the ACFE state) in DFT calculations. For SnS and SnSe, neither FE nor AFE has a complete energy landscape across the whole x–y sliding plane due to the spontaneous phase transition. Therefore, the FE and AFE energy landscapes were combined together (Supplementary Fig. 2), and the phase boundary is depicted with a dotted line in Fig. 2d, e. At the boundary, the FE and AFE states have equal total energy values. The middle region of the x–y sliding plane represents the stable AFE state. ACFE and ABAFE are stable states for SnS and SnSe, whereas AAFE and ADAFE are unstable states. Across the phase boundary, there is a significant Ps drop from 40–60 μC cm−2 to zero (Fig. 2d, e).
Similarly, Fig. 2f, g show the polarization-sliding map of GeS and GeSe, and Supplementary Fig. 3 illustrates the corresponding energy landscapes. Through DFT calculations, one energy landscape is obtained for the FE state and another one for the AFE states across the whole x–y sliding plane. The energy differences between the states are shown in Supplementary Fig. 3 c, f for GeS and GeSe, respectively. The intersection curves of the two energy landscapes are projected onto the x–y plane and indicated by dashed lines. They represent the theoretical phase boundaries that separate the stable FE and AFE regions. Combining the phase diagram (Supplementary Fig. 3) and polarization contour map (Supplementary Fig. 4), the theoretical polarization phase diagrams for GeS and GeSe can be obtained, as shown in Fig. 2f, g, respectively. A sharp change of Ps takes place across the boundary. Due to the energy barrier, the FE-to-AFE phase transitions cannot spontaneously take place during mechanical sliding, but can occur at a specific finite temperature.
The nudged elastic band (NEB) method44,45 was adopted in the DFT calculations to determine the energy barrier (Supplementary Fig. 5). In the vicinity of the phase boundary, the energy barriers of bilayer GeS and GeSe are about 78 and 33 meV per atom, respectively. They are comparable with the thermal excitation energy at ambient conditions (~26 meV per atom at 300 K). Thus, GeSe could exhibit the phase transition near room temperature, whereas GeS might need an elevated temperature for the phase transition to occur. From a thermodynamics perspective, mechanical sliding across the boundaries would lead to a reversible FE-to-AFE phase transition. In contrast, SnS and SnSe have an almost vanishing energy barrier near their phase boundary, which is consistent with the observed spontaneous phase transition.
Here DFT calculations clearly indicate that the FE-to-AFE phase transition is feasible upon mechanical interlayer sliding for these bilayer MXs. Such an anomalous behavior is distinctive from traditional ferroelectricity and ferroelectricity reported in 2D ferroelectrics, where the electrical polarization is usually manipulated by an external electric field2,30,31. Indeed, the ferroelectricity observed in this work originates from the layered crystal structures of vdW materials and the corresponding easy mechanical interlayer sliding. Additionally, the electric polarization can be changed from 0 to about 40–90 μC cm−2, which is higher than the polarization of the more commonly used BaTiO3, which exhibits a Ps of ~30 μC cm−2 in its tetragonal phase46,47, and of the interlayer ferroelectricity in bilayer WTe2 (less than 0.1 μC cm−2), and bilayer BN (less than 0.68 μC cm−2), whose polarization originates from the asymmetric stacking-induced charge transfer between layers5,20,21,23.
Physical origins of the observed tribo induced FE-to-AFE phenomena
The FE-to-AFE phase transition of the discovered phenomenon involves covalent bonds breaking and forming within the MX layer (Supplementary Fig. 1). This is surprising as conventional knowledge suggests that interlayer vdW interactions are much weaker than intralayer chemical bonds. In the past, to change the intralayer crystal structure and thus achieve polarization switching, either an external stress or an electric field had to be directly applied to the given layer11,28,30. Note that some recent studies have shown that the interlayer vdW interaction could stabilize stacked crystal structures in some few-layer vdW materials (e.g., the AA stacking of few-layer SnS and the AFE state of CuInP2S6 group) contrary to their bulk counterparts31,48,49. However, the reversible intralayer chemical bonds reconfiguration caused by interlayer interactions has not been reported before. It is thus relevant to investigate the physical origins of this anomalous phenomenon.
A careful inspection of the crystal structures reveals that interlayer sliding leads to structural distortions. When two fully relaxed monolayers stack together, the interlayer interaction lowers the total energy of the bilayer system, which is directly correlated to the interlayer vertical distance in the sliding process (Supplementary Fig. 6). It should be noted that one stacked layer is slightly different from the previous fully relaxed monolayer because the intralayer bonds and lattice constants are slightly changed by the interlayer interaction (Supplementary Fig. 7). As listed in Supplementary Table 1, the lattice strain in the x-direction became as large as 2%. The strain here is calculated related to the lattice constants of the corresponding ground state, ACFE stacking. For quantitative analysis, the total energy of bilayer MX was split into three components:
where EMX is the total energy of the fully relaxed monolayer MX, Eε is the strain energy of the top and bottom layers, and Einter is the interlayer interaction between the slightly deformed layers. The observed lattice distortion (Eε) should be attributed to the sliding-induced interlayer interaction changes (Einter). Taking SnSe as an example, we calculated the total energy of the rigid bilayer SnSe during its transition from the AC to the AD stacking and compared it with those of the relaxed cases (Supplementary Fig. 8). Figure 3a shows the Einter and Eε results separately. Comparing the relaxed curve (with lattice distortion) with the rigid case (no lattice distortion), it is noticed that the lattice distortion significantly reduces Einter while only slightly increasing Eε.
a Comparison of Einter/Eε of the relaxed and rigid bilayer SnSe upon mechanical sliding of the top layer. The significant interlayer energy Einter reduction dominates over the lattice strain energy increase in the relaxed SnSe bilayer, thus driving the lattice distortion. b Einter and c Eε of the relaxed bilayer SnSe upon mechanical sliding from ACFE to ADAFE. As the sliding distance from ACFE increases, Eε increases and exhibits a sudden drop at the FE-to-AFE transition. In the reverse sliding process, Eε first decreases and then increases before suddenly dropping at the AFE-to-FE transition. The change of Eε is consistent with that of Etot with a similar magnitude, indicating that the strain energy change is the origin for the observed spontaneous FE-to-AFE effect in bilayer SnSe. A similar conclusion can also be drawn for bilayer SnS. d Calculated energy barrier between the FE and AFE states of bilayer SnSe for different sliding positions along the pathway from ACFE to ADAFE. S0.050 denotes sliding at the position x = 0.05a. The energy barrier gradually vanishes. At a sliding distance of 0.09a (i.e., S0.09), the FE state has a higher total energy than the AFE state, but an energy barrier still exists. e Variation of the unit cell rectangularity of bilayer SnSe during the sliding process from ACFE to ADAFE. The spontaneous phase transition takes place at minimum values of the rectangularity, suggesting the correlation. f The phase transition energy barrier depends on the unit cell rectangularity for both bilayer SnSe and monolayer SnSe. Upon reducing the rectangularity, the energy barrier decreases and eventually disappears. The agreement between bilayer and monolayer SnSe indicates that the sliding-induced lattice distortion plays a primary role in the energy barrier.
To explore the driving force of the FE-to-AFE transition, an energy analysis for the FE and AFE phases was conducted for SnSe transitioning from the AC to the AD stacking. In principle, the drop of total energy is the driving force for phase transition. At the critical points, it is consisted of two parts, the interlayer interaction energy (Einter) and the structural strain energy (Eε). Figure 3b, c summarizes the variation of them, although their absolute value is comparable, their changes at the critical points are quite different. The former not drop but slightly rises at critical points, while the latter drops clearly, and the value of this energy drop is comparable with that drop of total energy in Fig. 2b, indicating that Eε is the driving force behind the transition. Specifically, it can be observed from Fig. 3c that Eε increases as the top layer slides away from the ACFE state and then exhibits a sudden drop of 4.2 meV per atom to the AFE state at the phase transition point. In the reverse sliding process, Eε gradually increases till the phase transition returns to the FE state, at which point an energy drop of 4.1 meV per atom is observed. The magnitude of the Eε change is close to that of Etot, indicating that the lattice strain energy relaxation is a key driving force for the tribo induced FE-to-AFE phase transition of bilayer SnSe. By further splitting Eε into the two different contributions from the top and bottom layers (Supplementary Fig. 9), the top layer strain energy undergoes a minor drop during the phase transition. The observed Eε change in Fig. 3c for bilayer SnSe originates from the bottom layer, indicating that the release of strain energy in the bottom layer contributes more to the FE-to-AFE phase transition. In the reverse ADAFE-to-ACFE process (Supplementary Fig. 9), the strain energy of the top and bottom layers decreases by 2.47 and 1.66 meV per atom, respectively, revealing that the release of strain energy for both layers contributes to the reverse phase transition. The Eε can be further split into the part from cell deformation (Eε-cell) and another part from internal degree of freedom (Eε-internal), which are defined in Supplementary Note 2. Within the AC-to-AD sliding process, the Eε-internal is dominant to release the strain energy, while during the backward sliding process, the Eε-cell becomes dominant to relax the system.
The lattice distortion also has a critical role in setting the energy barrier separating the FE from the AFE state. Figure 3d presents the energy barrier results between the FE and AFE states for bilayer SnSe at different sliding distances from ACFE to ADAFE. When the sliding distance is far away from the transition point, e.g., 0.05a, the FE state needs to overcome an energy barrier of 1.2 meV per atom to transform into the AFE state. Upon further sliding, the FE state gradually becomes metastable compared with the AFE state, and the energy barrier keeps decreasing. Upon reaching 0.127a (close to the critical point of 0.128a), the energy barrier is nearly zero. The phase transition thus happens spontaneously, which is consistent with Fig. 2b. In our energy barrier calculations, it was noticed that the transition state has a unit cell with an a/b ratio much closer to one (cubic-like) than those of the initial FE state and final AFE state. To quantitatively investigate the influence of the unit cell shape, the unit cell rectangularity is defined as:
where a and b are the lattice parameters in the armchair and zigzag direction, respectively. Figure 3e shows the rectangularity of bilayer SnSe during mechanical sliding. Upon sliding, the rectangularity continuously decreases from about 0.04 to a minimum value of about 0.02 and then shows a sudden jump at the FE-to-AFE phase transition (black line in Fig. 3e). The reverse process is similar, and the rectangularity in this case reaches a minimum value <0.01 at the phase transition (red line in Fig. 3e). These results indicate that a small rectangularity strongly correlates with the disappearance of the energy barrier. Indeed, Fig. 3f shows the quantitative confirmation of such correlation. This figure demonstrates that the energy barrier decreases with decreasing rectangularity. A near-zero energy barrier is achieved when the rectangularity becomes smaller than 0.025. Moreover, the energy barriers of bilayer SnSe (hollow symbols) were compared with those of monolayer SnSe (solid symbols) for the same lattice constants (thus, for the same rectangularity). The comparable energy barrier values clearly indicate that lattice strain is the physical origin behind the energy barrier change rather than the interlayer interaction.
Through the mechanical sliding process, the vdW force leads to a significant lattice strain for bilayer SnS and SnSe, drastically reducing their rectangularity. This gives rise to a vanishing energy barrier and, consequently, to a spontaneous phase transition. On the contrary, the ACFE states of bilayer GeS and GeSe have a large rectangularity, 0.20 and 0.12, respectively (Supplementary Fig. 10). These rectangularity values did not reduce, but instead increased to 0.22 and 0.13, upon sliding close to the phase boundary (Fig. 2). The relatively high rectangularity values are likely the reason for the calculated non-zero energy barrier in the vicinity of the phase boundary (Supplementary Fig. 5). For the FE-to-AFE phase transition to take place, some external stimulus, such as temperature, electric field, or applied stress, is required to assist the interlayer sliding for bilayer GeS and GeSe.
The above shows that vdW interaction is robust in layered MX materials. The presence of vdW interaction reduced the energy barrier of polarization switching, implying the low cost of intralayer bonds breaking. In fact, recent studies also demonstrated that the vdW forces are not weak at interfaces. In some cases, the vdW interactions may dominate the interfacial interactions, and lead to an equal stability (bistable) phenomenon as compared to the chemical bonds50,51. These findings present a breakthrough understanding of vdW interaction in condensed matter physics, offering strong support for our discovery.
Performance of the tribo induced FE-to-AFE device as NG
NGs are an emerging technology: they harvest energy from the ambient environment for self-powered micro/nanosystems. It is well established that the energy harvesting performance of NGs depends on the polarization-related displacement current:
Polarization change is the key factor for the electrical output52. In piezoelectric nanogenerators (PENGs), such as monolayer MoS2, polarization change is obtained by applying an external strain, a phenomenon that is known as piezoelectricity32,53. Triboelectric nanogenerators (TENGs) obtain polarized charges through contact electrification (triboelectricity) and convert mechanical energy into electricity via electrostatic induction54. Notice that the polarization change (~40 μC cm−2) induced by the FE-to-AFE phase transition herein is two orders of magnitude higher than that of PENGs (~0.27 μC cm−2 for monolayer MoS2), which should lead to a much higher open-circuit voltage (proportional to the polarization change). The time during which the polarization change occurs is only ~0.5 ns under a moderate interlayer sliding speed of 1 m s−1. In other words, the rate of polarization change of this behavior is ultrahigh and can generate a considerable displacement current in principle. Such an intrinsic superiority motivates us to propose a FE-to-AFE-based NG and estimate its potential electrical performance. For simplicity, bilayer SnSe flakes with an in-plane size of 10 × 10 nm were employed in this work (see the details in the Supplementary Information).
Taking bilayer SnSe as an example, Fig. 4a shows the schematic illustration of this mechanism-based NG in connection with an external load resistor, which is analogous to the previous model32,54,55. The tribo induced FE-to-AFE phenomenon in bilayer SnSe results in multiple repeated bursts of a significant electrical polarization change upon continuous interlayer sliding (over distances of several unit cells in Fig. 4a). Figure 4b illustrates the variation of polarization, source voltage, and short-circuit current of the proposed NG device in three sliding periods. The polarization Ps repeatedly changes between ~40 and 0 μC cm−2. Using a well-established theoretical model52, the source voltage can be estimated for the 10 × 10 nm bilayer MX device in the middle of Fig. 4b, showing an alternating change between ~25 and 0 V, as indicated by the dotted line. For simplicity, the source voltage is approximated as a simple sinusoidal alternating curve (the blue curve). The open-circuit voltage Voc can be obtained from this curve (see details in the Supplementary Information). The considerable output voltage benefits from the significant polarization change (~40 μC cm−2) during the interlayer sliding process. For monolayer MoS2-based PENGs with the same size55, the polarization change is only ~0.27 μC cm−2, and the voltage is only ~0.24 V. The voltage of the proposed NG (~25 V) is thus two orders of magnitude higher.
a Schematic illustration of a FE-to-AFE-based NG in connection with an external load resistor. The theoretical models were adopted from ref. 47 (see the main text and the SI for details). b Variation of polarization, source voltage (Vsource), and short-circuit current (Isc) of a 10 × 10 nm NG under a 1 m s−1 sliding speed. Three sliding periods are shown. The considerably large values of Vsource and Isc benefit from the large polarization change and large polarization rate during the interlayer sliding process (see the main text for details). The voltage exhibits a linear relation with the polarization change and is simplified as a sinusoidal alternating voltage in subsequent modeling and discussion. c Dependence of Voc and Isc on the interlayer sliding speed. The voltage is independent of the sliding speed because of the constant polarization change (see the main text). Isc is linearly related to the sliding speed because of its linear relation with the rate of polarization change. d Dependence of the voltage and current output under a 1 m s−1 sliding speed as a function of the load resistance. The inset is the equivalent circuit of the FE-to-AFE-based NG. e Power output as a function of the load resistance at different sliding speeds. f Maximum power at different sliding speeds obtained from the theoretical prediction.
For the proposed FE-to-AFE bilayer device, the polarization change rate depends on the sliding speed v:
The bottom plot of Fig. 4b shows the calculated sinusoidal short-circuit current Isc with an amplitude of ~35 and ~17 nA at a moderate sliding speed of 0.5 and 1 m s−1, respectively. A small phase difference in the source voltage can be observed (see details in the Supplementary Information). Note that the weak interlayer vdW interaction enables the ultralow friction and even the superlubricity in 2D materials. In the experiments, an interlayer sliding speed of 25–294 m s−1 has been achieved56,57. Fig. 4c summarizes the Voc and Isc outputs as a function of the sliding speed over a wide range, from 0.001 to 10 m s−1. Voc is independent of the sliding speed, while Isc depends linearly on the sliding speed. The electrical output of this NG can be tuned in a wide range by changing the sliding speed.
To quantitatively estimate the power output of the FE-to-AFE-based NG, the NG device is regarded as a simple resistor-capacitor (RC) circuit, as was done in previous works32,54. It is necessary to investigate the voltage and current outputs as a function of the load resistance, as shown in Fig. 4d. Taking the sliding speed of 1 m s−1 as an example, the output current is unchanged for a load resistance of up to ~10 MΩ, and then decreases with increasing the load. On the other hand, the output voltage remains ~0 V initially and starts to increase at the same point. As such, the maximum delivered power of 107 nW is achieved at an intermediate load of ~350 MΩ. Regarding other sliding speeds, the RC circuit model predicts a similar behavior for the voltage and current outputs. Figure 4e summarizes the power output as a function of the load resistance at different sliding speeds. For sliding speeds of 1 m s−1, 5 m s−1, and 10 m s−1, the power outputs are 107 nW, 533 nW, and 1057 nW, respectively. Furthermore, the derived optimal load resistances are about 350 MΩ, 70 MΩ, and 35 MΩ, respectively. The optimized maximum power output is found to be linearly related to the sliding speed, as shown in Fig. 4f. The difference in electrical output between bilayer SnSe and monolayer MoS2 can be found in Supplementary Table 2. For monolayer MoS2, a mechanical deformation of 0.5 GHz can generate an alternating current with the same frequency and a power output of 0.016 nW55, while a moderate mechanical sliding speed of 1 m s−1 can generate a current of 2.29 GHz and a power of 106.6 nW for bilayer SnSe.
It is worth to make a further comparison between the proposed FE-to-AFE-based NG and the well-known PENGs/TENGs. In addition to the high polarization change and charging rate, for the FE-to-AFE-based NGs, a moderate mechanical sliding speed can generate high-frequency alternating electrical output without the need for any high-frequency input signal. For example, a sliding speed of 1 m s−1 theoretically corresponds to a current of 35 nA and a frequency of ~2.29 GHz, which is nearly impossible for PENGs. Note that, in TENGs, increasing the number of grating units of dielectrics is a popular method to generate multiple electric outputs in one directional motion cycle54. However, these grating units requires sophisticated microfabrication techniques, and their sizes are of several micrometers. In the proposed NG, every unit cell (length of several angstroms) can be viewed as a grating unit. Moreover, the fragile grating units in TENGs may suffer mechanical failure (e.g., wear) under high-speed sliding and consequently a short lifetime54. The proposed FE-to-AFE-based NG clearly does not have these issues. The ultralow friction between vdW layers can enhance its lifetime 58.
Here we propose this promising phenomenon in present bilayer MX materials and its potential application with the idealized condition. In practice, the effects of defects and intrinsic ripples in 2D materials are nonnegligible, which can be further investigated in future works.
In summary, a sliding-induced FE-to-AFE phenomenon was discovered in bilayer MX (M = Ge, Sn; X = S, Se) using DFT calculations. Among the four possible types of high-symmetry stacking order for bilayer MX, the AA and AC stacking orders prefer an FE state with a parallel arrangement of the polarization, while the AB and AD stacking orders favor an AFE state with an anti-parallel arrangement of the polarization. Changing the stacking order through tribological interlayer sliding results in a reversible and hysteretic phase transition between the FE and AFE states. An in-depth analysis revealed that the lattice distortion caused by the interlayer vdW force plays a dominant role in the phase transition, which is surprising. Inspired by the intrinsically high magnitude of the electric polarization change and ultrahigh changing rate, we propose a bilayer MX-based energy harvesting NG. The performance predicted using a well-established theoretical model is superior compared with those of the widely studied PENG and TENG devices. This bilayer MX-based device is a promising candidate for future NGs.
Methods
The DFT calculations in this work were performed using the Vienna ab initio simulation package (VASP)59,60,61,62. The projector-augmented wave (PAW) potentials with the generalized gradient approximation63,64 in the Perdew-Burke-Ernzerhof (GGA-PBE) formulation65 were used with a cutoff energy of 600 eV. The Brillouin zone integration for structure relaxation was obtained using a 25 × 25 × 1 Monkhorst-Pack66 k-point grid. For the total energy calculation, the Brillouin zone was sampled with 45 × 45 × 1 k-points. A 30-Å-thick vacuum region was introduced to avoid interaction between the bilayers. The DFT-D2 method of Grimme was applied for the vdW corrections. The pairwise vdW approximations of D2 may alter the power-law scaling of interlayer vdW interactions67. To further verify the results, other vdW corrections, including the zero damping DFT-D3 method of Grimme68, the many-body dispersion energy method (MBD@rsSCS)69,70, and the vdW-DF functional of Langreth and Lundqvist et al. (optB86b-vdW)71,72,73 are also applied to further check the energy sequence of bilayer MX (Supplementary Fig. 11). All these methods agree that AA and AC stacking prefer FE state while AA and AD prefer AFE state. To verify the little impact of a substrate on the sliding-induced FE-to-AFE phenomenon, a substrate clamped model was also considered (Supplementary Fig. 12). The convergence criteria for electronic and ionic relaxations were 10−6 eV and 10−3 eV Å−1, respectively. The electric polarization was computed based on the Berry-phase theory of polarization74. To distinguish a stacking order from others, the relative position of a pair of atoms from the top and bottom layers was employed. The selective dynamics tag of VASP was used to fix the position of this pair of atoms. Further calculation details can be found in the Supplementary Information.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Information. Additional data related to this article may be requested from the authors.
References
Guan, Z. et al. Recent progress in two-dimensional ferroelectric materials. Adv. Electron. Mater. 6, 1900818 (2020).
Chang, K. et al. Discovery of robust in-plane ferroelectricity in atomic-thick SnTe. Science 353, 274–278 (2016).
Belianinov, A. et al. CuInP2S6 room temperature layered ferroelectric. Nano Lett. 15, 3808–3814 (2015).
Zhou, Y. et al. Out-of-plane piezoelectricity and ferroelectricity in layered α-In2Se3 nanoflakes. Nano Lett. 17, 5508–5513 (2017).
Fei, Z. et al. Ferroelectric switching of a two-dimensional metal. Nature 560, 336–339 (2018).
Yuan, S. et al. Room-temperature ferroelectricity in MoTe2 down to the atomic monolayer limit. Nat. Commun. 10, 1775 (2019).
Shirodkar, S. N. & Waghmare, U. V. Emergence of ferroelectricity at a metal-semiconductor transition in a 1T monolayer of MoS2. Phys. Rev. Lett. 112, 157601 (2014).
Chen, K. et al. Ferromagnetism of 1T’-MoS2 nanoribbons stabilized by edge reconstruction and its periodic variation on nanoribbons width. J. Am. Chem. Soc. 140, 16206–16212 (2018).
Ding, W. et al. Prediction of intrinsic two-dimensional ferroelectrics in In2Se3 and other III2-VI3 van der Waals materials. Nat. Commun. 8, 14956 (2017).
Xiao, C. et al. Elemental ferroelectricity and antiferroelectricity in group-V monolayer. Adv. Funct. Mater. 28, 1707383 (2018).
Wang, H. & Qian, X. Two-dimensional multiferroics in monolayer group IV monochalcogenides. 2D Mater. 4, 015042 (2017).
Chen, W. et al. Direct observation of van der Waals stacking-dependent interlayer magnetism. Science 366, 983–987 (2019).
Wang, Y. et al. Stacking-dependent optical conductivity of bilayer graphene. ACS Nano 4, 4074–4080 (2010).
Kim, C.-J. et al. Stacking order dependent second harmonic generation and topological defects in h-BN Bilayers. Nano Lett. 13, 5660–5665 (2013).
Dai, J. & Zeng, X. C. Bilayer phosphorene: effect of stacking order on bandgap and its potential applications in thin-film solar cells. J. Phys. Chem. Lett. 5, 1289–1293 (2014).
Liu, X., Pyatakov, A. & Ren, W. Magnetoelectric coupling in multiferroic bilayer VS2. Phys. Rev. Lett. 125, 247601 (2020).
Li, L. & Wu, M. Binary compound bilayer and multilayer with vertical polarizations: two-dimensional ferroelectrics, multiferroics, and nanogenerators. ACS Nano 11, 6382–6388 (2017).
Woods, C. R. et al. Charge-polarized interfacial superlattices in marginally twisted hexagonal boron nitride. Nat. Commun. 12, 347 (2021).
Vizner Stern, M. et al. Interfacial ferroelectricity by van der Waals sliding. Science 372, 1462–1466 (2021).
Yasuda, K., Wang, X., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Stacking-engineered ferroelectricity in bilayer boron nitride. Science 372, 1458–1462 (2021).
Xiao, J. et al. Berry curvature memory through electrically driven stacking transitions. Nat. Phys. 16, 1028–1034 (2020).
Liang, Y., Shen, S., Huang, B., Dai, Y. & Ma, Y. Intercorrelated ferroelectrics in 2D van der Waals materials. Mater. Horiz. 8, 1683–1689 (2021).
Yang, Q., Wu, M. & Li, J. Origin of two-dimensional vertical ferroelectricity in WTe2 bilayer and multilayer. J. Phys. Chem. Lett. 9, 7160–7164 (2018).
Liu, C., Wan, W., Ma, J., Guo, W. & Yao, Y. Robust ferroelectricity in two-dimensional SbN and BiP. Nanoscale 10, 7984–7990 (2018).
Wu, M. & Zeng, X. C. Bismuth oxychalcogenides: a new class of ferroelectric/ferroelastic materials with ultra high mobility. Nano Lett. 17, 6309–6314 (2017).
Fei, R., Kang, W. & Yang, L. Ferroelectricity and phase transitions in monolayer Group-IV monochalcogenides. Phys. Rev. Lett. 117, 097601 (2016).
Hu, T. & Kan, E. Progress and prospects in low-dimensional multiferroic materials. WIREs Comput. Mol. Sci. 9, e1409 (2019).
Wu, M. & Zeng, X. C. Intrinsic ferroelasticity and/or multiferroicity in two-dimensional phosphorene and phosphorene analogues. Nano Lett. 16, 3236–3241 (2016).
Bao, Y. et al. Gate-tunable in-plane ferroelectricity in few-layer SnS. Nano Lett. 19, 5109–5117 (2019).
Chang, K. et al. Microscopic manipulation of ferroelectric domains in SnSe monolayers at room temperature. Nano Lett. 20, 6590–6597 (2020).
Higashitarumizu, N. et al. Purely in-plane ferroelectricity in monolayer SnS at room temperature. Nat. Commun. 11, 2428 (2020).
Wu, W. et al. Piezoelectricity of single-atomic-layer MoS2 for energy conversion and piezotronics. Nature 514, 470–474 (2014).
Liu, Z. et al. Observation of microscale superlubricity in graphite. Phys. Rev. Lett. 108, 205503 (2012).
Hod, O., Meyer, E., Zheng, Q. & Urbakh, M. Structural superlubricity and ultralow friction across the length scales. Nature 563, 485–492 (2018).
Han, E. et al. Ultrasoft slip-mediated bending in few-layer graphene. Nat. Mater. 19, 305–309 (2020).
Kong, X. et al. Tunable auxetic properties in group-IV monochalcogenide monolayers. Phys. Rev. B 98, 184104 (2018).
Deng, J. et al. Electric field induced reversible phase transition in Li doped phosphorene: shape memory effect and superelasticity. J. Am. Chem. Soc. 138, 4772–4778 (2016).
Zhang, J.-J., Guan, J., Dong, S. & Yakobson, B. I. Room-temperature ferroelectricity in group-IV metal chalcogenide nanowires. J. Am. Chem. Soc. 141, 15040–15045 (2019).
Mehboudi, M. et al. Structural phase transition and material properties of few-layer monochalcogenides. Phys. Rev. Lett. 117, 246802 (2016).
Chang, K. et al. Enhanced spontaneous polarization in ultrathin SnTe films with layered antipolar structure. Adv. Mater. 31, 1804428 (2019).
Kaloni, T. P. et al. From an atomic layer to the bulk: low-temperature atomistic structure and ferroelectric and electronic properties of SnTe films. Phys. Rev. B 99, 134108 (2019).
Zhang, S., Ma, T., Erdemir, A. & Li, Q. Tribology of two-dimensional materials: from mechanisms to modulating strategies. Mater. Today 26, 67–86 (2019).
Berman, D., Erdemir, A. & Sumant, A. V. Approaches for achieving superlubricity in two-dimensional materials. ACS Nano 12, 2122–2137 (2018).
Henkelman, G., Uberuaga, B. P. & Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Sheppard, D., Xiao, P., Chemelewski, W., Johnson, D. D. & Henkelman, G. A generalized solid-state nudged elastic band method. J. Chem. Phys. 136, 074103 (2012).
Choi, K. J. Enhancement of ferroelectricity in strained BaTiO3 thin films. Science 306, 1005–1009 (2004).
Wu, X., Rabe, K. M. & Vanderbilt, D. Interfacial enhancement of ferroelectricity in CaTiO3/BaTiO3 superlattices. Phys. Rev. B 83, 020104 (2011).
Reimers, J. R., Tawfik, S. A. & Ford, M. J. van der Waals forces control ferroelectric-antiferroelectric ordering in CuInP2S6 and CuBiP2Se6 laminar materials. Chem. Sci. 9, 7620–7627 (2018).
Tawfik, S. A., Reimers, J. R., Stampfl, C. & Ford, M. J. van der Waals forces control the internal chemical structure of monolayers within the lamellar materials CuInP2S6 and CuBiP2Se6. J. Phys. Chem. C. 122, 22675–22687 (2018).
Su, G. et al. Modeling chemical reactions on surfaces: the roles of chemical bonding and van der Waals interactions. Prog. Surf. Sci. 94, 100561 (2019).
Su, G. et al. Switchable Schottky contacts: simultaneously enhanced output current and reduced leakage current. J. Am. Chem. Soc. 141, 1628–1635 (2019).
Wang, Z. L. On Maxwell’s displacement current for energy and sensors: the origin of nanogenerators. Mater. Today 20, 74–82 (2017).
Lee, J.-H. et al. Reliable piezoelectricity in bilayer WSe2 for piezoelectric nanogenerators. Adv. Mater. 29, 1606667 (2017).
Niu, S. & Wang, Z. L. Theoretical systems of triboelectric nanogenerators. Nano Energy 14, 161–192 (2015).
Zhou, Y. et al. Theoretical study on two-dimensional MoS2 piezoelectric nanogenerators. Nano Res. 9, 800–807 (2016).
Yang, J. et al. Observation of High-Speed Microscale Superlubricity in Graphite. Phys. Rev. Lett. 110, 255504 (2013).
Peng, D. et al. Load-induced dynamical transitions at graphene interfaces. Proc. Natl Acad. Sci. USA 117, 12618–12623 (2020).
Ambrosetti, A., Ancilotto, F. & Silvestrelli, P. L. van der Waals-corrected ab initio study of water ice-graphite interaction. J. Phys. Chem. C. 117, 321–325 (2013).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 6, 15–50 (1996).
Becke, A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098–3100 (1988).
Langreth, D. C. & Mehl, M. J. Beyond the local-density approximation in calculations of ground-state electronic properties. Phys. Rev. B 28, 1809–1834 (1983).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Ambrosetti, A., Ferri, N., DiStasio, R. A. & Tkatchenko, A. Wavelike charge density fluctuations and van der Waals interactions at the nanoscale. Science 351, 1171–1176 (2016).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Tkatchenko, A., DiStasio, R. A., Car, R. & Scheffler, M. Accurate and efficient method for many-body van der Waals Interactions. Phys. Rev. Lett. 108, 236402 (2012).
Ambrosetti, A., Reilly, A. M., DiStasio, R. A. & Tkatchenko, A. Long-range correlation energy calculated from coupled atomic response functions. J. Chem. Phys. 140, 18A508 (2014).
Dion, M., Rydberg, H., Schröder, E., Langreth, D. C. & Lundqvist, B. I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 92, 246401 (2004).
Román-Pérez, G. & Soler, J. M. Efficient implementation of a van der Waals density functional: application to double-wall carbon nanotubes. Phys. Rev. Lett. 103, 096102 (2009).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011).
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654 (1993).
Acknowledgements
The authors gratefully acknowledge the support of NSFC (Grant Nos. 11974269, 51728203), and the support by 111 project 2.0 (Grant No. BP0618008). J.D. also thanks the support of the National Key R&D Program of China (Grant No. 2018YFB1900104). J.Z.L. acknowledges the support from ARC discovery projects (DP180101744) and HPC from National Computational Infrastructure from Australia. This work is also supported by State Key Laboratory for Mechanical Behavior of Materials. The authors also thank Dr. X.D. Zhang and Mr. F. Yang at Network Information Center of Xi’an Jiaotong University for support of HPC platform.
Author information
Authors and Affiliations
Contributions
J.D. and J.Z.L. designed the simulations and the framework of this research. B.X. carried out the first-principles calculations. B.X., J.D., and J.Z.L. wrote the paper. J.S. and X.D. performed some data analysis and provide many suggestions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, B., Deng, J., Ding, X. et al. Van der Waals force-induced intralayer ferroelectric-to-antiferroelectric transition via interlayer sliding in bilayer group-IV monochalcogenides. npj Comput Mater 8, 47 (2022). https://doi.org/10.1038/s41524-022-00724-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00724-8
This article is cited by
-
Atomic-level polarization reversal in sliding ferroelectric semiconductors
Nature Communications (2024)
-
Multiresistance states in ferro- and antiferroelectric trilayer boron nitride
Nature Communications (2024)
-
Neuroprosthetic contact lens enabled sensorimotor system for point-of-care monitoring and feedback of intraocular pressure
Nature Communications (2024)
-
Strain engineering the spin-valley coupling of the R-stacking sliding ferroelectric bilayer 2H-VX2 (X = S, Se, Te)
npj Computational Materials (2024)
-
High-throughput computational stacking reveals emergent properties in natural van der Waals bilayers
Nature Communications (2024)