Introduction

Reflecting recent developments in computer hardware and algorithms, computer simulations have been increasingly employed, with remarkable success, to study the phase behavior and synthesis mechanisms of porous materials1,2,3,4. Several scales of such simulations exist, ranging from ab initio quantum mechanical calculations to classical molecular dynamics (MD) simulations, employing either atomistic (AA) or coarse-grained (CG) molecular models. First-principles calculations provide a great level of detail but are extremely limited in terms of size and time scale due to their high computational cost. Thus, large-scale processes, such as the formation of long-range ordered mesophases during synthesis of templated porous silica materials, have been addressed with classical MD5,6,7,8,9 or Monte Carlo (MC)10,11,12 simulations. However, the formation of ordered mesophases involves not only the self-assembly of the amphiphilic compounds that act as supramolecular templates, but also the simultaneous chemical reactions that contribute to the formation of the final material (e.g. silica polycondensation). Unfortunately, implementing chemical reactions in classical simulations is not straightforward. Several approaches have been followed by different authors, from MC lattice models13,14 to AA-MD simulations involving ad hoc reactive force fields15,16. However, the limited level of molecule description inherent to lattice models or the use of restricted force fields in AA-MD simulations has hampered the progress in this topic. In this paper, we present a reactive model of silica that can be directly incorporated in classical MD simulations to allow the first computationally efficient simulation of surfactant self-assembly and chemical reactions under experimentally realistic synthesis conditions within a single modeling framework.

Numerous experimental and computational studies can be found in the literature involving the mechanism of silica speciation and nucleation in the context of porous material synthesis2,3,14,17,18,19,20,21,22,23,24,25,26,27,28,29. Therefore, the mechanisms that govern the oligomerization of silica in simple aqueous solutions are often assumed to be well understood. What remains poorly described is the role of silica oligomerization in dynamic large-scale processes such as the surfactant self-assembly. This is critical for controlling the properties and structure of materials like zeolites and periodic mesoporous silicas (PMS), since the control of pore size and geometry defines the application of materials of these families18,21,23,30,31. However, this is a very challenging task. Since the synthesis process involves self-assembly in solution, mesophase formation, phase equilibrium, and silicate condensation reactions that lead to the simultaneous presence of a multitude of silica species in solution, it is rather difficult to extract information from individual events using only experimental data.

Theoretical models can, at least in principle, fill this gap; however, they also suffer from several drawbacks. Electronic structure calculations, either static32,33,34,35 or dynamic36,37,38,39, have been used to analyze the stability and condensation of silicates, both in the gaseous phase or in aqueous solution represented by implicit or explicit water. Those studies were limited to very small systems and/or very short simulation times (up to 200 picosecond), and focused on small silicate molecules, in most cases up to the trimer species only. Classical atomistic MD calculations5,6,40 have been used to probe the formation of zeolites and mesoporous materials, with systems containing up to 150 silicate monomers or a few oligomers with a few tens of atoms. The AA-MD simulations5,6,40 considered non-reactive force fields and, therefore, silica condensation was mimicked by replacing smaller fragments with larger ones (e.g. one dimer replacing two monomers). While those simulations could be run up to the nanosecond scale, they were not able to capture the much longer time and length scales of mesostructure formation4. In contrast, MD simulations using CG models have been able to shed light on this process by reaching the microsecond scale with molecular systems containing a few thousands of silicate monomers (or equivalent)7,8,9. Unfortunately, the CG models considered in those studies were not able to describe silica condensation reactions7,8,9.

Explicit silica condensation reactions have been embedded into lattice Monte Carlo models by Monson and co-workers13,14. Their approach was based on a previous lattice model of surfactant self-assembly41 in the presence of silica10,11 and included Reactive Monte Carlo steps between silica species using a tetrahedral model13. They were thus able to simultaneously simulate self-assembly and silica condensation reactions during the synthesis of MCM-41, the archetypal mesoporous silica material42, albeit within the strict assumptions of their simplified lattice model. Off-lattice models of silica condensation reactions, while potentially more realistic than lattice models, have suffered from different limitations. In most cases, explicitly describing chemical reactions in classical MD simulations has made use of AA reactive force fields, which have improved over the years in tandem with the increase in computer power43,44. Recently, this has included the parameterization and deployment of the general ReaxFF reactive force field for silicates16,42. Nevertheless, simulations with reactive force fields require unrealistic temperatures15,16 and densities, clearly inappropriate to reproduce the self-assembly of the amphiphilic compounds at comparatively much milder conditions (e.g. 25–100 °C)42. Similar MC-based reactive models20 as well as kinetic Monte Carlo simulations29,45,46,47 are also limited to small silica clusters in solution. A major recent development in this field is the off-lattice CG reactive model for silica developed by Malani et al.23,48,49. This model is based on a simplified description of silica networks as being built up of tetrahedral units held together by simple harmonic potentials; the tetrahedra are then allowed to undergo condensation reactions through a series of Monte Carlo trials, within an implicit solvent model formalism. Using this simple and elegant model, Malani et al. were able to describe, in agreement with experimental data, the evolution of the number of Qn species (silica moieties bonded to n others) along the process of silica condensation at realistic conditions and over long reaction times. However, this reactive MC algorithm has not yet been incorporated into simulations of surfactant self-assembly, which, as discussed above, have progressed mainly through highly parallelized MD simulations7,8,9.

Thereby, a model that can describe both the self-assembly and the chemical reactions under realistic conditions in a computationally efficient way is still lacking. This work fills this gap and presents a reactive CG-MD model that describes the orthosilicic acid chemical reactions (silica oligomerization) within the MARTINI 2.2 framework50,51 and an explicit solvent model formalism. Our approach is based on incorporating a series of virtual sites and sticky particles into the recently developed CG silica model of Pérez-Sánchez et al.7. This approach has allowed us to describe the self-assembly and encapsulation of a silica/surfactant micelle.

Results

Reactive CG silica model

The reactive CG silica model developed in this work is based on the PSN and QSI MARTINI beads introduced by Pérez-Sánchez et al.7 for modeling neutral and singly-charged anionic silicate monomers, respectively. Our adaptation of PSN/QSI consists of tweaking only the silicate-silicate interactions (namely the distance and isotropy, as described in detail below) while preserving all the other interactions of the original model. In their original model7, Pérez-Sánchez et al. established that each silicate monomer is enclosed inside a single PSN/QSI bead based on the MARTINI force field, with parameters adjusted to match results from AA simulations of silica/surfactant solutions. In a subsequent work8, to model more condensed silica species, e.g. a dimer or a trimer as shown in Fig. 1, those beads were connected by unbreakable harmonic bonds, such that each CG bead enclosed a single Si atom and adjacent oxygens (and hydrogens, when applicable). As such, by construction, the CG model of Pérez-Sánchez et al. is not able to describe the dynamics of bond making/breaking in the polymerization process; instead, solutions with higher degree of condensation were simulated by pre-loading the simulation box with silica oligomers with a speciation that matched the experimental pH of interest. In principle, one could potentially describe the silica condensation within this framework through a kind of dynamic bond-updating procedure, as has been done in the case of organic polymerization reactions52,53,54—at specified intervals during the simulation, one would check the inter silica bead distances, define a rule for making bonds, interrupt the simulation, create another topology with fresh bonds, and continue the simulation. This is rather cumbersome and time-consuming, being mainly appropriate for diffusion-limited polymerization since bond-breaking is not accounted for. Therefore, we have opted for a different approach in which the formation of different silicate species is accomplished by using continuous non-bonded potentials to dynamically form and break bonds on-the-fly between monomeric CG silica particles during a single MD simulation.

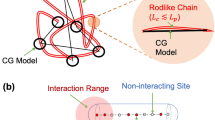
Fig. 1: Three modeling paradigms for silica dimer and trimer.
figure 1

Left. All-atom approach, with yellow, magenta and white spheres representing Si, O, and H atoms, respectively. Center. Standard non-reactive coarse-grained mapping, with simple CG beads (large gray spheres), representing each terminal Si(OH)3O- or central -OSi(OH)2O- fragment, connected by a fixed harmonic bond term. Right. Reactive coarse-grained model proposed in this work, in which the rigid bonds are replaced by dynamic bonds, achieved through a combination of virtual sites (teal spheres) and sticky particles (red spheres) and a proper interactive function. CG beads were scaled to ~50% of their sizes for clarity.

Full size image

In the original CG model8, covalently bonded silicate beads were connected by harmonic bonds of length 0.30 nm (reproducing experimental data for the Si-Si distance observed in several amorphous and crystalline silica structures55,56,57,58,59,60) while dispersion and repulsion interactions were excluded following the default prescription of the MARTINI model50. In order to replace these fixed bonds with continuous reversible potentials, one has to compensate for the mutual repulsion between approaching beads. After preliminary tests using the bead size of 0.47 nm from the original PSN/QSI particles, we concluded that the resulting silicate structures possessed unrealistically low densities. In order to overcome this difficulty, we decided to make use of a smaller type of particle (the S-type) included in the MARTINI 2.2 force field50 to obtain a SPSN/SQSI particle. In the description of the reactive model, we denote this as SSi for simplicity, but will revert to the original notation when distinguishing neutral (SPSN) and anionic (SQSI) silicates. The S-type beads display reduced interaction length and strength with other S-type particles—in particular, the interaction size parameter between S-type beads is reduced to 0.43 nm and the interaction energy is 25% lower, as illustrated in Table 1. Note that the interactions between S-type beads and all other beads in the system remain the same, therefore our modification only introduces changes in the silica-silica interactions—silica-water and silica-surfactant interactions remaining unchanged. We confirmed that the effect of this change on the performance of the original model was negligible (see Supplementary Fig. 1), since silica-silica interactions do not play a dominant role in the self-assembly process.

Table 1 Parameters of an RSi particle, composed of a central SSi MARTINI bead, four SP, and four VS.
Full size table

Our reactive CG approach consists in the incorporation of virtual sites (VS) and sticky particles (SP) to generate a monomeric silicate CG bead, which can emulate the tetrahedral directionality of silica condensation and the structural flexibility of the Si-O bonds and Si-O-Si angles in silica materials (see Fig. 1, right). More precisely, the silicate model is composed of an SSi bead surrounded by four VS and four SP, forming two tetrahedra in a stellated octahedron arrangement as shown in Fig. 2a. This topology is henceforth denominated as RSi (Reactive Silica). The philosophy behind our reactive model is as follows; each SP of an RSi particle is attracted to the SP of other RSi particles, while each VS repels SP of other RSi particles – the parameters for these non-bonded interactions are discussed below. Harmonic potentials were used to bond SP to the central SSi bead and to each other. The positions of the VS are defined by the GROMACS 3fad bond type61, i.e. with a fixed distance to the opposite SP (dSP-VS) and a fixed angle of 0° with that site and the central SSi bead, so as to enforce a tetrahedral configuration (see Fig. 2a). The total mass of an RSi is the standard mass of MARTINI S-type beads (45 a.m.u.) and is evenly distributed among the SSi and the SP (see Table 1), while the VS are massless. Note that, while silicic acid molecules polymerize through the formation of Si-O-Si bonds, the condensation within our CG approximation yields an SSi-SP-SP-SSi structure. For this reason, the center of the SP–SP bond should approximately match the location of an oxygen atom in atomistic models of silica oligomers. In order to achieve this, the SSi-SP bond lengths were set to a third of the inter-bead (SSi-SSi) ground state distance in the MARTINI force field, i.e., around 0.161 nm, while a Lennard-Jones σ value of 0.143 nm was assigned to SP–SP interactions so as to yield a mutual distance at the energy minimum of ~0.161 nm.

Fig. 2: Molecular models.
figure 2

a Representation of the stellated octahedron geometry of the RSi particle. The large spherical shadow is the SSi bead, bonded (dashed green lines) to the SP (red spheres). The latter are bonded to each other as shown by the dashed red lines. The bonds between the VS (teal spheres) and the SP are depicted as a teal dashed line. b Cross section of the potential energy profile of a Rsi particle, as exerted on the SP of a nearby Rsi particle, through a plane that passes through its center and contains one SP (at the lower end of the diagram) and one VS (at the top end), with εSP = 50 kJ mol−1 and εrep = 0.24 × 10−5 kJ mol−1. The small dots represent the projection on the cross-sectional plane of the positions of the SSi particle (yellow), the SP (red) and the VS (teal). c Reactive model for neutral silicic acid, showing the central SPSN bead (yellow, reduced to 1/3 of its diameter for clarity) and the reactive SP (red). d Reactive model for anionic silicic acid, showing the central SQSI bead (violet, reduced to 1/3 of its diameter for clarity), the reactive SP (red) and the inactive SP (gray). e CG model for the CTA+ surfactant, showing the cationic head bead (blue) and hydrophobic tail beads (green); the underlying atomistic representation is shown in the background.

Full size image

The role of each SP is to form a bond between one RSi and nearby RSi particles, since SP of different RSi particles are attracted to each other by a Lennard-Jones (LJ) potential with strength controlled by εSP. Because we are dealing with spherical potentials, the placement of four LJ centers in a tetrahedral fashion yields an RSi particle with a wide attractive volume, allowing each RSi to coordinate with up to 12 other RSi particles in a face-centered-cubic manner. This is highly unrealistic, since each real silica monomer contains only four oxygens and, therefore, can only form up to four bonds with other silica molecules. Therefore, to provide a realistic connectivity, four VS were added in diametrically opposed positions relative to the SP (Fig. 2a). These VS repel SP of neighboring RSi beads with a purely repulsive potential controlled by εrep; this is accomplished in GROMACS by defining the LJ interaction with the C12 parameter equal to εrep and the C6 parameter equal to zero. Furthermore, because each SP is surrounded by three VS, the magnitude of εrep helps straighten the SSi-SP-SP-SSi bond angles, as observed in porous silica structures62. It should be noted that other choices of potential model for the mutual interactions between VS and SP could have been made; the LJ potential was chosen for ease of implementation in multiple MD simulation codes and ease of integration into the MARTINI CG force field50, itself based on the LJ potential.

Model calibration

Our model was calibrated by testing various combinations of εrep and εSP, analyzing the fraction of RSi that are bonded to n other RSi as a function of time, and comparing the results to the experimental data of Devreux et al.63 and the Monte Carlo simulation results of Malani et al.48 for the condensation of neutral silica in aqueous solution at a pH of 2.5 and room temperature (corresponding to the experimental conditions63). The silica speciation is defined as usual by Qn (n = 0, 1, … , 4), where n refers to the number of coordinated neighbors, and we calculated qi(t), (i = 0, 1, … , 4) corresponding to the mole fraction of Qn silicon coordination environments. The degree of condensation as a function of the simulation time, c(t), is defined as follows:

$${{{{c}}}}\left( {{{{t}}}} \right) = \frac{1}{4}\mathop {\sum }\limits_{{{{{i}}}} = 0}^4 {{{{i}}}}\,{{{{q}}}}_{{{{i}}}}\left( {{{{t}}}} \right)$$
(1)

This formula yields a number between 0 and 1, such that c(t) = 0 when all RSi in the system are in the form of monomers and c(t) = 1 when all RSi are four–fold coordinated. Intermediate values of c(t) correspond to other combinations of oligomers. By multiplying c(t) by four, one obtains the average number of intermolecular bonds formed (between 0 and 4), among all RSi in the system.

The performance of the model relies on a delicate balance between the parameters εSP and εrep. On the one hand, the attractive SP-SP interactions need to be strong enough to promote binding that is sufficiently long-lived, as in the realistic case of a chemical reaction—if the magnitude of εSP is too low, the system is dominated by species of low degree of condensation (e.g. Q0–Q2). On the other hand, the repulsion term needs to be sufficiently strong to prevent each SP from bonding to more than one SP of other RSi particles, thus keeping the maximum coordination number of RSi close to four, as observed experimentally. Using a careful choice of parameters, we were able to keep the percentage of species with more than 4 bonded neighbors (labeled as Q5+) very close to zero, even though such bonds are not prohibited a priori as in most previous approaches to describe silica polymerization reactions (see Supplementary Fig. 2 and associated Supplementary Discussion for further details). Furthermore, an adequate balance between εSP and εrep promotes sufficient RSi-RSi bond breaking, thereby more realistically describing the silica oligomerization equilibrium (see sub-sections below and Supplementary Information). Despite the relatively strong attractive potential between two SP, the stellated configuration shown in Fig. 2a allows for collisions to take place that can sufficiently deform the structure of the bonded particles towards a region of the interaction potential where they are no longer bonded.

For model calibration, we carried out simulations of silica polymerization in aqueous solution close to the isoelectric point, to compare against existing experimental63 and simulation48 data. To achieve the same density considered by Malani et al.48, all simulations started with a random configuration having 1000 neutral RSi particles (Fig. 2c) that are far apart from each other. This system is therefore initially composed of 100% Q0 species. This system was equilibrated at 300 K in a 10.4 × 10.4 × 10.4 nm3 cubic box with the remaining empty space filled with 7700 water beads. Following the MARTINI philosophy, P4 particles were chosen to model the water molecules. To avoid any unrealistic freezing, 10% of them were replaced by BP4 particles50. Note that our simulations (and those of Malani et al.48) yield an effective silica concentration slightly higher than that in the experimental study of Devreux et al.63—more precisely, it is 1.45 mol/l for our simulation and 1.33 mol/l for the experimental system, estimated based on the molar ratios indicated in the original publication as well as the experimental densities of TEOS, ethanol and water. The small difference is unlikely to significantly affect the evolution of the Qn profiles or the comparison between experimental and simulation time scales. Note, also, that our model does not explicitly account for water participation in condensation/hydrolysis reactions, as the number of water beads remained the same throughout the simulations. While it is assumed that this approximation does not affect the physics related to the reactions themselves, it slightly affects the concentration of all the species in solution as the number of water molecules should increase upon silica condensation. We discuss the implications of these assumptions later in the paper.

To validate the model and demonstrate its practical applicability in templated material synthesis, we carried out simulations of micelle self-assembly and encapsulation at high pH, when a significant percentage of silicates are negatively charged. There are two main differences between a charged and a neutral RSi particle: i) the central bead contains a charge of −1 in the former and is denoted as SQSI; ii) one of the SP, meant to represent the charged oxygen atom, was rendered inactive by setting εSP = 0. This setup represents an Si(OH)3O− monomer, which is only able to take part in three Si-O-Si bonds, instead of four for the neutral monomer (Fig. 2d). The micelle was formed by cationic cetyltrimethylammonium (CTA+) surfactants, represented by the MARTINI model as described in our previous work7,8,9, i.e. with four hydrophobic tail beads corresponding to alkyl groups and one hydrophilic and positively charged bead representing the ammonium head group (Fig. 2e). The self-assembly simulation contained 100 CTA+ molecules, which corresponds to the experimental estimate of the average aggregation number for this molecule64,65, 100 anionic RSi- (hence ensuring overall neutrality of the simulation box), and 62500 water molecules (including 10% of the antifreeze type), i.e., close to the typical ~1 wt% concentration used experimentally. Since all silicates are ionized in this simulation, it corresponds to a pH higher than ~12. The encapsulation simulation was identical, but contained an additional 200 neutral RSi, thus corresponding to an overall silica/surfactant ratio of 3 and a pH of ~9.5. For comparison with the encapsulation simulation, we also simulated an identical solution but where the CTA+ molecules were replaced by 100 tetramethylammonium cations (TMA+) represented by a positively charged Qd particle50. Both simulations were run with the same parameters for the condensation reaction. Table S1 in Supplementary Information contains full details for each simulation carried out in this work.

Neutral polymerization

The first step in the development of our reactive CG silica model was to find the optimum values of the attractive and repulsive parameters that control the strength and directionality of the Si-O-Si bonds. After extensive testing, the values εSP = 50 kJ mol−1 and εrep = 0.24 × 10−5 kJ mol−1 were found to reproduce the condensation profiles of various Qn species with a remarkable level of accuracy, when compared with experimental results (see below). Figure 2b shows the corresponding energy profile experienced by a nearby RSi. As can be seen, most regions of space are colored in red, denoting very weak or no attraction. Four small regions (only one is fully visible in this plane of cross-section), are aligned with the positions of the SP and represented in green/blue, denoting strong attraction. The four small regions of stability, with energies comparable to activation energies calculated for the condensation of silica in aqueous solution38,46, are placed inside valleys of the central dark red region, confirming that this combination of values of εSP and εrep succeeds in limiting the number of interaction points to four, corresponding to the required tetrahedral orientation. Furthermore, the number of RSi which can be connected to each interaction point is also restricted by the short range of the attractive region, so that once two SP are bonded, the attractive region is sterically shielded from SP of other RSi particles.

Figure 3 shows the time evolution of each Qn species throughout an MD simulation of a solution starting from 1000 neutral monosilicic acid molecules in water. The corresponding Qn profiles obtained experimentally by Devreux et al.63 and from Monte Carlo simulations performed by Malani et al.48 are also shown for comparison. The first aspect to notice is that all three sets of profiles are qualitatively similar (compare left panels in Fig. 3). They show an initial rapid decrease in the percentage of Q0 species (i.e. unreacted monomers, Si(OH)4) due to the ongoing polymerization reactions. As the reaction progresses and the degree of polymerization increases, the profiles are alternately dominated by species of higher degree of condensation, i.e. first Q1 species (i.e. terminal Si(OH)3O fragments), then Q2 species (Si(OH)2O2 moieties in the middle of linear chains or rings), then Q3 species (Si(OH)O3 groups present in branched chains), and finally Q4 species (SiO4 moieties as in three-dimensional tetrahedral silica networks). The sequence of these stages, as well as the size and shape of the peaks, is similar in all three data sets, although some minor differences are apparent, as discussed in more detail below. The significant fluctuations observed in the Qn profiles from our model (Fig. 3, bottom) are a consequence of the frequent bond formation and breakage that takes place during the simulation. An example of the observed bond formation and bond breakage is shown in Supplementary Fig. 3. It is also worth noticing that the percentage of species with more than four bonded neighbors (yellow line in Fig. 3) is negligible throughout the simulations using our model, even though they are not prohibited a priori as in the MC approach of Malani et al.48. These observations give us the first indication that our model is providing a qualitatively correct description of the polymerization process. In the silica network formed by our model, the Si-Si average distance is ~0.482 nm, with a very narrow distribution (see Supplementary Fig. 4), which is still somewhat larger than the experimental distance of ~0.31 nm55,56,57,58,59,60. However, the Si-O-Si angle (measured here as the angle between two SPSN-SP vectors of bonded RSi particles) has a distribution centered around ~152°, in good agreement with angles observed in experimental silica materials66.

Fig. 3: Molar fraction profiles.
figure 3

Profiles for the molar fraction (qi) of the silicon coordination environments (Qn) obtained from the MC model of Malani et al.48 (top panels), from the experiments of Devreux et al.63 (middle panels), and from our CG-MD model (bottom panels). The panels on the left also show the degree of condensation (c), represented by the orange line. The results are presented on the left as a function of time (or MC steps in the case of the Malani et al. data) and on the right as a function of the degree of condensation.

Full size image

According to Devreux et al.63, the symmetry exhibited in the condensation curves is a result of three stages in the polymerization process; formation of silicic acid oligomers, followed by the growth of fractal aggregates from these oligomers and finally the gelation through agglomeration of the fractal aggregates. In our model, we observe a similar progression, which is also in agreement with the computational results of Shere and Malani49. Initially (until ~54 ps), the reaction undergoes rapid dimerization, which is manifested in a steep increase of Q1 species (red curves in Fig. 3). Subsequently, we observed monomer-dimer and dimer-dimer aggregation events, forming longer linear chains. This behavior is shown in more detail in Supplementary Fig. 5, with the exponential increase in the maximum size of the clusters in the initial simulation stage, and illustrated in the snapshot of Fig. 4a. Despite a few exceptions (see Supplementary Fig. 6a), however, the linear chains never grew much longer than 4 or 5 monomers, at which point they started to cyclize to form ring structures (Fig. 4b and Supplementary Fig. 6b). This leads to a quick transformation of Q1 species into Q2 species. In this initial stage of oligomerization and cyclization, a nearly exponential increase in the degree of condensation is observed, both in the experimental and MD simulation results (see orange curves in Fig. 3).

Fig. 4: Snapshots of the simulation with neutral monosilicic acid molecules in water.
figure 4

a Maximum q1 (54 ps). b Maximum q2 (380 ps). c Maximum q3 (8300 ps). d The final snapshot of the simulation (8.4 × 106 ps). SP are colored in red and the SPSN bead is colored in yellow. The VS and water beads were excluded for clarity. A: Linear tetramer; B: Linear nonamer (see also Supplementary Fig. 6a); C: Branched pentamer; D: Cyclic oligomer (see also Supplementary Fig. 6b); E: Dissolved monomer.

Full size image

When the maximum of the molar fraction of Q2 species is reached, at about 380 ps in the MD simulation, two phenomena can be observed: the degree of condensation loses its tendency of logarithmic growth (Fig. 3), and there is an inflection in the growth of the maximum size of the clusters (Supplementary Fig. 5). This is due to the fact that, from this moment on, lateral aggregation of rings takes place, which leads to the growth of some small three-dimensional silica clusters. Additionally, there is a gradual formation of silica bridges connecting these clusters, which culminates with the formation of a very large cluster when the maximum of Q3 is reached at ~8300 ps (Fig. 4c). However, as can be seen in the simulation snapshots, the structure was still quite branched and loose. The last phase of silica condensation, between ~10000 ps and the end of the simulation, occurs mainly through the structural rearrangement of these bridges, slowly bringing together the larger silica clusters. The constant rearrangement of silicate-silicate bonds, made possible by the fine balance between the attractive and repulsive parameters of the model, promotes the contraction of the branches, until a seemingly solid material is achieved. As is shown in Supplementary Fig. 5, although the maximum cluster size is limited by the number of silica particles in the simulation box, the number of clusters oscillates between 1 and 8 during this final stage. This is due to intra cluster rearrangement processes that lead to the hydrolysis of some interfacial silica units, forming mainly Q0 species that are dissolved in solution (see Fig. 4d). This means that the model is able to qualitatively describe the realistic dynamic equilibrium between a dense amorphous silicon dioxide phase and a surrounding aqueous solution of silica.

In terms of a more quantitative comparison between our MD simulations and experimental data, it can be seen in Fig. 3 that the time scales are mismatched by more than 10 orders of magnitude—i.e., the real condensation time of silica extends over several days, while in our simulations the same phenomenon occurs in less than 1 microsecond of simulation time. This is a consequence of the coarse-graining approximations introduced in our model, and indeed it is a necessity in order to allow for simulating the entire process with reasonable computational resources. The mismatch between real-time scales and those of CG models, even for simple diffusion processes, is well documented67,68. This becomes even more pronounced in the case of reactive events, since the highly simplified CG model does not represent realistic energy barriers or transition states usually observed during chemical reactions, and hence is not able to describe the realistic quantum-level dynamics of the reaction process.

It should, in principle, be possible to apply a scaling factor to the simulation time for mapping it to the real experimental dynamics, by comparing both Qn profiles. The results of this analysis are shown in Supplementary Fig. 7. As can be seen, although generally reasonable agreement is obtained between the two data sets when a scaling factor of ~2 × 1013 is applied to the simulation time, the agreement is not perfect – the reaction seems to be proceeding relatively faster in the MD simulations than in the experiments, particularly in the latter stages of the process, given that the intersection points between different Qn species are taking place earlier (see Supplementary Fig. 8). This could be a consequence of our approximation neglecting the creation of water molecules at each reaction step. As the reaction progresses in the MD, the solution becomes gradually more concentrated than in the experiment (where water molecules are actually formed during the reaction), leading to faster reaction rates. However, it is worth to note that for relatively dilute solutions, which are the most relevant systems in porous silica synthesis processes, this effect should be quite small.

An alternative approach to quantitatively compare simulations to experiments, which was also suggested by Malani et al. in their MC simulations48, is to calculate the distribution of molar fractions as a function of the degree of condensation (i.e. using the orange curve in the left panels of Fig. 3 as the x-axis). The results are shown on the right panels of Fig. 3, where we can see that the profiles obtained from our MD simulation are in agreement with the experimental ones. We extracted the coordinates of key stages in the reaction from the plots, namely the positions of each peak in qn distributions and the intersection points between adjacent qn curves (e.g. where qn = qn+1), as shown in Table 2.

Table 2 Coordinates of the peaks and intersections between mole fractions of each Si environment when plotted against the overall degree of condensation.
Full size table

According to the experimental data obtained by Devreux et al.63 (middle-right plot of Fig. 3), every Qn species appears to reach approximately the same maximum molar fraction, around 60%, as well as the same molar fraction value for the crossing between different n; Qn/Qn+1 occurring at ~44%, Qn/Qn+2 occurring at ~22% and Qn/Qn+3 occurring at ~8%. Our simulation results exhibited peak maxima 6–11% below the experimental values, but values for the intersections that were in very close agreement with experiment. The lower peak heights observed in the simulations could once more be due to the progressive increase in concentration discussed above. This leads to a comparatively higher reactivity than in experiments, promoting a faster formation of more coordinated species, which in turn has an impact on the maximum value of the molar fraction of each species. Nevertheless, the fact that the points of intersection are accurately described confirms that our model is able to reproduce the main experimental condensation mechanisms. It is worth noting that lower peak heights had also been observed in the work of Malani et al.48. In fact, the quantitative performance of our model, in terms of predicting the correct experimental peak and intercept coordinates, is at least as good as that of the MC model of Malani et al.48 (see Table 2).

Micelle self-assembly and encapsulation

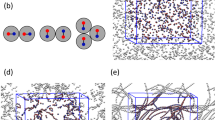
In the previous section, we showed that our reactive CG model can reproduce the experimental behavior for neutral silica polymerizing in aqueous solution, and that the results are competitive with a state-of-the-art reactive Monte Carlo model. The great advantage of our approach, however, is the possibility of describing both chemical reactions and surfactant self-assembly at realistic conditions within the same modeling framework, which had hitherto not been achieved. Here, we demonstrate this capability for a simple test-system, the self-assembly and encapsulation of a single spherical micelle of a cationic ammonium surfactant. Figure 5 shows several snapshots obtained during the self-assembly simulation, corresponding to a solution with a very high pH (above 12, where all silica monomers are anionic) and a silica/surfactant ratio of 1. Soon after the start of the simulation, small surfactant aggregates are formed, surrounded by anionic silicates (Fig. 5a). This is followed by fusion of those small aggregates to form micelles, which are stabilized by electrostatic interactions between the silica and surfactant heads (Fig. 5b). Finally, those micelles fuse together in a slower process until the final equilibrium state ─ a single micelle of CTA+ with silica adsorbed on its surface ─ is obtained (Fig. 5c).

Fig. 5: Snapshots of the micelle self-assembly simulation with polymerization reaction.
figure 5

a Initial formation of small proto-micelles with a few silica dimers marked with blue arrows and a silica tetramer marked with a gray arrow; b Fusion of aggregates to form small micelles surrounded by silica monomers and small oligomers; c Final snapshot with a single surfactant micelle surrounded by anionic silicates; d Blow-up of a small micelle (~40 surfactants) formed during the reactive self-assembly simulations, highlighting a linear silica trimer (red circle and arrow) and a branched tetramer (orange circle and arrow). Surfactant tails are shown in green, surfactant heads in dark blue, the central anionic silica beads are shown in purple, and reactive/inactive SP are shown in red/gray. Water and VS were removed for ease of visualization.

Full size image

The self-assembly process shown in Fig. 5 is qualitatively similar to that observed in our previous non-reactive CG simulations starting from either anionic silica monomers7 or small oligomers8. The main difference, of course, is that now the silicate molecules are allowed to react during the self-assembly. In fact, already at an early stage of the simulation (Fig. 5a), we can see a few silica dimers forming at the surface of the micelles. In Fig. 5d, we show a close-up of one of the intermediate-sized micelles observed in the simulation, highlighting the presence of a few linear and branched silica oligomers. The presence of these small, compact and highly charged oligomers qualitatively agrees with experimental measurements of silica speciation in dilute solutions at high pH in the presence of ammonium ions69,70,71,72.

Although the previous simulation demonstrates the capability of our model to simultaneously describe self-assembly and reaction processes, due to the low concentration of silica, we did not observe the formation of a large silica network that could encapsulate the micelle. Therefore, we simulated a solution with a silica/surfactant ratio of 3 and corresponding to a lower pH (around 9.5), where 2/3 of silicates are in their neutral form. The simulations were carried out in two steps in order to more realistically mimic the experimental synthesis process: i) micelle formation in the presence of silica monomers with the reaction turned off (i.e. the attractive SP–SP interaction set to zero); ii) micelle encapsulation with the reaction turned on. We note, however, that an analogous simulation where the reaction was turned on from the start of the self-assembly process ultimately led to the same equilibrium state (see Supplementary Figs. 9 and 10).

In Fig. 6 (top), we show snapshots of the encapsulation simulation. After ~1µs, the CTA+ micelle is fully formed, driven by hydrophobic forces between alkane tail atoms and stabilized by electrostatic interactions between the cationic head groups and the surrounding anionic silica monomers (see purple silicates at the micelle surface in Fig. 6b, with a magnified image provided in Supplementary Fig. 11a). When activated, the reactive model enables the formation of small condensed silicate species in solution, composed mostly of neutral silicates. Crucially, however, we also observe the condensation of anionic silicates at the micelle surface with each other and with some neutral units adsorbed from solution (Figs. 6c and S11b). After enough time, the majority of silicates are adsorbed onto the micelle and polymerize to form a single silica layer encapsulating the micelle. From the snapshot in Fig. 6d, we can see that the silicate molecules are closely interconnected to form a practically two-dimensional network, with only a few molecules protruding to the outside of the micelle (Supplementary Fig. 11c).

Fig. 6: Silica polymerization in aqueous solutions with CTA+ or TMA+ cations.
figure 6

Top. Snapshots of the micelle encapsulation simulation: a Initial snapshot with all molecules starting from random positions and RSi reactivity turned off; b Formation of the micelle, with RSi- adsorbed at the surface (frame obtained at 1.6 µs but a single micelle was already formed at t = 1 µs); from this point on (i.e., after 1.6 µs), RSi reactivity is activated; c Formation of small oligomers in solution, and some condensation of RSin at the micelle surface enabled by the RSi-; d Snapshot at ~3 µs (after reactivity was turned on) where a single layer of silica (neutral and anionic) covers the micelle. Bottom. Snapshots of the simulation with small TMA+ cations: e Initial snapshot with all molecules starting from random positions; f Formation of some small oligomers, and two small clusters that trapped some cations in their structure; g Increase in size of the clusters by the deposition of monomers and small oligomers; h Final snapshot at 3 µs, with coalescence of the two clusters into a single amorphous silica structure incorporating several cations. Color code is the same as in Fig. 5, but the central bead of neutral silicates is colored in yellow and the TMA+ ions are colored in cyan. Water and VS were removed for ease of visualization.

Full size image

The silica polymerization mechanism observed during the micelle encapsulation process is in marked contrast with an analogous system where the surfactants are replaced by TMA+ ions (i.e. equivalent to loose head groups), shown in Fig. 6 (bottom). In this system, silica condensation was turned on from the start and took place mainly in the bulk solution, initially forming small disordered clusters (Fig. 6f; please refer to Supplementary Fig. 12a,b for closer views of the aggregates), which subsequently merged to form a large three-dimensional silica aggregate (Fig. 6h; please refer to Supplementary Fig. 12c for a closer view). Interestingly, we can see that a significant number of TMA+ cations were initially adsorbed outside the small silica clusters (Fig. 6f), but were subsequently incorporated inside the growing aggregate (Fig. 6g–h), presumably due to the fusion of smaller clusters. Detailed views of the amorphous structure of the neutral/charged silica | TMA+ aggregate are provided in Supplementary Fig. 13. A similar behavior has been observed in more simplified models of silica/TMA+ solutions, aiming to describe the initial stages of the synthesis of zeolites templated by TMA+19,73,74. In the future, it would be worth exploring to which extent the incorporation of these cations inside growing nuclei leads to the onset of crystalline order, which is a critical step in the zeolite formation mechanism. Our model opens up an avenue to explore this mechanism, although much longer simulations, using special techniques like parallel tempering or metadynamics, would likely be required.

A more quantitative comparison between the two systems shows some significant differences induced by the presence of the surfactant micelle. In Fig. 7, we can observe the polymerization profile along the micelle encapsulation simulation (left panels), together with the same data for the TMA+ cation solution (right panels). In this Figure, we show the total condensation profile (top panels), but also the separate contributions from reactions involving only anionic silicates (middle panels) and those involving only neutral silicates (bottom panels). By comparing the curves in Fig. 7c and e up to 300 ps, it is clear that the first phase of the reaction in the micelle solution after self-assembly is mainly driven by the condensation of anionic silicates with each other (Fig. 7c). Only after this stage does condensation between neutral monomers take off, leading to the formation of more highly condensed species (Fig. 7e). In contrast, condensation in the TMA+ cationic solution is dominated by reactions between neutral silicates (Fig. 7f), with condensation between anionic monomers playing a very minor role and only taking place much later in the simulation (Fig. 7d). This difference is a consequence of the dramatic increase in the local concentration of anionic silicates at the micelle surface, which facilitates the start of the silica polymerization. In fact, the requirement for balancing the electrostatic forces at the surface of the micelle causes the formation of a rather stable arrangement where anionic silicates of opposite charge can be located in quite close proximity. This view is further supported by the results of Supplementary Fig. 9, where the reactive potential was turned on at the start of the self-assembly process. Although some small silica oligomers are formed in solution during the early stages of the simulation (Supplementary Fig. 9b), significant polymerization only takes place once micellar aggregates start to form (Supplementary Fig. 9c), hence further supporting our conclusion that the micelles act as pseudo-catalysts by creating a local silica concentration enhancement that promotes the reaction. Such a local concentration enhancement does not take place in the cationic solution, where the ions are much more mobile and spread out across the aqueous phase. Therefore, the electrostatic repulsion between anionic silicates is not overcome, and condensation in that system takes place mostly by formation of isolated clusters in the bulk solution.

Fig. 7: Time dependence of the molar fraction of each Qn species.
figure 7

Left panels. Reactive MD simulation of the micelle encapsulation. Right panels. Reactive MD simulation of the TMA+ cation solution. The top panels (a, b) show data for reactions between all RSi particles in the system, the middle panels (c, d) are for reactions between anionic RSi- particles only, and the bottom panels (e, f) are for reactions between neutral RSin particles only. Note that in all profiles, the time is counted from the point at which the reactive potential was turned on (i.e. the left panels start from a pre-formed micelle).

Full size image

As the encapsulation simulation progresses, small neutral species are deposited at the micelle surface and react with the anionic silica layer, leading to a significant increase in the formation of Q3 and even some Q4 species. Furthermore, we observe a significant degree of rearrangement in the silica network covering the micelle during the latter stages of the simulation, such that anionic silicates become more uniformly dispersed throughout the micelle surface to minimize their mutual electrostatic repulsion. This is what leads to the observed increase in the percentage of Q0 species in the anionic-anionic profiles beyond ~2000 ps (see black line in Fig. 7c)—initially anionic silicates were primarily connected to other anionic silicates on the micelle surface, but with the progress of the reaction, they become mostly connected to neutral silicate groups instead. In fact, looking at all the left-hand side panels in Fig. 7 together leads us to conclude that the more highly condensed species most often involve a combination of anionic and neutral moieties. This emphasizes the role of neutral silicates as a kind of glue that contributes towards the cohesion of the silica layer at later stages of material synthesis. Such a role has been postulated to take place in the synthesis of amine-templated mesoporous silica materials at pH ~ 9, leading to materials with much thicker walls than their high-pH counterparts, although in those simulations no silica reactions took place75. Further studies are needed to explore these effects in the context of nanoporous silica material formation.

Overall, the cationic solution leads to the formation of a significantly higher proportion of Q4 species than in the micellar solution (compare top panels in Fig. 7). This is because, in this solution, there is no need for silica to wrap around a large micelle structure, and therefore it forms more disordered three-dimensional aggregates. In contrast, the micellar solution leads to the formation of a rather uniform nearly two-dimensional layer, dominated by Q2 and Q3 species, that fully encapsulates the micelle. In fact, removing the surfactant molecules from the inside of the micelle (mimicking, for example, the experimental processes of calcination or solvent extraction), we obtain a hollow silica shell (Supplementary Fig. 14) that is reminiscent of experimentally synthesized hollow silica nanospheres76,77,78. In those cases, the template surfactant micelles are typically much larger due to the presence of swelling agents (e.g. oils or alcohols), and the silica walls tend to be thicker to impart robustness to the particles. A synthesis mechanism of such systems has been proposed79, based on adsorption of silicates at the micelle surface, followed by polycondensation reactions to form a hollow silica shell. This is remarkably similar to the results of our reactive MD simulations.

Discussion

We have developed a classical reactive coarse-grained model to study the silica polymerization process that can be implemented in molecular dynamics simulation software, hence allowing for efficient simulation of these reactions under realistic experimental conditions. The formation and breakage of siloxane bonds is described through continuous Lennard-Jones interactions between virtual sites and sticky particles, suitably placed around a central silica particle so as to reproduce the correct tetrahedral bonding structure of silica. In the sense that it represents chemical reactions by coupling smaller particles with larger CG beads, our approach shares some similarities with the recently developed titratable MARTINI model80, although the latter does not aim to describe explicit chemical bonding between CG beads but rather the pH-dependent protonation/deprotonation equilibrium in individual CG beads representing acids or bases. Our model is compatible with the widely used MARTINI 2.0 coarse-grained force field, thus allowing for the simulation of chemical reactions and surfactant self-assembly from solution at realistic conditions with an explicit solvent representation.

The parameters of the reactive model were calibrated against experimental data63 for the evolution of silica connectivity during condensation at room temperature and at the isoelectric point of silica (i.e. pH = 2.5, where all silicates are neutral). Our model accurately reproduces the experimental distribution of the different Qn silica species as a function of time, and performs at least as well as a state-of-the-art Reactive Monte Carlo model48 with implicit solvent. Nevertheless, the model still has some limitations. First, the formation of water molecules in the polycondensation reactions is not explicitly accounted for, leading to a gradual densification of the solution as the degree of condensation increases. One could, in principle, correct for this effect by adding water molecules at specific points of the simulation proportionally to the number of Si-O-Si bonds formed; however, this would lead to unphysical jumps in the concentration, which we prefer to avoid at this stage. Furthermore, the distance between silica beads that have reacted is limited by the size of the MARTINI S-bead, and hence is larger than that observed in real Si-O-Si covalent bonds. This leads to the formation of silica structures of unrealistically low density, and may prevent the formation of ordered silica phases. One option to solve this problem would be to use even smaller silica beads, as introduced in the very recent MARTINI 3 model81. We are actively working on improved strategies to circumvent these limitations of our reactive model, and will report the outcomes in subsequent publications.

The features of our reactive coarse-grained model enable it to take advantage of highly parallelized molecular dynamics codes and efficiently simulate the processes of silica polymerization and surfactant self-assembly at the same time. We have demonstrated this capability by simulating the formation of a micelle of a cationic ammonium surfactant and its encapsulation by a two-dimensional layer of silica. Although this set-up is rather simplistic, it is reminiscent of the synthesis of micelle-templated hollow silica nanospheres and sheds light on the process of porous silica synthesis. In particular, we found that the density enhancement of anionic silicates at the surface of the cationic micelle, brought about by attractive electrostatic interactions, promotes the condensation between those silicates – in other words, surfactant micelles effectively act as catalysts for the polymerization reaction. This is a key step in the now widely accepted co-operative synthesis mechanism of mesoporous silica82, which had hitherto remained unproven. Additional simulations at higher concentrations, enabling the formation of higher-order surfactant/silica mesophases, are necessary to fully explore this issue, and we intend to report on these in due course.

The modeling paradigm reported here has the potential to be transferable to other systems that involve polymerization reactions of organic or inorganic reactants. In principle, the virtual sites and sticky particles can be arranged to describe other reaction topologies, such as in chain polymerization or cross-linking. The parameters of the model can also be tuned to capture the degree of reversibility of each reaction – e.g. by shifting the balance between formation and breakage of bonds through the relative magnitude of the attractive and repulsive potentials. Crucially, the simplicity of the model and its compatibility with existing force fields and widely used MD simulation software mean that it is likely to play an important role in processes where both chemical reactions are self-assembly processes are taking place.

Methods

All molecular dynamics simulations considered periodic boundary conditions and were carried out using the GROMACS 2016 package61 using the leap-frog algorithm83 to integrate the equations of motion. The initial energy minimization to avoid any overlapping particles was carried out in two steps, first using the steepest-descent method and then the conjugate gradient algorithm. In both cases, the convergence criterion for energy differences between consecutive iterations was 0.1 kJ mol−1. In order to set the initial temperature, an equilibration step in the NVT ensemble was used over 10 ps, with an integration time step of 0.1 fs using the velocity rescale thermostat84 at 300 K. This was followed by an equilibration step in the NpT ensemble for 500 ps with an integration time step of 2 fs, also employing the velocity rescale thermostat, and isotropic pressure scaling with the Berendsen barostat85 to maintain the pressure at 1 bar. In both steps, the cut-off scheme was used with 1.2 nm, and the potential-shift-Verlet modifier was applied both in the electrostatic and Lennard-Jones interactions. An additional NpT step with a simulation time of 10 ns and a time step of 5 fs, using the isotropic Parrinello-Rahman barostat86 and the Nosé-Hoover thermostat87, was carried out with positional restraints on all RSi molecules (i.e. preventing silica polymerization) to ensure that water molecules were realistically distributed before the production runs. The production runs followed the same setup as in the last equilibration stage, differing only in the integration time step. The use of particles with shorter non-bonded interactions, which is the case of VS and SP, requires the use of a smaller time step than that used in our previous studies7,8,9, otherwise the integration of the equations of motion may diverge and cause the system to collapse. We found that for time steps of 8 fs or above, the simulation was unstable leading to occasional divergences in the energy, and hence we applied a conservative time step of 6 fs throughout. We confirmed that for timesteps of 6 fs or less, there was no significant variation of the polymerization process over time.