Abstract
Despite governing heat management in any realistic device, the microscopic mechanisms of heat transport in all-solid-state electrolytes are poorly known: existing calculations, all based on simplistic semi-empirical models, are unreliable for superionic conductors and largely overestimate their thermal conductivity. In this work, we deploy a combination of state-of-the-art methods to calculate the thermal conductivity of a prototypical Li-ion conductor, the Li3ClO antiperovskite. By leveraging ab initio, machine learning, and force-field descriptions of interatomic forces, we are able to reveal the massive role of anharmonic interactions and diffusive defects on the thermal conductivity and its temperature dependence, and to eventually embed their effects into a simple rationale which is likely applicable to a wide class of ionic conductors.
Similar content being viewed by others
Introduction
The lithium-rich antiperovskite solid-state electrolyte (SSE) Li3ClO has emerged in the last decade as a promising candidate for all-solid-state lithium-metal batteries: it is superionic at room temperature (RT) with a large ionic conductivity; it is environmental friendly and made of light and cheap elements; it is not flammable and has demonstrated a good cyclability1. Furthermore, its wide electronic band gap leads to a very low electronic conductivity and a large electrochemical stability window2. Finally, it is also chemically stable against Li-metal formation, which would negatively affect the battery performance via dendritic short-circuits.
A proper account of heat dissipation is key in the design and actual production of batteries: in fact, an excessively low thermal conductivity may lead to overheating, especially during fast charging cycles, which may itself prompt catastrophic incidents, such as melting or explosion. In light of this, thermal runaway can be rightly considered “the key scientific problem in battery safety research” (verbatim from Ref. 3). In addition, thermal dissipation governs energy saving and scavenging: a compromise must be established between minimising heat losses while maximising electric flow during the charging cycle.
A relatively small number of experimental studies on heat dissipation in fast ionic conductors have been reported, as compared to the extensive literature on electric transport. Measurement were performed on superionic materials such as α-LiIO3 and \({{{{\rm{L{i}}}_{2}{\rm{{B}}}_{4}{\rm{O}}}}}_{{{{\rm{7}}}}}\)4,5; sulfates \({{{{\rm{L{i}}}_{2}{\rm{SO}}}}}_{{{{\rm{4}}}}}\) and \({{{{\rm{A{g}}}_{2}{\rm{SO}}}}}_{{{{\rm{4}}}}}\)6; the quasi-1D material LiCuVO47; lithium aluminium germanium phosphate glass-ceramics compounds of the form \({{{{\rm{Li}}}}}_{1+x}{{{{\rm{Al}}}}}_{x}{{{{\rm{Ge}}}}}_{2-x}{({{{{\rm{PO}}}}}_{4})}_{{{{\rm{3}}}}}\)8; yttrium-stabilised lithium zirconate phosphates, of the form \({{{{\rm{Li}}}}}_{1+x+y}{{{{\rm{Y}}}}}_{x}{{{{\rm{Zr}}}}}_{2-x}{({{{{\rm{PO}}}}}_{4})}_{{{{\rm{3}}}}}\)9. Of these, only the last two classes of materials can can be directly used as SSEs. From the theoretical standpoint, even fewer works are to be found. Even though some models that account for the contribution of the diffusing ions to thermal transport were introduced in the past decades10,11, a thorough study of heat dissipation in Li3ClO—and in SSE in general—is still missing. At the best of our knowledge, there exists only one calculation of the thermal conductivity, κ, of Li3ClO, reporting κ = 22.49 W m−1 K−1 at ambient temperature, i.e., more than one order of magnitude larger than the standard value found in ceramic SSEs8,9. Nonetheless, this seemingly promising result is obtained via a rather crude approximation to the Peierls–Boltzmann transport equation (BTE), namely the Slack model, known since its development to have a satisfactory agreement with the experiments (i.e., within ±20%) only for exceedingly simple materials, such as the rare-gas solids, while it is in general poorer for other systems12. Furthermore, the Slack approximation totally neglects the effects of defects/vacancies and, just like any BTE-based model, it cannot handle the spurious contributions to heat transport induced by the diffusion of Li ions. These limitations, stemming from a phonon(/normal-mode)-based approach to heat transport, can be naturally and easily bypassed through the Green–Kubo (GK) theory of linear response13,14,15,16,17,18, which holds for solids with anharmonic interactions of any strength, as well as for diffusing systems, such as liquids and superionic solids. Recently, the GK theory of thermal transport has been combined with state-of-the art quantum simulation methods based on density-functional theory (DFT)17,19,20 and successfully employed to evaluate κ from equilibrium molecular dynamics (MD) simulations of superionic systems, even at extreme pressure and temperature conditions21,22.
In this paper we first address the structural and mechanical properties of Li3ClO, along with their temperature dependence, by means of state-of-the-art ab initio (AI) calculations based on DFT. Leveraging these results, we then explore the thermal transport of Li3ClO by calculating its thermal conductivity within (1) the Slack model; (2) a state-of-the art implementation of the BTE; and (3) the GK theory of linear response and classical MD simulations using both classical force fields (FF) and machine-learnt interatomic potentials, trained on DFT data. Our results show that the presence of LiCl divacancies in nonstoichiometric systems, though increasing the Li-ion diffusivity, strongly reduces the thermal conductivity—and thus heat dissipation within the electrolyte—with respect to stoichiometric conditions. We find that the dependence of κ on temperature is also reduced, thus making it potentially easier to engineer devices that can safely and efficiently operate in a wide range of temperatures.
Results
Summary
Before addressing thermal transport, which represents the main goal of our work, we investigate the structural, electronic, vibrational, and mechanical properties of Li3ClO, along with their temperature dependence, and we extensively compare our AI results with the existing literature. These results are not only preliminary to the calculation of transport coefficients, but they also make it possible to draw some general conclusions on the deployment of Li3ClO for mass production of SSE-based batteries: ductility, stiffness, the magnitude of the mismatch in the lattice constants or in the thermal expansion coefficients between the SSE and the electrodes govern the extent and amplitude of local stresses, particularly at the SSE-electrode junction, and affect the overall performance of Li3ClO in a real device by either hindering or inducing cracks, mechanical instabilities, or spurious electric fields.
Structural properties
The crystal structure of Li3ClO has the \({{{\rm{Pm}}}}\overline{3}{{{\rm{m}}}}\) perovskite space group. The dependence of the lattice parameter on temperature is obtained in the quasi-harmonic approximation (QHA)23, using the vibrational frequencies computed as explained in section “Vibrational properties” and the Murnaghan equation of state24. The resulting zero temperature value, explicitly accounting for zero-point vibrational effects, is 3.91 Å, while the full temperature dependence is reported in Fig. 1.
The lattice parameter and thermal expansion coefficient computed at RT (RT = 300 K) are 3.93 Å and 2.77 ⋅ 10−5 K−1, respectively, in good agreement with the values previously obtained in other works: Zhang et al.25, Emly et al.26, and Wu et al.27 reported an optimised lattice parameter without the zero-point of 3.85, 3.90, and 3.91 Å, respectively; Braga et al.1 provided both experimental and theoretical data in accordance with one another, namely 3.91 Å1,28. For the linear thermal expansion coefficient, Zhang et al.25 reported a value of 2.11 × 10−5 K−1 using MD simulations in the NPT ensemble, while Wu et al.27 reported α = 3.12 × 10−5 K−1 within the QHA, in good agreement with our calculation. Braga et al.1 found the larger value 4.65 × 10−5 K−1 from the slope of the lattice parameter as a function of temperature.
Electronic band structure
The electronic band structure of Li3ClO (Fig. 2) exhibits a direct band gap of 6.46 eV at the M in the BZ at the HSE06 level of theory, in good agreement with the values obtained by Wu et al.27 (6.26 eV) and by Emly et al.26 (6.39 eV), thus making Li3ClO a wide band gap insulator and preluding a good electrochemical stability.
Vibrational properties
The phonon dispersion along high-symmetry lines in the BZ are plotted in Fig. 3 together with the corresponding vibrational density of states. Notice the presence of a large longitudinal-transverse (LO-TO) splitting in the infrared-active mode at the centre of the BZ (Γ point), due to the non-analytic behaviour of the dynamical matrices induced by the long-range (Coulomb) tails of the interatomic interactions. It has been pointed out that a proper account of these tails is essential not only for a correct qualitative description of the vibrational spectrum in the optic region, but also for an accurate evaluation of the thermal conductivity, which is more sensitive to the low-frequency portion of the spectrum29. The effect of a proper account of the LO-TO splitting on the value of the lattice thermal conductivity of Li3ClO is examined in the Supplementary Information.
The stability at zero temperature of this material has been debated, with different authors claiming the system to be either unstable30 or stable27: methods are employed, the authors find soft modes (imaginary frequencies) at the M and R points in the BZ using a 6 × 6 × 6 supercell. Since the instability is larger when a smaller (3 × 3 × 3) supercell is used, the occurrence of lattice instabilities may be an artefact due to lack of convergence even when a supercell as large as 6 × 6 × 6 unit cells is used in finite-difference calculation. Using perturbation theory at the zone-centre of a supercell (this by construction does not include NAC), the authors of Ref. 27 do not find any dynamical instabilities. Our calculations, performed within density-functional perturbation theory (DFPT), confirm the dynamical stability of this system.
Temperature dependence of the mechanical properties
Mechanical properties can have a deep influence on the fabrication of any device and, in particular, of alkali-ion solid-state batteries. An important aspect is that there must be a good contact between electrolyte and electrodes during the activity of a device. A good SSE candidate must be able to sustain large strains31 to prevent the interfaces with cathode and anode to deteriorate in response to the deformation thereof. In this light, excessive stiffness is a feature to be avoided. Another element to consider is the problem of Li deposition at the interface with the cathode, and the subsequent dendrite formation32, that affects especially liquids. A solid material may partially overcome this obstacle by fine-tuning elastic properties such as the shear modulus and Poisson’s ratio33, even if it has been reported that dendrite growth can still occur for other reasons34.
The three elastic moduli, namely the bulk modulus B, the Young modulus E, and the shear modulus G, measure how a material responds to volumetric, tensile, and shear stress, respectively; Poisson’s ratio, ν, measures the strain response in a direction perpendicular to an applied strain; Pugh’s ratio, B/G, is related to how materials are ductile as opposed to brittle. The Chung–Buessem35 elastic anisotropy index, AG, and the universal elastic anisotropy36, AU, provide a measure to quantify the extent of anisotropy in the elastic response of a crystal, and are obtained from the Voigt and Reuss estimates of B and G36. The Grüneisen parameter γ is the variation of pressure with thermal energy density at constant volume37. All these quantities are computed as a function of temperature within the QHA. The isothermal and adiabatic elastic constants (Cij) as a function of temperature are computed within the quasi-static approximation (QSA).
The temperature dependence of these quantities is shown in Fig. 4. Their values at RT and at T = 0 are reported in Table 1, together with results already available in the literature25,31. While our results at T = 0 are comparable with the ones found in other works, at the working temperature the quantities have lower values, in accordance to the fact that the material becomes softer when temperature is increased. In particular, the temperature dependence of B and G entails that Pugh’s ratio is also decreased, hinting at a greater brittleness38 of Li3ClO than previously predicted27,31. Furthermore, the computed value of AG is higher than what found in the literature, suggesting that Li3ClO is slightly more anisotropic than previously thought; this is confirmed by the value of AU, that allows a broader comparison with other materials.
Thermal conductivity
Thermal conductivity (κ) plays a key role in the quest for promising SSE for battery production. A high value of the thermal conductivity is a favourable quality for a SSE candidate to have, since efficient heat dissipation allows the manufacture of safer batteries that do not overheat. A quite high value κ = 22.49 W m−1 K−1 was previously reported27. This result was obtained from Slack’s model (SM)12, which is based on a rather crude approximation of the BTE39,40,41. We briefly review SM in the Supplementary Information. At the same level of theory, we obtain 16.55 W m−1 K−1 that is 26% lower and it is likely to be closer to a realistic value. Yet, the coarseness of the approximation makes it impossible to draw conclusions: as already mentioned in the Introduction, SM is known, since its formulation dating back to 1960s, to be fairly accurate (to within 20%) only for simple systems such as rare-gas crystals, while it grossly fails for more complex materials. The main issue is to be addressed to the cubic dependence of κ on the Debye temperature ΘD of the crystal, which itself depends dramatically on the parameters used to estimate it. For instance, if the lattice parameter is reduced by less than 2%, i.e., from the value we compute (3.91 Å) to a value found in the literature25 (3.85 Å), ΘD increases by 4% (from 630 to 653 K) and κ by 12% (from 16.6 to 18.5 W m−1 K−1). This and further approximations of the model—it is for instance insensible to the crystal structure of the material—makes it impossible to produce reliable estimates for κ within SM. For a realistic calculation the BTE must be treated in a detailed fashion relying on the explicit calculation (and inversion) of the phononic scattering-rate matrix to obtain the out-of-equilibrium occupation numbers of the phonons. A quick review of the BTE-based approach we follow is given in the Supplementary Information.
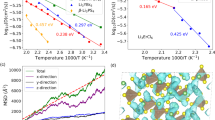
The lattice thermal conductivity in the Single Mode Relaxation Time Approximation (SMRTA) is computed AI via genuine third-order perturbation theory as implemented in the D3Q code42 distributed with QUANTUM ESPRESSO, and is displayed in Fig. 5 as a function of the temperature. For a comparison, we also report our calculation within the SM, which agrees qualitatively to the AI SMRTA result better than the existing literature27. We test the reliability of the classical FF in probing thermal properties of Li3ClO by employing it to compute the lattice thermal conductivity in the SMRTA. In general, a full solution of the linearised BTE may change significantly the computationally cheaper SMRTA result. In practice, we explicitly verified that the full solution reduces the SMRTA value of up to 0.5%, so we can safely keep all the calculations at the SMRTA level. Details can be found in the Supplementary Information. Figure 5 shows that classical FF and AI results are in good agreement, suggesting that the chosen classical FF is suited for investigating the thermal transport properties of Li3ClO.
BTE calculations are within SMRTA with 3-phonon scattering. Unfortunately, due to the large anharmonicity, 3-phonon scattering is not sufficient and further terms must be included, as discussed in the main text and shown quantitatively in Fig. 6.
As recently pointed out43,44, higher-order scattering events can drastically reduce the value of the lattice thermal conductivity; therefore, we test the effect of the inclusion of four phonon scattering into the computation of κ. As shown in Fig. 6, four phonon scattering is found to have a major role in determining the value of the lattice thermal conductivity, being able to reduce κ of at least 15% at RT, the reduction being larger for larger temperatures. Details on the calculation can be found in the Supplementary Information. This facts calls for a method able to include higher-order scattering: MD simulations together with GK linear response theory (see section “Green–Kubo linear-response theory”), which automatically include all the orders of interactions among phonons, are a fitting candidate for this role. Notice that, in BTE, the occupation numbers follow the Bose–Einstein distribution, \(n={\left({{{{\rm{e}}}}}^{\hslash \omega /{k}_{B}T}-1\right)}^{-1}\), while, in MD, n = kBT/ℏω, according to classical equipartition. This always leads to an underestimation of thermal conductivity in MD with respect to BTE, at the same level of the theory. An account on the relationship between GK and BTE approaches to thermal transport can be found in Ref. 45. Further details can be found in the Supplementary Information.
The choice of MD comes with an additional benefit: since fast ion conduction in SSE materials such as Li3ClO is due to diffusing defects, lattice dynamical methods are inadequate, as they require the atoms to have fixed equilibrium positions. MD simulations are not subject to this prerequisite and, therefore, they allow us to access thermal transport in the diffusive regime where fast ion diffusion is mediated by vacancy hopping.
According to the comprehensive studies of Mouta et al.46 and Lu et al.47, LiCl Schottky pairs—divacancies generated by the removal of neutral groups of atoms that are deposited at the surface of the material—are more likely to appear and give rise to a high Li-ion mobility than both other Schottky (Li2O or Li3ClO vacancies) and Frenkel (Li vacancies and interstitials) defects. Thus, the nonstoichiometric systems we study are of the form Li3−xCl1−xO, with x the concentration of vacancies that varies between 0 (perfect crystal) and 0.1.
The classical FF described in section “Classical molecular dynamics” is used to carry out the MD simulations and sample the heat flux according to Eq. (6), which in turn is employed to compute κ as in Eq. (7). To validate this, we compare classical FF calculations to estimates of κ extracted from (1) a Car–Parrinello MD simulation, on which a DFT energy flux is computed according to Ref. 17 as implemented in Ref. 48; (2) a model obtained via machine learning techniques.
The AI GK thermal conductivity requires a computationally demanding DFT energy flux (it requires roughly twice the computational time of the AIMD simulation the trajectory is sampled from): therefore, a single calculation at RT is carried out for the sake of checking the accuracy of the FF. We obtain κDFT = 6.5 ± 1.0 W m−1 K−1 at T = 306 K on a 4 × 4 × 4 supercell of crystalline Li3ClO, in close agreement with results from classical FF (see below).
As for the machine learning model, a DeepPot-SE NN49,50 is trained on a 3 × 3 × 3 supercell of Li3ClO with a LiCl pair removed. Details on the model and its validation can be found in the Supplementary Information. NN based MD simulations are carried out for x = 0 and x = 0.1 across the whole temperature range of interest. Thermal conductivity for the NN model is computed using the methodology developed in Ref. 51. In Fig. 7, we show a comparison between the GK thermal conductivity obtained with classical FF- and the NN potentials for these two systems. Results from NN simulations are in close agreement with the AI ones available at RT and, remarkably, with those obtained from classical FFs, over a broad temperature range, thus further validating the accuracy of the latter for the purposes of the present work.
Results are obtained from MD simulations with the classical FF and with the NN model for the perfect crystalline system (x = 0) and the highest concentration (x = 0.1) of vacancies we investigate. The 1/T fit of the high temperature behaviour of the FF data at x = 0 is shown in orange. The yellow star is the ab initio GK result at RT. Error bars represent standard deviations.
Having thoroughly verified that the classical FF closely mimics AI-quality results, we use it to perform a systematic analysis of the thermal transport properties of Li3ClO in a broad range of temperatures and vacancy concentrations. MD simulations are carried out on 10 × 10 × 10 supercells. The desired vacancy concentration is obtained by randomly removing the corresponding number of LiCl pairs from the supercell by means of the Atomsk code52. For each temperature, we employed the temperature-dependent AI lattice parameter computed in section “Structural properties” in the QHA (independently of vacancy concentration). In the equilibration phase, the canonical ensemble is sampled via the CSVR thermostat53 for 200 ps. At this point, the thermostat is removed and a microcanonical (NVE) production run of 5 ns is carried out to collect the desired data.
The dependence of the thermal conductivity on T and x is shown in Fig. 8. The numerical data measured in the MD simulations are then fitted to a simple function, Eq. (3), as described below. The functional form of such dependence should account for the Peierls–Boltzmann asymptotic 1/T behaviour (Eucken’s law)54, holding for crystals (x = 0) at large temperatures, but should also be able to take into account the breakdown of crystalline order when vacancies are present (x ≠ 0). The presence of vacancies, while providing access to Li-ion conduction channels, on shorter time-scales establishes an effective local disorder, that would result in a contribution to the thermal conductivity describable at different levels of accuracy18,55,56,57. The simplest significant approach is to consider the Allen–Feldman model56 of thermal conduction in harmonic glasses, where the thermal conductivity, κAF, takes the form:
Here, λ is a label for the modes, nλ(T) is the Bose–Einstein occupation number at temperature T, and Dλ is the (temperature-independent) mode diffusivity; asymptotic expansion of (1) in the high temperature limit yields:
i.e., the leading order is constant in temperature. Notice that MD with classical nuclei sample, by definition, classical distributions: the occupation of a mode of energy ℏωλ is thus the first order expansion of Bose–Einstein distribution, nλ(T) ≈ kBT/ℏωλ, and the heat capacity per mode reduces to the Dulong–Petit result, Cλ ≈ kB. All in all, we take as fitting function for κ(T, x):
where CEuck(x) and CAF(x) are vacancy-dependent fitting parameters, incorporating both the Eucken and the Allen–Feldman asymptotics. Their values are reported in the Supplementary Information and shown in the inset of Fig. 8. As expected, CAF is compatible with zero in the case x = 0, while sensibly different in the other cases. It is also comforting to notice that CEuck(x) vanishes as x increases, while CAF(x) saturates. To have a clear picture of the relative importance of these contributions, we explicitly report, in Fig. 9, the decomposition of κ vs T into the Eucken and AF terms at the different vacancy concentrations inspected in MD simulations. This picture suggests that, at least in this class of SSE, ionic diffusion may contribute very little to κ, which is instead dominated by the lattice component at low temperature, and by disorder at high temperature. This was recently investigated experimentally in Ref. 58 for Ag+ fast ion conductors.
Our GK calculations show that the thermal conductivity strongly depends on the presence of defects: in the considered temperature range, even a few-% concentration of defects is able to almost halve the κ with respect to its value for the perfect crystal. This behaviour is particularly evident at low temperature, due to the suppression of the Eucken law when x increases. Nonetheless, when compared to other candidates for battery-oriented SSE, Li3ClO is characterised by a relatively high thermal conductivity, and meets the requirements for safe heat dissipation and management.
Discussion
We conclude with a summary of our results and some perspectives on the possible use of Li3ClO in realistic devices. In the first part of our work we have reported state-of-the art calculations on the structural and mechanical properties of Li3ClO, including the zero-point lattice contribution and non-analytical corrections. According to our calculations, Li3ClO is mechanically stable, and characterised by a larger brittleness and anisotropy than previously thought. From the thermal transport standpoint, we extensively showed, by comparing different levels of theory, that current estimates of the thermal conductivity are fully unreliable, overestimating the value obtained via more accurate theory by several times in the temperature window at which SSE are supposed to operate. We explicitly demonstrated that, due to strong anharmonicity, not even the full solution of the Peierls–BTE with three-phonon scattering is sufficient and higher order contributions must be considered, which tend to further decrease the thermal conductivity of Li3ClO. We performed MD simulations and employed the GK theory of linear response and newly developed data-analysis tools to automatically incorporate all scattering orders and deal with vacancies and charge carrier diffusion as well. We observed that increasing the number of vacancies induces local disorder, which leads to a glass-like behaviour where the thermal conductivity saturates at large T rather than vanishing like 1/T according to Eucken’s law. Ionic diffusion per se seems instead to affect thermal transport only marginally. Our calculations indicate that, even if the capability of Li3ClO to dissipate heat in a realistic device must be scaled back, Li3ClO should still have a good thermal conductivity in a quite large temperature range and may be safely employed as a battery-oriented SSE. We hope that our work will encourage an experimental assessment of thermal transport properties of Li3ClO, and will also serve as a valid methodological reference, aimed at numerical-simulation practitioners, on how to investigate the thermal transport properties of generic SSE ionic conductors through state-of-the-art theoretical and data-analysis tools.
Methods
Summary
In this work, we follow a multi-method approach, hinging on a combination of classical simulations based on FF, AI computations based on density-functional (perturbation) theory, and neural-network (NN) modelling of AI data. In all cases, the accuracy of empirical FFs and NN potentials is thoroughly benchmarked against AI data.
Electronic, structural, mechanical, and vibrational properties are studied using DFT. The thermal conductivity is evaluated both through a Boltzmann–Peierls kinetic approach and via the GK theory of linear response and classical MD. BTE calculations are performed both AI, and using classical FFs. AI data are used as a reference, while FF simulations allow us to estimate the magnitude of finite-size and anharmonic effects, whenever AI calculations would be unfeasible, as well as the role of vacancies in thermal transport in nonstoichiometric conditions.
Electronic and atomic structure
All the electronic structure calculations are performed within DFT and the plane-wave pseudopotential method using QUANTUM ESPRESSO59,60,61 and SG15 Optimized Norm-Conserving Vanderbilt pseudopotentials62. Structural optimisation and lattice dynamical calculations were performed using the generalised gradient approximation to the exchange-correlation functional in the Perdew–Burke–Ernzerhof flavour63, while the electronic band structure is computed using the Heyd-Scuseria-Ernzerhof (HSE06)64 hybrid functional. The electronic structure is obtained starting from a self-consistent calculation on a coarse k-point grid in the Brillouin zone (BZ) leveraging a fast implementation of the Fock-exchange operator65, followed by a transformation to the Wannier basis, performed with WANNIER9066. and a subsequent non-self-consistent calculation to interpolate the energy bands. All calculations are performed using a plane-wave kinetic energy cutoff of 200 Ry (such an unusually high cutoff was needed for an optimal convergence of equilibrium thermal properties, vide infra) and the BZ sampling is done via a Monkhorst-Pack grid67 of 12 × 12 × 12 points displaced by half a grid step along the (1, 1, 1) direction. Vibrational properties are computed via DFPT68. dynamical matrices have been calculated on a 7 × 7 × 7 q-point grid, and Fourier-interpolated on a 192 × 192 × 192 mesh to evaluate the temperature dependence of the free energy in the QHA23, with the aid of the thermo_pw QUANTUM ESPRESSO driver69.
Classical molecular dynamics
MD simulations have been carried out with LAMMPS70,71, using different kinds of FF. Specifically, we adopt both an empirical FF and a NN interatomic potential trained and validated on AI data. We anticipate that the overall very good agreement between FF and NN simulations safely justifies the extended use of the empirical FF to study thermal transport across a wide range of temperatures and vacancy concentrations in a computationally affordable way.
The empirical force-field, which was fitted to structural and dielectric properties from experiments and AI calculations, is taken from Ref. 46. We adopt the simplified version based on a rigid-ion model, as opposed to core-shell models that are necessary when addressing specifically the electronic polarisability. The rigid-ion approximation has been used by other authors to investigate charge transport47,72. The short-range interatomic interaction is modelled by a Buckingham potential of the form:
where i and j label the two atoms separated by a distance rij, while Aij, ρij and Qij are fitting parameters. The long-range (Coulomb) interaction among point charges is computed via the Ewald summation technique73. The time-step for the dynamics is of 1 fs.
A Deep Potential–Smooth Edition (DeepPot-SE) NN model49,50,74 is employed to accurately mimic AI atomic forces in a computationally affordable way. The model is trained on a set of configurations sampled from Car–Parrinello simulations75 enriched with additional configurations chosen by the dpgen software76. Further details are provided in the Supplementary Information.
Boltzmann transport equation
The BTE is solved by real-space techniques with the ShengBTE code77 and its successor, almaBTE78, using harmonic and higher-order interatomic force constants (IFC) from both classical FFs, so as to make a comparison with GK-MD results handy, and first-principles methods based on DFT. In the first case, IFCs are obtained in real space using phonopy79. Details on size effects and the choice of the parameters can be found in the Supplementary Information. Quadratic and cubic force constants AI IFCs are obtained from second- and third-order DFPT, using the ph.x and D3Q42,80 components of QUANTUM ESPRESSO, respectively.
Green–Kubo linear-response theory
In the linear-response regime, the thermal conductivity, κ, is defined as the ratio between the energy flux and the negative of the temperature gradient in the absence of any convection. For solids and one-component fluids this last prescription is trivially satisfied in practical MD simulations performed in the barycentric reference frame. Within the GK theory of linear response, the thermal conductivity is given by the celebrated GK formula13,14,15,16,19
where the energy flux, JE(t), reads:
Here Ω is the system’s volume, ϵi is the energy assigned to the ith atom, Vi and Ri its velocity and position, respectively, and \({{{{\bf{F}}}}}_{ji}=-\frac{\partial {\epsilon }_{i}}{\partial {{{{\bf{R}}}}}_{j}}\).
For a multicomponent system such as the superionic phase of Li3ClO, Eq. (5) cannot be applied as it is, since the prescription of vanishing convection is not automatically satisfied in a standard MD simulation: in fact, keeping the barycentre of the whole system fixed does not imply that the barycentres of each atomic species S (with S = Li, Cl, O) stay fixed. Therefore, the mass fluxes of two of the three species, say \({{{{\bf{J}}}}}_{{{{\rm{Li}}}}}(t)=\frac{{M}_{{{{{\rm{Li}}}}}}}{{{\Omega }}}{\sum }_{i\in {{{\rm{Li}}}}}{{{{\bf{V}}}}}_{i}(t)\) and \({\bf{J}}_{\rm{Cl}}(t)=\frac{{M}_{\rm{Cl}}}{{{\Omega }}}{\sum }_{i \in {{{\rm{Cl}}}}}{{{{\bf{V}}}}}_{i}(t)\), where MS is the atomic mass of species S, i.e. the total momenta of each atomic species, are independent and in general non vanishing. Notice that, from a more fundamental point of view, even the concept of atomic energy ϵi appearing in Eq. (6) is intrinsically flawed, in that (1) there is no a priori “correct” decomposition of the total energy of a system of interacting atoms among its constituents, and (2) the zero of the atomic energies (i.e. the energy of isolated atoms) is arbitrary. A theoretically sound solution to both these problems has been provided in refs. 17,19,81, where it is rigorously proved that these apparent inconsistencies must disappear when a measurable quantity, such as κ, is correctly calculated, leading to the formulation of so-called invariance principles of transport coefficients20,82. Furthermore, a multivariate technique83,84 for the analysis of the energy flux time series obtained from MD simulations has been developed, which allows one to compute κ for multicomponent systems, like the superionic Li3ClO, in an efficient and rigorous way. We redirect the reader to refs. 83,84 for a thorough description of the method. Suffice it here to say that the thermal conductivity for Li3ClO is estimated in terms the ω → 0 limit of the power spectrum of the energy flux, after removing its coupling to the mass fluxes. This is achieved by computing the Schur complement of the matrix whose entries are the power spectra between fluxes JA, JB, i.e. \({S}_{AB}(\omega )=\int\nolimits_{-\infty }^{\infty }{e}^{i\omega t}\langle {{{{\bf{J}}}}}_{A}(t)\cdot {{{{\bf{J}}}}}_{B}(0)\rangle {{{\rm{d}}}}t\), where A, B ∈ {E, Li, Cl} refer to energy flux, Li mass flux, and Cl mass flux, respectively:
Since Li3ClO is a three-components material, two of the three mass fluxes are independent (the third being fixed by conservation of total momentum) and as such must, in general, be decoupled from the energy flux. In the case where some mass component were non-diffusive, they would contribute nothing to the value of the decoupled spectrum at zero frequency. Nonetheless, it was shown numerically that the decoupling at finite frequency allows a better estimate of the value at ω = 084. The numerical tools needed to evaluate the power spectra of time series of JE, and JLi and JCl have been implemented in the open-source SPORTRAN code85, which we extensively adopted in the present work.
References
Braga, M. H., Ferreira, J. A., Stockhausen, V., Oliveira, J. E. & El-Azab, A. Novel Li3ClO based glasses with superionic properties for lithium batteries. J. Mater. Chem. A 2, 5470 (2014).
Lü, X. et al. Li-rich anti-perovskite Li3OCl films with enhanced ionic conductivity. Chem. Commun. 50, 11520 (2014).
Feng, X. et al. Thermal runaway mechanism of lithium ion battery for electric vehicles: a review. Energy Storage Mater. 10, 246 (2018).
Abdulchalikova, N. & Aliev, A. Thermal properties of Li conducting superionic matirials. Synth. Met. 71, 1929 (1995).
Aliev, A. E., Krivorotov, V. F. & Khabibullaev, P. K. Specific heat and thermal conductivity of superionic conductors in the superionic phase. Phys. Solid State 39, 1378 (1997).
El-Rahman, A. A., El-Desoky, M. M. & El-Sharkawy, A. E.-W. A. Electrical and thermal properties of polycrystalline Li2SO4 and Ag2SO4. J. Phys. Chem. Solids 60, 119 (1999).
Parfen’eva, L. S. et al. Heat transport over nonmagnetic lithium chains in LiCuVO4, a new one-dimensional superionic conductor. Phys. Solid State 45, 2093 (2003).
Cui, Y., Mahmoud, M. M., Rohde, M., Ziebert, C. & Seifert, H. J. Thermal and ionic conductivity studies of lithium aluminum germanium phosphate solid-state electrolyte. Solid State Ion. 289, 125 (2016).
Yazdani, S. et al. Thermal transport in phase-stabilized lithium zirconate phosphates. Appl. Phys. Lett. 117, 011903 (2020).
Rice, M. & Roth, W. Ionic transport in super ionic conductors: a theoretical model. J. Solid State Chem. 4, 294 (1972).
Yonashiro, K. Thermal conductivity in superionic conductors. Solid State Ion. 27, 157 (1988).
Slack, G. A. The thermal conductivity of nonmetallic crystals. Solid State Phys. 34, 1 (1979).
Green, M. S. Markoff random processes and the statistical mechanics of time-dependent phenomena. J. Chem. Phys. 20, 1281 (1952).
Green, M. S. Markoff random processes and the statistical mechanics of time-dependent phenomena. II. Irreversible processes in fluids. J. Chem. Phys. 22, 398 (1954).
Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 12, 570 (1957).
Kubo, R., Yokota, M. & Nakajima, S. Statistical-mechanical theory of irreversible processes. II. Response to thermal disturbance. J. Phys. Soc. Jpn. 12, 1203 (1957).
Marcolongo, A., Umari, P. & Baroni, S. Microscopic theory and quantum simulation of atomic heat transport. Nat. Phys. 12, 80 (2015).
Isaeva, L., Barbalinardo, G., Donadio, D. & Baroni, S. Modeling heat transport in crystals and glasses from a unified lattice-dynamical approach. Nat. Commun. 10, 1 (2019).
Baroni, S., Bertossa, R., Ercole, L., Grasselli, F. & Marcolongo, A. Heat Transport in Insulators from Ab Initio Green-Kubo Theory. In Handbook of Materials Modeling: Current and Emerging Materials, (eds. Andreoni, W. & Yip, S.), 809 (Springer, Cham, 2020).
Grasselli, F. & Baroni, S. Invariance principles in the theory and computation of transport coefficients. Eur. Phys. J. B 94, 160 (2021).
Grasselli, F., Stixrude, L. & Baroni, S. Heat and charge transport in H2O at ice-giant conditions from ab initio molecular dynamics simulations. Nat. Commun. 11, 1 (2020).
Stixrude, L., Baroni, S. & Grasselli, F. Thermal and tidal evolution of Uranus with a growing frozen core. Planet. Sci. J. 2, 222 (2021).
Baroni, S., Giannozzi, P. & Isaev, E. Density-functional perturbation theory for quasi-harmonic calculations. Rev. Mineral. Geochem. 71, 39 (2010).
Murnaghan, F. D. The compressibility of media under extreme pressures. Proc. Natl Acad. Sci. USA 30, 244 (1944).
Zhang, Y., Zhao, Y. & Chen, C. Ab initiostudy of the stabilities of and mechanism of superionic transport in lithium-rich antiperovskites. Phys. Rev. B 87, 1 (2013).
Emly, A., Kioupakis, E. & Van der Ven, A. Phase stability and transport mechanisms in antiperovskite Li3OCl and Li3OBr superionic conductors. Chem. Mater. 25, 4663 (2013).
Wu, M., Xu, B., Lei, X., Huang, K. & Ouyang, C. Bulk properties and transport mechanisms of a solid state antiperovskite Li-ion conductor Li3OCl: Insights from first principles calculations. J. Mater. Chem. A 6, 1150 (2018).
Zhao, Y. & Daemen, L. L. Superionic conductivity in lithium-rich anti-perovskites. J. Am. Chem. Soc. 134, 15042 (2012).
Shafique, A. & Shin, Y.-H. The effect of non-analytical corrections on the phononic thermal transport in InX (X = s, se, te) monolayers. Sci. Rep. 10, 1 (2020).
Chen, M.-H., Emly, A. & Van der Ven, A. Anharmonicity and phase stability of antiperovskite Li3OCl. Phys. Rev. B 91, 214306 (2015).
Deng, Z., Wang, Z., Chu, I.-H., Luo, J. & Ong, S. P. Elastic properties of alkali superionic conductor electrolytes from first principles calculations. J. Electrochem. Soc. 163, A67 (2015).
Xu, W. et al. Lithium metal anodes for rechargeable batteries. Energy Environ. Sci. 7, 513 (2014).
Monroe, C. & Newman, J. The impact of elastic deformation on deposition kinetics at lithium/polymer interfaces. J. Electrochem. Soc. 152, A396 (2005).
Dollé, M., Sannier, L., Beaudoin, B., Trentin, M. & Tarascon, J.-M. Live scanning electron microscope observations of dendritic growth in Lithium/Polymer cells. Electrochem. Solid State Lett. 5, A286 (2002).
Chung, D. H. & Buessem, W. R. The elastic anisotropy of crystals. J. Appl. Phys. 38, 2010 (1967).
Ranganathan, S. I. & Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 101, 055504 (2008).
Stacey, F. D. & Hodgkinson, J. H. Thermodynamics with the grüneisen parameter: Fundamentals and applications to high pressure physics and geophysics. Phys. Earth Planet. Inter. 286, 42 (2019).
Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 45, 823 (1954).
Peierls, R. Zur kinetischen theorie der wärmeleitung in kristallen. Ann. Phys. 395, 1055 (1929).
Ziman, J. Electrons and Phonons (Oxford University Press, 2001).
McGaughey, A. J. H., Jain, A. & Kim, H.-Y. Phonon properties and thermal conductivity from first principles, lattice dynamics, and the Boltzmann transport equation. J. Appl. Phys. 125, 011101 (2019).
Paulatto, L., Mauri, F. & Lazzeri, M. Anharmonic properties from a generalized third-orderab initioapproach: theory and applications to graphite and graphene. Phys. Rev. B 87, 214303 (2013).
Feng, T. & Ruan, X. Quantum mechanical prediction of four-phonon scattering rates and reduced thermal conductivity of solids. Phys. Rev. B 93, 045202 (2016).
Feng, T., Lindsay, L. & Ruan, X. Four-phonon scattering significantly reduces intrinsic thermal conductivity of solids. Phys. Rev. B 96, 161201 (2017).
Puligheddu, M., Xia, Y., Chan, M. & Galli, G. Computational prediction of lattice thermal conductivity: a comparison of molecular dynamics and Boltzmann transport approaches. Phys. Rev. Mater. 3, 085401 (2019).
Mouta, R., Melo, M. A. B., Diniz, E. M. & Paschoal, C. W. A. Concentration of charge carriers, migration, and stability in Li3OCl solid electrolytes. Chem. Mater. 26, 7137 (2014).
Lu, Z. et al. Defect chemistry and lithium transport in Li3OCl anti-perovskite superionic conductors. Phys. Chem. Chem. Phys. 17, 32547 (2015).
Marcolongo, A., Bertossa, R., Tisi, D. & Baroni, S. QEHeat: an open-source energy flux calculator for the computation of heat-transport coefficients from first principles. Comput. Phys. Commun. 269, 108090 (2021).
Han, J., Zhang, L., Car, R. & E, W. Deep potential: a general representation of a many-body potential energy surface. CiCP 23, 629 (2018).
Zhang, L. et al. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. Adv. Neur. 2018, 4436 (2018).
Tisi, D. et al. Heat transport in liquid water from first-principles and deep neural network simulations. Phys. Rev. B 104, 22 (2021).
Hirel, P. Atomsk: a tool for manipulating and converting atomic data files. Comput. Phys. Commun. 197, 212 (2015).
Bussi, G., Donadio, D. & Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101 (2007).
Eucken, A. über die temperaturabhängigkeit der wärmeleitfähigkeit fester nichtmetalle. Ann. Phys. 339, 185 (1911).
Einstein, A. Elementare betrachtungen über die thermische molekularbewegung in festen körpern. Ann. Phys. 340, 679 (1911).
Allen, P. B. & Feldman, J. L. Thermal conductivity of disordered harmonic solids. Phys. Rev. B 48, 12581 (1993).
Simoncelli, M., Marzari, N. & Mauri, F. Unified theory of thermal transport in crystals and glasses. Nat. Phys. 15, 809 (2019).
Bernges, T. et al. Diffuson-mediated thermal and ionic transport in superionic conductors. Preprint at https://doi.org/10.33774/chemrxiv-2021-3zxh4 (2021).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Giannozzi, P. et al. Advanced capabilities for materials modelling with quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).
Giannozzi, P. et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 152, 154105 (2020).
Schlipf, M. & Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Comput. Phys. Commun. 196, 36 (2015).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207 (2003).
Carnimeo, I., Baroni, S. & Giannozzi, P. Fast hybrid density-functional computations using plane-wave basis sets. Electron. Struct. 1, 015009 (2019).
Pizzi, G. et al. Wannier90 as a community code: new features and applications. J. Phys. Condens. Matter 32, 165902 (2020).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515 (2001).
Malica, C. & Dal Corso, A. Quasi-harmonic temperature dependent elastic constants: applications to silicon, aluminum, and silver. J. Phys. Condens. Matter 32, 315902 (2020).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1 (1995).
Thompson, A. P. et al. LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022).
Sagotra, A. K. & Cazorla, C. Stress-mediated enhancement of ionic conductivity in fast-ion conductors. ACS Appl. Mater. Interfaces 9, 38773 (2017).
Ewald, P. P. Die berechnung optischer und elektrostatischer gitterpotentiale. Ann. Phys. 369, 253 (1921).
Wang, H., Zhang, L., Han, J. & E, W. DeePMD-kit: a deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 228, 178 (2018).
Car, R. & Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55, 2471 (1985).
Zhang, Y. et al. DP-GEN: a concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun. 253, 107206 (2020).
Li, W., Carrete, J., Nebil, A. K. & Mingo, N. ShengBTE: a solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 185, 1747 (2014).
Carrete, J. et al. almaBTE: a solver of the space–time dependent Boltzmann transport equation for phonons in structured materials. Comput. Phys. Commun. 220, 351 (2017).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1 (2015).
Fugallo, G., Lazzeri, M., Paulatto, L. & Mauri, F. Ab initiovariational approach for evaluating lattice thermal conductivity. Phys. Rev. B 88, 045430 (2013).
Ercole, L., Marcolongo, A., Umari, P. & Baroni, S. Gauge invariance of thermal transport coefficients. J. Low. Temp. Phys. 185, 79 (2016).
Marcolongo, A., Ercole, L. & Baroni, S. Gauge fixing for heat-transport simulations. J. Chem. Theory Comput. 16, 3352 (2020).
Ercole, L., Marcolongo, A. & Baroni, S. Accurate thermal conductivities from optimally short molecular dynamics simulations. Sci. Rep. 7, 1 (2017).
Bertossa, R., Grasselli, F., Ercole, L. & Baroni, S. Theory and numerical simulation of heat transport in multicomponent systems. Phys. Rev. Lett. 122, 255901 (2019).
Ercole, L., Bertossa, R., Bisacchi, S. & Baroni, S. SPORTRAN: a code to estimate transport coefficients from the cepstral analysis of a multi-variate current stationary time series. https://github.com/lorisercole/sportran (2017–2021).
Talirz, L. et al. Materials cloud, a platform for open computational science. Sci. Data 7, 1 (2020).
Pegolo, P., Baroni, S. & Grasselli, F. Temperature- and vacancy-concentration-dependence of heat transport in Li3ClO from multi-method numerical simulations, Materials Cloud Archive, https://doi.org/10.24435/materialscloud:hf-qj (2022).
Acknowledgements
This work was partially funded by the EU through the MAX Centre of Excellence for supercomputing applications (Project No. 824143) and by the Italian Ministry of Research and education through the PRIN 2017 FERMAT grant. F.G. acknowledges funding from the Swiss National Science Foundation (SNSF), through Project No. 200021-182057, and from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Action IF-EF-ST, grant agreement No. 101018557 (TRANQUIL). We thank Cristiano Malica for his support with ab initio thermodynamics methods; Davide Tisi and Cesare Malosso for their support with machine learning methods; Pietro Delugas, Riccardo Bertossa and Alfredo Fiorentino for technical support and useful discussions. We thank Kevin Rossi for a critical reading of the manuscript.
Author information
Authors and Affiliations
Contributions
This work was jointly supervised by S.B. and F.G. Computer simulations were run and analysed by P.P. The paper was jointly written by all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pegolo, P., Baroni, S. & Grasselli, F. Temperature- and vacancy-concentration-dependence of heat transport in Li3ClO from multi-method numerical simulations. npj Comput Mater 8, 24 (2022). https://doi.org/10.1038/s41524-021-00693-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00693-4
This article is cited by
-
Predicting lattice thermal conductivity via machine learning: a mini review
npj Computational Materials (2023)
-
Hydrodynamic finite-size scaling of the thermal conductivity in glasses
npj Computational Materials (2023)
-
Viscosity in water from first-principles and deep-neural-network simulations
npj Computational Materials (2022)