Abstract
Manipulating valley-dependent Berry phase effects provides remarkable opportunities for both fundamental research and practical applications. Here, by referring to effective model analysis, we propose a general scheme for realizing topological magneto-valley phase transitions. More importantly, by using valley-half-semiconducting VSi2N4 as an outstanding example, we investigate sign change of valley-dependent Berry phase effects which drive the change-in-sign valley anomalous transport characteristics via external means such as biaxial strain, electric field, and correlation effects. As a result, this gives rise to quantized versions of valley anomalous transport phenomena. Our findings not only uncover a general framework to control valley degree of freedom, but also motivate further research in the direction of multifunctional quantum devices in valleytronics and spintronics.
Similar content being viewed by others
Introduction
Recent advances in valleytronics are mainly based on the paradigm of time-reversal-connected valleys, which generates valley polarization by an external field, dynamically or statically1,2,3. However, for achieving widespread applications of valleytronics, intrinsic properties are to be prioritized higher than external tunability. More importantly, intrinsic valleytronics materials hosting spontaneous valley polarization are most desirable, owing to their advantages of robustness, power efficiency, and simplicity in operation. In this regard, alternatives to the existing paradigms are intensively sought after. Recently, the proposal of two-dimensional (2D) ferrovalley materials has laid out a magneto-valleytronics composite paradigm based on spontaneous valley polarization induced by the integrated effects of magnetic order and spin-orbit coupling (SOC), which can radically reduce additional costs of the applied external fields4. Specifically, when valley couples with intrinsic ferromagnetic order, the valley-dependent Berry phase effects can generate emergent valley anomalous transport phenomena − e.g., valley Hall effect5,6,7,8,9,10,11 and valley Nernst effect12,13) − making it possible to realize high-performance quantum devices and thus raising an intensive interest in materials systems which host magneto-valley traits.
From the perspective of potential applications in valleytronics, exploring various phase transitions in 2D magneto-valley materials has played a vital role in promoting our understanding, discovery, and characterization of emerging quantum states of matter. A general law of phase transitions is that they can drive not only rich quantum states but also intriguing physical properties. However, possibly due to the fewer number of 2D ferrovalley materials4,14,15,16,17,18 and the difficulty in characterizing the magnetic ordering and topological phase transitions, high-quality magneto-valley material candidates with a wide range of phase transitions have been scarcely discussed. On the other hand, an interplay between different phase transitions accompanied by distinct valley anomalous transport manifestations in such materials has not been seriously considered yet, which poses a great challenge for the research on potential high-performance valleytronics devices.
A crucial but thought-provoking issue for magneto-valley coupling is finding a way to effectively generate spontaneous valley polarization utilizing the spin degree of freedom, and thereby lead to a revolution in magneto-valley-based information storage and operation principles. To tackle the current challenges of valleytronics, we break out the present ferrovalley paradigm to provide a general classification of magneto-valley coupling states through an effective model analysis, where the low energy electronic inter-valley nature enjoys a giant valley splitting with fully spin-polarized fermions. Consistent with the model, as a concrete example, VSi2N4 showcases emerging magneto-valley coupling phases − including valley-half-semiconductor, valley-half-semimetal as well as valley-unbalanced quantum anomalous Hall states (see Fig. 1) − transitions between which can be controlled by using external stimuli such as biaxial strain, electric field, and correlation effects. Remarkably, we find that topological phase transitions with magneto-valley coupling can exhibit valley-dependent Berry phase effects which manifest in prominent valley sign-reversible anomalous transport fingerprints.
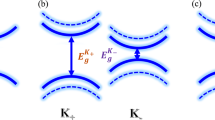
The balanced system is a valley-half-semiconductor (VHSC) state (a), which simultaneously exhibits valley polarized, full spin-polarized, and semiconducting properties. With increasing the parameter e1, K\({}^{\prime}\) and K valleys close successively at the critical points ec1 and ec2 respectively, corresponding to the valley-half-semimetal (VHSM) states (b, d), which simultaneously exhibits valley polarized, full spin-polarized, and semi-metallic properties. The fully spin-polarized valley-unbalanced quantum anomalous Hall states (VQAH) state (c) is expected between two VHSM states, which harbors valley index and quantum anomalous Hall effect simultaneously. Beyond ec2, the gap at K valley reopens and the VHSC state restores (e). A phase diagram as a function of the model parameters r2 and e1 (r1 = 2) is summarized in (f).
Results and discussion
Valley-half-semiconductors and their topological phase transitions
According to the relationship between the valence band maximum and conduction band minimum of the same spin channel at the Fermi level, magneto-valley coupling (MVC) gives rise to a wide spectrum of quantum phase transitions ranging from gapped to gapless ones. To better capture the key physics underlying topological phase transitions, we construct a simple tight-binding (TB) model for describing the topological phase transitions of MVC states. Without loss of generality, we take a 2D triangular lattice with a magnetic space group \(P\bar{6}m^{\prime} 2^{\prime}\) as an example, and assume that the direction of the spins of magnetic atoms is parallel to the z-axis (i.e., out of the plane). To conveniently describe the atomic basis of \(P\bar{6}m^{\prime} 2^{\prime}\) symmetry, the minimal set of \(|{d}_{{x}^{2}-{y}^{2}}\uparrow \rangle\) and \(|{d}_{xy}\uparrow \rangle\) (or \(|{p}_{x}\uparrow \rangle\) and \(|{p}_{y}\uparrow \rangle\)) orbitals is taken as the basis in our TB model. The Hamiltonian containing only the nearest-neighbour hopping reads:
where \({c}_{i\alpha }^{{\dagger} }\) (cjβ) is the electron creation (annihilation) operator for the orbital α (β) on site i (j). By using the MagneticTB package19 that was recently developed to incorporate the group representation theory, all independent nearest-neighbour hopping integrals \({t}_{ij}^{\alpha \beta }\) can be screened under a given symmetry constraint. Under the magnetic space group of \(P\bar{6}m^{\prime} 2^{\prime}\), the topological phase transitions of MVC states can be achieved with only three parameters [r1, r2, and e1, see Eqs. (23) and (24)]. The Chern number for characterizing topologically nontrival phases can be analytically written as,
For our model, Fig. 1a schematically shows that K and K\({}^{\prime}\) valleys bare semiconductor characteristics with full spin-polarization in the same spin channel. Such a valley-half-semiconductor (VHSC) state is highly promising for generating, transporting, and manipulating spin currents in spin-valleytronics. Topological phase transitions starting from the VHSC state can be realized by changing the model parameters r2 and e1 simultaneously. When the bandgap at K valley decreases, the other one at K\({}^{\prime}\) valley is reduced as well. During the transition, a critical state, namely the valley-half-semimetal (VHSM) state, is inevitably encountered [Fig. 1b]: it is gapless at K\({}^{\prime}\) valley but it is gapped at K valley. The gapless crossing point is two-fold degenerate with linear dispersion, similar to that of Weyl semimetals. In Fig. 1c, the gap reopening at K\({}^{\prime}\) valley indicates a topological phase transition, and the valley-unbalanced quantum anomalous Hall state (VQAH) state is confirmed by a nonzero Chern number (\({{{\mathcal{C}}}}=1\)), which is contributed by both K and K\({}^{\prime}\) valleys. The VQAH state predicted here differs from the previously considered quantized valley Hall state or valley-polarized quantum anomalous Hall state. The quantized valley Hall state is found in spatial inversion broken non-magnetic materials, in which both K and K\({}^{\prime}\) valleys host nonzero Chern numbers but with opposite signs, while the valley-polarized quantum anomalous Hall state is predicted in magnetic materials with nonzero Chern number originating from only one valley5,20,21. Further increasing the parameter e1 will force K valley to first close the gap and then reopen it again, as shown in Fig. 1d, e. The summary of topological phase transitions is shown in Fig. 1f. Note that the SOC has been taken into account in our model, and therefore the emergence of MVC states having 100% spin polarization is remarkable and promising for spin-valleytronics22,23,24,25.
An interplay between valley degree of freedom, magnetism, and topology provides an excellent platform for researching valley-related anomalous transport properties of MVC states, realizing a rich set of exotic quantum phenomena, such as valley anomalous Hall effect (VAHE), valley anomalous Nernst effect (VANE), as well as valley magneto-optical Kerr effect (VMOKE) and valley magneto-optical Faraday effect (VMOFE). Specifically, pursuing a single material that simultaneously exhibits topological phase transitions and valley sign-reversible Berry phase effects has been rarely done to date, although such a material would be highly valuable for multi-functional miniaturized devices. In addition to considering artificially constructed MVC heterostructures, an alternative is to seek intrinsic MVC materials that can harbor topological phase transitions driven by external means, such as biaxial strain, electric field, and correlation effects.
High-quality candidate materials
In this work not only do we provide a classification of MVC states, but also propose a series of MVC materials [Fig. 2a, b], including 2D ferromagnetic VSi2N4 as well as other eleven MA2Z4 (M = V, Nb; A = Si, Ge; Z = N, P, As) candidates26,27. All these candidate materials form on a hexagonal lattice with the same magnetic space group that has been employed above, which can be regarded as the magnetic counterparts of the valley Hall semiconductors MoSi2N4 family28,29. While aforementioned MVC states and their topological phase transitions exist in all materials, below we focus on one representative − VSi2N4 − and discuss the rest of the materials in the Supplemental Material (see Supplementary Figs. 1 and 2).
a, b The top and side views of MA2Z4 materials family. The dashed lines in (a) indicate the 2D primitive cell. c The Brillouin zone of MA2Z4. d The band structures of VSi2N4 were calculated by the hybrid functional without SOC (left panel) and with SOC (right panel). (e) The stress-strain curve of VSi2N4. The top x-axis plots the whole strain range of 0–30%, while the bottom x-axis plots the small strain range of 0–3%. The colors indicate the magnitudes of the bandgap, and the corresponding Chern number (\({{{\mathcal{C}}}}\)) is marked. The evolution of band structure (f) and orbital compositions at band edge (g) under the strain of 0–2%. Various fully spin-polarized valley topological states emerge, including VHSC (0%), VHSM (1.4%), VQAH (1.6%), VHSM (1.75%), and VHSC (2%).
The electronic band structure of VSi2N4, which is a fully spin-polarized semiconductor with a small direct bandgap (0.24 eV) at K/K\({}^{\prime}\) valley in the spin-up channel and with a large indirect bandgap (3.19 eV) in the spin-down channel, is shown in Fig. 2d. When SOC is taken into account, VSi2N4 evolves into a VHSC state with a giant valley splitting of 102.3 (27.3) meV at the valence (conduction) band edge, which is originated from the simultaneous breaking of time-reversal and spatial inversion symmetries. Its physical origin is similar to the resonant photovoltaic effect in doped magnetic semiconductors30. More importantly, VSi2N4 possesses an "ultra-clean” linear band dispersion around K and K\({}^{\prime}\) valleys in the energy range of [− 0.7, + 1.2] eV, which suppresses the influence of irrelevant trivial bands for valley performance. The linear band dispersion ensures a high Fermi velocity of about 0.4 − 0.5 × 106 m/s along with different momentum directions, which is of the same order as that of graphene31. This promotes VSi2N4 into one of the most appealing candidates when comparing it with currently considered ferrovalley materials. Note that the VHSC state of VSi2N4 has been previously discovered in a recent work32.
While VSi2N4 is a long-sought VHSC material, it can also host various fully spin-polarized MVC topological states under external means such as biaxial strain, electric field, and correlation effects. Taking biaxial strain as an example (the cases of electric field and correlation effects are shown in Supplementary Figs. 5 and 6), we predict strained VSi2N4 to exhibit various MVC states, covering VHSC, VHSM, and VQAH states. As shown in Fig. 2f, by increasing strain within a reasonable range (0–2%), the VHSC state (0%) undergoes topological phase transitions that can be identified by the closing and reopening of band gaps at K\({}^{\prime}\) and K valleys, resulting in the VHSM (1.4%), VQAH (1.6%), VHSM (1.75%), and VHSC (2%) states. The gap evolution together with corresponding Chern numbers is summarized in Fig. 2e. Furthermore, the orbital-projected band structures of MVC states [Fig. 2g] are another indicator for topological phase transitions. In the balanced state of VSi2N4, the valence band maximum is dominated by the dxy and \({d}_{{x}^{2}-{y}^{2}}\) orbitals of V atoms, and the conduction band minimum mainly comes from the \({d}_{{z}^{2}}\) orbital. At the strain of 1.4%, the orbital compositions reverse at K\({}^{\prime}\) valley, driving the system into the VQAH state; further increasing strain to 1.75%, the orbital inversion occurs also at K valley, restoring the system to the VHSC state. This valley-related topological phase transition can be also driven by the correlation effect, as realized in FeCl217 and VSi2P433,34.
Sign reversal of valley-dependent Berry phase effects
An in-depth investigation of MVC topological phase transitions provides a platform for exploring valley-related anomalous transport phenomena. In this context, it is remarkable that VSi2N4, while hosting topological phase transitions, exhibits also sign change of valley-dependent Berry phase effects. Regarding the VHSC state (0%), for which the calculated k-resolved Berry curvature Ω(k) is shown in Fig. 3a, one can clearly identify the hot spots in the Berry curvature around two valleys with opposite signs and different magnitudes. By introducing a tiny biaxial strain, the VHSC state experiences a topological phase transition into the VQAH state, bridged by the VHSM state. Within the strain of 1.4–1.6%, the sign of Ω(k) at K\({}^{\prime}\) valley flips [Fig. 3b]. Further increasing strain from 1.6–2%, K valley also experiences a topological phase transition, akin to the case of K\({}^{\prime}\) valley, resulting in the sign change of Ω(k) at K valley [Fig. 3c]. Such dynamics of Ω(k) is bound to influence valley-related anomalous transport phenomena such as VAHE, VANE, VMOKE, and VMOFE.
The Berry curvature Ω(k) (first row), VAHE (second row), VANE (third row), and VMOKE (fourth row) under three different strains of 0% (a), 1.6% (b), and 2% (c), respectively. The results of VMOFE (not shown here) are rather similar to that of VMOKE. The unit of VANE is set to be α0 = kBe/h (e is the elementary charge, kB and h are Boltzmann and Planck constants, respectively). Yellow shaded areas indicate the regions of large valley splitting. The Berry curvature is plotted at the energy where the anomalous Hall conductivity reaches its maximum. The legends of K, K\({}^{\prime}\), and TOT represent contributions from K valley, K\({}^{\prime}\) valley, and the entire Brillouin zone, respectively.
Our predictions concerning the valley-related anomalous transport phenomena are presented in Fig. 3. Since VAHE is calculated by the integration of Ω(k) in a small region centered at each valley, the sign changes of VAHE are in full accordance with Ω(k) during the topological phase transitions. This is also the case for VANE as well as VMOKE and VMOFE. The former is calculated by integrating the Berry curvature together with a weighting factor around each valley (see Eq. (4)). The latter phenomenon can be actually regarded as the ac counterpart of VAHE. Physically, these anomalous transport phenomena are intimately related to each other. Therefore, the change in their signs strongly depends on the nature of topological phase transitions, exhibiting exotic sign reversal of valley-dependent Berry phase effects.
Interestingly, due to the different magnitudes of Ω(k) at two valleys, a net fully spin-polarized valley current is produced by the anomalous Hall, anomalous Nernst, and magneto-optical effects. Notably, the VQAH phase emerges during the phase transition, accompanied by a quantized anomalous Hall conductivity σxy = e2/h [second row of Fig. 3b]. Besides, one can utilize the non-contact magneto-optical technique35,36,37 to detect this topological phase38,39,40,41. For a VQAH state, the central physical idea is that Maxwell’s equations have to be modified by adding an axion term (Θα/4π2) E ⋅ B (here Θ is magnetoelectric polarizability and α = e2/ℏc is the fine structure constant) into the usual Lagrangian42. In this way, the magneto-optical Kerr (θK) and Faraday (θF) rotation angles turn out to be quantized in the low-frequency limit, that is, θK ≃ − π/2 and \({\theta }_{F}\simeq {{{\mathcal{C}}}}\alpha\) (\({{{\mathcal{C}}}}\) is the Chern number)43,44. In the bottom of Fig. 3b, one can clearly observe the quantization behavior of θK and θF in the low-frequency limit.
Generally, the tunable sign of Ω(k) has been witnessed by reversing the magnetization4 and ferroelectric polarization45. However, these two means seem to be sub-optimal and often suffer from various drawbacks, making it difficult to utilize this effect. As an alternative avenue, the manipulation by a small biaxial strain is more suitable for practical purposes. It is worth noting that topological phase transitions through biaxial strain may not only change the sign of anomalous transport characteristics but also modify their magnitude, and more importantly, the mediated quantization of transport characteristics is indispensable for experimental observation. We further calculate the effects of temperature and disorder on the valley-dependent Berry phase effects, and the results (see Supplementary Fig. 10) show that the sign changes of VAHE and VANE, being the key feature of topological phase transitions, are robust against disorder and temperature.
In this work, we introduce a general framework to realize topological magneto-valley phase transitions in 2D VHSC, and we propose a series of feasible candidate materials harboring valley-dependent Berry phase effects, which are triggered by external means such as biaxial strain, electric field, and correlation effects. Taking VSi2N4 as a representative, we demonstrate that such intrinsic VHSC states display long-sought fully spin-polarized valley index. The proposal of sign reversal of valley-dependent Berry phase effects and high-quality materials realization greatly expand the ferrovalley family and provide an exciting playground for spintronics and valleytronics applications.
Methods
First-principles calculations
The first-principles calculations were carried out employing the projected augmented wave method46, as implemented in the Vienna ab initio simulation package (VASP)47. The exchange-correlation effect was treated by the Perdew-Burke-Ernzerhof parameterized generalized-gradient approximation (PBE-GGA)48. The energy cut-off of 500 eV and the k-mesh of 25 × 25 × 1 were used in the static calculations. The force and energy convergence criteria were set to be 10−3 eV/Å and 10−7 eV, respectively. The on-site Coulomb correlation of V and Nb atoms is considered within the GGA + U scheme49. Different effective Hubbard energy U were tested in Supplementary Fig. 5 and the U = 3 eV was used in the main text, which has been also used in ref. 32. The more accurate Heyd-Scuseria-Ernzerhof hybrid functional method (HSE06)50 was used to check the electronic structure. A vacuum space of 13 Å was used to avoid the interactions between the neighboring slabs. The phonon spectrum was performed based on the density functional perturbation theory (DFPT)51. The mostly localized Wannier functions including the d-orbitals of V atom, the s- and p-orbitals of Si atom, and the p-orbitals of N atom were constructed on a k-mesh of 8 × 8 × 1, using the WANNIER90 package52.
Anomalous Hall and anomalous Nernst effects
The intrinsic anomalous Hall conductivity (AHC) and anomalous Nernst conductivity (ANC) were calculated on a dense k-mesh of 501 × 501 × 1, using the Berry phase theory53,54,
where \({{{\Omega }}}_{xy}^{n}({{{\bf{k}}}})\) is the band- and momentum-resolved Berry curvature
Here, {x, y} denote the Cartesian coordinates, \({\hat{v}}_{x,y}\) are the velocity operators, and ψnk (ℏωnk = Enk) is the eigenvector (eigenvalue) at band index n and momentum k. The two unitless weighting factors wn(k) and Wn(k) in Eqs. (3) and (4) are written as
where fn(k) = 1/[exp((Enk − μ)/kBT) + 1] is the Fermi-Dirac distribution function, T is temperature, μ is chemical potential, and kB is the Boltzmann constant.
Physically, the anomalous Hall effect can be influenced by disorder55,56,57. To model the variation of intrinsic anomalous Hall conductivity against disorder, a constant Γ approximation of the Kubo formula was used55,
where vi, EF, and Γ are the velocity operator, Fermi energy, and band broadening parameter, respectively. The anomalous Nernst conductivity under the effect of the disorder can be then calculated through the generalized Mott relation,
where f, E, μ, T, and σxy are the Fermi-Dirac distribution function, energy, chemical potential, temperature, and anomalous Hall conductivity, respectively. When Γ → 0, the anomalous Hall and Nernst conductivities calculated from Eqs. (8) and (9) have to be identical to the results of Eqs. (3) and (4), respectively.
Magneto-optical Kerr and Faraday effects
Extending the AHC to the ac case, the optical Hall conductivity52,
was evaluated on a k-mesh of 1001 × 1001 × 1. Here, Vc is the cell volume, Nk is the number of k-points, ℏω is the photon energy, and η is the smearing parameter.
The MO Kerr and Faraday effects in topologically trivial two-dimensional (2D) magnetic materials are given by58,59,60,61,
here θK and θF are the MO Kerr and Faraday rotation angles, respectively. c is the speed of light in vacuum, ℏω is the photon energy, d is the effective thickness of the 2D magnetic material, \({\sigma }_{xx}^{s}\) is the diagonal element of the optical conductivity for a non-magnetic substrate (the SiO2 is used, and the substrate effect was discussed in our previous works62,63), σxy is the off-diagonal element of the optical conductivity of the 2D magnetic materials, and \({n}_{\pm }={[1+\frac{4\pi {{\mbox{i}}}}{\omega }({\sigma }_{xx}\pm {{\mbox{i}}}{\sigma }_{xy})]}^{1/2}\) are the eigenvalues of the dielectric tensor of the 2D magnetic materials.
The MO Kerr and Faraday rotation angles in the Chern insulator are written by64,
in which \({E}_{\pm }^{r,t}={E}_{x}^{r,t}\pm \,{{\mbox{i}}}\,{E}_{y}^{r,t}\) are the left (+) and right (−) circularly polarized components of the reflected (r) and transmitted (t) outgoing electric fields. When the thickness of the Chern insulators is much thinner than the incident light wavelength, the reflected and transmitted fields can be obtained64,
with \(A=1/[{(2+4\pi {\sigma }_{xx})}^{2}+{(4\pi {\sigma }_{xy})}^{2}]\). In the low-frequency limit (ω → 0), the optical conductivity in Chern insulators gives \({\sigma }_{xx}^{R}=0\), \({\sigma }_{xx}^{I}=0\), \({\sigma }_{xy}^{R}={{{\mathcal{C}}}}{e}^{2}/h\), and \({\sigma }_{xy}^{I}=0\) (\({{{\mathcal{C}}}}\) is the Chern number; the superscripts R and I are the real and imaginary parts, respectively). Then, the Eqs. (13)–(18) can be simplified to43,44,64,
Thus, in the low-frequency limit, the magneto-optical Kerr and Faraday rotation angles in Chern insulators are quantized to θK = − π/2 and \({\theta }_{F}={{{\mathcal{C}}}}\alpha\), respectively.
Curie temperature
Regarding the ferromagnetic VSi2N4, a key physical quantity is Curie temperature (Tc), which can be estimated by carrying out the Monte Carlo simulations based on the Ising Hamiltonian model65,
Here, Jij is the nearest-neighboring exchange interaction, S is the spin magnetic moment on the V or Nb atom. The calculated Tc for strain-free (ε = 0%) VSi2N4 is about 100 K [see Supplementary Fig. 3b], which is more than two times larger than CrI3 of 45 K36 and Cr2Ge2Te6 of less than 30 K37, indicating the potential applications of 2D spintronics. The Tc (75 K) of strained structure (ε = 1.6%) is slightly smaller than that of the balanced system but is much larger than that of the famous antiferromagnetic topological insulator MnBi2Te4 (24 K)66, suggesting the great application prospects to realize the high-temperature VQAH state.
Tight-binding model
The magnetic space group of monolayer VSi2N4 with out-of-plane magnetization is \(P\bar{6}m^{\prime} 2^{\prime}\). Considering the magnetic V atoms, it is a 2D triangular lattice with out-of-plane ferromagnetic order. We now introduce a two-band tight-binding model using a minimal basis set of \(\left|{d}_{{x}^{2}-{y}^{2}}\uparrow \right\rangle\) and \(\left|{d}_{xy}\uparrow \right\rangle\) (or \(\left|{p}_{x}\uparrow \right\rangle\) and \(\left|{p}_{y}\uparrow \right\rangle\)) orbitals, where ↑ means spin up. Then, the generators of the magnetic space group \(P\bar{6}m^{\prime} 2^{\prime}\) are represented by \({S}_{3z}={e}^{2\pi {{\mbox{i}}}{\sigma }_{y}/3-\pi {{\mbox{i}}}{\sigma }_{0}/6}\) and \({M}_{x}{{{\mathcal{T}}}}=-\,{{\mbox{i}}}\,{\sigma }_{z}\), respectively. By including only the nearest-neighbour hopping, the symmetry-adapted tight-binding Hamiltonian can be written by,
where \({c}_{i\alpha }^{{\dagger} }\) (cjβ) is the electron creation (annihilation) operator for the orbital α (β) on-site i (j). Note that this Hamiltonian is in general including spin-orbit coupling and magnetic interaction. By using the MagneticTB package19 that is recently developed on the top of group representation theory, all independent nearest-neighbour hopping integrals \({t}_{ij}^{\alpha \beta }\) can be screened under a given symmetry constrain. Under magnetic space group of \(P\bar{6}m^{\prime} 2^{\prime}\), we found there are only three parameters are necessary to realize the magneto-valley coupling states and their topological phase transitions. The Hamiltonian is recast to
where \(\tilde{k}={k}_{x}+{k}_{y}\), r1 = t1 + t2, r2 = t1 − t2, and e1 are real parameters. Specifically, t1 and t2 are the nearest-neighbor hopping integrals and e1 is the on-site hopping integral from different orbitals. When r2 ≪ r1, such a model with different bandgaps at K and K\({}^{\prime}\) valleys are actually a modified Haldane’s model67. We can further expand this Hamiltonian around K and K\({}^{\prime}\) valleys:
where H(K) = H+ and \(H(\,{{\mbox{K}}}\,^{\prime} )=-{H}^{-}\). The Chern number for characterizing topological nontrival phases can be analytically written as,
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
Code availability
The first principle and tight-binding codes that support the findings of this study are available from the corresponding author on reasonable request.
References
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343 (2014).
Mak, K. F., Xiao, D. & Shan, J. Light-valley interactions in 2D semiconductors. Nat. Photonics 12, 451 (2018).
Yu, Z. M., Guan, S., Sheng, X. L., Gao, W. & Yang, S. A. Valley-layer coupling: a new design principle for valleytronics. Phys. Rev. Lett. 124, 037701 (2020).
Tong, W. Y., Gong, S. J., Wan, X. & Duan, C. G. Concepts of ferrovalley material and anomalous valley Hall effect. Nat. Commun. 7, 13612 (2016).
Xiao, D., Yao, W. & Niu, Q. Valley-contrasting physics in graphene: magnetic moment and topological transport. Phys. Rev. Lett. 99, 236809 (2007).
Xiao, D., Liu, G. B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489 (2014).
Lee, J., Mak, K. F. & Shan, J. Electrical control of the valley Hall effect in bilayer MoS2 transistors. Nat. Nanotechnol. 11, 421 (2016).
Farooq, M. U., Hashmi, A., Ono, T. & Huang, L. Spin-valley Hall phenomena driven by Van Hove singularities in blistered graphene. npj. Comput. Mater. 6, 197 (2020).
Liu, J. & Dai, X. Anomalous Hall effect, magneto-optical properties, and nonlinear optical properties of twisted graphene systems. npj. Comput. Mater. 6, 57 (2020).
Mu, X., Pan, Y. & Zhou, J. Pure bulk orbital and spin photocurrent in two-dimensional ferroelectric materials. npj. Comput. Mater. 7, 61 (2021).
Yu, X. Q., Zhu, Z. G., Su, G. & Jauho, A. P. Thermally driven pure spin and valley currents via the anomalous Nernst effect in monolayer group-VI dichalcogenides. Phys. Rev. Lett. 115, 246601 (2015).
Dau, M. T. et al. The valley Nernst effect in WSe2. Nat. Commun. 10, 5796 (2019).
Li, X., Cao, T., Niu, Q., Shi, J. & Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl Acad. Sci. (USA) 110, 3738 (2013).
Song, Z. et al. Spontaneous valley splitting and valley pseudospin field effect transistors of monolayer VAgP2Se6. Nanoscale 10, 13986 (2018).
Zhao, P. et al. Single-layer LaBr2: two-dimensional valleytronic semiconductor with spontaneous spin and valley polarizations. Appl. Phys. Lett. 115, 261605 (2019).
Hu, H., Tong, W. Y., Shen, Y. H., Wan, X. & Duan, C. G. Concepts of the half-valley-metal and quantum anomalous valley Hall effect. npj. Comput. Mater. 6, 129 (2020).
Peng, R. et al. Intrinsic anomalous valley Hall effect in single-layer Nb3I8. Phys. Rev. B 102, 035412 (2020).
Zhang, Z., Yu, Z. M., Liu, G. B. & Yao, Y. MagneticTB: a package for tight-binding model of magnetic and non-magnetic materials. Comput. Phys. Commun. 270, 108153 (2021).
Pan, H. et al. Valley-polarized quantum anomalous Hall effect in silicene. Phys. Rev. Lett. 112, 106802 (2014).
Ren, Y., Qiao, Z. & Niu, Q. Topological phases in two-dimensional materials: a review. Rep. Prog. Phys. 79, 066501 (2016).
Zhang, R. W., Zhang, Z., Liu, C. C. & Yao, Y. Nodal line spin-gapless semimetals and high-quality candidate materials. Phys. Rev. Lett. 124, 016402 (2020).
Feng, B. et al. Discovery of Weyl nodal lines in a single-layer ferromagnet. Phys. Rev. Lett. 123, 116401 (2019).
Zhou, X. et al. Fully spin-polarized nodal loop semimetals in alkaline-metal monochalcogenide monolayers. J. Phys. Chem. Lett. 10, 3101 (2019).
Zhang, R. W., Ma, D. S., Zhang, J. M. & Yao, Y. Weyl nodal-line surface half-metal in CaFeO3. Phys. Rev. B 103, 195115 (2021).
Hong, Y. L. et al. Chemical vapor deposition of layered two-dimensional MoSi2N4 materials. Science 369, 670 (2020).
Novoselov, K. S. Discovery of 2D van der waals layered MoSi2N4 family. Natl Sci. Rev. 7, 1842 (2020).
Li, S. et al. Valley-dependent properties of monolayer MoSi2N4, WSi2N4, and MoSi2As4. Phys. Rev. B 102, 235435 (2020).
Yang, C., Song, Z., Sun, X. & Lu, J. Valley pseudospin in monolayer MoSi2N4 and MoSi2As4. Phys. Rev. B 103, 035308 (2021).
Bhalla, P., MacDonald, A. H. & Culcer, D. Resonant photovoltaic effect in doped magnetic semiconductors. Phys. Rev. Lett. 124, 087402 (2020).
Kim, S. et al. Direct measurement of the Fermi energy in graphene using a double-layer heterostructure. Phys. Rev. Lett. 108, 116404 (2012).
Cui, Q., Zhu, Y., Liang, J., Cui, P. & Yang, H. Spin-valley coupling in a two-dimensional VSi2N4 monolayer. Phys. Rev. B 103, 085421 (2021).
Li, S., Wang, Q., Zhang, C., Guo, P. & Yang, S. A. Correlation-driven topological and valley states in monolayer VSi2P4. Phys. Rev. B 104, 085149 (2021).
Feng, X. et al. Valley-related multiple Hall effect in monolayer VSi2P4. Phys. Rev. B 104, 075421 (2021).
Antonov, V., Harmon, B. & Yaresko, A. Electronic structure and magneto-optical properties of solids (Chap. 1.4). (Kluwer Academic Publishers, Dordrecht, 2004).
Huang, B. et al. Layer-dependent ferromagnetism in a van der waals crystal down to the monolayer Limit. Nature 546, 270 (2017).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der waals crystals. Nature 546, 265 (2017).
Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124 (2016).
Okada, K. N. et al. Terahertz spectroscopy on Faraday and Kerr rotations in a quantum anomalous Hall state. Nat. Commun. 7, 12245 (2016).
Shuvaev, A., Dziom, V., Kvon, Z. D., Mikhailov, N. N. & Pimenov, A. Universal Faraday rotation in HgTe wells with critical thickness. Phys. Rev. Lett. 117, 117401 (2016).
Dziom, V. et al. Observation of the universal magnetoelectric effect in a 3D topological insulator. Nat. Commun. 8, 15197 (2017).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Maciejko, J., Qi, X.-L., Drew, H. D. & Zhang, S.-C. Topological quantization in units of the fine structure constant. Phys. Rev. Lett. 105, 166803 (2010).
Tse, W.-K. & MacDonald, A. H. Giant magneto-optical Kerr effect and universal Faraday effect in thin-film topological insulators. Phys. Rev. Lett. 105, 057401 (2010).
Liu, X., Pyatakov, A. P. & Ren, W. Magnetoelectric coupling in multiferroic bilayer VS2. Phys. Rev. Lett. 125, 247601 (2020).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Dudarev, S. L., Botton, G. A., Savrasov., S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study. Phys. Rev. B 57, 1505 (1998).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207 (2003).
Baroni, S., Gironcoli, S. D., Corso, A. D. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515 (2001).
Mostofi, A. A. et al. Wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685 (2008).
Yao, Y. et al. First principles calculation of anomalous Hall conductivity in ferromagnetic bcc Fe. Phys. Rev. Lett. 92, 037204 (2004).
Xiao, D., Yao, Y., Fang, Z. & Niu, Q. Berry-phase effect in anomalous thermoelectric transport. Phys. Rev. Lett. 97, 026603 (2006).
Czaja, P., Freimuth, F., Weischenberg, J., Blügel, S. & Mokrousov, Y. Anomalous Hall effect in ferromagnets with Gaussian disorder. Phys. Rev. B 89, 014411 (2014).
Spencer, C. S. et al. Helical magnetic structure and the anomalous and topological Hall effects in epitaxial B20 Fe1−yCoyGe films. Phys. Rev. B 97, 214406 (2018).
Keser, A. C., Raimondi, R. & Culcer, D. Sign change in the anomalous Hall effect and strong transport effects in a 2D massive Dirac metal due to spin-charge correlated disorder. Phys. Rev. Lett. 123, 126603 (2019).
Suzuki, Y., Katayama, T., Yoshida, S., Tanaka, K. & Sato, K. New magneto-optical transition in ultrathin Fe(100) films. Phys. Rev. Lett. 68, 3355 (1992).
Guo, G. Y. & Ebert, H. Band-theoretical investigation of the magneto-optical Kerr effect in Fe and Co multilayers. Phys. Rev. B 51, 12633 (1995).
Ravindran, P. et al. Magnetic, optical, and magneto-optical properties of MnX (X=As, Sb, or Bi) from full-potential calculations. Phys. Rev. B 59, 15680 (1999).
Feng, W., Guo, G. Y. & Yao, Y. Tunable magneto-optical effects in hole-doped group-IIIA metal-monochalcogenide monolayers. 2D Mater. 4, 015017 (2017).
Zhou, X., Feng, W., Li, F. & Yao, Y. Large magneto-optical effects in hole-doped blue phosphorene and gray arsenene. Nanoscale 9, 17405 (2017).
Li, F., Zhou, X., Feng, W., Fu, B. & Yao, Y. Thickness-dependent magneto-optical effects in hole-doped GaS and GaSe multilayers: a first-principles study. N. J. Phys. 20, 043048 (2018).
Tse, W.-K. & MacDonald, A. H. Magneto-optical Faraday and Kerr effects in topological insulator films and in other layered quantized Hall systems. Phys. Rev. B 84, 205327 (2011).
Evans, R. F. L. et al. Atomistic spin model simulations of magnetic nanomaterials. J. Phys.: Condens. Matter 26, 103202 (2014).
Otrokov, M. M. et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 576, 416 (2019).
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the "parity anomaly”. Phys. Rev. Lett. 61, 2015 (1988).
Acknowledgements
This work is supported by the National Key R&D Program of China (Grant No. 2020YFA0308800), the National Natural Science Foundation of China (Grant Nos. 11734003, 11874085, 12047512, and 12004028), and the Project Funded by China Postdoctoral Science Foundation (Grant Nos. 2020M680011 and 2021T140057). Y.M. acknowledges the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) − TRR 288 - 422213477 (project B06). Y.M., W.F., and Y.Y. acknowledge the funding under the Joint Sino-German Research Projects (Chinese Grant No. 12061131002 & German Grant No. 1731/10-1) and the Sino-German Mobility Programme (Grant No. M-0142).
Author information
Authors and Affiliations
Contributions
W.F. and Y.Y. conceived the research. X.Z., and R.-W.Z. performed the first-principles calculations. Z.Z. carried out the model analysis. X.Z., R.-W.Z., and Z.Z. contributed equally to this work. All authors contributed to the discussion of the data. X.Z., R.-W.Z., W.F., and Y.M. wrote the paper with discussion from and Y.Y.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhou, X., Zhang, RW., Zhang, Z. et al. Sign-reversible valley-dependent Berry phase effects in 2D valley-half-semiconductors. npj Comput Mater 7, 160 (2021). https://doi.org/10.1038/s41524-021-00632-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00632-3
This article is cited by
-
A new family of septuple-layer 2D materials of MoSi2N4-like crystals
Nature Reviews Physics (2024)
-
Controlled transmission of multiband acoustic waves based on composite resonant cavities
Applied Physics A (2024)
-
First-principles investigation of two-dimensional iron molybdenum nitride: A double transition-metal cousin of MoSi2N4(MoN) monolayer with distinctive electronic and topological properties
Frontiers of Physics (2024)
-
Proposal for valleytronic materials: Ferrovalley metal and valley gapless semiconductor
Frontiers of Physics (2024)
-
Correlation-driven threefold topological phase transition in monolayer OsBr2
Frontiers of Physics (2023)