Introduction

Surface and bulk electrochemical phenomena are particularly important in ferroelectrics, whose switchable remanent polarisation modulates their electrochemical reactivity, determining fundamental material responses and giving rise to promising catalysis and sensing applications1,2. Electrochemistry has been linked to all aspects of ferroelectric switching and screening3,4,5, with recent studies highlighting its influence on catalytic effects and functionality-modifying phenomena6,7. These effects can be amplified by the additional presence of adsorbates, such as surface water ubiquitous under ambient conditions8,9.

As ferroelectric surfaces with different domain orientations exhibit varying polarisation-induced fields and chemical compositions7,9, the interplay of their electrochemistry with surface water generates a wide range of complex phenomena. Structurally, preferential adsorption can modulate the usual humidity dependent molecular arrangement observed on simple dielectric materials10 of 1–2 monolayers of ice-like water, followed by less ordered liquid layers. Chemically, varying dissociation rates into OH− and protons vs. molecular water and even modulation of the surface and bulk material composition as a function of polarisation orientation and relative humidity have been reported11,12.

The observed effects are further enhanced under the application of an electric field, with radical water-mediated changes and time-dependent processes taking place, as also seen in non-polar materials13. In addition, sufficiently high fields will enhance oxidation reactions at the surface and promote charge injection and/or polarisation switching14,15,16,17, leading to a strong dependence of electrochemical response on the electrostatic (switching and charging) history of the material. The combination of all these phenomena gives rise to a highly non-trivial mixed response of ferroelectrics to changes in relative humidity or surface bias, with widely ranging timescales and magnitudes, as demonstrated previously by local probe Kelvin probe force microscopy (KPFM) contact potential difference imaging12,18.

Over the last decade, investigation of complex phenomena with multiple parameters have been made possible by incremental advances in experimental techniques and acquisition hardware, yielding rich datasets of correlated responses at a broad range of timescales. Additionally, tremendous progress has been made in tools designed to analyse the resulting hyperdimensional datasets, based on Big Data approaches such as machine learning and dimensional reduction. These have been successfully applied to studies of ferroelectric materials, enabling a better understanding of the competing and correlated processes involved in switching and surface screening under ambient conditions19,20,21.

Here, we investigate the mechanisms of surface charge dissipation on ferroelectric thin film surfaces as a function of time, applied voltage, writing history from as-grown through final polarisation, and relative humidity. Local probe imaging of the contact potential difference was performed on two Pb(Zr0.2Ti0.8)O3 (PZT) thin films of opposite polarisation, after the writing of a predefined structure. The resulting time-dependent datasets were dimensionally stacked and analysed by means of Dictionary Learning in order to unravel the underlying physical and chemical behaviours. A simplified reaction–diffusion model complements the experimental work, allowing the results of the machine learning analysis to be interpreted in terms of physical/chemical processes. Our observations unequivocally demonstrate that whilst both positive and negative surface charges decay with time, only negative charges spread laterally on the surface, diffusing far beyond the originally written areas.

Results and discussion

Imaging surface charge dissipation

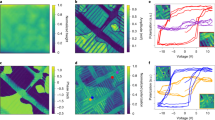
Surface charge dissipation was imaged by Kelvin probe force microscopy on 100 nm thick PZT films (presenting either up- or down-oriented as-grown monodomain polarisation) and tracked as a function of relative humidity, polarisation, applied voltages, and time. Domain structures were patterned by scanning the biased atomic force microscope tip in contact with the surface: first, to define three lateral stripe regions with positive (+8 V), zero, and negative (−8 V) tip bias; then, three overlaid vertical stripe regions, again with positive, zero, and negative tip bias, as illustrated in Fig. 1a. The sequential writing is performed in order to take into account possible effects of polarisation switching history and varying intensity of charge injection (areas scanned twice with negative or positive voltages). Once the writing was completed, KPFM imaging was carried out until dissipation of the contact potential difference (CPD) signal contrast, approximately 9 to 12 hours. An illustration of the resulting KPFM image is shown in Fig. 1b, with the writing structure overlaid. We note that whilst the piezoresponse force microscopy image of the ferroelectric domains generated through the writing process follows the writing structure exactly, the CPD signal usually extends outwards due to charge diffusion, especially at high humidity. We note that a 20% overscan generated by the atomic force microscope used in this study, required for the operation of the closed-loop scanner, results in the extension of the stripe regions along their length, giving rise to additional sharp contrast regions outside the formally defined writing structure. The procedure was repeated at each relative humidity setpoint (ten different values spanning 6% to 80%), for both samples (up- and down-oriented as-grown polarisation). The control of relative humidity was performed with a in-house-built flow-based, low noise humidity controller, which enables fast and precise in situ control in the atomic force microscope chamber22,23.

Fig. 1: Experimental protocol for mapping charge dissipation on the ferroelectric thin film surface.
figure 1

In each sample and at each humidity setpoint, a biased atomic force microscope tip was scanned over the surface: first defining lateral stripe regions with positive (+8 V), zero, and negative bias (−8 V) at 0∘; then defining vertical stripe regions with identical positive, zero, and negative bias at 90∘. a Schema of the target writing pattern. b Typical contact potential difference (CPD) image of the resulting structure, with overlaid writing bias pattern. c Ferroelectric domain structure resulting from voltage application on the down-polarised sample (PFM phase image).

Full size image

The first five resulting contact potential difference images (approximately 70 min after writing) are shown in Fig. 2 for both samples at all ten humidity levels probed. Several trends can be identified from simple visual inspection. First, in both samples, faster surface charge dissipation and larger spatial spread of the CPD signal beyond the boundaries of the stripe domains can be observed at higher humidities. Second, the positive charges seem to be much more localised (bright yellow contrast) than the negative charges (dark blue contrast), regardless of the initial sample polarisation. Finally, the charge contrast seems to be more intense in areas where the polarisation was switched from its as-grown state—i.e. where negative tip bias was applied for the down-polarised film and positive tip bias for the up-polarised film—hinting at the role of switching history in the dissipation. These observations are in line with previous investigations of the dynamics of charged species on ferroelectric thin films, showing a strong effect of relative humidity on charge dissipation. Indeed, via the presence of ambient water and through bias-induced electrochemistry, multiple species co-exist at the surface—including hydroxyl and carboxyl groups, as well as surface bound oxygen. Being charged, these species will interact with the surface and follow different dissipation/passivation dynamics, investigated in previously studies12. However, the supplementary parameter of history yields additional insight: in both samples the first writing (horizontal stripes) can be readily distinguished at low humidities, but is not discernible at high humidities, suggesting faster dynamics in presence of high water content at the surface.

Fig. 2: KPFM contact potential difference imaging.
figure 2

The first five images from the complete humidity dataset are shown as a function of time and humidity for the (a) down-polarised and (b) up-polarised samples. A new structure is written at each relative humidity setpoint and then monitored continuously until complete contact potential difference signal dissipation. At low humidities the charges seem to be more localised and retained longer than at high humidities. Additionally, at higher humidities the horizontal lines corresponding to the first writing step are not visible, suggesting much faster charge dynamics in presence of high water content at the surface. Lastly, the written pattern remains visible in the up-polarised films at much higher humidity levels than in the down-polarised films.

Full size image

Dictionary learning analysis

Due to the complex and correlated nature of the full dataset, any analysis beyond simple visual inspection is challenging as it will introduce human error and bias: regions over which observed behaviour is to be averaged may be selected arbitrarily, outliers and/or unexpected data might be ignored, and overall the spatial distribution of information within the images will be lost as most analysis would concentrate on average signals. Indeed, a more classical statistical analysis performed on the dataset by extracting individual regions defined from the writing pattern12 (presented in the Supplementary Materials), demonstrates not only that such arbitrary region selection is rather ambiguous—especially at the higher humidity where spatial spread of charge occurs—but also that the quality and selectivity of the analysis are severely limited by the inhomogeneous nature of the CPD signal within each region. To address these issues, machine learning-based techniques were leveraged for the correlative analysis of the acquired data, having been established as a reliable way to objectively extract regions with different characteristic behaviours in multidimensional datasets19,20,21.

The KPFM images for all ten humidities and two samples (one up-polarised and one down-polarised) were stacked along the spatial dimension in order to induce a time correlation, and are shown in the Supplementary Materials, Fig. S1. Such stacking, yielding a set of 10240 × 512 images at 33 distinct time steps, imposes a constraint of identical behaviour(s) across polarisation, time and humidity values21, thus enabling a direct comparison of the evolution of the behaviours as a function of initial sample polarisation and relative humidity. Dictionary Learning was selected as the machine learning dimensional reduction technique for the further analysis of the dataset due to its intrinsically sparse nature24. Indeed, as a result of the spatial separation and uniform nature of the regions written with different voltage sequences, we expect only a few behaviours to be spatially co-located at each given location (each behaviour potentially being a combination of multiple physical processes). The number of components n is a free parameter and was evaluated from two to ten, allowing us to track which behaviours are associated with the different regions as they successively segregate out, as detailed in the Supplementary Materials, Fig. S3.

The resulting decomposition, presented in Fig. 3 for n = 10, shows three distinct types of components, each associated with the relevant spatial distribution weight maps. The components are directly interpretable as combinations of physical behaviours, and are common to the complete dataset. The prevalence of each component within a measurement series (sample and humidity pair) is dictated by the corresponding weight maps which show the spatial location or co-location of the components related thereto, and in the case of a successful decomposition, each spatial location will be contained in at least one of the weight maps. The first component, C1, has a low magnitude and is spatially located in the regions that can be identified as a background—i.e., locations outside of the written structure or where zero tip bias was applied during writing—and is identifiable as a distinct component for n ≥ 8. This component is also present within the written areas at higher humidities, and specifically in the locations where the surface charge has already dissipated. An inspection of its time evolution indicates that this component is essentially stable with a very slight linear drift, possibly caused by the change in tip-sample interactions over time, as shown in the exponential-plus-linear fit C1 in Fig. 3d. The second component, C2, decays with time from an initial high positive value, and is present in areas of positive voltage application only, regardless of the initial polarisation state of the films. These areas separate out as distinct from those written with negative bias at n = 6. Increasing n does not change the C2 component. The last three components present negative decays, starting at a low CPD value and evolving towards the background signal value as the surface charges dissipate. This is most prominent at high humidity values, where the positive decay components tend to be less present, and for these measurements, the data effectively split between two complementary component sets: the negative components (in particular C5), and the background (C1). Additionally, the three negative decay components are co-located within each other and spread outwards around areas of negative voltage application, with the highest intensity decay (C3) on the inside, and the lowest intensity decay (C5) on the outside of the negative charge distributions—a structure reminiscent of Matryoshka dolls, and suggesting the possible presence of lateral diffusion. This characteristic structure is apparent from n = 7, and increasing n simply refines the areas written with negative bias into increasingly fine concentric segments.

Fig. 3: Dictionary Learning analysis of the KPFM data.
figure 3

The spectral decomposition of the complete dataset of contact potential difference signal evolution measured in the two samples and at ten humidities yields five components. The weight maps for the (a) down-polarised and (b) up-polarised sample demonstrate spatially localised features, which once correlated with the (c) time-dependent components yield a clear separation between the background response (C1), and the areas of positive (C2) and negative (C3–5) charge. The negative charge region is split into co-located concentric structures, reminiscent of Matryoshka dolls. Components C2–C5 can be fitted with double exponential decays, each yielding (d) two very different time constants.

Full size image

To quantify the time evolution of the positive and negative decays, the corresponding components—C2 to C5—were fitted to a double exponential decay function, \({\rm{CPD}}(t)={A}_{0}+{A}_{1}\exp -t/{\tau }_{1}+{A}_{2}\exp -t/{\tau }_{2}\), with CPD the contact potential difference, and A0 the offset corresponding to the final CPD value, A1, A2 the amplitudes, and τ1, τ2 the time constants of the decays. From the parameters shown in Fig. 3d, two behaviours seem to be present in all decaying components, each with two substantially different time constants. The latter differ by at least an order of magnitude, as reported previously for this material, suggesting the coexistence of a surface charge dissipation and passivation process and a slow material-dependent electrochemically-driven process12. The fast process, of the order of 1000 s, can be related to the re-equilibration of surface screening charges along or through the surface as it has a time scale similar to previously observed dynamics of charged species on surfaces13,25,26,27. The slow process, on the other hand, is of the order of 10,000 s, and can be specifically attributed to the properties of the material—with charges being retained for polarisation screening or due to local chemical-bias-induced electrochemical modification of the surface9,12.

In all cases, however, the overall mechanisms (background, positive and negative decay) are present in both films and share the same parameters, varying in intensity with humidity and initial polarisation, but mostly depending on the polarity of the applied voltage. The positive voltage related component, C2, for instance is found in both films below 50% RH, but seems to be more present at the higher humidity only in the up-polarised films, where a positive voltage application switches the polarisation. Conversely, negative voltage related components, C3, C4 and C5 seem to be more present within the down-polarised film, where such a voltage polarity switches the polarisation. The coexistence of the same physical dissipation processes (as fitted above) in both samples suggests that the initial polarisation orientation does not affect the dissipation mechanisms which seem to be primarily dominated by voltage and surface electrochemistry. Last, the history of polarisation is important, as switching processes during voltage application will result in higher surface charge density and/or longer charge retention, especially at higher humidities. This is evidenced by the higher surface charge density of C3–C5 for the down-polarised film, as well as by the presence of C2 at higher humidity values for the up-polarised film. In both cases, switching has occurred in the films for the respective voltage polarities, concurring with previous studies on the same material12.

Reaction–diffusion simulation

To better understand the influence of the spatial and temporal trends observed in the experimental data and the resulting Machine Learning analysis, a simplified reaction–diffusion model was constructed, based on the FitzHugh–Nagumo system. This is an excitable system model, ideal for describing the distributions of different species during their relaxation to equilibrium, as for example in neural synapses28. Specifically, we tailored the model to clarify the influence of a time-dependent spatial spread on the resulting spatio-temporal charge distributions, and in turn what effect such physical processes would have on the Machine Learning analysis. As the experimental data suggest the presence of lateral spread acting together with surface and bulk electrochemistry, the parameters of the model were tuned to reproduce the observations qualitatively, with a spatially localised and negligibly diffusive positive charge distribution, and an initially more spread and highly diffusive negative charge distribution.

The resulting time evolution of the combined distributions is shown in Fig. 4. As a function of time, or the number of simulation iterations, the intensity of both distributions appears to decay, as illustrated in the plot of the evolution of each distribution’s centre point intensity. However, the difference in diffusivity of the two distributions is apparent when a cross-section is taken at the centre of each image. Whilst the positive charges (red) seem to simply decay (i.e. reduce in intensity as a function of time), the negative charge distribution spreads outwards via lateral diffusion, as indicated by the characteristic crossing points.

Fig. 4: FitzHugh–Nagumo reaction–diffusion model of the surface charge dissipation.
figure 4

a Time evolution of the positive (red) and negative (blue) surface charge distributions shows spatially localized vs. highly diffusive behaviour, qualitatively reproducing the experimental observations. Maxima (b) and cross-sections (c) of the positive and negative charge distributions show that both positive and negative charge intensities decay with time, but that only negative charges show a lateral diffusion, as evidenced by the increased width of the signal, leading to characteristic crossing points (green circles).

Full size image

The model data were subjected to the same computational treatment as the experimental data with Dictionary Learning analysis. The resulting components and weight maps are shown in Fig. 5, separated into behaviours for positively and negatively charged regions. For the positive regions, only simple decays are observed, with the second component identifying mostly the interaction of charges at the boundary between positively and negatively charged regions. In comparison, the negative charge decay shows a striking resemblance to the experimental data analysis, with concentric shell structures in the weight maps.

Fig. 5: Dictionary learning analysis of reaction–diffusion analysis.
figure 5

The maps shown in (a) and corresponding components shown in (b) demonstrate two specific behaviours: positive and negative decays. The latter show a decreasing amplitude following a characteristic concentric structure, consistent with the presence of a diffusion process.

Full size image

Last, the components associated with the weight maps are also consistent with the original experimental observations: the most and least intense behaviours are located at the centre and at the periphery of each charged regions, respectively. Per model parameters, the species that shows this behaviour is associated with a reaction and diffusion process—as opposed to the other species which is constrained to reaction only. Thus, the introduction of diffusion into the model brings out the characteristic concentric shell structure of decreasing intensity in the Dictionary Learning analysis. This result confirms the intuition that lateral diffusion is taking place within our experimental data based on the similarity to the machine learning analysis features, making this—to the authors’ knowledge—the first reported observation of a signature of such behaviour observed by machine learning methods.

In conclusion, in this investigation of the interplay of time, relative humidity, polarisation and voltage with the surface charge dissipation of ferroelectric thin films, polarised regions written by scanning probe microscopy were analysed with Dictionary Learning spectral decomposition. The results highlight two separate voltage-mediated behaviours, characteristic of a combined surface/bulk electrochemical process and of surface charge passivation. Negative charges are additionally observed to diffuse laterally, as demonstrated by the characteristic concentric shell structure in machine learning analysis, while positive charges are mostly confined to their original location with very limited lateral diffusion. Our interpretation is corroborated by a reaction–diffusion model set up to reproduce the experimental contact potential difference observations, whose resulting time evolution was analysed with the same spectral decomposition technique, yielding similar characteristic concentric structures in the case of the diffusing species. The cumulative evidence points to a non-trivial behaviour of surface charges, with the positive and negative charges exhibiting a substantially different diffusion/dissipation mechanism that is modulated by the underlying ferroelectric polarisation. The coexistence of these electrochemical processes opens a pathway towards polarisation-directed catalysis, with a highly localised control of charges.

Methods

Materials growth

Films of 100 nm thick Pb(Zr0.2Ti0.8)O3 (PZT) have been grown on Nb:SrTiO3 single crystalline substrates by RF-magnetron sputtering, as described elsewhere29. The films used in this study were up- and down-polarised as grown, respectively, with a smooth sub-nanometre roughness topography.

Kelvin probe force microscopy

The scanning probe microscopy imaging was performed on an Asylum Research Cypher microscope equipped with an environmental control chamber, using Bruker SCM-PtSi cantilevers with a resonance frequency of ~75 kHz and a spring constant of ~2.8 N/m. Sample temperature was kept constant at 30 ∘C, and relative humidity was varied through the use of a home-build controller22,23. The humidity was stabilised for at least an hour prior to each measurement series. Topographic imaging was performed in intermittent contact mode (AC Mode), with a free oscillation amplitude of ~10 nm and a setpoint of ~5 nm. The contact potential difference between the tip and the sample was acquired over 12 × 12 μm2 areas at a scan speed of 0.5 Hz in single-pass Kelvin probe force microscopy mode with the following parameters: 3 V excitation voltage, 5 kHz frequency, −90∘ phase, 5 proportional gain, 10 integral gain. Domain writing was done in contact mode with a 0.5 V setpoint over 8 × 8 μm2 areas at a scan speed of 0.5 Hz and applied voltages of ± 8 V, as detailed in Fig. 1a.

Data processing

Due to the lack of an absolute surface potential reference, the acquired KPFM data were processed through line-by-line offset subtraction for each measurement. This resulted in an effective 0 V background CPD value. Additionally, prior to machine learning analysis, all data were shifted by its global minimum value, −0.74 V, in order for it to be non-negative, as required for input to the machine learning analysis algorithms.

Dictionary learning analysis

Time-dependent data were stacked into data cubes, and the data cubes at each humidity and for each sample were concatenated along the spatial dimension x, yielding a correlated dataset. A similar stacking method was performed for the reaction–diffusion modelling dataset. The Dictionary Learning implementation of the scikit-learn library was then used on the flattened dataset with the following parameters: 3–10 n_components, 1000000 max_iter, 8 n_jobs, lasso_lars transform_algorithm, 15 transform_n_nonzero_coefs, lars fit_algorithm, and 0 random_state. The code and data used for the analysis are freely available on the paper repository30.

Reaction–diffusion modelling

The reaction–diffusion model used is based on a 2D Fitzhugh-Nagumo excitable system model28. The implementation used is adapted from existing Python code, recipe 12.4 in31. The specific form of the model is a set of two differential equations: \(\frac{\partial u}{\partial t}=a{{\Delta }}u+u-{u}^{3}-v+k\) and \(\tau \frac{\partial v}{\partial t}=b{{\Delta }}v+u-v\), with u, v denoting the two species, a, b their corresponding diffusion factors, k the intensity of the external stimulus, and tau the time constant providing the separation of the timescales of the evolution of the two species. For the comparison to surface charge dissipation, the two species were initially set up in separate bands and allowed to relax. The parameter set, selected up to allow for single species diffusion only, is a = 0, b = 0.1, τ = 0.1, and k = −0.005. The resulting spatio-temporal evolution was analysed through the same Dictionary Learning workflow as the experimetnally obtained dataset. The code and data used for the simulation and analysis are freely available on the paper repository30.