Abstract
We present the EVONANO platform for the evolution of nanomedicines with application to anti-cancer treatments. Our work aims to decrease both the time and cost required to develop nanoparticle designs. EVONANO includes a simulator to grow tumours, extract representative scenarios, and simulate nanoparticle transport through these scenarios in order to predict nanoparticle distribution. The nanoparticle designs are optimised using machine learning to efficiently find the most effective anti-cancer treatments. We demonstrate EVONANO with two examples optimising the properties of nanoparticles and treatment to selectively kill cancer cells over a range of tumour environments. Our platform shows how in silico models that capture both tumour and tissue-scale dynamics can be combined with machine learning to optimise nanomedicine.
Similar content being viewed by others
Introduction
Cancer is known to be a complex and multiscale disease, where tumour growth is caused by multifactorial effects spanning multiple scales, such as individual cell stressors, mutations in cell signalling pathways, changes in the local tumour microenvironment, and the overall disruption of tissue homeostasis1,2,3,4. Nanoparticle-based drug vectors have the potential for improved targeting of cancer cells when compared to free drug delivery through the design of cell-specific binding moieties and the encapsulation of drugs within nanoparticles that improve bioavailability5,6. Furthermore, nanoparticles can be used to create novel treatment strategies that rely on, for example, delayed release, local photo-thermal therapies, as well as treatments that take advantage of the collective dynamics of the nanoparticles7,8,9.
Novel anti-cancer nanomedicines are possible due to the expansive range of design parameters that can be altered. These include the four ‘S’s (size, shape, stiffness and surface coating) as well as more complicated designs, such as encapsulated nanoparticles, self-assembling nanoparticles, and nanoparticles that self-amplify a signal in order to increase localised distribution10,11,12,13. However, given the vast parameter space, effective design of nanoparticles is a considerable challenge, as each of the chosen particle parameters impacts how they behave in the body7,14,15. To improve nanoparticle design, in silico models have been shown to be efficient at both the prototyping and the hypothesis testing stage, preventing costly trial-and-error search routines for potential test candidates16,17,18,19,20,21. For a recent review of how in silico models have been used to further nanoparticle design, see, for example, refs. 22,23,24. In addition, machine learning and AI methods have been used to optimise nanoparticle design, for example, by predicting the properties of nanoparticles or reducing their overall toxicity25,26,27,28. However, many of these in silico models focus on singular aspects of the nanoparticles’ journey through the body and are unable to systematically generate virtual tumour scenarios.
In this paper, we present a platform for drug discovery, EVONANO, that combines models at the scale of an individual cell to the growth dynamics of a virtual tumour, while also applying machine learning to more efficiently explore the nanoparticle design space. The tumour growth dynamics are simulated using PhysiCell, an open-source package for simulating large cellular systems29. This simulator creates a virtual tumour using an agent-based model (ABM) which allows for a high level of adaptability, such as the inclusion of heterogeneity in the cell phenotypes (cancer cells, cancer stem cells, macrophages). The virtual tumour models are then used to generate representative scenarios for testing nanoparticles in silico.
Modelling nanoparticles over a whole tissue is computationally expensive and limits the degree to which nanoparticle parameters influence tumour dynamics. Instead, we systematically designate representative sections of tissue to test nanoparticle and treatment designs. We use in a stochastic simulator, the STochastic Engine for Pathways Simulations (STEPS), which allows for simulations of stochastic networks over complex spatial domains through the discretisation of the well-mixed domain into smaller well-mixed subunits (known as voxels)30,31,32. We specifically focus on a stochastic simulator to capture the inherent randomness that occurs within biochemical reaction networks. Nanoparticle–cell interactions are modelled using such reaction networks, where complicated signalling pathways can be introduced using the systems biology markup language (SBML) standard33. Finally, the optimisation of nanoparticle design is done using a custom-built evolutionary algorithm, similar to previous attempts34,35,36.
We present two examples demonstrating the EVONANO platform. The first designs nanoparticles that are able to penetrate an optimum distance to cover the majority of what is assumed to be a homogeneous tumour mass. We optimise over the concentration, size, binding affinity, and payload of nanoparticles. We show how an evolutionary algorithm is able to effectively choose parameters that result in more than 90% of cancer cells successfully treated with low overall injected dosage. We then give an example of optimisation of treatments targeting a heterogeneous tumour mass, containing both cancer cells and cancer stem cells and where cancer stem cells are a minority cell population that are responsible for treatment resistance, metastatic growth and tumour recurrence, providing a promising target for nanomedicine and anti-cancer therapies37. We increase the complexity of the design space by introducing two nanoparticle–drug vectors, one that is specifically lethal to cancer cells and a second that is lethal to cancer stem cells only. In both of these examples, we find parameters that can preferentially kill cancer cells (and cancer stem cells) while minimising the overall dosage.
We end with a discussion of current and future developments for the EVONANO platform, such as integrating molecular dynamic simulations and validation using in vitro/in vivo experiments and clinical or patient data, before making our concluding remarks.
Results
EVONANO description
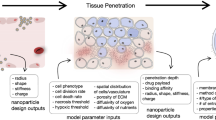
The EVONANO platform uses modular design principles to implement and explore multiscale simulations over large parameter spaces. The pipeline consists of three central modules: simulation of a virtual tumour, simulation of nanoparticle-tissue interactions, and evolutionary optimisation routines for nanoparticle design. Figure 1 illustrates an abstract workflow of the EVONANO platform.
The EVONANO platform begins by (A) specifying tumour and possible nanocarrier properties which are then used as assumptions within the EVONANO simulation platform. This proceeds as follows: (i) we first grow a virtual tumour to a sufficient size using the virtual tumour model, (ii) summary statistics, such as necessary penetration distance, are calculated from the virtual tumour and used to generate representative treatment scenarios, (iii) we then optimise the parameter values using the tissue module and machine learning module. The nanocarrier and treatment parameters can then be designed and tested using in vitro/in vivo methods.
Virtual tumour module
The EVONANO platform begins by generating a virtual tumour, as shown in Fig. 2. The virtual tumour models a representative tumour grown under certain assumptions. For example, here we focus on two aspects of tumour growth, the vasculature of the tumour and the inclusion of cancer stem cells. Tumour-specific features, such as the initial size and distribution of cells, structure of the vasculature, and the existence of resistant sub-populations, can all be modelled in the virtual tumour module. The virtual tumour is then used to generate biologically relevant scenarios for testing nanoparticles. Further details of the virtual tumour module are provided in the ‘Methods’ section.
Tumours are grown in silico by (a) initialising tumour with several cells (shown as green circles) and vessel points (shown as red circles) and running simulation until the tumour population is sufficiently large. All simulations are performed using PhysiCell, where (b), (c) show example outputs of a tumour with VPs and oxygen gradients where VPs are represented by red circles, green circles are CCs and brown circles are CC undergoing necrosis due to oxygen depletion. We use simulation output to (d) calculate the distance required for nanoparticles to penetrate from VPs and cover 95% of the tumour as well as (e) construct treatment scenarios such as those shown in (f), where red squares represent VPs, green squares represent CCs and blue squares represent ECM.
To demonstrate the EVONANO platform, we generate two virtual tumours, one with only cancer cells (homogeneous) and one with both cancer cells and cancer stem cells (heterogeneous). We assume that the tissue surrounding the cancer cells is made up of healthy cells and that the space between cells within the tumour represents the tumour extracellular matrix (ECM). The cancer stem cells (CSCs) have an altered cellular behaviour so that, in contrast to cancer cells (CCs), they cannot enter an apoptotic or necrotic state. When in conditions of reduced oxygen concentration, they became dormant. CSCs are generated either by dedifferentiation of CCs or by (symmetric or asymmetric) division of CSCs. In the case of dedifferentiation, two daughter cells are created: 1 CC and 1 CSC.
We also include a vasculature which grows with the tumour. The growing vasculature is discrete, made up of individual vessel points (VPs) and network-like. We assume that nanoparticles enter into the tumour only from VPs, either through extravasation or transendothelial transport38. Furthermore, we assume that the extravasation rate is constant across all VPs. We consider extensions regarding the rate of extravasation in the ‘Discussion’ section.
Virtual tissue module
To effectively capture the movement of nanoparticles through tissue, and their interaction with cells, we have designed a virtual tissue module which uses stochastic reaction–diffusion simulations to model nanoparticle transport through the tissue. An example schematic of the virtual tissue module is given in Fig. 3.
We use STEPS to solve the stochastic reaction network, shown in (a), for nanoparticles that diffuse from vessel points (shown in red) into well-mixed compartments (shown as green cubes) representing tumour cells (shown as a green sphere). In (b), we show the total penetration profile of nanoparticles within a homogeneous tumour, such as the number of nanoparticles (NP) and internalised nanoparticles (NPi) within each cellular compartment. Here the nanoparticle and treatment parameters are able to successfully penetrate and kill all cancer cells. Each cell contains example Cell–nanoparticle dynamics such as increased number of nanoparticle–receptor complexes (NPR), and a decrease in overall receptors over time. We also show, in (c) the two optimum solutions of a heterogeneous cell population.
In the virtual tissue module, nanoparticles interact with cell features such as the cell membrane and receptors within a single well-mixed domain with dimensions equal to that of a single cell. Interactions between nanoparticles and cells are modelled using a stochastic Michaelis–Menten reaction network18,39, with further details provided in the ‘Methods’ section. Nanoparticles are able to actively target and bind to receptors on the cell membrane, as well as be released from these receptors and be uptaken by a cell. Furthermore, nanoparticles are able to diffuse through the tissue, potentially binding and unbinding with several cells or diffusing sufficiently fast to interact with cells far away from the vessel point. The virtual tissue model allows for testing of specific nanoparticle designs in biologically realistic scenarios and, when combined with the machine learning module, allows for the optimisation of nanoparticles to have higher overall bio-distribution within the tissue.
The virtual tissue module also allows for treatment-specific details to be included. Using considerations of the overall dosage of nanoparticles into the body, the efficacy of the payload carried by nanoparticle-based drug vectors, and the number of drug molecules contained within a nanocarrier, we can calculate the number of nanoparticles that are able to extravasate into the tumour as well as the cytotoxicity of a nanoparticle–drug vector. Further details are included within the ‘Methods’ section. These calculations allow for optimisation of nanoparticle-based anti-cancer treatments, such as treatments with lower dosage but high efficacy.
Machine learning module
Nanoparticles are highly customisable, covering a large design space of properties such as their size, material, shape, stiffness, binding moieties and charge7. Simulations at the tissue scale allow for the simulation of multiple particles as well as cell types. Nanoparticles can be optimised with different binding properties and diffusion coefficients, or drugs and targeting moieties specialised for individual cell types. For example, nanoparticles can be introduced that have specific binding to cancer cells but with a higher internalisation rate for cancer stem cells.
This creates an extremely large parameter space to search for the most effective treatment parameters. The computational cost of simulation is prohibitive of unbound multiple tests and intelligent optimisation tactics are required instead. Consequently, the optimisation of the treatment parameters can be implemented with an amalgam of conventional, well-established algorithms, such as genetic algorithms34, as well as more unconventional and innovative methods, such as novelty search and metameric representations35,36,40,41.
In this work, we optimise nanoparticle-based treatments using a genetic algorithm, as shown in Fig. 4a, with a custom fitness function that optimises for increased efficacy and low dosage and where the tradeoff between efficacy and dosage is controlled by a weighting factor. Further details are provided in the ‘Methods’ section. We use the EVONANO platform to optimise nanoparticles that can penetrate deep into the tumour tissue, induce cell death in all cancer cells but where the overall injected dose is low. The EVONANO machine learning module allows for the flexible and customisable optimisation of nanoparticle treatments. We are able to achieve these optimum results for both homogeneous and heterogeneous tumour cell populations, as we describe below.
We use (a) an evolutionary algorithm to optimise nanoparticle design. This optimisation routine first initialises a population of different parameter sets and evaluates the fitness of each parameter set using the tissue module. Parameter sets with high fitness are selected for (using a tournament procedure) and these sets are used to generate a new population of nanoparticle parameters using the crossover operator (where the information of the two parent solutions are combined to make new solutions), and the mutation operator. This process is repeated for a prescribed number of generations, resulting in an overall increase in the fitness of the parameters and effective nanoparticle treatments. We show in (b) the mean, maximum and minimum change in fitness across generations and highlight the changes of importance in parameters as we optimise the nanoparticle treatment, where parameter changes are shown in the table.
Optimizing NPs in a homogeneous tumour cell population
We present results from two example scenarios, as described in the ‘Methods’ section. We first consider a homogeneous tumour cell population, where all nanoparticles have equal efficacy on CCs. We then consider a heterogeneous tumour cell population containing both CCs and CSCs.
For the first scenario, we use the EVONANO platform to generate a virtual tumour. We use our sampling procedure, described in the ‘Methods’ section, to generate scenarios that are optimised using the machine learning module and evaluated at the tissue scale. Using the EVONANO platform, we find parameter values that result in 99% of all CCs killed within 95% of VPs with a dosage of 7.8 mg/kg. Optimum nanoparticle-based treatment parameters are given in Table 1.
Overall, more effective solutions (which kill more CCs) were found when nanoparticle treatments were tested on the worst-case scenario representing one VP and 22 CCs. This is likely due to the presence of multiple VPs in some scenarios, increasing the number of nanoparticles in the system and leading to fewer constraints on nanoparticle parameters. As a result, we focus only on this scenario, as solutions tended to have low dosage (10 mg/kg and below) while still killing a large number of CCs. We found that, for the homogeneous case, the weighting factor did not influence nanoparticle parameters in a meaningful way.
We show results from running the evolutionary optimisation in Fig. 4b. We find that we are able to correctly identify the combination of parameters that allow for almost all cancer cells to be killed with low dosage. These parameters are D = 1 × 10−6 cm2/s, ka = 700,000 (Ms)−1 (equivalent to a nanoparticle radius of R = 2.5 nm and KD = 70 nM), NP0 = 60,000 and E = 5000, which has an overall fitness of 0.85. The nanoparticles that killed the largest number of cells followed the same trend as that observed in ref. 18, in which those with high diffusion and disassociation constants were found to penetrate and kill cells furthest from the vessel point. However, far fewer particles were shown to be required.
Optimizing NPs in a heterogeneous tumour cell population
We next use the EVONANO platform to design nanoparticles within a heterogeneous tumour mass. In this scenario, a virtual tumour is generated using the virtual tumour module which consists of 527,000 cells with 517,000 CCs, 5000 VPs and 5000 CSCs. The CSCs have altered cellular behaviour as described in ‘Methods’. We repeat the same sampling process for the generated tumour mass, resulting in 100 scenarios. Again, we find that the penetration distance from VPs required to cover 95% of the tumour mass is ~22 cells deep.
We use the machine learning module to find a parameter set that successfully kills 99% of CCs and 82% of CSCs within all scenarios. For NP1, D = 9.8 × 10−7 cm2/s, ka = 217,000 (Ms)−1 (equivalent to a radius of R = 2.5 nm and KD = 22 nM), NP0 = 923,000 and E = 400, while for NP2, D = 6.4 × 10−7 cm2/s, ka = 117,000 (Ms)−1 (equivalent to a radius of R = 4 nm and KD = 12 nM), NP0 = 150,000 and E = 2500. This reflects a total dosage of 9.4 mg/kg for NP1 and 9 mg/kg for NP2.
This solution was found when the weighting factor was set to 5 and where nanoparticles were tested only on the worst-case scenario. Overall, we did not see significant differences for those solutions where the weighting factors were above one. On the other hand, for those treatment designs found using weighting factor equal to one, i.e., where the efficacy and dosage gave equal contributions to the overall fitness, we found that solutions failed to kill all the cancer cells and the overall dosage was low. This highlights the importance of fine-tuning the fitness function for the desired outcome. In the future, we will consider other fitness functions as we increase the complexity of the optimization problem.
For nanoparticles tested on several randomly selected scenarios, we found that the solution would often fail to kill CSCs due to their low prevalence within the total cell population. However, when we heavily bias the gain in fitness according to the combined efficacy of the nanoparticle, by setting w = 10 in Eq. (5), we find a second solution that has significantly different nanoparticle parameters but where the total dosage is high. These parameters are, for NP1, D = 9.7 × 10−9 cm2/s, ka = 8300 (Ms)−1 (equivalent to a nanoparticle radius of R = 264 nm and KD = 0.8 nM), NP0 = 236,000 and E = 7600, while for NP2, D = 5.7 × 10−7 cm2/s, ka = 791,000 (Ms)−1 (equivalent to a radius of R = 4.5 nm and KD = 80 nM), NP0 = 828,000 and E = 1200. This reflects a total dosage of 46.4 mg/kg for NP1 and 25.9 mg/kg for NP2, relatively high for nanomedicine treatment. However, this solution deviates from previous solutions in that the nanoparticles are much larger with high binding affinity and demonstrates that by tuning the fitness and randomly sampling from generated scenarios, we are able to find effective nanoparticle designs.
Discussion
In this paper, we have introduced the EVONANO platform for the automatic optimisation of nanoparticle design parameters in tumour tissue. This modular simulation tool builds on two open-source simulation frameworks, PhysiCell and STEPS, extending them to model tumour growth, extract representative worst-case tumour tissue scenarios, and then model nanoparticle penetration within these tumour tissues. Finally, we use machine learning to optimise nanoparticle designs.
In the first example, we show that we can use machine learning to find nanoparticle designs that are able to distribute and kill large proportions of tumour mass, while keeping dosage low. Overall, we find that high diffusion values (small nanoparticle radius) and low binding affinity (high KD) are most effective, and that low nanoparticle concentration (tens of thousands of nanoparticles) will suffice, provided their drug payload is in the thousands (of molecules). This allows nanoparticles to both penetrate the tumour, and avoid binding site barriers, as already demonstrated in previous work18. Alternatively, concentrations of several million nanoparticles can also be effective, and require a payload of only some several hundred drug molecules. The idea that a high concentration of nanoparticles may lead to more effective cancer treatments complements other work that emphasises the importance of increasing nanoparticle dosage42.
For the second example, consisting of a heterogeneous tumour with cancer stem cells, we successfully find nanoparticle designs that have high efficacy with low dosage. Again, we find that the solutions tend towards designs with a high diffusion coefficient (representing small nanoparticles), low binding affinity (representing high disassociation constants), high nanoparticle concentration and a low number of drug molecules. This indicates that successful nanoparticle treatments may be those with a high concentration of nanoparticles and low drug loading, as discussed above.
We also find an unexpected solution for the heterogeneous tumour: relatively large nanoparticles with high binding affinity. The diffusion coefficient and disassociation constant for these nanoparticles are within the parameter ranges that were expected to be unsuitable for nanoparticle designs, based on previous work in ref. 18. Instead, this solution demonstrates that nanoparticles with low diffusion coefficient and high binding affinity are able to successfully kill a high proportion of CCs, provided the total number of nanoparticles that reach the tumour is high. This reaffirms recent conclusions that the success of nanoparticle treatments may be highly dose dependent42. This strategy requires a total dosage of 46 mg/kg for NP1, near to the assumed upper limit of 55 mg/kg, we note that this is based on the assumption of systemic circulation and that only 1% will make it to the tumour. For Doxil, it has been reported that the percentage injected dose that is able to make it to the tumour can be as high as 3.5%43, which would reflect, using Eq. (2), a reduced dosage of only 13 mg/kg. These findings, along with the design principles described above, highlights that it is possible to obtain more flexibility in nanoparticle design. Furthermore, our platform gives specific nanoparticle parameter values which can then be tested. Future work will look to synthesize nanoparticles that meet these evolved parameters and test them within representative in vitro environments.
In this paper, we present the first extension to homogeneous cancer models through the inclusion of cancer stem cells. We note that, both cancer de-differentiated and stem cells were assumed to be homogeneous in both size and shape. This limitation can be easily relaxed, with heterogeneous cells of any size, shape or type included within the virtual tumour as input for the optimisation routine. For example, stromal cells such as fibroblasts or cancer cells with increased resistance can be included. The impact of nanoparticle treatment can then be returned to the virtual tumour to assess how treatment impacts tumour progression, based on targeting some or all of these cell types. By adapting and including further biological details into the virtual tumour and nanoparticle properties, the EVONANO platform has the potential to link to clinical data and to develop and evaluate potential treatments before choosing a specific course of action for a patient. Clinical data, such as histology samples or image results, can be used to determine model parameters such as the cell proliferation rate or tumour heterogeneity. Since all of the processes in the virtual tumour and tissue module are based on well-characterized physical laws, the time needed to set up the virtual tumour simulation is not long as it amounts to setting up a handful of pre-existing parameters from these data. The inclusion of these data into the pipeline would be a significant step towards the long sought-after objective of personalised (patient-specific) medicine44,45.
In the future, we see several interesting avenues to extend and apply the EVONANO platform. This includes investigating the potential toxicity of nanocarriers and the role of the tumour microenvironment, such as the pH. For example, recent work on gold nanoparticles shows that gold carriers mostly remain in fibroblast lysosomes where they slowly degrade46. Given the abundance of cancer-associated fibroblast (CAFs), up to 80% of the tumour mass in pancreatic tumour47, it is reasonable to expect that most of the internalized gold carriers will remain within the tumour cells. This highlights the fate of nanocarriers within the tumour environment and the importance of modelling the tumour stroma. Furthermore, in order to reach clinical practice, nanocarriers need to pass rigorous regulatory requirements, where several nanocarrier types, such as biocompatible PLA/PLGA (poly-lactic acid/poly-lactic-co-glycolic acid) have been shown to be safe and non-toxic48. Future work will look at how these nanoparticle types can be implemented in EVONANO and how these nanoparticles leave the tumour and are then cleared, which is essentially the reverse problem to the one studied here. We also intend to consider how the acidity of the tumour microenvironment can change nanoparticle dynamics of release. For example, the pH sensitivity of drug delivery systems can be used for the rapid release of drugs once nanocarriers extravasate out of blood vessels and approach an acidic tumour environment. In this work, our model deals only with the local tumour environment and, as such, the pH-sensitive drug release can be indirectly modelled via drug concentration. This is reflected in Table 2, where we have tested a two-thousand-fold range of drug concentrations. Finally, we note that Eq. (1) represents a simplified model of nanoparticle–cell interactions, which ignores details such as the exocytosis rate of nanoparticles from the cells, transendothelial transport into the tumour, how retention rates affect nanoparticle accumulation as well as how the rate of drug release from the NPs can vary. Here, we choose this simplified model to act as a baseline to demonstrate the EVONANO platform. Future work will consider how to both extend and calibrate our model to consider these effects.
One of the benefits of the modular design of the EVONANO platform is that two powerful open-source-packages are used. For example, STEPS is able to simulate stochastic pathways across spatially discrete domains. These features allow for simulating nanoparticle interactions with whole-cell models where nanoparticle binding can be modelled at the resolution of individual receptor types, and nanoparticle transport and internalisation can be a function of cell cycle or the distribution of nanoparticles within intracellular compartments, all of which have been shown to impact nanoparticle treatment efficacy49,50,51. Alternatively, extensions to the PhysiCell codebase allow for increased complexity in tumour models. The vasculature network added into PhysiCell allows us to more precisely control the spatial effect of nanoparticle extravasation. This could lead to the better parameterisation of nanoparticle delivery to the tumour and enables simulation of the effect of drugs that disrupt the vasculature network (such as the tumour necrosis factor) or those that block vasculature growth factors (for example, Bevacizumab, Cabozantinib, Pazopanib). These aspects will be investigated in our future work. Alternatively, nanoparticles can be introduced that, when binding together, lead to larger particles with lower diffusion coefficients. Both of these reflect realistic nanoparticle designs that have been demonstrated in vitro52,53. Finally, both PhysiCell and STEPS supports SBML models. This means that both cell-based models, nanoparticle signalling, and reaction networks can be developed, validated and shared between researchers to greater increase standardisation within the field of nanomedicine54.
By disconnecting the model of tissue-scale dynamics from the virtual tumour (which includes the dynamics of hundreds of thousands, if not millions, of individual cells), we decrease computing time and allow for large parameter spaces to be explored at the physio-chemically relevant scale for nanoparticle design. In the future, we plan to use high-performance computing to meet the computational needs of the EVONANO platform. This will facilitate the development of personalised treatments and will allow for the exploration of more computationally complex environments as well as novel and emergent nanoparticle designs7,35. Furthermore, we will increase the level of parallelisation within each EVONANO module to execute simulation processes simultaneously.
The richness that can be accessed through the inclusion of nanoparticle-scale models also allows for downstream integration of molecular dynamics simulations. These simulations can, for example, explore the influence of a drug’s chemical properties on the NP coating, the dependency of binding moieties on diffusion due to particle self-aggregation or the formation of protein coronas55,56,57,58. By including molecular dynamics, specific rules for nanoparticle synthesis can be found such as the number of binding ligands on the nanoparticle surface. Furthermore, these simulations give another scale that can be optimised, whereby machine intelligence applied at the molecular scale learns overall impacts on tumour progression, as mediated by the nanoparticle–cell interactions.
Finally, the EVONANO platform can be used to develop future design principles that, when combined with high-throughput testing, would give an integrated and calibrated tool for testing the efficacy of proposed anti-cancer therapies. By including data from in vitro tools, such as measuring the extravasation properties of nanoparticles into tumour tissue, testing for toxicity, the impact of the extracellular matrix on nanoparticle transport dynamics, or the interactions of nanoparticles with individual cells59,60,61, we can further improve nanoparticle designs as well as perform testing for potential bottlenecks in nanomedicine engineering.
We have presented EVONANO, a software platform for the design and optimisation of anti-cancer nanomedicine. Our open-source platform combines multiscale and modular simulations with machine learning techniques, testing the properties of both nanocarriers and treatments against biologically relevant tissue scenarios, generated from an in silico virtual tumour. We first demonstrate our platform by finding nanoparticle treatments that lead to the successful treatment of 95% of cancer cells within the virtual tumour while minimising dosage. We then introduce a second cell type, cancer stem cells, into the virtual tumour and find parameters for a combined treatment that successfully kills 99% of cancer cells and more than 80% of cancer stem cells within the tumour tissue. The platform addresses a significant clinical challenge in automatically designing nanocarriers with appropriate transport properties. Future work will concentrate on combining our simulator with details from cell biology, molecular dynamic simulations, and the validation and calibration of in silico results with in vitro and in vivo data.
Methods
Virtual tumour module
To generate the virtual tumour, we use a modified version of the open-source PhysiCell platform, a cross-platform agent-based modelling framework for 2-D and 3-D multicellular simulations29. Agent-based models allow for high adaptability by modelling the interactions of individual subunits (cells) which follow some system of rules and relevant dynamics. PhysiCell combines two modelling approaches: agent-based at the individual cell level and reaction–diffusion calculations for modelling diffusing substrates62. Each cancer cell is represented as individual agent and agents are associated with a library of sub-models for simulating cell, fluid, and solid volume changes, cycle progression, apoptosis, necrosis, mechanics, and motility. Since PhysiCell only supports differentiated cancer cells (CCs), we also modified its source code to include cancer stem cells (CSCs) and vasculature growth, modelled as vessel points (VPs).
In this work, virtual tumours are initialised in PhysiCell with a single cancer cell (CC) and then grown until they reach the size of ~500,000 CCs at which point the simulation is stopped. When simulating the growth of a tumour containing CSCs, we use pre-defined probabilities of division. We found no reliable empirical data that describes the relative ratio of normal CC division to dedifferentiation, so we used a fixed probability of 99.5% (normal CC division) and 0.5% (dedifferentiation). CSC division can either be asymmetric giving a generation of 1 CC and 1 CSC, or symmetric and generating either 2 CSCs or 2 CCs. We set the probability of asymmetric division of CSC to 99%. The symmetric division, with probability of 1%, is further divided into 99% probability of creating 2 CSCs, and 1% of creating 2 CCs. We find that this distribution of probabilities leads to a virtual tumour with ~1% of CSCs, which is consistent with experimental data63. While the probabilities used above have not been calibrated to experimental data, they are used to obtain simulated tumours with the same observed percentages of CSCs as in ref. 63.
To model the vascular network, we rely on a discrete approach which allows us to produce vascular networks of desired topologies. While it is possible to include a higher fidelity model of the interaction between nanoparticles and vascular flow such as a combination of computational fluid dynamics and agent-based or Brownian particles modelling, we chose an option that will minimally increase complexity of the pipeline. Therefore, we implemented a simplified model of vasculature directly into the PhysiCell by creating a new type of dividing agents with the following properties: they secrete oxygen; they are not movable and cannot enter apoptosis and necrosis; they are connected to each other apically. When dividing, vasculature agents can keep or change spatial direction by inserting a branching point. At the beginning of the simulation the following parameters are set: the initial position of vasculature agents, the maximum number of vasculature agents, and the frequency of branching.
PhysiCell also models diffusing substrates using a multi-substrate diffusion solver, BioFVM, that divides the simulation domain into a collection of non-intersecting voxels. BioFVM supports diffusion, decay, cell-based secretions/uptake, and bulk supply/uptake functions for each individual substrate and is used here to capture the diffusion of oxygen and nutrients across the virtual tumour.
Virtual tissue module
We use the open-source package STEPS for simulating the cell–nanoparticle interactions in the virtual tissue module30,31,32. For the virtual tissue module, the length, L, of each well-mixed compartment is 10 μm. This reflects the mean diameter of many carcinomas, including breast and lung carcinomas as well as travelling tumour cells64,65,66. We note that changes to cell sizes can be implemented in a straightforward manner. Though we refer to the diameter of the cell, we assume that the cells are axes-symmetric in both the virtual tumour and tissue module. We ignore the influence of spatiality as introduced by the discretisation of the domain into sub-volume elements (voxels) and consider penetration of the nanoparticles linearly from the vessel point. We assume that drugs diffusing out from the tumour slice would also diffuse laterally from the neighbouring tissue. We note that recent work has shown that these spatial assumptions do not make significant impact for high nanoparticle concentration67. We model interactions between nanoparticles and cells using a stochastic Michaelis–Menten reaction network18,43,
where NPF is the free nanoparticles, R is the receptors on the cell membrane, C is nanoparticle–receptor complexes, and NPi is internalised nanoparticles. We assume that nanoparticles are able to actively target and bind to the receptors on CCs with binding rate, ka, to release from receptors with dissociation rate kd, and to internalise according to internalisation rate ki. Nanoparticles move from neighbouring well-mixed compartments with probability D/L2 where D is the diffusion coefficient of the nanoparticles and L is the compartment length. We also assume that nanoparticles have uniform binding to cell receptors and will explore alternate nanoparticle designs in future work.
To calculate the number of nanoparticles that are able to extravasate into the tumour within an idealised murine model, NP0, we use
where ID is the total injected dose of nanomedicine, W is the weight of the mouse, PID is the percentage of the injected dose that reaches the tumour, S is the characteristic length scale of the cell, L is the total required penetration depth, Vt is the volume of the tumour, M the molecular mass of the nanoparticle payload, E the total number of payload molecules, and NA is Avogadro’s constant. Parameter values are given in Table 2.
We assume that the cytotoxic effect of the nanoparticle is a function on the total payload carried by the nanoparticle, such that the threshold of nanoparticles required to induce cell death is given by
where the potency, P, is chosen to be the IC90 of the anti-cancer drug (the drug concentrations that achieve 90% growth inhibition of cancer cells) and we assume that the properties of the drug are not altered by the nanoparticle vector. Hence, altering E changes both the total dosage as well as the threshold of nanoparticles required to kill a cell.
For all simulations, we assume that nanoparticles circulate for 48 h, that there is a constant release of nanoparticles from vessel points and that 1% of the injected dose will eventually extravasate into the tumour. Furthermore, we choose to link the potency to the IC90 of the drug rather than the IC50 or IC75 as we require the lethal levels of nanoparticles needed to kill a cell, and where IC90 is very close to that lethality point. These assumptions (circulation time, release rate, percentage injected dose that reaches the tumour and how we define potency) are based on previously published results on the modelling of nanoparticle dynamics18, and serve as a baseline to demonstrate the platform. In future work, we intend to examine these assumptions using a combination of in vitro and in vivo methods and pass results into the EVONANO platform to further improve nanoparticle design. When testing nanoparticle designs, we adjust both the number of payload molecules per nanoparticle (E), as well as the total number of nanoparticles within the treatment dose (NP0). Altering both of these reflects changes to the total injected dose that is administered to the mouse model.
Machine learning module
As a first instance, we used an evolutionary algorithm which operates as follows: A population of randomly initialised individuals is produced, where each individual represents one solution (group of parameters) defining the functionality of the nanoparticles. These individuals are evaluated using the virtual tissue module described above, with an appropriate score assigned to each individual based on the proportion of cell types killed and the overall drug dosage. The score represents the fitness of the individual and is described in more detail below. Given the assigned fitness, the best individuals are then selected through a tournament procedure and the crossover operator is applied to produce offspring individuals. These offspring individuals are then updated with the mutation operator and represent the next generation of individuals. This population is evaluated again to find a new fitness and the process repeated until a predetermined number of generations has passed.
The parameters of the evolutionary algorithm are as follows: the search space is initially four-dimensional (having four parameters to optimise), the population size is P = 20, the tournament size for replacement and selection procedures is T = 2, while the mutation operator is applied with probability of p = 0.2 and it alters one parameter with random step size of s = [−5; 5]%. During the replacement process (with tournament size T = 2), one offspring solution is compared to one parent solution and the fittest of them is added to the next generation. Finally, the evolution of the population of individuals lasts for 100 generations.
Generating nanocarrier test scenarios
To develop realistic scenarios for testing nanoparticle design, we create tissue profiles using the virtual tumour, as shown in Fig. 2b–c. We first calculate the minimum distance to VPs for all CCs and use this to find the distance which would account for 95% of CCs being reached, given maximum penetration. We find this to be ~220 µm, or the distance of 22 cells, for both homogeneous and heterogeneous tumour scenarios, shown in Fig. 2d. Similar penetrations depths have been highlighted in experimental work by Jain and Stylianopoulos68.
Having calculated the necessary penetration distance required for maximal nanoparticle coverage, we then create simple scenarios consisting of 22 cells, generated from the PhysiCell simulations. We first randomly choose a VP from which we assume nanoparticles will release. We measure a distance of 220 µm from this VP, where we assume each cell is 10 µm. This distance, which represents the necessary penetration distance that nanoparticles are required to cover, is split into compartments of cubic compartments of length 10 µm. The cell type within this compartment reflects the PhysiCell cell definition, such as VP, CC, CSC. In this work, we specify regions without cells as extracellular matrix (ECM). These 22 cells, spanning 220 µm, constitute a test scenario for nanoparticle design which is then passed to the tissue module of EVONANO. Examples of both cell sampling and resulting scenarios are given in Fig. 2e, f.
Using the process described above, we generate 100 representative tissue-scale scenarios which are used for optimising nanoparticle design. However, in some scenarios, such as where multiple VPs are present, nanoparticle designs can become sufficiently under-constrained such that solutions have a misleadingly high fitness. As a result, we also choose a single scenario that represents the ‘worst-case’ scenario. For the homogeneous case, this is one VP and 22 CCs without any ECM or additional VPs. For the heterogeneous case, we first run the machine learning module on randomly selected tissue-scale scenarios before identifying which scenarios consistently had lower fitness than other scenarios. We specify these scenarios as the heterogeneous ‘worst-case’ scenario. We found these to be a VP with 20 CCs and 2 CSCs, where the first CSC is 140 µm from the VP and the second CSC is 180 µm from the VP. The fitness for this scenario was lower than other scenarios due to the high number of CSCs and because the CSCs were located further away from the VP than other scenarios. After finding an optimum solution using either random sampling or the ‘worst-case’ scenario, we then evaluated the solution on all 100 generated scenarios.
Optimising nanoparticle-based treatments
We first consider the homogeneous case, where the tumour contains only cancer cells (CCs) and where we aim to find nanoparticle designs that cover the largest volume of the tumour and kill the highest proportion of CCs while keeping dosage low.
To grade the success of nanoparticle designs, we calculate the maximum number of nanoparticles that a cell can internalise before cell death is triggered. This is a function of the number of drug molecules, E, carried by the nanoparticle, given in Eq. (3). To demonstrate our methods, we consider nanoparticles that are loaded with Doxorubicin, a well-known and relatively common anti-cancer drug. We assume an IC90 of Doxorubicin to be 10 µM69 and that the nanoparticles can carry between 100 and 10,000 drug molecules. This corresponds to a maximum lethal dose, per cell, of between 600 and 60,000 nanoparticles. We include large ranges to allow for the machine learning module to search through the state space in order to find an optimal solution. In this work, we make several critical simplifying assumptions, such as constant rate of extravasation, a fixed percentage injected dose, that nanoparticles circulate for 48 h regardless of their size or binding affinity and we link the potency of the treatment to the IC90 of the drug (the drug concentrations that achieve 90% growth inhibition of cancer cells). We make many of these assumptions as they represent a worst-case scenario for nanoparticle transport. Future work will investigate the extent to which these assumptions can be relaxed.
Here, we look to optimise two nanoparticle-specific parameters; the diffusion coefficient (D) and the binding affinity (ka), relating to the respective size and, for example, a nanoparticle targeting ligand that is agnostic to cell type. We consider the diffusion coefficient, D, to be in the range of 10−8 to 10−6 cm2/s. Using the Stokes–Einstein equation70 and assuming biologically realistic values for the viscosity of the surrounding medium, this reflects a range of 10 nm to 1 μm sized nanoparticles. We vary the binding affinity, ka, of 103 to 106 (Ms)−1, while keeping disassociation rate, kd, and internalisation rate, ki, for particles fixed at 10−4 and 10−5 s−1, respectively. This relates to a disassociation constant, KD = kd/ka, of between 10−1 and 102 nM.
We also consider the influence of two treatment-specific parameters, the concentration of nanoparticles within the treatment dose as well as the number of molecules per nanoparticle. As described above, we assume that extravasation rates are equal across all VPs, such that scenarios with additional VPs will have a linear increase in the total number of nanoparticles released. The change in concentration of nanoparticles will result in a different number of nanoparticles being released from the VPs. We explore nanoparticle concentration within the range of 10,000 to 1 million nanoparticles, which we assume circulates for 48 h and that 1% of the nanoparticles reach the tumour. We also assume that nanoparticles can carry between 100 and 10,000 drug molecules, giving an upper and lower bound for dosage of 0.025 to 250 mg/kg, calculated using Eq. (2). However, dosages higher than 55 mg/kg of Doxorubicin have been reported to lead to toxic effects in mice71. As a result, we do not evaluate any parameter solutions that result in dosage higher than 55 mg/kg.
Finally, given the test scenarios and parameters above, we use the machine learning module to optimise nanoparticle design. The fitness of each individual parameter set for each test scenario is calculated as the proportion of cancer cells killed minus the total dosage,
where CC is the number of killed cancer cells and NCC is the total number of cancer cells before treatment. We normalize the dosage constraint by dividing the dosage with the maximum possible dosage (set at 55 mg/kg as described above). By doing so, we have an intuitive way of understanding changes in the fitness where dosages close to the maximum will offset a nanoparticle treatment which kills all cells. Alternatively, a very low dosage will offer less constraint. We chose this normalization to account for the fact that any dosage will have some cost penalty attached to it, even at very low concentrations. Hence, a higher fitness represents both more cancer cells killed and a lower overall dosage. The average fitness is then calculated across all 5 scenarios. We also test the importance of the efficacy term (CC/NCC) by introducing a weighting factor, w, that biases the machine learning towards higher efficacy, where w = 1, 2, 5, 10. We run the optimisation routine three times for each different weight and either by randomly selecting five scenarios and taking the average fitness or using the single ‘worst-case’ scenario.
We have method the scenario of optimising nanoparticle transport into a homogeneous tumour in which there is only one cancer cell type which has shared features across the tumour. These CCs have no difference in their differentiation and are assumed to be equally relevant targets for nanocarriers. We next generate a heterogeneous virtual tumour which contains both cancer cells and cancer stem cells (CSCs) and then optimise nanoparticles that are lethal to specific cell types.
To compare optimisation across the two virtual tumours populations, both homogeneous and heterogeneous, we keep optimisation parameters the same. We are interested in altering the diffusion and binding coefficient of the nanoparticles as well as the initial concentration and drug payload for two nanoparticle types, where lethality of both nanoparticles depends on cell type. We assume that cell death of CCs is triggered only beyond a threshold of internalised NP1s (CC-specific nanoparticles), while cell death of CSCs occurs only beyond a threshold of internalised NP2s (CSC-specific nanoparticles). These CSC-specific nanoparticles are supported by work reported in, for example, ref. 72. As before, we model both nanoparticle properties on Doxorubicin, such as the drug molecular mass and IC90 but note that other nanoparticle–drug models can be used.
We now optimise an 8-dimension parameter space, in which we alter the diffusion coefficient, binding affinity, nanoparticle concentration and number of drug molecules for each of the nanoparticles but where we do not assume cell-specific properties other than the number of nanoparticles required to induce cell death.
We use the same evolutionary algorithm as before, but now with adapted fitness function,
where CSC is the number of killed cancer stem cells and NCSC is the total number of cancer stem cells before treatment within a scenario. We again explore the importance of drug efficacy but consider the combined efficacy for both CCs and CSCs, \((CC/NCC + CSC/NCSC)\). We run the optimisation routine three times, taking the average fitness calculated across 5 randomly selected scenarios within one generation, or using the ‘worst-case’ scenario, and use the same weighting factors as above, namely w = 1, 2, 5, 10.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
Code is available at https://bitbucket.org/hauertlab/evonano_methods/.
References
Basanta, D. & Anderson, A. R. Homeostasis back and forth: an ecoevolutionary perspective of cancer. Cold Spring Harb. Perspect. Med. 7, a028332 (2017).
Deisboeck, T. S., Wang, Z., Macklin, P. & Cristini, V. Multiscale cancer modeling. Annu. Rev. Biomed. Eng. 13, 127–155 (2011).
Sawyers, C. Targeted cancer therapy. Nature 432, 294–297 (2004).
Sever, R. & Brugge, J. S. Signal transduction in cancer. Cold Spring Harb. Perspect. Med. 5, a006098 (2015).
Bazak, R., Houri, M., El Achy, S., Kamel, S. & Refaat, T. Cancer active targeting by nanoparticles: a comprehensive review of literature. J. Cancer Res. Clin. Oncol. 141, 769–784 (2015).
Roberts, W. G. & Palade, G. E. Increased microvascular permeability and endothelial fenestration induced by vascular endothelial growth factor. J. Cell Sci. 108, 2369–2379 (1995).
Hauert, S. & Bhatia, S. N. Mechanisms of cooperation in cancer nanomedicine: towards systems nanotechnology. Trends Biotechnol. 32, 448–455 (2014).
Tong, R., Hemmati, H. D., Langer, R. & Kohane, D. S. Photoswitchable nanoparticles for triggered tissue penetration and drug delivery. J. Am. Chem. Soc. 134, 8848–8855 (2012).
Von Maltzahn, G. et al. Nanoparticles that communicate in vivo to amplify tumour targeting. Nat. Mater. 10, 545–552 (2011).
Fu, Y. et al. A feasible strategy for self-assembly of gold nanoparticles via dithiol-PEG for photothermal therapy of cancers. RSC Adv. 8, 6120–6124 (2018).
Kumari, P., Ghosh, B. & Biswas, S. Nanocarriers for cancer-targeted drug delivery. J. Drug Target. 24, 179–191 (2016).
Li, Y. et al. Cell and nanoparticle transport in tumour microvasculature: the role of size, shape and surface functionality of nanoparticles. Interface Focus 6, 20150086 (2016).
Simberg, D. et al. Biomimetic amplification of nanoparticle homing to tumors. Proc. Natl Acad. Sci. USA 104, 932–936 (2007).
Blanco, E., Shen, H. & Ferrari, M. Principles of nanoparticle design for overcoming biological barriers to drug delivery. Nat. Biotechnol. 33, 941 (2015).
Angioletti-Uberti, S. Theory, simulations and the design of functionalized nanoparticles for biomedical applications: a Soft Matter Perspective. NPJ Comput. Mater. 3, 1–15 (2017).
Ginsburg, G. S. & McCarthy, J. J. Personalized medicine: revolutionizing drug discovery and patient care. Trends Biotechnol. 19, 491–496 (2001).
Goldie, J. H. Drug resistance in cancer: a perspective. Cancer Metastasis Rev. 20, 63–68 (2001).
Hauert, S., Berman, S., Nagpal, R. & Bhatia, S. N. A computational framework for identifying design guidelines to increase the penetration of targeted nanoparticles into tumors. Nano Today 8, 566–576 (2013).
Singh, A. V. et al. Anisotropic gold nanostructures: optimization via in silico modeling for hyperthermia. ACS Appl. Nano Mater. 1, 6205–6216 (2018).
Ozik, J. et al. High-throughput cancer hypothesis testing with an integrated PhysiCell-EMEWS workflow. BMC Bioinforma. 19, 483 (2018).
Chamseddine, I. M., Frieboes, H. B. & Kokkolaras, M. Multi-objective optimization of tumor response to drug release from vasculature-bound nanoparticles. Sci. Rep. 10, 1–11 (2020).
Mascheroni, P. & Schrefler, B. A. In Silico models for nanomedicine: recent developments. Curr. Med. Chem. 25, 4192–4207 (2018).
Stillman, N. R., Kovacevic, M., Balaz, I. & Hauert, S. In silico modelling of cancer nanomedicine, across scales and transport barriers. NPJ Comput. Mater. 6, 92 (2020).
Kashkooli, F. M., Soltani, M., Souri, M., Meaney, C. & Kohandel, M. Nexus between in silico and in vivo models to enhance clinical translation of nanomedicine. Nano Today 36, 101057 (2021).
Jones, D. E., Ghandehari, H. & Facelli, J. C. A review of the applications of data mining and machine learning for the prediction of biomedical properties of nanoparticles. Comput. Methods Prog. Biomed. 132, 93–103 (2016).
Singh, A. V. et al. Artificial intelligence and machine learning in computational nanotoxicology: unlocking and empowering nanomedicine. Adv. Healthc. Mater. 9, 1901862 (2020).
Singh, A. V. et al. Artificial intelligence and machine learning empower advanced biomedical material design to toxicity prediction. Adv. Intell. Syst. 2, 2000084 (2020).
Singh, A. V. et al. Machine-learning-based approach to decode the influence of nanomaterial properties on their interaction with cells. ACS Appl. Mater. Interfaces 13, 1943–1955 (2020).
Ghaffarizadeh, A., Heiland, R., Friedman, S. H., Mumenthaler, S. M. & Macklin, P. PhysiCell: an open source physics-based cell simulator for 3-D multicellular systems. PLoS Comput. Biol. 14, e1005991 (2018).
Chen, W. & de Schutter, E. Parallel STEPS: large scale stochastic spatial reaction-diffusion simulation with high performance computers. Front. Neuroinform. 11(February), 1–15 (2017).
Hepburn, I., Wils, S. & De Schutter, E. STEPS: reaction-diffsion simulation in complex 3D geometries. BMC Neurosci. 10, 1–2 (2009).
Hepburn, I., Chen, W., Wils, S. & De Schutter, E. STEPS: efficient simulation of stochastic reaction–diffusion models in realistic morphologies. BMC Syst. Biol. 6, 1–19 (2012).
Hucka, M. et al. The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics 19, 524–531 (2003).
Preen, R. J., Bull, L. & Adamatzky, A. Towards an evolvable cancer treatment simulator. Biosystems 182, 1–7 (2019).
Tsompanas, M. A., Bull, L., Adamatzky, A. & Balaz, I. In silico optimization of cancer therapies with multiple types of nanoparticles applied at different times. Comput. Methods Prog. Biomed. 200, 105886 (2021).
Balaz, I., Petrić, T., Kovacevic, M., Tsompanas, M. A. & Stillman, N. Harnessing adaptive novelty for automated generation of cancer treatments. Biosystems 199, 104290 (2020).
Gener, P. et al. Cancer stem cells and personalized cancer nanomedicine. Nanomedicine 11, 307–320 (2016).
Sindhwani, S. et al. The entry of nanoparticles into solid tumours. Nat. Mater. 19, 566–575 (2020).
Lauffenburger, D. A. & Linderman, J. J. Receptors: Models for Binding, Trafficking, and Signaling (Oxford University Press on Demand, 1996).
Tsompanas, M. A., Bull, L., Adamatzky, A. & Balaz, I. Novelty search employed into the development of cancer treatment simulations. Inform. Med. Unlocked 19, 100347 (2020).
Tsompanas, M. A., Bull, L., Adamatzky, A. & Balaz, I. Metameric representations on optimization of nano particle cancer treatment. Biocybern. Biomed. Eng. 41, 352–361 (2021).
Ouyang, B. et al. The dose threshold for nanoparticle tumour delivery. Nat. Mater. 19, 1362–1371 (2020).
Man, F., Lammers, T. & de Rosales, R. T. Imaging nanomedicine-based drug delivery: a review of clinical studies. Mol. Imaging Biol. 20, 683–695 (2018).
Ryu, J. H. et al. Theranostic nanoparticles for future personalized medicine. J. Control. Release 190, 477–484 (2014).
Shin, S. J., Beech, J. R. & Kelly, K. A. Targeted nanoparticles in imaging: paving the way for personalized medicine in the battle against cancer. Integr. Biol. 5, 29–42 (2013).
Balfourier, A. et al. Unexpected intracellular biodegradation and recrystallization of gold nanoparticles. Proc. Natl Acad. Sci. USA 117, 103–113 (2020).
Yu, M. & Tannock, I. F. Targeting tumor architecture to favor drug penetration: a new weapon to combat chemoresistance in pancreatic cancer? Cancer Cell 21, 327–329 (2012).
Elmowafy, E. M., Tiboni, M. & Soliman, M. E. Biocompatibility, biodegradation and biomedical applications of poly (lactic acid)/poly (lactic-co-glycolic acid) micro and nanoparticles. J. Pharm. Investig. 49, 347–380 (2019).
Behzadi, S. et al. Cellular uptake of nanoparticles: journey inside the cell. Chem. Soc. Rev. 46, 4218–4244 (2017).
Deng, H., Dutta, P. & Liu, J. Stochastic modeling of nanoparticle internalization and expulsion through receptor-mediated transcytosis. Nanoscale 11, 11227–11235 (2019).
Liu, M. et al. Real-time visualization of clustering and intracellular transport of gold nanoparticles by correlative imaging. Nat. Commun. 8, 1–10 (2017).
Hoshyar, N., Gray, S., Han, H. & Bao, G. The effect of nanoparticle size on in vivo pharmacokinetics and cellular interaction. Nanomedicine 11, 673–692 (2016).
Sun, J. et al. A distinct endocytic mechanism of functionalized-silica nanoparticles in breast cancer stem cells. Sci. Rep. 7, 1–13 (2017).
Macklin, P., Friedman, S. H. & Project, M. Open-source tools and standardized data in cancer systems biology. Preprint at BioRxiv https://doi.org/10.1101/244319 (2018).
Babakhani, P. The impact of nanoparticle aggregation on their size exclusion during transport in porous media: One-and three-dimensional modelling investigations. Sci. Rep. 9, 1–12 (2019).
Treuel, L., Docter, D., Maskos, M. & Stauber, R. H. Protein corona–from molecular adsorption to physiological complexity. Beilstein J. Nanotechnol. 6, 857–873 (2015).
Villaverde, G. & Baeza, A. Targeting strategies for improving the efficacy of nanomedicine in oncology. Beilstein J. Nanotechnol. 10, 168–181 (2019).
Kovacevic, M., Balaz, I., Marson, D., Laurini, E. & Jovic, B. Mixed-monolayer functionalized gold nanoparticles for cancer treatment: atomistic molecular dynamics simulations study. Biosystems 202, 104354 (2021).
Cunha-Matos, C. A., Millington, O. R., Wark, A. W. & Zagnoni, M. Real-time assessment of nanoparticle-mediated antigen delivery and cell response. Lab Chip 16, 3374–3381 (2016).
Savage, D. T., Hilt, J. Z. & Dziubla, T. D. in Nanotoxicity 1–29 (Humana Press, 2019).
McCormick, S. C., Stillman, N., Hockley, M., Perriman, A. W. & Hauert, S. Measuring nanoparticle penetration through bio-mimetic. Gels. Int. J. Nanomed. 16, 2585 (2021).
Ghaffarizadeh, A., Friedman, S. H. & Macklin, P. BioFVM: an efficient, parallelized diffusive transport solver for 3-D biological simulations. Bioinformatics 32, 1256–1258 (2016).
Bao, B., Ahmad, A., Azmi, A. S., Ali, S. & Sarkar, F. H. Overview of cancer stem cells (CSCs) and mechanisms of their regulation: implications for cancer therapy. Curr. Protoc. Pharmacol. 61, 14–25 (2013).
Lee, T. K., Silverman, J. F., Horner, R. D. & Scarantino, C. W. Overlap of nuclear diameters in lung cancer cells. Anal. Quant. Cytol. Histol. 12, 275–278 (1990).
Montcourrier, P. et al. Characterization of very acidic phagosomes in breast cancer cells and their association with invasion. J. Cell. Sci. 107, 2381–2391 (1994).
Shashni, B. et al. Size-based differentiation of cancer and normal cells by a particle size analyzer assisted by a cell-recognition PC software. Biol. Pharm. Bull. 41, 487–503 (2018).
Stillman, N. R. & Hauert, S. How spatiality impacts in silico experiments of nanoparticle-cell interactions. IEEE 21st international conference on nanotechnology (NANO), 279-282 (2021).
Jain, R. K. & Stylianopoulos, T. Delivering nanomedicine to solid tumors. Nat. Rev. Clin. Oncol. 7, 653 (2010).
Abraham, S. A. et al. In vitro and in vivo characterization of doxorubicin and vincristine coencapsulated within liposomes through use of transition metal ion complexation and pH gradient loading. Clin. Cancer Res. 10, 728–738 (2004).
Lindsay, S. Introduction to Nanoscience (Oxford University Press, 2010).
Parr, M. J., Masin, D., Cullis, P. R. & Bally, M. B. Accumulation of liposomal lipid and encapsulated doxorubicin in murine Lewis lung carcinoma: the lack of beneficial effects by coating liposomes with poly (ethylene glycol). J. Pharmacol. Exp. Ther. 280, 1319–1327 (1997).
Gener, P. et al. Zileuton™ loaded in polymer micelles effectively reduce breast cancer circulating tumor cells and intratumoral cancer stem cells. Nanomedicine 24, 102106 (2020).
Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 800983.
Author information
Authors and Affiliations
Contributions
N.R.S., I.B. and S.H. developed the initial concept. N.R.S. designed the tissue module, connected the tumour module to the tissue module and carried out the optimisation. I.B. and M.K. designed the tumour module. M.A.T. wrote the scripts used for optimisation and helped with interpretation of optimisation results. N.R.S. wrote the initial draft and had primary writing responsibilities. S.H. supervised the work and helped in interpretation of the results. All authors discussed and modified the paper together.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stillman, N.R., Balaz, I., Tsompanas, MA. et al. Evolutionary computational platform for the automatic discovery of nanocarriers for cancer treatment. npj Comput Mater 7, 150 (2021). https://doi.org/10.1038/s41524-021-00614-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00614-5
This article is cited by
-
Vesicle and reaction-diffusion hybrid modeling with STEPS
Communications Biology (2024)
-
Predicting efficacy of drug-carrier nanoparticle designs for cancer treatment: a machine learning-based solution
Scientific Reports (2023)