Abstract
First-principles techniques for electronic transport property prediction have seen rapid progress in recent years. However, it remains a challenge to predict properties of heterostructures incorporating fabrication-dependent variability. Machine-learning (ML) approaches are increasingly being used to accelerate design and discovery of new materials with targeted properties, and extend the applicability of first-principles techniques to larger systems. However, few studies exploited ML techniques to characterize relationships between local atomic structures and global electronic transport coefficients. In this work, we propose an electronic-transport-informatics (ETI) framework that trains on ab initio models of small systems and predicts thermopower of fabricated silicon/germanium heterostructures, matching measured data. We demonstrate application of ML approaches to extract important physics that determines electronic transport in semiconductor heterostructures, and bridge the gap between ab initio accessible models and fabricated systems. We anticipate that ETI framework would have broad applicability to diverse materials classes.
Similar content being viewed by others
Introduction
Semiconductor heterostructures have brought about tremendous changes in our everyday lives in the form of telecommunication systems utilizing double-heterostructure lasers, heterostructure light-emitting diodes, or high-electron-mobility transistors used in high-frequency devices, including satellite television systems1. Silicon (Si)/germanium (Ge) heterostructures, in particular, have emerged as key materials in numerous electronic2,3,4,5, optoelectronic6,7 and thermoelectric devices8,9, and promising hosts of spin qubits10. Recent developments of nanofabrication and characterization techniques achieved great control over the growth of Si/Ge heterostructures11,12,13,14,15. Nevertheless, fabrication of heterostructures is strongly affected by strain relaxation in component layers5, and the resulting electronic properties show high variability due to fabrication-dependent structural parameters9,16,17. A few theoretical studies discussed the effect of non-idealities on electronic properties of heterostructures18,19, however, these studies were parametric in nature. It is essential to acquire a comprehensive understanding of the complex relationship between growth-dependent parameters and electronic properties, to attain targeted semiconductor heterostructure design with reliable electronic performance. Ab initio techniques enable prediction of materials properties with minimal experimental input, however, often come with large computational costs. In particular, the calculations of electronic transport coefficients (such as, thermopower or conductivity) require large number of individual energy calculations and computational costs can accrue quickly. It remains a challenge to model electronic transport coefficients of technologically relevant heterostructures incorporating full structural complexity, representing the vast fabrication-dependent structural parameter space.
Recent studies demonstrated the remarkable successes of machine-learning (ML) models in accelerating atomistic computations, and extending applicability of ab initio approaches to predict properties of larger systems20,21,22. ML-based materials informatics (MI) approaches are increasingly being used to accelerate design and discovery of new materials and structures with targeted properties23,24,25,26,27, facilitated by large amounts of data available through databases28,29,30 or generated with high-throughput density functional theory (DFT) calculations31. In the context of thermoelectric materials, ML studies aim to identify new compounds, materials, or structures with optimized thermoelectric properties, such as electronic power factor, thermal conductance, or the figure of merit, by scanning large physical or chemical property space, primarily following combinatorial approaches26,27,30. However, few studies exploited ML techniques to establish relationships between local atomic environment and global electronic transport coefficients, going beyond the optimization strategy. Recently, some attempts have been made to use ML techniques to learn and predict atomic-scale dynamics32. A vast amount of information is generated during a single ab initio electronic structure property calculation. Therefore, there is a great benefit to develop frameworks that can harness information available from ab initio calculations and formulate transferable atomic structure-global electronic property relationships. Transferability of the formulated relationships will then facilitate the prediction of electronic properties of new similar size or even larger systems, from the knowledge of local atomic structures. Such an approach will establish a bridge ab initio models with fabricated systems, exhibiting complex fabrication-dependent structural variability.
In this work, we propose a first-principles-based electronic-transport-informatics (ETI) framework that is trained on ab initio atomic structures and electronic bands properties of small models, and predicts electronic transport coefficients, namely the thermopowers of fabricated semiconductor heterostructures. The framework is built on the hypothesis that functional relationships between local atomic configurations, CN(r), and their contributions to global electronic energy bands, E, remain preserved when the local configurations are part of larger nanostructures with different compositions. The rationale for the hypothesis is rooted in the fundamental insight that material’s physical properties, ranging from mechanical to electronic, are intimately tied to the underlying crystal structure33. We test this hypothesis by (i) formulating transferable local configurations-energy bands relationships, f(CN(r), E), from few-atom fragment training units with varied local atomic environments, and (ii) extrapolating the relationships to predict \(f(CN({\bf{r}}),\hat{E})\)’s of larger nanostructures with known CN(r)’s. We train our ML algorithms to learn f(CN(r), E) from first-principles (DFT) electronic structure properties of 16-atom model systems, and use them to predict \(f(CN({\bf{r}}),\hat{E})\)’s of larger heterostructures. We provide information about local structures of fabricated heterostructures as input to the ML models and task them to predict the energy bands. The use of ML techniques helps us bypass the task of performing first-principles calculation of energy bands of these large systems, which is mostly unfeasible due to computational costs. We use the ML-predicted energy bands to compute Seebeck coefficients (S) or thermopowers, and validate against results obtained with first-principles methods, or measured data. Our ETI framework thus demonstrates the usefulness of ML techniques to bridge the gap between ideal ab initio accessible models and fabricated systems.
Results and discussion
Overview of the electronic-transport-informatics framework
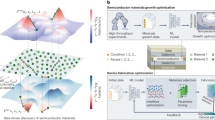
Figure 1 shows the outline of our ETI framework that results in first-principles-based prediction of thermopowers of fabricated Si/Ge heterostructures. As depicted in the figure, we train ML algorithms on the relationships, f(CN(r), E), between local atomic configurations, CN(r) and energy bands E (panel (b)) of 16-atom fragment units (cartoons in panel (a)), and task the algorithms to predict energy bands of larger heterostructures (panels (c, e)). The components of our ETI framework are (1) creation of a data resource to harvest f(CN(r), E), (2) formulation of descriptors that can uniquely define CN(r), and help characterize f(CN(r), E), in training or test structures, (3) choice of ML algorithms to discover correlations in training data, and, (4) validating ML predictions for new structures against known data. We use the term CN(r) to refer to the atomic configuration at position r and identify features to describe it. We incorporate physics awareness into the framework especially through components (1) and (2), as we elucidate below.
a Ordered and disordered 16-atom fragment units of varied compositions. Features describing local atomic configurations, CN(r), of these units are used to train ML algorithms. b Property value corresponding to features: energy bands, E(k, b), computed with DFT, where b is band index and k-points sample Brillouin zones of the units. Neural networks and random forests algorithms are used to learn relationships between local configurations and energy bands, f(CN(r), E(k, b))’s. c Trained ML algorithms are tasked to predict \(\hat{E}(k,b)\)’s for input CN(r)’s, corresponding to larger structures of varied compositions. Predicted \(\hat{E}(k,b)\)’s are validated against DFT-computed effective band structures51,52. d Thermopower or Seebeck coefficients (S) are calculated using semi-classical Boltzmann transport equation (BTE). Cross-validation is carried out by comparing S calculated from \(\hat{E}(k,b)\) and direct DFT results. e Representative configuration of a fabricated heterostructure. Target S of fabricated heterostructures are computed from \(\hat{E}(k,b)\) using BTE, and f compared with measured data.
(1) Creation of data resource: We found that electronic structure property data of only limited number of Si/Ge structures are available in databases, such as Materials Project28 and NOMAD Repository & Archive29. In addition, the available data do not provide sufficient sampling of the Brillouin zones (BZ) of the structures to converge electronic transport coefficients, requiring us to create our own data resource. The remarkable successes shown by MI approaches using DFT data22,31 inspired us to use DFT to generate training data. In order to minimize data generation efforts, we perform DFT calculations of limited number of training systems, and mine the large amount of information generated through these calculations. To that end, we follow two strategies during data generation: (i) selection of training units using physics insight, and (ii) utilization of information generated from individual energy calculations of the units as training data.
We implement the first strategy by choosing Si/Ge systems with varied strain environment as training fragments. The choice is guided by the fact that electronic bands of Si/Ge heterostructures are significantly affected by strain34,35,36,37. Strain engineering has led to more than an order of magnitude variation in electronic properties over the non-strained materials38,39,40. In heterostructures, strain environment is variable and contributed by various mechanisms including structural (lattice mismatch, presence of defects), thermal expansion or chemical (phase transition) changes. In our recent publications, we presented extensive investigations of the electronic structure and transport properties of Si/Ge heterostructures34,35,36,41. These past data and insights greatly facilitate the development of the ETI framework. Panel (a) of Fig. 1 shows cartoon representations of the two categories of the fragment training units with diverse lattice strain environement. The 16-atom models include ordered layered Si/Ge superlattices (SLs) and disordered Si–Ge “alloys” (see “Methods” section for details). We acknowledge that the small size of the units along with the imposed periodic boundary conditions do not reflect true randomized alloy configurations. Nevertheless, the models allow us to explore f(CN(r), E) in these binary systems with diverse atomic environments. We implement the second strategy in two ways: (a) utilizing DFT predicted atomic structures to formulate the descriptors, as described in the next paragraph (component (2)), and (b) using k-mesh resolved energy bands, E(k, b), as training data and benchmark for cross-validation tests. Here, b is band index and k-points sample respective BZ. We use E(k, b) as training data, instead of integrated transport coefficients such as thermopower or electronic conductivity, with the objective to train the ML algorithms on finer variations of the energy bands associated with diverse local environments. These variations mostly disappear while performing k-space integration of E(k, b) to calculate transport coefficients.
(2) Formulation of representation: We task ourselves to identify a feature subset that is strongly correlated with the electronic transport properties, from a large parameter space. The success of MI approaches has been shown to crucially depend on selection of features that help formulate relevant structure–property relationships22,42,43. A diverse set of elemental properties are used as features in MI studies42. However, the widely employed elemental-property-based features differ only slightly across various configurations of the binary (Si/Ge) heterostructures, and we do not expect these features to provide unique information to characterize f(CN(r), E). Instead, we exploit the insight that electronic transport in a heterostructure is highly sensitive to local structural environment34,35,36,37,38,39,40. Taking this fact into consideration, we include only one elemental-property-based feature in our model, computed from the electronegativity difference of the species (Si, Ge) and multiple global and local structural features that reflect changes of CN(r). Through this strategy, we aim to influence the ML algorithms to learn physically relevant f(CN(r), E) relationships. f(CN(r), E)’s in heterostructures are expected to be multivariate and highly nonlinear. We construct descriptors that capture fine sub-Angstrom-scale variations of CN(r) and guide the ML algorithms to formulate transferable f(CN(r), E)’s.
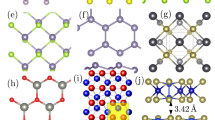
Global features include overall composition of the structures (e.g., Ge concentrations) and lattice constants (a, b, c). To determine local features of CN(r), we perform Voronoi tessellations (VT) of the crystal structures. MI studies incorporating VT-derived features have shown great success in predicting formation enthalpies42. The VT approach is particularly beneficial for our study since the tessellations uniquely define local environments of a structure, and are insensitive to global dimensions. Figure 2a shows VT of a representative Si4Ge4 SL configuration and Fig. 2b shows a typical Voronoi cell of an atom X in a Si/Ge configuration. The neighbors of X occupy adjoined cells and share faces in the tessellations. Thus, each face of a Voronoi cell corresponds to a specific nearest neighbor of the selected atom, X. We connect a given atom with its neighbors, identified by the tessellations, and describe Si/Ge configurations as crystal graphs. Crystal graphs encode both atomic information and bonding environments44,45,46, and are being increasingly used in ML models for successful materials property prediction42,44,45,46. Figure 2c shows representative crystal graphs G of a Si/Ge configuration. The atom X and the neighboring atoms form nodes, and the interatomic distances constitute the edges. Figure 2c shows crystal graphs that include paths connecting atom X with all neighboring atoms up to a specified order, e.g., G(1) (blue), G(2) (red). We demonstrate in this article that crystal graph and VT-derived features help formulate transferable f(CN(r), E)’s across structures of varied dimensions. The relative feature importance data shown in Supplementary Figure 7 reflects the strong influence of VT-derived features on the performance of the ETI framework. In total, we describe each configuration with 100 features. Below, we provide detailed explanation of one of the physics-aware VT-derived features, the order parameters, used in the ETI framework. We provide extensive discussions of all features in the Supplementary Information document.
a Voronoi tessellations of a model Si4Ge4 SL. b Voronoi cell of atom X in a SiGe model heterostructure. c Representative crystal graphs connecting atom at node X with order = 1 (G(1) (blue)) and 2 (G(2) (red)) neighbors. d Selected configurations to illustrate order parameter concept: (i) Si4Ge4 SL, (ii) Si8Ge8 disordered “alloy”. e Order parameters of relaxed ordered and disordered training units.
We fingerprint the spatial ordering of atoms around atom X in a given local configuration CN(r), using order parameters, \({Q}_{X}^{\rm{order}}\), defined by42,47:
and calculated using VT and crystal graphs. We consider crystal graphs up to a specified order (=3), because higher order graphs do not affect the predictions significantly, however, raise computational cost proportionally with the neighborhood volume, ~order3. We only consider species-aware crystal graphs that include paths connecting atoms of same type as X. The restriction is implemented by the Kronecker delta function in the numerator, δnX. Figure 2c shows some example species-aware graphs: the paths connecting Si (yellow) or Ge (green) circles are constructed assuming the atom X to be of type Si (yellow) or Ge (green), respectively. A typical step along a path is shown by the arrow (green) in Fig. 2b. The step crosses a Voronoi face of index n and area An (magenta), normal to its direction. The ratio between area, An, and the sum over all areas the step could possibly cross, Aa, that are part of other non-backtracking paths, determines the fractional weight (Eq. 1). The fractional weight of each step can be understood as the probability of taking the step. The product of fractional weights of all steps yields the effective weight, the probability of choosing the path. The sum of the effective weights of all possible non-backtracking paths in G(1), G(2), and G(3) results in \({Q}_{X}^{\rm{order}}\) (See Supplementary Figs. 2–4 for examples and discussions). Figure 2e shows the variations of \({Q}_{\rm{Si}}^{\rm{order} = 1,2,3}\) and \({Q}_{\rm{Ge}}^{\rm{order} = 1,2,3}\), for relaxed 7 ordered and 350 disordered training units, averaged over all atoms of the configurations. As a reference, the order parameters of bulk structures are equal to 1. The scatter plot shows a pictorial representation of the training set and demonstrates the diversity of CN(r) in the training units. The scatter plot illustrates that \({Q}_{\rm{Si}}^{\rm{order}}\) and \({Q}_{\rm{Ge}}^{\rm{order}}\) are highly effective in classifying SiGe configurations with different degrees of structural ordering. The distinct clusters of data points representing layered SL and “alloy” units can be noted. The order parameters decrease at a fast rate with increasing order for disordered units compared to SLs, as shown in panels from left to right in Fig. 2e.
To further fingerprint the anisotropic atomic environment of a SL compared to a disordered structure, we define directional order parameters, \({Q}_{X}^{{{\Omega }} = (x,y,z),{\rm{order}}}\). We consider only projections of An along a chosen direction to calculate the fractional weights in Eq. (1) and obtain directional Q’s (see Supplementary Information Eq. 10). In Table 1, we show \({Q}_{X}^{{{\Omega }},{\rm{order}}}\)’s corresponding to individual atoms in a representative Si4Ge4 SL (See Fig. 2d). The in-plane order parameters, \({Q}_{X}^{x,{\rm{order}}}\), \({Q}_{X}^{y,{\rm{order}}}\), are equal, corresponding to the rotational symmetry of the atomic ordering around the z-axis, along [001]. In comparison, the cross-plane order parameters, \({Q}_{X}^{z,{\rm{order}}}\), are smaller and decrease faster with the order number, due to the heterogeneous stacking along the z direction. \({Q}_{X}^{z,{\rm{order}}}\)’s reflect the different atomic environments along z direction, e.g., Qz,1 ~ 0.5 to 0.6 for interface atoms and Qz,1 ~ 0.9 to 1.0 for inner atoms. The higher inner values arise due to the presence of greater number of same species neighbors, resulting in more paths contributing to Q’s of inner atoms. The order parameters also highlight the reflection symmetry with respect to the x − y plane, yielding identical values for atom pairs such as (1, 2) ≡ (4, 3) and (5, 6) ≡ (8, 7). In comparison, \({Q}_{X}^{{{\Omega }},{\rm{order}}}\)’s of a representative Si8Ge8 “alloy” configuration, shown in Fig. 2d, do not show any specific trend and decrease fast with increasing order, reflecting the disordered atomic environment (See Supplementary Table 3). In Supplementary Fig. 6, we show \({Q}_{X}^{{{\Omega }},{\rm{order}}}\)’s of all SL and “alloy” training units. The order parameters \({Q}_{X}^{{{\Omega }},{\rm{order}}}\) are particularly important features in the ETI framework, since directional ordering dictates how atomic orbitals contribute to energy bands of Si/Ge heterostructures35.
(3) Choice of ML algorithm: We compare the performances of supervised neural network (NN) and random forests (RF) algorithms in predicting \(\hat{E}\) for input CN(r) of respective test structures. The input to the algorithms is determined by number of features considered. We list the training sets and test data in Table 2. The algorithms are tasked to produce an output equal to the number of energy values, \(\hat{E}(k,b)\): kx × ky × kz × b. We consider 21 × 21 × 21 × 12 E(k, b) values for each configuration: a 21 × 21 × 21 k-point mesh to sample the respective BZ, and six valence and six conduction bands (b). The choice is determined by performing tests that such sampling of E-values yields necessary convergence of Seebeck coefficients34,35 (See Supplementary Figs. 8 and 9). We provide detailed information regarding the implementation of the algorithms in the “Methods” section.
In the following, we (4) validate the performance of the two ML algorithms in predicting electronic bands of three classes of SiGe heterostructures: (1) ideal superlattices, strained or relaxed, (2) non-ideal heterostructures with irregular layer thicknesses and imperfect layers, and (3) fabricated heterostructures (See Table 2 for a data summary).
Ideal superlattices: strained & relaxed
We test the effectiveness of our ETI framework in predicting the thermopowers of ideal SLs, considered to be grown on substrates inducing epitaxial strain. We use the term ideal to refer to SLs with sharp interfaces. We consider seven applied strain values ranging uniformly from −1.1% to +6.1%, resulting in 49 different SLs, depicted by cartoons in Fig. 3a. Strain values ~3 to 4% have been observed in Si/Ge nanowire heterostructures with compositionally abrupt interfaces, grown via the VLS process48. We consider some extreme strains to probe the predictive power of our ML models. The models are trained on 40 and tested on 9 SLs. In Fig. 3b, we show the bands of a relaxed Si4Ge4 SL along symmetry directions of a tetragonal BZ. Both NN and RF algorithms predict energies remarkably close to DFT results, with mean absolute errors (MAE) given by 13.2 meV and 27.0 meV, respectively. The MAE is calculated over all energy values, E(k, b) (Eq. 2). We show more conduction bands since these bands control the thermopower in the technologically relevant high doping regime of our interest. The NN-predicted degenerate bands at ~0.8 eV along Γ − Z compare well with DFT results but the RF predictions deviate moderately. The bandgap is also predicted slightly better by the NN algorithm. For example, for the results shown in Fig. 3b, the bandgap values are as follows: 0.947 eV (DFT), 0.944 eV (NN) and 0.914 eV (RF) (See “Methods” section for discussion). The train and test MAE for the two predictions are shown in Fig. 3d, e. MAE is relatively small for small strain systems and higher for high strain values. Both algorithms yield small train MAE while their testing errors are considerably different. In Fig. 3c, we show S of relaxed n-type Si4Ge4 SLs as a function of carrier concentration, ne, which can be controlled by chemical or electrostatic doping methods49. Within BTE, S is obtained by integrating a function including energy bands, Fermi-Dirac distribution function and transport distribution function50 over the respective BZ, as outlined in the "Methods" section. Thus, the discrepancy in predicted bands leads to an accumulated error in S prediction. The closer match of the NN-predicted lowest conduction bands with the DFT results in a better prediction of the resulting S. Figure 3c shows that the predictions significantly improve when the ML models are trained using global plus VT-derived features (solid curves) in comparison to using only global features (dashed curves). This result highlights the importance of considering local environment features in order to predict thermopowers with higher accuracy.
a Representative configurations of 16-atom train and test units: ideal superlattices (SL) with varied compositions and external strain. Colored and gray cartoons represent train and test units, respectively. Each configuration is subjected to global in-plane substrate strains of varied magnitude. The unit structure in the middle correspond to a relaxed Si4Ge4 SL (see arrow). b Energy bands of relaxed Si4Ge4 SL calculated with DFT (black solid lines) and predicted by neural network (NN) (red circle) and random forests (RF) (blue inverted triangle) algorithms. c Thermopower calculated from bands obtained with DFT (black solid line) and predicted by NN (red) and RF (blue) algorithms. Dashed and solid lines represent predictions from ML models trained with only global features and global plus local features from Voronoi tessellations (VT) except order parameters, respectively. d, e Mean absolute errors (MAE) of ML-predicted bands of train and test structures.
Here, we demonstrate further the effectiveness of training ML models with features describing local atomic configurations. In Fig. 4a, b, we show the bands of a relaxed Si4Ge4 SL along with the corresponding S. Similar to Fig. 3b, the predictions match DFT results closely, with MAEs of 34.2 meV (NN) and 38.2 meV (RF), respectively. The remarkable aspect of these results is that the ML models are trained only on disordered fragment units and the predictions are made for ordered structures. These results provide a direct demonstration of our central hypothesis that the local atomic configurations-energy bands relationship, f(CN(r, E), is transferable across configurations with different compositions. Figure 4b further establishes that training ML models including order parameter features improves S predictions (solid curves). The MAE for the 7 relaxed SL configurations of varying Ge concentrations are shown in Fig. 4c. The high MAEs for the lowest and the highest Ge concentration SLs can be attributed to the lack of training data. As can be noted from Fig. 2e, our training set contained limited number of disordered training units with similar Ge concentrations. Thus, the order parameter maps provide great insight into the expected performance of the ML models on test structures, a priori. These results demonstrate that our ML models capture the necessary information regarding transferable f(CN(r, E)’s present in these binary heterostructures. We leverage this knowledge to predict the energy bands and transport coefficients of larger heterostructures as demonstrated below.
a Energy bands of relaxed Si4Ge4 SL predicted with ML algorithms and compared with DFT results. ML model is trained on 350 disordered units, and tested on 7 relaxed SL structures. b Comparison between thermopowers obtained with DFT (black) and ML algorithms, NN (red) and RF (blue). ML models are trained with all Voronoi tessellations (VT) derived features except the order parameters (Q) (dashed) and including order parameters (VT+Q) (solid), respectively. Improved match upon including Q features can be noted. c Train and test MAE of ML-predicted energies.
Non-ideal heterostructures
We task our ML models, trained on 16-atom relaxed ordered and disordered fragment units, to predict electronic transport properties of 32-atom non-ideal SLs. The two types of “non-idealities” we probe are represented by SLs with irregular layer thicknesses (Fig. 5b), and imperfect layers (Fig. 5d). These systems are larger in size compared to the 16-atom training units. As a result, we face a challenge to validate ML-predicted bands against DFT results, due to the different size BZs of train and test structures. The ML models predict energy bands sampling the first BZ of 16-atom models, as shown in Figs. 3 and 4. However, the 32-atom test systems have a smaller BZ and as a result, several bands are zone-folded. In addition, the number of valence and conduction bands increases with increasing system size, making it challenging to keep track of. We resort to a band structure unfolding technique that allows to identify effective band structures (EBS), by projecting onto a chosen reference BZ51,52. We obtain the EBS of 32-atom test configurations by projecting the DFT-computed bands onto the BZ of 16-atom reference BZs, and compare with the ML-predicted bands, that sample a similar size BZ (see “Methods” section for details). This technique has been proposed for different random substitutional alloy compositions, to probe to which extent band characteristics are preserved at different band indices, and k-points, compared to the respective bulk systems. Although this technique has not been applied to probe SL bands, we argue that our test structures, especially non-ideal SLs, are close to alloy systems due to broken translational symmetry. In Fig. 5a, we show the EBS of a 32-atom irregular layered heterostructure, Si4Ge4Si5Ge3. Here the indices represent the number of MLs in each component layers, as depicted by the configuration in the inset of Fig. 5b. Figure 5c shows the EBS of a 32-atom imperfect layer heterostructure, as represented by the configuration in the inset of Fig. 5d. The remarkable agreement between ML-predicted bands and EBS can be noted from both the figures. Similar to the example shown in Fig. 3, the NN algorithm provides a slightly better estimate of bandgap: the predicted band gaps are 0.996 eV (NN) and 1.005 eV (RF) for Fig. 5a; 1.022 eV (NN) and 1.009 eV (RF) for Fig. 5c, compared to the corresponding 0.978 eV and 1.035 eV obtained from DFT. As demonstrated in Fig. 5b, d, the inclusion of the order parameters (Q) is crucial for accurate prediction of thermopower. We tested the ML models on several such non-ideal heterostructures and include other results in Supplementary Information (see Supplementary Fig. 10).
a Effective band structure (EBS) (gray) of Si4Ge4Si5Ge3 multilayered system compared with ML-predicted bands. b Thermopower calculated from DFT (black) and ML bands (NN-red and RF-blue). c EBS of an imperfect layer heterostructure (gray) compared with predicted bands. d Thermopower calculated from DFT (black) and ML bands (NN-red and RF-blue). Insets show representative test structure configurations. Dashed and solid lines represent predictions from ML models, trained with all Voronoi tessellations (VT) derived features except order parameters (Q), and including them (VT+Q), respectively.
Fabricated heterostructures
As we discussed previously, the domain of application of first-principles approaches is often limited to ideal systems that do not capture the structural complexity of fabricated heterostructure, mainly due to computational expenses. As a consequence, we resort to parametric approaches to predict electronic properties of fabricated systems. It is highly desirable to establish a bridge between the domains of (A) ab initio accessible ideal systems and (B) fabricated systems, to acquire parameter-free predictions of electronic properties of real systems. Below, we demonstrate that our ETI framework successfully predicts electronic properties of test systems representing domain (B), after being trained on 16-atom training units from domain (A), and thus establishes a bridge between the two domains.
In Fig. 6, we demonstrate the agreement between ML-predicted thermopowers (solid (NN) and dashed (RF)) and measured values (circle and triangles)17,53,54. We chose three representative fabricated systems to demonstrate the predictive power of our ETI framework. The circle (red) in Fig. 6a represents cross-plane thermopower of n-type Si(5Å)/Ge(7Å) SL grown along [001] direction at 300K53. The triangles (green) represent in-plane thermopowers of n-type Si(20Å)/Ge(20Å) SL grown along [001] direction at 300K17. The inverted triangles (blue) represent thermopowers of n-type Si0.7Ge0.3 alloys at 300K54. We relax the geometry of atomistic models of the test structure using DFT and compute the features from the relaxed configurations. The relaxation is performed to ensure that the initial bias in preparing the model configurations does not affect our ML predictions (see “Methods” section for details). We provide features of the test structures as input to the ML models and task it to predict the electronic bands. We then use the ML-predicted bands to compute thermopowers implementing the BTE framework. The ML predictions show a good agreement for both cross-plane and in-plane thermopowers at different carrier concentrations. The small deviations between ML results and measured data can be attributed to the differences between local environments in the models and the fabricated samples. We anticipate that the error in ML prediction would fall within experimental uncertainties. We considered multiple randomized configurations for the alloy results shown in Fig. 6a and did not observe any significant variation in the predicted thermopower. The modulations of the cross-plane S’s at different carrier concentrations is rooted to the formation of minibands in the SL configuration, due to potential perturbation and intervalley mixing effects34,35,36. The comparison shown in Fig. 6a reveals that ML predictions can be utilized to optimize the thermopowers of these systems by varying carrier concentrations.
Each model is trained with DFT data obtained from 16-atom fragment units: a Predicted thermopower (NN (solid lines), RF (dashed lines)) of n-type SLs and alloys compared to measured data17,53,54. b Representative model Si/Si0.7Ge0.3 SL. Length (L) of Si region is varied while keeping length of Si0.7Ge0.3 region fixed. c S of p-type Si/Si0.7Ge0.3 SLs at carrier concentration, ne = 1.5 × 1019 cm−3 predicted with NN algorithm and compared with measured data55. Predicted S’s converge to measured value from below with increasing L. Spread in NN predictions represent five randomized Si0.7Ge0.3 configurations, considered for each L.
In Fig. 6c, we further establish that the ETI framework can guide the design of heterostructures to optimize electronic transport properties. We show the NN-predicted cross-plane thermopowers of p-type Si/SiGe SLs at a carrier concentration, ne = 1.5 × 1019 cm−3, as a function of varying Si layer thickness (L). A representative configuration of a Si/Si0.7Ge0.3 SL is shown in Fig. 6b. We construct model configurations with a fixed-length alloy region and varied Si region lengths, L. For each model with Si region of length L, we considered five different randomized substitutional alloy configurations yielding the spread in ML predictions. As can be noted from the figure that our predictions approach the measured value obtained for a Si(80Å)/Si0.7Ge0.3(40Å) SL grown on a Si substrate55, as we approach L ~ 80Å. Our results reveal that thermopower of Si/SiGe SLs can be optimized by choosing an appropriate system size guided by ML prediction, and also, establish the remarkable extrapolating power of the framework. We argue that the extension of the prediction domain is enabled by our central hypothesis that local environment–energy bands relationships are transferable across configurations with different compositions. This physics-based extrapolation is thus possible because of accumulating knowledge from “known” environments.
Scalability of the ETI framework
In order to further establish the claim that our ETI framework will help bridge the gap between ab initio accessible and fabricated systems, we explore the scalability of our framework with increasing system size. In Fig. 7, we compare the computational cost of using ETI framework to predict electronic properties against direct DFT calculations, with increasing system size. The ML runtime is divided in two parts: generation of training data with DFT, indicated by the constant baseline, shown with the dashed line in inset of Fig. 7b; and the feature extraction of DFT-relaxed test configurations. The plot shows that runtime for DFT calculations scales as ~N2 while that for feature extraction scales linearly with N, where N is a number of atoms. Figure 7 establishes the remarkable advantage of the ETI framework for parameter-free prediction of thermopowers of large structures that cannot be fully accessed with DFT. We acknowledge that identifying the upper bound of this plot would be beneficial but leave it for future work.
In summary, we demonstrate that the problem of predicting electronic properties of technologically relevant heterostructures can be solved by combining first-principles methods with ML techniques into a physics-aware ETI framework. We incorporate the physics awareness in the ML approach in two ways: (1) providing carefully chosen training data to bias the learning and (2) formulating descriptors that can successfully characterize functional relationships, f(CN(r), E), between local atomic configurations and global energy bands. We illustrate that physics-informed ML models are capable of formulating transferable relationships, f(CN(r), E), from the large body of atomistic data generated with individual DFT calculations of 16-atom ordered (layered) and disordered (alloy) semiconductor structures with diverse atomic environments. We exploit the transferability and task the ML models to predict energy bands (\(\hat{E}\)) of fabricated nanostructures. We thus use ML techniques to overcome the challenges to calculate energy bands using first-principles techniques, and compute thermopower from the predicted \(\hat{E}\)’s. The predicted thermopowers of fabricated heterostructures show remarkable agreement with measured data. The proposed ETI framework, thus, help establishes a bridge between ideal systems accessible with first-principles approaches and real systems realized with nanofabrication techniques.
The relationship between fabrication-dependent structural parameters and electronic properties of heterostructures is complex and often cannot be fully explored with first-principles approaches. Our study demonstrates that physics-informed ML techniques can be successfully exploited to formulate them. We establish that functional relationships between local atomic configurations, and their contributions to global energy bands remain preserved when the local configurations are part of a nanostructure with different composition and/or dimensions. Transferability of these functional relationships is the key physical understanding that is revealed by our study. Our framework proposes a data driven approach to extract important physics that determines electronic properties of heterostructures, and allows to extend the applicability of first-principles techniques for technologically relevant heterostructures. For example, this approach will allow the predictions of properties of alloyed thermoelectric materials with diverse nanostructures, formed by segregated structures, partial solid solutions or completely random solid solutions, which appear in real materials. It will allow researchers to predict the best nanostructure to achieve maximum Seebeck coefficient for different classes of thermoelectric materials. We anticipate that this viewpoint would give the ETI framework broad applicability to diverse materials classes.
Methods
Training and testing model details
Ordered units
We construct model SinGem SL fragment units with different compositions to generate the training data, where n and m refer to the number of Si and Ge monolayers (ML), respectively. We create a SinGem (n + m = 8) fragment unit supercell by replicating an 8-atom conventional Si unit cell (CC) twice along the symmetry direction [001] and replacing m Si ML with Ge atoms, since both Si and Ge have stable FCC diamond lattice structures56,57. By replacing Si ML with Ge, we obtain 7 Si8−xGex SLs, where x is the number of MLs: x = [1, 2, …7]. To generate train and test strained SL structures, we consider applied strains ranging uniformly from −1.1% to +6.1% with a total of 7 different strain values, resulting in 49 different SLs, as shown in Fig. 3. To simulate SLs under applied strain we fix in-plane lattice constants: (−1.1%, 0.1%, 1.3%, 2.5%, 3.7%, 4.9%, 6.1% of bulk Si lattice constant), keep the volume of the cell fixed and let the atomic positions and shape of the cell relax along cross-plane [001] direction. We estimate the in-plane strain in the SLs from the lattice constants by ϵ∥ = (a∥/aSi − 1) with aSi = 5.475 Å58.
Disordered units
We model the disordered SinGem fragment units with different compositions to generate the training data, where n and m refer to the number of Si and Ge atoms, respectively. The disordered SiGe structures are prepared with similar 16 atom supercells, two conventional 8-atom cells (CC) stacked along the [001] direction. For each chosen Ge concentration (5/16, 6/16, 7/16, 8/16, 9/16, 10/16, 11/16), we generate 50 substitutional “alloy” configurations, resulting in 350 total disordered fragment training units.
Non-Ideal Heterostructure Models
The non-ideal heterostructures shown in Fig. 5b, d are modeled with 32-atom supercells (4 CCs). The systems are constructed by stacking 16-atom units with atomic composition SinGem, where n + m = 8, along z direction for the multilayered systems and along x direction for the imperfect layer heterostructures. The resulting stoichiometry of the test configurations can be represented as SinGemSikGel with n + m + k + l = 32, n ≠ k, and m ≠ l.
Fabricated heterostructure models
We model the Si(5Å)/Ge(7Å) SL shown in Fig. 6a with 1 × 1 × 2 CCs that include 8 Si and 8 Ge atoms. We construct the model Si(20Å)/Ge(20Å) SL with 2 × 2 × 7 CCs including 112 Si and 112 Ge atoms. The Si0.7Ge0.3 alloy is modeled using a randomly substituted 64-atom 2 × 2 × 2 CCs system that includes 45 Si and 19 Ge atoms. The fabricated structures shown in Fig. 6b are modeled with a Si0.7Ge0.3 random alloy region (2 × 2 × 7 CCs: 157 Si and 67 Ge atoms) and a Si layer of varied lengths between 0 and 10 CCs (0–320 Si atoms). We model systems with total size varied from 2 × 2 × 7 (157 + 67 = 224 atoms) to 2 × 2 × 17 CCs (157 + 67 + 320 = 544 atoms) by increasing L and keeping the width of the alloy region constant to 2 × 2 × 7 CCs. For each system with a given L, we model the substitutional alloy region with five different randomized configurations.
We compute the features of the test non-ideal and fabricated heterostructures from their relaxed geometry configurations, to ensure that the initial bias in preparing the model configurations does not affect our ML predictions. In this study, we use the Broyden–Fletcher–Goldfarb–Shanno Quasi-Newton algorithm, as implemented in the Vienna Ab Initio Simulation Package (VASP) package, for geometry relaxation without any applied constraints (as discussed below). We provide the test features as input to the ML models and task them to predict the energy bands.
DFT computational details
The relaxed geometries of the structures are obtained VASP. The lattice constants and the atomic positions in SinGem structures are optimized using Broyden–Fletcher–Goldfarb–Shanno Quasi-Newton algorithm, sampling the BZ with 8 × 8 × 8 k-point mesh. To simulate SLs under applied strain, we keep the cell volume fixed and relax the cell shape in cross-plane [001] direction. We perform the electronic structure calculations with DFT using the generalized gradient approximation (GGA) implemented in VASP59,60 with the Perdew–Burke–Ernzenhof (PBE) exchange-correlation functional61. The ultra-soft projector-augmented wave pseudopotential62,63 with a cutoff energy of 400 eV was used to describe the interaction between the valence electrons and the ions. For the self-consistent calculations, the energy convergence threshold was set to 10−6 eV. We have not included spin–orbit interaction in our analysis since the magnitude of the lattice strain induced splittings is larger than the spin–orbit splittings64. The electronic bands are plotted along the Γ − Z symmetry direction of the BZ with 11 points resolution. Following relaxation, we perform non self-consistent field calculations to obtain the energy bands using a dense Γ-centered 21 × 21 × 21 Monkhorst–Pack k-point mesh65, to sample the irreducible Brillouin zone (IBZ). Such sampling is necessary to converge the calculation of the electronic transport coefficients34,35 (see Supplementary Figs. 8 and 9). Once the electronic structure calculations are completed, we employ the semi-classical Boltzmann transport theory66 as implemented in BoltzTraP code67 to compute the room temperature Seebeck coefficients. The k-point mesh is chosen after performing systematic studies to converge Seebeck coefficients with increasing mesh size. In Supplementary Figs. 8 and 9, we show the convergence of S of two representative configurations with increasing k-sampling and number of included bands, respectively.
ML algorithm implementations
NN model
The NN model is tasked to formulate f(CN(r), E), relating features of CN(r) and the target electronic states \(\hat{E}\), parametrized by weights W. Our model consists of a 128-node input layer, three fully connected hidden layers each with 256 nodes, and an output layer with nodes equal to the number of energy values, \(\hat{E}(k,b)\): kx × ky × kz × b. We consider a 21 × 21 × 21 k-point mesh to sample the respective BZ, and six valence and six conduction bands (b), resulting in 21 × 21 × 21 × 12 E(k, b) values for each training configuration. The model input is determined by the number of features considered. We list the training sets and test data in Table 2. The training sets are split into random batches of size 32 at each epoch during training. Sequential random samplings (e.g., 32/40, 32/350 or 32/357) are performed during each training epoch. The last batch will be of size less than 32 if the remainder is not zero. The NN model is trained for 500 epochs. The training is performed by iteratively updating the weights to minimize the MAE between actual and predicted energies,
We employ the ADAM stochastic optimization method for gradient descent to minimize the loss function (MAE). The high-level NNs are implemented using the Keras library68 written in Python. In all NN models, the Rectified Linear Unit activation functions are utilized. Fivefold cross-validation tests are performed to avoid overfitting. The optimized weights,
are then used to predict 21 × 21 × 21 × 12 \(\hat{E}\) values for unknown test structures.
RF model
We use RF models69 since they are computationally inexpensive and shown to be robust to overfitting of data42. Our model assembles results of several decision trees, each built from random selection of training data that include both features and training energy values. The selected training data are further partitioned into subsets based on decision rules. For example, the subsets can be formed based on order parameter values, e.g., Qz,1 ~ 0.5 to 0.6, representing different atomic environments (see Table 1). The decision rules identify features that minimize the intrasubset variation of electronic energies and constitute branches of the trees. The leaves of the tree are then assigned to an energy value that maximizes fitting over the subset data. Such tree generation process is then repeated for other random subsets of training data. The final predictions are obtained by averaging the predicted energies over all trees. We implement the RF module available in the scikit-learn Python package70. The input and output are identical to the ones used for the NN algorithm (Table 2). We use 100 regression trees per ensemble and set all other parameters to default values recommended for the package. We did not observe any notable change in the predicted energies by increasing the number of trees to 200 and 300.
Effective band structures
Following the approach outlined in ref. 51, we transform the band structures of larger configurations into EBS of a reference cell consisting of 16 atoms, using spectral decomposition71. The reference cell contains the same number of atoms as the training units and is approximately of the same size as 2 CCs stacked along [001] direction. However, the dimensions of the reference cells that each test configuration is projected to are different, and are obtained by dividing the supercells as multiples of 2 CCs and taking an average. We calculate the eigenstates \(|\vec{K}m\rangle\) of the test supercells using DFT, sampling the BZ with a 21 × 21 × 21 K-point mesh, where m is the band index. The spectral weight that quantifies the amount of character of Bloch states \(|\vec{{k}_{i}}n\rangle\) of the reference unit cell preserved in \(|\vec{K}m\rangle\) at the same energy Em = En, can be written as
Here, ki = K + Gi, Gi being the translational vector of a reciprocal lattice of the supercell BZ in the reference cell BZ51. The spectral function (SF) can then be defined as
where E is a continuous variable of a chosen range over which we probe for the preservation of the Bloch character of the supercell eigenstates. The delta function in Eq. (5) is modeled with a Lorentzian function with width 0.002 eV. \(A(\vec{{k}_{i}},E)\) are normalized by dividing the SF by \(ma{x}_{\{\vec{{k}_{i}},E\}}[A(\vec{{k}_{i}},E)]\).
Seebeck coefficients
We compute the Seebeck coefficients using the semi-classical BTE as implemented in the BoltzTraP code67. All thermopower calculations are performed at room temperature and for technologically relevant high doping regime ranging from ne = 1018 to 1021 cm−3. S is obtained from \((1/eT)({{\mathcal{L}}}^{(1)}/{{\mathcal{L}}}^{(0)})\), where e is the electron charge, T is temperature, and the generalized in-plane (∥) or cross-plane (⊥) nth-order conductivity moments are
The integrand is computed from the energy difference (ϵ − ϵF) to the nth power, the Fermi energy level (ϵF), the derivative of the Fermi-Dirac distribution function (f) with respect to energy ϵ, and the transport distribution function (TDF)50. TDF can be expressed as
within the constant relaxation time (τ) approximation (CRTA). The area-integral is given by the density of states (DOS) (\(\propto {\oint }_{{\epsilon }_{{\bf{k}}} = \epsilon }\frac{d{\mathcal{A}}}{| {{\bf{v}}}_{{\bf{k}}}| }\)) weighted by the squared group velocities, \({({{\bf{v}}}_{{\bf{k}},(\parallel ,\perp )})}^{2}\). The carrier concentrations ne are obtained from the knowledge of the electronic bands and the Fermi level: \({n}_{e}=\int d\epsilon \,{\rm{DOS}}(\epsilon )\,{f}_{{\epsilon }_{f}}(\epsilon ,T).\)
It is known that the PBE-GGA approach poorly predicts semiconductor band gaps72,73, as opposed to using hybrid functionals74. Nevertheless, the PBE-GGA approximation has been regularly employed to compute the electron/hole transport coefficients of semiconductors, including thermoelectric properties of [111]-oriented Si/Ge SLs37. These studies demonstrate the effectiveness of the PBE-GGA approximation to highlight the role of lattice environment on electronic properties of Si-based systems. In previous publications, we discussed the discrepancy in bandgap predictions in detail34 as well as shown comparisons of S of Si4Ge4 SLs predicted using the Heyd–Scuseria–Ernzerhof75 and the PBE functionals35. We find that the PBE-predicted S vs ne relationship closely follows the HSE prediction for low strain cases, and shows small deviations at low doping concentrations for high strain cases, which can be attributed to bandgap discrepancies35. In addition, we tested that using a scissors operator for bandgap correction using the HSE predicted gaps (See ref. 35) or experimental bandgap (see Supplementary Fig. 8), essentially leaves the S vs ne curve unchanged. This systematic analysis showed the robustness of our results highlighting the relationship between lattice environment and electronic transport in heterostructures, independent of the numerical approach used, and motivated us to use PBE-GGA-BTE approach to analyze the thermopowers of SinGem heterostructures. In the present article, we use a static correction (UGGA = 0.52 eV37) to match the PBE-predicted bandgap to the measured bandgap value for bulk silicon. The PBE approach is especially suited for data driven studies since it is far less expensive compared to a more accurate hybrid functional. For example, the electronic bands calculation of a Si4Ge4 SL using PBE, over a 21 × 21 × 21 k-point mesh, required 31 CPU hours and compared to 1075 hours of CPU time when using the hybrid functional.
We used a CRTA for all the calculations presented in this article. This approximation allows us to calculate S without any free parameters. It is a common practice to obtain τ by fitting experimental mobility data for specific carrier concentrations with empirical approximations, and adjust the first-principle results accordingly to reproduce experimental findings. For example, the first-principles estimation of electronic transport properties of strained bulk Si used relaxation times fitted from the measured mobility data of unstrained Si37. One main reason is that first-principles computation of τ is highly expensive for model systems containing greater than a few atoms. As a result, only a handful of previous studies exist that analyzed the electronic properties of highly technologically relevant Si/Ge heterostructures using first-principle methods, especially including the complex effects of strain or non-idealities. It is known that strain could alter the dominant scattering processes in bulk Si76, however, the role of different scattering mechanisms on electron relaxation in Si/Ge heterostructures is relatively unexplored. We acknowledge that CRTA may not capture the full physics, particularly, the effects of electrons scattering due to phonons and ionized impurities on the electronic transport properties of our interest. In an earlier publication, we estimated the relaxation time assuming that the electron–phonon scattering rates in non-polar semiconductors generally are proportional to the DOS, and provided a comparison between S, computed with constant τ and with τ(ϵ) ∝ 1/DOS (See Supplementary Materials of ref. 34). We noted that S trends match quite well between the two approximations, although the exact values differ. These observations motivated us to employ CRTA to compute the electronic transport coefficients in this article. We acknowledge that a detailed analysis of the validity of this approximation would be highly beneficial. However, such a study is out of scope of the present article, especially since we needed to perform these calculations for a large number of samples for training our ML models, or to test the predictions on systems containing 100s of atoms. Our aim here is to establish that the local functional relationships present in small models can be harnessed to achieve parameter-free prediction of the electronic transport properties of fabricated heterostructures. And we have provided a proof of concept by demonstrating that our predictions, made using a constant relaxation time, match the measured data for three classes of fabricated heterostructures. We primarily use ML techniques to overcome the challenges of calculating energy bands using first-principles techniques. We anticipate that one can predict electronic properties with higher accuracy using our ETI framework by providing training set data, obtained using higher accuracy models or implementing sophisticated transport models.
Data availability
We declare that the data supporting the findings of this study are available within the main article and the Supplementary Information document. In addition, we have made an example data set available through public GitHub repository77. The example data set includes 49 Si/Ge superlattice (SL) configurations with external strain. We have included the SL geometry data before and after DFT relaxation, and the DFT calculated energy values.
Code availability
We have made the Python scripts available for extracting the geometrical features from the example data set through a public GitHub repository77.
References
Alferov, Z. I. Nobel lecture: the double heterostructure concept and its applications in physics, electronics, and technology. Rev. Mod. Phys. 73, 767 (2001).
Thompson, S. E. et al. A 90-nm logic technology featuring strained-silicon. IEEE Trans. Electron Devices 51, 1790–1797 (2004).
Meyerson, B. S. High-speed silicon-germanium electronics. Sci. Am. 270, 62–67 (1994).
Nissim, Y. & Rosencher, E. Heterostructures on Silicon: One Step Further with Silicon, Vol. 160 (Springer Science & Business Media, 2012).
Paul, D. J. Si/SiGe heterostructures: from material and physics to devices and circuits. Semicond. Sci. Technol. 19, R75 (2004).
Koester, S. J., Schaub, J. D., Dehlinger, G. & Chu, J. O. Germanium-on-SOI infrared detectors for integrated photonic applications. IEEE J. Sel. Top. Quantum Electron. 12, 1489–1502 (2006).
Liu, J., Sun, X., Camacho-Aguilera, R., Kimerling, L. C. & Michel, J. Ge-on-Si laser operating at room temperature. Opt. Lett. 35, 679–681 (2010).
Alam, H. & Ramakrishna, S. A review on the enhancement of figure of merit from bulk to nano-thermoelectric materials. Nano Energy 2, 190–212 (2013).
Taniguchi, T. et al. High thermoelectric power factor realization in Si-rich SiGe/Si superlattices by super-controlled interfaces. ACS Appl. Mater. Interfaces (2020).
Shi, Z. et al. Tunable singlet-triplet splitting in a few-electron Si/SiGe quantum dot. Appl. Phys. Lett. 99, 233108 (2011).
Euaruksakul, C. et al. Heteroepitaxial growth on thin sheets and bulk material: exploring differences in strain relaxation via low-energy electron microscopy. J. Phys. D: Appl. Phys. 47, 025305 (2013).
Brehm, M. & Grydlik, M. Site-controlled and advanced epitaxial Ge/Si quantum dots: fabrication, properties, and applications. Nanotechnology 28, 392001 (2017).
Lee, C. et al. Interplay of strain and intermixing effects on direct-bandgap optical transition in strained Ge-on-Si under thermal annealing. Sci. Rep. 9, 1–9 (2019).
Chen, P. et al. Role of surface-segregation-driven intermixing on the thermal transport through planar Si/Ge superlattices. Phys. Rev. Lett. 111, 115901 (2013).
David, T. et al. New strategies for producing defect free SiGe strained nanolayers. Sci. Rep. 8, 2891 (2018).
Samarelli, A. et al. The thermoelectric properties of Ge/SiGe modulation doped superlattices. J. Appl. Phys. 113, 233704 (2013).
Koga, T., Cronin, S., Dresselhaus, M., Liu, J. & Wang, K. Experimental proof-of-principle investigation of enhanced Z3DT in (001) oriented Si/Ge superlattices. Appl. Phys. Lett. 77, 1490–1492 (2000).
Watling, J. R. & Paul, D. J. A study of the impact of dislocations on the thermoelectric properties of quantum wells in the Si/SiGe materials system. J. Appl. Phys. 110, 114508 (2011).
Vargiamidis, V. & Neophytou, N. Hierarchical nanostructuring approaches for thermoelectric materials with high power factors. Phys. Rev. B 99, 045405 (2019).
Snyder, J. C., Rupp, M., Hansen, K., Müller, K.-R. & Burke, K. Finding density functionals with machine learning. Phys. Rev. Lett. 108, 253002 (2012).
Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 145, 170901 (2016).
Ramprasad, R., Batra, R., Pilania, G., Mannodi-Kanakkithodi, A. & Kim, C. Machine learning in materials informatics: recent applications and prospects. npj Comput. Mater. 3, 1–13 (2017).
Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 1–7 (2016).
Meredig, B. et al. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B 89, 094104 (2014).
Jain, A., Shin, Y. & Persson, K. A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 1, 1–13 (2016).
Wang, T., Zhang, C., Snoussi, H. & Zhang, G. Machine learning approaches for thermoelectric materials research. Adv. Funct. Mater. 30, 1906041 (2020).
Gaultois, M. W. et al. Perspective: web-based machine learning models for real-time screening of thermoelectric materials properties. APL Mater. 4, 053213 (2016).
Jain, A. et al. The Materials Project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Draxl, C. & Scheffler, M. The NOMAD laboratory: from data sharing to artificial intelligence. J. Phys. Mater. 2, 036001 (2019).
Gaultois, M. W. et al. Data-driven review of thermoelectric materials: performance and resource considerations. Chem. Mater. 25, 2911–2920 (2013).
Schleder, G. R., Padilha, A. C., Acosta, C. M., Costa, M. & Fazzio, A. From dft to machine learning: recent approaches to materials science–a review. J. Phys. Mater. 2, 032001 (2019).
Xie, T., France-Lanord, A., Wang, Y., Shao-Horn, Y. & Grossman, J. C. Graph dynamical networks for unsupervised learning of atomic scale dynamics in materials. Nat. Commun. 10, 1–9 (2019).
Nye, J. F. et al. Physical properties of crystals: their representation by tensors and matrices (Oxford University Press, 1985).
Proshchenko, V. S., Settipalli, M. & Neogi, S. Optimization of Seebeck coefficients of strain-symmetrized semiconductor heterostructures. Appl. Phys. Lett. 115, 211602 (2019).
Proshchenko, V. S., Settipalli, M., Pimachev, A. K. & Neogi, S. Role of substrate strain to tune energy bands–seebeck relationship in semiconductor heterostructures. J. Appl. Phys. 129, 025301 (2021).
Settipalli, M. & Neogi, S. Theoretical prediction of enhanced thermopower in n-doped si/ge superlattices using effective mass approximation. J. Electron. Mater. 49, 4431–4442 (2020).
Hinsche, N., Mertig, I. & Zahn, P. Thermoelectric transport in strained Si and Si/Ge heterostructures. J. Phys. Condens. Matter 24, 275501 (2012).
Peter, Y. & Cardona, M. Fundamentals of Semiconductors: Physics and Materials Properties (Springer Science & Business Media, 2010).
Ridley, B. Quantum Processes in Semiconductors (Oxford Univ. Press, 1999).
Schäffler, F. High-mobility Si and Ge structures. Semicond. Sci. Technol. 12, 1515 (1997).
Proshchenko, V. S., Dholabhai, P. P., Sterling, T. C. & Neogi, S. Heat and charge transport in bulk semiconductors with interstitial defects. Phys. Rev. B 99, 014207 (2019).
Ward, L. et al. Including crystal structure attributes in machine learning models of formation energies via voronoi tessellations. Phys. Rev. B 96, 024104 (2017).
Ghiringhelli, L. M., Vybiral, J., Levchenko, S. V., Draxl, C. & Scheffler, M. Big data of materials science: critical role of the descriptor. Phys. Rev. Lett. 114, 105503 (2015).
Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).
Xie, T. & Grossman, J. C. Hierarchical visualization of materials space with graph convolutional neural networks. J. Chem. Phys. 149, 174111 (2018).
Gong, S. et al. Predicting charge density distribution of materials using a local-environment-based graph convolutional network. Phys. Rev. B 100, 184103 (2019).
Cowley, J. An approximate theory of order in alloys. Phys. Rev. 77, 669 (1950).
Wen, C.-Y., Reuter, M. C., Su, D., Stach, E. A. & Ross, F. M. Strain and stability of ultrathin Ge layers in Si/Ge/Si axial heterojunction nanowires. Nano Lett. 15, 1654–1659 (2015).
Gupta, G., Rajasekharan, B. & Hueting, R. J. Electrostatic doping in semiconductor devices. IEEE Trans. Electron Devices 64, 3044–3055 (2017).
Mahan, G. & Sofo, J. O. The best thermoelectric. Proc. Natl. Acad. Sci. USA 93, 7436–7439 (1996).
Popescu, V. & Zunger, A. Extracting E versus \(\overrightarrow{k}\) effective band structure from supercell calculations on alloys and impurities. Phys. Rev. B 85, 085201 (2012).
Boykin, T. B., Kharche, N., Klimeck, G. & Korkusinski, M. Approximate bandstructures of semiconductor alloys from tight-binding supercell calculations. J. Phys.: Condens. Matter 19, 036203 (2007).
Yang, B., Liu, J., Wang, K. & Chen, G. Characterization of cross-plane thermoelectric properties of Si/Ge superlattices. In Proceedings ICT2001. 20 International Conference on Thermoelectrics (Cat. No. 01TH8589), 344–347 (IEEE, 2001).
Dismukes, J., Ekstrom, L., Steigmeier, E., Kudman, I. & Beers, D. Thermal and electrical properties of heavily doped Ge-Si alloys up to 1300 K. J. Appl. Phys. 35, 2899–2907 (1964).
Zhang, Y. et al. Measurement of Seebeck coefficient perpendicular to SiGe superlattice. In Thermoelectrics, 2002. In Proceedings ICT’02. Twenty-First International Conference on, 329–332 (IEEE, 2002).
Pearsall, T. P. Strained-Layer Superlattices: Materials Science and Technology, Vol. 33 (Academic Press, 1991).
Manasreh, M. O., Pantelides, S. T. & Zollner, S. Optoelectronic Properties of Semiconductors and Superlattices, Vol. 15 (Taylor & Francis Books, INC, 1991).
Van de Walle, C. G. & Martin, R. M. Theoretical calculations of heterojunction discontinuities in the Si/Ge system. Phys. Rev. B 34, 5621 (1986).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Hybertsen, M. S. & Schlüter, M. Theory of optical transitions in Si/Ge (001) strained-layer superlattices. Phys. Rev. B 36, 9683 (1987).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Ziman, J. M. Electrons and Phonons: the Theory of Transport Phenomena in Solids (Oxford University Press, 1960).
Madsen, G. K. & Singh, D. J. BoltzTraP. a code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71 (2006).
Chollet, F. et al. Keras (Internet) (GitHub, 2015). https://github.com/fchollet/keras.
Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).
Pedregosa, F. et al. Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
Wang, L.-W., Bellaiche, L., Wei, S.-H. & Zunger, A. "majority representation” of alloy electronic states. Phys. Rev. Lett. 80, 4725 (1998).
Perdew, J. P. et al. Understanding band gaps of solids in generalized Kohn–Sham theory. Proc. Natl. Acad. Sci. USA 114, 2801–2806 (2017).
Morales-García, Á., Valero, R. & Illas, F. An empirical, yet practical way to predict the band gap in solids by using density functional band structure calculations. J. Phys. Chem. C 121, 18862–18866 (2017).
Hummer, K., Harl, J. & Kresse, G. Heyd-scuseria-ernzerhof hybrid functional for calculating the lattice dynamics of semiconductors. Phys. Rev. B 80, 115205 (2009).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Dziekan, T., Zahn, P., Meded, V. & Mirbt, S. Theoretical calculations of mobility enhancement in strained silicon. Phys. Rev. B 75, 195213 (2007).
Cuantam lab - github repository. https://github.com/CUANTAM.
Acknowledgements
We gratefully acknowledge funding from the Defense Advanced Research Projects Agency (Defense Sciences Office) [Agreement No.: HR0011-16-2-0043]. We acknowledge funding from the National Science Foundation Harnessing the Data Revolution NSF-HDR-OAC-1940231. This work utilized resources from the University of Colorado Boulder Research Computing Group, which is supported by the National Science Foundation (awards ACI-1532235 and ACI-1532236), the University of Colorado Boulder, and Colorado State University. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation grant number ACI-1548562.
Author information
Authors and Affiliations
Contributions
A.K.P contributed to the acquisition and the analysis of data and the creation of new scripts used in the study. S.N. contributed to the conception and the design of the work, the interpretation of data, drafting and revision of the article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pimachev, A.K., Neogi, S. First-principles prediction of electronic transport in fabricated semiconductor heterostructures via physics-aware machine learning. npj Comput Mater 7, 93 (2021). https://doi.org/10.1038/s41524-021-00562-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00562-0
This article is cited by
-
Designing semiconductor materials and devices in the post-Moore era by tackling computational challenges with data-driven strategies
Nature Computational Science (2024)
-
Descriptor engineering in machine learning regression of electronic structure properties for 2D materials
Scientific Reports (2023)
-
Phase classification of multi-principal element alloys via interpretable machine learning
npj Computational Materials (2022)