Abstract
The search of direct-gap Si-based semiconductors is of great interest due to the potential application in many technologically relevant fields. This work examines the incorporation of He as a possible route to form a direct band gap in Si. Structure predictions and first-principles calculations show that He and Si, at high pressure, form four dynamically stable phases of Si2He (oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He). All phases adopt host–guest structures consisting of a channel-like Si host framework filled with He guest atoms. The Si frameworks in oP36-Si2He, tP9-Si2He, and mC12-Si2He could be retained to ambient pressure after removal of He, forming three pure Si allotropes. Among them, oP36-Si2He and mC12-Si2He exhibit direct band gaps of 1.24 and 1.34 eV, respectively, close to the optimal value (~1.3 eV) for solar cell applications. Analysis shows that mC12-Si2He with an electric dipole transition allowed band gap possesses higher absorption capacity than cubic diamond Si, which makes it to be a promising candidate material for thin-film solar cell.
Similar content being viewed by others
Introduction
With the growth of population and the development of science and economy, human beings need more energy to create a better living environment. However, burning traditional fossil fuels is causing climate change, global warming, air pollution, acid rain, and a serious of other environmental problems1,2,3,4. Thus, energy becomes one of the most important issues on the international environment and development agenda. Photovoltaic modules provide a clean, reliable, and abundant way to convert solar energy into electricity to meet the growing demand for energy5,6,7,8. A good photovoltaic material should possess an electric dipole transition allowed direct band gap9 and the Shockley–Queisser limit predicts that a band gap of 1.34 eV achieves the highest solar conversion efficiency (33.7%) for a single p–n junction10. Due to the relative abundance and environmental friendliness of silicon, silicon solar cells have attracted much attention in the field of photovoltaic market in the past several decades. However, the indirect electric band gap and the large optical gap (larger than 3 eV) make the thin-film silicon not a competitive candidate11. Thicker silicon can increase the efficiency of solar conversion but with a higher commercial cost11,12. Therefore, to search for potential Si allotropes or Si-based compounds with an electric dipole transition allowed direct band gap is of great interest.
Much effort has been devoted to the search for new Si allotropes with direct or quasi-direct band gaps13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34. A series of new Si structures formed by phase transformations under high pressure have been observed experimentally13,14,15,16,17,18,19,20. Direct-gap BC8-Si was formed after releasing the pressure from the high-pressure β-Sn phase to 2 GPa13. However, the relatively narrow direct band gap of 30 meV precludes BC8-Si as a photovoltaic material18. Irradiation of amorphous Si film with a coherent electron beam stabilized a new Si9 phase with a direct band gap of ~1.59 eV, indicating a potentially useful photovoltaic material20. In particular, the hexagonal 2H-allotrope phase was well studied both theoretically35 and experimentally36,37,38,39 and can be viewed as a better potential photovoltaic material than cubic silicon.
First-principle calculations are important in the search for new Si structures. Structure searches based on Crystal structure AnaLYsis by Particle Swarm Optimization (CALYPSO) have found four channel-like Si allotropes (oF16-Si, tP16-Si, mC12-Si, and tI16-Si) with direct band gaps of 0.81–1.25 eV21. A cubic Si20-T phase with a quasi-direct band gap of 1.55 eV was designed using a new inverse-band structure design approach based on CALYPSO22. Conformational space annealing calculations have uncovered two new Si allotropes, Q135 and D135, with direct band gaps of 0.98 and 1.33 eV, respectively, both of which were proposed to be good photovoltaic materials with estimated photovoltaic efficiency of ~ 30%23. Ab initio random structure searching has also revealed a new Si structure with space group Pbam and a direct band gap of 1.4 eV24. By substituting C or Ge atoms in their structures with Si atoms, at least 17 candidate structures were predicted25,26,27,28,29,30, of which nine27,28,29 (M585, Pbam-32, P6/mmm, \(Im\bar{3}m\), C2/c, I4/mcm, I4/mmm, P21/m, and P4/mbm) have direct band gaps of 0.65–1.51 eV. Ab initio minima hopping structure predictions have also predicted more than 44 Si structures, of which eleven (\(R\bar{3}m\)-1, \(R\bar{3}m\)-2, C2/m, Immm-1, Immm-2, Immm-3, Pmma, I41md, Pnma, \(I\bar{4}2d\) and I212121) exhibit direct band gaps of 1.0–1.8 eV31,32. All these direct or quasi-direct Si structures are metastable, possessing a high energy relative to CD-Si, and thus are difficult to synthesize directly.
Si-rich compounds with open framework structures formed at high pressures are good precursors to obtain new Si allotropes. A two-step synthesis method has made two metastable allotropes (a clathrate Si13633 and a channel-like Si2434) by removing Na from high-pressure Na–Si compounds. Channel-like Si24 was prepared by first synthesizing at high pressure a Na4Si24 precursor that contained a channel-like sp3 Si host structure filled with linear Na chains. Na atoms were removed along the open channels via thermal degassing, leaving the pure Si24 allotrope. Electrical conductivity and optical absorption measurements confirmed a quasi-direct band gap of 1.3 eV, making Si24 a potential photovoltaic material.
The noble gas He becomes reactive at high pressure, leading to several new compounds, including some materials which are synthsized on experiment, such as Na2He40 and NeHe241, and some predicted materials, such as HeN442, He–alkali oxides (sulfides)43, He–Fe44, FeO2He,45 Mg(Ca)F2He46, He–H2O47,48, He–CH449, and He–NH350,51,52. Although most of these materials are predicted under extreme condition, the results provide a clear indication that He can break through the chemical inert barrier and react with other substances. The incorporation of inert He tends to form open framework structures with weak interactions between He and the host sublattice. For example, our previous calculations predicted a HeN4 compound formed at high pressure42, which consists of open channels of N atoms holding He. Their weak interactions allow the removal of the He from the structure, leading to a pure t-N structure. Therefore, He may be regarded as a good intermediate for preparing new materials. A recent molecular dynamics (MD) simulation has demonstrated that Si and He react to form hP6-Si2He at 7 GPa and 1500 K53, which is a host–guest structure compared by a hexagonal diamond Si sublattice encapsulating He atoms. In addition, the scientists screened a series of stable potential photovoltaic Si phase by substituting other atoms, including He atom54. These results, especially for the t-N phase and Si24 obtained from high-pressure phases of HeN442 and Na4Si2434, respectively, give us a clear indication of the reaction between He and other substances and motivate us to study whether new Si allotropes could be formed from high pressure Si–He compounds.
This work reports extensive structure searches on Si2He which uncover four energetically favorable channel-like phases (oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He) in addition to hP6-Si2He53. The He atoms trapped inside the channels are easily removed from oP36-Si2He, tP9-Si2He, and mC12-Si2He to form oC24-Si, tP6-Si, and mC8-Si, respectively. Interestingly, oP36-Si2He and mC12-Si2He are direct-gap semiconductors with band gaps of 1.24 and 1.34 eV, respectively, proximately to the Shockley–Queisser limit (1.34 eV). In particular, mC12-Si2He has an electric dipole transition allowed direct band gap, making it a good candidate photovoltaic material.
Results
Crystal structure searches
Structure predictions are first performed for Si2He at 10 GPa with a maximum of eight formula units (f.u.) in a simulation cell. The previously proposed hP6-Si2He53 is successfully predicted, but with much higher enthalpy, as shown in Fig. 1. Instead, the four structures we predicted are energetically favorable than hP6-Si2He53. Crystal structures of four phases are shown in Fig. 2 and the lattice parameters of these structures are listed in the Supplementary Table 1. The four structures with increasing energy are oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He, namely ~0.13, ~0.08, ~0.05, and ~0.04 eV/f.u. energetically lower than hP6-Si2He53 at 10 GPa, respectively. We also calculate the related enthalpies of Si–He compounds as a functions of pressure by including different van der Vaals (vdW) functionals (optPBE-vdW, optB88-vdW, and DFT-D3)55,56, as shown in Supplementary Fig. 1. The results reveals that the vdW interaction almost has no influence in the phase transition sequence of Si2He. Static-lattice enthalpy calculations reveal that oP36-Si2He remains energetically most stable up to 18 GPa, above which hP6-Si2He53 takes over, see Fig. 1. A previous MD simulation suggests that hP6-Si2He53 could be formed at 7 GPa and 1500 K. Therefore, we examine the effect of temperature on the relative stability using the quasi-harmonic approximation and find that temperature does not change the phase diagram of Si2He, but rather postpones the transition pressure to 26 GPa at 1500 K. This result indicates that the predicted four phases are more favorable than hP6-Si2He in experimental synthesis at low pressures. The MD calculations also include vdW interactions.
Enthalpy of oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He relative to previously proposed hP6-Si2He53 as a function of pressure at 0 and 1500 K.
Structural configurations of predicted phases
All structures are channel frameworks composed of four coordination Si atoms and filled with He atoms in the voids, as shown in Fig. 2. The energetically most stable structure oP36-Si2He is orthorhombic with space group Pnnm (12 f.u. in a unit cell), as shown in Fig. 2a. The Si sublattice of oP36-Si2He along the a-axis shows a one-dimensional channel structure composed of ten-, six-, and five-membered rings. The Si–Si bond lengths are ranging from 2.28 to 2.33 Å, slightly shorter than that of hP6-Si2He (2.35 Å)53. Helium atoms are stacked in triangles in quasi-circular channels of ten membered rings (see Supplementary Fig. 2). The triclinic tP9-Si2He has a symmetry of P3212 (3 f.u. in a unit cell), as shown in Fig. 2b. The silicon atoms form a spiral staircase configuration with a six-membered circular channel, and the helium atoms are distributed in three vertical columns in the channel with the He–He distance of 2.34 Å. The mC18-Si2He phase is monoclinic with the symmetry of C2/m (6 f.u. in a unit cell). The Si atoms form six- and five-membered rings, and two six-membered rings are connected by two layers of five-membered rings dislocated and stacked along the c-axis, as shown in Fig. 2c. The Si–Si bond lengths are ranging from 2.30 to 2.37 Å. The He atoms form a tilted triangle arranged along the channel. The mC12-Si2He is monoclinic with space group C2/m (4 f.u. in a unit cell), as shown in Fig. 2d. Two kinds of channels sharing edges are found along the b-axis formed by five- or seven-membered rings of Si atoms. A zigzag arrangement of He atoms is located inside the larger channels formed by the seven-membered rings. The shortest distances between He and the Si channel in structures of oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He are 2.73, 2.56, 2.64, and 2.49 Å, respectively, which are shorter than the Na–Si distance (3.01 Å) in Na4Si2434. Similar host–guest structures have been reported in several other compounds, such as Na4Si2434 and HeN442. The previously proposed hP6-Si2He53 can also be regarded as a host–guest structure with a distorted diamond hexagonal host Si sublattice encapsulating guest He atoms inside the hexagonal channels. The lowest enthalpy of oP36-Si2He compared with hP6-Si2He suggests that Si can form larger channels for the incorporation of He. The dynamic stability of oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He at 10 and 0 GPa are confirmed by phonon dispersion calculations, as shown in Supplementary Figs. 4 and 5 (including the vdW interaction). The MD simulation (with the vdW interaction) reveals that all structures exhibit thermodynamic stability at ambient pressure and temperature (300 K), suggesting that all of them could be quenched and recovered at ambient conditions once formed (see Supplementary Fig. 6).
Charge transfer and CI-NEB energy barrier of silicides
Electron localization function calculations exclude the existence of Si–He covalent bonds in both compounds given the absence of electron localization between them (see Supplementary Fig. 3). Bader charge analysis57 suggests slight charge transfer from the Si framework to each He atom of (0.03 electrons in oP36-Si2He, 0.05 electrons in tP9-Si2He, 0.09 electrons in mC18-Si2He, and 0.05 electrons in mC12-Si2He), similar to those predicted in Na2He40 and FeO2He45. The weak interaction between the Si frameworks and He atoms provides a good priori condition for removal of the He from the structures, but the process can also be influenced by different Si frameworks. Therefore, we examine the energy barriers of He diffusing along the channels, see Fig. 3a. CI-NEB calculates energy barriers of 0.08, 0.01, 1.51, and 0.37 eV for oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He, respectively. We also checked the calculations with including vdW interaction, as shown in Supplementary Table 3. The vdW interaction has no effect on the energy barrier of all structures.The energy barriers of all structures except mC18-Si2He are much lower than that (0.74 eV) of Na4Si24 for removing Na34, see Fig. 3b and Supplementary Fig. 7 (with the vdW interaction), indicating comparatively easy removal of He atoms from oP36-Si2He, tP9-Si2He, and mC12-Si2He. For the mC18-Si2He, there exhibits a hexagonal channel structure both along a- and b-axis with a diameter of only about 3.9 Å and is much shorter than that of oP36-Si2He (6.4 Å), which induces a high energy barrier of 1.51 eV and indicates that He is difficult to be removed. This suggests that the structural configuration also plays a very important role in removing helium atoms.
a Migration pathways of He atoms from site A to site B along the channels in oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He. The shaded regions indicate the longitudinal section of the channels. b Energy barriers for He migration along the channels at zero pressure, as well as Na migration in Na4Si2434.
Figure 4a–c shows three pure Si structures obtained by removing He from oP36-Si2He, tP9-Si2He, and mC12-Si2He, denoted as oC24-Si, tP6-Si, and mC8-Si, respectively. Both Si allotropes retain Si frameworks nearly identical to those of the corresponding compounds. Phonon dispersion calculations confirm the stability of three allotropes (see Supplementary Fig. 4). A literature survey surprisingly found that these three Si structures have been previously predicted with much higher energies (~80 meV) than CD-Si21,58,59. Metastable structures with higher energies are generally difficult to synthesize directly. Here, we provide a potential chemical pathway for the synthesis these metastable Si allotropes, namely removing He atoms from pressure-stabilized Si–He compounds by thermal degassing.
Electronic and optical properties
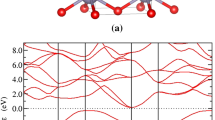
Photovoltaic materials require a suitable direct band gap to ensure a large overlap with the solar spectrum in the visible range, and thus strong solar absorption. Electronic band gaps of the compounds are calculated by using the HSE06 functional and the band structures are shown in Fig. 5. Although the HSE06 functional can well evaluate the band gaps, we still make a test of the Fock exchange percentage to check its accuracy with GW method60 and including vdW interaction. The comparisons are shown in Supplementary Tables 2 and 3. The results show that the original parameter of HSE06 (Fock exchange percentage in 0.25) can well evaluate the band gaps of our Si–He system. Take the cubic silicon as an example, the band gap of CD-Si is about 1.17 eV on experiment, our calculated value is about 1.18 eV (HSE06) and 1.14 eV (GW). While for mC12-Si2He, the band gap is about 1.34 eV in HSE06 and 1.26 eV in GW, respectively. So the band gap values obtained by using the HSE06 original parameter (Fock exchange percentage in 0.25) is reasonable. From Supplementary Fig. 3, we can see that when we include the vdW interaction, the electronic band gaps change a little. Take mC12-Si2He as an example, the band gap is about 1.35 eV (with the vdW interaction), while is 1.34 eV without considering vdW interaction. From our calculations (see Fig. 5), we can clearly find that tP9-Si2He and mC18-Si2He are indirect-gap semiconductors with indirect band gaps of 2.18 and 0.91 eV, respectively, which excludes the possibility of being good photovoltaic materials. Interestingly, oP36-Si2He and mC12-Si2He have direct band gaps of 1.24 and 1.34 eV, respectively, close to the Shockley–Queisser limit (1.34 eV), which indicate that they can be viewed as good potential photovoltaic materials. We also calculated the Si allotropes electronic band structure after the removal of He atoms in oP36-Si2He, tP9-Si2He, and mC12-Si2He (see Fig. 6). After removing the He atoms, the electronic band gaps of these Si allotropes decrease and degenerate from the direct band gaps to the indirect band gaps. As shown in Fig. 6, the band gap of oC24-Si can be viewed as a quasi-direct gap with a value of 0.95 eV, while for tP6-Si and mC8-Si are indirect with values of 2.12 and 0.84 eV, respectively. These results reveal that the incorporation of He benefits to forming the direct-gap semiconductor compounds for the Si–He system.
Electronic band structures of a oP36-Si2He, b tP9-Si2He, c mC18-Si2He, and d mC12-Si2He at 0 GPa calculated based on the HSE06 functional. Red solid and blue hollow circles represent the valence band maximum and conduction band minimum, respectively. The lower panels in each figure are the square of the transition dipole moment89.
To evaluate the sunlight absorption abilities of a direct band gap material, the imaginary parts of the dielectric constant of oP36-Si2He, mC12-Si2He and three silicon allotropes (oC24-Si, tP6-Si, and mC8-Si) were calculated by HSE06 functional, compared with that of CD-Si, as shown in Fig. 7. We also checked the results with the independent-quasiparticle approximation and solving the Bethe–Salpeter equation (BSE) to include excitonic and local-field effects61. The HSE06 results are in good agreement with that was obtained by GW + BSE method. The GW + BSE results are shown in Supplementary Fig. 8. The calculation results show that the absorption spectra of oP36-Si2He is slightly higher than that of mC12-Si2He and both have much better solar absorption capacities than the other three silicon allotropes and the CD-Si, as indicated by their broader overlap with the AM1.5 solar spectrum62. The optical absorption in oP36-Si2He and mC12-Si2He have an increasing trend at 1.2 and 1.4 eV, respectively. Another critical factor for a good photovoltaic material is a dipole-allowed direct transition. Therefore, further calculation of the square of the transition dipole moment (P2) explores the transition permissibility between the direct band gaps (see the lower panels in Figs. 5 and 6). The direct band gap of oP36-Si2He is located at Γ point in the first Brillouin zone, and the P2 at Γ point is close to 0, which indicates that oP36-Si2He is dipole-forbidden and same to the other three silicon allotropes (oC24-Si, tP6-Si, and mC8-Si). Instead, mC12-Si2He shows a dipole-allowed direct transition with large P2 value at the Γ point, suggesting good potential as a photovoltaic material.
Imaginary part of the dielectric functions of oP36-Si2He, mC12-Si2He, and the three silicon alltropes (oC24-Si, tP6-Si, and mC8-Si) calculated with the HSE06 functional, as well as the reference air mass 1.5 (AM1.5) solar spectral irradiance62 and CD-Si.
Other predicted Si–He compounds
To search for other possible Si–He compounds, structural predictions are also performed for Si3He and Si4He at 10 GPa using a maximum of 20 atoms in a simulation cell. Supplementary Fig. 9 summarizes the formation enthalpies of the stoichiometries with respect to decomposition into β-Sn Si and hcp He. Unfortunately, the formation enthalpy of all the Si–He compounds are positive. In fact, this does not completely rule out the possibility of experimental synthesis. A recent data mining study found that more than 60th percentile of the 0 K DFT-calculated metastability of all of the compounds within the Inorganic Crystal Structure Database was 150 meV/atom above the convex hull63. Actually, some silicon-contained compounds with high formation enthalpy have been successfully experimentally synthesized. For example, the theoretical calculated formation enthalpy of clathrate (type-I) I9.5Si46 is above convex hull 130 meV/atom, and SiB6 has the formation enthalpy of 289 meV/atom, both of which have been synthesized64,65,66,67. The crystal structures and electronic structures of Si3He and Si4He are shown in Supplementary Figs. 10–13. The formation enthalpies of Si3He and Si4He phases are both <130 meV/atom and they have direct band gap, which could be potential photovoltaic materials.
Discussion
He, which has two electrons, is the most chemically inert natural element, although several recent works have predicted or synthesized He-containing compounds42,53. Despite this, He can be regarded as chemically inert in Si–He, as the atoms are almost completely independent of the surrounding structure with negligible charge gained from Si. He appears to be chemically inert in all its known compounds (e.g., Na2He40 and HeN442), allowing it to be removed easily from the surrounding structure without changing the structure substantially. Interestingly, the incorporation of He in Si allotrope can form direct band gap semiconductors with the suitable band gaps, with the dipole-allowed direct band gap confirmed by mC12-Si2He. Therefore, He appears to be a good intermediate for designing potential functional materials.
In conclusion, through extensive structure searches of Si2He systems, we predict four dynamically stable phases (oP36-Si2He, tP9-Si2He, mC18-Si2He, and mC12-Si2He) with open framework structures comprising Si channels containing triangle or zigzag arrangements of He atoms. CI-NEB calculations reveal that the He atoms could be easily removed along the channels in them to leave the pure Si allotropes, oC24-Si, tP6-Si, and mC8-Si, respectively. oP36-Si2He and mC12-Si2He exhibit direct-gap semiconductive property, while others possess indirect band gaps. The dipole-allowed direct band gap of 1.34 eV in mC12-Si2He makes it a potential thin-film photovoltaic material. The current results demonstrate that He is an excellent element for regulating the properties of materials, as well as a good medium to synthesize functional materials.
Methods
Structural prediction and relaxation
Structure predictions for the Si–He system were performed using CALYPSO68,69, which has correctly predicted many stable compounds under high pressure70,71,72,73,74,75,76,77,78,79. The structural optimization and electronic and optical properties were calculated using density functional theory as implemented in the Vienna ab initio simulation package80, adopting the Perdew–Burke–Ernzerhof exchange-correlation functional under the generalized gradient approximation81,82.
Electronic and optical properties calculations
The Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional was employed to correct the electronic band structures83 and calculate the optical properties. We also make a test of the Fock exchange percentage to check its accuracy with GW method60 and the Fock exchange percentage is adopted the defaut value of 0.25. All electron projector augmented wave pseudopotentials with 1s2 and 3s23p2 valence configurations were chosen for He and Si atoms, respectively84. A plane wave cutoff energy of 800 eV and k-point mesh of 2π × 0.03 Å−1 were set to ensure total energy and forces convergence better than 1 meV/atom and 1 meV/Å, respectively. VASPKIT85 was used to resolve the results of the transition dipole moment and the optical absorption spectra (the imaginary part of the dielectric function, ε2). Specially, we have checked our calculations (structural relaxation, band gap calculation, MD, and CI-NEB) with including the vdW interactions56.
Phonon and CI-NEB energy barrier calculations
Phonon calculations were carried out using a supercell approach as implemented in PHONOPY code86. First-principles MD simulations using N (number of particles), V (volume), and T (temperature) were performed at 0 GPa and 300 K87. In total, 3 × 1 × 2 supercells for oP36-Si2He (216 atoms), 3 × 3 × 2 supercells for tP9-Si2He (162 atoms), 2 × 1 × 2 supercells for mC18-Si2He (144 atoms), and 1 × 3 × 2 supercells for mC12-Si2He (144 atoms) were employed. The migration barriers were calculated using the climbing image nudged elastic band (CI-NEB) method88 based on supercells containing one He atom and 48 host Si atoms for oP36-Si2He, tP9-Si2He, mC18-Si2He, mC12-Si2He, and Na4Si2434.
Data availability
The authors declare that the main data supporting the findings of this study are contained within the paper and its associated Supplementary Information. All other relevant data are available from the corresponding author upon reasonable request.
References
Peng, J., Lu, L. & Yang, H. Review on life cycle assessment of energy payback and greenhouse gas emission of solar photovoltaic systems. Renew. Sust. Energ. Rev. 19, 255–274 (2013).
Bhattacharya, T., Chakraborty, A. K. & Pal, K. Effects of ambient temperature and wind speed on performance of monocrystalline solar photovoltaic module in Tripura, India. J. Sol. Energy 2014, 1–5 (2014).
Tyagi, V., Rahim, N. A., Rahim, N., Jeyraj, A. & Selvaraj, L. Progress in solar PV technology: research and achievement. Renew. Sust. Energ. Rev. 20, 443–461 (2013).
El-Ghonemy, A. Photovoltaic solar energy: review. Int. J. Sci. Eng. Res. 3, 1–43 (2012).
Kazmerski, L. L. Solar photovoltaics R&D at the tipping point: a 2005 technology overview. J. Electron Spectrosc. Relat. Phenom. 150, 105–135 (2006).
Jelle, B. P., Breivik, C. & Røkenes, H. D. Building integrated photovoltaic products: a state-of-the-art review and future research opportunities. Sol. Energy Mater. Sol. Cells 100, 69–96 (2012).
Kannan, N. & Vakeesan, D. Solar energy for future world: a review. Renew. Sust. Energ. Rev. 62, 1092–1105 (2016).
Zhang, L., d’Avezac, M., Luo, J.-W. & Zunger, A. Genomic design of strong direct-gap optical transition in Si/Ge core/multishell nanowires. Nano Lett. 12, 984–991 (2012).
Walsh, A. et al. Nature of the band gap of In2O3 revealed by first-principles calculations and X-ray spectroscopy. Phys. Rev. Lett. 100, 167402 (2008).
Shockley, W. & Queisser, H. J. Detailed balance limit of efficiency of p−n junction solar cells. J. Appl. Phys. 32, 510–519 (1961).
Lautenschlager, P., Garriga, M., Vina, L. & Cardona, M. Temperature dependence of the dielectric function and interband critical points in silicon. Phys. Rev. B 36, 4821–4830 (1987).
Hybertsen, M. S. & Louie, S. G. First-principles theory of quasiparticles: calculation of band gaps in semiconductors and insulators. Phys. Rev. Lett. 55, 1418–1421 (1985).
Wentorf, R. & Kasper, J. Two new forms of silicon. Science 139, 338–339 (1963).
Zhao, Y.-X., Buehler, F., Sites, J. R. & Spain, I. L. New metastable phases of silicon. Solid State Commun. 59, 679–682 (1986).
Crain, J. et al. Reversible pressure-induced structural transitions between metastable phases of silicon. Phys. Rev. B 50, 13043–13046 (1994).
Rapp, L. et al. Experimental evidence of new tetragonal polymorphs of silicon formed through ultrafast laser-induced confined microexplosion. Nat. Commun. 6, 1–10 (2015).
Kurakevych, O. O. et al. Synthesis of bulk BC8 silicon allotrope by direct transformation and reduced-pressure chemical pathways. Inorg. Chem. 55, 8943–8950 (2016).
Zhang, H. et al. BC8 Silicon (Si-III) is a narrow-gap semiconductor. Phys. Rev. Lett. 118, 146601 (2017).
Wong, S. et al. Formation of an r8-dominant Si material. Phys. Rev. Lett. 122, 105701 (2019).
Huang, W.-Q., Huang, Z.-M., Liu, S.-R. & Peng, H.-Y. Synthesis of new Si9 material with a direct bandgap and its unique physical properties. Mater. Res. Express 6, 105905 (2019).
Wang, Q. et al. Direct band gap silicon allotropes. J. Am. Chem. Soc. 136, 9826–9829 (2014).
Xiang, H. J., Huang, B., Kan, E., Wei, S.-H. & Gong, X. G. Towards direct-gap silicon phases by the inverse band structure design approach. Phys. Rev. Lett. 110, 118702 (2013).
Lee, I.-H., Lee, J., Oh, Y. J., Kim, S. & Chang, K. J. Computational search for direct band gap silicon crystals. Phys. Rev. B 90, 115209 (2014).
Mujica, A., Pickard, C. J. & Needs, R. J. Low-energy tetrahedral polymorphs of carbon, silicon, and germanium. Phys. Rev. B 91, 214104 (2015).
Malone, B. D., Louie, S. G. & Cohen, M. L. Electronic and optical properties of body-centered-tetragonal Si and Ge. Phys. Rev. B 81, 115201 (2010).
Wu, F., Jun, D., Kan, E. & Li, Z. Density functional predictions of new silicon allotropes: electronic properties and potential applications to Li-battery anode materials. Solid State Commun. 151, 1228–1230 (2011).
He, C. et al. Direct and quasi-direct band gap silicon allotropes with remarkable stability. Phys. Chem. Chem. Phys. 18, 9682–9686 (2016).
He, C. et al. Complex low energy tetrahedral polymorphs of group IV elements from first principles. Phys. Rev. Lett. 121, 175701 (2018).
Wei, Q., Tong, W., Wei, B., Zhang, M. & Peng, X. Six new silicon phases with direct band gaps. Phys. Chem. Chem. Phys. 21, 19963–19968 (2019).
Oreshonkov, A., Roginskii, E. & Atuchin, V. New candidate to reach Shockley–Queisser limit: the DFT study of orthorhombic silicon allotrope Si (oP32). J. Phys. Chem. Solids 137, 109219 (2020).
Botti, S., Flores-Livas, J. A., Amsler, M., Goedecker, S. & Marques, M. A. L. Low-energy silicon allotropes with strong absorption in the visible for photovoltaic applications. Phys. Rev. B 86, 121204(R) (2012).
Amsler, M., Botti, S., Marques, M. A. L., Lenosky, T. J. & Goedecker, S. Low-density silicon allotropes for photovoltaic applications. Phys. Rev. B 92, 014101 (2015).
Gryko, J. et al. Low-density framework form of crystalline silicon with a wide optical band gap. Phys. Rev. B 62, R7707–R7710 (2000).
Kim, D. Y., Stefanoski, S., Kurakevych, O. O. & Strobel, T. A. Synthesis of an open-framework allotrope of silicon. Nat. Mater. 14, 169–173 (2015).
Rödl, C. et al. Wurtzite silicon as a potential absorber in photovoltaics: tailoring the optical absorption by applying strain. Phys. Rev. B 92, 045207 (2015).
Vincent, L. et al. Shear-driven phase transformation in silicon nanowires. Nanotechnology 29, 125601 (2018).
Dixit, S. & Shukla, A. Optical properties of lonsdaleite silicon nanowires: a promising material for optoelectronic applications. J. Appl. Phys. 123, 224301 (2018).
Rodichkina, S. et al. Photo-induced cubic-to-hexagonal polytype transition in silicon nanowires. CrystEngComm 21, 4747–4752 (2019).
Tizei, L. H. G. & Amato, M. Electronic structure and optical properties of semiconductor nanowires polytypes. Eur. Phys. J. B 93, 16 (2020).
Dong, X. et al. A stable compound of helium and sodium at high pressure. Nat. Chem. 9, 440–445 (2017).
Loubeyre, P., Jean-Louis, M., LeToullec, R. & Charon-Gérard, L. High pressure measurements of the He-Ne binary phase diagram at 296 K: evidence for the stability of a stoichiometric NeHe2 solid. Phys. Rev. Lett. 70, 178 (1993).
Li, Y. et al. Route to high-energy density polymeric nitrogen t-N via He-N compounds. Nat. Commun. 9, 1–7 (2018).
Gao, H., Sun, J., Pickard, C. J. & Needs, R. J. Prediction of pressure-induced stabilization of noble-gas-atom compounds with alkali oxides and alkali sulfides. Phys. Rev. Mater. 3, 015002 (2019).
Monserrat, B., Martinez-Canales, M., Needs, R. J. & Pickard, C. J. Helium-iron compounds at terapascal pressures. Phys. Rev. Lett. 121, 015301 (2018).
Zhang, J. et al. Rare helium-bearing compound FeO2He stabilized at deep-earth conditions. Phys. Rev. Lett. 121, 255703 (2018).
Liu, Z. et al. Reactivity of He with ionic compounds under high pressure. Nat. Commun. 9, 1–10 (2018).
Liu, H., Yao, Y. & Klug, D. D. Stable structures of He and H2O at high pressure. Phys. Rev. B 91, 014102 (2015).
Liu, C. et al. Multiple superionic states in helium–water compounds. Nat. Phys. 15, 1065–1070 (2019).
Gao, H. et al. Coexistence of plastic and partially diffusive phases in a helium-methane compound. Natl. Sci. Rev. 7, 1540–1547 (2020).
Bai, Y. et al. Electrostatic force driven helium insertion into ammonia and water crystals under pressure. Commun. Chem. 2, 1–7 (2019).
Liu, C. et al. Plastic and superionic helium ammonia compounds under high pressure and high temperature. Phys. Rev. X 10, 021007 (2020).
Shi, J. et al. Formation of ammonia–helium compounds at high pressure. Nat. Commun. 11, 1–7 (2020).
Bi, Y., Xu, E., Strobel, T. A. & Li, T. Formation of inclusion type silicon phases induced by inert gases. Commun. Chem. 1, 1–9 (2018).
Sluydts, M., Pieters, M., Vanhellemont, J., Van Speybroeck, V. & Cottenier, S. High-throughput screening of extrinsic point defect properties in Si and Ge: database and applications. Chem. Mater. 29, 975–984 (2017).
Klimeš, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys.: Condens. Matter 22, 022201 (2009).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Henkelman, G., Arnaldsson, A. & Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 36, 354–360 (2006).
Von Schnering, H.-G., Schwarz, M. & Nesper, R. The lithium sodium silicide Li3NaSi6 and the formation of allo-silicon. J. Less Common Met. 137, 297–310 (1988).
Pickard, C. J. & Needs, R. Hypothetical low-energy chiral framework structure of group 14 elements. Phys. Rev. B 81, 014106 (2010).
Hedin, L. New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 139, A796 (1965).
Onida, G., Reining, L. & Rubio, A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601 (2002).
ASTM Standard G173-03(2008). Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37° Tilted Surface (ASTM International, 2008).
Sun, W. et al. The thermodynamic scale of inorganic crystalline metastability. Sci. Adv. 2, e1600225 (2016).
Vlasse, M., Slack, G., Garbauskas, M., Kasper, J. & Viala, J. The crystal structure of SiB6. J. Solid State Chem. 63, 31–45 (1986).
Yuan, Z., Xiong, M. & Yu, D. A novel metallic silicon hexaboride, Cmca-B6Si. Phys. Lett. A 384, 126075 (2020).
Reny, E., Yamanaka, S., Cros, C. & Pouchard, M. High pressure synthesis of an iodine doped silicon clathrate compound. Chem. Commun. 24, 2505–2506 (2000).
Cerqueira, T. F. et al. Prediction and synthesis of a non-zintl silicon clathrate. Chem. Mater. 28, 3711–3717 (2016).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. CALYPSO: a method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Zhu, L., Liu, H., Pickard, C. J., Zou, G. & Ma, Y. Reactions of xenon with iron and nickel are predicted in the Earth’s inner core. Nat. Chem. 6, 644 (2014).
Li, Y., Hao, J., Liu, H., Li, Y. & Ma, Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 140, 174712 (2014).
Li, Y., Hao, J., Liu, H., Lu, S. & Tse, J. S. High-energy density and superhard nitrogen-rich B-N compounds. Phys. Rev. Lett. 115, 105502 (2015).
Li, Y. et al. Metallic icosahedron phase of sodium at terapascal pressures. Phys. Rev. Lett. 114, 125501 (2015).
Li, Y. et al. Dissociation products and structures of solid H2S at strong compression. Phys. Rev. B 93, 020103(R) (2016).
Cui, W. & Li, Y. The role of CALYPSO in the discovery of high-Tc hydrogen-rich superconductors. Chin. Phys. B 28, 107104 (2019).
Liu, B. et al. Effect of covalent bonding on the superconducting critical temperature of the H-S-Se system. Phys. Rev. B 98, 174101 (2018).
Xu, M. et al. Electrical control of magnetic phase transition in a type-I multiferroic double-metal trihalide monolayer. Phys. Rev. Lett. 124, 067602 (2020).
Cui, W. et al. Route to high-Tc superconductivity via CH4-intercalated H3S hydride perovskites. Phys. Rev. B 101, 134504 (2020).
Shi, J., Cui, W., Botti, S. & Marques, M. A. L. Nitrogen-hydrogen-oxygen ternary phase diagram: new phases at high pressure from structural prediction. Phys. Rev. Mater. 2, 023604 (2018).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Perdew, J. P. et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46, 6671–6687 (1992).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Wang, V., Xu, N., Liu, J. C., Tang, G. & Geng, W.-T. VASPKIT: a user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 108033, https://doi.org/10.1016/j.cpc.2021.108033. (2021). Inpress.
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984).
Henkelman, G., Uberuaga, B. P. & Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Meng, W. et al. Parity-forbidden transitions and their impact on the optical absorption properties of lead-free metal halide perovskites and double perovskites. J. Phys. Chem. Lett. 8, 2999–3007 (2017).
Acknowledgements
The authors acknowledge funding from the NSFC under grants Nos. 12074154, 11804129, 11722433, and 11804128, and the funding from the Science and Technology Project of Xuzhou under grant No. KC19010. Y.L. acknowledges the funding from the Six Talent Peaks Project and 333 High-level Talents Project of Jiangsu Province. S.D. acknowledges the founding from Postgraduate Research and Practice Innovation Program of Jiangsu Province No. KYCX20_2223. All the calculations were performed at the High Performance Computing Center of the School of Physics and Electronic Engineering of Jiangsu Normal University.
Author information
Authors and Affiliations
Contributions
J.S. and Y.L. designed the project. S.D. and J.S. performed the calculations. S.D., J.S., J.X., W.C., P.Z., K.Y., J.H., L.Z. and Y.L. analyzed the data. S.D., J.S., W.C. and Y.L. wrote the paper. All the authors checked the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ding, S., Shi, J., Xie, J. et al. Helium incorporation induced direct-gap silicides. npj Comput Mater 7, 89 (2021). https://doi.org/10.1038/s41524-021-00558-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00558-w