Abstract
Metal additive manufacturing provides remarkable flexibility in geometry and component design, but localized heating/cooling heterogeneity leads to spatial variations of as-built mechanical properties, significantly complicating the materials design process. To this end, we develop a mechanistic data-driven framework integrating wavelet transforms and convolutional neural networks to predict location-dependent mechanical properties over fabricated parts based on process-induced temperature sequences, i.e., thermal histories. The framework enables multiresolution analysis and importance analysis to reveal dominant mechanistic features underlying the additive manufacturing process, such as critical temperature ranges and fundamental thermal frequencies. We systematically compare the developed approach with other machine learning methods. The results demonstrate that the developed approach achieves reasonably good predictive capability using a small amount of noisy experimental data. It provides a concrete foundation for a revolutionary methodology that predicts spatial and temporal evolution of mechanical properties leveraging domain-specific knowledge and cutting-edge machine and deep learning technologies.
Similar content being viewed by others
Introduction
Additive manufacturing (AM), sometimes called three-dimensional (3D) printing, is a rapidly growing advanced manufacturing paradigm that promises unparalleled flexibility in the production of metal or non-metal parts with complex geometries. However, the nature of the process creates position-dependent microstructures, residual stresses, and mechanical properties that complicate printing process design, part qualification, and manufacturing certification. Metal additive manufacturing, such as laser powder bed fusion (L-PBF) and directed energy deposition (DED), have most of the relevant physical processes occurring in the vicinity of the melt pool. This region is where a laser melts an alloy powder feedstock material that then solidifies with cooling rates up to 107 K/s1. The laser rapidly heats the metal causing localized melting and vaporization. The melt pool surface extends behind the moving laser producing large thermal gradients with corresponding variations in surface tension, that may produce turbulence within the melt pool through the Marangoni effect. During rapid solidification, dendritic growth with micro-segregation of the alloy constituents can produce non-equilibrium phases and anisotropic grain morphologies that strongly affect the local component properties and performances. These multiscale and multiphysics phenomena involve interactions and dependencies of a large number of process parameters and material properties leading to complex process-structure-properties (PSP) relationships2. Tremendous effort has been directed at conducting in/ex-situ experimental characterization3,4,5,6,7,8 and physics-based modeling9,10,11,12,13,14,15 to understand the effects of process conditions on microstructure and mechanical properties. This allows for the creation of defect-free materials with favorable microstructure and performance. The prediction of as-built mechanical properties (e.g., ultimate tensile strength (UTS)) remains very challenging because of the multiphysics involved, such as thermal-fluid dynamics, laser-powder interactions, phase transformation, and fracture and damage mechanics. Several governing equations have been proposed16,17,18, but extremely high complexity and associated high computational cost (upwards of a month for each printing condition) limits the potential industrial applications of these mechanistic models.
In recent years, many researchers have explored data-driven methods and machine learning for AM and other manufacturing processes19,20. Popova et al.21 developed a data-driven surrogate model to correlate process parameters with complex grain structure inherently produced by AM process. The Potts-kinetic Monte Carlo (kMC) approach22 was used to create process-structure datasets. Du et al.23 developed a decision tree and a Bayesian neural network to classify conditions for void formation in friction stir welding. Li et al.24 proposed a functional Gaussian process-based surrogate model from finite element simulations and thermal imaging data for temperature field prediction. Zhang et al.25 employed neural networks to represent nonlinear relationships between powder spreading parameters. Optimized spreader parameters can be determined based on the networks to save the total time for printing. Gan et al.26 used self-organizing map (SOM) to visualize high-dimensional datasets generated by experiments and simulations. Optimized process parameters that determine desired mechanical properties can be obtained from the SOMs. Lu et al.27 created an adaptive reduced-order model for AM thermal fluid analysis. Recently, Wang et al.28 proposed a data-driven framework based on high-throughput AM simulations and AM benchmark experiments10. They developed a Bayesian calibration approach to calibrate experimental parameters and correct the model, which improves the validity of the surrogate model. A few authors focused on real-time models for defect identification during the AM process. Scime and Beuth et al.29 combined computer vision techniques and unsupervised machine learning to identify flaw formation based on in-situ melt pool images captured by a visible-light high-speed camera. Zhang et al.30,31 designed a convolutional neural network (CNN) model to recognize patterns in melt pool images to predict porosity.
Elucidating the effect of process conditions, such as process parameters and temperature history, on resulting mechanical properties is a central goal in advanced manufacturing and material science1,2. Traditionally in metal additive manufacturing, some thermal-related factors like solidification cooling rate and solid cooling rate, are computed based on local derivatives of the thermal history13. These cooling rates are used to correlate and predict microstructure and mechanical proprieties10,32. However, those arbitrarily extracted factors lose much of the information involved in the complex thermal histories. Machine learning algorithms allow us to use and manipulate the whole thermal histories for regression and reveal dominant thermal-related features purely from data.
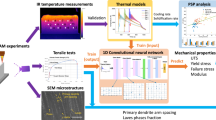
The state-of-the-art data-driven models mentioned above focused on the optimization of process parameters. At the same time, these models ignored the variability of thermal history and mechanical properties within the as-built parts caused by location-dependent melting/solidification behaviors and scanning toolpaths. In this study, we provide a systematic study on predicting mechanical property distributions over as-built additively manufactured parts based on location-dependent thermal histories. The study consists of several parts, which are outlined in Fig. 1. Infrared (IR) thermographic measurements are made of multiple thin wall parts fabricated using a DED AM process. Time-temperature thermographic data (i.e., thermal histories) from 135 select regions-of-interest (ROIs) are transformed to wavelet-based scalograms, which are related to the DED processing dynamics. A CNN is then mapped the wavelet scalograms to mechanical properties. We call this mechanistic data-driven approach using CNN with wavelet transform as WT_CNN. The mechanical properties obtained from miniature tensile specimens, with the gauge region nominally aligned with the 135 ROIs. This trained model is then used to predict mechanical properties at other spatial locations (5000 per wall) throughout the DED-fabricated thin walls, where tensile specimens are not obtained, but IR thermographic data is obtained. This is the path 1 of this study, i.e., predictive relationship, shown in Fig. 1. The mechanical properties of interest include ultimate tensile strength (UTS), yield strength, and elongation. It is noted that predicting UTS using physics-based models remains challenging due to the complexity of fracture and damage mechanics. This makes the UTS a good quantity of interest for demonstrating the data-driven modeling. Additionally, a feature/parameter is developed using the thermal history measured via IR thermography, that is based on accumulated occurrence of temperature data within discrete temperature ranges within a thermal history data. A Random forest (RF) algorithm is then applied to relate this parameter to mechanical properties such as UTS, and identify which temperature range(s) has greatest importance. These identified temperature ranges are then related to material phase transition temperatures and measured dendritic arm spacing. This is the path 2, i.e., importance analysis, shown in Fig. 1. The proposed approach is then compared with machine learning methods (including Regression Tree33, Random Forest33, Gradient Boosting Regression34, etc.) to confirm its effectiveness given a small amount of noisy experimental data for model training.
The proposed framework includes two modeling paths for different objectives but share the same experimental data. The path 1 is designed to correlate and predict mechanical properties based on process-induced thermal histories. It links thermal histories, multiresolution analysis based on wavelet transforms, a convolutional neural network (CNN), and ultimate tensile strength (UTS) predictions. The path 2 is designed to identify dominant mechanistic features from the dataset. It links thermal histories, importance analysis of thermal features, and UTS at regions-of-interest.
Results
Predictive relationships between thermal histories and mechanical properties
We proposed a data-driven supervised learning approach to capture complex nonlinear mapping between local thermal history and as-built mechanical properties such as UTS. We extracted 12 sets of thermal histories by IR in-situ measurements for twelve additively manufactured thin walls. Five thousand thermal histories were extracted from 5000 uniformly spaced measurement locations (see Supplementary Fig. 9) of each wall. Each thin wall was built using a single track and multilayer laser DED process. Experimental additive manufacturing details are provided in “Directed energy deposition” section. We cut 135 specimens for mechanical tensile tests at predetermined regions-of-interest (ROIs). The definition of the ROIs is shown in Supplementary Fig. 8. We used 135 thermal histories extracted from the center of the ROIs as input and corresponding 135 UTS measurements as labeled output for the proposed data-driven model. Detailed information for thermal history extraction is provided in “Infrared (IR) thermal measurement and calibration” section and for mechanical tensile tests is provided in “Microstructure and mechanical properties characterization” section. All the thermal histories (5000 per wall) were then used as input of trained data-driven model to predict 2D high-resolution UTS maps for each thin wall fabricated by a specific process condition.
To extract mechanistic meanings of the thermal histories and improve predictive capability of the model given a small amount of noisy data, we transformed the high-dimensional thermal histories into time-frequency scalograms using wavelet transforms. A CNN was developed for capturing the complex relationships between the process-induced wavelet scalograms and resulting as-built mechanical properties such as UTS. The CNN structure and training details are provided in “Convolutional neural networks” section. This mapping assumes that the as-built mechanical properties of additively manufactured material at a specific spatial location highly depends on the process-induced thermal history at this location. This assumption is plausible because many researchers have reported that the thermal-related factors, such as cooling rate during solidification or solid-state phase transformation significantly impact microstructure and resulting mechanical properties32,35,36.
To clearly describe our methods and results, we define/describe important terminologies as follow:
-
As-built thin wall: A DED-manufactured part built by a single track and multilayer process.
-
Thermal history: A temperature sequence with different time at a specific thermal measurement location.
-
Thermal measurement location: A location at a thin wall where a thermal history is extracted.
-
A set of thermal histories: A collection of thermal histories for a thin wall.
-
Region-of-interest (ROI): A predetermined region of a thin wall. Gauge region of a tensile specimen is nominally aligned with the ROI.
-
Tensile specimen: A specimen for mechanical tensile tests.
-
Data point: A thermal history and corresponding mechanical properties extracted from a thermal measurement location. A collection of data points constructs the dataset for model training.
-
Image: A wavelet scalogram, which is the input of the CNN model.
Five CNN models for UTS predictions were trained to reduce the variance of model predictions. The mean value of the predictions is used as the final predictions, while the standard deviation is used to analyze the variance of predictions.
Once five CNN models for UTS were trained and tested, 5000 thermal histories at different thermal measurement locations (where tensile specimens are not necessarily obtained) were used as inputs of trained models to predict a 2D UTS map for each thin wall. Detailed information for the extraction of 5000 thermal histories is provided (see Supplementary Fig. 9). Figure 2 shows the predicted UTS maps for three process conditions by averaging five CNN outputs. The three UTS maps on the left denote the original average outputs of the CNN models and the three maps on the right are the associated locally averaged results for clearly demonstrating the spatial variation of the UTS distribution. The two maps in the first-row are associated with the AM process without intentional dwell process and melt pool control. The two maps at the second-row are associated with the AM process with 5 s dwell time between layers but without melt pool control. The third-row maps are associated with the AM process without dwell time but with melt pool control (see “Directed energy deposition” section for more details). The CNN predicted UTS (in black) and experimental values (in red) at ROIs are marked in Fig. 2 as well. The proposed data-driven approach can predict the UTS very well as compared with the experimental measurements. More quantitative comparisons will be conducted in “Comparison with classical machine learning methods” section.
Several interesting trends can be clearly visualized from the UTS maps. First, fabricated parts with 5 s dwell time generally have higher UTS than the parts without dwell time. Second, as-built material at two sides of the wall has higher UTS than that in the middle or at the top. Third, using melt pool control slightly increases the spatial variance of UTS within the part, which can be seen from Supplementary Fig. 5. The UTS distribution over as-built thin wall #10 (with melt pool control) has a wider range than that over as-built thin wall #4 (without melt pool control). Those effects result from the process-induced thermal histories and can be interpreted using multiresolution analysis in the following sections (“Mechanistic insights from wavelet transforms of thermal histories” section and “Importance of thermal features on mechanical properties” section).
Statistical analysis of model predictions is useful to analyze and illustrate uncertainties in the data-driven model. Figure 3 shows the standard deviation distributions for three as-built thin walls. Three sub-figures on the left side are location-dependent maps of standard deviation (MPa) for three process conditions. The sub-figures on the right side are corresponding statistical distributions. As compared to wall #4 (without dwell time and melt pool control) and wall #10 (with melt pool control), wall #7 (with 5 s dwell time) have higher standard deviations. The standard deviations at two sides of the walls are higher than those at the center because most of the labeled thermal histories (i.e., training data) are located at the center of the walls.
The predicted UTS results are obtained by averaging five CNN outputs. The process conditions include 120 mm wall without any dwell time and melt pool control, 120 mm wall with 5 s dwell time, and 120 mm wall with melt pool control. The positions of tensile specimens are marked as black dots on the left side of sub-figures. Three sub-figures on the right side show the standard deviation distribution for three process conditions. The distribution analyzes 5000 predicted UTS values at different locations of the thin wall.
We emphasize that the proposed data-driven model is flexible and can be easily extended for predicting other mechanical properties by changing the labeled outputs. Predictions of yield stress and elongation are provided in the Supplementary Information. Figure 4 presents the correlation matrix of mechanical properties. UTS is positively correlative with yield stress and failure stress, but negatively correlative with elongation. These results align with the strength-ductility trade-off37 in material science, i.e., most metallurgical mechanisms for increasing strength leads to ductility loss. The correlation matrix of mechanical properties helps to quantify the strength-ductility trade-off, which benefits the design of high-performance additively manufactured materials.
Pearson correlation coefficient defined in ref. 56 is used to quantify the correlation between properties.
Mechanistic insights from wavelet transforms of thermal histories
Feature engineering was performed by applying wavelet analysis on the experimental time-temperature histories (i.e., thermal histories). Details of the technique are given in “Wavelet transform” section. Underlying mechanistic information can be revealed by wavelet transformed time-frequency maps (i.e., wavelet scalograms). Figure 5 presents a case, where we consider the wall without dwell time and converted the time-temperature histories at different thermal measurement locations into time-frequency maps (wavelet scalograms) using wavelet transform. Thermal histories vary depending on the thermal measurement location on the wall38. For example, at the top-left of the wall (thermal measurement location 1 in Fig. 5), the thermal history shows dual peaks. This happens because the thermal measurement location is slight to the left, and the location does not get sufficient cooling time before being reheated again. The heating–cooling cycles are manifested as periodic in nature in the time-temperature history. The time-temperature history from the bottom-right of the wall (thermal measurement location 2 in Fig. 5) has a shorter period for heating–reheating as the location is near the corner. If we compare the wavelet scalograms of both locations, the wavelet scalogram for the location from the bottom-right of the wall shows comparatively more high frequencies. Both of these plots have a common fundamental frequency of approximately 0.1 Hz. This frequency is related to the scan speed of the AM process. Solidification cooling time (SCT) differs in these two cases as well, with the bottom-right of the wall seeing a smaller SCT. The SCT is defined as the time interval between the start and the end of solidification. It can be computed based on the thermal history, material solidus temperature (i.e., 1260 °C39) and liquidus temperature (1336 °C39). Detailed computation procedure of the SCT is provided in the literature38. Smaller SCT means higher cooling rates, which results in finer dendrite arms10 and increased volume fraction of \({\gamma }^{\prime}\) or γ″40. This results in a strengthening of Inconel 718. This explains the fact that the UTS of thermal measurement location 2 (side of the wall) is higher than that of thermal measurement location 1 (middle of the wall). Wavelet analysis is essentially a multiresolution analysis. As a consequence, signals from multiple time-scales are captured by the wavelets. For example, for thermal measurement location 2, there is a presence of both low and high frequencies. This can be interpreted as a result of the fluctuation of the melt pool near the edge of the wall. At the thermal measurement locations near two sides of the wall, the gap between two subsequent cycles of heating and cooling is not even. For thermal measurement location 2, when the laser is traveling to the right of the wall and comes back, the material at this location is reheated almost immediately after heating. However, the next heating cycle takes some time to travel to the left and then come back. These nuances affect the thermal field at multiple scales, with changes in the shape of the melt pool occurring at the scale of microseconds.
Similar trends are also observed in Fig. 6 where the process has a 5 s dwell time. For a fair comparison, we consider two thermal measurement locations with the same locations as the previous case. It is observed that for 5 s dwell time, the fundamental frequency coming from the scan speed remains. However, in general, the signature of higher frequency signals have increased. A general trend of higher frequency signatures can be observed. The SCT is smaller compared to the no dwell time case for both locations. Consequently, there are higher values of UTS. Because of the dwell time, all the peaks and valleys in time-temperature histories are very well developed. This is manifested in the high-frequency signature in wavelet figures.
Figure 7 presents a comparison of the wavelet transforms with and without melt pool control. The results in Fig. 7a–c are for without melt pool control and the results in Fig. 7d–f are with melt pool control. It is obvious from the time-temperature histories of these two cases that when melt pool control is applied the thermal history has fluctuations. These fluctuations come from the continuous adjustments of laser power. These adjustments are reflected in wavelet transforms as more frequency signatures can be observed when the melt pool is controlled. As with the other cases, the fundamental frequency is present here too. The consequence of controlling laser power is translated into a local variation of the mechanical properties such as UTS. It is difficult to capture these nuances by directly using the time-temperature history for the machine learning model input since very high data resolution is required. Wavelet transformed time-frequency map serves the purpose with information available at multiple time scales.
In melt pool control mode DED, laser power is adjusted frequently to stabilize melt pool size, which however might lead to local fluctuation of thermal history and resulting mechanical properties. This work demonstrates this effect clearly using machine learning approach. The first row for a–c shows the results for the right bottom of wall #4 (without melt pool control). a A 200 s thermal history, b a sub-range thermal history ranging from 0 s to 25 s, c the wavelet scalogram of the 200 s thermal history. The second row for d–f shows the results for the right bottom of wall #10 (with melt pool control). d A 200 s thermal history, e a sub-range thermal history ranging from 0 to 25 s, f the wavelet scalogram of the 200 s thermal history.
Importance of thermal features on mechanical properties
To identify the relative importance of temperature range(s) for a specific mechanical property such as UTS, we reduced each high-dimensional thermal history into a low-dimensional vector. Each component of the vector represents the time that the material point spends at a specific temperature range with about 50.88 °C interval (details of this approach are provided in “Dimension reduction by Discrete Binning (DB)” section). The thermal history represented by a low-dimensional vector was mapped to associated UTS using the RF method, which inherently enables importance analysis (the detailed algorithm is provided in “Random forest and feature importance analysis” section).
Figure 8 shows the calculated relative importance of temperature intervals on UTS. Each statistical bar indicates the relative importance of a temperature range between the value on the x-axis and that value plus 50.88 °C. The sum of all the values of relative importance equals one. Our analysis identifies two dominant temperature ranges: 1212.99–1365.35 °C and 654.32–857.47 °C. The first temperature range is very close to the solidus and liquidus temperatures of the material used in the study (Inconel 718), i.e., 1260–1336 °C39. The symbol t1314.56 indicates the time that a material point spends at temperature range between 1314.56–1365.35 °C and t806.68 indicates the time that a material point spends at temperature range between 806.68–857.47 °C. They have high relative importance values as shown in Fig. 8. Our experimental measurements support the importance analysis. Scanning electron microscope (SEM) results extracted from three different as-built thin walls are presented in Fig. 9. Corresponding t1314.56, measured primary dendrite arm spacing (PDAS) and UTS are listed at the bottom of the figure. Since the temperature range indicated in the t1314.56 (i.e., 1314.56–1365.35 °C) is close to the material solidification temperature range (i.e., 1260–1336 °C), a lower t1314.56 as shown in Fig. 9a implies a higher solidification cooling rate. A higher solidification cooling rate leads to a smaller PDAS and thus a higher UTS, which aligns with many other reported experimental data10,41. The second important temperature range identified, 654.32–857.47 °C, is assumed to be related to precipitate formation during solid-state transformation. It aligns with the formation temperature of \(\gamma ^{\prime}\) and γ″ phases (649–760 °C) in the literature40,42. The first dominant temperature range is more important than the second one. For example, the mean of the relative importance for t806.68 is around 0.14, while the mean of the relative importance for t1314.56 is only slightly more than 0.09.
We randomly split the total dataset 150 times to obtain statistical bars for the relative importance spectrum, including maximum, third quartile, median, first quartile, and minimum. Each statistical bar indicates the relative importance of a temperature range between the value on the x-axis and that value plus the temperature interval (50.88 °C).
Three specimens were cut from the similar ROI of different as-built thin walls. The value of t1314.56, measured primary dendrite arm spacing (PDAS) and ultimate tensile strength (UTS) are listed at the bottom. a specimen from wall #9:120 mm in length with 5 s dwell time, b specimen from wall #10:120 mm in length without dwell time with melt pool control, c specimen from wall #1:80 mm in length without dwell time. Detailed experimental setup is provided in “Directed energy deposition” section. Credit: Jennifer Glerum.
In this study, the important temperature ranges are identified purely from experimental data without a prior knowledge of process conditions or governing equations. The identified dominant temperature ranges will benefit process-structure-properties quantification and materials design. This study demonstrates a new possibility to discover dominant features of process conditions and quantify their effects on mechanical properties by leveraging machine learning. It can be applied to not only additive manufacturing but broader areas of advanced manufacturing and material design.
Comparison with classical machine learning methods
We compared the proposed WT_CNN model with several classical machine learning methods. We confirmed that our proposed approach has the best predictive capability given the small amount of experimental data with uncertainty. Figure 10 presents the comparisons based on four metrics: coefficient of determination (R2), mean squared error (MSE), mean relative error (MRE), and mean absolute error (MAE)43. Definitions of those metrics are shown in the figure, where n is the number of the dataset, yi is the value of ith data in the dataset, \({\hat{y}}_{{\rm{i}}}\) is the model prediction of ith data, and \(\bar{y}\) is the mean of the data points in the dataset. We distinguished metrics computed using data points in training, validation, and test sets. Ten candidate models are compared as shown in Fig. 10. by using the same training, validation, and test set for the model comparison. A red line profiles the value of the metric for the test set in each sub-figure because it exhibits the predictive performance of each model. The error bars show the standard deviation for each metric based on five trained models, which come from 5-fold cross-validation. The proposed WT_CNN approach achieves the highest R2 score (0.7) and lowest errors including MSE, MRE, and MAE as compared with other models, which exhibits a great predictive capability of the proposed approach given such a small amount of available data.
The error bars indicate the standard deviations of the five model results based on 5-fold cross-validation. Name of a model includes two parts separated by an underline. The first part indicates the method used for reducing the dimension of the input (thermal history). The method includes Discrete Binning (DB) (“Dimension reduction by Discrete Binning (DB)” section), PCA, and WT (“Wavelet transform” section). The second part indicates the regression method including Regression Tree (RT)33, Feed-forward Neural Network (FNN)57, Lasso58, Bayesian Ridge Regression (BRR)59, Gradient Boosting Regression (GBR)34, K-Nearest Neighbors (KNN)60, Random Forest (RF)33,61, and CNN62. a Coefficient of determination (R2), b mean squared error (MSE), c mean relative error (MRE), d mean absolute error (MAE).
The values of R2 are not close to 1 because of noisy experimental data and uncertainties in the models. Supplementary Fig. 6 shows the Bayesian Ridge Regression (BRR) result that includes predictions of mean and standard deviation (SD). Experimental data points are also marked for comparison. The results clearly present the uncertainty in the experimentally measured UTS. The Bayesian method can approximate the range of uncertainty, which is useful for model section and evaluation.
Discussion
Previous researchers have explored machine learning for additive manufacturing of metals, but machine and deep learning to predict as-built mechanical properties using basic IR thermal history measurements has not been studied. It is valuable to predict the mechanical property variability within a part to evaluate the weakest position and improve the final performance of additively manufactured materials. We’ve also demonstrated that meaningful mechanistic features, like critical temperature ranges or critical frequencies, can be extracted using the data-driven approach. This provides an alternative way to identify dominant process conditions for a new material system.
The presented method embeds multiresolution analysis of thermal histories for mechanistic feature extraction, which can reduce the amount of data required in training for achieving reasonably good performance. The challenges of using a data-driven approach for the prediction include data uncertainty in thermal histories and mechanical properties, risk of overfitting, and non-optimal learning models and parameters. This study demonstrated the use of IR measurements of thermal images as the input of supervised learning, which provides a solid foundation on not only the prediction of mechanical properties from process-induced thermal histories but also the real-time control of microstructure and mechanical properties during additive manufacturing process.
We provide two reasons for the better performance of the WT_CNN model compared with other machine learning methods. (1) Wavelet transform extracts multiscale time-frequency information from the high-dimensional thermal history data. Wavelet scalogram clearly shows the time-dependent frequencies, which are intrinsic mechanistic features in additive manufacturing. Those frequencies represent the multiscale nature of the AM process. It is noted that the timescale of the thin wall fabrication is about 103 s and the timescale of a single layer manufacturing is about 10 s, while the timescale of melt pool dynamics ranges from 10−3 s to 1 s. (2) The CNN model is a powerful model which can capture both local and global frequency relationships from the wavelet scalograms by a hierarchical structure of convolutions. The performance is also improved by a customized design of the architecture and training strategies with hyper-parameters. Figure 3 shows that model uncertainty due to the utilization of various CNNs can result in less than 5% variations on the predicted UTS values.
Future work may include (1) a rigorous uncertainty quantification for the mechanistic data-driven model (2) using computational thermal histories as input. Uncertainty quantification provides a confidence degree of the prediction which is valuable for decision making. Leveraging the proposed data-driven approach with high-fidelity simulations, spatial and temporal mechanical properties could be predicted. This methodology provides a mechanistic data-driven framework as a digital twin of physical AM process. It will significantly accelerate AM process optimization and printable material discovery by avoiding an Edisonian trial and error approach.
Methods
Directed energy deposition
We built 12 thin walls, i.e., single track and multilayer structures, using directed energy deposition (DED). All of the walls were 120 layers tall (the width of walls is about 3 mm). The programmed layer height was 0.5 mm. Inconel 718 powders were deposited on stainless steel 304 substrates using the DMG MORI LaserTec 65, which is a hybrid additive and subtractive 5-axis machine. The powder particle size ranged from 50 to 150 μm. The walls were manufactured with a laser power of 1800 W, a powder flow rate of 18 g/min, a scanning speed of 1000 mm/min, and a laser spot of 3 mm. A bidirectional (zigzag) tool path was used. The laser was powered off while the laser moved vertically to the next layer. As shown in Supplementary Fig. 7, three of the walls (#1–3) were 80 mm in length and three of the walls (#4–6) were 120 mm in length. Those six walls were created without intentional dwell process or melt pool control. Walls #7–9 were 120 mm in length with 5 s dwell time between each layer. Walls #10–12 were 120 mm in length with melt pool control during the process. The melt pool controller native to the DMG MORI LaserTec 65 machine uses a charge coupled device (CCD) camera with a resolution of 180 × 250 and a pixel size of about 30 μm2 to view the melt pool. It counts all pixels above a certain user-defined threshold as part of the melt pool and then modulates the laser power during the process, depending on the pixel count, in order to maintain the user-specified melt pool size. These walls and their thermal measurements were further analysed an empirical study relating tensile properties to thermal metrics44.
Infrared (IR) thermal measurement and calibration
A FLIR A655s digital infrared (IR) camera was used to measure the temperature field on the side wall in-situ. The IR camera recorded the surface emission with equivalent radiance temperature ranging from 300 to 2000 °C with an accuracy of ±2 °C. The spectral range of the camera is from 7.5 to 14 μm. The resolution of the IR camera was 640 × 480 pixels and the field of view was 128 mm × 96 mm, and the pixel size was 200 μm2. The frame rate of the IR camera was 6–25 fps. Multiple small ROIs were selected at each wall for extracting time-dependent temperature curves, i.e., the thermal histories, and mechanical properties. The size of a ROI is 2 mm × 2 mm, which is comparable with the gauge section of a miniature tensile specimen. Illustrative IR results for two walls (#1 and #12) with detailed information of those ROIs are shown in Supplementary Fig. 8a, b, respectively. Supplementary Fig. 8c shows an illustrative thermal history for a specific ROI at wall #1. Supplementary Fig. 8d shows an illustrative thermal history for a specific ROI at wall #12. Wall #1–3 (80 mm length) have nine predetermined ROIs, and Wall #4–12 (120 mm length) have 12 predetermined ROIs. Thus, 135 (3 × 9 + 9 × 12) high-dimensional thermal histories were extracted from the center of ROIs of the walls for further model training and testing. The mechanical properties were obtained from miniature tensile specimens, with the gauge region nominally aligned with the 135 ROIs. We used the thermal history at the center of each ROI instead of averaging the thermal histories over the ROI because thermal histories in a small neighboring region are highly correlated. Detailed information is provided in supplementary information (Supplementary Discussion: Correlation matrix of thermal histories). Then, to build high-resolution as-built mechanical property maps, we divided each wall into a uniform grid of 50 × 100 based on its width and height, and extracted 5000 thermal histories for each wall at the locations of the grid. The corresponding pixel locations of at the IR measurement were identified based on the coordinates of the grid for data extraction. A schematic of the thermal measurement locations is shown in Supplementary Fig. 9. The 80 mm length walls and 120 mm length walls have the same number of extracted thermal histories, i.e., 5000 thermal histories.
The temperature measured by the IR camera was the radiation temperature, rather than the absolute temperature, because of the lack of knowledge of the true value of emissivity at the measurement location. We calibrated the extracted thermal histories using the solidification features based on a method detailed in the ref. 38.
Microstructure and mechanical properties characterization
We cut an 0.8 mm thick sheet from the center of the wall thickness using wire EDM. Wire EDM was also used to cut miniaturized ASTM E8 tensile specimens in the vertical (build) orientation from this sheet. To obtain stress–strain curves of the local material at each ROI, the gauge section of the specimens coincided with each ROI as shown in Supplementary Fig. 10a for wall #1, and the nominal dimensions of the gauge section were 0.8 mm thick by 1.2 mm wide by 2.5 mm long. More details of the coupon dimensions can be found in the ref. 38. The specimens were tested under displacement control until complete failure on a Sintech 20G tensile test machine. Mechanical properties extracted from the stress–strain curve included Young’s modulus, yield strength, yield strain, ultimate tensile strength, fracture strength, and fracture strain, as shown in Supplementary Fig. 10b. Thus, we obtained total 135 sets of mechanical properties at the predetermined ROIs of the twelve walls. Fractured tensile specimens from identical locations on wall #9, #4, and #1 were examined with a FEI Quanta 650 scanning electron microscope. In preparation for imaging, the specimens were mounted in epoxy, polished to a 0.02 μm finish, and etched with Carapella’s reagent for 15–30 s. A further investigation of the evolution of microstructure and hardness of the walls in this work after heat treatment and HIP post-processing can be found in the ref. 45.
Dimension reduction by discrete binning (DB)
The dimension of an as-measured thermal history is more than 103 for a frame rate of 6 fps. Directly using this kind of high dimensional vector as the input of a machine learning algorithm will lead to overfitting and reduce the generalization capability of the algorithm if the amount of the data is not very large. Thus, to reduce the dimension of thermal histories, we used a pre-processing technique, called the discrete binning (DB) approach. An illustrative thermal history is shown in Supplementary Fig. 11. We only use the thermal history after the peak temperature because (1) the detected radiation signal before the peak has more noise and uncertainty that are difficult to be eliminated through a calibration process; (2) many authors reported that the solidification microstructure and mechanical properties during additive manufacturing are highly correlated with the cooling stage, where the temperature is lower than the peak temperature1,46,47. We divided the temperature range of each thermal history into small temperature segments, or discrete bins (Supplementary Fig. 11b). To cover the maximum and minimum temperatures of the thermal histories, we set 37 temperature segments/bins in our study, and thus the corresponding temperature interval is about 50.88 °C. Then we computed the total time that the material spends at each temperature segment/bin. Then we transformed 135 high dimensional (103) thermal history to 135 low dimensional (37) vectors. Each component of those vectors presents the accumulated time during each discrete temperature bin (Supplementary Fig. 11c).
Wavelet transform
Wavelet transform is used as a feature engineering mechanism. The time-temperature histories (i.e., thermal histories) are converted to frequency-time plots (i.e., wavelet scalogram) which are later used as inputs for convolutional neural networks. We investigated different techniques including Fourier and Hilbert–Huang transformations to come to the final choice of using wavelet transformation. However, the resulting correlation had room for improvement. The reason for apparent lower efficiency of the Fourier techniques and relative success of the wavelet-based analysis is that the Gabor or Fourier based transforms have a fixed basis and window size that transforms any signal. For Fourier analysis, this basis is sine or cosine function. This is restrictive as the information or signal content in our experiments are not necessarily stationary and periodic. For example, the variation in thermal history signal can be attributed to different sources: it can come from the melt pool shape change, change in the direction of the laser, local composition of the powder, or uncertainties in the process. These phenomena are occurring at different timescales as well. Hence, to retain the information during feature engineering, we had to adopt a technique that retains the information in the time-temperature signal. In addition, there is uncertainty principle acting in the Short time Fourier Transform. It means, we cannot get exact data for both frequency and time. If we get high resolution of data in time domain, we lose data in frequency domain and vice versa. Wavelet analysis is a suitable candidate in this case. The non-circular basis function and coupled with flexibility to vary the width of the window function for convolution, wavelet transform can do a much better job to retain the multiresolution and locally variant information. In wavelet analysis, we define a mother wavelet which is given by48,
Here a and b are the parameters controlling the scaling and translating of the function ψa,b(t). If the function to be transformed is given by f(t), the transformation is defined as,
Here, \({\bar{\psi }}_{{\rm{a,b}}}(t)\) is the complex conjugate of ψa,b(t). In the context of this work, f(t) is the temperature-time histories and mother wavelet is the Morse wavelets49. The sampling rate used in wavelet transform was based on the thermal camera frame rate. To have consistent frame rate recordings, we down-sampled the higher frame rate recordings (25 fps) to lower frame rate recordings (6 fps) by using a function called linspace in the NumPy package50. Thus, the sampling frequency used in this work is 6 Hz.
The fundamental theory of wavelet analysis involves convolving a mother wavelet to the original signal. The mother wavelet traverses across the time domain to create the wavelet coefficient. Now because of the size of the mother wavelet, near the edge, there is a region where the wavelet coefficients have some uncertainty. This effect is called the boundary effect and the boundary of this uncertain region is called the cone of influence. Supplementary Fig. 12 shows sample wavelet scalograms of the thermal histories on the wall #2 and #7. The red lines show the cone of influence. Outside the boundary of this cone, the wavelet coefficient will suffer from edge effect. However, since we are not really directly interpreting the wavelet images as such, the consistency in the cone of influence across the thermal histories makes sure that the correlation achieved by the CNN is valid. Therefore, we ignored the boundary effect when making the image database.
Convolutional neural networks (CNNs)
CNNs51 are powerful deep learning architectures to analyze visual imagery like images or videos. Generally, CNNs are composed of convolution layers, activation layers, pooling layers, fully-connected layers. But with the network depth increasing, the notorious vanishing gradient problem occurs, which can stop the network from further training and updating parameters. Residual Networks (ResNet)52, one of the most famous CNNs architectures, used identity shortcut connection to solve this problem. The inserted shortcut connections allow gradient information to pass through layers directly and help to train deeper networks.
The proposed WT_CNN approach used ResNet1852, an 18-layer CNN, as the base structure. Important modifications were made to fit the wavelet scalogram dataset and improve model performance. First, the input image to the WT_CNN, based on the wavelet scalogram, was set to 64 × 64 × 3. We used 64 × 64 in the spatial size (height and width) because larger spatial size (124 × 124 or 256 × 256) can easily cause overfitting problems considering we have 135 thermal histories in total. The input image based on wavelet scalogram has three channels (RGB) instead of one channel (magnitude value). The first reason why we used three channels is that converting grayscale image with actual magnitude value to color image does not loss information but increase two channels, which might boost the CNN training. The usage of RGB images or grayscale images will produce very similar results because the mapping between them is linear in this case. The second reason is that many state-of-the-art CNN architectures (including the one used in this study) are implemented based on three channels’ inputs. Thus, to take advantage of those standard libraries, we did not directly use the actual magnitude value (i.e., one channel inputs). Second, in the first convolution layer, the filter size was 3 and the stride was 1 and the padding was 1. These parameters help the network maintain most of the information from the inputs. Third, we used eight residual blocks52 as the main structure of our network. Each residual block has a residual connection (or shortcut connection). This technique can improve the feature extraction capacity and avoid vanishing gradient problem at the same time. Fourth, after eight residual blocks and the global average pooling layer, two fully-connected (FC) layers were used to fit the output label. ReLU activation functions were only used in the first two FC layers. The network architecture is shown in Supplementary Fig. 12.
We trained the network using the Adam optimizer53 with 1.0 × 10−3 weight decay. Mean square error was used in the loss function. There were several hyper-parameters including learning rate (1.0 × 10−3), the number of epoch (50), batch size (8). Besides, 5-fold cross-validation was used to choose the optimal network. Thus, the total dataset was split into three parts: training set (64%), validation set (16%), and test set (20%).
RF and feature importance analysis
In this study, the RF algorithm54 was used to fit the relationship between discrete temperature bins and mechanical properties. This algorithm is an ensemble learning method that constructs a multitude of base models and integrates each prediction to make a final prediction. For our problem, base models are regression trees55. Besides, RF has two main characteristics: random subsets of the original training set and random feature selection when building each tree54. These two techniques help to increase the randomness of models and de-couple the correlation between base models. Thus, RF has low variance and low bias of the final model.
For a fair comparison, we used the same test set with CNN approach and also applied 5-fold cross-validation. Due to the limited number of the total dataset and the high sensitivity of the number of trees in our dataset, we set the number of trees to range from 30 to 100 with an interval of 10. During training, the RF model was designed to automatically search for the best parameter and then fit the training set.
To find important features, we calculated Mean Decrease Impurity (MDI) Imp(Xj)55 for each feature Xj. The value of Imp(Xj) can be calculated by summing the total impurity reduction of all tree nodes where the feature Xj appears. The higher value of Imp(Xj) means the higher importance for Xj. Imp(Xj) is defined as:
Here M is the number of trees, t is a node of trees, φm is a set of nodes for each tree, jc is the feature used in node c, p(c) is a fraction of the number of data points (thermal histories in our study) belongs to node c and is defined as \(\frac{{N}_{c}}{N}\), where Nc the number of data points in node c and N is the number of total data points, Δi(c) is the impurity reduction at node c and is defined as:
where impurity i(c) is Mean Square Error (MSE), Nc is the number of data points of node c, \({N}_{lef{t}_{c}}\) is the number of data points in the left of node c, \({N}_{{\rm{righ}}{{\rm{t}}}_{{\rm{c}}}}\) is the number of data points in the right of node c.
When analyzing feature importance, we split the total dataset as a training set (80%) and a test set (20%) randomly for 150 times instead of using a validation set. In this way, we can use the most data for model training and get a stable distribution of each feature’s importance, which avoids the randomness impact when splitting the total dataset.
Data availability
The datasets required to reproduce the results in this study are provided at https://github.com/xiaoyuxie-vico/DL_AM_Data. The data includes thermal histories, wavelet scalogram, and mechanical properties.
Code availability
The Python code required to reproduce the results is available at https://github.com/xiaoyuxie-vico/DL-AM.
References
DebRoy, T. et al. Additive manufacturing of metallic components–process, structure and properties. Prog. Mater. Sci. 92, 112–224 (2018).
Khairallah, S. A., Anderson, A. T., Rubenchik, A. & King, W. E. Laser powder-bed fusion additive manufacturing: physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 108, 36–45 (2016).
Cunningham, R. et al. Keyhole threshold and morphology in laser melting revealed by ultrahigh-speed x-ray imaging. Science 363, 849–852 (2019).
Ye, J. et al. Energy coupling mechanisms and scaling behavior associated with laser powder bed fusion additive manufacturing. Adv. Eng. Mater. 21, 1900185 (2019).
Hojjatzadeh, S. M. H. et al. Pore elimination mechanisms during 3d printing of metals. Nat. Commun. 10, 1–8 (2019).
Zhao, C. et al. Real-time monitoring of laser powder bed fusion process using high-speed x-ray imaging and diffraction. Sci. Rep. 7, 3602 (2017).
Martin, J. H. et al. 3d printing of high-strength aluminium alloys. Nature 549, 365 (2017).
Gray III, G. T. et al. Structure/property (constitutive and spallation response) of additively manufactured 316l stainless steel. Acta Mater. 138, 140–149 (2017).
King, W. E. et al. Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges. Appl. Phys. Rev. 2, 041304 (2015).
Gan, Z. et al. Benchmark study of thermal behavior, surface topography, and dendritic microstructure in selective laser melting of inconel 625. Integr. Mater. Manuf. Innov. 8, 1–16 (2019).
Lian, Y. et al. A cellular automaton finite volume method for microstructure evolution during additive manufacturing. Mater. Des. 169, 107672 (2019).
Herriott, C. F. et al. A multi-scale, multi-physics modeling framework to predict spatial variation of properties in additive-manufactured metals. Model. Simul. Mater. Sci. Eng. 27, 025009 (2018).
Gan, Z., Yu, G., He, X. & Li, S. Numerical simulation of thermal behavior and multicomponent mass transfer in direct laser deposition of co-base alloy on steel. Int. J. Heat. Mass Transf. 104, 28–38 (2017).
Thompson, S. M., Bian, L., Shamsaei, N. & Yadollahi, A. An overview of direct laser deposition for additive manufacturing; part i: transport phenomena, modeling and diagnostics. Addit. Manuf. 8, 36–62 (2015).
Markl, M. & Körner, C. Multiscale modeling of powder bed–based additive manufacturing. Annu. Rev. Mater. Res. 46, 93–123 (2016).
Bayat, M., Mohanty, S. & Hattel, J. H. Multiphysics modelling of lack-of-fusion voids formation and evolution in in718 made by multi-track/multi-layer l-pbf. Int. J. Heat. Mass Transf. 139, 95–114 (2019).
Wei, H. et al. Mechanistic models for additive manufacturing of metallic components. Prog. Mater. Sci. 116, 100703 (2020).
DebRoy, T., Mukherjee, T., Wei, H., Elmer, J. & Milewski, J. Metallurgy, mechanistic models and machine learning in metal printing. Nat. Rev. Mater. 2, 1–21 (2020).
Goh, G. D., Sing, S. L. & Yeong, W. Y. A review on machine learning in 3d printing: applications, potential, and challenges. Artif. Intell. Rev. 54, 1–32 (2020).
Johnson, N. et al. Invited review: machine learning for materials developments in metals additive manufacturing. Addit. Manuf. 36, 101641 (2020).
Popova, E. et al. Process-structure linkages using a data science approach: application to simulated additive manufacturing data. Integr. Mater. Manuf. Innov. 6, 54–68 (2017).
Rodgers, T. M., Madison, J. D. & Tikare, V. Simulation of metal additive manufacturing microstructures using kinetic monte carlo. Comput. Mater. Sci. 135, 78–89. (2017).
Du, Y., Mukherjee, T. & DebRoy, T. Conditions for void formation in friction stir welding from machine learning. npj Comput. Mater. 5, 1–8 (2019).
Li, J., Jin, R. & Hang, Z. Y. Integration of physically-based and data-driven approaches for thermal field prediction in additive manufacturing. Mater. Des. 139, 473–485 (2018).
Zhang, W., Mehta, A., Desai, P. S. & Higgs, C. Machine learning enabled powder spreading process map for metal additive manufacturing (am). In Solid Freeform Fabrication 2017: Proceedings of the 28th Annual International Solid Freeform Fabrication Symposium, 1235–1249. University of Texas at Austin (2017).
Gan, Z. et al. Data-driven microstructure and microhardness design in additive manufacturing using a self-organizing map. Engineering 5, 730–735 (2019).
Lu, Y., Jones, K. K., Gan, Z. & Liu, W. K. Adaptive hyper reduction for additive manufacturing thermal fluid analysis. Comput. Methods Appl. Mech. Eng. 372, 113312 (2020).
Wang, Z. et al. Uncertainty quantification and reduction in metal additive manufacturing. npj Comput. Mater. 6, 1–10 (2020).
Scime, L. & Beuth, J. Using machine learning to identify in-situ melt pool signatures indicative of flaw formation in a laser powder bed fusion additive manufacturing process. Addit. Manuf. 25, 151–165 (2019).
Zhang, B., Liu, S. & Shin, Y. C. In-process monitoring of porosity during laser additive manufacturing process. Addit. Manuf. 28, 497–505 (2019).
Zhang, B., Hong, K.-M. & Shin, Y. C. Deep-learning-based porosity monitoring of laser welding process. Manuf. Lett. 23, 62–66 (2020).
Wolff, S. J. et al. Experimentally validated predictions of thermal history and microhardness in laser-deposited inconel 718 on carbon steel. Addit. Manuf. 27, 540–551 (2019).
Lewis, R. J. An introduction to classification and regression tree (cart) analysis. In Annual Meeting of the Society for Academic Emergency Medicine in San Francisco, California (2000).
Friedman, J., Hastie, T. & Tibshirani, R. The Elements of Statistical Learning vol. 1 (Springer, 2001).
Irwin, J., Reutzel, E. W., Michaleris, P., Keist, J. & Nassar, A. R. Predicting microstructure from thermal history during additive manufacturing for ti-6al-4v. J. Manuf. Sci. Eng. 138, 11107 (2016).
Yan, W. et al. An integrated process–structure–property modeling framework for additive manufacturing. Comput. Methods Appl. Mech. Eng. 339, 184–204 (2018).
Wei, Y. et al. Evading the strength–ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 5, 1–8 (2014).
Bennett, J. L. et al. Cooling rate effect on tensile strength of laser deposited inconel 718. Proced. Manuf. 26, 912–919 (2018).
MatWeb, L. Material property data. MatWeb [Online]. http://www.matweb.com (2016).
Paulonis, D., Oblak, J. & Duvall, D. Precipitation in nickel-base alloy 718. Technical Report (Pratt and Whitney Aircraft, 1969).
Knapp, G. et al. Building blocks for a digital twin of additive manufacturing. Acta Mater. 135, 390–399 (2017).
Keiser, D. & Brown, H. Review of the physical metallurgy of alloy 718. Technical Report (Idaho National Engineering Lab, 1976).
Devore, J. L. Probability and Statistics for Engineering and the Sciences (Cengage Learning, 2011).
Bennett, J., Glerum, J. & Cao, J. Relating additively manufactured part tensile properties to thermal metrics. CIRP Ann. 70 (2021).
Glerum, J., Bennett, J., Ehmann, K. & Cao, J. Mechanical properties of hybrid additively manufactured inconel 718 parts created via thermal control after secondary treatment processes. J. Mater. Process. Technol. 291, 117047 (2021).
He, X., Fuerschbach, P. & DebRoy, T. Heat transfer and fluid flow during laser spot welding of 304 stainless steel. J. Phys. D 36, 1388 (2003).
Elmer, J., Palmer, T., Babu, S., Zhang, W. & DebRoy, T. Phase transformation dynamics during welding of ti–6al–4v. J. Appl. Phys. 95, 8327–8339 (2004).
Brunton, S. L. & Kutz, J. N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control (Cambridge University Press, 2019).
Olhede, S. C. & Walden, A. T. Generalized morse wavelets. IEEE Trans. Signal Process. 50, 2661–2670 (2002).
Harris, C. R. et al. Array programming with NumPy. Nature 585, 357–362 (2020).
Krizhevsky, A., Sutskever, I. & Hinton, G. E. Imagenet classification with deep convolutional neural networks. Commun. ACM 60, 84–90 (2017).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 770–778. IEEE (2016).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. https://arxiv.org/1412.6980 (2014).
Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).
Breiman, L., Friedman, J., Stone, C. J. & Olshen, R. A. Classification and Regression Trees (CRC Press, 1984).
Benesty, J., Chen, J., Huang, Y. & Cohen, I. Noise Reduction in Speech Processing 1–4 (Springer, 2009).
Svozil, D., Kvasnicka, V. & Pospichal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 39, 43–62 (1997).
Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 58, 267–288 (1996).
Shi, Q., Abdel-Aty, M. & Lee, J. A bayesian ridge regression analysis of congestion’s impact on urban expressway safety. Accid. Anal. Prev. 88, 124–137 (2016).
Fukunaga, K. & Narendra, P. M. A branch and bound algorithm for computing k-nearest neighbors. IEEE Trans. Comput. 100, 750–753 (1975).
Saha, S. et al. Hierarchical deep learning neural network (hidenn): an artificial intelligence (ai) framework for computational science and engineering. Comput. Methods Appl. Mech. Eng. 373, 113452 (2020).
Lecun, Y. & Bengio, Y. Convolutional networks for images, speech, and time series. Handb. Brain Theory Neural Netw. 3361, 1995 (1995).
Acknowledgements
This study was supported by the National Science Foundation (NSF) through grants CMMI-1934367. We thank Jennifer Glerum for performing the SEM imaging and Mark Fleming for his detailed review and helpful suggestions. J. Bennett and J. Cao would like to acknowledge the support from the Army Research Laboratory (ARL W911NF-18-2-0275). J. Bennet acknowledeg the ARL Oak Ridge Associated Universities (ORAU) Journeyman Fellowship.
Author information
Authors and Affiliations
Contributions
Z. Gan proposed the original ideas, supervised the project, designed the machine learning models, analyzed the results, co-wrote the manuscript, revision response and supplementary information. X. Xie constructed the datasets (wavelet scalogram, raw thermal history, and discrete binning data), designed and implemented WT_CNN and machine learning models, analyzed and visualized the results, co-wrote the manuscript, and wrote revision response and supplementary information. J. Bennett conducted and analyzed DED experiments, calibrated thermal histories, and conducted mechanical properties tests. S. Saha conducted and analyzed wavelet transform, contributed to discussions, computed correlation matrix, co-wrote the manuscript and revision response. Y. Lu analyzed the results. J. Cao supervised the experiments. W. Liu contributed to discussions and supervised the project. All the authors reviewed and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xie, X., Bennett, J., Saha, S. et al. Mechanistic data-driven prediction of as-built mechanical properties in metal additive manufacturing. npj Comput Mater 7, 86 (2021). https://doi.org/10.1038/s41524-021-00555-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00555-z
This article is cited by
-
Data-driven modeling of process-structure-property relationships in metal additive manufacturing
npj Advanced Manufacturing (2024)
-
State-space reconstruction from partial observables using an invertible neural network with structure-preserving properties for nonlinear structural dynamics
Nonlinear Dynamics (2024)
-
In Situ, Parallel Monitoring of Relative Temperature, Material Emission, and Laser Reflection in Powder-Blown Directed Energy Deposition
JOM (2024)
-
A deep learning framework for layer-wise porosity prediction in metal powder bed fusion using thermal signatures
Journal of Intelligent Manufacturing (2023)
-
A structure-preserving neural differential operator with embedded Hamiltonian constraints for modeling structural dynamics
Computational Mechanics (2023)