Abstract
Grain boundary (GB) dynamics are largely controlled by the formation and motion of disconnections (with step and dislocation characters) along with the GB. The dislocation character gives rise to shear coupling; i.e. the relative tangential motion of two grains meeting at the GB during GB migration. In a polycrystal, the shear coupling is constrained by the presence of other grains and GB junctions, which prevents large-scale sliding of one grain relative to the other. We present continuum equations of motion for GBs that is based upon the underlying disconnection dynamics and accounts for this mechanical constraint in polycrystals. This leads to a reduced-order (zero-shear constrained) model for GB motion that is easily implemented in a computationally efficient framework, appropriate for the large-scale simulation of the evolution of polycrystalline microstructures. We validated the proposed reduced-order model with direct comparisons to full multi-disconnection mode simulations.
Similar content being viewed by others
Introduction
Grain boundaries (interfaces between domains/grains of different crystallographic orientations) are major components of polycrystalline microstructures. The dynamical properties of grain boundary (GB) networks play essential roles in the mechanical response of materials and influence a wide range of other properties (e.g., electrical resistance, optical transmission, thermoelectric efficiency)1. Traditional models for isotropic GB dynamics are based on capillarity-driven GB migration; i.e., the driving force for migration is proportional to the local GB mean curvature κ2,3 such that the normal GB velocity vn (isotropic limit) is vn = MGBγκ, where MGB is the GB mobility and γ is the GB energy. Theoretical predictions and experimental observations demonstrate that GB migration, in general, is controlled by the motion of discrete line defects constrained to the GBs known as disconnections4,5,6,7,8,9,10,11,12,13. Motion by mean curvature-based continuum models are unable to adequately account for many GB migration phenomena such as stress-driven GB motion associated with disconnection dynamics.
Disconnection is a line defect that is characterised by a dislocation Burgers vector b and a step height H; i.e., (b, H). We recently developed a continuum model for GB migration that is based upon disconnection migration14,15. These models naturally include GB migration under a wide range of driving forces (internal and applied stress, chemical potential jumps, capillarity), as well as the effect of temperature. We also proposed a continuum model that accounts for the concurrent migration of GB and the junctions along which they meet in a disconnection-based framework16,17.
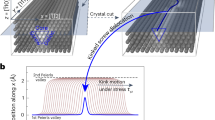
One important consequence of GB migration by disconnection motion is shear coupling18,19,20; the translation of one grain relative to the other in a direction parallel to the GB plane during migration (associated with the disconnection Burgers vector) (Fig. 1a, b). The shear coupling has been observed in bicrystals in both experiments and simulations21,22,23,24,25,26,27,28,29,30,31,32,33. On the other hand, in a polycrystal, constraints imposed by the presence of other grains prevents large-scale sliding of one grain relative to the other (Fig. 1c). Grain boundary migration in such constrained systems requires the simultaneous action of disconnections of multiple modes such that there is zero-net-shear16. Continuum models14,15 can, in principle, incorporate this collective behaviour through the long-range stress field generated by all of the disconnections on all of the GBs in the microstructure16,17. However, such calculations are too complex and computationally inefficient for widespread adoption in microstructure evolution simulations.
A bicrystal with free top and bottom surface a before and b after GB migration with accompanying shear deformation. The dashed blue line is a fiducial marker (e.g., a scratch) in the bicrystal. The shear-coupling factor β is the inverse of the slope of this line between the initial and final GB positions (red solid and dashed lines in b, respectively). c A grain in a polycrystal with GBs 1–5 and Junctions A–E. The shear of GB ① is constrained by junctions A and B and by the elastic interactions between Grain I and surrounding grains, III–VI. d GB migration in the bicrystal of a where the top and bottom surface do not translate to mimic the effects of Grains IV and V on the shear of GB ①.
In this paper, we propose a reduced-order description of GB migration that accounts for the constraints imposed by other grains in the polycrystalline microstructure (Fig. 1c) that is both disconnection-based and is sufficiently computationally tractable to be broadly applied. The result is a disconnection migration-based equation of motion for a mechanically constrained GB; one for which there is zero-net-shear (see an example in Fig. 1d). To validate our proposed approach, we compare model predictions with a multi-disconnection migration-based approach for GB migration in the presence of different mechanical constraints (as appropriate for microstructural evolution in a polycrystal)15.
Results
Equation of motion for a constrained grain boundary
On the microscopic level, a high-angle GB may be viewed as being composed of flat sections and disconnections (the stepped, black curve in Fig. 2). The motion of disconnections in one direction translates the GB while motion of a pair of disconnections such that they meet and annihilate with each other changes the GB curvature. Hence, both GB migration and change in GB shape can be characterised by disconnection motion. On a continuum level, a high-angle GB may be modelled as a smoothly varying curve (not resolving the underlying disconnection/step structure—see the red curve in Fig. 2).
Consider a slightly curved GB, deviating from a flat reference parallel to x. The GB profile may be described by y = h(x, t), where ∣∂xh∣ ≪ 1. The disconnection mode is characterised by a Burgers vector and step height (b, H), where the Burgers vectors b = (b, 0) is, here, in x and the step height vector H in y (Fig. 2). There are many possible Burgers vectors bn and for each a set of possible step heights {Hnk} on each GB, as determined by the misorientation between the grains13. Although in principle, the number of possible disconnection modes is infinite, the modes likely to be found are quite limited, depending on thermodynamic variables, bonding, disconnection core structure. The density of disconnections of mode j (b(j), H(j)) is denoted ρ(j) and positive/negative ρ(j) value represents the density of disconnection (b(j), H(j))/(−b(j), −H(j)). Evolution equations for the GB profile h(x, t) and disconnection densities ρ(j)(x, t) on the GB can be described by disconnection fluxes J(j),
In a polycrystalline microstructure, two grains meeting at a GB cannot slide with respect to one another without limit. This is because of the mechanical constraint from the other grains surrounding the two grains meeting at the GB in question and/or because of the presence of a nearby GB junction12,13. (Note that since different GBs have different crystallographically allowed disconnection Burgers vectors and step heights, disconnections can rarely move across GB junctions.) These constraints give rise to a macroscopic zero-net-shear across a GB constraint; i.e.
Since disconnections have both dislocation and step character, this implies a constrained evolution problem: the GB profile and disconnection densities evolve as per (1) and (2) subject to the constraint (3).
The evolution of the GB profile ht is determined by the disconnection fluxes (1). The flux of disconnections of each mode contributes to the change in GB profile via their step heights H(j). The disconnection density evolution is consistent with both the Burgers vector and step conservation. The flux J(j) of the jth disconnection mode is
where \({c}^{(j)}=\frac{1}{a}{{\rm{e}}}^{-{E}^{* (j)}/({k}_{{\rm{B}}}T)}\) is the thermal equilibrium disconnection density on the GB (which enables the motion of an initially flat GB), a is an atomic spacing, kB is the Boltzmann constant, T is the temperature, E*(j) is half the disconnection pair formation energy13, and v(j) is the disconnection glide velocity
Here, \({M}_{{\rm{d}}}^{(j)}\) is the disconnection mobility, τ is the total internal shear stress, and Ψ is the chemical potential-jump across the GB. We assume that the disconnection glide velocity (5) is overdamped, such that it is proportional to the driving force \({f}_{{\rm{d}}}^{(j)}\), i.e. \({v}^{(j)}={M}_{{\rm{d}}}^{(j)}\cdot {f}_{{\rm{d}}}^{(j)}\).
With (4) and (5), the assumption of zero-net-shear across the GB as described in (3) becomes
where
Here β(j) is the shear-coupling factor associated with disconnection mode j19. The zero-net-shear constraint (3) implies the development of a shear stress τ on the GB induced by GB migration:
With this effective shear stress, the GB profile and disconnection density evolution, (1) and (2), can be expressed as
where β(j) and A(j) are given in (7) and (8). This is our reduced-order model for GB motion and disconnection density evolution subject to the zero-net-shear constraint.
Solution of the original dynamical equations (1) and (2) requires the determination of the total, non-local, shear stress τ. However, with the zero-net-shear constraint, the dynamical equations (10) and (11) are local and can be solved much more efficiently than the original ones.
Before concluding our discussion of a GB equation of motion, it is appropriate to note a few limitations. First, the full disconnection description of GB migration explicitly depends on the crystallinity of the grains on either side of the GB. It will not describe GB migration in systems where the GB is a thick amorphous between the crystal grains. Second, the disconnection model described here assumes that the disconnections move in a glissile manner; disconnections with Burgers vector components perpendicular to the GB plane may move by absorption/emission of point defects - disconnection climb. We do not consider climb here since the climb is typically much slower than glide (even on a GB) and, hence, disconnection climb is expected to make a much smaller contribution to GB migration than that associated with glide. Third, we ignore the fact that GBs may exhibit multiple metastable states34, in which case, disconnections may be partial disconnections separated by stacking faults. While such effects may be included in a discrete disconnection model, they are not incorporated here.
Flat grain boundary dynamics
We first apply the GB evolution equations to GB migration driven by a chemical potential-jump Ψ across the GB. Consider the simple case of an infinitely large, initially flat GB h(x, 0) = 0 with no disconnections ρ(j) = 0 for all j. Here, the GB profile evolves as
where
This expresses the GB velocity ht as the product of the chemical potential-jump Ψ and an effective GB mobility which is determined by the properties/parameters of the disconnections. Here the GB remains flat and moves with a constant velocity and the disconnection densities are zero ρ(j) = 0 for all j at all time (i.e., the equal density of positive and negative disconnections). The internal stress τ (9) is proportional to the chemical potential-jump Ψ with a negative factor that depends on the disconnection properties; this exerts a back stress that opposes the chemical potential-jump Ψ,
We now compare the zero-net-shear model (see (12) and (13)) with the predictions of the full continuum disconnection model15, as represented by (1), (2), (4), and (5) for the migration of a flat GB. More specifically, we assume a bicrystal geometry where the top and bottom surfaces of the bicrystal (flat horizontal, centred GB) are fixed (see Fig. 1d and ref. 15 for details) to provide no net bicrystal shear. In the full continuum disconnection model, we explicitly evolve two-disconnection modes and evaluate the stresses at every point (x, y) in the bicrystal that arise from all disconnections along the GB and the image stresses generated by the fixed top and bottom surface of the bicrystal boundary conditions.
We choose parameters appropriate for a nominally flat, Σ13[100](015) symmetric tilt GB in Cu driven by a chemical potential-jump of Ψ = −1 meV ⋅ Å−3. More specifically, we consider the two lowest formation energy disconnections modes (b(1), H(1)) and (b(2), H(2)); i.e. \({b}^{(1)}={b}^{(2)}={a}_{0}/\sqrt{26}\), \({H}^{(1)}=4{a}_{0}/\sqrt{26},{H}^{(2)}=-2.5{a}_{0}/\sqrt{26}\), where the lattice constant a0 = 3.615 Å13,15,35. When T = 800 K, the nucleation rate of these disconnections are estimated to be 2c(1) = 0.2188/L0 and 2c(2) = 0.6930/L0, where L0 = 100 Å is the length of the GB13,15,36,37. In these simulations, we set the distance between the top and bottom surfaces as 2L0 and the GB is initially located in the centre of the simulation cell. These are consistent with a grain size of ~L0.
The migration velocity of this flat GB (see (12) and (13)) is independent of time, as seen in Fig. 3a for T = 800 K (red line). This constant velocity agrees well with that found at a late time from the simulation based upon the full multi-mode disconnection model15 (the blue curve). In the full multi-mode disconnection simulation, the velocity starts at a large value but relaxes quickly to the steady-state solution founding the zero-shear model.
Migration of a nominally flat, Σ13[100](015) symmetric tilt GB in Cu driven by a chemical potential-jump across the GB of Ψ = −1 meV ⋅ Å−3 using the zero-shear, reduced-order model and the full multi-disconnection mode model15. The GB migration velocity in a and internal stress in b at T = 800 K predicted by the reduced-order model (red lines) and the full multi-disconnection mode model with fixed boundary conditions (blue curves). The predicted steady state GB migration velocity in c and internal stress in d are shown as a function of T (blue points: full multi-disconnection mode model). Stress is normalised by τ0 = − ΨH(2)/b(2), GB velocity by the T = 1300 K velocity v0, and t0 = L0/v0.
This transient in the full multi-mode disconnection simulation can be understood as follows: (i) the GB starts to migrate by the motion of the lowest formation energy disconnection mode, (ii) shear coupling and the constraint set up a back stress that counteracts the chemical jump driving force12, (iii) continued motion requires the formation of disconnection of opposite shear-coupling factor with higher formation energy and (iv) continued migration is limited by the rate of formation of the more difficult to form secondary (or higher order) disconnections. The concerted motion of these different modes is required for steady-state migration.
This ‘back stress’ picture is confirmed by a consideration of the internal stress during GB migration τ as described by (14) and the full continuum model15 (Fig. 3b). While the zero-shear model accurately predicts the steady-state internal stress, the full multi-mode disconnection simulation shows the transient development of the internal stress which asymptotically approaches the reduced-order model steady-state stress. Figure 3c, d show the T-dependence of the GB mobility and the internal stress from the zero-shear model and the full multi-mode disconnection simulations. The agreement is excellent. The duration of the transient, not captured by the zero-shear model, depends on both the GB bicrystallography as well as the microstructure (e.g. large grain sizes imply longer transients). It is important to note that since the full multi-mode continuum disconnection model successfully reproduces atomistic simulation results15 and the reduced-order model agrees with the steady-state of that model, the reduced-order model too is consistent with the steady-state obtained from atomistic simulations12.
While the flat GB velocity in the zero-shear model is explicitly given by (12), in the full multi-disconnection mode model15 it depends on the shear stress τ which evolves during disconnection/GB migration during migration (must be determined via elasticity calculations with the appropriate boundary conditions). Calculation of the stress generated by disconnections in the full model has computational complexity \({\mathcal{O}}\left((m+1){N}^{2}\right)\), where m and N are the number of disconnection modes and points in the GB mesh. Calculation of the image stress arising from the boundary conditions in a general full multi-disconnection model is calculated over the entire domain via, for example, the finite element method. (For the simulation geometries/domain considered in the full multi-disconnection mode model, we employ the Airy stress function and Fourier analysis methods.) Elimination of the stress field calculation makes the reduced-order model local and efficient.
Curved grain boundary dynamics
We now consider the dynamics of the capillarity-driven migration of a curved GB. The geometric constraint that connects the disconnection densities with the GB profile is
The GB profile and disconnection density evolution equations (1) and (2) imply that \(\left(\right.\mathop{\sum }\nolimits_{j = 1}^{m}{\rho }^{(j)}{H}^{(j)}-{h}_{x}{\left)\right.}_{t}=0\). Thus, the geometric constraint (15) applies at all times. The disconnection density evolution and the zero-net-shear constraints, (2) and (3), imply that \(\mathop{\sum }\nolimits_{j = 1}^{m}\left(\right.{\rho }^{(j)}{b}^{(j)}{\left)\right.}_{t}=0\); i.e.
This means that the net Burgers vector vanishes at every point on the GB.
We first consider the two-disconnection mode cases: (b(1), H(1)) and (b(2), H(2)), with initial disconnection densities chosen to satisfy constraints (15) and (16):
This yields an explicit expression for the disconnection densities,
Substituting these into the GB profile evolution equation (10), we obtain an explicit expression for the GB evolution:
where
Note, we assumed that the equilibrium disconnection densities c(1) and c(2) are small and only keep their leading order terms.
We performed a series of numerical simulations to study the evolution of a curved GB with two-disconnection modes using the reduced-order (20) and full continuum models15. We again focus on the Σ13[100](015) (near) symmetric tilt GB in Cu (shear modulus μ = 45 GPa and Poisson ratio ν = 0.36) in the two-mode limit (parameters above); the symmetric GB has energy γ = 0.878 J ⋅ m−2 19. The GB has an initially sinusoidal profile \(h=0.03{L}_{0}\sin (2{\rm{\pi }}x/{L}_{0})\) with period L0 = 100 Å. While the initial disconnection densities in the full multi-disconnection mode model are arbitrary chosen (we examine two cases below), in the reduced-order model these satisfy (19).
First, we examine the case where the initial disconnection densities in the reduced-order and full model are identical (19) (Fig. 4a–c). As shown in Fig. 4a, b, the reduced-order model predictions for the evolution of both the GB profile and densities of the two-disconnection modes are in excellent agreement with the predictions from the full continuum model with the same number of modes. To provide a more quantitatively comparison of the two sets of predictions, we also calculated the differences of the GB migration velocities and the differences in the rates of changes of the disconnection densities between the reduced-order model and the full model, as shown in Fig. 4c. The differences between the two models decay rapidly to zero; indicating again that the errors intrinsic to the reduced-order model are associated with small, short-lived transients.
The temporal evolution of the GB profile in a, d and density in b, e of each disconnection mode using the reduced-order model (solid lines) and the full multi-disconnection mode model (dashed lines with circles) for two-disconnection modes. The arrows indicate the direction of the evolving curves. c, f The difference between the predictions of the reduced-order model and the full multi-disconnection mode model for the GB velocity and rates of change of the disconnection densities during the evolution of the initially sinusoidal profile GB. These data are calculated at the positions of the arrows in a, b, d and e. Panels a–c correspond to the case where the initial disconnection densities in both models are the same (19), and d–f correspond to a case where the initial densities are different—as described in the text.
In the second comparison, we choose the initial disconnection densities in the full multi-disconnection mode model to be different from those in (19) in the reduced-order model; i.e. the initial disconnection densities in the full multi-disconnection mode model was ρ(1) = hxc(1)/(c(1)H(1) − c(2)H(2)), ρ(2) = hxc(2)/(c(2)H(2) − c(1)H(1)). The comparisons, shown in Fig. 4d–f, indicate that the GB profiles evolution are well-predicted by the reduced-order model and the full multi-disconnection mode model disconnection densities rapidly decay to those predicted from the reduced-order model. While the differences decay rapidly, the magnitude of the initial differences in the evolution rates (Fig. 4f) is an order of magnitude larger than when the initial disconnection densities are the same, as expected. These results demonstrate that there are two sources of error associated with the reduced-order model. The first is associated with the zero-shear assumption (the heart of the reduced-order formalism) and the second is associated with the initial disconnection densities which are inevitably unknown (in most applications). Fortunately, both of these only affect transient behaviour, such that the reduced-order and full multi-disconnection mode models match after a short-time transient.
In the present two-disconnection-mode examples, the constraints (17) and (18) in the reduced-order model uniquely determine the densities of the two modes of disconnections (19) and the GB evolution equation (20) is an explicit expression for the GB profile evolution, without requiring the tracking of the evolution of the disconnection densities. However, in the general m-disconnection modes (m ≥ 3) case, the two constraints (15) and (16) are not sufficient to uniquely determine the disconnection densities, i.e. there is an infinite set of possible disconnection densities for any given GB profile h. In this case, we must solve both the equations for the GB motion (10) and the evolution of the disconnection densities (11) in the reduced-order model; here the disconnection density and GB profile evolution are coupled; see Supplementary Fig. 1 for simulation results for GB evolution with three disconnection modes.
While the results presented above demonstrated that the reduced-order model provides accurate predictions for the evolutions of arbitrarily curved GBs and the disconnection densities on them, a major advantage of the reduced-order model (as compared with the full continuum multi-disconnection mode model) is computational efficiency. As discussed in the previous section, the reduced-order model avoids the time-consuming \({\mathcal{O}}({N}^{2})\) calculation (N is the number of numerical grid/mesh points on GBs) of singular integrals for the stress generated by disconnections and the auxiliary elasticity problem over the entire computational domain associated with elastic boundary conditions. Hence, the reduced-order model provides a simple, efficient and accurate method to track GB motion based upon a mechanistically accurate disconnection mechanism.
Discussion
We presented a reduced-order, local continuum model for GB migration appropriate for microstructure evolution in polycrystals that accounts for mechanical constraints through the zero-net-shear condition. Our reduced-order model is based on the underlying microscopic mechanism of GB dynamics, in which GB migration and shear are associated with disconnection migration along with a GB. Our model leads to explicit evolution equations for the GB profile and disconnection densities. The strong zero-net-shear constraint implies that the reduced-order model does not capture short-time, transient effects but accurately describes long-time (steady-state) GB dynamics. The zero-net-shear assumption implies that the reduced-order model does not capture GB sliding or grain rotation.
When the GB is flat, Eq. (12) implies that the GB migration velocity is proportional to the driving force (chemical potential-jump Ψ). The migration of a general curved GB is described by ht = − B(Ψ − γhxx)(∣hx∣ + D), where B and D are functions of disconnection parameters (20). D is associated with the equilibrium disconnection densities c(j) and is small at low T. At high T, with large equilibrium disconnection densities c(j), D is large and ∣hx∣ ≪ D. In this limit, the GB equation of motion reduces to classical curvature flow ht = − MGB(Ψ − γhxx) (MGB = BD).
The reduced-order model implies that two or more disconnection modes must be active on a GB to satisfy the zero-net-shear constraint (unless the lowest formation energy disconnection is a pure step). If there is only one disconnection mode active on a GB, the constraint (3) reduces to \(\dot{\epsilon }=bJ=0\). This constraint directly implies that GB motion is described by \({h}_{t}=-HJ=-\frac{1}{\beta }bJ=0\); in other words, GBs in polycrystals cannot migrate with a single disconnection mode. This conclusion is consistent with the observation of GB stagnation in bicrystal atomistic simulations12 and the observations that most GBs do not move at low temperature, where only one disconnection mode is activated. The internal stress on the GB can be obtained from the constraint,
which is satisfied only when βτ + (Ψ − γhxx) = 0. When the GB is flat, we have hxx = 0 and τ = −Ψ/β, which implies that if a chemical potential-jump Ψ is applied to the GB, its migration will generate a back stress τ. Their relationship τ = −Ψ/β is in agreement with molecular dynamics simulations12.
The character of different disconnection modes active on a GB influences GB dynamics. Figure 5 compares the GB evolution when there are two and three disconnection modes active. At T = 800 K, the GB profiles evolve almost identically (Fig. 5a). On the other hand, at the relatively high temperature of T = 1200 K, the GB profile evolves more quickly when three modes are included (relatively to the two-mode case) (Fig. 5b). The disconnection formation energies increase and formation rates decrease with increasing mode number13,15,36,37. The thermally nucleated disconnections have a non-negligible effect at high T, while disconnection migration dominates GB evolution at low T.
Comparison of the GB profile evolution in the case of two and three disconnection modes. The arrows indicate the direction of the evolving curves. The three disconnections modes share the same Burgers vector \({b}^{(i)}=b={a}_{0}/\sqrt{26}\), and H(1) = 4b, H(2) = −2.5b, H(3) = − 9b. The initial disconnection densities for the first two modes are as per (19), while in the three mode calculations in a, b, we also set the initial values of ρ(3) = 0. In c, the initial disconnection densities are as per (15) and (16) with ρ(1):ρ(2):ρ(3) = 1:−0.65:−0.35.
We also compare the evolution of the GB profile and disconnection densities in the two and three disconnection mode cases for arbitrary initial disconnection densities (see Fig. 5c and the Supplementary Information for details). Again, we see that the observation that GB migration is faster when more disconnections modes are included at high temperature is a general phenomenon. We reiterate that with a single disconnection mode GB migration does not occur, at low T GB migration with two or three (or more) modes are nearly identical and adding more modes increases the migration rate at high T.
The present paper presents a reduced-order model for GB motion in a two-dimensional continuum dynamics framework based upon the underlying (discrete) disconnection dynamics mechanism; our formulation is computationally efficient and appropriate for large-scale simulations. Here, we described the model and showed examples specifically for the case of GB migration in a two-dimensional system. This two-dimensional model can be extended to three dimensions, appropriate for application to polycrystalline microstructures in typical materials. While the main ideas and model present here easily translate to three dimensions, there are some important differences. First and foremost, disconnections in three dimensions are lines rather than points and hence the model must include disconnection topology and its evolution. Second, disconnection nucleation in three dimensions includes a wider range of option than considered here in two dimensions; including disconnection bowing, disconnection loop formation, etc. The three-dimensional continuum framework for the dynamics of low angle grain boundaries incorporating dislocation structures38,39 can be adopted. Alternatively, the three-dimensional model can also be implemented in a discrete dislocation dynamics-type of framework, albeit constrained to a plane (similar to dislocation dynamics where dislocations are constrained to a slip plane; see e.g. refs. 40,41,42,43,44). The constraint of disconnections lines to a GB plane rather than dislocation lines in three dimensions means that such calculations need only be codimension 1 rather than 2 in the three-dimensional dislocation dynamics case; hence such three-dimensional simulations are much easier to implement than full, three-dimensional dislocation dynamics simulations. Such discrete dislocation-dynamic like calculations may be implemented in either sharp or diffuse dislocation/disconnection dynamics formulations.
Methods
Derivation of disconnection velocity
The disconnection glide velocity expression (5) is applicable to the case where the motion is overdamped; i.e. the velocity is proportional to the driving force \({f}_{{\rm{d}}}^{(j)}\), i.e., \({v}^{(j)}={M}_{{\rm{d}}}^{(j)}\cdot {f}_{{\rm{d}}}^{(j)}\), where \({M}_{{\rm{d}}}^{(j)}\) is the disconnection mobility. The driving force on a jth mode disconnection is
which has contributions from the stress τ (both applied stress and that originating from all other disconnections), the jump in the energy/chemical potential across the GB Ψ, and capillarity where γ is the GB energy density. Positive/negative disconnection density ρ(j) implies disconnections of type (b(j), H(j))/(−b(j), −H(j)) with velocities v(j)/ − v(j). The disconnection flux is J(j) = v(j)(∣ρ(j)∣ + c(j)), as per (4).
Numerical methods of the grain boundary evolution
In the numerical simulations, we employ a forward Euler and finite difference methods in time and space. The GB length L0 is discretised into N equally spaced intervals [xi−1, xi], where xi = x0 + iΔx, Δx = L0/N, i = 0, 1, … , N. h(x) and ρ(x) are evaluated at spatial discrete points and hx is calculated using a backward difference scheme and hxx using a centre difference scheme. ∣ρ(j)∣ in \({A}^{(j)}={M}_{{\rm{d}}}^{(j)}{{b}^{(j)}}^{2}(| {\rho }^{(j)}| +2{c}^{(j)})\) is calculated using an upwind scheme. The discretised temporal points are tn = nΔt, n = 0, 1, 2, …. The numerical value of a function g(x, t) at the discrete spacial point xi and temporal point tn is denoted as \({g}_{i}^{n}\).
Specifically, the GB evolution in Eq. (20) is numerically implemented as
The GB profile and disconnection density evolution equations (10) and (11) are numerically implemented as
where
Periodic boundary conditions are applied at the endpoints of the GB.
Data availability
The data and codes that support the findings of this study are available from the authors upon reasonable request.
References
Sutton, A. P. and Balluffi, R. W. Interfaces in Crystalline Materials (1995).
Hillert, M. On the theory of normal and abnormal grain growth. Acta Metall. 13, 227–238 (1965).
Mullins, W. Two-dimensional motion of idealized grain boundaries. J. Appl. Phys. 27, 900–904 (1956).
Ashby, M. F. Boundary defects, and atomistic aspects of boundary sliding and diffusional creep. Surface Sci. 31, 498–542 (1972).
Bollmann, W. Crystal Defects and Crystalline Interfaces (1970).
King, A. H. & Smith, D. A. The effects on grain-boundary processes of the steps in the boundary plane associated with the cores of grain-boundary dislocations. Acta Cryst. A36, 335–343 (1980).
Hirth, J. P. & Pond, R. C. Steps, dislocations and disconnections as interface defects relating to structure and phase transformations. Acta Mater. 44, 4749–4763 (1996).
Khater, H. A., Serra, A., Pond, R. C. & Hirth, J. P. The disconnection mechanism of coupled migration and shear at grain boundaries. Acta Mater. 60, 2007–2020 (2011).
Rajabzadeh, A., Mompiou, F., Legros, M. & Combe, N. Elementary mechanisms of shear-coupled grain boundary migration. Phys. Rev. Lett. 110, 265507 (2013).
Rajabzadeh, A., Legros, M., Combe, N., Mompiou, F. & Molodov, D. A. Evidence of grain boundary dislocation step motion associated to shear-coupled grain boundary migration. Philos. Mag. 93, 1299–1316 (2013).
Mompiou, F., Legros, M., Ensslen, C. & Kraft, O. In situ TEM study of twin boundary migration in sub-micron be fibers. Acta Mater. 96, 57–65 (2015).
Thomas, S. L., Chen, K. T., Han, J., Purohit, P. K. & Srolovitz, D. J. Reconciling grain growth and shear-coupled grain boundary migration. Nature Commun. 8, 1764 (2017).
Han, J., Thomas, S. L. & Srolovitz, D. J. Grain boundary kinetics: a unified approach. Prog. Mater. Sci. 98, 386–476 (2018).
Zhang, L. C., Han, J., Xiang, Y. & Srolovitz, D. J. Equation of motion for a grain boundary. Phys. Rev. Lett. 119, 246101 (2017).
Wei, C. Z., Thomas, S. L., Han, J., Xiang, Y. & Srolovitz, D. J. A continuum multi-disconnection-mode model for grain boundary motion. J. Mech. Phys. Solids 133, 103731 (2019).
Thomas, S. L., Wei, C. Z., Han, J., Xiang, Y. & Srolovitz, D. J. Disconnection description of triple junction motion. Proc. Natl. Acad. Sci. USA 116, 8756–8765 (2019).
Wei, C. Z., Zhang, L. C., Han, J., Srolovitz, D. J. & Xiang, Y. Grain boundary triple junction dynamics: a continuum disconnection model. SIAM J. Appl. Math. 80, 1101–1122 (2020).
Cahn, J. W. & Taylor, J. E. A unified approach to motion of grain boundaries, relative tangential translation along grain boundaries, and grain rotation. Acta Mater. 52, 4887–4898 (2004).
Cahn, J. W., Mishin, Y. & Suzuki, A. Coupling grain boundary motion to shear deformation. Acta Mater. 54, 4953–4975 (2006).
Taylor, J. E. & Cahn, J. W. Shape accommodation of a rotating embedded crystal via a new variational formulation. Interfaces Free Boundaries 9, 493–512 (2007).
Winning, M., Gottstein, G. & Shvindlerman, L. S. Stress induced grain boundary motion. Acta Mater. 49, 211–219 (2001).
Winning, M., Gottstein, G. & Shvindlerman, L. S. On the mechanisms of grain boundary migration. Acta Mater. 50, 353–363 (2002).
Gottstein, G., Molodov, D. A., Shvindlerman, L. S., Srolovitz, D. J. & Winning, M. Grain boundary migration: misorientation dependence. Curr. Opin. Solid State Mater. Sci. 5, 9–14 (2001).
Molodov, D. A., Ivanov, V. A. & Gottstein, G. Low angle tilt boundary migration coupled to shear deformation. Acta Mater. 55, 1843–1848 (2007).
Rupert, T. J., Gianola, D. S., Gan, Y. & Hemker, K. J. Experimental observations of stress-driven grain boundary migration. Science 326, 1686–1690 (2009).
Molteni, C., Francis, G. P., Payne, M. C. & Heine, V. First principles simulation of grain boundary sliding. Phys. Rev. Lett. 76, 1284–1287 (1996).
Molteni, C., Marzari, N., Payne, M. C. & Heine, V. Sliding mechanisms in aluminum grain boundaries. Phys. Rev. Lett. 79, 869–872 (1997).
Hamilton, J. C. & Foiles, S. M. First-principles calculations of grain boundary theoretical shear strength using transition state finding to determine generalized gamma surface cross sections. Phys. Rev. B 65, 064104 (2002).
Chen, L. Q. & Kalonji, G. Finite temperature structure and properties of Σ = 5 (310) tilt grain boundaries in NaCl a molecular dynamics study. Philos. Mag. A 66, 11–26 (1992).
Shiga, M. & Shinoda, W. Stress-assisted grain boundary sliding and migration at finite temperature: a molecular dynamics study. Phys. Rev. B 70, 054102 (2004).
Sansoz, F. & Molinari, J. F. Mechanical behavior of Σ tilt grain boundaries in nanoscale Cu and Al: a quasicontinuum study. Acta Mater. 53, 1931–1944 (2005).
Trautt, Z., Adland, A., Karma, A. & Mishin, Y. Coupled motion of asymmetrical tilt grain boundaries: molecular dynamics and phase field crystal simulation. Acta Mater. 60, 6528–6546 (2012).
Homer, E. R., Foiles, S. M., Holm, E. A. & Olmsted, D. L. Phenomenology of shear-coupled grain boundary motion in symmetric tilt and general grain boundarie. Acta Mater. 61, 1048–1060 (2013).
Han, J., Vitek, V. & Srolovitz, D. J. Grain-boundary metastability and its statistical properties. Acta Mater. 104, 259–273 (2016).
Mishin, Y., Mehl, M. J., Papaconstantopoulos, D. A., Voter, A. F. & Kress, J. D. Structural stability and lattice defects in copper: ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B Condens. Matter 63, 224106 (2001).
Chen, K. T., Han, J., Thomas, S. L. & Srolovitz, D. J. Grain boundary shear coupling is not a grain boundary property. Acta Mater. 167, 241–247 (2019).
Hirth, J. P. and Lothe, J. Theory of Dislocations. 2nd ed (1982).
Qin, X. X., Zhang, L. C. & Xiang, Y. A three-dimensional continuum simulation method for grain boundary motion incorporating dislocation structure. Preprint at https://arxiv.org/abs/2102.00386 (2021).
Zhu, X. H. & Xiang, Y. Continuum framework for dislocation structure, energy and dynamics of dislocation arrays and low angle grain boundaries. J. Mech. Phys. Solids 69, 175–194 (2014).
Wang, Y. U., Jin, Y. M., Cuitino, A. M. & Khachaturyan, A. G. Nanoscale phase field microelasticity theory of dislocations: model and 3D simulations. Acta Mater. 49, 1847–1857 (2001).
Koslowski, M., Cuitino, A. M. & Ortiz, M. A phase-field theory of dislocation dynamics, strain hardening and hysteresis in ductile single crystals. J. Mech. Phys. Solids 50, 2597–2635 (2002).
Rodney, D., Le Bouar, Y. & Finel, A. Phase field methods and dislocations. Acta Mater. 51, 17–30 (2003).
Shen, C. & Wang, Y. Phase field model of dislocation networks. Acta Mater. 51, 2595–2610 (2003).
Xiang, Y., Cheng, L. T., Srolovitz, D. J. & Weinan, E. A level set method for dislocation dynamics. Acta Mater. 51, 5499–5518 (2003).
Acknowledgements
L.Z. acknowledges support from the Hong Kong Research Grants Council General Research Fund 16301720. J.H. acknowledges support from CityU in the form of a Start-up Grant 7200667 and a Strategic Research Grant 7005466. D.J.S. and Y.X. acknowledge support from the Hong Kong Research Grants Council Collaborative Research Fund C1005-19G. D.J.S. also acknowledges partial support from the US Army Research Office under Grant Number W911NF-19-1-0263.
Author information
Authors and Affiliations
Contributions
L.Z., J.H., D.J.S. and Y.X. developed the reduced-order model. L.Z. and Y.X. derived analytical formulations and designed the numerical scheme. J.H. and D.J.S. designed simulation examples and analysed the implications. L.Z. performed the numerical simulations. L.Z., J.H., D.J.S. and Y.X. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, L., Han, J., Srolovitz, D.J. et al. Equation of motion for grain boundaries in polycrystals. npj Comput Mater 7, 64 (2021). https://doi.org/10.1038/s41524-021-00532-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00532-6
This article is cited by
-
Advances in Experimental Studies of Grain Growth in Thin Films
JOM (2024)
-
Symmetric or asymmetric glide resistance to twinning disconnection?
npj Computational Materials (2022)