Abstract
Predicting the properties of materials prior to their synthesis is of great importance in materials science. Magnetic and superconducting materials exhibit a number of unique properties that make them useful in a wide variety of applications, including solid oxide fuel cells, solid-state refrigerants, photon detectors and metrology devices. In all these applications, phase transitions play an important role in determining the feasibility of the materials in question. Here, we present a pipeline for fully integrating data extracted from the scientific literature into machine-learning tools for property prediction and materials discovery. Using advanced natural language processing (NLP) and machine-learning techniques, we successfully reconstruct the phase diagrams of well-known magnetic and superconducting compounds, and demonstrate that it is possible to predict the phase-transition temperatures of compounds not present in the database. We provide the tool as an online open-source platform, forming the basis for further research into magnetic and superconducting materials discovery for potential device applications.
Similar content being viewed by others
Introduction
Experimentally driven materials discovery is costly, inefficient and largely reliant on scientific intuition1,2. Materials informatics is an emerging field of research that aims to enhance this materials discovery process through computational methods. Although still developing, materials informatics has demonstrated the effectiveness of machine learning for property prediction and materials discovery2,3,4,5,6. Spearheaded by the Materials Genome Initiative7, a variety of big-data projects have since emerged. By far, the majority of such projects are high-throughput computational methods; examples include the Harvard Clean Energy Project8 and the Materials Project9, focussed on the discovery of photovoltaic and battery materials, respectively. Although computationally expensive, these approaches present significant savings in time and cost compared with experimentally driven research, thereby decreasing the timeline of materials discovery from decades to months. High-throughput projects that integrate computational and experimental data are rare, but afford actual materials discovery where they do exist10.
Despite the rapid increase in the use of machine learning for materials discovery over the last decade, relatively little has been reported for the prediction of properties of inorganic compounds that exhibit magnetism and superconductivity. Some recent work has used machine learning to investigate inorganic materials and properties, such as the ferroelectric Curie points in perovskites11, superconducting critical temperatures in cuprates12, bandgaps in double perovskites13 and thermal hysteresis and glass-forming abilities in alloys6. Across the experimental and computational spectrum, a great deal of attention has been paid to the identification of previously unobserved structure–property relationships. However, the relationships between bulk properties, materials composition and structure are non-linear, and the dimensionality of the data space is far too large to analyse experimentally. As such, machine learning has the potential for great utility in magnetic and superconducting materials science.
For example, the phase space of magnetic and superconducting materials is highly influential on the possible device applications. For magnetic materials, the Curie and Néel temperatures, which denote the points at which a material transitions to a ferromagnetic or antiferromagnetic state, respectively, are important properties for solid-state refrigerants14, generators and spintronic or data-storage devices15. Similarly, in the domain of superconductivity, experimental research has been dedicated to the discovery of near-room-temperature superconductors that would have applications in magnetometers, digital circuits, photon detection and power conversion16.
A key barrier to the widespread use of machine learning for materials discovery is the lack of large and structured materials property databases upon which machine-learning techniques can be applied. Previous studies make use of small-scale, manually compiled databases or repositories that are not freely available17,18,19. Thus, the research does not make full use of the vast amount of data available in the scientific literature, and often focusses on small subsets of data that are not fully representative. Manual compilation of scientific literature data is clearly unfeasible, but with recent advances in the field of natural language processing (NLP), it is now possible to automate data mining from text and tables. This provides an opportunity for the automated generation of materials property databases and complete integration of data extracted from the scientific literature into machine-learning pipelines. Such NLP-driven materials science has yielded novel embeddings for structure–property relationships20, large autogenerated property databases21 and mappings of quantum materials databases22.
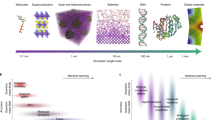
To that end, we herein present a complete and general pipeline that fully integrates the scientific literature into a machine- learning and property prediction toolkit. Our combined workflow is shown in Fig. 1.
1. Using the advanced ‘chemistry aware’ NLP toolkit, ChemDataExtractor (Version 1.3), we extract chemical names and their associated phase-transition temperatures from the scientific literature. 2. These data are automatically standardised and paired with relevant atomic and structural features to form a highly detailed database of materials properties. 3. Using machine learning, we are able to accurately reconstruct phase diagrams and predict phase transitions for unseen compounds. 4. An ‘Associated Data’ facility enables backward validation of predictions against DOI-tagged experimental data.
From a corpus of 74,000 scientific journal articles that are scraped from the webpages of Elsevier, Springer and Royal Society of Chemistry publishers, we use the advanced NLP pipeline within the ‘chemistry aware’ ChemDataExtractor toolkit23 to autogenerate a database of \(\approx\)20,400 magnetic and superconducting phase-transition temperature records and their associated chemical compound names. These data are automatically cleaned and paired with elemental and structural data present in existing data repositories24. We freely provide the complete database in the form of an online magnetic materials-discovery web application at http://magneticmaterials.org. Based on user input of the desired material compositions, the web application automatically reconstructs the phase diagram from the mined data. This gives the user an ability to explore previously unseen structure-phase relationships across multiple independent source documents. Beyond visualisation, the user is able to make use of machine-learning methods to predict phase transitions for materials not present in the database. These predictions can be further validated though an ‘Associated Data’ facility that allows for backward validation of predictions against DOI-tagged experimental research.
In this paper, we demonstrate, through case studies of the perovskite-type oxides and pnictide superconductors, that the reconstructed phase diagrams and associated predictions are highly accurate and directly relatable to the underlying physical theory of magnetism and superconductivity.
Results
Case study of perovskite manganites: reconstructing phase diagrams
We begin with a case study of the perovskite-type oxides. The properties and phase diagrams of the common perovskite series have been widely reported, making these materials ideal candidates to evaluate our database and phase-transition prediction toolkit. The perovskite-type oxides are inorganic compounds with the general formula \({\mathrm{AB}}{\mathrm{O}}_{3}\), where A is a large 12-coordinated cation and B is a smaller 6-coordinated cation. The generic perovskite structure is cubic; however, this form is rarely found owing to structural deformation25. These deformations cause perovskites to exhibit a wide variety of interesting and useful properties, including ferroelectricity, piezoelectricity, superconductivity and magnetism26. As such, perovskite materials are found in a vast number of applications.
Magnetism in perovskites arises through the incorporation of paramagnetic cations. Commonly, cationic species are lanthanides or transition metals, which have partially filled d and f orbitals. Through the crystal-field interaction, local-coordination environments determine the orbital energy levels and hence the magnetic moment of the cation. The large dependence of the magnetic properties on the crystal field leads to a substantial variation in magnetic state with temperature and composition. With only minor changes in doping concentration of the A- and B-site cations, the compounds undergo transitions between multiple magnetic phases. A prime example of this is the \({\mathrm{L}}{{\mathrm{a}}}_{1-x}{\mathrm{S}}{{\mathrm{r}}}_{x}{\mathrm{Mn}}{{\mathrm{O}}}_{3}\) (\(0\le x\le 1\)) system27 that displays a bulk metallic ferromagnetic phase and four different antiferromagnetic phases.
An example of the reported phase diagram of \({\mathrm{L}}{{\mathrm{a}}}_{1-x}{\mathrm{S}}{{\mathrm{r}}}_{x}{\mathrm{Mn}}{{\mathrm{O}}}_{3}\) is shown in Fig. 2a. Owing to the costly nature of producing experimental data, research articles often focus on a small subsection of magnetic and superconducting phase diagrams, or alternatively present general trends with little specificity, as shown in Fig. 2a. The first key contribution of our work is the ability to automatically aggregate materials property data across a vast number of source documents. These data contain independent experimental results, and therefore our toolkit visualises previously unseen chemical property relationships where previous data were highly fragmented.
a Reported phase diagram of the perovskite-type oxide series \({\mathrm{L}}{{\mathrm{a}}}_{1-x}{\mathrm{S}}{{\mathrm{r}}}_{x}{\mathrm{Mn}}{{\mathrm{O}}}_{3}\), reproduced with permission from Tilley25. AFM A, AFM C and AFM G refer to the A-, C- and G-type antiferromagnetic phases, respectively. b The autoreconstructed phase diagram created using our text-mining and visualisation toolkit. The diagram clearly exhibits a bulk ferromagnetic phase for \(0.1\le x\le 0.6\) and antiferromagnetic phases for \(x\le 0.1\) and \(x\ge 0.5\). Error bars show the standard deviation between values of individual measurements mined for each composition where multiplicate data exist.
The corresponding phase diagram that has been automatically reconstructed from the scientific literature using our NLP pipeline is shown Fig. 2b. The reconstructed diagram shows high correlation with the generally reported trend, and clearly distinguishes the ferromagnetic (\(0.1\le x\le 0.6\)) and the antiferromagnetic (\(x\le 0.1\) and \(x\ge 0.5\)) phases, although currently we are unable to distinguish between the A-, C- and G-type antiferromagnetism. As shown in Fig. 2b, each transition temperature has associated error bars. The phase-transition temperature at each composition is calculated as the mean of all text-mined values, with the error bars taken to be 1 standard deviation. All values can be easily referenced back to their original sources since our toolkit tracks the DOI associated with each data point in the reconstruction. This permits backward validation and investigation of spurious or interesting values.
Case study of antiferromagnetic perovskites: predicting Néel temperatures in rare-earth manganites
Antiferromagnetic interactions in perovskites originate from the superexchange mechanism25. This is defined as an indirect exchange interaction between non-neighbouring magnetic cations that is mediated by a non-magnetic anion (Fig. 3).
Such examples include the rare-earth manganite series \({\mathrm{LNMn}}{{\mathrm{O}}}_{3}\) where \({\mathrm{LN}}\) is a lanthanide ion. The Néel temperature dependence of the series, reconstructed using our NLP pipeline, is shown in Fig. 4 vs. the ionic radius of the LN cation. We also show reference values28,29, taken from articles not present in our text-mining corpus, for comparison. Both the reference and reconstructed diagrams show a clear non-linear dependence. This non-linearity results from a structural phase transition. For LN = Dy, Ho, Er, Yb, Lu, the compounds typically crystallise in a stable hexagonal structure30. In these perovskites, the linkage between the cations can be either \(18{0}^{\circ }\) or \(9{0}^{\circ }\) (Fig. 3b), yielding very different superexchange mechanisms to the typically orthorhombic manganite compounds for LN = La, Pr, Nd, Sm, Eu, Gd, Tb, which show a roughly linear Néel temperature dependence.
The autoreconstructed phase diagram of \({\mathrm{LNMn}}{{\mathrm{O}}}_{3}\) series vs. ionic radius of the 6-coordinated LN cation alongside reported values28,29 not present in the text-mined corpus. The series demonstrates non-linear dependence of Néel temperature due to the structural transition between \({\mathrm{LN=Dy}}\) and \({\mathrm{LN=Tb}}\). Error bars show the standard deviation between values of individual measurements mined for each composition where multiplicate data exist.
Case study of antiferromagnetic perovskites: predicting Néel temperatures in rare-earth orthochromites
In the orthorhombic perovskite structure, which displays \(18{0}^{\circ }\) superexchange, the geometry favours antiferromagnetic alignment, and thus, the orthorhombic perovskites typically demonstrate a clear Néel transition. Another example of the orthorhombic perovskites are the rare-earth orthochromite series \({\mathrm{LNCr}}{{\mathrm{O}}}_{3}\). Here, the theory of superexchange indicates that the strength of the antiferromagnetic interaction, and hence the Néel temperature of the material, depends on the degree of the orbital overlap between the cations and their mediating anion. Figure 5a shows the reported Néel temperature of the \({\mathrm{LNCr}}{{\mathrm{O}}}_{3}\) series as a function of the LN ionic radius. In accordance with the superexchange theory, increasing ionic radius causes a roughly linear increase in Néel temperature. Figure 5b shows the corresponding phase diagram reconstructed using our text-mined database. Again, we see a highly accurate reconstruction of the phase diagram. However, the reconstruction tool is not only useful for visualising these trends. A distinct contribution of this work is that the text-mined phase-transition records are automatically paired with bulk structural features and elemental properties of the constituent elements. Using these features, we are able to construct physically interpretable machine-learning models of phase transitions, and therefore perform phase-transition temperature prediction.
a Reported Néel phase diagram of the \({\mathrm{LNCr}}{{\mathrm{O}}}_{3}\) (\({\mathrm{LN=Lanthanide}}\)) series vs. ionic radius of the 6-coordinated LN cation, values reproduced from Goodenough and Longo34. b The corresponding phase diagram that has been autoreconstructed with our text-mining pipeline. We also show the predicted Néel phase-transition temperatures (orange) of the Tm, Eu, Sm, Nd, Pr and Ce members, obtained using Automatic Relevance Determination with K-best feature selection on our combined database. Error bars show the standard deviation between values of individual measurements mined for each composition where multiplicate data exist.
To this end, we note that the text-mined series in Fig. 5b is missing the Tm, Eu, Nd, Pr and Ce members. Making use of the machine-learning and feature-selection algorithms outlined in the Methods, the mined data are used to create a predictive model for the Néel temperature in these rare-earth orthochromites.
Table 1 shows the reported and predicted Néel temperatures for the missing compounds achieved with various different prediction methods. As shown, the best model, using ridge regression (RR) with K-best feature selection (KB) (K = 5), achieved a mean absolute error (MAE) of 3.1% (for a discussion of the different methods, see the Methods).
By virtue of the automated feature-selection algorithms, we are able to determine the most predictive elemental and structural features, and thus relate the machine-learning model back to the underlying theory. The KB feature selection determined the most predictive features of Néel temperature to be the ionic radius, charge-to-ionic radius ratio and Pauling electronegativity of the LN cation, all of which can be directly related to the orbital theory of superexchange given above.
It is important that the end user is able to backward validate their predictions. We enable this in our platform via an ‘Associated Data’ facility that directly links the property prediction to DOI-tagged experimental and computational data. Given the high cost of generating experimental results from large facilities such as neutron sources, it is now the norm for national laboratories to DOI-tag unpublished experimental data. By linking predictions to these unpublished data, we empower researchers to begin further investigation on a predicted property. Although this is a simple step, it completes the integration of data extracted from scientific literature sources with machine-learning tools and experimental validation procedures.
We demonstrate this through validation of our Néel temperature predictions shown in Fig. 5 and Table 1. For \({\mathrm{CeCr}}{{\mathrm{O}}}_{3}\), Datacite reveals neutron diffraction data created at the Institut Laue-Langevin (ILL)31. These experimental data are still under embargo, and are therefore not currently available for further analysis. However, through publications associated with the experimental data authors, we are able to find reference values for the Néel temperature in CeCrO3, which confirm our predictions32,33.
Although our associated data facility is not strictly needed to find validation of phase-transition temperature predictions, we believe that the Datacite facility greatly enriches the property prediction pipeline through direct linking to first-hand experimental data. For example, while experimental data for our Néel temperature prediction of PrCrO3 can be validated by data tables34, the Datacite DOI linkup from our web application reveals that neutron diffraction data on PrCrO3 have also been collected at high pressure, via the ISIS Neutron and Muon Facility, UK. Although these data are yet to be published, their existence suggests that high-pressure phases of PrCrO3 may yet enrich our current understanding of the Néel temperature in praseodymium orthochromites.
In contrast, a neutron diffraction study on TmCrO3 appears to have been performed in 201335. These data are sufficiently old that they are publicly available. The neutron proposal for this experiment is also available on Datacite. It suggests that there is a complicated multiferroic phase of TmCrO3 whose Néel temperature lies at around 125 K. The experimental metadata show that TmCrO3 was studied above and below this expected Néel temperature. The lack of published research associated with these data gives the potential for researchers to download and re-analyse the raw or processed experimental data to further understand the complicated multiferroic phases in TmCrO3.
Case study of ferropnictide superconductors: unconventional superconductivity
As described in the ‘Introduction', phase transitions also play an important role in the applications of superconducting materials. The ferropnictides are a series of recently discovered iron-based superconductors formed from layers of iron and a pnictide material (see the inset in Fig. 7). The theory of superconductivity in these compounds diverges from the conventional Bardeen–Cooper–Schrieffer (BCS) model in which superconductivity arises as a direct result of electron–phonon coupling36. Instead, ferropnictide superconductivity is caused by electron–electron Coulomb interactions37. This unconventional superconductivity is indicated in the phase diagrams of the ‘1222-type’ superconductors. Thereby, the superconducting state arises near the onset of antiferromagnetic order in metals with very low electrical conductivity.
An example of such a system is \({\mathrm{BaF}}{{\mathrm{e}}}_{2-x}{\mathrm{N}}{{\mathrm{i}}}_{x}{\mathrm{A}}{{\mathrm{s}}}_{2}\), whose phase diagram is shown in Fig. 6. The compound is a typical 1222-type superconductor and its end member, \({\mathrm{BaF}}{{\mathrm{e}}}_{2}{\mathrm{A}}{{\mathrm{s}}}_{2}\) (\(x=0\)), exhibits antiferromagnetism up to around 140 K. Above this temperature, it is a paramagnetic ‘bad-metal’ with high resistivity. As the Ni content, \(x\), is increased, the Néel temperature decreases until a superconducting phase begins to emerge below 20 K. At a certain critical doping concentration, \({x}_{c}\approx 0.07\), the antiferromagnetic and superconducting states coincide at \(T\approx 40\) K. For higher concentrations, the Néel phase is suppressed, and superconductivity below 20 K is observed. For doping concentrations above \(x=0.20\), the system returns to a non-superconducting paramagnet. This is reflected clearly in our autoreconstructed phase diagram shown in Fig. 6b.
a The reported phase diagram, reproduced with permission from Si et al.37, and b the autoreconstructed phase diagram created using our toolkit. Both diagrams clearly show that the transition to the superconducting state arises from an antiferromagnetic metallic state. The reconstructed diagram is highly specific, pinpointing a mixed AFM and superconducting state in the region of \({x}_{c}\approx 0.07\). Error bars show the standard deviation between values of individual measurements mined for each composition where multiplicate data exist.
Predicting \({T}_{C}\) across the lanthanides
The first measurement of superconductivity in ferropnictides was reported in 2008, where a critical temperature of 26 K was discovered in \({\mathrm{LaFeAs}}{{\mathrm{O}}}_{0.89}{{\mathrm{F}}}_{0.11}\)38. Subsequently, the highest critical temperature of any non-cuprate superconductor has been measured above 50 K in \({\mathrm{LNFeAs}}{{\mathrm{O}}}_{1-x}{{\mathrm{F}}}_{x}\) where LN = La, Ce, Pr, Nd, Sm39.
Figure 7 shows a plot of the reconstructed superconducting critical temperature presented as a function of \({\mathrm{LN}}\) electronegativity for the \({\mathrm{LNFeAs}}{{\mathrm{O}}}_{1-x}{{\mathrm{F}}}_{x}\) series.
This series has been shown to exhibit the highest critical temperature of any non-cuprate compounds, with superconductivity over 50 K. We also present \({T}_{C}\) predictions for LN = Pm, Eu, Tb − Lu generated via random forest regression with K-best feature selection (K = 5). Error bars show the standard deviation between values of individual measurements mined for each composition where multiplicate data exist. Inset: crystal structure of a typical oxypnictide superconductor \({\mathrm{GdFeAs}}{{\mathrm{O}}}_{0.53}{{\mathrm{F}}}_{0.47}\) with atoms (colours): Gd (magenta), Fe (gold), As (green), O (red) and F (silver).
Again, we see that the text-mined data are limited to \({\mathrm{LN=La-Gd}}\). Thus, we can use our predictive tools to create a model for the superconducting critical temperature in \({\mathrm{LNFeAs}}{{\mathrm{O}}}_{1-x}{{\mathrm{F}}}_{x}\). The plot in Fig. 7 shows the predicted superconducting critical temperature for LN = Tb, Dy, Ho, Er, Tm, Yb, Lu achieved using random forest regression and K-best feature selection (K = 5). Analysis of the chosen features of this model indicates a dependence of \({T}_{C}\) on the work function, atomic number and ionic radius of the \({\mathrm{LN}}\) ion.
Table 2 shows the \({T}_{C}\) predictions and the associated reference values where they could be found. It is interesting here that the reference values for the LN = Pm, Er, Tm, Yb, Lu compounds have not yet been reported at the time of publication. We are therefore ahead of experimental research in this regard.
Discussion
The pipeline and methodology presented here demonstrate the ability to fully integrate data extracted from the scientific literature into machine-learning pipelines for materials discovery. By aggregating data over a large number of independent sources, we negate the limitations of relying on small annotated datasets. Furthermore, the methodology presented herein is entirely general, and can therefore be applied to any set of materials properties.
Overall, these case studies demonstrate that we can accurately reproduce phase diagrams and predict phase-transition temperatures for magnetic and superconducting materials, using their elemental and structural features as a basis. This allows us to relate a collection of independent observations to physical theories of magnetism and superconductivity. This provides a solid foundation for further data-driven magnetic materials discovery. In the first instance, we can now embark on the data-driven mapping of phase diagrams that have yet to be reported. To this end, our web platform is sufficiently versatile that it can accommodate mixtures of computational and experimental data, and machine-learning predictions in its phase-diagram mappings, rather than just assume the default of employing experimental data. This may lead to the discovery of new magnetic and superconducting phases.
Data bestow the core power of our approach. Looking ahead, we will therefore continue to enhance our materials-discovery platform by augmenting its underpinning materials database via extracting data from more articles across a greater number of literature sources. We will also add new properties to the existing database, such as temperature and field-dependent magnetic susceptibility and magnetisation data, as well as superconductivity parameters such as coherence length and penetration depth. We can further enrich these data by providing the experimental or computational parameters associated with each measurement, indicating how the data were derived in the original source article.
As the database continues to grow, and more properties are added, we can build predictive models with even more detail and predictive power. While our current models enable us to predict phase-transition temperatures for known compounds, our ultimate goal is to predict and experimentally validate new classes of compounds for magnetic and superconducting applications. While data-driven materials discovery has been achieved in other fields of research10,40,41, it remains a distant goal in the magnetic and superconductivity domain. Yet, our toolkit is poised for this endeavour since its databank utility could be reverse engineered with some toolkit adaptations to predict material compositions that have desired phase transitions. New material predictions could then be synthesised and verified experimentally. Associated data from the Datacite Metadata Search Tool could prove very effective in aiding such predictions or validating them experimentally. Our web platform linkup to Datacite also provides a rare two-way channel between raw and processed experimental data within a materials prediction framework. Amongst other benefits, the two-way mixing of such data knowledge could be exploited to unravel a new realm of materials prediction that couples raw and processed data through, as yet unknown, forms of data correlations. Irrespective of the actual predictive models that end up being used to realise data-driven materials discovery for magnetic and superconducting applications, the important endgame is that they will accelerate discovery to drive innovation down from its current ‘molecule-to-market’ timeframe of 20 years towards the 5-year goal of the Materials Genome Initiative7.
Methods
Autogenerated data extraction and database creation
The methodology for this work can be summarised in seven stages: data acquisition, database generation, data standardisation, database evaluation, phase-diagram reconstruction, phase-transition temperature prediction and the ‘Associated Data’ facility. The main dataset for this work is a database of magnetic and superconducting phase transitions for inorganic compounds. These data were automatically mined from text and tables contained within journal articles of Elsevier, Springer and the Royal Society of Chemistry publishers, using the ‘chemistry-aware’ NLP toolkit, ChemDataExtractor23 (Version 1.3). This information-retrieval stage particularly targeted journals in the area of condensed-matter physics, superconductivity, magnetism and inorganic chemistry, since these were judged to be particularly relevant to the data type sought. For a full list of search queries and publishers used, see Supplementary Table 1. Automated web-scraping techniques sourced a corpus of 74,000 articles from these academic publishers.
The mining procedure applied to these data used solely text-parsing methods, as described in the original ChemDataExtractor v1.3.0 publication23, in which the toolkit utilises machine-learning processes, such as Brown clustering42, to identify and associate chemically named entities to their properties. The built-in interdependency-resolution system enables ChemDataExtractor to correctly associate chemicals to the correct compound even when multiple compounds are present in the text.
This process yielded a set of 29,000 mutually consistent data records from a total of 4728 unique articles. These data were collated in the Database Management Framework, MongoDB43, containing the chemical formula of a compound and its associated phase-transition temperature. Each entry was tagged with the information that identifies its document source; these tags include the Digital Object Identifier (DOI), title, authors and the year of publication.
Data standardisation
In their raw form, the chemical data record outputs by ChemDataExtractor23 are noisy and non-standardised, making them relatively unusable for large-scale analysis and machine learning. Therefore, an automated data-cleaning process was applied to standardise the form of the records and remove incorrect entries. This standardisation process contains four distinct stages:
-
Ambiguous \({T}_{C}\) specifier resolution
-
Conversion of inorganic chemical formulae to Hill Formula notation
-
Temperature unit conversion to Kelvin
-
Resolution of doped compound labels and informal chemical symbols
It is often the case that two separate domains of science use identical abbreviations to denote different properties. A case in point is found within the general condensed-matter physics literature. A Curie temperature is commonly denoted with the specifier \({T}_{C}\), which is also used within the superconductivity literature to denote the superconducting critical temperature. This causes a problem for text extraction methods when the definition of a specifiers is implied by general context, but not explicitly defined. Moreover, magnetism and superconductivity properties are increasingly being reported together; two distinct \({T}_{C}\) values can even appear within the same document. Automated text-parsing techniques are then unable to determine the meaning of the \({T}_{C}\) occurrence.
In our database, it was found that 3959 records had ambiguous \({T}_{C}\) occurrences that were undefined or could not be distinguished as a Curie or superconducting critical temperature, thus limiting the precision of these records. Fortunately, we were able to make this distinction via a machine-learning technique, whereby text classification was used to classify ambiguous \({T}_{C}\) occurrences as pertaining to either superconductivity or magnetism.
All source documents in our corpus were vectorised using the term frequency–inverse document frequency (TF-IDF) method. The training set of the classifiers consisted of \({T}_{C}\) occurrences that were clearly defined as being a Curie temperature or superconducting critical temperature. The test set, comprising the ambiguous \({T}_{C}\) occurrences, was then classified with three standard methods: the support vector machine (SVM), naive Bayes (NB) and K-nearest-neighbour (KNN) classifiers. A peak F1 score of 82% was achieved with the NB classifier (full text-classification results are given in Supplementary Methods 1). Although this approach uses very basic text-classification methods, the main benefit is that no annotation of the training data was required. Therefore, our database was able to self-learn from the existing data in an unsupervised manner in order to clean the records and improve precision.
Phase-transition data record format
Following the specifier ambiguity resolution, each record is further standardised through conversion of compound names to Hill Formula notation, and temperature values converted to units of Kelvin. Finally, any chemical labels found in the text are resolved and associated with the appropriate compound.
At each stage, records that could not be standardised were removed to increase database precision; the number of records at each stage of the standardisation pipeline is shown in Table 3. In total, the standardisation processes yielded a final set of 20,389 records that were retrieved from a small set of only 3668 articles, thus showing that the relevant data were highly sparse within our 74,000-paper corpus.
Overall, this four-stage process affords a single, consistent and highly standardised set of data records. The final format of the records is given in Supplementary Table 2.
Database evaluation
The precision of the database was determined using Eq. (1), where TP is the true-positive rate, FN is the false-negative rate and FP is the false-positive rate.
A sample of 300 records (100 Curie, 100 Néel and 100 superconductivity) were uniformly and randomly sampled from the database, and then evaluated against the original source material. A record was considered to be a true positive if all elements of the record were correct when compared with the original source literature, and all standardisation processes had succeeded. If any part of the record was incorrect, then it was marked as a false positive. Table 4 shows the level of precision of the different record types, and the overall (average) precision of the database, which was calculated to be 82%.
Creating a web-based application that autoreconstructs phase diagrams
A web-based platform was created that automatically reconstructs magnetic and superconducting phase diagrams from the mined data. The platform is interactive and freely available at http://magneticmaterials.org, so that users can explore structure–property relationships in magnetism and superconductivity. Based on user input of any number of elements and their relative material compositions, the phase diagram of the series of these compounds is generated. Curie and Néel temperatures for magnetism, and critical temperatures for superconductivity, can be visualised against a number of material descriptors to explore the phase space.
These compound descriptors include bulk and ionic properties of their constituent elements (e.g. melting points, density and atomic volume; ionic radii, coordination numbers and oxidation states), which were mined from well-established data repositories6,44,45 and associated with the database records during extraction. Some descriptors employed structural information; accordingly, 403,814 crystallographic information files (CIFs), accessed from the open-source Crystallography Open Database (COD)46,47,48,49, provided atomic positions of the mined materials. In total, 36 property features were manually compiled (for a full list of features, see Supplementary Table 3).
Prediction and feature-selection methods
Machine-learning capabilities were also embedded into the web platform, so that the user can predict phase-transition temperatures. Four machine-learning methods were employed: ridge regression (RR), support vector regression (SVR)50, automatic relevance determination (ARD)51 and random forest regression (RFR)52.
Selection of the optimal features to predict phase-transition temperatures is very difficult, especially without expert knowledge of the underlying physics. In order to overcome this difficulty, we provided three methods for feature selection on our web platform: manual feature selection (MFS), K-best feature selection (KB) and recursive feature elimination (RFE).
The following paragraphs provide a brief description of each prediction and feature-selection method with guidance as to where their use is best suited. All of the prediction and feature-selection methods were implemented using the Scikit-Learn Python library53.
Ridge regression is a regularised form of linear least-squares regression, in which the model was designed to reduce overfitting and improve generalisability. The solution finds the optimal weight, \(w\), that minimizes the objection function
where \(y\) is the target phase-transition temperature, \(X\) is the feature matrix and \(| | .| {|}_{2}\) represents the L2 norm. The regularisation parameter, \(\alpha\), controls the level of regularisation. This method is best suited to out-of-sample prediction as it attempts to fit a more general set of model coefficients.
In a simple regression model, the weights are optimised to minimise the error rate. In SVR, we attempt to fit the error within a defined threshold. This forms a decision boundary that reflects a given tolerance threshold for the associated error.
The hyperparameters of the SVR are the kernel, tolerance threshold, \(\epsilon\) and the penalty, \(C\). The model implemented in our toolkit allows for multiple choices of kernel, radial basis function, linear or polynomial, which should be chosen depending on how the data are best represented. The epsilon argument defines the distance of the decision boundary from the true values, and the penalty term controls how much to penalise misclassification of the data points. Overall, SVR is best used when attempting to fit regression models that have non-linear data distributions.
Automatic relevance determination, or Bayesian ridge regression, is used to perform standard ridge regression under a probabilistic model. That is, the coefficient \(w\), is probabilistic with a spherical Gaussian prior defined by
where the priors on \(\lambda\) and \(\alpha\) are gamma distributions. All parameters are estimated jointly during the model fit, and therefore the full implementation is highly nonparametric. ARD is a very useful ‘general-purpose’ regression method.
Random forest regression is an ensemble regression method that uses multiple independent decision trees to predict the target variable. These predictions are then aggregated to form an overall prediction. The main parameters for RFR are the number of decision trees (the total number of predictions) and the depth of each tree.
Overall, RFR can form a highly accurate regression model on datasets with high-dimensional input data. However, by virtue of this, they can be prone to overfitting. It should also be noted from a practical standpoint that RFR can be computationally expensive.
All of the regression-based methods rely on an appropriate choice of features. As such, we employ three main feature-selection routines. The MFS method enables the user to define their own predictive model. This is best used when attempting to explore known relationships or ‘sanity-check’ other models. The KB method chooses the K most optimal features under a choice-scoring function. In our toolkit, the features are scored using a simple linear f score. Finally, RFE recursively reduces the number of features according to a ranking function in an attempt to minimise the number of features required to explain the data.
The choice of these methods allows varying degrees of control over the model parameters, ranging from full control, in the case of MFS, to completely automated model selection with RFE.
Associated data to corroborate phase-transition temperature predictions
The phase diagrams and phase-transition temperature predictions autoreconstructed by our web platform all depend on the knowledgebase of the underpinning material database that we have sourced from the academic literature. However, not all data in materials science are published in academic journals. There is also the growing trend for data to be published through other forms of media, and in formats that are at different stages of data processing. In addition, while data continue to be generated from experiments, materials data are increasingly computed; examples of high-throughput computational databases in materials science have already been mentioned above8,9,10. Many computational data hosted by online databases, as well as raw data from high-end experiments, are being given DOIs so that they can be identified just like a journal article. The field of magnetism and superconductivity is no exception. The materials project contains a wealth of computational data in this field of science, whose entries carry DOIs. Meanwhile, neutron institutes around the world are sources of niche experimental data on magnetic and superconducting materials, since a neutron can interact with magnetic materials at the atomic level, by virtue of its magnetic moment. Neutron data are sufficiently rare and expensive to create, that DOIs are now being minted to tag and catalogue their raw data at several institutes (ISIS Neutron and Muon Facility, UK, and Institut Laue-Langevin, Grenoble, France). The Datacite Metadata Search tool, available at http://datacite.org, collates all forms of data that are tagged with a DOI, thus providing a massive resource of unpublished data on materials that complements our literature-mined database.
Accordingly, we set up an ‘Associated Data’ section on our web platform that links any predicted material to its bespoke entry of the Datacite Metadata Search tool. This offers our materials predictions a possible route to validation through non-literature resources, or at least provides enriched information about the material under scrutiny, such as details on who has synthesised, computed or characterised the material in a certain fashion, with the raw data being openly accessible for fresh data analysis. While simple in its implementation, the establishment of a two-way channel between raw and processed experimental data in a materials prediction platform, as linked to a large corpus of literature-mined data, is rare, if not unprecedented. Yet, such data channelling has enormous scope since it invites the development of artificially intelligent data-analytics machinery to operate autonomously in the middle of these data types. On the one hand, this machinery could tension the consistency of putative results with their raw data, leading to highly optimised, self-consistent results, which are void of potential human bias. On the other hand, it will enable a new dimension of materials prediction that couples raw and processed data through, as yet unknown, forms of data correlations.
Data availability
The web application associated with this work is available on http://magneticmaterials.org. This contains all underpinning data, a data analysis user interface with associated demo, usage documentation and source code references with citing and licensing information.
Code availability
All the source code used in this work is made freely available under the MIT license. The code used to generate the database is available at http://github.com/cjcourt/magdb. A clean build of the ChemDataExtractor toolkit is available at http://chemdataextractor.org/download.
References
Rajan, K. Materials informatics. Mater. 8, 38–45 (2005).
Jain, A., Hautier, G., Ong, S. P. & Persson, K. New opportunities for materials informatics: resources and data mining techniques for uncovering hidden relationships. J. Mater. Res. 31, 977–994 (2016).
Liu, Y., Zhao, T., Ju, W. & Shi, S. Materials discovery and design using machine learning. J. Materiomics 3, 159–177 (2017).
Lu, W., Xiao, R., Yang, J., Li, H. & Zhang, W. Data mining-aided materials discovery and optimization. J. Materiomics 3, 191–201 (2017).
Agrawal, A. & Choudhary, A. Perspective: Materials informatics and big data: realization of the “fourth paradigm” of science in materials science. PLl Materials 4, 053208 (2016).
Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. NPJ Comput. Mater. 2, 16028 EP (2016).
Holdren, J. P. et al. Materials Genome Initiative for Global Competitiveness (National Science and technology council OSTP, Washington, 2011).
Pyzer-Knapp, E. O., Li, K. & Aspuru-Guzik, A. Learning from the harvard clean energy project: The use of neural networks to accelerate materials discovery. Adv. Funct. Mater. 25, 6495–6502 (2015).
Jain, A. et al. Commentary: The Materials Project: a materials genome approach to accelerating materials innovation. APL Materials 1, 011002 (2013).
Cooper, C. B. et al. Design-to-device approach affords panchromatic co-sensitized solar cells. Adv. Energy Mater. 9, 1802820 (2019).
Zhai, X., Chen, M. & Lu, W. Accelerated search for perovskite materials with higher Curie temperature based on the machine learning methods. Comput. Mater. Sci. 151, 41–48 (2018).
Stanev, V. et al. Machine learning modeling of superconducting critical temperature. NPJ Comput. Mater. 4, 29 (2018).
Pilania, G. et al. Machine learning bandgaps of double perovskites. Sci. Rep. 6, 19375 EP (2016).
Ram, N. R. et al. Review on magnetocaloric effect and materials. J. Supercond. Nov. Magn. 31, 1971–1979 (2018).
Coey, J. M. D. Magnetism and Magnetic Materials (Cambridge University Press, 2010).
Sarker, M. M. & Flavell, W. R. Review of applications of high-temperature superconductors. J. Supercond. 11, 209–213 (1998).
Gallego, S. V. et al. MAGNDATA: towards a database of magnetic structures. I. The commensurate case. J. Appl. Crystallogr. 49, 1750–1776 (2016).
Gallego, S. V. et al. MAGNDATA: towards a database of magnetic structures. II. The incommensurate case. J. Appl. Crystallogr. 49, 1941–1956 (2016).
Springer Nature. Springer Nature: SpringerMaterials Database. Online https://materials.springer.com (2019).
Tshitoyan, V. et al. Unsupervised word embeddings capture latent knowledge from materials science literature. Nature 571, 95 (2019).
Court, C. J. & Cole, J. M. Auto-generated materials database of Curie and Néel temperatures via semi-supervised relationship extraction. Sci. Data. 5, 180111 EP (2018).
Venugopal, V. & Broderick, S. R. A picture is worth a thousand words: applying natural language processing tools for creating a quantum materials database map. MRS Comms. 9, 1134–1141 (2019).
Swain, M. C. & Cole, J. M. ChemDataExtractor: a toolkit for automated extraction of chemical information from the scientific literature. J. Chem. Inf. Model. 56, 1894–1904 (2016).
Wolfram|Alpha ElementData. Retrieved January, 2019, from http://wolframalpha.com/ (2009).
Tilley, R. J. Perovskites: Structure-property Relationships (John Wiley & Sons, 2016).
Kasap, S. & Capper, P. Springer Handbook of Electronic and Photonic Materials (Springer International Publishing, 2017).
Paraskevopoulos, M. et al. Magnetic properties and the phase diagram of La1−xSrxMnO3 for x < 0.2. J. Phys. Condens. Matter 12, 3993 (2000).
Laverdiere, J. et al. Spin-phonon coupling in orthorhombic RMnO3 (R = Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Y): a Raman study. Phys. Rev. B 73, 214301 (2006).
Kimura, T. et al. Distorted perovskite with eg1 configuration as a frustrated spin system. Phys. Rev. B 68, 060403 (2003).
Zhou, J.-S. et al. Hexagonal versus perovskite phase of manganite RMnO3 (R = Y, Ho, Er, Tm, Y b, Lu). Phys. Rev. B. 74, 014422 (2006).
Kremer, R. K. Cerium magnetic ordering in the cerium orthochromite CeCrO3. https://doi.org/10.5291/ILL-DATA.5-31-2594 (2018).
Taheri, M., Kremer, R. K., Trudel, S. & Razavi, F. S. Exchange bias effect and glassy-like behavior of EuCrO3 and CeCrO3 nano-powders. J. Appl. Phys. 118, 124306 (2015).
Shukla, R. Multifunctional nanocrystalline CrCrO3: antiferromagnetic, relaxor, and optical properties. J. Phys. Chem. C 113, 12663–12668 (2009).
Goodenough, J. B. & Longo, M. Part A Table 6, Part 2: Datasheet from Landolt-Börnstein - Group III Condensed Matter\(\cdot\) Volume 4A: “Part A” in SpringerMaterials (1970).
Nenert Gwilherm. Investigation of the complex magnetic phase diagram of the recently reported multiferroic chromite TmCrO3. https://doi.org/10.5291/ILL-DATA.5-31-2279 (2013).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175 (1957).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 EP (2016).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-based layered superconductor LaO1−xFxFeAs (x = 0.05–0.12) with Tc = 26 K. J. Amer. Chem. Soc. 130, 3296–3297 (2008).
Zhi-An, R. et al. Superconductivity at 55 K in iron-based F-doped layered quaternary compound SmO1−xFxFeAs. Chinese Phys. Lett. 25, 2215 (2008).
Gómez-Bombarelli, R. et al. Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach. Nature materials 15, 1120 (2016).
Cole, J. M. et al. Data mining with molecular design rules identifies new class of dyes for dye-sensitised solar cells. Phys. Chem. Chem. Phys. 16, 26684–26690 (2014).
Brown, P. F., Desouza, P. V., Mercer, R. L., Pietra, V. J. D. & Lai, J. C. Class-based n-gram models of natural language. Computat. Linguist. 18, 467–479 (1992).
MongoDB, Inc. MongoDB. Online https://mongodb.com (2019).
Cardarelli, F. Materials Handbook: A Concise Desktop Reference (Springer Science & Business Media, 2008).
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta. Crystallogr. A. 32, 751–767 (1976).
Merkys, A. et al. COD::CIF::Parser: an error-correcting CIF parser for the Perl language. J. Appl. Crystallogr. 49, 292–301 (2016).
Grazulis, S. D. et al. Crystallography Open Database (COD): an open-access collection of crystal structures and platform for world-wide collaboration. Nucleic Acids Res. 40, D420–D427 (2012).
Grazulis, S. et al. Crystallography Open Database—an open-access collection of crystal structures. J. Appl. Crystallogr. 42, 726–729 (2009).
Downs, R. T. & Hall-Wallace, M. The American Mineralogist crystal structure database. Am. Mineral. 88, 247–250 (2003).
Cortes, C. & Vapnik, V. Support-vector networks. Mach. Learn. 20, 273–297 (1995).
MacKay, D. J. Bayesian interpolation. Neural computation 4, 415–447 (1992).
Ho, T. K. Random decision forests. in Proceedings of 3rd International Conference on Document Analysis and Recognition, vol. 1, 278–282 (IEEE, 1995).
Pedregosa, F. et al. Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
Solovjov, A. et al. Fluctuation conductivity and possible pseudogap state in feas-based superconductor EuFeAsO0.85F0.15. Mater. Res. Express 3, 076001 (2016).
Yates, K. et al. Investigation of superconducting gap structure in TbFeAsO0.9F0.1 using point contact Andreev reflection. New J. Phys. 11, 025015 (2009).
Johnson, P. D., Xu, G. & Yin, W.-G. Iron-Based Superconductivity Vol. 211 (Springer, 2015).
Rodgers, J. A. et al. Suppression of the superconducting transition of RFeAso1−xFx (R = Tb, Dy, and Ho). Phys. Rev. B. 80, 052508 (2009).
Acknowledgements
C.J.C. would like to thank the EPSRC Computational Methods in Materials Science Centre for Doctoral Training for PhD funding (reference EP/L015552/1). J.M.C. is grateful for the 2014 Design Fellowship from the Royal Commission for the Exhibition 1851, hosted by Argonne National Laboratory, where work done was supported by DOE Office of Science and Office of Basic Energy Sciences, and used research resources of the Argonne Leadership Computing Facility (ALCF), which is a DOE Office of Science Facility, all under contract No. DEAC02-06CH11357. J.M.C. is also grateful for the BASF/Royal Academy of Engineering Research Chair in Data-Driven Molecular Engineering of Functional Materials, which is partly supported by the STFC via the ISIS Neutron and Muon Facility.
Author information
Authors and Affiliations
Contributions
C.J.C. and J.M.C. conceived and designed the research. C.J.C. collected the data, performed the data analysis and created the web platform, assisted by J.M.C. who supervised C.J.C. on the project. C.J.C. drafted the paper with help from J.M.C. Both authors reviewed the final paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Court, C.J., Cole, J.M. Magnetic and superconducting phase diagrams and transition temperatures predicted using text mining and machine learning. npj Comput Mater 6, 18 (2020). https://doi.org/10.1038/s41524-020-0287-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-0287-8
This article is cited by
-
A materials terminology knowledge graph automatically constructed from text corpus
Scientific Data (2024)
-
Extracting accurate materials data from research papers with conversational language models and prompt engineering
Nature Communications (2024)
-
Superstrength permanent magnets with iron-based superconductors by data- and researcher-driven process design
NPG Asia Materials (2024)
-
Crystal structure graph neural networks for high-performance superconducting critical temperature prediction
Science China Materials (2024)
-
A study of machine-learning-derived formulas using artificially generated dataset
Journal of the Korean Physical Society (2024)