Abstract
Computing electron–defect (e–d) interactions from first principles has remained impractical due to computational cost. Here we develop an interpolation scheme based on maximally localized Wannier functions (WFs) to efficiently compute e–d interaction matrix elements. The interpolated matrix elements can accurately reproduce those computed directly without interpolation and the approach can significantly speed up calculations of e–d relaxation times and defect-limited charge transport. We show example calculations of neutral vacancy defects in silicon and copper, for which we compute the e–d relaxation times on fine uniform and random Brillouin zone grids (and for copper, directly on the Fermi surface), as well as the defect-limited resistivity at low temperature. Our interpolation approach opens doors for atomistic calculations of charge carrier dynamics in the presence of defects.
Similar content being viewed by others
Introduction
The interactions between electrons and defects control charge and spin transport at low temperature, and give rise to a range of quantum transport phenomena1,2,3,4,5. Understanding such electron–defect (e–d) interactions from first principles can provide microscopic insight into carrier dynamics in materials in the presence of point and extended defects, and accelerate materials discovery. Currently, e–d interactions can be computed ab initio mainly through the all-electron Korringa–Kohn–Rostoker Green’s function method6, which is based on multiple-scattering theory. Several properties have been computed with this approach, including the magnetoresistance due to impurity scattering7, the residual resistivity of metals and alloys8, and spin relaxation9,10,11,12 and the spin Hall effect13,14,15. In contrast, ab initio e–d calculations using pseudopotentials or projector augmented waves16,17,18 have progressed more slowly, mainly due to the high computational cost of obtaining the e–d interaction matrix elements needed for perturbative calculations19.
We recently developed an ab initio method18 to compute efficiently the e–d interactions and the associated matrix elements. Our approach uses only the wave functions of the primitive cell, thus significantly reducing computational cost compared to e–d calculations that use supercell wave functions16,17. As our method uses a plane-wave (PW) basis set and pseudopotentials, it is compatible with widely used density functional theory (DFT) codes. A different method developed by Kaasbjerg et al.20 uses an atomic orbital (AO) basis to compute the e–d matrix elements; its advantage is that one can compute the e–d matrix elements using only a small set of AOs, although one is limited by the quality and completeness of the AO basis set21.
To benefit from both the completeness and accuracy of the PW basis and the versatility of a small localized basis set, approaches combining PWs and AOs22 or Wannier functions (WFs)23,24 have been developed for electron–phonon (e–ph) interactions. They have enabled efficient interpolation of the e–ph matrix elements and have been instrumental to advancing carrier dynamics calculations25,26,27. To date, such an interpolation scheme does not exist for e–d interactions to our knowledge; thus, performing demanding Brillouin zone (BZ) integrals needed to compute e–d relaxation times (RTs) and defect-limited charge transport remains an open problem. Interpolating the interaction matrix elements to uniform, random, or importance-sampling fine BZ grids is key to systematically converging the RTs and transport properties25,28, and it has been an important development in first-principles calculations of e–ph interactions and phonon-limited charge transport.
In this work, we develop a method for interpolating the e–d interaction matrix elements using WFs. Through a generalized double-Fourier transform, our approach can efficiently transform the matrix elements from a Bloch representation on a coarse BZ grid to a localized WF representation and ultimately to a Bloch representation on an arbitrary fine BZ grid. We show the rapid spatial decay of the e–d interactions in the WF basis, which is crucial to the accuracy and efficiency of the method. Using our approach, we investigate e–d interactions due to charge-neutral vacancies in silicon and copper. In both cases, we can accurately interpolate the e–d matrix elements and converge the e–d scattering rates and defect-limited carrier mobility or resistivity. In copper, we map the e–d RTs directly on the Fermi surface and show their dependence on electronic state. We demonstrate computations of e–d matrix elements on random and uniform BZ grids as dense as 600 × 600 × 600 points, whose computational cost would be prohibitive for direct computation. We expect that our efficient e–d computation and interpolation approaches will enable a wide range of studies of e–d interactions in materials ranging from metals to semiconductors and insulators, and for applications such as electronics, nanodevices, spintronics, and quantum technologies.
Results
Theory
The perturbation potential ΔVe−d introduced by a point defect in a crystal couples different Bloch eigenstates of the unpertured (defect-free) crystal. The matrix elements associated with this e–d interaction are defined as
where \(\left|n{\boldsymbol{k}}\right\rangle\) is the Bloch state with band index n and crystal momentum k. To handle these e–d interactions, one needs to store and manipulate a matrix Mmn of size \({N}_{\mathrm {b}}^{2}\) (Nb is the number of bands) for each pair of crystal momenta \({\boldsymbol{k}}^{\prime}\) and k in the BZ. Within DFT, the perturbation potential ΔVe−d can be computed as the difference between the Kohn–Sham potential of a defect-containing supercell and that of a pristine supercell with no defect18.
We compute the e–d matrix elements in Eq. (1) with the method we developed in ref. 18, which uses only the Bloch wave functions of the primitive cell and does not require computing or manipulating the wave functions of the supercell, thus significantly reducing computational cost. The Bloch states can be expressed in terms of maximally localized WFs using
where \(\left|j{\boldsymbol{R}}\right\rangle\) is the WF with index j centered at the Bravais lattice vector R. The unitary matrices U in Eq. (2) maximize the spatial localization of the WFs29
where Nk is the number of k-points in the BZ. The e–d matrix element \({M}_{ij}({\boldsymbol{R}}^{\prime} ,{\boldsymbol{R}})\) between two WFs centered at the lattice vectors \({\boldsymbol{R}}^{\prime}\) and R in the Wannier representation is defined as
If the center of the perturbation potential lies in the unit cell at the origin, the absolute value of the e–d matrix elements, \(| {M}_{ij}({\boldsymbol{R}}^{\prime} ,{\boldsymbol{R}})|\), decays rapidly (within a few lattice constants) for increasing values of the lattice vectors \({\boldsymbol{R}}^{\prime}\) and R due to the short-ranged nature of the perturbation potential from the defect, which is assumed to be charge-neutral in this work. As a result, only a small number of lattice vectors R, which we arrange in a Wigner–Seitz (WS) supercell centered at the origin, is needed to compute the e–d matrix elements in the Wannier representation.
Using Eqs. (1)–(4), the e–d matrix elements in the Wannier representation can be written as a generalized double-Fourier transform of the matrix elements in the Bloch representation, which are first computed on a coarse BZ grid with points kc:
Here and below, we omit all band indices for clarity. Through the inverse transform, we can interpolate the e–d matrix elements to any desired pair of fine BZ grid points \({{\boldsymbol{k}}}_{{\rm{f}}}^{\prime}\) and kf, using
Although \({U}_{{{\boldsymbol{k}}}_{{\rm{c}}}}\) in Eq. (5) is the coarse-grid unitary matrix used to construct the WFs [see Eq. (3)], the unitary matrix on the fine grid, \({U}_{{{\boldsymbol{k}}}_{{\rm{f}}}}\) in Eq. (6), is obtained by diagonalizing the fine-grid Hamiltonian,
where H(R) is the electronic Hamiltonian in the Wannier basis. These equations are analogous to those used for interpolating the e–ph matrix elements22,23,24, except that here the lattice vectors \({\boldsymbol{R}}^{\prime}\) and R are both associated with electronic states. The lattice vectors \({\boldsymbol{R}}^{\prime}\) and R in the WS supercell are determined—through the periodic boundary conditions—by the \({{\boldsymbol{k}}}_{{\rm{c}}}^{\prime}\) and kc coarse grids, respectively. In practice, we choose a uniform coarse BZ grid and the size of the WS supercell is equal to the size of this coarse grid. It is noteworthy that our e–d matrix elements in the Wannier representation require WFs only for the primitive cell, whereas a method developed in ref. 30 requires WFs for the defect-containing supercells.
Similar to the e–ph case22, the rapid spatial decay of the e–d matrix elements in the WF basis is crucial to reducing the computational cost, as it puts an upper bound to the number of lattice sites \({\boldsymbol{R}}^{\prime}\) and R at which \(M({\boldsymbol{R}}^{\prime} ,{\boldsymbol{R}})\) needs to be computed. In particular, computing \(M({{\boldsymbol{k}}}_{{\rm{f}}}^{\prime},{{\boldsymbol{k}}}_{{\rm{f}}})\) at small \({{\boldsymbol{k}}}_{{\rm{f}}}^{\prime}\) and kf vectors would in principle require summing the Fourier transform in Eq. (6) up to correspondingly large lattice vectors of length \(| {\boldsymbol{R}}^{\prime} | =2\pi /| {{\boldsymbol{k}}}_{{\rm{f}}}^{\prime}|\) and ∣R∣ = 2π∕∣kf∣; in practice, this is not needed due to the rapid spatial decay. The choice of a WS supercell and its relation to the DFT supercell are discussed in detail in the Supplementary Information.
Interpolation workflow and validation
The workflow for interpolating the e–d matrix elements to a fine grid with points kf consists of several steps (see Fig. 1) as follows: (i) compute the e–d matrix elements in the Bloch representation on a coarse BZ grid with points kc using Eq. (1); (ii) obtain the e–d matrix elements in the Wannier representation using Eq. (5); (iii) interpolate the Hamiltonian using Eq. (7) and diagonalize it to obtain the fine-grid unitary matrices \({U}_{{{\boldsymbol{k}}}_{{\rm{f}}}}\); (iv) interpolate the e–d matrix elements to any desired pair of fine-grid points \({{\boldsymbol{k}}}_{{\rm{f}}}^{\prime}\) and kf using the matrix elements in the Wannier representation and the fine-grid unitary matrices [see Eq. (6)].
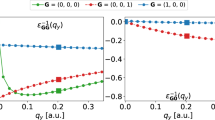
We validate our WF-based interpolation method using vacancy defects in silicon as an example (see Methods). The relaxed symmetry of the vacancy in our calculation is Td, whereas previous work and experiment find a D2d symmetry31. The reason for this inconsistency is that we do not randomly displace the atoms before relaxation, which is needed to break the symmetry and obtain the lower-energy D2d vacancy structure. Although our calculations use a vacancy with Td rather than D2d symmetry, the results we present are not affected by this choice. Figure 2a compares the e–d matrix elements calculated directly using Eq. (1) with the same matrix elements obtained by interpolation starting from two different coarse BZ grids with respectively 43 and 103 points kc (here and below, we denote an N × N × N uniform grid as N3). The interpolated results can qualitatively reproduce the direct computation for both coarse grids, but the results from the 103 coarse grid achieve a superior quantitative accuracy as the interpolated matrix elements agree with the directly computed ones within 1% over the entire BZ. The accuracy can be systematically improved by increasing the size of the coarse kc-grid (see Table 1). This trend implies that the e–d perturbation potential decays to a negligible value over >4 but <10 lattice constants.
a Absolute value of the e–d matrix elements, computed along high-symmetry BZ lines. The initial state is set to the lowest valence band at Γ, whereas the final states span all four valence bands and possess crystal momenta chosen along the high-symmetry lines shown in figure. Panels b and c show the spatial decay of the e–d matrix elements in the Wannier basis, \(| | M({\boldsymbol{R}}^{\prime} ,{\boldsymbol{R}})| |\), which are plotted in b as a function of \(| {\boldsymbol{R}}^{\prime} |\) for R = 0 and in c as a function of ∣R∣ for \({\boldsymbol{R}}^{\prime} ={\bf{0}}\). The highest value of \(| | M({\boldsymbol{R}}^{\prime} ,{\boldsymbol{R}})| |\) is normalized to 1 in both cases and the plots use a logarithmic scale.
The spatial decay of the matrix elements in the WF basis is essential for the accuracy of our approach. To analyze the spatial behavior of the matrix elements in the WF basis, we define for each pair of lattice vectors \({\boldsymbol{R}}^{\prime}\) and R the maximum absolute value of the e–d matrix elements as \(| | M({\boldsymbol{R}}^{\prime} ,{\boldsymbol{R}})| | ={\max }_{ij}| {M}_{ij}({\boldsymbol{R}}^{\prime} ,{\boldsymbol{R}})|\). Figure 2b, c show the spatial behavior of \(| | M({\boldsymbol{R}}^{\prime} ,{\boldsymbol{R}})| |\) for a vacancy defect in silicon as a function of \(| {\boldsymbol{R}}^{\prime} |\) while keeping R = 0 and as a function of ∣R∣ while keeping \({\boldsymbol{R}}^{\prime} ={\bf{0}}\), respectively. Note that \(| M({\boldsymbol{R}}^{\prime} ,0)|\) and ∣M(0, R)∣ in Fig. 2b, c are identical, because the defect perturbation potential is centered at the origin of the WS supercell. This result does not hold in general for an arbitrary position of the defect in the WS supercell. We find that the matrix elements in the WF basis decay exponentially over a few unit cells, thus confirming that the WFs are a suitable basis set for interpolating the e–d matrix elements.
Relaxation times and defect-limited transport
The e–d RTs and the defect-limited carrier mobility are key to characterizing carrier dynamics at low temperatures and also near room temperature in highly doped or disordered materials. We compute the e–d RTs, τnk, associated with elastic carrier-defect scattering using the lowest-order Born approximation3,18:
where ℏ is the reduced Planck constant, nat the number of atoms in a primitive cell, Cd the (dimensionless) defect concentration (defined as the number of defects divided by the number of atoms), \({N}_{{\boldsymbol{k}}^{\prime} }\) the number of k-points used in the summation, and εnk the unperturbed energy of the Bloch state \(\left|n{\boldsymbol{k}}\right\rangle\) in the primitive cell. The delta function is implemented as a normalized Gaussian with a small broadening η, \({\delta }_{\eta }(x)={e}^{-{x}^{2}/2{\eta }^{2}}/\sqrt{2\pi }\eta\). The e–d RTs are proportional to the defect concentration because our approach assumes that the scattering events are independent and uncorrelated18.
For defect-limited carrier transport, we first compute the conductivity tensor σ(T) at temperature T using25
where e is the electron charge and E the electron energy, f(T, E) the Fermi-Dirac distribution, and \(\Sigma \left(E\right)\) the transport distribution function (TDF) at energy E, defined as
where α and β are Cartesian directions, and Ωuc the volume of the primitive cell. The TDF is computed with a tetrahedron integration method25, using our calculated e–d RTs and Wannier-interpolated band velocities vnk32,33. The mobility is obtained as μ = σ∕nce, where nc is the carrier concentration, whereas the resistivity is obtained by inverting the conductivity tensor.
We first study the e–d RTs and hole carrier mobility in silicon with vacancy defects (see Methods). We use interpolated e–d matrix elements and focus on the accuracy and convergence of our interpolation method. The results given here assume a defect concentration of one vacancy in 106 silicon atoms (1 p.p.m. concentration), but results for different defect concentrations can be obtained by rescaling these reference RTs to a different defect concentration [using Eq. (8)]; this approach is valid only within the concentration range in which the Born approximation holds. Figure 3a compares the RTs obtained from directly computed and interpolated e–d matrix elements. The two sets of RTs are in close agreement with each other for both electrons and holes, confirming the accuracy of our interpolation method. Figure 3b shows the convergence of the defect-limited hole mobility with respect to the size of the fine BZ grids, for BZ grids ranging from 403 to 6003 points; the convergence is studied at two temperatures (10 K and 100 K) and for two types of grids, random and uniform. At 10 K, the mobilities are fully converged for fine grids with 2003 points, for both random and uniform grids. We observe a similar trend at 100 K. The converged values of the mobility are consistent with our previous calculations using directly computed (rather than interpolated) matrix elements18.
a Electron–defect RTs obtained from directly computed and interpolated e–d matrix elements. Here, εc is the conduction band minimum and εv the valence band maximum. b Convergence of the hole mobility with respect to the size of the fine BZ grid used for interpolation, shown for both uniform and random grids. The computed hole mobilities at 10 K and 100 K from ref. 18 are also shown. A reference vacancy concentration of 1 p.p.m. is used in all calculations.
The interpolation method allows us to use extremely dense BZ grids with up to 6003 points due to its superior computational efficiency. Let us briefly analyze the overall speed-up of the interpolation method for a carrier mobility calculation. To converge the mobility at low temperature, one needs to consider only fine BZ grid points in a small energy window, roughly within 100 meV of the band edges in semiconductors18,25 or of the Fermi energy in metals; these are the only states contributing to the conductivity in Eq. (9). In this small energy window, the number of k-points is a small fraction α of the total number of points \({N}_{{{\boldsymbol{k}}}_{{\rm{f}}}}\) in the entire fine BZ grid. In the direct computation, one computes the e–d matrix elements \(M({{\boldsymbol{k}}}_{{\rm{f}}}^{\prime},{{\boldsymbol{k}}}_{{\rm{f}}})\) between all crystal momentum pairs and thus a number of matrix elements of order \({(\alpha {N}_{{{\boldsymbol{k}}}_{{\rm{f}}}})}^{2}\). In the interpolation approach, the most time-consuming step is directly computing the \({N}_{{{\boldsymbol{k}}}_{{\rm{c}}}}^{2}e\)-d matrix elements on the coarse grid [step (i) in Fig. 1], whereas interpolating the matrix elements per se is orders of magnitude less computationally expensive. In our machine, the average central processing unit (CPU) time to directly compute one matrix element is ~0.2 s for silicon (with an electronic kinetic energy cutoff of 40 Ry), whereas the same calculation done with our interpolation method requires only ~80 μs. The speed-up of the interpolation scheme for computing matrix elements is thus around three orders of magnitude. As a result, the overall speed-up of the interpolation approach over the direct computation is \(\sim\! {(\alpha {N}_{{{\boldsymbol{k}}}_{{\rm{f}}}})}^{2}/{N}_{{{\boldsymbol{k}}}_{{\rm{c}}}}^{2}\). The typical value of \({N}_{{{\boldsymbol{k}}}_{{\rm{f}}}}\) is around 103 – 104\({N}_{{{\boldsymbol{k}}}_{{\rm{c}}}}\). For our silicon calculations, the value of α is of order 10−2, so the interpolation approach speeds up the mobility calculation by at least two to four orders of magnitude.
The method for directly computing the e–d matrix elements we developed in ref. 18 and the interpolation method shown here are general, and can be applied to metals, semiconductors, and insulators. As an example, we show a calculation on a metal, copper, containing vacancy defects (see Methods). In metals, the fine grids required to compute the e–d RTs near the Fermi energy and the resistivity are a major challenge for direct e–d calculations without interpolation. Figure 4a shows the e–d RTs computed at k-points on the Fermi surface of copper, using interpolated e–d matrix elements obtained from a moderate size (8 × 8 × 8) coarse kc-grid. The e–d RTs for a reference vacancy concentration of 1 p.p.m. are between 0.3 and 1.4 ps. Interestingly, these e–d RTs are orders of magnitude shorter than the electron RTs in silicon for the same vacancy concentration, which suggests that scattering due to vacancy defects in copper is significantly stronger than in silicon (see the Supplementary Information). The e–d RTs in copper are strongly state-dependent—we find values of order 0.3 ps on the majority of the Fermi surface and values as large as 1.4 ps near the regions of the Fermi surface close to the X points of the BZ. Similar state-dependent RTs due to impurity scattering in copper have been predicted using the all-electron Korringa–Kohn–Rostoker Green’s function method9,10. These results show that our first-principles approach can access microscopic details of the e–d scattering processes.
a RTs mapped on the Fermi surface, obtained using interpolated e–d matrix elements for a reference vacancy concentration of 1 p.p.m. b Defect-limited resistivity as a function of temperature for an assumed reference vacancy concentration of 1 p.p.m., compared with experimental data from ref. 34.
Figure 4b shows the calculated defect-limited resistivity for vacancy defects in copper, at low temperatures between 2 and 50 K (see Methods). The calculated resistivity is independent of temperature, in agreement with experimental results34,35, even though the conductivity formula we use [Eq. (9)] depends on temperature via the Fermi-Dirac distribution. The low-temperature defect-limited resistivity for a reference 1 p.p.m. vacancy concentration is ~10−9 Ω⋅m. However, the equilibrium vacancy concentration (see Methods) of copper at 50 K is negligible (of order 10−119), and the corresponding resistivity is of order 10−122 Ω⋅m. This value is negligible in comparison with the measured resistivity of ~10−12 Ω⋅m in a highly pure copper Cu(7N) sample at low temperature, where 7N means 99.99999% purity (see Fig. 4b). We conclude that the resistivity of real copper samples at low temperature is not limited by intrinsic vacancy defects, but rather is controlled by impurities. This is a well-known result36,37,38,39,40 and our calculations are consistent with it.
Our method can predict a lower bound of the residual resistivity due to intrinsic defects in an ideally pure material. Alternatively, if the main type of defect or impurity is known from experiment, our approach can estimate the defect concentration present in the sample. The so-called residual resistivity ratio (RRR) between the low temperature and room temperature resistivities is used as a figure of merit for sample quality, and a large collection of data exists41 for RRR in metals. As at room temperature the resistivity is usually phonon-limited, combined with e–ph calculations25,42, our approach allows one to compute RRR for a wide range of materials and defect types. Taken together, these capabilities expand the tool box of first-principles methods for investigating carrier dynamics in complex materials.
Discussion
Our e–d interpolation method can be extended to charged defects, for which the long-range Coulomb interactions can be added in reciprocal space similar to what is done for e–ph interactions25,43. By including spin–orbit coupling, our approach can also be extended to study spin-flip processes and e–d interactions in magnetic and topological materials. Future work will also attempt to include multiple e–d scattering events and higher-order e–d interactions, e.g., using the T-matrix formalism20,44. Other applications include investigating carrier scattering due to extended defects such as dislocations and grain boundaries, a topic of prime relevance to materials science. In summary, the applications of the method discussed in this work are broad and so are its possible future extensions.
In conclusion, we developed a WF-based interpolation approach to efficiently compute e–d interactions and the associated matrix elements on fine BZ grids. We have shown that the interpolation method is accurate and that it can effectively compute demanding BZ integrals requiring up to 108–109 k-points. The ability to efficiently interpolate e–d matrix elements starting from moderate BZ coarse grids is a stepping stone toward perturbative calculations of defect-limited charge and spin transport, and to investigate quantum transport regimes governed by e–d interactions.
Methods
DFT calculations
The ground state of a primitive cell and of supercells with size N × N × N (where N is the number of primitive cells along each lattice vector) are computed using DFT within the local density approximation. We use a PW basis set and norm-conserving pseudopotentials45 with the QUANTUM ESPRESSO code46. The total energy is converged to within 10 meV/atom in all structures. In the defect-containing supercells, the atomic forces are relaxed to within 25 meV/Å to account for structural changes induced by the defect. For silicon, we use an experimental lattice constant of 5.43 Å and a PW kinetic energy cutoff of 40 Ry. For copper, we use an experimental lattice constant of 3.61 Å and a PW kinetic energy cutoff of 90 Ry. We employ a 12 × 12 × 12 k-point grid47 for the primitive cells of both materials to converge the charge density and total energy, and interpolate their band structures using maximally localized WFs29 with the Wannier90 code32,33. Coarse kc-grids between 4 × 4 × 4 and 10 × 10 × 10, as given in the text, are used in the non-self-consistent DFT calculations and in the wannierization procedure. The dense kf-grid used in the matrix element interpolation or relaxation time (RT) calculations is unrelated to the WF generation. In silicon, we wannierize the four highest valence and four lowest conduction bands together, using sp3 orbitals centered on the silicon atoms as the initial guess, to compute the e–d matrix elements used for electron and hole RTs. A different wannierization is employed to compute the e–d matrix elements along high-symmetry BZ lines in Fig. 2; in this case, we wannierize only the four highest valence bands, using four s orbitals centered at the fractional coordinates (−1/8, 3/8, −1/8), (−1/8, −1/8, −1/8), (3/8, −1/8, −1/8), and (−1/8, −1/8, 3/8). In copper, we exclude the four lowest (core) 3sp-bands and wannierize the next seven bands using five d orbitals centered at the copper atom and two s orbitals centered at the fractional coordinates (1/4, 1/4, 1/4) and (−1/4, −1/4, −1/4) as the initial guess.
Electron–defect matrix elements, RTs, and resistivity calculations
The methods to directly compute the e–d matrix elements and from them obtain the RTs, mobility, and conductivity (or resistivity) are described in detail in ref. 18. Briefly, we compute the coarse-grid e–d matrix elements using the wave functions of the primitive cell and obtain the perturbation potential due to a vacancy defect using a 6 × 6 × 6 supercell with a 2 × 2 × 2 k-point grid. The atomic positions around the vacancy are relaxed up to the third nearest-neighbor shell in both silicon and copper. The potential alignment for the supercell containing the relaxed vacancy is chosen as the core-averaged potential of the farthest atom from the vacancy in the same (but unrelaxed) supercell. In Fig. 3a, the directly computed matrix elements are calculated using the wave functions obtained from non-self-consistent calculations on a dense grid with 3003 kf-points, whereas the interpolated matrix elements are calculated on the same dense grid starting from a coarse grid with 103 kc-points. In the e–d RT and defect-limited mobility calculations in silicon, we use only electronic states in a small (~100 meV) energy window near the band edges, as these are the only states contributing to the mobility25; similarly, in copper we use only states within 100 meV of the Fermi energy. In silicon, we use a broadening value η = 5 meV to compute the delta function in Eq. (8) and a uniform BZ grid with 3003 points for the RTs; for the mobility, we use a 1 meV broadening and e–d matrix elements interpolated from a 103 coarse BZ grid. In copper, we compute the RTs and resistivity on a fine BZ grid with 2403 points, using a 1 meV broadening and e–d matrix elements interpolated from a coarse 83 BZ grid. The equilibrium vacancy concentration at temperature T in copper is estimated using48
where ΔHv and ΔSv are the vacancy formation enthalpy and entropy, respectively, and kB the Boltzmann constant. In copper, ΔSv = 3.0 kB and ΔHv = 1.19 eV48.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code developed in this work will be released in the future at http://perturbo.caltech.edu/.
References
Economou, E. N. Green’s Functions in Quantum Physics (Springer, 1983).
Datta, S. Electronic Transport in Mesoscopic Systems (Cambridge Univ. Press, 1997).
Bruus, H. & Flensberg, K. Many-Body Quantum Theory in Condensed Matter Physics: An Introduction (Oxford Univ. Press, 2004).
Akkermans, E. & Montambaux, G. Mesoscopic Physics of Electrons and Photons (Cambridge Univ. Press, 2007).
Mahan, G. D. Many-Particle Physics (Springer US, 2000).
Ebert, H., Ködderitzsch, D. & Minár, J. Calculating condensed matter properties using the KKR-Green’s function method-recent developments and applications. Rep. Prog. Phys. 74, 096501 (2011).
Zahn, P., Mertig, I., Richter, M. & Eschrig, H. Ab initio calculations of the giant magnetoresistance. Phys. Rev. Lett. 75, 2996–2999 (1995).
Mertig, I. Transport properties of dilute alloys. Rep. Prog. Phys. 62, 237 (1999).
Fedorov, D. V., Zahn, P., Gradhand, M. & Mertig, I. First-principles calculations of spin relaxation times of conduction electrons in Cu with nonmagnetic impurities. Phys. Rev. B 77, 092406 (2008).
Gradhand, M., Fedorov, D. V., Zahn, P. & Mertig, I. Fully relativistic ab initio treatment of spin-flip scattering caused by impurities. Phys. Rev. B 81, 020403 (2010).
Fedorov, D. V. et al. Impact of electron-impurity scattering on the spin relaxation time in graphene: a first-principles study. Phys. Rev. Lett. 110, 156602 (2013).
Long, N. H. et al. Spin relaxation and the Elliott-Yafet parameter in W (001) ultrathin films: surface states, anisotropy, and oscillation effects. Phys. Rev. B 87, 224420 (2013).
Gradhand, M., Fedorov, D. V., Zahn, P. & Mertig, I. Spin Hall angle versus spin diffusion length: tailored by impurities. Phys. Rev. B 81, 245109 (2010).
Gradhand, M., Fedorov, D. V., Zahn, P. & Mertig, I. Extrinsic spin Hall effect from first principles. Phys. Rev. Lett. 104, 186403 (2010).
Hönemann, A., Herschbach, C., Fedorov, D. V., Gradhand, M. & Mertig, I. Spin and charge currents induced by the spin Hall and anomalous Hall effects upon crossing ferromagnetic/nonmagnetic interfaces. Phys. Rev. B 99, 024420 (2019).
Restrepo, O. D., Varga, K. & Pantelides, S. T. First-principles calculations of electron mobilities in silicon: phonon and Coulomb scattering. Appl. Phys. Lett. 94, 212103 (2009).
Lordi, V., Erhart, P. & Åberg, D. Charge carrier scattering by defects in semiconductors. Phys. Rev. B 81, 235204 (2010).
Lu, I.-T., Zhou, J.-J. & Bernardi, M. Efficient ab initio calculations of electron-defect scattering and defect-limited carrier mobility. Phys. Rev. Mater. 3, 033804 (2019).
Bernardi, M. First-principles dynamics of electrons and phonons. Eur. Phys. J. B 89, 239 (2016).
Kaasbjerg, K., Martiny, J. H., Low, T. & Jauho, A.-P. Symmetry-forbidden intervalley scattering by atomic defects in monolayer transition-metal dichalcogenides. Phys. Rev. B 96, 241411 (2017).
Ulian, G., Tosoni, S. & Valdrè, G. Comparison between Gaussian-type orbitals and plane wave ab initio density functional theory modeling of layer silicates: Talc [Mg3Si4O10(OH)2] as model system. J. Chem. Phys. 139, 204101 (2013).
Agapito, L. A. & Bernardi, M. Ab initio electron-phonon interactions using atomic orbital wave functions. Phys. Rev. B 97, 235146 (2018).
Giustino, F., Cohen, M. L. & Louie, S. G. Electron-phonon interaction using Wannier functions. Phys. Rev. B 76, 165108 (2007).
Calandra, M., Profeta, G. & Mauri, F. Adiabatic and nonadiabatic phonon dispersion in a Wannier function approach. Phys. Rev. B 82, 165111 (2010).
Zhou, J.-J. & Bernardi, M. Ab initio electron mobility and polar phonon scattering in GaAs. Phys. Rev. B 94, 201201 (2016).
Zhou, J.-J., Hellman, O. & Bernardi, M. Electron-phonon scattering in the presence of soft modes and electron mobility in SrTiO3 perovskite from first principles. Phys. Rev. Lett. 121, 226603 (2018).
Lee, N.-E., Zhou, J.-J., Agapito, L. A. & Bernardi, M. Charge transport in organic molecular semiconductors from first principles: the bandlike hole mobility in a naphthalene crystal. Phys. Rev. B 97, 115203 (2018).
Park, J., Zhou, J.-J. & Bernardi, M. Elliott-Yafet spin-phonon relaxation times from first principles. Phys. Rev. B 101, 045202 (2019).
Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).
Berlijn, T., Volja, D. & Ku, W. et al. Can disorder alone destroy the \({e^{\prime}}_{g}\) hole pockets of Nax CoO2? a Wannier function based first-principles method for disordered systems. Phys. Rev. Lett. 106, 077005 (2011).
Corsetti, F. & Mostofi, A. A. System-size convergence of point defect properties: The case of the silicon vacancy. Phys. Rev. B 84, 035209 (2011).
Yates, J. R., Wang, X., Vanderbilt, D. & Souza, I. Spectral and Fermi surface properties from Wannier interpolation. Phys. Rev. B 75, 195121 (2007).
Mostofi, A. A. et al. An updated version of Wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Nakane, H., Watanabe, T., Nagata, C., Fujiwara, S. & Yoshizawa, S. Measuring the temperature dependence of resistivity of high purity copper using a solenoid coil (srpm method). IEEE Trans. Instrum. Meas. 41, 107–110 (1992).
Cho, Y. C. et al. Copper better than silver: electrical resistivity of the grain-free single-crystal copper wire. Cryst. Growth Des. 10, 2780–2784 (2010).
Jongenburger, P. The extra-resistivity owing to vacancies in copper. Phys. Rev. 90, 710–711 (1953).
Blatt, F. J. Effect of point imperfections on the electrical properties of copper. I. conductivity. Phys. Rev. 99, 1708–1716 (1955).
Overhauser, A. & Gorman, R. Resistivity of interstitial atoms and vacancies in copper. Phys. Rev. 102, 676–681 (1956).
Friedel, J. Electronic structure of primary solid solutions in metals. Advances in Physics 50, 539–595 (2001).
Rossiter, P. L. The electrical resistivity of metals and alloys (Cambridge University Press, 1991).
Hall, L. Survey of Electrical Resistivity Measurements on 16 Pure Metals in The Temperature Range 0 to 273 K, vol. 365 (US Dept. of Commerce, National Bureau of Standards, 1968).
Mustafa, J. I., Bernardi, M., Neaton, J. B. & Louie, S. G. Ab initio electronic relaxation times and transport in noble metals. Phys. Rev. B 94, 155105 (2016).
Sjakste, J., Vast, N., Calandra, M. & Mauri, F. Wannier interpolation of the electron-phonon matrix elements in polar semiconductors: polar-optical coupling in GaAs. Phys. Rev. B 92, 054307 (2015).
Kaasbjerg, K. Atomistic T-matrix theory of disordered two-dimensional materials: bound states, spectral properties, quasiparticle scattering, and transport. Phys. Rev. B 101, 045433 (2020).
Van Setten, M. et al. The PseudoDojo: training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 226, 39–54 (2018).
Giannozzi, P. et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. Matter 21, 395502 (2009).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Hehenkamp, T., Berger, W., Kluin, J.-E., Lüdecke, C. & Wolff, J. Equilibrium vacancy concentrations in copper investigated with the absolute technique. Phys. Rev. B 45, 1998–2003 (1992).
Acknowledgements
This work was supported by the Air Force Office of Scientific Research through the Young Investigator Program, grant FA9550-18-1-0280. J.-J.Z. was supported by the National Science Foundation under grant number ACI-1642443, which provided for code development, and CAREER-1750613, which provided for part of the theory development. J.P. acknowledges support by the Korea Foundation for Advanced Studies.
Author information
Authors and Affiliations
Contributions
I.-T.L. derived the equations, implemented the code, and carried out the numerical calculations. J.P. and J.-J.Z. contributed to developing the code. M.B. supervised the research. M.B. and I.-T.L. analyzed the results and wrote the manuscript. All authors edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lu, IT., Park, J., Zhou, JJ. et al. Ab initio electron-defect interactions using Wannier functions. npj Comput Mater 6, 17 (2020). https://doi.org/10.1038/s41524-020-0284-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-0284-y
This article is cited by
-
Semiclassical electron and phonon transport from first principles: application to layered thermoelectrics
Journal of Computational Electronics (2023)
-
Machine learning sparse tight-binding parameters for defects
npj Computational Materials (2022)