Abstract
Atomic-level qubits in silicon are attractive candidates for large-scale quantum computing; however, their quantum properties and controllability are sensitive to details such as the number of donor atoms comprising a qubit and their precise location. This work combines machine learning techniques with million-atom simulations of scanning tunnelling microscopic (STM) images of dopants to formulate a theoretical framework capable of determining the number of dopants at a particular qubit location and their positions with exact lattice site precision. A convolutional neural network (CNN) was trained on 100,000 simulated STM images, acquiring a characterisation fidelity (number and absolute donor positions) of >98% over a set of 17,600 test images including planar and blurring noise commensurate with experimental measurements. The formalism is based on a systematic symmetry analysis and feature-detection processing of the STM images to optimise the computational efficiency. The technique is demonstrated for qubits formed by single and pairs of closely spaced donor atoms, with the potential to generalise it for larger donor clusters. The method established here will enable a high-precision post-fabrication characterisation of dopant qubits in silicon, with high-throughput potentially alleviating the requirements on the level of resources required for quantum-based characterisation, which will otherwise be a challenge in the context of large qubit arrays for universal quantum computing.
Similar content being viewed by others
Introduction
Of the leading platforms for the implementation of quantum computing architectures, qubits based on the spin of individual dopant atoms in silicon1,2,3,4,5,6,7 are growing in interest given the nexus with nanoelectronics engineering and the long coherence times8,9. For the exchange-based quantum computer design proposals1,2,10 where the physical separations between atomic qubits are small (10–15 nm), the pathway for scale-up to large two-dimensional arrays generally relies on uniformity of control of qubits and their interactions. Even small variations at the level of one lattice site for qubits based on single or multiple dopant atoms can significantly affect the design and control of logical operations. While the details of few qubit systems can be determined using electrostatics and electron spin resonance11 and variations in interactions mitigated by designing appropriate pulse schemes12,13, for large-scale arrays a reliable and fast method of identification (atom count per qubit) and characterisation (exact spatial location of atoms in lattice) is critical.
Machine intelligence techniques have been extremely productive in a wide range of applications, including material design, medical imaging, and data science, where the design space is enormously large14,15,16,17 and/or autonomous predictions are required from big data analysis18. In quantum devices, the application of deep learning for the automated fabrication of atomic-scale surface defects has been proposed19,20. This work integrates the high efficiency of machine learning algorithms towards pattern recognition21 with multi-million-atom simulations of scanning tunnelling microscopic (STM) images of donor wave functions22,23 to formulate a theoretical framework with the capability of high-throughput and automated spatial metrology of the donor qubits in silicon. The ability to pinpoint the donor locations with exact atom precision in large two-dimensional arrays will provide crucial input in the design and implementation of the fault-tolerant quantum computer architectures.
STM has been extensively used to measure the spatially resolved images of wave functions corresponding to the individual subsurface impurity atoms in various semiconductors, such as group V impurities in silicon22,24, Mn25, and N26,27 atoms in GaAs and Bi atoms in InP28. Recently, STM imaging technique has been applied to determine the exact locations of single dopant atoms in silicon23,29, which has opened new avenues to perform STM-based qubit characterisation and wave function benchmarking30. The idea underpinning the STM-based dopant position metrology23 was that the high-resolution images of donor wave functions exhibit a map of features, in which the brightness and symmetry of the features directly encodes the information about the locations of atoms. A direct pixel-by-pixel comparison of a measured image with a library of theoretically computed STM images provided direct information about the exact dopant locations. This rigorous comparison approach worked well for the individual atoms, but its scalability towards full-scale quantum computer arrays consisting of O(106) qubits, where each qubit may consist of small clusters of closely spaced donor atoms, is still an open problem and requires further development of computational techniques to efficiently process and characterise several thousand STM images. This work demonstrates that a machine learning algorithm when trained on simulated STM images is capable of characterising atomic-level qubits based on STM images including noise levels commensurate with the previously reported measurements. Furthermore, the published high-level agreement between the theory and experimental measurements for these STM images23 at the pixel and feature levels opens up the future possibility of training a machine learning algorithm over thousands of simulated images, which could then be implemented within an experimental set-up. As the generation of large experimental data sets is a highly tedious task, such transfer learning approach could provide an efficient pathway for the large-scale implementation of the spatial metrology technique as required for scalable quantum computer architectures.
Single-atom STM fabrication techniques4 can achieve the placement of phosphorus (P) atoms in silicon with accuracy in position of one lattice site, and the number of P atoms can in principle be controlled. However, the tunability of exchange interaction between a single P atom and two closely spaced P atoms (2P) makes it an attractive qubit system31, and the recent work has also studied qubits formed by three to four closely spaced P atoms32. Therefore, the generalisation of the spatial metrology technique23 beyond single donor atoms will broaden its scope for a wide range of qubit systems being considered for quantum computing applications. As the donor count per qubit increases, the number of available donor placement configurations drastically increase and impose stringent computational requirements for characterisation of qubits in large-scale devices. For example, merely increasing the number of dopant atoms per qubit from one to two leads to an increase in the possible position configurations from 60 to 1250 within 5 nm depth from the silicon surface. To enable an autonomous and robust spatial metrology of single donors and 2P dots in silicon, we perform the training of a convolutional neural network (CNN). The CNN learns the relationship between STM image features and the corresponding donor count and the exact spatial positions based on 105 simulated training images. The testing of the trained CNN over a large test data set consisting of 17,600 simulated images including noise demonstrated a highly robust performance with fidelities >98% across the selected four depth planes. In principle, the donor atoms can be fabricated with a single target depth plane4, in which case the qubit characterisation fidelities of 100% are achievable from the established CNN framework.
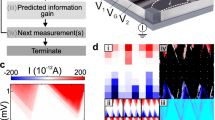
Figure 1 provides an overview of the proposed theoretical framework. To demonstrate the working of our technique, we have restricted each qubit formation to 1P and 2P configurations. The technique can be readily generalised to larger clusters consisting of a few closely spaced P atoms per qubit. In part (a), one electron STM images are computed, where each image encodes the information about underpinning donor positions and count. In the next step, the computed STM images are processed via image reduction algorithms to increase the computational and storage efficiency of the machine learning framework. Two complementary methods are developed for image reduction, namely edge detection and feature averaging. Both methods drastically enhance the speed of the CNN. We also introduced various levels of planar and blurring noise to test the resilience of the trained CNN against realistic image distortions. Figure 1b illustrates that the processed STM images are used to train a CNN. The testing of the trained CNN can be performed based on experimentally measured data and/or simulated STM images including noise as shown in Fig. 1c. In this work, we have used simulated STM images with various levels of blurring and planar noise to test the performance of the CNN due to the unavailability of experimental data at present. The computation of the STM images have previously shown an unprecedented accuracy when compared directly with the STM measurements23, capturing both the symmetry and the brightness of the measured wave function features. Therefore, we expect that the training and testing of the machine learning framework performed in this study will be directly applicable to the experimental data sets available in the future. Figure 1d shows the output of the CNN, indicating that it can accurately characterise each qubit by identifying donor count (1P or 2P) and their exact spatial locations in Si lattice.
a A qubit is formed by electrons confined to either a single donor atom (1P) or a pair of closely spaced atoms (2P) in silicon. Theoretically computed tunnelling current images of one electron wave functions confined on dopant qubits in silicon are generated. After including the application of noise typical of experimental images, the images are processed using an edge or feature detection analysis to reduce the computational and storage requirements. b A large set (100,000) of the processed images is used to train a machine learning algorithm such as a convolutional neural network (CNN). c The testing of the CNN is performed by generating a new set of 17,600 simulated STM images with varying levels of planar and blurring noise. It is noted that this work does not include experimental testing; however, the previously reported excellent agreement between theory and measurements23 imply that the trained ML framework could be directly applied to future experimental data sets. d The trained CNN performs the exact-atom characterisation of qubits by precisely determining the spatial locations and count of dopant atoms corresponding to each test image.
Results and discussion
Image classification and symmetry analysis
The STM images are computed by coupling the atomistic tight-binding calculations of the subsurface phosphorus dopant wave functions33 with the Bardeen’s tunnelling formalism34 and Chen’s derivative rule35. Note that we have performed this study for P in silicon system; however, the developed machine learning framework can also be trained and applied to other group V donor atoms in silicon. In recent years, advancements in the atomic precision fabrication techniques4 have led to a donor atom placement accuracy to within ±a0 in-plane variation for P donors in silicon, where a0 is the silicon lattice constant. It was also shown that the donor atoms experience no diffusion along the growth direction (depth direction) when fabricated with a target depth of 4.75a023. In accordance with these published studies, we have assumed that the two closely spaced dopant atoms in the case of 2P qubits are placed at the same depth from the Si surface. Furthermore, the distance between the two P atoms is within 2a0. We note that these are not limiting factors for our technique and robust qubit characterisation can be performed in the presence of donor depth variations and/or for larger donor separations.
A systematic labelling scheme was formulated to represent single donor atoms in silicon crystal23, which is extended in this work for a general case of qubits, where each qubit can be formed by either one donor atom (P) or two closely spaced donor atoms (2P). Note that here 2P is defined as a donor cluster where two donor atoms are within the 2a0 distance. The schematic diagram of a small portion of the Si crystal structure is shown in Fig. 2a to illustrate the possible locations for a dopant atoms to within a few nanometres from the z = 0 surface. The z = 0 surface is hydrogen passivated (shown by purple atoms and marked with H) and exhibits the formation of Si dimer rows (shown by light blue atoms), which are aligned perpendicular to the page (along the [110] direction). The area is shaded underneath the dimers to indicate the positioning of Si atomic sites with respect to the dimers. In our new notation, we represent each donor atom location by \({L}_{m}^{i,j}(n)\) and the corresponding STM images by (n, m, i, j), where n selects a plane group, m ∈ {0, 1∕4, 1∕2, 3∕4} represents a plane within the group at depth d[PGm] = (m + n)a0, i identifies the positioning with respect to the surface dimer rows, and j denotes the individual location(s) of the dopant atom(s) inside a selected plane defined by (n, m, i). Further details about this classification scheme are provided in Supplementary Section 1.
a Schematic diagram of a small portion of the silicon lattice is shown, along with the positioning of the P donor atoms within a few nanometres of the z = 0 surface. The z = 0 surface is hydrogen passivated (purple atoms) and exhibits the formation of Si dimer rows (light blue atoms at z = 0), which are aligned perpendicular to the page (along the [110] direction). The area is shaded underneath the dimers to provide guidance on the positioning of atomic sites with respect to the dimers. b Based on symmetry of donor positions with respect to the location of surface dimer rows, six planes at n = 4 are shown highlighting possible locations for donor atom placement. In each plane, the positioning of donor atoms is labelled by a number j, whose value varies from 0 to 24 as shown for m = 0 and i = 1 case. The position labels are same for the other five (n, m) cases. The central atom is marked as j = 0 and the numbering in the inner ring is from 1 to 8 and in the outer ring is from 9 to 24 clockwise. c Theoretically computed STM images are plotted for all possible positions (j = 0, 1, 2, ..., 24) at n = 4, m = 3/4, and i = 7. The images clearly exhibit a well-defined symmetry of wave function features convoluted with the surface dimer positions. Based on the symmetry analysis, we find that the 2P images are identical when the second P atom is symmetrically distributed around the reference P atom at j = 0. All distinct images are highlighted by a red coloured boundary.
For a given target depth based on (n, m), the dopant atoms are placed in the same plane. The in-plane positioning of the dopant atoms is shown in Fig. 2b. To demonstrate the working of the machine learning framework, we have selected four target depths: 4a0, 4.25a0, 4.5a0, 4.75a0, corresponding to n = 4 plane group. Owing to the symmetry of the silicon crystal, the STM images exhibit same symmetry for other plane groups, therefore this particular set of planes at n = 4 represents all types of STM images that repeat for other values of n23. We have separately plotted six planes corresponding to n = 4. Note that for m = 0 and 1/4, we have only plotted one value of i (1 and 3). The positions corresponding to i = 2 and 4 are at the other edge of the dimer rows and symmetrically similar to the positions at i = 1 and 3, respectively. This will result in exactly the same STM images, rotated by 270°. The exact positions corresponding to these images can be determined by overlaying dimer row atoms23. In our classification scheme, we assume that one dopant atom is always at the centre marked by j = 0. The second donor in the case of 2P will occupy one of the locations at the boundaries of the two diamonds with distances a0 and 2a0 from the centre dopant atom. These positions are labelled anti-clockwise from j = 1–8 for the inner diamond and j = 9–24 for the outer diamond as illustrated for (n, m, i) = (4, 0, 1) in Fig. 2b. Note that, in each plane, the atom position at j = 0 is same as the i value in that plane.
Based on the dopant locations plotted in Fig. 2b, each dopant plane offers 25 possible configurations to place P/2P donor atoms, leading to 25 STM images. For the n = 4 plane group, we computed in total 125 STM images. Figure 2c plots the STM images for one selected plane corresponding to m = 3/4 and i = 7. Each STM image is labelled with the corresponding value of j. The STM images for the other five configurations are provided in Supplementary Figs 1–5.
From Fig. 2b, we note that a number of dopant positions are equivalent due to their symmetrical distance from the centre location at j = 0. This implies that the corresponding STM images would also exhibit the same feature map with a possible rotation or reflection with respect to the axes parallel or normal to the dimer rows direction. For example, in Fig. 2c, the images corresponding to j = 4 and j = 8 will be same if one of them is reflected with respect to the diagonal direction as shown in Supplementary Fig. 6. A careful examination of all images for (4, 3/4, 7, j) reveals that, out of the 25 images, only 9 images are distinct. We classify the 25 images for the (4, 3/4, 7, j) group in 9 distinct image classes in Supplementary Table 1. Further details about the classification of the STM images in distinct image classes is provided in Supplementary Section 1. Each class has been labelled by (m, n, i, min(j)), where min(j) is the minimum value of j in that class. For n = 4, there are 50 distinct image classes. The 50 images representing the distinct classes are highlighted by the red colour boundaries in Fig. 2c and also in Supplementary Figs 1–5. The machine learning framework recognises dopant positions and count based on the feature maps, therefore it will only identify images with respect to these 50 classes. For example, in Fig. 2c, the images corresponding to the positions j = 1, 3, 5, and 7 will be assigned to the same image class (3/4, 4, 7, 1). The determination of the exact dopant locations within an image class can be subsequently performed based on its relative symmetry with respect to the positions of the surface dimer rows, which can be done by overlaying dimer atom positions on top of the image.
Application of noise and image size reduction
The computed STM images demonstrate a perfect symmetry and sharp bright features, whereas the published measured images22,23,29 may consists of features that are asymmetrical in brightness and/or blurred around the edges. In order to test the resiliency of the machine learning framework in the presence of feature asymmetry and blurriness, we artificially apply a range of two types of noise to the computed images. A planar noise (σP) leads to an asymmetry of the features and a blurring noise (σB) causes the features to spread across their edges, making adjacent features harder to distinguish. The computation of noise and its application to the exemplary images is provided in Supplementary Section 2. Supplementary Figs 8 and 12 plot computed STM images as a function of various strengths of the planar and blurring noise, respectively. Based on the plotted images, we infer that σP ≤ 0.4 and σB ≤ 4.0 are the reasonable range of noise strengths beyond which the computed STM images become significantly distorted and cannot be accurately recognised. As part of the STM image preparation process, the application of noise is performed in the second step as illustrated in Fig. 3a.
a For the demonstration of the working of our machine learning framework, we have selected one STM image corresponding to n = 4, m = 3/4, i = 7, and j = 2. The STM image is converted from RGB colour plot to greyscale colour plot to reduce the storage size. The STM image is further processed to extract either edges of the bright features or based on the average values over each bright feature (see Supplementary Sections 3 and 4 for details). b Kernels are shown with size 32 (3 × 3) and 16 (2 × 2) for the edge detection and the feature averaging schemes, respectively. Each training image is convoluted with the kernels to generate a set of 32 or 16 convoluted images. The convoluted images are used to train a neural network with one input layer, one hidden layer, and one output layer. The outcomes of the trained neural network classifies the STM images in accordance with the exact donor atom positions and count.
After the addition of noise, the computed STM images are further processed to reduce their size. The size of a computed image is 535 × 535 pixels, which is quite large for the purpose of training and testing of a machine learning framework, which generally requires processing of several thousand images (105 training and 17,600 test images in our study). To reduce the computational burden, we apply image reduction steps. Each coloured pixel represented by the RGB format is first converted to the greyscale format. We note that the STM images are computed over a large area (8 × 8 nm2); however, the area around the features is dark indicating negligible tunnelling current. As the information about the donor positions is encoded in the bright features, we crop the dark region to further reduce the image sizes. This is done by first rotating the image clockwise by 45° and then removing the pixels with the tunnelling current values below a threshold value. Further details of this process are provided in Supplementary Sections 3 and 4, along with Supplementary Figs. 13 and 14. At the end of this process, the image size is reduced from 535 × 535 pixels to about 237 × 189 pixels.
The information about the donor positions is present in the size, arrangement, and brightness of the image features. It is noted that each image consists of 20–30 bright features, which distinctly describe the corresponding position(s) and count of dopant atom(s). To further reduce the size of an image, we focus on the bright features and apply two techniques to extract the feature properties while preserving the donor position information. The first method that focusses on the shape of the features is called feature edges in Fig. 3a. Further details about this method are described in Supplementary Section 3. In this technique, we apply a filter operation that extracts the edges of the features. The image is then 3 × 3 sub-sampled or max-pooled to obtain a final image consisting of about 79 × 63 pixels. Note that in this method, each image is of slightly different size based on the number of features and their spatial distributions. Overall, the size of the computed images after the edge detection processing is always below 90 × 90 for all the images studied in this work.
The second method is labelled as feature averages in Fig. 3a and is described in detail in Supplementary Section 4. In this scheme, we represent each feature by its overall average brightness with respect to the dimer positions. This drastically reduces the size of an image to 11 × 10 pixels. Moreover, the size of the final processed images is also fixed for all cases. We do not apply any max-pooling function to feature averaged images. Following the image processing steps, we train and test a machine learning framework for both methods separately. A comparison is performed between the two image reduction schemes based on the computational efficiency and robustness against the application of noise.
Training of the CNN
The processed STM images are used to train a CNN. The robust training of a CNN generally requires a very large data set, typically consisting of sample spaces with O(103) sizes. We used ideal images and the images with various levels of planar noise (σP) to train the CNN. To construct a sufficiently large training data set, we randomly vary σP between 0 and 0.4 and compute 2000 images corresponding to each of the 50 classes, accumulating a library of 105 training images. These images are separately processed through the edge detection and feature averaging schemes and are used to train two independent CNNs with one input, one hidden, and one output layers.
Figure 3b displays the work flow of the CNN for the established high-throughput qubit characterisation scheme. Each image in the training data set is passed through the convolution layer before setting up the CNN. In the case of the edge detection scheme, the CNN consists of a convolutional layer with 32, 3 × 3 kernels along with 2 × 2 max-pooling, followed by a hidden layer of 256 rectified linear units (ReLu) activated neurons. The images are scaled to 48 × 48 pixels. Training on 105 images with 30 epochs achieved a learning accuracy of >99.5% and completed in about 5 h on an average desktop machine. For the case of the feature averaging scheme, a hidden layer of 64 ReLu activated neurons, and the training was performed on 105 images with 20 epochs, which was completed in about 30 min on an average desktop machine and resulted in a learning accuracy of 100%. In both cases, the output layer is a densely connected layer with Softmax activation function. The CNN was compiled based on the Adam algorithm36 with the learning rate of 104 and the categorical cross-entropy for optimisation and as the loss function, respectively. The number of neurons is optimised by testing out various configurations of the CNN, and a sufficiently low number of neurons that will maintain the near perfect learning is chosen. The implementation of the CNN was performed by using Keras37, utilising TensorFlow as the underlying platform38.
Qubit characterisation fidelities including noise
To test the performance of the machine learning framework, we define two parameters as the fidelity (f) of the qubit characterisation and the confidence level (CL). For a given test image, the trained CNN returns a set of 50 values (between 0 and 1), where each value indicates CL for that image to be in 1 of the 50 image classes. The test image is characterised as belonging to a particular image class based on the highest CL value. If the highest CL correctly identifies the image class, it is assigned a value of f = 1, otherwise f = 0. To test the robustness of the CNN, we prepared three separate test sets for both the edge detection and the feature averaging schemes. The first test set consists of 50 ideal STM images without the application of noise and the trained machine learning framework resulted in f = 1 with CL = 1 for all images. This confirmed that the CNN has been properly trained based on the prepared training images.
The second case consisted of test images after the application of blurring noise only for both the edge detection and the feature averaging schemes. To establish a sufficiently large test set, we arbitrarily selected 16 STM image classes (see Supplementary Section 5 and Supplementary Fig. 15 for details) and applied the blurring noise (σB) with its strength varying from 0 to 5.0 pixels with an increment of 0.5. At each value of σB, its orientation is randomly varied and 100 images are computed. The total test set consisted of 17,600 STM images from the 16 classes. In Supplementary Figs. 16 and 17, we have plotted the percentage of fidelity values (number of correctly classified images out of the 100 noisy images) obtained from the CNN for each image class independently. Figure 4a plots the average values computed from the 1600 images (16 classes × 100 noise orientations) at each value of σB. The error bars indicate two standard deviations of the mean value. As expected, fidelities decrease when σB increases and the images become harder to recognise. Based on the plotted results, we infer that the feature averaging scheme provides much higher fidelities compared to the edge detection scheme for large values of σB. The higher fidelity values for the feature averaging scheme are also coupled with about an order of magnitude better computational efficiency and two orders of magnitude lower storage requirements. Therefore, we conclude that the feature averaging scheme offers superior performance for the established machine learning-based qubit characterisation compared to the edge detection scheme. Interestingly, we find that the fidelity drop varies between different image classes and some images offer very high resiliency against the application of σB. This information may provide a useful input for the selection of a target depth during donor atom fabrication processes incorporating this autonomous characterisation scheme.
a The average fidelities from the CNN are plotted as a function of σB. At each value of σB, the average fidelity is computed based on 1600 test images (16 classes and 100 images per class). The error bars indicate two standard deviations of the mean value. b A set of 16 processed STM images are shown after the application of the edge detection procedure to test the working of the trained CNN. The images are applied random strengths of noise selected from 0 ≤ σP ≤ 0.4 and 0 ≤ σB ≤ 2.0 range. The corresponding unprocessed STM images are provided in Supplementary Fig. 15. In each case, the CNN correctly identifies the donor positions and count with the CL values as provided on top of the images. c A set of 16 processed STM images are shown after the application of the feature averaging procedure to test the working of the trained CNN. The images are applied random strengths of noise selected from 0 ≤ σP ≤ 0.4 and 0 ≤ σB ≤ 4.0 range. The corresponding unprocessed STM images are provided in Supplementary Fig. 15. In each case, the CNN correctly identifies the donor positions and count with the CL values as provided on top of the images.
In the final test set, we simultaneously apply both planar and blurring noise to the set of STM images plotted in Supplementary Fig. 15. In the case of the edge detection scheme, we randomly vary noise orientation and strength from 0 ≤ σP ≤ 0.4 and 0 ≤ σB ≤ 2.0 range, whereas for the feature average scheme, we randomly vary noise levels from 0 ≤ σP ≤ 0.4 and 0 ≤ σB ≤ 4.0 due to its higher resiliency against the application of σB. The final processed images including noise are shown in Fig. 4b, c. For both image-reduction schemes, the CNN characterises each image correctly (f = 1), with the CL values shown in the figure. Based on these results, we conclude that the CNN has been trained to accurately identify the STM images in the presence of both planar and blurring noise.
Summary and outlook
In summary, this work takes a first step towards implementation of a machine learning framework for autonomous characterisation of a large-scale quantum computer architectures based on dopant impurities in silicon. The input to the established framework are simulated STM images of one electron wave functions confined on single dopants or on small clusters of closely spaced dopants. The images are processed to optimise the exploitation of information known about the system (e.g. lattice geometry and surface dimers) and to reduce computational burden by developing and applying two feature-detection methods, namely edge detection and feature averages. Our results showed that both feature-detection methods enable high-fidelity qubit characterisation at low noise level, with the feature averaging method providing considerably superior performance in the presence of large blurring noise. A CNN is trained to characterise the noisy STM images and pinpoint the corresponding dopant atom position(s) and count with an exact lattice site precision. For the purpose of demonstrating the working of the established methods, the CNN was trained and tested on simulated STM images, including noise levels commensurate with the published measurements. We note that the computed STM images have previously shown an extremely good agreement with the measured images at both pixel-by-pixel and feature-by-feature levels23, therefore we expect that the trained CNN will be able to characterise experimental images with an accuracy equivalent to the simulated images with noise. As the training of CNN requires several thousand images, the capability to train based on simulated images eliminates the need for performing large-scale experimental measurement, saving a lot of time and effort.
A second outcome of this work is that the trained ML framework enables the pinpointing of dopant locations in the donor-dot qubits consisting of two dopant atoms in the nearest-neighbour and second nearest-neighbour configurations. Given the considerable recent interest in donor-dot qubits for two-qubit exchange-based quantum gates39, this work significantly broadens the scope of the established spatial metrology technique, which was previously demonstrated for qubits made up of single impurity atoms only23. We note that, in this work, the image classification was performed by implementing a CNN. The selection of the CNN technique was based on its recent success for the experimental work on silicon dangling bond qubits19 and electronic quantum matter visualisation40. In our study, the training of the CNN over 100,000 STM images worked efficiently, attaining a learning of 99.5% in about 5 h on an average desktop machine. In this proof-of-concept work, we have shown that the CNN approach has been very effective; in future work, a comparative study might be carried out of the application of other machine learning techniques such as support vector machine and random forest classifier scheme to this problem.
The established automated characterisation of atomic qubits with such a high level of accuracy will assist in the design and implementation of two-qubit quantum gates. The underpinning experimental expertise, the atomic-precision fabrication of dopant atoms in silicon via STM lithography4, and the STM images of dopant wave functions by low-temperature tunnelling of single electron22 has already been demonstrated. Augmentation of the formulated machine learning set-up with these experimental techniques is expected to enable high-throughput characterisation post-fabrication with minimal human interaction. We envision that, as the number of qubits in quantum devices grows, the characterisation by direct quantum measurements will be increasingly onerous, and a fast, reliable, and autonomous methodology may play a crucial role in the scale-up process.
Methods
Tight-binding wave function calculations
The computation of phosphorus dopant wave functions is performed by solving an atomistic sp3d5s* tight-binding Hamiltonian41. The P donor atom is placed in a large silicon box consisting of roughly four million atoms. The confining potential on the P atom is represented by a comprehensive description of the central-cell effects, which include non-static dielectric screening of donor potential33:
where A, α, β, and γ are fitting constants and have been numerically fitted as described in the literature42. In addition, the nearest-neighbour bond lengths of Si:P are strained by 1.9% in accordance with the recent density functional theory study43. The value of U0 at the donor atom site is adjusted to empirically fit the binding energies of 1s manifold of states44. The calculation of wave functions also included the effect of 2 × 1 surface reconstruction, leading to the formation of dimer rows at the z = 0 surface23,45. The impact of the surface strain due to the 2 × 1 reconstruction is included in the tight-binding Hamiltonian by a generalisation of the Harrison’s scaling law, where the inter-atomic interaction energies are modified with the strained bond length d as \({(\frac{{d}_{0}}{d})}^{\eta }\), where d0 is the unperturbed bond length of Si lattice and η is a scaling parameter whose magnitude depends on the type of the interaction being considered and is fitted to obtain hydrostatic deformation potentials41. The boundary conditions for the silicon box are selected as closed, with dangling bond energies shifted by large values to exclude their effect in the working range of energy46. The theoretical calculations were performed using the NEMO-3D framework47,48.
Computation of STM Images
The computation of the STM images is performed by coupling the atomistic tight-binding wave function calculation with the Bardeen’s tunnelling current formalism34. The wave function is decayed in the vacuum region above the reconstructed silicon surface based on the Slater orbital real-space representation49. For the calculation of the tunnelling current, the dominant contribution has been found to come from the \({d}_{{z}^{2}\!-\frac{1}{3}{r}^{2}}\) tip orbital23, which is computed by applying the derivative rule reported by Chen35:
where ΨD is the donor wave function and r0 is the position of the STM tip.
Each computed STM image is spanned over 8 × 8 nm2 area and consists of about 535 × 535 pixels represented in the RGB colour scheme.
Data availability
The data that support the findings of this study are available within the article and its Supplementary Information File. Further requests can be made to the corresponding author.
References
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133 (1998).
Loss, D. & Divincenzo, D. Quantum computation with quantum dots. Phys. Rev. A 57, 120 (1998).
Zwanenburg, F. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961 (2013).
Fuechsle, M. et al. A single-atom transistor. Nat. Nanotechnol. 7, 242 (2012).
Salfi, J. et al. Valley filtering in spatial maps of coupling between silicon donors and quantum dots. Phys. Rev. X 8, 031049 (2018).
Pla, J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541 (2012).
Morello, A. et al. Single-shot readout of an electron spin in silicon. Nature 467, 687 (2010).
Tyryshkin, A. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 11, 143 (2012).
Saeedi, K. et al. Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830 (2013).
Pica, G., Lovett, B. W., Bhatt, R. N., Schenkel, T. & Lyon, S. A. Surface code architecture for donors and dots in silicon with imprecise and nonuniform qubit couplings. Phys. Rev. B 93, 035306 (2016).
Wang, Y., Chen, C.-Y., Klimeck, G., Simmons, M. & Rahman, R. Characterizing Si:P quantum dot qubits with spin resonance techniques. Sci. Rep. 6, 31830 (2016).
Testolin, M., Hill, C., Wellard, C. & Hollenberg, L. A precise cnot gate in the presence of large fabrication induced variations of the exchange interaction strength. Phys. Rev. A 76, 012302 (2007).
Hill, C. Robust controlled-not gates from almost any interaction. Phys. Rev. Lett. 98, 180501 (2007).
Butler, K., Davies, D., Cartwright, H., Isayev, O. & Walsh, A. Machine learning for molecular and materials science. Nature 559, 547 (2018).
Luna, P., Wei, J., Bengio, Y., Aspuru-Guzik, A. & Sargent, E. Use machine learning to find energy materials. Nature 552, 23 (2017).
Libbrecht, M. & Noble, W. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 16, 321 (2015).
Murphy, R. An active role for machine learning in drug development. Nat. Chem. Biol. 7, 327 (2011).
Heureux, A., Grolinger, K., Elyamany, H. & Capretz, M. Machine learning with big data: challenges and approaches. IEEE Access 5, 7776 (2017).
Rashidi, M. & Wolkow, R. Autonomous scanning probe microscopy in situ tip conditioning through machine learning. ACS Nano 12, 5185 (2018).
Rashidi, M. et al. Autonomous atomic scale manufacturing through machine learning. Preprint at https://arxiv.org/abs/1902.08818 (2019).
Bishop, C. M. Pattern Recognition and Machine Learning (Springer, 2006).
Salfi, J. et al. Spatially resolving valley quantum interference of a donor in silicon. Nat. Mater. 13, 605 (2014).
Usman, M. et al. Spatial metrology of dopants in silicon with exact lattice site precision. Nat. Nanotechnol. 11, 763 (2016).
Sinthiptharakoon, K. et al. Investigating individual arsenic dopant atoms in silicon using low-temperature scanning tunnelling microscopy. J. Phys. Condens. Matter 26, 012001 (2014).
Garleff, J. K. et al. Atomically precise impurity identification and modification on the manganese doped GaAs(110) surface with scanning tunneling microscopy. Phys. Rev. B 78, 075313 (2008).
Ishida, N. et al. Direct visualization of the N impurity state in dilute GaNas using scanning tunneling microscopy. Nanoscale 7, 16773 (2015).
Plantenga, R. et al. Spatially resolved electronic structure of an isovalent nitrogen center in GaAs. Phys. Rev. B 96, 155210 (2017).
Krammel, C. et al. Incorporation of Bi atoms in InP studied at the atomic scale by cross-sectional scanning tunneling microscopy. Phys. Rev. Mater. 1, 034606 (2017).
Brazdova, V. et al. Exact location of dopants below the Si(001):H surface from scanning tunneling microscopy and density functional theory. Phys. Rev. B 95, 075408 (2017).
Usman, M., Voisin, B., Salfi, J., Rogge, S. & Hollenberg, L. C. L. Towards visualisation of central-cell-effects in scanning tunnelling microscope images of subsurface dopant qubits in silicon. Nanoscale 9, 17013 (2017).
Wang, Y. et al. Highly tunable exchange in donor qubits in silicon. npj Quantum Inf. 2, 16008 (2016).
Pakkiam, P. et al. Single-shot single-gate rf spin readout in silicon. Phys. Rev. X 8, 041032 (2018).
Usman, M. et al. Donor hyperfine stark shift and the role of central-cell corrections in tight-binding theory. J. Phys. Condens. Matter 27, 154207 (2015).
Bardeen, J. Tunnelling from a many-particle point of view. Phys. Rev. Lett. 6, 57 (1961).
Chen, C. J. Tunneling matrix elements in three-dimensional space: the derivative rule and the sum rule. Phys. Rev. B 42, 8841 (1990).
Kingma, D. & Ba, J. Adam: a method for stochastic optimization. In 3rd International Conference for Learning Representations (ICLR, 2015).
Chollet, F. et al. Keras. https://github.com/fchollet/keras (2015).
Abadi, M. et al. TensorFlow: large-scale machine learning on heterogeneous systems. https://www.tensorflow.org/ (2015).
He, Y. et al. A two-qubit gate between phosphorus donor electrons in silicon. Nature 571, 371–375 (2019).
Zhang, Y. et al. Machine learning in electronic-quantum-matter imaging experiments. Nature 570, 484–490 (2019).
Boykin, T. B., Klimeck, G. & Oyafuso, F. Valence band effective-mass expressions in the sp3d5s* empirical tight-binding model applied to a si and ge parametrization. Phys. Rev. B 69, 115201 (2004).
Nara, H. Screened impurity potential in Si. J. Phys. Soc. Jpn. 20, 778 (1965).
Overhof, H. & Gerstmann, U. Ab initio calculation of hyperfine and superhyperfine interactions for shallow donors in semiconductors. Phys. Rev. Lett. 92, 087602 (2004).
Usman, M. et al. Strain and electric field control of hyperfine interactions for donor spin qubits in silicon. Phys. Rev. B 91, 245209 (2015).
Craig, B. I. & Smith, P. V. The structure of the si(100)2×1: H surface. Surf. Sci. 226, L55–L58 (1990).
Lee, S., Oyafuso, F., von Allmen, P. & Klimeck, G. Boundary conditions for the electronic structure of finite-extent embedded semiconductor nanostructures. Phys. Rev. B 69, 045316 (2004).
Klimeck, G. et al. Atomistic simulation of realistically sized nanodevices using NEMO 3-D: Part II—applications. IEEE Trans. Electron. Dev. 54, 2090–2099 (2007).
Ahmed, S. et al. In Springer Encyclopedia of Complexity and Systems Science (ed. Meyers, R. A.) 5745–5783 (Springer, Heidelberg, 2009).
Slater, J. C. & Koster, G. F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 94, 1498 (1954).
Acknowledgements
This work was supported by the Australian Research Council (ARC) funded Center for Quantum Computation and Communication Technology (CE170100012) and partially funded by the USA Army Research Office (W911NF-08-1-0527). Computational resources were provided by the National Computing Infrastructure (NCI) and Pawsey Supercomputing Center through National Computational Merit Allocation Scheme (NCMAS).
Author information
Authors and Affiliations
Contributions
L.C.L.H. conceived the initial idea, subsequently developed by all authors. M.U. and L.C.L.H. planned and supervised the project. M.U. and Y.Z.W. computed and processed the STM images with input from L.C.L.H. Y.Z.W., M.U., and C.D.H. formulated and applied the machine learning framework. All authors contributed to the discussions and analysis of the data. M.U. wrote the manuscript with inputs from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial or non-financial interests. A provisional patent application has been submitted based on the aspects of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Usman, M., Wong, Y.Z., Hill, C.D. et al. Framework for atomic-level characterisation of quantum computer arrays by machine learning. npj Comput Mater 6, 19 (2020). https://doi.org/10.1038/s41524-020-0282-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-0282-0
This article is cited by
-
Challenges to extracting spatial information about double P dopants in Si from STM images
Scientific Reports (2024)
-
Study of structural, electrical and magnetic properties of co-substituted Co1−2xNixMgxFe2O4 (0 ≤ x ≤ 0.25) nanoferrite materials
Applied Physics A (2024)
-
A solid-state quantum microscope
Nature Electronics (2023)
-
Scanning tunneling microscopy of buried dopants in silicon: images and their uncertainties
npj Computational Materials (2022)