Abstract
Ferroelectric Rashba semiconductors (FERSCs) have recently emerged as a promising class of spintronics materials. The peculiar coupling between spin and polar degrees of freedom responsible for several exceptional properties, including ferroelectric switching of Rashba spin texture, suggests that the electron’s spin could be controlled by using only electric fields. In this regard, recent experimental studies revealing charge-to-spin interconversion phenomena in two prototypical FERSCs, GeTe and SnTe, appear extremely relevant. Here, by employing density functional theory calculations, we investigate spin Hall effect (SHE) in these materials and show that it can be large either in ferroelectric or paraelectric structure. We further explore the compatibility between doping required for the practical realization of SHE in semiconductors and polar distortions which determine Rashba-related phenomena in FERSCs, but which could be suppressed by free charge carriers. Based on the analysis of the lone pairs which drive ferroelectricity in these materials, we have found that the polar displacements in GeTe can be sustained up to a critical hole concentration of over ~1021/cm3, while the tiny distortions in SnTe vanish at a minimal level of doping. Finally, we have estimated spin Hall angles for doped structures and demonstrated that the spin Hall effect could be indeed achieved in a polar phase. We believe that the confirmation of spin Hall effect, Rashba spin textures and ferroelectricity coexisting in one material will be helpful for design of novel all-in-one spintronics devices operating without magnetic fields.
Similar content being viewed by others
Introduction
Employing electron’s spin for information processing is one of the main goals of semiconductor spintronics.1,2 The electric and nonvolatile control of spins in recently discovered ferroelectric Rashba semiconductors (FERSCs) holds a promise to combine storage, memory and computing functionalities.3,4 The exceptional properties of these novel materials arise from the unique property that the spin degrees of freedom are coupled to the electric polarization, whereby the polar axis intrinsically breaks the inversion symmetry (IS). The giant Rashba spin-splitting of the bulk electronic states can be then switched with the ferroelectric orientation and controlled by an electric field. On the other hand, the large spin–orbit coupling (SOC) required in these materials could also give rise to charge-to-spin interconversion phenomena, such as spin Hall effect (SHE),5,6,7,8 Edelstein–Rashba effect9 or spin galvanic effect10 allowing the electric control of spin currents.11 In this paper, we have theoretically studied the intrinsic SHE in two prototype FERSC compounds, GeTe and SnTe, and explored its compatibility with the polar distortion, a fundamental property in these materials.
The ferroelectric XTe (X = Ge, Sn) monochalcogenides share rhombohedrally distorted rocksalt structure (space group R3m, Fig. 1). Both possess spontaneous electric polarization \(\overrightarrow{P}\) parallel to [111] direction, but the high Curie temperature of GeTe (TC = 700 K)12,13 allowed in-depth experimental studies of the ferroelectric phase, which proved the polarization switching,14 electronic structures15,16,17 and reversible Rashba spin textures.18 Importantly, spin-to-charge conversion has been recently measured via spin pumping experiments in Fe/GeTe bilayers demonstrating high potential of such interfaces for multifunctional spintronics applications.19,20,21 On the other hand, ferroelectric phase of SnTe (TC = 100 K)22 has been known mainly from the theoretical side.23 Although the intermediate topological phases predicted at the phase transition still await an experimental confirmation, even the room temperature cubic crystal is intriguing, as it represents a prototypical example of a topological crystalline insulator.24 Finally, recent spin pumping experiments performed for the high-symmetry paraelectric bulk revealed strong SHE whose origin remains elusive.25
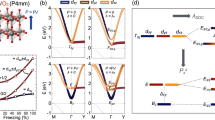
a Crystal structure of distorted GeTe with the polar axis along [111] direction. b BZ corresponding to the rhombohedral unit cell shown in a. The labels denote high-symmetry points used to evaluate band structures. c Schematic view of spin Hall effect in the configuration \({\sigma }_{yx}^{z}\). Directions of charge and spin currents are marked by the arrows. Red and blue shades denote spin polarization parallel and antiparallel to electric polarization, respectively.
Our calculations based on density functional theory (DFT) allowed us to quantitatively estimate spin Hall conductivities (SHCs) for low- and high-symmetry structures of both materials. First, we have unveiled that the ferroelectric phase could indeed enhance the SHE as compared with the paraelectric structure. We have interpreted this effect in terms of additional contributions to spin Berry curvature, originating from spin-splitted electronic states in the polar phase. Second, since the realization of SHE in semiconductors requires doping, we have studied the evolution of polar distortion with respect to the charge carrier concentration and estimated critical levels of doping that can sustain the low-symmetry phase. Finally, we have calculated spin Hall angles for doped structures and explored their potential for practical realization of SHE and electric control of Rashba effect (RE) at the same time.
Results and discussion
Electronic properties and SHE
Spin Hall materials are usually found either among elemental metals with strong SOC26,27,28 or novel topological phases, such as Weyl and Dirac nodal line semimetals where spin–orbit-protected gaps between the electronic bands are crossed by the Fermi level.29,30,31 It has also been known that a giant RE could induce large SHC as long as the Fermi level can be tuned and brought between lower and upper Rashba bands.32 In a polar material, the IS breaking gives rise to giant Rashba spin–orbit-derived spin splittings of the electronic states. Therefore, we expect that the ferroelectric structure could, in principle, enhance the SHC over the paraelectric phase at specific values of the chemical potential.
Before we start a more detailed analysis of the relationship between electronic structures and SHCs in polar and nonpolar phases, let us briefly comment on the accuracy of our calculations, essential for realistic evaluation of the SHC. Figure 2a shows the band structure calculated for the ferroelectric GeTe (blue line) along the high-symmetry directions defined in Fig. 1b. The ferroelectric distortion of the rhombohedral structure gives rise to inequivalent hexagonal faces in the Brillouin zone (BZ), two of them perpendicular to the polar axis and centered at Z points, and six corresponding to other hexagons centered at L, as marked in the scheme. The band structure agrees perfectly with earlier theoretical predictions and experimental results. In particular, our band gap Eg = 0.65 eV is very close to the experimental one (0.61 eV)33 and coincides exactly with the value obtained previously with Heyd–Scuseria–Ernzerhof (HSE) hybrid functional.3 We note that a simple PBE calculation yields an incorrect energy gap of only 0.3 eV. Importantly, the reliable value of the band gap is relevant for the estimation of Rashba spin splittings. They can be easily noticed in Fig. 2a, especially close to the valence band maximum (VBM) and highest conduction band minimum (HBM) along the ZU direction. Their values, 250 meV and 100 meV for valence and conduction bands, respectively, are again in excellent agreement with the HSE calculations and with experimental results reporting giant RE in bulk electronic states of GeTe.3,17,18 The corresponding Rashba parameters (6.4 and 2.4 eVÅ) are comparable with the values in different polar materials, such as BiTeI.34
Panels a and b show fully relativistic band structures of distorted (blue) and centrosymmetric (red) GeTe, respectively. Black lines denote results of scalar-relativistic calculations. c Different components of spin Hall conductivity tensor as a function of chemical potential. Blue and red lines correspond to distorted and undistorted structures in accordance with band structures in a–b. a′–c′ Same as a–c for SnTe. The Fermi energy is set at the VBM in all panels. We also note that the CBM does not lie along any of the high-symmetry lines.
Surprisingly, despite much smaller polar displacement, the electronic properties of the ferroelectric SnTe are quite similar to those described above. The strong SOC combined with the small band gap (0.33 eV) induces giant Rashba splittings (parameters) of the valence and conduction bands along ZU path, estimated to approximately 180 and 290 meV (4.0 and 8.3 eVÅ), respectively, again in good agreement with earlier hybrid functional calculations.23
As a next step, we will analyze the intrinsic SHE in both compounds. By using Bilbao Crystallographic Server,35,36 we have determined non-zero elements of \({\sigma }_{ij}^{k}\) and expressed them in terms of four independent components identified in the ferroelectric phase (space group no. 160). The third rank tensor of SHC can be written by treating different spin polarizations as separate matrices in the following form:
We have also performed an analogous symmetry analysis for the paraelectric phase (space group no. 225) and found only one independent component of the SHC tensor; more specifically, the elements of the matrices above are all identical, except for \({\sigma }_{xx}^{x}\) which vanishes in such a case.
Figure 2c–c′ shows SHC components \({\sigma }_{xy}^{z}\), \({\sigma }_{yz}^{x}\) and \({\sigma }_{zx}^{y}\) representing typical experimental geometries. We note that the elements \({\sigma }_{yx}^{y}={\sigma }_{xy}^{y}={\sigma }_{yy}^{x}=-{\sigma }_{xx}^{x}\) describe either rarely occuring configurations with spin polarizations aligned along spin/charge current or so-called longitudinal spin currents flowing in the direction of charge current. Because it is not yet clear whether they should be classified as SHEs,37 we have omitted them in the discussion below (\({\sigma }_{xx}^{x}\) is reported in the Supplementary Fig. 1). The plotted SHCs strongly suggest a sizable SHE in either ferroelectric (blue) or centrosymmetric (red) configuration. It emerges due to the significant impact of SOC on the electronic states, as deduced from the comparison between fully-relativistic and scalar-relativistic electronic structures. Nevertheless, it is evident that the magnitudes of SHCs are not identical in the two phases. Although the difference could arise either from the unit cell deformation or the polar displacement itself, a closer analysis revealed that the component \({\sigma }_{yz}^{x}\) changes mostly because of the deviation from the cubic unit cell, while the modifications in \({\sigma }_{xy}^{z}\) and \({\sigma }_{zx}^{y}\) arise predominantly from differences in the internal positions. As the latter leads to the IS breaking and Rashba spin-splitting in several regions of the BZ, we are convinced that it must be also a cause of a slight change in the magnitudes of SHC.
Finally, we note that in both materials the enhancement in the ferroelectric phase is rather small; for example, the feature that may really contribute to SHE in polar GeTe is a small peak of \({\sigma }_{xy}^{z}\) just below the Fermi level achievable in the presence of moderate doping. The difference is even more difficult to notice in SnTe, as all SHC components have comparable magnitudes, similar to the cubic phase (Fig. 2c′). We also emphasize that the band structures might change significantly upon the charge injection, thus the analysis based on the rigid shift of the chemical potential in Fig. 2c–c′ anyway provides only a rough approximation of SHC in doped materials. In order to obtain more realistic predictions, we have performed additional calculations which explicitly takes charge carriers into account.
Doping-induced evolution of polar displacements
The idea of realizing SHE in a device based on FERSC raises the question whether ferroelectricity, the key property of these materials, can be sustained upon doping which is required to achieve a non-zero SHC. In fact, the existence of ferroelectric metals has been debated for several years,38,39 as not only do the conduction charges screen the external electric fields, but they also suppress the Coulomb interactions that give rise to polar distortions. Although true ferroelectric metals are rare,40,41,42 it has been shown that the polar phase can survive in some materials upon doping. For example, ferroelectric distortions in BaTiO3 are sustained up to a critical concentration of 0.11e per unit cell volume (u.c.),43,44 whereas in BiFeO3, PbTiO3 and other lone-pair-driven ferroelectrics the charge injection even enhances the polar structures.45,46 Since the response to doping will depend, in general, on the origin of ferroelectricity (e.g. short-range vs long-range interactions among other factors),47,48 a careful analysis is needed to confirm the compatibility between SHE and the polar phase.
The ferroelectric displacement in both GeTe and SnTe is driven by the lone pair of the cation. As it has been shown in detail by Waghmare et al., the stereochemical activity of the latter is determined by the interacting s and p states of the cation mediated by the mixing with the anion p states.49 The strictly chemical origin of the ferroelectricity suggests that the displacement might be sustained even in the presence of free charges screening the Coulomb interaction. We note, however, that the previous studies demonstrating the persistence of polar distortion in lone-pair-driven ferroelectrics were focused on electron doping, while GeTe and SnTe are always p-type doped due to the vacancies that naturally form in these materials.50 In the analysis below, we consider both signs of charge in order to provide a complete picture of the physics behind.
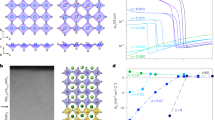
Figure 3a shows the evolution of polar displacement in GeTe as a function of charge carrier concentration. We can immediately notice that n- and p-type doping yield two completely different structural scenarios. In case of the former, the displacements are indeed enhanced, similarly as in the previous studies of lone-pair-driven ferroelectrics. In contrast, p-type doped structures reveal a rather fast decay of polar distortions which vanish above the critical hole concentration of n = 0.13∣e∣/u.c. corresponding to about 2.2 × 1021/cm3, closely resembling the behavior of BaTiO3 with ferroelectric instability ensured by the Coulomb force.43 This indicates that the lone pairs in GeTe might become less active upon p-type doping. We also notice that the volumes of the unit cell, Fig. 3b, follow quite similar trend, i.e. a larger displacement tends to increase the volume, while paraelectric structures favor smaller unit cells. Finally, ferroelectric to paraelectric transition in p-type doped regime is further confirmed by the phonon calculations of the doped cubic cells shown in Fig. 3c. Ferroelectric instabilities manifest as the imaginary frequencies of phonons that soften close to the point of phase transition.
Panel a shows the relative displacement τ of the atom from the centrosymmetric 0.5a position (black diamonds) and the angle between lattice vectors (red squares), b reports the changes in the unit cell volume (blue circles) and c the corresponding phonon frequencies (green circles). The negative numbers indicate imaginary values of the frequency. Dashed lines denote the phase transition. d Electron localization function plotted in the plane of distortion [0-11] for the centrosymmetric (upper left) and distorted (upper right) structures without doping and assuming the same rhombohedral unit cell for both. The bottom panels report p-type (left) and n-type doped (right) polar phases. In this case, the unit cells correspond to the relaxed volumes displayed in b. The highest localization is displayed in red, thus the orange/redish lobes are interpreted as the lone pairs of Ge.
In order to shed more light on these intriguing findings, we have calculated the electron localization function (ELF) which helps to identify regions associated with electron pairs. Figure 3d compares ELF plotted for selected configurations from Fig. 3a–c as well as for an undistorted structure. The lone pairs are seen as pronounced red regions around the Ge atoms, rather spherical in the centrosymmetric configuration (upper left) and distorted in the ferroelectric structure (upper right). The asymmetric lobe confirms the activity of the lone pair in the polar phase and demonstrates dominant role that it plays in the mechanism of ferroelectricity. Furthermore, the comparison of the heavily p- and n-type ‘ferroelectrics’ (bottom right and left, respectively) clearly shows that in the former the lobes resemble those observed in the centrosymmetric structure. In contrast, the asymmetric lobe in the electron-doped configuration is even more enhanced with respect to the undoped ferroelectric, which indicates a stronger stereochemical activity of Ge.
The reason of the distinct evolution of the hole and electron doped structures can be further rationalized by the analysis of the projected density of states (PDOS) calculated for the corresponding cubic cells (Fig. 4). As discussed in ref. 49, the primary cause of the distortion is mixing between s and p states of the cation (dark and light blue, respectively) resulting from a delicate balance of their bonding/antibonding with the anion p states (orange lines). Since this effect occurs predominantly at the top of valence bands, it is thus not surprising that the lone pair remains unaffected by n-type doping which shifts the Fermi level in opposite direction (Fig. 4a). On the other hand, in the presence of holes as shown in Fig. 4c, all the involved states reconstruct, slightly hybridizing with conduction bands which in turn suppresses the distortion.
a Density of states projected on s and p states of cation (dark and light blue, respectively) and p states of anion (orange) in n-type doped cubic and distorted rhombohedral unit cell of GeTe. b Same as a without doping. c Same as a with opposite p-type doping of 0.1∣e∣/u.c. All the structures were fully relaxed.
In SnTe, the calculations of structural parameters with varying carrier concentration revealed trends very similar to those observed in GeTe. We emphasize that the polar displacement, even without doping, is very tiny (τ ~ 0.01). Moreover, as can be observed in Fig. 5a, τ decays much faster than in GeTe; the polar phase is completely suppressed at the carrier concentration of n = 0.03∣e∣/u.c. equivalent to around 4.0 × 1020/cm3, a doping commonly observed in experiments. We believe that the weaker ferroelectricity in this material can be assigned to a smaller and less active lone pair, resulting in a decreased tendency to a covalent bond formation.
Panel a shows the relative displacement τ of the atom from the centrosymmetric 0.5a position (black diamonds) and the angle between lattice vectors (red squares), b reports the changes in the unit cell volume (blue circles) and c the corresponding phonon frequencies (green circles). The negative numbers indicate imaginary values of the frequency. Dashed lines denote the phase transition.
Finally, let us comment on the practical realization of polarization reversal, which can be challenging in a doped semiconductor. Recent experimental study by Kolobov et al. based on piezoresponse force microscopy have demonstrated that the ferroelectric switching is possible in p-type doped epitaxial GeTe films.14 As estimated above, the polar displacements should survive even at the high doping level of over 1021 e/cm3 above the typically measured values,51,52 but the applied electric field might still be screened by free carriers induced by the vacancies. We believe that the successful realization of ferroelectric switching in GeTe samples could be related to a strong electric field applied locally with the PFM tip which allows to switch the domains. As pointed out by Kolobov et al., the reduced thickness of the film might also play a role in the overall mechanism of the switching. These indicate that the ferroelectric switching in this material has to be further explored from both fundamental and practical sides; ideally, the polarization reversal should be achieved by applying an opposite voltage with the electrode contacts. On the other hand, the ferroelectric switching has never been reported in a similar rhombohedral SnTe, most likely due to the weak ferroelectricity and low temperature of phase transition, which also impedes the realization of FERSC in this material.
SHE in doped FERSCs
Finally, we will focus on the SHE in the doped structures discussed in the previous section. Figure 6 reports the values of spin Hall angle, defined as a ratio of spin and charge conductivity. We have compared the values estimated for XTe at moderate and high concentrations of holes with the calculations for known spin Hall materials. The highest SHCs in GeTe within the considered range of carrier concentrations are ~30–80 (\(\hbar\)/e)(Ω × cm)−1 with the maximum value found at n = 0.1∣e∣/u.c. = 2.0 × 1021∣e∣/cm3 for \({\sigma }_{yz}^{x}\). The calculated spin Hall angle θSH ~ 0.01 (green circle) is lower than in case of Pt and much below the value estimated for (nodal line) semimetal IrO2.30,31 It can be assigned to the large charge conductivity in doped GeTe. On the other hand, θSH is higher at n = 0.02∣e∣/u.c. ≈ 3 × 1020/cm3 (green square), as the charge conductivity changes faster than the SHC. This confirms that the sizable SHE could be explored in GeTe at hole concentrations of 1020–1021/cm3, which genuinely sustains the polar phase and is typically observed in experiments. In fact, recent results based on unidirectional spin Hall magnetoresistance in Fe/GeTe bilayer seem to be in good agreement with the above estimation.21 In those experiments, the SHE was observed in GeTe with holes concentration of ~2.2 × 1020/cm3.
Spin Hall conductivities were calculated using PAOFLOW code, whereas charge conductivities σC for specific carrier concentrations were estimated from the experimental data in ref. 68 for GeTe, ref. 69 for SnTe and ref. 70 for IrO2. We note that the actual σC will strongly depend on sample preparation and structure. The dashed lines indicate large (0.1) and moderate (0.01) spin Hall angles.
Analogous trends can be noticed for SnTe displayed as blue square and circle in Fig. 6. We have found that the SHCs are much above those estimated for GeTe, similarly as in case of previously reported 2D-XTe.53 Notably, the values of SHCs continuously grow with doping, achieving 170–250 (\(\hbar\)/e)(Ω × cm)−1 for hole concentrations of 0.02–0.1∣e∣/u.c., which results in very high spin Hall angles of 0.03–0.15. Because the polar distortions of SnTe are suppressed already at 0.02∣e∣/u.c., the giant SHE should rather be attributed to the paraelectric phase. In fact, the estimated spin Hall angle is in good agreement with the experimental value of 0.01 measured in the high-temperature rocksalt structure by Ohya et al.25 Although it has been suggested that the topological surface states could enhance the efficiency of SHE, our analysis shows that the large spin Hall angle can be entirely assigned to the strong SOC of bulk electronic states in the cubic structure. Thus, despite the realization of FERSC seems difficult in this material, it is extremely promising for spintronics applications based on SHE.
Summary
In summary, we have studied SHE in prototype Rashba ferroelectrics GeTe and SnTe. Although such an idea might appear contradictory, we have demonstrated that the SHE could be indeed observed in a doped polar (or ferroelectric) material. We have explored several aspects related to the realization of SHE in polar structures. First, we have noticed that the Rashba splittings of the electronic bands can enhance SHC, but they play a minor role at the hole concentrations usually observed in the considered materials. Second, we have investigated the evolution of polar distortions under carrier doping and found that the lone pair driven ferroelectricity is robust against electron injection, whereas in the presence of holes the polar displacements can be sustained up to ~0.13 (0.03) ∣e∣/u.c. in GeTe (SnTe). Finally, we have reported spin Hall angles for both materials at the typical concentrations of holes 1020–1021/cm3. The values in GeTe are close to 0.01 and refer to the polar phase, while giant SHE in SnTe characterized by the angles of ~0.1 is likely to be found in paraelectric structures. In conclusion, our results indicate that the SHE could be realized in FERSCs. This opens a new perspective to integrate different functionalities within one material, and combine spin injection/detection with electric spin manipulation in a device similar to recently presented all-electric spin transistor.54 We believe that our study will stimulate further search of FERSCs with complementary spin-dependent electronic properties, whereby the interplay of charge-to-spin conversion, Rashba-related physics and ferroelectricity could bring novel spintronics applications.
Methods
First-principles calculations based on DFT were performed using QUANTUM ESPRESSO package55,56 interfaced with the AFLOWπ infrastructure.57 We treated the exchange and correlation interaction within the generalized gradient approximation (GGA),58 and the ion–electron interaction with the projector augmented-wave fully-relativistic pseudopotentials59 from the pslibrary database.60 The electron wave functions were expanded in a plane wave basis set with the cutoff of 85 Ry. The electronic properties were calculated using the pseudo-hybrid Hubbard density functional ACBN0.61 We remark that this parameter-free alternative of traditional DFT+U methods was proven to yield extremely accurate values of energy gaps and relative positions of different bands in wide-gap semiconductors or perovskite oxides,62,63 in good agreement with more demanding beyond-DFT approaches,64 such as hybrid functionals or GW approximation.
The rhombohedral unit cells were fully relaxed until the forces on each atom became smaller than 10−3 Ry/bohr; the optimized lattice constants of the ground-state ferroelectric GeTe (SnTe) are equal to 4.37 Å (4.57 Å), respectively. The BZ sampling at the level of DFT was performed following the Monkhorst-Pack scheme using a 16 × 16 × 16 k-points grid. The electron/hole doping was simulated by adding extra charge to the system with the compensating amount of opposite charge in the background.
The intrinsic SHCs were calculated as implemented in the PAOFLOW code65 following the Kubo’s formula:66,67
where \({\Omega }_{n,ij}^{k}\) is the spin Berry curvature of nth band assuming spin polarization along k and spin (charge) current along i (j), \({f}_{n}(\overrightarrow{k})\) is the Fermi-Dirac distribution function and \({j}_{i}^{k}=\{{s}_{k},{v}_{i}\}\) is the spin current operator, where s and v stand for spin and velocity operators, respectively. In order to properly resolve the rapid variation of spin Berry curvatures, we have interpolated the k-points mesh to 48 × 48 × 48 using the adaptive smearing in the final SHC calculations. The corresponding convergence test is reported in the Supplementary Information.
Data availability
Data are available from the authors upon reasonable request.
Code availability
The PAOFLOW code can be downloaded from http://aflowlib.org/src/paoflow/.
References
Xu, Y., Awschalom, D. D. & Nitta, J. Handbook of Spintronics (Springer Publishing Company, Incorporated, 2015).
Datta, S. & Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 56, 665–667 (1990).
Di Sante, D., Barone, P., Bertacco, R. & Picozzi, S. Electric control of the giant Rashba effect in bulk GeTe. Adv. Mater. 25, 509–513 (2013).
Picozzi, S. Ferroelectric Rashba semiconductors as a novel class of multifunctional materials. Front. Phys. 2, 10 (2014).
Sinova, J., Valenzuela, S. O., Wunderlich, J., Back, C. H. & Jungwirth, T. Spin Hall effects. Rev. Mod. Phys. 87, 1213–1260 (2015).
Hirsch, J. E. Spin Hall effect. Phys. Rev. Lett. 83, 1834–1837 (1999).
Kato, Y. K., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Observation of the spin Hall effect in semiconductors. Science 306, 1910–1913 (2004).
Sinova, J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004).
Nakayama, H. et al. Rashba-Edelstein magnetoresistance in metallic heterostructures. Phys. Rev. Lett. 117, 116602 (2016).
Ganichev, S. D. et al. Spin-galvanic effect. Nature 417, 153 (2002).
Sih, V. & Awschalom, D. D. Electrical manipulation of spin-orbit coupling in semiconductor heterostructures. J. Appl. Phys. 101, 081710 (2007).
Rabe, K. M. & Joannopoulos, J. D. Ab initio determination of a structural phase transition temperature. Phys. Rev. Lett. 59, 570–573 (1987).
Kriegner, D. et al. Ferroelectric self-poling in GeTe films and crystals. Crystals 9, 335 (2019).
Kolobov, A. V. et al. Ferroelectric switching in epitaxial GeTe films. APL Mater. 2, 066101 (2014).
Liebmann, M. et al. Giant Rashba-type spin splitting in ferroelectric GeTe(111). Adv. Mater. 28, 560–565 (2016).
Elmers, H. J. et al. Spin mapping of surface and bulk Rashba states in ferroelectric α -GeTe(111) films. Phys. Rev. B 94, 201403 (2016).
Krempasky, J. et al. Disentangling bulk and surface Rashba effects in ferroelectric α -GeTe. Phys. Rev. B 94, 205111 (2016).
Rinaldi, C. et al. Ferroelectric control of the spin texture in GeTe. Nano Lett. 18, 2751–2758 (2018).
Rinaldi, C. et al. Evidence for spin to charge conversion in GeTe(111). APL Mater. 4, 032501 (2016).
Sławińska, J. et al. Fe/GeTe(111) heterostructures as an avenue towards spintronics based on ferroelectric Rashba semiconductors. Phys. Rev. B 99, 075306 (2019).
Varotto, S. et al. Investigation of charge-to-spin conversion in GeTe. In Proc. Spintronics XI, Vol. 10732 (eds Drouhin, H. -J. et al.) 27–34 (International Society for Optics and Photonics, SPIE, 2018).
Iizumi, M., Hamaguchi, Y., Komatsubara, K. F. & Kato, Y. Phase transition in SnTe with low carrier concentration. J. Phys. Soc. Jpn. 38, 443–449 (1975).
Plekhanov, E., Barone, P., Di Sante, D. & Picozzi, S. Engineering relativistic effects in ferroelectric SnTe. Phys. Rev. B 90, 161108 (2014).
Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 982 (2012).
Ohya, S. et al. Observation of the inverse spin Hall effect in the topological crystalline insulator SnTe using spin pumping. Phys. Rev. B 96, 094424 (2017).
Guo, G. Y., Murakami, S., Chen, T.-W. & Nagaosa, N. Intrinsic spin Hall effect in platinum: first-principles calculations. Phys. Rev. Lett. 100, 096401 (2008).
Guo, G. Y. Ab initio calculation of intrinsic spin Hall conductivity of Pd and Au. J. Appl. Phys. 105, 07C701 (2009).
Sagasta, E. et al. Unveiling the mechanisms of the spin Hall effect in Ta. Phys. Rev. B 98, 060410 (2018).
Sun, Y., Zhang, Y., Felser, C. & Yan, B. Strong intrinsic spin Hall effect in the TaAs family of Weyl semimetals. Phys. Rev. Lett. 117, 146403 (2016).
Sun, Y., Zhang, Y., Liu, C.-X., Felser, C. & Yan, B. Dirac nodal lines and induced spin Hall effect in metallic rutile oxides. Phys. Rev. B 95, 235104 (2017).
Das, P. K. et al. Role of spin-orbit coupling in the electronic structure of IrO2. Phys. Rev. Mater. 2, 065001 (2018).
Xiao, C. Semiclassical Boltzmann theory of spin Hall effects in giant Rashba systems. Front. Phys. 13, 137202 (2017).
Chang, L. L., Stiles, P. J. & Esaki, L. Electron barriers in Al-Al2O3-SnTe and Al-Al2O3-GeTe tunnel junctions. IBM J. Res. Dev. 10, 484–486 (1966).
Ishizaka, K. et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 10, 521–526 (2011).
Aroyo, M. I. et al. Bilbao crystallographic server: I. Databases and crystallographic computing programs. Z. Kristallogr. Cryst. Mater. 221, 15–27 (2006).
Aroyo, M. I., Kirov, A., Capillas, C., Perez-Mato, J. M. & Wondratschek, H. Bilbao crystallographic server. II. Representations of crystallographic point groups and space groups. Acta Crystallogr. A 62, 115–128 (2006).
Zhang, Y. et al. Spin-orbitronic materials with record spin-charge conversion from high-throughput ab initio calculations. Preprint at https://arxiv.org/abs/1909.09605 (2019).
Anderson, P. W. & Blount, E. I. Symmetry considerations on martensitic transformations: "ferroelectric" metals? Phys. Rev. Lett. 14, 217–219 (1965).
Benedek, N. A. & Birol, T. Ferroelectric metals reexamined: fundamental mechanisms and design considerations for new materials. J. Mater. Chem. C 4, 4000–4015 (2016).
Shi, Y. et al. A ferroelectric-like structural transition in a metal. Nat. Mater. 12, 1024 (2013).
Filippetti, A., Fiorentini, V., Ricci, F., Delugas, P. & Íñiguez, J. Prediction of a native ferroelectric metal. Nat. Commun. 7, 11211 (2016).
Puggioni, D., Giovannetti, G., Capone, M. & Rondinelli, J. M. Design of a Mott multiferroic from a nonmagnetic polar metal. Phys. Rev. Lett. 115, 087202 (2015).
Wang, Y., Liu, X., Burton, J. D., Jaswal, S. S. & Tsymbal, E. Y. Ferroelectric instability under screened Coulomb interactions. Phys. Rev. Lett. 109, 247601 (2012).
Iwazaki, Y., Suzuki, T., Mizuno, Y. & Tsuneyuki, S. Doping-induced phase transitions in ferroelectric BaTiO3 from first-principles calculations. Phys. Rev. B 86, 214103 (2012).
He, X., Jin, K.-J, Guo, H.-Z & Ge, C. Evolution of the electronic and lattice structure with carrier injection in BiFeO3. Phys. Rev. B 93, 174110 (2016).
He, X. & Jin, K.-J. Persistence of polar distortion with electron doping in lone-pair driven ferroelectrics. Phys. Rev. B 94, 224107 (2016).
Chandra, H. K., Gupta, K., Nandy, A. K. & Mahadevan, P. Ferroelectric distortions in doped ferroelectrics: BaTiO3:m (m = V − Fe). Phys. Rev. B 87, 214110 (2013).
Liu, J. et al. Understanding doped perovskite ferroelectrics with defective dipole model. J. Chem. Phys. 149, 244122 (2018).
Waghmare, U. V., Spaldin, N. A., Kandpal, H. C. & Seshadri, R. First-principles indicators of metallicity and cation off-centricity in the IV-VI rocksalt chalcogenides of divalent Ge, Sn, and Pb. Phys. Rev. B 67, 125111 (2003).
Edwards, A. H. et al. Electronic structure of intrinsic defects in crystalline germanium telluride. Phys. Rev. B 73, 045210 (2006).
Campi, D., Paulatto, L., Fugallo, G., Mauri, F. & Bernasconi, M. First-principles calculation of lattice thermal conductivity in crystalline phase change materials: GeTe,Sb2Te3 and Ge2Sb2Te5. Phys. Rev. B 95, 024311 (2017).
Shaltaf, R., Gonze, X., Cardona, M., Kremer, R. K. & Siegle, G. Lattice dynamics and specific heat of α -GeTe: theoretical and experimental study. Phys. Rev. B 79, 075204 (2009).
Sławińska, J. et al. Giant spin Hall effect in two-dimensional monochalcogenides. 2D Mater. 6, 025012 (2019).
Choi, W. Y. et al. Ferromagnet-free all-electric spin Hall transistors. Nano Lett. 18, 7998–8002 (2018).
Giannozzi, P. et al. Quantum Espresso: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).
Supka, A. R. et al. AFLOWπ : a minimalist approach to high-throughput ab initio calculations including the generation of tight-binding hamiltonians. Comput. Mater. Sci. 136, 76–84 (2017).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Corso, A. D. Pseudopotentials periodic table: from H to Pu. Comput. Mater. Sci. 95, 337–350 (2014).
Agapito, L. A., Curtarolo, S. & Buongiorno Nardelli, M. Reformulation of DFT+ U as a pseudohybrid Hubbard density functional for accelerated materials discovery. Phys. Rev. X 5, 011006 (2015).
Gopal, P. et al. Improved predictions of the physical properties of Zn- and Cd-based wide band-gap semiconductors: a validation of the ACBN0 functional. Phys. Rev. B 91, 245202 (2015).
May, K. J. & Kolpak, A. M. Improved description of perovskite oxide crystal structure and electronic properties using self-consistent Hubbard U corrections from the ACBN0 functional. Preprint at https://arxiv.org/abs/1905.08328 (2019).
Tancogne-Dejean, N., Oliveira, M. J. T. & Rubio, A. Self-consistent DFT + U method for real-space time-dependent density functional theory calculations. Phys. Rev. B 96, 245133 (2017).
Buongiorno Nardelli, M. et al. PAOFLOW: A utility to construct and operate on ab initio Hamiltonians from the projections of electronic wavefunctions on atomic orbital bases, including characterization of topological materials. Comput. Mater. Sci. 143, 462–472 (2018).
Guo, G. Y., Yao, Y. & Niu, Q. Ab initio calculation of the intrinsic spin Hall effect in semiconductors. Phys. Rev. Lett. 94, 226601 (2005).
Gradhand, M. et al. First-principle calculations of the Berry curvature of Bloch states for charge and spin transport of electrons. J. Phys. Condens. Matter 24, 213202 (2012).
Madelung, O., Rössler, U. & Schulz, M. (eds) in Non-Tetrahedrally Bonded Elements and Binary Compounds I 1–16 (Springer, Berlin, Heidelberg, 1998).
Mandale, A. Transport properties of tin telluride films. Mater. Lett. 9, 389–395 (1990).
Fujiwara, K. et al. 5d iridium oxide as a material for spin-current detection. Nat. Commun. 4, 2893 (2013).
Acknowledgements
We are grateful to Naiwrit Karmodak, Christian Rinaldi, Riccardo Bertacco, Marcio Costa and Frank Cerasoli for valuable discussions. The members of the AFLOW Consortium (http://www.aflow.org) acknowledge the grant ONR-MURI N000141310635. Finally, we acknowledge the High Performance Computing Center at the University of North Texas and the Texas Advanced Computing Center at the University of Texas, Austin.
Author information
Authors and Affiliations
Contributions
J.S. coordinated the project, providing calculations, data analysis and writing the manuscript; H.W. initiated the project and performed the calculations; P.G. performed the calculations; M.B.N. and S.C. analyzed the results; S.P. and M.B.N. conceived the idea of spin Hall effect in Rashba ferroelectrics. All the authors contributed to the discussion of the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, H., Gopal, P., Picozzi, S. et al. Spin Hall effect in prototype Rashba ferroelectrics GeTe and SnTe. npj Comput Mater 6, 7 (2020). https://doi.org/10.1038/s41524-020-0274-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-0274-0
This article is cited by
-
Nonreciprocal charge transport up to room temperature in bulk Rashba semiconductor α-GeTe
Nature Communications (2021)
-
Room-temperature ferroelectric switching of spin-to-charge conversion in germanium telluride
Nature Electronics (2021)
-
Dynamical amplification of electric polarization through nonlinear phononics in 2D SnTe
npj Computational Materials (2020)