Abstract
We analyze a data set comprising 370 GW band structures of two-dimensional (2D) materials covering 14 different crystal structures and 52 chemical elements. The band structures contain a total of 61716 quasiparticle (QP) energies obtained from plane-wave-based one-shot G0W0@PBE calculations with full frequency integration. We investigate the distribution of key quantities, like the QP self-energy corrections and QP weights, and explore their dependence on chemical composition and magnetic state. The linear QP approximation is identified as a significant error source and we propose schemes for controlling and drastically reducing this error at low computational cost. We analyze the reliability of the 1/N basis set extrapolation and find that is well-founded with a narrow distribution of coefficients of determination (r2) peaked very close to 1. Finally, we explore the accuracy of the scissors operator approximation and conclude that its validity is very limited. Our work represents a step towards the development of automatized workflows for high-throughput G0W0 band structure calculations for solids.
Similar content being viewed by others
Introduction
In computational materials science, the high-throughput mode of operation is becoming increasingly popular1. The development of automatized workflow engines capable of submitting, controlling, and receiving thousands of interlinked calculations2,3,4 with minimal human intervention has greatly expanded the range of materials, and properties, that can be investigated by a single researcher. Several high-throughput studies have been conducted over the past decade mostly with the aim of identifying new prospect materials for various applications including catalysis5, batteries6,7, thermoelectrics8,9, photocatalysts10, transparent conductors11, and photovoltaics12,13, just to mention some. The vast amounts of data generated by such screening studies have been stored in open databases14,15,16,17 making them available for further processing, testing, and comparison of methods and codes, training of machine learning algorithms, etc. With very few exceptions, the high-throughput screening studies and the generation of materials databases, have been based on density functional theory (DFT) at the level of the generalized gradient approximation (GGA).
While DFT is fairly accurate for structural parameters and other properties related to the electronic ground state, it is well known that electronic band structures, in particular the size of band gaps, are not well reproduced by most xc-functionals18. This holds in particular for the LDA and GGA functionals, which hugely underestimate band gaps, often by about a factor of 2 or more19,20. Hybrid functionals and certain metaGGAs perform significantly better21, but are not fully ab-initio and miss fundamental physics such as nonlocal screening effects22. Instead, the gold standard for quasiparticle band structure calculations of solids is the many-body GW method23,24,25,26, which explicitly accounts for exchange and dynamical screening. In its simplest non-self-consistent form, i.e., G0W0, this approximation reproduces experimental band gaps to within 0.3 eV (mean absolute error) or 10% (mean relative error)19,20,27. We note in passing that for partially self-consistent GW020 or when vertex corrections are included28,29, the deviation from experiments falls below 0.2 eV, which is comparable to the uncertainty of the experimental reference data. The improved accuracy of the GW method(s) comes at the price of a significantly more involved methodology both conceptually and numerically as compared to DFT. While DFT calculations can be routinely performed by non-experts using codes that despite very different numerical implementations produce identical results30, GW calculations remain an art for the expert.
The high complexity of GW calculations is due to several factors including (i) The basic quantities of the theory, i.e., the Greens function (G) and screened Coulomb interaction (W) are dynamical quantities that depend on time/frequency. Several possibilities for handling the frequency dependence exists including the formally exact direct integration19 and contour deformation techniques31 as well as the controlled approximate analytic continuation methods32 and the rather uncontrolled but inexpensive plasmon-pole approximations24. (ii) The formalism involves infinite sums over the unoccupied bands. While most implementations perform the sum explicitly up to a certain cutoff, schemes to avoid the sum over empty states have been developed33,34. (iii) The basic quantities are two-point functions in real space (or reciprocal space) that couple states at different k-points. This leads to large memory requirements and makes it unfeasible to fully converge GW calculations with respect to the basis set. Consequently, strategies for extrapolation to the infinite basis set limit must be employed35,36. (vi) Unless the GW equations are solved fully self-consistently, which is rarely done and does not improve accuracy29,37, there is always a starting point dependence. This has been systematically explored for molecules where it was found that LDA/GGA often comprise a poor starting point whereas hybrids perform better in the sense that they lead to better agreement with experimental ionization potentials and produce more well-defined spectral peaks with higher quasiparticle weights38,39. These and other factors imply that GW calculations not only become significantly more demanding than DFT in terms of computer resources, but they also involve more parameters making it difficult to assess whether the obtained results are properly converged or perhaps even erroneous.
Successful application of the high-throughput approach to problems involving excited electronic states, e.g., light absorption/emission, calls for the development of automatized and robust algorithms for setting the parameters of many-body calculations such as GW (according to available computational resources and required accuracy level), extrapolating the basis set, and assessing the reliability of the obtained results. The first step towards this goal is to analyze and systematize the data from large-scale GW studies. With a similar goal in mind, van Setten et al. compared G0W0@PBE band gaps, obtained with the plasmon-pole approximation, to the experimental band gaps. They analyzed the correlations between different quantities and concluded that that G0W0 (with plasmon-pole approximation) is more accurate than using an empirical correction of the PBE gap, but that, for accurate predictive results for a broad class of materials, an improved starting point or some type of self-consistency is necessary.
In this work we perform a detailed analysis of an extensive GW data set consisting of G0W0@PBE band structures of 370 two-dimensional semiconductors comprising a total of 61,716 QP energies. Our focus is not on the ability of the G0W0 to reproduce experiments, i.e., its accuracy, which is well established by numerous previous studies, but rather on the numerical robustness and reliability of the method and the basis set extrapolation procedure. The calculations employ a plane-wave basis set and direct frequency integration; thus the use of projector augmented wave (PAW) potentials represent the only significant numerical approximation. We investigate the distribution of self-energy corrections and quasiparticle weights, Z, and explore their dependence on the materials composition and magnetic state. By investigating the full frequency-dependent self-energy for selected materials we analyze the error caused by the linear approximation to the QP equation and propose methods to estimate and correct this error. We assess the reliability of a plane-wave basis set extrapolation scheme finding it to be very accurate with a coefficient of determination, r2, values above 0.95 in more than 90% of the cases when extrapolation is performed from 200 eV. Finally, we assess the accuracy of the scissors operator approach and conclude that it should only be used when the average (maximal) band energy errors of 0.2 eV (2 eV) are acceptable.
Results and discussion
The G0W0 data set
The 370 G0W0 calculations were performed as part of the Computational 2D Materials Database (C2DB) project40. Below we briefly recapitulate the computational details behind the G0W0 calculations and refer to Ref. 40 for more details. All calculations were performed with the projector augmented wavefunction code GPAW41.
The C2DB database contains about 4000 monolayers comprising both known and hypothetical 2D materials constructed by decorating experimentally known crystal prototypes with a subset of elements from the periodic table40. Currently, G0W0 calculations have been performed for 370 materials covering 14 different crystal structures and 52 different chemical elements. Figure 1a illustrates the distribution of elements. The number of materials containing a given element is shown below the element symbol. The number of magnetic materials containing the elements is shown in parenthesis next to the total number.
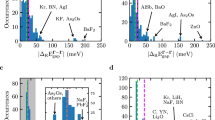
a The representation of individual elements in the G0W0 data set. The number of materials containing a given element is shown under the element’s symbol. The number of magnetic materials, if any, is shown in the parenthesis next to the total number. b Histograms of quasiparticle energy corrections calculated from G0W0 . The blue histogram shows the three topmost occupied valence bands, while the orange shows the three lowest unoccupied conduction bands. c A scatter plot of the PBE energy vs. the G0W0 energy. The colors show the Z value truncated to the interval [0.5, 1.0]. The points are plotted so that a point with smaller Z is plotted on top of a point with larger Z if the two points overlap.
To give an overview of some of the data analyzed in this work, the distribution of the 61716 G0W0 corrections for the six bands around the bandgap is shown in Fig. 1b. The distribution for the valence bands is shown in blue and for the conduction in orange. It is usually the case in GW studies that the DFT valence bands are shifted down and the conduction bands are shifted up. Similar behavior is found for the main part of our data, but we also observe a small subset of states for which the correction has the opposite sign. It is difficult to provide a clear physical explanation for why some occupied states are shifted up and some empty states are shifted down. We stress, however, that the GW corrections are measured relative to the PBE band energies, which is a somewhat arbitrary reference. For example, G0W0@LDA and G0W0@HSE would give different results—not so much for the resulting QP energies, which are relatively independent of the starting point—but for the size and sign of the GW corrections, which would now be measured relative to the LDA and HSE energies, respectively.
Figure 1c shows a scatter plot of the PBE energies versus the G0W0 energies. We only show energies from −10 to 10 eV for clarity. The color of a point shows the Z value. The latter has been truncated to the region [0.5, 1.0] to show the variation of the main part of the distribution. The main observation we can make from this figure is that there is no obvious correlation between the energies and the Z values. This is also verified by the calculated correlation coefficient, C, between EPBE and Z (C = 0.27), \({E}_{{\text{G}}_{0}{\text{W}}_{0}}\) and Z (C = 0.23) and between the G0W0 correction, \({E}_{{\text{G}}_{0}{\text{W}}_{0}}-{E}_{\text{PBE}}\), and Z (C = 0.10). We conclude that there is no significant correlation between the energies and Z, meaning that low Z values (which signals a break down of the QP approximation) may occur in any energy range.
Quasiparticle weight Z
The quasiparticle weight, Z, gives a rough measure of the validity of the quasiparticle picture, i.e., how well the charged excitations of the interacting electron system can be described by single-particle excitations from the ground state. In the “Methods” section, we prove a physical interpretation of the quasiparticle weight.
In the following, we analyze the 61,716 calculated QP weights, Z, contained in the C2DB database. As discussed in the Methods section, for the QP approximation to be well-founded Z should be close to 1. We split the Z values into two classes: quasiparticle-consistent (QP-c) for Z ∈ [0.5, 1.0] and quasiparticle-inconsistent (QP-ic) for Z ∉ [0.5, 1.0]. With this definition, QP-c states will have at least half of their spectral weight in the quasiparticle peak, but there is no deeper principle behind the threshold value of 0.5. We can expect that the QP approximation is more accurate for QP-c states than for QP-ic states.
Figure 2 shows a histogram of the Z-values (all extrapolated to the infinite plane-wave limit) corresponding to the 3 highest valence bands and 3 lowest conduction band of 370 semiconductors. The vast majority of the values are distributed around ≈0.75 with only 0.28% lying outside the physical range from 0 to 1 (0.16% are larger than one and 0.12% are negative). We find that 97.5% of the states are QP-c.
Histogram of QP weights, Z, for the 61716 QP states in the C2DB40. The Z values have been extrapolated to the infinite plane-wave limit (see next section). The main panel shows the distribution of Z values within the range, Z ∈ [0, 1], while the upper and lower insets show the distribution outside the physical range, i.e., Z > 1 and Z < 0, respectively. 0.16% of points lie in the Z > 1 range, while 0.12% lie in the Z < 0 range.
It is of interest to investigate if there are specific types of materials/elements that are particularly challenging to describe by G0W0. Figure 3 shows a barplot of the percentage of QP-ic states in materials containing a given element (note the logarithmic scale). The result of this analysis performed on the non-magnetic (ferromagnetic) materials is shown in blue (orange). For example, a large percentage (about 65%) of the states in Co-containing materials are QP-ic. It is clear that magnetic materials contribute a large fraction of the QP-ic states. In fact, 0.36% of the non-magnetic states are QP-ic while 22% of the magnetic states are QP-ic. In general, it thus seems that the QP approximation is generally worse for magnetic materials.
We note that the employed PAW potentials are not strictly norm-conserving. It has previously been found that the use of norm-conserving pseudopotentials can be crucial for the quantitative accuracy of G0W0 results for materials with localized d or f states35,42,43. To investigate this potential issue, we checked the distributions of G0W0 corrections and QP weights for materials containing at least one element with a pseudo partial wave of norm <0.5, i.e., materials where the norm-conservation could potentially be strongly violated for certain states. Out of the 370 materials, there were 279 materials in this category. The resulting distributions were not found to deviate qualitatively from those of all the materials (shown in Figs. 1b and 2, respectively), and the strongest indicator of unphysical Z values or opposite-sign G0W0 corrections remained the magnetic state of the material. On basis of this analysis, we conclude that the use of non-norm-conserving PAW potentials does not affect the conclusions of our study.
Based on the distribution of QP weights in Fig. 2, it appears that the QP approximation is valid for essentially all the states in the non-magnetic materials and most of the states in the magnetic materials. However, while a QP-c Z value is likely a necessary condition for predicting an accurate QP energy from the linearized QP equation [Eq. (6) in the “Method” section], it is not sufficient. This is because the assumption behind Eq. (6), i.e., that Σ(ε) varies linearly with ε in the range between the KS energy and the QP energy, is not guaranteed for QP-c states. This is illustrated in Fig. 4, which shows the full frequency-dependent self-energy for three states in the ferromagnetic FeCl2. Case (a) is a typical example where the self-energy of a QP-c state (Z = 0.61) varies linearly around εKS and the 1st order approximation works well. The second case (b) shows an example where the 1st order approximation breaks down for a QP-ic state (Z = 1.19). The final case (c) illustrates that the 1st order approximation can break down even in cases where Z is very close to 1. Unfortunately, there is no simple way to diagnose such cases from the information available in a standard G0W0 calculation (Σ(εKS) and Z). We stress that the example in Fig. 4c is a special case and that in general, the linear approximation is significantly more likely to hold for QP-c states than for QP-ic states (see discussion below).
Frequency-dependent self-energy (blue) for three electronic states with different quasiparticle weights, Z. The red line indicates ω − ϵKS while the black line is the linear approximation of the self-energy. The intersection of the blue and red lines indicate the solution to the quasiparticle equation, while the intersection between the red and black lines indicate the solution given by the linear approximation to the self-energy.
Beyond the linear QP approximation
Under the assumption that the KS wave functions constitute a good approximation to the QP wave functions so that off-diagonal elements can be neglected, the solution to the QP equation reduces to solving an equation of the form
where Σ(ω) = ΣGW(ω) − vxc is the frequency-dependent self-energy (see “Methods” section).
In this section, we investigate different root-finding schemes to estimate the size of the error introduced by the linear approximation and obtain an improved QP energy. With high-throughput computations in mind, a good algorithm provides a reasonable balance between computation time (number of Σ/Z evaluations) and accuracy. To benchmark the different schemes we computed the full frequency-dependent self-energy for 3192 states, corresponding to the 3 highest valence bands and 3 lowest conduction bands, for 12 of the 370 2D materials (including two ferromagnetic materials). The two ferromagnetic materials were chosen at random from materials that had some Z ∉ [0, 1]. The remaining 10 materials were chosen at random from materials with all Z ∈ [0, 1] and typical Z distributions. An overview of the materials is shown in Table 1. The self-energy is evaluated on a uniform frequency grid and interpolated using cubic splines. The “true” solution of the QP equation is then determined and used to evaluate the errors of the approximate schemes. In cases where there are multiple solutions, the smallest correction is selected.
We first determine the errors introduced by the linear approximation. Histograms of the errors for QP-c and QP-ic states are shown in Fig. 5. This shows that QP-ic generally has larger error and thus warrant particular attention.
The distributions of the error incurred by the linear approximation as estimated from 3192 states in 12 different materials for which we have calculated the full frequency-dependent self-energy and determined the exact QP energy (see main text). The distribution for QP-c states is shown in blue, while the distribution for QP-ic states is shown in orange. The inset shows the full distribution for QP-ic states.
We first consider the iterative Newton–Raphson (NR) method where we limit ourselves to 1 and 2 iterations to keep the number of self-energy evaluations and thus the computational cost low. We note that 1 iteration (NR1) is equivalent to the linear approximation. The distribution of the errors is shown in Fig. 6a. Although 87% of the errors from NR1 are below 0.1 eV, the mean absolute error (MAE) is 0.11 eV due to outliers. Most of these errors are significantly reduced by performing one more iteration of Newton–Raphson (NR2), but again outliers increase the MAE. If we evaluate the MAE without the outliers (those lying outside the displayed error range), the MAE reduces to only 0.006 eV.
a The error distributions for first-order Newton–Raphson (NR1) (blue) and second-order Newton–Rahpson (NR2) (orange). NR1 is equivalent to solving the linearized QP equation. b The NR1 distribution from a is again shown in blue for comparison. The orange distribution shows the error for the empirical empZ scheme. c The NR1 distribution is again shown in blue. The orange distribution is the error when the empZ scheme is applied only to the QP-ic states.
Motivated by the relatively narrow distribution of Z values in Fig. 2, we consider an empirical solution estimate consisting of replacing the actual Z value with the mean value of the distribution, i.e., we simply set Z = 0.75. This has the advantage of being simple, computationally cheap, and robust in the sense of avoiding outlier Z-values arising from local irregularities in Σ at the KS energy (Fig. 4b). The resulting error distribution is shown in Fig. 6b. While the central part of the distribution is slightly broadened compared to the 1st order approximation, the MAE is reduced due to a reduction of outliers (enhanced robustness). As shown in Fig. 6c, the central part of the distribution can be narrowed by applying the empirical approach only for QP-ic states, i.e., when Z ∉ [0.5, 1]. In fact, this approach (empZ@QP-ic) has a MAE equal to that of NR2 but with half the computational cost (two Σ/Z evaluations compared to four).
Next, we examine the polynomial fitting of the self-energy. We construct second and fourth-order polynomials, Pn(ω), from the self-energy at energies in a range of ±1 eV around the KS energy. The cost of the second and fourth-order fits is equivalent to three and five self-energy evaluations, respectively. In general, the polynomial fits have rather low correlation coefficients of C < 0.9 and are sensitive to the choice of frequency points and self-energy data used for the fit. As a consequence, the resulting errors are large (not shown) and the approach is not suitable. We attribute this to our observation that self-energies are often irregular (on the relevant scale of 1 eV) and not well-described by low-order polynomials.
Finally, we consider a scheme that we refer to as ΣdE, which estimates the error as
The motivation for this expression is the following. If the linear approximation is exact, then δ vanishes as it should. Moreover, if the self-energy has a non-zero curvature it can be shown that δ equals the true error to leading order in the curvature. In that sense, it is similar to the second-order polynomial fit, but with the important difference that whereas the polynomial fit was based on uniformly distributed points, ΣdE uses the value and slope at EKS and the value at EQP,lin.
In Fig. 7a, the distribution of the ratios of the estimated error and true error is shown and the errors resulting from Eq. (2) are shown in Fig. 7b. Compared to the linear approximation, the ΣdE reduces the MAE from 0.11 to 0.05 eV, at the cost of one additional self-energy evaluation. Interestingly, Eq. (2) systematically overestimates the error as shown in Fig. 7a. A Gaussian fit to the distribution (red curve) has a mean value of α0 = 1.5 and a standard deviation of 0.2. Since the distribution of α is fairly narrow, it is tempting to correct for the systematic error using α = α0, i.e., replacing δ → δ/α0. We denote this estimate as ΣdE-corrected. To verify this procedure we randomly bisect the data into a “training” and a “test” set of equal size. α0 is determined from the training set and the MAE is calculated on the test set. The MAEs thus found were always 0.02–0.03 eV. We performed the same analysis using different sizes of the training set and found that an MAE of 0.03 eV is robust with a training set down to ≥5% of data points. This indicates the approach is insensitive to data used to determine α0. In Fig. 7c, the ΣdE-corrected values are shown, where α0 was determined from the full distribution for simplicity. The ΣdE-corrected scheme shows excellent performance with an almost four-fold reduction of the MAE from 0.11 eV for the linear approximation to only 0.03 eV at a computational overhead of just one additional self-energy evaluation.
a The distribution of the ratio of the estimated error and the true error. Also shown in red is a gaussian fit to the distribution. The text annotations are shown the definition of α (top), the mean of the fitted gaussian, α0 (middle), and the standard deviation of the fitted gaussian, σ, (bottom). b Distribution of the error of the linear approximation (blue) and the error of solution derived from the estimated error (orange). c Correcting for the mean of α yields improved solution estimates (orange).
The performance of the different correction schemes is summarized in Table 2.
Plane-wave extrapolation
The self-energy and the derivative of the self-energy (both evaluated at the KS energy) are calculated at three cutoff energies: 170, 185, and 200 eV. These values are then extrapolated to infinite cutoff, or an infinite number of plane waves, NPW → ∞, by assuming a linear dependence on the inverse number of plane waves44. An example of this fitting procedure is shown in Fig. 8a. The extrapolation procedure saves computational time while improving the accuracy of the results—provided the extrapolation is sufficiently accurate. Extrapolation can fail if convergence as a function of the plane-wave cutoff for the given quantity does not follow the expected 1/NPW behavior in the considered cutoff range.
a Example of the plane-wave extrapolation procedure for the G0W0 self-energy and its derivative. The quantity of interest, e.g., the self-energy, is calculated for three different cutoff energies, here 170, 185, and 200 eV, and the assumed linear dependence on 1/NPW (NPW is the number of plane waves) is extrapolated to the infinite basis set limit. The coefficient of determination for the fit, r2, is shown in the box. b Histogram of the coefficient of determination, r2, for the 61,716 plane-wave extrapolations of self-energies (blue) and the derivatives of the self-energy (orange). The plot shows the distribution for the coefficient of determination r2 ≥ 0.99, while the insets show values outside this range. A total of 5.5% and 14.1% of the values are <0.99 for the self-energy and its derivative, respectively.
To validate this approach, we investigate the distribution of the r2 values for all 61716 extrapolations in C2DB. We split them into two cases: extrapolation of the self-energy and extrapolation of the derivative of the self-energy. The distributions are shown as histograms in Fig. 8b. The distributions are clearly peaked very close to 1, and in general, it seems that the extrapolation is very good. The distribution for the derivatives is somewhat broader, and the extrapolation is generally less accurate than for the self-energies, which indicates a slower convergence with plane waves than for the self-energies. If we choose r2 = 0.8 as an acceptable threshold, we find that 1.7% of the r2 values of the self-energy extrapolation fall below this criterion while 5.0% are below for the derivative extrapolation. While these numbers might seem large, the problem is readily diagnosed (by the r2 value) and can be alleviated by using higher plane-wave cutoffs.
Scissors operator approximation
Within the so-called scissors operator approximation (SOA) it is assumed that the G0W0 correction is independent of band- and k-index. Consequently, the G0W0 correction calculated at, e.g., the Γ point is applied to all the eigenvalues thus saving computational time as only one G0W0 correction is required. In Fig. 9a, the idea is illustrated for a generic band. With the notation from the figure, the SOA consists of setting Δ(k) = Δ (or Δnσ(k) = Δnσ when more than one band and spin is involved).
a Illustration of the scissors operator approximation for a generic band. The G0W0 correction (Δ) is calculated at, e.g., the Γ-point and is used to correct the energies at all every k-point. This yields the scissors shifted band structure, here labeled “PBE + Δ”. The actual G0W0 correction at the point k is labeled Δ(k). b Histogram showing the mean absolute error. c Maximum absolute error (b) of the scissors operator approximation. In both b and c, the average (maximum) is taken over the 3 highest valence bands and 3 lowest conduction bands in each of the 370 2D materials considered in this work.
To test the accuracy of the SOA, we evaluate the mean absolute error (\(\left\langle | \epsilon | \right\rangle\)) and maximum absolute error (\(\max (| \epsilon | )\)) of the band energies obtained with the SOA for each of the 370 materials:
and
The distribution of these errors is shown in Fig. 9b, c. From Fig. 9b, we see that the mean error exceeds 100 meV for about half of all materials—a rather large error, comparable to the target accuracy of the G0W0 method itself. Furthermore, it follows from Fig. 9c that the maximum absolute error is often 0.5–1.0 eV. We conclude that while the average error of the SOA might be acceptable, it can produce significant errors for specific bands and should be used with care.
Summary and conclusions
As high-throughput computations are gaining popularity in the electronic structure community, it becomes important to establish protocols for performing various types of calculations in an automated, robust, and error-controlled manner. In this work, we have taken steps towards the development of automated workflows for G0W0 band structure calculations of solids. With G0W0 representing the state-of-the-art for predicting QP energies in condensed matter systems, such workflows are essential for continued progress in the field of computational materials design.
Based on our detailed analysis of 61,716 G0W0 self-energy evaluations for the eigenstates of 370 two-dimensional semiconductors we were able to draw several conclusions relevant to large-scale GW studies. First of all, we found it useful to divide the states into two categories, namely quasiparticle-consistent (QP-c) and quasiparticle-inconsistent (QP-ic) states defined by Z ∈ [0.5, 1.0] and Z ∉ [0.5, 1.0], respectively. Importantly, we found that the QP energies obtained from the standard linearized QP equation are significantly more accurate for QP-c states than for QP-ic state. Moreover, we found the fraction of QP-ic states to be much larger in magnetic materials (22%) than in non-magnetic materials (0.36%). Thus, extra care must be taken when performing G0W0 calculations for magnetic materials; in particular, such materials might require special treatment in high-throughput workflows.
The mean absolute error (MAE) on the QP energies resulting from the linearized QP equation was found to be 0.11 eV. The MAE evaluated separately for QP-c and QP-ic states were 0.04 and 0.27 eV, respectively. In comparison, the accuracy of the GW approximation itself (compared to experiments) is on the order of 0.2 eV. It is therefore of interest to reduce or at least estimate the numerical error bar on the QP energies obtained from G0W0 calculations. We found that an empirical scheme, where we set Z = 0.75 (corresponding to the mean of the Z-distribution) for QP-ic states, reduces the MAE from 0.11 to 0.06 eV with no computational overhead. Similarly, the method dubbed the corrected ΣdE scheme reduces the MAE to 0.03 eV, at the cost of one additional self-energy evaluation. From these studies, it seems natural to accompany the QP energies obtained from G0W0 with estimated error bars derived from one of these correction schemes. In fact, we have used the empZ@QP-ic method to correct all the GW band structures in the C2DB database.
Our analysis of the well known and widely used scissors operator approximation shows that the errors introduced on the individual QP energies when averaged over all bands (specifically the 3 highest valence and 3 lowest conduction bands) typically is on the order of 0.1 eV while the maximum error typically exceeds 1 eV. We stress that our scissors operator fits each of the six bands separately using the G0W0 corrections at the Γ-point. Thus the errors introduced by the more standard scissors approximation that fits only the bandgap, are expected to be even larger. We conclude that the scissors operator should be used with care and only in cases where errors on specific band energies of 1–3 eV are acceptable.
Finally, the plane-wave extrapolation scheme was found to be highly reliable for our PAW calculations when applied to cutoff energies in the range 180–200 eV. In fact, only 1.7% (5.0%) of the self-energy (a derivative of self-energy) extrapolations had an r2 below 0.8. However, for the purpose of high-throughput studies, it may be prudent to store and make available information on the r2 for the extrapolation so that the quality of the extrapolation can always be examined and improved calculations with higher cutoff can be performed if deemed necessary.
Methods
G0W0 calculations
For the materials considered here, DFT calculations using PBE45 were performed using an 800 eV plane-wave cutoff. Spin–orbit coupling is included by diagonalizing the spin–orbit Hamiltonian in the k-subspace of the Bloch states found from PBE.
Those materials that have a finite gap and up to 5 atoms in the unit cell are selected for G0W0 calculations. The QP energies in C2DB are calculated for the 8 highest occupied and the 4 lowest unoccupied bands, however, in this study we only use the 6 bands closest to the Fermi level (3 valence and 3 conduction bands). Furthermore, we only include materials with a PBE gap greater than 0.2 eV as the accuracy of G0W0 for materials with very small PBE gaps is questionable. Three energy cutoffs are used: 170, 185, and 200 eV. The results are then extrapolated to infinite energy, i.e., to an infinite number of plane waves. This extrapolation is done by expressing the self-energies in terms of the inverse number of plane waves, 1/NPW, performing a linear fit, and determining the value of the fit at 1/NPW = 035,46.
The screened Coulomb interaction entering in the self-energy is calculated using full frequency integration in real frequency space. To avoid effects from the (artificially) repeated layers. A Wigner–Seitz truncation scheme is used for the exchange part of the self-energy47 and a 2D truncation of the Coulomb interaction is used for the correlation part44,48. A truncated Coulomb interaction leads to significantly slower k-point convergence because the dielectric function strongly depends on q around q = 0; this is remedied by handling the integral around q = 0 analytically49,50. A k-point density of 5.0/Å−1 was used.
The statistical analyses performed here use the data from all spins, k-points, and the three highest occupied bands, and the three lowest unoccupied bands. In section IV B we consider several examples of the full frequency-dependent self-energies for a randomly selected spin, k-point, and band combination, subject to some requirements on the quasiparticle weight, Z, which are described below.
Quasiparticle theory
The G0W0 quasiparticle energies are found by solving the quasiparticle equation (QPE)37:
Here ψnkσ is the Kohn–Sham wavefunction for band n, crystal momentum k, and spin σ, HKS is the single-particle Kohn–Sham Hamiltonian, Σ(ω) = ΣGW(ω) − vxc is the self-energy, and vxc is the exchange-correlation potential.
Typically, and in C2DB, the QPE is solved via one iteration of the Newton–Raphson method starting from the KS energy, ϵnkσ, which is equivalent to making a linear approximation of the self-energy. This yields the solution
Z is known as the quasiparticle weight. The G0W0 correction is defined as the difference between the G0W0 energy and KS energy, \({{\Delta }}{E}_{nk\sigma }={E}_{nk\sigma }^{\,\text{QP}\,}-{\epsilon }_{nk\sigma }\).
Following ref. 49, we provide here a physical interpretation of Z. We denote the many-body eigenstates for the N particle system by \(\left|{{{\Psi }}}_{i}^{N}\right\rangle\), where i is the excitation index. An interesting question is how well the state \(\left|{{{\Psi }}}_{i}^{N+1}\right\rangle\) can be described as the addition of a single electron to the ground state \(\left|{{{\Psi }}}_{0}^{N}\right\rangle\). In other words, can we find a state ϕ such that \(\left|{{{\Psi }}}_{i}^{N+1}\right\rangle \approx {c}_{\phi }^{\dagger }\left|{{{\Psi }}}_{0}^{N}\right\rangle\)? The optimal ϕ is determined from maximizing the overlap, i.e.,
If the maximal overlap is close to 1 the excited many-body state is well approximated by a single-particle excitation.
It turns out that the square of this maximal overlap is exactly equal to the QP weight Z defined by Eq. (6) if it is evaluated at the true QP energy and with the true QP wavefunction rather than at the KS energy and with the KS wavefunction. Furthermore, Z can be shown to be equal to the squared norm of the QP wavefunction, which is defined as
For proof of these results, we refer to ref. 49. In standard G0W0 calculations, the self-energy is evaluated at the KS energy using KS eigenstates. In this case, Z is no longer equal to the exact QP weight but only approximates it. If Z deviates significantly from 1, we can only conclude that either (1) the system is strongly correlated so that the QP approximation fails, or (2) the Kohn–Sham energy and/or wavefunction are a bad approximation to the true QP energy and/or wavefunction. In either case, we would expect that the G0W0 calculation is problematic and requires special attention.
Data availability
Data are available as an ASE51 database at https://cmr.fysik.dtu.dk/htgw/htgw.html.
References
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Jain, A. et al. Fireworks: a dynamic workflow system designed for high-throughput applications. Concurr. Comput. 27, 5037–5059 (2015).
Pizzi, G., Cepellotti, A., Sabatini, R., Marzari, N. & Kozinsky, B. Aiida: automated interactive infrastructure and database for computational science. Comput. Mater. Sci. 111, 218–230 (2016).
Mortensen, J., Gjerding, M. & Thygesen, K. Myqueue: Task and workflow scheduling system. J. Open Source Softw. 5, 1844 (2020).
Greeley, J., Jaramillo, T. F., Bonde, J., Chorkendorff, I. & Nørskov, J. K. Computational high-throughput screening of electrocatalytic materials for hydrogen evolution. Nat. Mater. 5, 909–913 (2006).
Kirklin, S., Meredig, B. & Wolverton, C. High-throughput computational screening of new li-ion battery anode materials. Adv. Energy Mater. 3, 252–262 (2013).
Zhang, Z. et al. Computational screening of layered materials for multivalent ion batteries. ACS Omega 4, 7822–7828 (2019).
Chen, W. et al. Understanding thermoelectric properties from high-throughput calculations: trends, insights, and comparisons with experiment. J. Mater. Chem. C 4, 4414–4426 (2016).
Bhattacharya, S. & Madsen, G. K. High-throughput exploration of alloying as design strategy for thermoelectrics. Phys. Rev. B Condens. Matter 92, 085205 (2015).
Castelli, I. E. et al. Computational screening of perovskite metal oxides for optimal solar light capture. Energy Environ. Sci. 5, 5814–5819 (2012).
Hautier, G., Miglio, A., Ceder, G., Rignanese, G.-M. & Gonze, X. Identification and design principles of low hole effective mass p-type transparent conducting oxides. Nat. Commun. 4, 1–7 (2013).
Yu, L. & Zunger, A. Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials. Phys. Rev. Lett. 108, 068701 (2012).
Kuhar, K., Pandey, M., Thygesen, K. S. & Jacobsen, K. W. High-throughput computational assessment of previously synthesized semiconductors for photovoltaic and photoelectrochemical devices. ACS Energy Lett. 3, 436–446 (2018).
Thygesen, K. S. & Jacobsen, K. W. Making the most of materials computations. Science 354, 180–181 (2016).
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B. & Wolverton, C. Materials design and discovery with high-throughput density functional theory: the open quantum materials database (oqmd). JOM 65, 1501–1509 (2013).
Jain, A. et al. Commentary: The materials project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Curtarolo, S. et al. Aflow: an automatic framework for high-throughput materials discovery. Comput. Mater. Sci. 58, 218–226 (2012).
Godby, R., Schlüter, M. & Sham, L. Accurate exchange-correlation potential for silicon and its discontinuity on addition of an electron. Phys. Rev. Lett. 56, 2415 (1986).
Hüser, F., Olsen, T. & Thygesen, K. S. Quasiparticle GW calculations for solids, molecules, and two-dimensional materials. Phys. Rev. B Condens. Matter 87, 235132 (2013).
Shishkin, M. & Kresse, G. Self-consistent GW calculations for semiconductors and insulators. Phys. Rev. B Condens. Matter 75, 235102 (2007).
Borlido, P. et al. Exchange-correlation functionals for band gaps of solids: benchmark, reparametrization and machine learning. Npj Comput. Mater. 6, 1–17 (2020).
Garcia-Lastra, J. M., Rostgaard, C., Rubio, A. & Thygesen, K. S. Polarization-induced renormalization of molecular levels at metallic and semiconducting surfaces. Phys. Rev. B Condens. Matter 80, 245427 (2009).
Hedin, L. New method for calculating the one-particle green’s function with application to the electron-gas problem. Phys. Rev. 139, A796 (1965).
Hybertsen, M. S. & Louie, S. G. Electron correlation in semiconductors and insulators: band gaps and quasiparticle energies. Phys. Rev. B Condens. Matter 34, 5390 (1986).
Aryasetiawan, F. & Gunnarsson, O. The GW method. Rep. Prog. Phys. 61, 237 (1998).
Golze, D., Dvorak, M. & Rinke, P. The GW compendium: a practical guide to theoretical photoemission spectroscopy. Front. Chem. 7, 377 (2019).
Nabok, D., Gulans, A. & Draxl, C. Accurate all-electron G0W0 quasiparticle energies employing the full-potential augmented plane-wave method. Phys. Rev. B Condens. Matter 94, 035118 (2016).
Shishkin, M., Marsman, M. & Kresse, G. Accurate quasiparticle spectra from self-consistent GW calculations with vertex corrections. Phys. Rev. Lett. 99, 246403 (2007).
Schmidt, P. S., Patrick, C. E. & Thygesen, K. S. Simple vertex correction improves GW band energies of bulk and two-dimensional crystals. Phys. Rev. B Condens. Matter 96, 205206 (2017).
Lejaeghere, K. et al. Reproducibility in density functional theory calculations of solids. Science 351, aad3000 (2016).
Faber, C., Attaccalite, C., Olevano, V., Runge, E. & Blase, X. First-principles GW calculations for dna and rna nucleobases. Phys. Rev. B Condens. Matter 83, 115123 (2011).
Caruso, F., Rinke, P., Ren, X., Scheffler, M. & Rubio, A. Unified description of ground and excited states of finite systems: The self-consistent GW approach. Phys. Rev. B Condens. Matter 86, 081102 (2012).
Umari, P., Stenuit, G. & Baroni, S. GW quasiparticle spectra from occupied states only. Phys. Rev. B Condens. Matter 81, 115104 (2010).
Govoni, M. & Galli, G. Large scale GW calculations. J. Chem. Theory Comput. 11, 2680–2696 (2015).
Klimeš, J., Kaltak, M. & Kresse, G. Predictive GW calculations using plane waves and pseudopotentials. Phys. Rev. B Condens. Matter 90, 075125 (2014).
Rasmussen, F. A. & Thygesen, K. S. Computational 2d materials database: electronic structure of transition-metal dichalcogenides and oxides. J. Phys. Chem. C 119, 13169–13183 (2015).
Shishkin, M. & Kresse, G. Implementation and performance of the frequency-dependent GW method within the paw framework. Phys. Rev. B Condens. Matter 74, 035101 (2006).
Rostgaard, C., Jacobsen, K. W. & Thygesen, K. S. Fully self-consistent gw calculations for molecules. Phys. Rev. B Condens. Matter 81, 085103 (2010).
Bruneval, F. & Marques, M. A. Benchmarking the starting points of the gw approximation for molecules. J. Chem. Theory Comput. 9, 324–329 (2013).
Haastrup, S. et al. The computational 2d materials database: high-throughput modeling and discovery of atomically thin crystals. 2D Mater. 5, 042002 (2018).
Enkovaara, J. E. et al. Electronic structure calculations with gpaw: a real-space implementation of the projector augmented-wave method. J. Phys. Condens. Matter 22, 253202 (2010).
Jiang, H. & Blaha, P. GW with linearized augmented plane waves extended by high-energy local orbitals. Phys. Rev. B Condens. Matter 93, 115203 (2016).
Jiang, H. Revisiting the GW approach to d-and f-electron oxides. Phys. Rev. B Condens. Matter 97, 245132 (2018).
Rozzi, C. A., Varsano, D., Marini, A., Gross, E. K. & Rubio, A. Exact coulomb cutoff technique for supercell calculations. Phys. Rev. B Condens. Matter 73, 205119 (2006).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Tiago, M. L., Ismail-Beigi, S. & Louie, S. G. Effect of semicore orbitals on the electronic band gaps of Si, Ge, and GaAs within the GW approximation. Physical Rev. B 69, 125212 (2004).
Sundararaman, R. & Arias, T. Regularization of the coulomb singularity in exact exchange by wigner-seitz truncated interactions: Towards chemical accuracy in nontrivial systems. Phys. Rev. B Condens. Matter 87, 165122 (2013).
Ismail-Beigi, S. Truncation of periodic image interactions for confined systems. Phys. Rev. B Condens. Matter 73, 233103 (2006).
Hüser, F., Olsen, T. & Thygesen, K. S. Quasiparticle gw calculations for solids, molecules, and two-dimensional materials. Phys. Rev. B Condens. Matter 87, 235132 (2013).
Rasmussen, F. A., Schmidt, P. S., Winther, K. T. & Thygesen, K. S. Efficient many-body calculations for two-dimensional materials using exact limits for the screened potential: Band gaps of mos 2, h-bn, and phosphorene. Phys. Rev. B Condens. Matter 94, 155406 (2016).
Larsen, A. H. et al. The atomic simulation environment—a python library for working with atoms. J. Phys. Condens. Matter 29, 273002 (2017).
Acknowledgements
We acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant No. 773122, LIMA). The Center for Nanostructured Graphene is sponsored by the Danish National Research Foundation, Project DNRF103. This project has received funding in the European Union’s Horizon 2020 research and innovation program under the European Union’s Grant Agreement No. 951786 (NOMAD CoE). T.D. acknowledges financial support from the German Research Foundation (DFG Project No. DE 2749/2-1).
Author information
Authors and Affiliations
Contributions
A.R. performed the statistical analyses and full, frequency-dependent self-energy calculations. T.D. performed the G0W0 calculations. K.S.T. conceptualized the project. All authors interpreted the analyses and wrote the article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rasmussen, A., Deilmann, T. & Thygesen, K.S. Towards fully automated GW band structure calculations: What we can learn from 60.000 self-energy evaluations. npj Comput Mater 7, 22 (2021). https://doi.org/10.1038/s41524-020-00480-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00480-7
This article is cited by
-
A robust, simple, and efficient convergence workflow for GW calculations
npj Computational Materials (2024)
-
Efficient GW calculations in two dimensional materials through a stochastic integration of the screened potential
npj Computational Materials (2023)
-
Towards high-throughput many-body perturbation theory: efficient algorithms and automated workflows
npj Computational Materials (2023)
-
Representing individual electronic states for machine learning GW band structures of 2D materials
Nature Communications (2022)
-
A universal similarity based approach for predictive uncertainty quantification in materials science
Scientific Reports (2022)