Abstract
We introduce machine-learned potentials for Ag-Pd to describe the energy of alloy configurations over a wide range of compositions. We compare two different approaches. Moment tensor potentials (MTPs) are polynomial-like functions of interatomic distances and angles. The Gaussian approximation potential (GAP) framework uses kernel regression, and we use the smooth overlap of atomic position (SOAP) representation of atomic neighborhoods that consist of a complete set of rotational and permutational invariants provided by the power spectrum of the spherical Fourier transform of the neighbor density. Both types of potentials give excellent accuracy for a wide range of compositions, competitive with the accuracy of cluster expansion, a benchmark for this system. While both models are able to describe small deformations away from the lattice positions, SOAP-GAP excels at transferability as shown by sensible transformation paths between configurations, and MTP allows, due to its lower computational cost, the calculation of compositional phase diagrams. Given the fact that both methods perform nearly as well as cluster expansion but yield off-lattice models, we expect them to open new avenues in computational materials modeling for alloys.
Similar content being viewed by others
Introduction
The technology frontier relies on the exceptional performance of next-generation materials. First-principles calculations of material properties provide one way to discover new materials or optimize existing ones. However, calculating properties from a first-principles approach is resource-intensive, restricting its applicability. For example, molecular dynamics simulations using density functional theory (DFT) are currently capable of handling fewer than a thousand atoms at picosecond time scales. However, many interesting materials science problems and technologically important processes can only be described with millions of atoms on micro- to millisecond time scales.
Conventional interatomic potentials (IPs), such as Lennard–Jones, embedded atom method (EAM), modified EAM, Tersoff, Stillinger–Weber, and so on, typically provide six to eight orders of magnitude speed-up compared to DFT calculations, and due to their simple, physically motivated forms, they are somewhat robust in the sense that their predictions for low energy structures are plausible. However, their quantitative accuracy is typically quite poor compared to DFT, especially in reproducing macroscopic properties. Machine-learned IPs tend to be much more accurate, but they are typically three to four orders of magnitude slower than conventional IPs. Importantly, the range of their applicability may be quite restricted. In typical parlance, their transferability can be limited. This transferability problem requires researchers to take care of constructing, applying, and validating IPs, and in particular makes it a rather tenuous proposition to use them to discover and predict new structures and novel properties.
In 2010, the Gaussian approximation potential (GAP)1 was introduced as an approach to create IPs with ab initio accuracy, using kernel regression and invariant many-body representations of the atomic neighborhood. Since their introduction, they have been effective at modeling potential energy surfaces2,3,4 and reactivity5 of molecules6 and solids7,8, defects9, dislocations10, and grain boundary systems11. Recently Bartók et al.12 showed that a GAP model using a smooth overlap of atomic position (SOAP) kernel can be systematically improved to reproduce even complex quantum-mechanical effects13. SOAP-GAP has thus become a standard by which to judge the effectiveness of numerical approximations to ab initio data. There are a number of other machine-learned potentials that also perform well and have overlapping applications with SOAP-GAP, although applications of several of these methods to alloys are still nascent14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31. While recent work32 compares the performance of multiple methods for alloy systems, it does not address dynamical quantities such as phonon dispersion or temperature-composition dependence in phase diagrams. Note that although the GAP framework can be used with arbitrary kernels, for simplicity we will use the GAP abbreviation to mean SOAP-GAP exclusively in the rest of this paper.
The moment tensor potential (MTP)33 is another approach to learning quantum-mechanical potential energy surfaces. Due to the efficiency of its polynomial basis of interatomic distances and angles, MTP is significantly faster than GAP and has already been shown to be capable of reaching equivalent accuracy for modeling chemical reactions34, single-element systems35,36, single-phase binary systems37, or ground states of multicomponent systems25. In this work, we demonstrate that both GAP and MTP are capable of fitting the potential energy function of a binary metallic system, the Ag-Pd alloy system, with DFT accuracy across the full space of configuration and composition for solid and liquid systems. In addition to reproducing energies, forces, and stress tensor components with near-DFT accuracy, we show that these potentials can also approximate phononic band structure quite well and can be used to model compositional phase diagrams. These new capabilities of quantum-accurate IPs for alloys would pave the way to accelerated materials discovery and optimization.
The Ag-Pd system provides a stringent test for a machine-learned IP that shows whether it can compete with the cluster expansion (CE) method despite the much simpler “lattice gas” formalism of the latter. The chemical similarity of silver and palladium and their similar atomic sizes (leading to small atomic mismatch)38 make it an ideal system for CE and a challenging test for competing methods. Ultimately, the challenging aspect for competing methods is handling both the structural and compositional degrees of freedom. For a system with matched atom sizes, the structural degrees are less of an issue for CE and it shines because of its effectively compositional basis functions. Since methods that use continuous basis functions, like the ones we test, typically perform better for structural rather than compositional variation, this system is a challenging test.
Phonon band structures directly describe phase stability at moderate temperatures via the quasi-harmonic approximation. We first show that both SOAP-GAP and MTP potentials can accurately reproduce DFT-calculated phonon band structures for alloy configurations that are not in the training set. As a demonstration of speed and transferability, we use the MTP potential to calculate melting lines and transition temperatures for the Ag-Pd phase diagram using the nested sampling (NS) method39,40,41. We then compare the performance of GAP and MTP across a low energy transition pathway between two stable configurations to demonstrate the importance of regularization and active learning.
Methods
Datasets
In this section, we describe the datasets used to fit and validate the potentials. Both the MTP and GAP potentials were fitted to the same active-learned dataset, while a liquid dataset provided validation for energies, forces, and “virials” (volume-weighted coefficients of the stress tensor). Although only the active-learned dataset was used for building the models, there was some overlap between the seed configurations in the active-learned dataset and the configurations for which phonons are predicted (discussed later), both having their origin in enumerated42 supercells.
Active-learned dataset
We use the MTP potential and its associated tools to create a database via active learning25,43 as described below. We start with a catalog of small fcc- and body-centered cubic (bcc)-based derivative superstructures. The energies, forces, and virials of these structures are computed by DFT and are then used to fit an MTP potential. This potential is then used to perform structural relaxation for all structures in the database. Active learning25,43 is based on a geometric criterion determining whether extrapolation was attempted while predicting energies, forces, and virials. If, during the relaxation of a particular structure, the estimated degree of extrapolation of the potential is too large, then that (partially relaxed) structure is computed with DFT and added to the training set. When the potential can reliably relax all structures in the enumerated database, the database is expanded to include larger unit cells, and the process is repeated.
For this work, an initial catalog of 58 enumerated structures42 with bcc and fcc derivative superstructures containing four atoms or less were calculated. We iterated the active-learning process until the MTP was able to successfully relax all enumerated structures with cell sizes up to 12 (a total of 10,850 structures). This final active-learning dataset has 774 configurations.
All the DFT data for these potentials were calculated with the Vienna Ab initio Simulation Package (VASP)44,45,46,47,48 using the PBE functional49. The k-points were selected using either Monkhorst-Pack50 or WMM51 schemes as described below. PREC = Accurate and EDIFF = 1e − 4 were used for all calculations unless otherwise specified.
During active learning, we used a k-point density setting of MINDISTANCE = TRUE and an energy convergence target of EDIFF = 1e - 4 for the self-consistent loop. However, for the final fit, we found it necessary to recompute the DFT for this dataset with higher k-point density and a tighter EDIFF setting in order to get good convergence of phonon dispersions. In our experience, a linear k-point density of 0.015 k-points per Å−1 is a reliable density for alloy fits.
The final dataset for training the GAP and MTP potentials used the original 774 configurations discovered through active learning but computed with MINDISTANCE = 65 in Mueller’s scheme and EDIFF = 1e − 8.
Liquid dataset
We built a dataset of liquid-like configurations by performing MD simulations using VASP at a high temperature. These calculations were performed at compositions of 25, 50, and 75 at.% Ag in cells with 32 atoms. The temperature for each simulation was set around the theoretical melting point (linearly interpolated from atomic melting points). Thus, 2766, 3063, and 3360 K were set as target temperatures for the MD runs and the thermostat parameters were SMASS = 3 and POTIM = 1.0. The simulation ran for 100,000 fs with snapshots taken every 50 fs. NELMIN = 4 ensured sufficient electronic steps were taken at each MD step. For this MD data, only the k-point at Γ was used. After the MD runs, each independent snapshot was evaluated again with VASP, but using a 4 × 4 × 4 MP k-point grid.
Potential fitting
The GAP model was fitted to the active-learned dataset using the QUIP package available from https://github.com/libAtoms/QUIP, using a sum of a two-body term with Gaussian kernels of pairwise distances and a many-body term with a SOAP kernel, a combination that has produced successful fits of materials in the past52,53,54,55. Parameters for the two- and many-body parts of the GAP model are summarized in Tables 1 and 2, and are broadly in line with what were used in the previous works. The σ values control regularization in the GAP model, and can be broadly thought of as target accuracies; they were set to 10−3 eV for energies (per atom), 10−3 eV/Å for forces, and 0.02 eV for virials (per atom). Their relative magnitudes also control the trade-off between the fit accuracies in energies, forces, and virials.
The MTP model with polynomial degree up to 1625 with 188 adjustable fitting parameters was trained on the same dataset as GAP. Table 3 summarizes the parameters needed to recreate the MTP model. The fitting weights (roughly corresponding to σ parameters of GAP) were 10−3 eV, 1.4 × 10−2 eV/Å, and 0.04 eV for energy, force, and stress, respectively. This is somewhat different from the parameters used for GAP; however, as we verified, this does not significantly affect the results.
NS: dataset augmentation
As described below, NS simulates atoms at extremely high temperatures that are well outside of the typical active-learned dataset described above. The MTP potential used for NS had to be trained using a slightly augmented dataset, to avoid the formation of dimers in the gaseous phase.
As the first step to constructing the augmented dataset, we identified 67 structures that are within 5 meV/atom from the convex hull of stable Ag-Pd structures. These structures were periodically repeated to form supercells with 32–64 atoms. These structures were used as initial configurations for molecular dynamics, running for 0.1 ns, while the MTP potential was trained on-the-fly25,43 at the range of temperatures from nearly zero to temperatures ensuring melting.
NS: methodology
The constant pressure NS method40,41 was used to calculate phase diagrams by sampling the entire potential energy surface with corresponding configuration space volumes to calculate the isobaric-isothermal partition function. The specific heat, which is the second derivative with respect to the temperature of the partition function, shows peaks at phase transitions, and we use temperatures of specific heat maxima as estimates of the corresponding transition temperatures. While the NS method has previously been applied to multicomponent systems, those simulations assumed constant composition. However, it is possible for phase separation to occur in temperature-composition space, which would be neglected by this constraint. Here we have extended the constant pressure NS method to a semi-grand-canonical (sGC) version56, where the total number of atoms is constant, but the numbers of the individual species are allowed to vary. This is implemented by carrying out the NS procedure on a free energy F defined as
where Ni and μi are the number of atoms and chemical potential of species i, respectively, and the sum is carried out over all species. To explore these degrees of freedom, we also added Monte-Carlo steps that propose the changing of the species of a randomly selected atom. Note that since the procedure is invariant to shifts in the total energy, the total number of particles is conserved, and only two species are present; the simulation is entirely characterized by the difference in chemical potentials Δμ.
To calculate the phase diagram in temperature-composition space, as it is usually plotted, we carry out sGC NS runs at a range of values of Δμ. In the sGC framework, the composition is an output of the simulation, and its value can be calculated as a function of temperature using the same ensemble average (with NS phase space volumes and Boltzmann weights) as any other quantity in the NS approach. For phase transitions that cross phase-separated regions, we would in principle expect discontinuous changes in composition (analogous to discontinuous changes in structure, internal energy, etc.) across the transition, but these will be broadened by finite-size effects. We also compare these results to constant composition NS runs, where a single transition temperature is identified with the peak of the Cp(T) curve. For one composition, 50%, we continue one of those NS runs to a sufficiently low temperature to search for solid-state phase transitions. The parameters used for both types of NS runs are listed in Table 4 in the notation of ref. 41, and in all NS simulations one configuration per NS iteration was removed (Kr = 1).
Results
Energy, force, and virial predictions
We now compare the performance of GAP and MTP models for the Ag-Pd system. Both the MTP and GAP models were validated against the liquid dataset for energy, force, and virial predictions. Table 5 summarizes the root mean square error (RMSE) in each of these properties for both GAP and MTP. No liquid data were included in the original active-learned dataset. Thus, these predictions represent severe extrapolation. The fact that both machine-learned IPs perform so well in this dataset is evidence of their transferability. The relatively simple approach to building the training set (iterative fitting and relaxing of enumerated superstructures) resulted in IPs that would be reliable in most solid or liquid simulations.
In Fig. 1, a cumulative probability distribution of errors for energy, force, and virial predictions are plotted for GAP and MTP, where errors are calculated relative to DFT. For energy, MTP has a lower cumulative probability of error overall. This difference is less pronounced for the force errors where MTP is only marginally better. Interestingly, the probability of error for virial predictions in MTP deviates significantly from GAP at larger errors. These error statistics are consistent with the ratio of energy, force, and virial weights (σ parameters) for the two models: on the one hand, MTP has >10× higher weights (lower σ values) for energies relative to forces, whereas GAP uses the same; meanwhile, GAP uses twice the weights (half σ) for the virials.
The liquid dataset consists of ~6000 configurations from a subsampled MD run. From left to right, energy, force, and virial error probabilities are plotted, where the error is calculated relative to DFT. Mean errors are given in Table 5.
Phonon predictions
The phonon eigenvalues computed from a force-constants matrix for a crystal structure describe the energy required to excite a specific vibrational mode within the crystal. For a potential to closely reproduce a phonon spectrum, it must accurately approximate the curvature of the potential energy surface for small deformations from its relaxed geometry. Thus, while energy and force validation provides useful insights into the accuracy of a potential for specific points and their slopes on the potential energy surface, validating against phonons gives insight into the second derivatives of the energy surface. Historically, potentials have successfully reproduced phonon spectra for certain compositions and configurations, but not generally for an entire alloy system. To demonstrate the ability of our potentials to produce accurate phonon band structures, we compare DFT- and IP-calculated band structures for face-centered cubic (fcc)-type derivative superstructures42 of cell sizes from 2 to 6; there are 65 of these cells.
DFT phonon dispersion curves
First, with DFT, we relaxed each configuration twice using IBRION = 2 and ISIF = 3, which allows both cell shape and volume to change during relaxation.
We then used phonopy to generate frozen phonon displacements. For selecting the supercell, we enumerated the list of all possible hermite normal form (HNF) matrices for each structure and selected the HNF in each case that maximized the distance between periodic images with a supercell size of >32 atoms. When two HNFs were equivalent for both size and distance metric, we selected the one with the larger point group. This procedure allowed us to choose the smallest possible supercell with the highest symmetry subject to the constraint of the maximal distance between periodic images. See the discussion in the appendix of ref. 57 for the utility of using HNF matrices in this context.
Each of the displaced structures from phonopy were computed using EDIFF = 1e − 8, ADDGRID = TRUE, ENCUT = 400, and MINDISTANCE = 55 in Mueller’s k-point scheme.
Machine-learned phonon dispersion curves
Using both GAP and MTP, we demonstrate here that a single, machine-learned potential can simultaneously approximate phonons across the full compositional space for many configurations, and with good accuracy. In Supplementary Figs. 1 –11, we include additional phonon plots that cover a broad structure-composition range. In this section, we have chosen two that are interesting for discussion purposes.
In Fig. 2, we plot a typical phonon spectrum for a 50 at.% Ag configuration with four atoms. For this structure, both GAP and MTP approximate the eigenvalues along the special path well. The RMSE, reported within parentheses, is the integrated error across all eigenvalues in the Brillouin zone (BZ), sampled on a 13 × 13 × 13 grid. Figure 3 shows a structure with a dynamic instability (i.e., negative phonons), as reported by DFT. For this structure, both GAP and MTP learn and reproduce this instability, albeit with different accuracies. Both figures demonstrate that the ability of the IPs predicts dynamic changes due to small perturbations. In Supplementary Figs. 1–11, we similarly plot 65 phonon spectra.
Both the RMS errors within parentheses represent the integrated error across all eigenvalues sampled on a 13 × 13 × 13 grid in the Brillouin zone. GAP and MTP both provide good approximations to the curves along the special path, although each makes different errors in over- and underestimating the eigenvalues at different k-points. Note that this configuration was not included in the fitting dataset (“Prediction” in the plot title).
Both the RMS errors within parentheses represents the integrated error across all eigenvalues sampled on a 13 × 13 × 13 grid in the Brillouin zone. According to DFT, this structure is not dynamically stable. Both GAP and MTP recover this dynamic instability, although GAP is more accurate. Note that this seed configuration was included in the active-learned dataset that the potentials were fitted to.
Table 6 provides statistics for the integrated error across all 65 structures for GAP and MTP. Both GAP and MTP predictions for integrated error are close to 0.1 THz across the full validation set. Similar training and prediction errors indicate a good bias/variance trade-off (not over-fitting). Importantly, these aggregated results show that across a broad range of alloy compositions and structures for Ag-Pd, machine-learned IPs are in good agreement with DFT in the harmonic approximation for vibrational modes.
Transition pathway
As discussed in the “Introduction,” reduced transferability is the price we pay for approximating quantum mechanics with high accuracy. In general, a machine-learned IP is only valid within the subspace in which it was trained. Although it is possible to apply an IP outside of that space, the results will not be trustworthy. We demonstrate this by computing the energy along a smooth, but high energy, transition pathway between two structures. Figure 4 shows two Ag-Pd structures that are connected by a smooth transition (essentially these two structures are identical, except that the upper two atoms switch places). Although the cell must enlarge slightly and distort, the atoms have a clear path to transition from the starting configuration (index 1) to the final configuration (index 11) without colliding. The total energy along the path is also shown in Fig. 4. Note that in the figure, the y-axis is the total energy, not the energy difference between distorted and undistorted cases. Also note that y-axis scale is linear between −1 and +1 eV and logarithmic elsewhere in the upper plot. In the starting configuration, the total energy is ~−16 eV. At its highest point on the transition path, the energy is ~9.5 eV, a total difference of ~25 eV. Such a high energy structure is not problematic for DFT, but it is a big ask to expect a machine-learned IP to accurately extrapolate to this kind of a structure if similar structures were not included in the training dataset. Nevertheless, the GAP does quite well. Although the absolute error of its prediction for the top of the barrier is several eVs, the qualitative behavior is correct.
Since there were no configurations in the training set along the middle of the path, the MTP prediction is purely extrapolative and presents a false, deep, local minimum. Because of its tight regularization, the GAP prediction for this transition is reasonable. It underestimates the barrier significantly due to the lack of training data, but does not introduce a false minimum. Note the symmetric log scale (linear between −1 and +1) on the y-axis in the upper plot. Above the plots are configurations along the pathway. The upper Pd atom (blue) at index 1 moves further into the page as the unit cell distorts. The furthest Ag atom (red) simultaneously moves out of the page. The lowest panel plots the expected variance of the GAP model and the extrapolation grade of the MTP model. Predictive variance is essentially the expected error per atom (in eV) along the transition pathway and the extrapolation grade is a dimensionless quantity indicating that if it exceeds ~10, then a configuration must be added to the training set because the prediction of its energy is not reliable.
Due to its more local basis functions and built-in regularization, the GAP model provides reasonable physical behavior for the transition between the starting and final configurations. MTP, with its global polynomial basis functions, relies on active learning to ensure that its predictions fall within the interpolation regime. As part of its framework, MTP (like GAP) provides the extrapolation grade25,43 to distinguish between configurations that can be evaluated reliably and configurations that should be added to the training set to avoid large extrapolation errors. In our test, MTP correctly detects extrapolation, but has a much poorer extrapolation behavior compared to GAP, and this is the price one pays for using unregularised global basis functions. The active-learning approach is general and could be applied to GAP too (using the predicted variance of the underlying Gaussian process as a proxy for extrapolation52), which would be expected to make its predictions better too. This demonstration should be seen as a warning in the application of machine-learned IPs generally. Using such models safely requires understanding the properties of the basis functions, how the training set was built, which parts of the configuration space were included, and on. In the case of MTP, the extrapolation grade should be used to check against representative samples from the configurations that are expected to be encountered before embarking on large-scale molecular dynamics simulations.
Phase diagram results
The success of the models in learning basic properties and phonons motivates examining the temperature–concentration phase diagram for the alloy system. We used NS with the MTP model to find the liquidus–solidus line, calculate order–disorder transition temperatures, and so on. The MTP model is significantly faster than the current implementation of GAP, and this makes the exploration of the phase space more practical. With respect to speed, the final GAP potential uses 1075 basis functions vs. 569 for the MTP potential. Note that MTP basis functions are polynomial, whereas in our current GAP-SOAP, basis functions require the calculation of an overlap integral. For example, investigation of a single temperature slice of the phase space (for fixed composition and pressure) requires >2 billion evaluations of the potential. This cost is presently prohibitive for GAP but reasonable with MTP.
Liquid–solid transition
Inasmuch as NS cools down from a high-temperature gas phase, we first reproduce the liquid transition behavior as a function of temperature. Each solid line in Fig. 5 shows a trace of the ensemble-averaged composition as a function of temperature that results from a NS run at fixed Δμ = μAg − μPd. In the high-temperature liquid and low-temperature solid regions, the composition varies smoothly with temperature. The solid–liquid transition is indicated by a sharper horizontal (along the composition x-axis) jump, which we expect would become discontinuous in the large system size limit. The width of the approximate discontinuity indicates the width of the phase-separated region.
Solid lines show sGC NS composition as a function of temperature for each Δμ = μAg − μPd, with approximately horizontal jogs indicating finite-size broadened discontinuities associated with the liquidus–solidus (L–S) gap. Dotted lines indicate experimentally observed L–S gap. Circles indicate constant composition NS specific heat maxima corresponding to liquid–solid and solid–solid phase transition temperatures. We have shifted all simulation results in this figure up by 200 K to make it easier to compare the width of the L–S gap with the experiment. The experimental liquidus and solidus are adapted from several sources, refs. 66,67,68. The slight difference between the NS results and coexistence results can be explained by the system size: 64 atoms for NS and 16,384 atoms for coexistence. Error bars for fixed-composition NS are the full-width half-maximum obtained from the heat capacity peaks.
As is clear from Fig. 5, the melting behavior of our MTP potential qualitatively matches the experimental line58,59,60,61,62. However, although the entire line has roughly the same shape, it is shifted from the experimental results by ~200 K. The liquidus–solidus gaps are also in reasonable agreement with experimental data when the same shift of 200 K is included (added in Fig. 5 to facilitate comparison). This shift in temperature is expected for DFT with a Perdew–Burke–Ernzerhof (PBE) functional and has been discussed in the context of other ab initio studies63,64,65. Since the shift does not appear to be composition-dependent, the trends are still reliable.
To further verify our NS results, we have also performed a coexistence simulation of an equimolar Ag-Pd system with 16,384 atoms (8 × 8 × 64 four-atom cubic fcc cells). We ran a combined molecular dynamics and Monte-Carlo simulation to model the disordered phase. The coexistence simulations predicted the melting point of ~1315 K as compared to ~1380 K as predicted by our NS simulations. This is consistent with previous work showing that for NS simulations the finite-size errors in the melting temperature estimated using the full-width at half-maximum of the heat capacity peak was ~200 K for 64 particles and 100 K for 128 particles (see the Supplementary information of ref. 40).
Solid–solid transition
Another stringent test of the potential is whether it can recover the transition from a disordered solid solution to an ordered phase. Experimentally, it appears that ordered phases are kinetically inhibited by low transition temperatures and would be unlikely to appear in experimental constitutional phase diagrams. All reported phase diagrams59,66,67,68 typically show just solidus and liquidus lines and indicate a solid solution below the solidus (see Fig. 5), although one proposed phase diagram guesses two solid–solid transitions, based on some reports of ostensibly ordered phases58, reliable evidence for first-order transformations in the solid state is lacking69. A careful review of relevant experimental literature70,71,72,73,74,75,76 since 1961 (after ref. 58) suggests that, when Ag-Pd samples are annealed in the air or otherwise exposed to oxygen, the formation of oxide phases can be misinterpreted as the effects of ordering. The experimental literature does not agree on the stoichiometry of these oxide phases, such phases have not been reported in samples not exposed to oxygen, and no structural information for these phases (e.g., from X-ray diffraction (XRD) studies) have been reported. It seems reasonable that there is no formation of intermetallic phases in the temperature ranges reported in the phase diagrams.
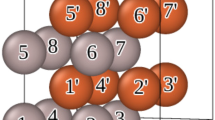
Since the melting transition was underestimated, we expected that any disorder–order transition would also take place at a reduced temperature, hence for the 1:1 composition system we continued the sampling well below the melting temperature. As shown in Fig. 5, which includes a region of the phase diagram outside the experimental data, the order–disorder transition does exist at 125 K for this system. Other computational works find the transition temperatures to be similar to what we report here77,78,79,80. In Fig. 6, we show the atomic ordering before and after this transition. While the atomic views in panels (a) and (b) clearly show ordering in the stacking planes, we also show simulated XRD in panel (c) where the ordering is clearly discernible.
Panel a is at 150 K, while panel b is at 100 K. For both panels a and b, the crystal is viewed edge-on at [111] planes. The lower temperature structure shows clear ordering as stacking planes. This ordering is confirmed by simulated XRD in panel (c). Ag atoms replaced H atoms to artificially boost the difference in structure factors for the simulation.
Comparison to CE
As a reference, we include a comparison of the GAP and MTP models to a state-of-the-art CE of the same Ag-Pd system81. Table 7 compares the training and validation errors of the GAP, MTP, and CE models on the validation dataset used while building the CE model. Note, however, that the training error reported for each model is with respect to the training set used for that model. Since CE does not train on off-lattice data, its training dataset is different. We also include the number of basis functions in each model. Because the CE basis is well suited to the configurational degrees of freedom, relatively few basis functions are needed compared to GAP and MTP. However, it is worth remembering that the computational cost in evaluating a basis function in each method is different so that these values are only somewhat representative of computational cost.
Discussion
CE has been a go-to tool for computing energies across configuration space for alloys. Because of its speed and applicability over the full range of compositions, it is useful for performing ground-state searches, and even for temperature-dependent phase mapping in certain systems. However, it cannot address dynamic processes that involve structural perturbations, which often limits its usefulness.
This work demonstrates that machine-learned IPs are nearly as good as CE for on-lattice computation of energies81. Nevertheless, for on-lattice systems where the atomic displacements are small, CE is still the best choice. Ref. 38 discusses metrics to determine when CE performs well as a function of atomic displacement. But unlike CE, the machine-learned IPs can compute forces, virials, and hessians across the compositional space as well. These additional derivatives of the potential energy surface are sufficiently accurate to approximate dynamic properties like phonon dispersion curves, as well as map out the temperature-composition phase diagram for an alloy. Software for creating datasets and fitting potentials is readily available and easy to use. These potentials, therefore, offer a viable alternative to CE models, and arguably represent the future direction of first-principles computational alloy design.
Although the fitting errors are a factor of 2–3 larger for the GAP and MTP on-lattice predictions, this could be due to lower k-point errors in the DFT data for the CE work, where an “equivalent k-point” scheme was used to provide fortuitous cancellation for some of this error (but this is only possible in systems with small lattice mismatch38). The predictions in all three methods are nearly at DFT accuracies and sufficient for many practical alloy questions.
Data availability
Data and models are available at https://github.com/msg-byu/agpd.
Code availability
Code to produce GAP models is available at libatoms Download. The code implementing MTPs can be obtained for academic purposes free of charge by sending a request to A. Shapeev.
References
Bartók, A. P., Payne, M. C., Kondor, R. & Gábor, C. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403 (2010).
Szlachta, W. J., Bartók, A. P. & Csányi, G. Accuracy and transferability of Gaussian approximation potential models for tungsten. Phys. Rev. B 90, 104108 (2014).
Mocanu, F. C. et al. Modeling the phase-change memory material, Ge2Sb2Te5, with a machine-learned interatomic potential. J. Phys. Chem. B 122, 8998–9006 (2018).
John, S. T. & Csányi, G. Many-body coarse-grained interactions using gaussian approximation potentials. J. Phys. Chem. B 121, 10934–10949 (2017).
Caro, M. A., Aarva, A., Deringer, V. L., Csányi, G. & Laurila, T. Reactivity of amorphous carbon surfaces: rationalizing the role of structural motifs in functionalization using machine learning. Chem. Mater. 30, 7446–7455 (2018).
Cisneros, G. A. et al. Modeling molecular interactions in water: from pairwise to many-body potential energy functions. Chem. Rev. 116, 7501–7528 (2016).
De, S., Bartók, A. P., Csányi, G. & Ceriotti, M. Comparing molecules and solids across structural and alchemical space. Phys. Chem. Chem. Phys. 18, 13754–13769 (2016).
Sosso, G. C., Deringer, V. L., Elliott, S. R. & Csányi, G. Understanding the thermal properties of amorphous solids using machine-learning-based interatomic potentials. Mol. Simul. 44, 866–880 (2018).
Dragoni, D., Daff, T. D., Csányi, G. & Marzari, N. Achieving dft accuracy with a machine-learning interatomic potential: thermomechanics and defects in bcc ferromagnetic iron. Phys. Rev. Mater. 2, 013808 (2018).
Maresca, F., Dragoni, D., Csányi, G., Marzari, N. & Curtin, W. A. Screw dislocation structure and mobility in body centered cubic Fe predicted by a Gaussian approximation potential. npj Comput. Mater. 4, 69 (2018).
Rosenbrock, C. W., Homer, E. R., Csányi, G. & Hart, G. L. W. Discovering the building blocks of atomic systems using machine learning: application to grain boundaries. npj Comput. Mater. 3, 29 (2017).
Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
Bartók, A. P. et al. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 3, 12 (2017).
Pilania, G., Wang, C., Jiang, X., Rajasekaran, S. & Ramprasad, R. Accelerating materials property predictions using machine learning. Scientific Rep. 3, 2810 (2013).
Handley, C. M. & Behler, J. Next generation interatomic potentials for condensed systems. Eur. Phys. J. B 87, 152 (2014).
Lorenz, S., Groß, A. & Scheffler, M. Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks. Chem. Phys. Lett. 395, 210–215 (2004).
Ishida, T. & Schatz, G. C. A local interpolation scheme using no derivatives in quantum-chemical calculations. Chem. Phys. Lett. 314, 369–375 (1999).
Mills, M. J. L. & Popelier, P. L. A. Polarisable multipolar electrostatics from the machine learning method kriging: an application to alanine. Theor. Chem. Acc. 131, 1137 (2012).
Crespos, C., Collins, M. A., Pijper, E. & Kroes, G. J. Multi-dimensional potential energy surface determination by modified shepard interpolation for a molecule-surface reaction: H2. pt (1 1 1). Chem. Phys. Lett. 376, 566–575 (2003).
Brown, A., Braams, B. J., Christoffel, K., Jin, Z. & Bowman, J. M. Classical and quasiclassical spectral analysis of CH 5+ using an ab initio potential energy surface. J. Chem. Phys. 119, 8790–8793 (2003).
Hansen, K. et al. Assessment and validation of machine learning methods for predicting molecular atomization energies. J. Chem. Theory Comput. 9, 3404–3419 (2013).
Rupp, M., Tkatchenko, A., Müller, K.-R. & Lilienfeld, O. A. V. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).
Von Lilienfeld, O. A., Tavernelli, I., Rothlisberger, U. & Sebastiani, D. Optimization of effective atom centered potentials for London dispersion forces in density functional theory. Phys. Rev. Lett. 93, 153004 (2004).
Montavon, G. et al. Learning invariant representations of molecules for atomization energy prediction. In Advances in Neural Information Processing Systems 440–448 (NIPS, 2012).
Gubaev, K., Podryabinkin, E. V., Hart, G. L. W. & Shapeev, A. V. Accelerating high-throughput searches for new alloys with active learning of interatomic potentials. Comput. Mater. Sci. 156, 148–156 (2019).
Faber, F., Lindmaa, A., von Lilienfeld, O. A. & Armiento, R. Crystal structure representations for machine learning models of formation energies. Int. J. Quantum Chem. 115, 1094–1101 (2015).
Seko, A., Togo, A. & Tanaka, I. Group-theoretical high-order rotational invariants for structural representations: Application to linearized machine learning interatomic potential. Phys. Rev. B 99, 214108 (2019).
Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials. Phys. Rev. B 99, 014104 (2019).
van der Oord, C., Dusson, G., Csányi, G. & Ortner, C. Regularised atomic body-ordered permutation-invariant polynomials for the construction of interatomic potentials. Machine Learning: Science and Technology 1, 015004 (2020).
Bachmayr, M. et al. Atomic Cluster Expansion: Completeness, Efficiency and Stability. Preprint at https://arxiv.org/abs/1911.03550 (2019).
Allen, A., Dusson, G., Ortner, C., & Csanyi, G. Atomic permutationally invariant polynomials for fitting molecular force fields. Machine Learning: Science and Technology. https://doi.org/10.1088/2632-2153/abd51e (2020).
Nyshadham, C. et al. Machine-learned multi-system surrogate models for materials prediction. npj Comput. Mater. 5, 51 (2019).
Shapeev, A. V. Moment tensor potentials: a class of systematically improvable interatomic potentials. Multiscale Model. Simul. 14, 1153–1173 (2016).
Novikov, I. S., Suleimanov, Y. V. & Shapeev, A. V. Automated calculation of thermal rate coefficients using ring polymer molecular dynamics and machine-learning interatomic potentials with active learning. Phys. Chem. Chem. Phys. 20, 29503–29512 (2018).
Podryabinkin, E. V., Tikhonov, E. V., Shapeev, A. V. & Oganov, A. R. Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys. Rev. B 99, 064114 (2019).
Novoselov, I. I., Yanilkin, A. V., Shapeev, A. V. & Podryabinkin, E. V. Moment tensor potentials as a promising tool to study diffusion processes. Comput. Mater. Sci. 164, 46–56 (2019).
Novikov, I. S. & Shapeev, A. V. Improving accuracy of interatomic potentials: more physics or more data? a case study of silica. Mater. Today Commun. 18, 74–80 (2019).
Nguyen, A. H., Rosenbrock, C. W., Reese, C. S. & Hart, G. L. W. Robustness of the cluster expansion: assessing the roles of relaxation and numerical error. Phys. Rev. B 96, 014107 (2017).
Pártay, L. B., Bartók, A. P. & Csányi, G. Efficient sampling of atomic configurational spaces. J. Phys. Chem. B 114, 10502–10512 (2010).
Baldock, R. J. N., Pártay, L. B., Bartók, A. P., Payne, M. C. & Csányi, G. Determining pressure-temperature phase diagrams of materials. Phys. Rev. B 93, 174108 (2016).
Baldock, R. J. N., Bernstein, N., Salerno, K. M., Pártay, L. B. & Csányi, G. Constant pressure nested sampling with atomistic dynamics. Phys. Rev. E. 96, 043311 (2017).
Hart, G. L. W. & Forcade, R. W. Algorithm for generating derivative structures. Phys. Rev. B 77, 224115 (2008).
Podryabinkin, E. V. & Shapeev, A. V. Active learning of linearly parametrized interatomic potentials. Comput. Mater. Sci. 140, 171–180 (2017).
Georg, K. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Georg, K. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 49, 14251 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Peter, E. B Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Wisesa, P., McGill, K. A. & Mueller, T. Efficient generation of generalized monkhorst-pack grids through the use of informatics. Phys. Rev. B 93, 155109 (2016).
Bartók, A. P., Kermode, J., Bernstein, N. & Csányi, G. Machine learning a general-purpose interatomic potential for silicon. Phys. Rev. X 8, 041048 (2018).
Deringer, V. L., Csányi, G. & Proserpio, D. M. Extracting crystal chemistry from amorphous carbon structures. ChemPhysChem 18, 873–877 (2017).
Deringer, V. L., Pickard, C. J. & Csányi, G. Data-driven learning of total and local energies in elemental boron. Phys. Rev. Lett. 120, 156001 (2018).
Deringer, V. L., Proserpio, D. M., Csányi, G. & Pickard, C. J. Data-driven learning and prediction of inorganic crystal structures. Faraday Discuss. 211, 45–59 (2018).
Kofke, D. A. & Glandt, E. D. Nearly monodisperse fluids. I. Monte carlo simulations of Lennard-Jones particles in a semigrand ensemble. J. Chem. Phys. 87, 4881–4890 (1987).
Hart G. L. W., Jorgensen, J. J., Morgan, W. S. & Forcade, R. W. A robust algorithm for k-point grid generation and symmetry reduction. J. Phys. Commun. 3, 065009 (2019).
Savitskii, E. M. & Pravoverov, N. L. Kurnakov phases in the palladium-silver system. Russ. J. Inorg. Chem. 6, 253–254 (1961).
Okamoto, H. Phase diagrams for binary alloys. ASM Int. 268, 2–24 (2000).
Naidu, S. V. N. & Houska, C. R. X-ray determinations of the debye temperatures and thermal expansions for the Pd-Ag-Au system. J. Appl. Phys. 42, 4971–4975 (1971).
Ellner, M. Partial atomic volume and partial molar enthalpy of formation of the 3d metals in the palladium-based solid solutions. Metall. Mater. Trans. A 35, 63–70 (2004).
DosSantos, D. S., Miraglia, S. & Fruchart, D. A high pressure investigation of Pd and the Pd-H system. J. Alloys Compd 291, L1–L5 (1999).
Hong, Q.-J. & van de Walle, A. Prediction of the material with highest known melting point from ab initio molecular dynamics calculations. Phys. Rev. B 92, 020104 (2015).
Pozzo, M. & Alfe, D. Melting curve of face-centered-cubic nickel from first-principles calculations. Phys. Rev. B 88, 024111 (2013).
Taioli, S., Cazorla, C., Gillan, M. J. & Alfè, D. Melting curve of tantalum from first principles. Phys. Rev. B 75, 214103 (2007).
Morioka, S. & Hasebe, M. Thermodynamic constraints to describe gibbs energies for binary alloys. J. Phase Equil. 20, 244 (1999).
Ghosh, G., Kantner, C. & Olson, G. B. Thermodynamic modeling of the Pd-X (X= Ag, Co, Fe, Ni) systems. J. Phase Equil. 20, 295 (1999).
Karakaya, I. & Thompson, W. T. The Ag-Pd (silver-palladium) system. Bull. Alloy Phase Diagrams 9, 237–243 (1988).
Darling, A. S. Some properties and applications of the platinum-group metals. Int. Met. Rev. 18, 91–122 (1973).
Allison, E. G. & Bond, G. C. The structure and catalytic properties of palladium-silver and palladium-gold alloys. Catal. Rev. 7, 233–289 (1972).
Brouers, F. & Brauwers, M. On the temperature dependence of electrical resistivity in concentrated disordered transition binary alloys. J. Phys. Lett. 36, 17–21 (1975).
Dawei, F. & Taskinen, P. Thermodynamic properties of silver-palladium alloys determined by a solid state electrochemical method. J. Mater. Sci. 49, 5790–5798 (2014).
Terry, G. & Rodriguez, M. Behavior of silver and palladium mixtures during heating. J. Am. Ceram. Soc. 83, 2709–2714 (2000).
Luef, C., Paul, A., Flandorfer, H., Kodentsov, A. & Ipser, H. Enthalpies of mixing of metallic systems relevant for lead-free soldering: Ag-Pd and Ag-Pd-Sn. J. Alloys Compd 391, 67–76 (2005).
Sopousek, J., Zemanová, A., Vřešt’ál, J. & Broz, P. Experimental determination of phase equilibria and reassessment of Ag-Pd system. J. Alloys Compd 504, 431–434 (2010).
Rao, P. R. & Rao, K. K. X-ray measurements of faulting in Ag-Pd alloys. J. Appl. Phys. 39, 4563–4568 (1968).
Ruban, A. V., Simak, S. I., Korzhavyi, P. A. & Johansson, B. Theoretical investigation of bulk ordering and surface segregation in Ag-Pd and other isoelectornic alloys. Phys. Rev. B 75, 054113 (2007).
Stefan, M. & Zunger, A. First-principles predictions of yet-unobserved ordered structures in the Ag-Pd phase diagram. Phys. Rev. Lett. 87, 165502 (2001).
Gonis, A., Butler, W. H. & Stocks, G. M. First-principles calculations of cluster densities of states and short-range order in AgcPd1-c alloys. Phys. Rev. Lett. 50, 1482 (1983).
Takizawa, S., Terakura, K. & Mohri, T. Electronic theory for phase stability of nine AB binary alloys, with A=Ni, Pd, or Pt and B=Cu, Ag, or Au. Phys. Rev. B 39, 5792 (1989).
Nelson, L. J., Hart, G. L. W. & Curtarolo, S. Ground-state characterizations of systems predicted to exhibit L11 or L13 crystal structures. Phys. Rev. B 85, 054203 (2012).
Acknowledgements
C.W.R. and G.L.W.H. were supported under ONR (MURI N00014-13-1-0635). L.B.P. acknowledges support from the Royal Society through a Dorothy Hodgkin Research Fellowship. N.B. acknowledges support from the US Office of Naval Research through the US Naval Research Laboratory’s core research program, and computer time from the US DoD’s High-Performance Computing Modernization Program Office at the Air Force Research Laboratory Supercomputing Resource Center. A.V.S. was supported by the Russian Science Foundation (grant number 18-13-00479). This collaboration might not have been possible had the authors not met at the Institute of Pure and Applied Mathematics, UCLA. We thank Andrew Huy Nguyen for his help with several NS calculations.
Author information
Authors and Affiliations
Contributions
Datasets were created by C.W.R., G.L.W.H., and A.V.S. G.C., C.W.R., and G.L.W.H. created GAP models and fine-tuned phonon calculations. K.G. and A.V.S. created MTP models. L.B.P. and C.W.R. performed calculations for fixed-composition Nested Sampling calculations. sGC Nested Sampling calculations were done by N.B. All authors contributed to the discussion, analysis, and writing of the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rosenbrock, C.W., Gubaev, K., Shapeev, A.V. et al. Machine-learned interatomic potentials for alloys and alloy phase diagrams. npj Comput Mater 7, 24 (2021). https://doi.org/10.1038/s41524-020-00477-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00477-2
This article is cited by
-
Complexity of many-body interactions in transition metals via machine-learned force fields from the TM23 data set
npj Computational Materials (2024)
-
Machine-learning potentials for nanoscale simulations of tensile deformation and fracture in ceramics
npj Computational Materials (2024)
-
Accurate machine learning force fields via experimental and simulation data fusion
npj Computational Materials (2024)
-
Machine learned force-fields for an Ab-initio quality description of metal-organic frameworks
npj Computational Materials (2024)
-
Recent advances in machine learning interatomic potentials for cross-scale computational simulation of materials
Science China Materials (2024)