Abstract
Band degeneracy is effective in optimizing the power factors of thermoelectric (TE) materials by enhancing the Seebeck coefficients. In this study, we demonstrate this effect in model systems of layered oxyselenide family by the density functional theory (DFT) combined with semi-classical Boltzmann transport theory. TE transport performance of layered LaCuOSe and BiCuOSe are fully compared. The results show that due to the larger electrical conductivities caused by longer electron relaxation times, the n-type systems show better TE performance than p-type systems for both LaCuOSe and BiCuOSe. Besides, the conduction band degeneracy of LaCuOSe leads to a larger Seebeck coefficient and a higher optimal carrier concentration than n-type BiCuOSe, and thus a higher power factor. The optimal figure of merit (ZT) value of 1.46 for n-type LaCuOSe is 22% larger than that of 1.2 for n-type BiCuOSe. This study highlights the potential of wide band gap material LaCuOSe for highly efficient TE applications, and demonstrates that inducing band degeneracy by cations substitution is an effective way to enhance the TE performance of layered oxyselenides.
Similar content being viewed by others
Introduction
The thermoelectric (TE) effect can realize direct and reversible conversion between heat and electric energy, and thus provides a promising technology for green power generation and refrigeration systems1. The conversion efficiency of TE materials can be evaluated by the figure of merit ZT = S2σT/κ, in which, S is Seebeck coefficient, σ is electrical conductivity, T is absolute temperature2. The thermal conductivity κ consists of electronic thermal conductivity κe and lattice thermal conductivity κ1. Generally, narrow band gap semiconductors are considered suitable for TE applications due to relatively high doping efficiency and excellent electronic transport properties3,4.
Recently, layered compounds show great promise in TE applications due to the intrinsic low lattice thermal conductivities with phonon anharmonicity induced by the interactions between adjacent layers5,6. Especially, the band structures of layered materials with multiple chemical bonding typically show multi-band and/or multi-band valleys behaviors around the Fermi level, which provides the possibility of optimizing their TE transport properties by modifying electronic band structures, i.e., enhancing the power factors resulted from enlarged Seebeck coefficients5,7. As illustrated in Fig. 1, band valleys that next to the conduction band minimum (CBM) or valence band maximum (VBM), can be modify to move toward their respective band edges in higher energy direction through band engineering approaches, leading to a highly degenerated band structure with reduced energy difference. This band degeneracy helps to confine extra effective density of state (DOS) near the band edge region beyond the original effective DOS that only determined by VBM or CBM, resulting in enhanced Seebeck coefficient7,8,9. Therefore, layered semiconductors with narrow bandgaps and multiple chemical bonding have attracted wide attention in the quest for the TE materials5,6,10. Among them, p-type quaternary oxyselenides BiCuOSe (as shown in Fig. 2a, b) is an emerging TE material due to the moderate Seebeck coefficient, narrow band gap (~0.8 eV)11 and low lattice thermal conductivity (~0.88 W m−1 K−1)12.
BiCuOSe has been reported as a potential TE material for the first time by Bleijs et al., and the ZT value of single phase BiCuOSe has been measured to be 0.53 at 873 K12. It is also found that the σ of BiCuOSe is found to be only 112 S m−1 at room temperature because of the weak interactions between the adjacent layers13. Such low σ drives the follow-up research works toward improving its electronic transport property. The most common way to increase the electrical conductivity of BiCuOSe is to dope divalent metal ions into its Bi atoms sites14,15,16. Recently, both experimental and theoretical investigations suggest n-type doping of BiCuOSe may achieve a larger σ and thus enhanced ZT value5,17. The optimal ZT value can be improved by 32% for n-type BiCuOSe and reach to 1.2 at 920 K, as compared with the p-type doping approach17. Yet, n-type BiCuOSe is shown to exhibit an intrinsically lower Seebeck coefficient than p-type BiCuOSe due to lower density of states in the conduction band minimum (CBM) than in the valence band maximum (VBM)17. From this perspective, single method of n-type doping is still restricted by low Seebeck coefficient, thus limiting further ZT optimization for this material.
Control of electronic structure, in this case the band degeneracy, might offer another approach to promote the thermoelectric properties of these layered oxyselenides. In BiCuOSe, CBM is occupied by Bi elements with 6 s character18, which intrinsically shows larger orbital bandwidth than that of d orbitals due to symmetry restriction19,20,21. Thus if more localized metal d-bands can be successfully introduced into the CBM of layered oxyselenides, it might be helpful to enhance the band-edge convergence thus the effective density of state at the CBM, leading to further improvement of Seebeck coefficient and PF value (Fig. 1b, c). Considering this, La element is better than Bi due to its significant contribution of 5d orbitals in the unoccupied states. Layered LaCuOSe, with similar isostructure of BiCuOSe (as shown in Fig. 2a, b), exhibits excellent photoelectric, magnetic and electronic transport properties22,23,24,25. It is proposed to be a candidate for TE materials since the work of Yasukawa et al., who found that its σ can be significantly enhanced by Sr-doping26. Follow-up studies also found that the carrier mobility, effective mass, and thermal conductivity of LaCuOSe are of anisotropic character due to its layered crystal structure27,28. However, study on the TE properties of LaCuOSe is rare, and there is no reliable report for ZT value of this crystal so far in whether the theoretical or the experimental studies.
Furthermore, the potential of LaCuOSe as a thermoelectric material is considered to be lower than BiCuOSe due to its wide band gap (~2.8 eV)29 and higher lattice thermal conductivity (~2.1 W m−1 K−1)26 than BiCuOSe. Recently, some wide band gap materials (1.5–3.5 eV) have been found to exhibit excellent TE performance due to high motilities and low lattice thermal conductivities30,31,32. For example, the σ of LaCuOSe has been reported to be 2560 S m−1 at 300 K33, which is more than 20 times larger than that of BiCuOSe. To make it clear, although BiCuOSe has higher S and lower κ1, LaCuOSe exhibits larger σ, thus leading to an open question that which one shows better overall TE performance? Existing literatures are mainly focused on the comparison of other properties, such as elastic27, thermal34 and optoelectronic18 properties. Direct comparison of electronic and thermal transport properties between BiCuOSe and LaCuOSe have not been reported yet. Hence, in order to reevaluate the potential of layered LaCuOSe for TE applications, it is necessary to understand the electronic structure and intrinsic TE transport properties of the two crystals.
In this work, the TE performance of LaCuOSe and BiCuOSe are systematically investigated by means of the first-principles calculations combined with Boltzmann transport theory. The calculated results show that as compared with BiCuOSe, La elements in LaCuOSe can effectively induce conduction band degeneracy and further enhance the Seebeck coefficient. As a result, the optimal ZT value of n-type LaCuOSe can reach to 1.46 at 900 K, which is larger than that of 1.2 for n-type BiCuOSe, demonstrating wide band gap semiconductor LaCuOSe exhibits better TE performance than BiCuOSe. This study unveils the critical role of La element in optimizing the electronic structure and further promoting thermoelectric properties of layered oxyselenides, which will provide useful information for further experimental and theoretical studies on these and other related layered TE materials.
Results and discussion
Crystal structure and electronic structure
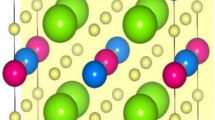
Both LaCuOSe and BiCuOSe crystals belong to tetragonal structure with P4/nmm space group (No.129)29,35. As shown in Fig. 2a, b, the anti-fluorite (Cu2Se2)2− chalcogenide layers and fluorite-like (La2O2)2+/(Bi2O2)2+ oxide layers are stacked perpendicularly along c-axis. The optimized lattice parameters of LaCuOSe and BiCuOSe are in good agreement with the experimental results (see Table 1)29,35. On the other hand, the bond lengths and interlayer spacing for layered compounds provide information about the physical nature of the chemical bonds27. Our results show that the bond lengths and interlayer spacing for BiCuOSe are slightly shorter than those of LaCuOSe, which are consistent with previous reports27,34. See Table 1 for more detailed comparison with other reported values.
The calculated electronic band structures and DOS distributions near the Fermi level of LaCuOSe and BiCuOSe are plotted in Fig. 2c–f. It shows that the difference of A-site cations affects the electronic structures of layered oxyselenides markedly. The band gap of BiCuOSe exhibits indirect character, i.e., the CBM is positioned at Z point and the VBM is on the M-G line, while LaCuOSe is exhibits direct gap with both CBM and VBM locate at Gamma (G) point. The band gaps of LaCuOSe and BiCuOSe are 2.59 eV and 0.87 eV without vdW, respectively, which are consistent with the previous experimental data of 2.8 eV for LaCuOSe and 0.8 eV for BiCuOSe11,26. It is found that the CBM of LaCuOSe is mostly contributed by the 5d orbitals of La atoms, and the 6p orbitals of Bi atoms contribute to the CBM of BiCuOSe (see Fig. 2e, f). It also shows that the VBMs of both LaCuOSe and BiCuOSe are mostly contributed by the 3d orbitals of Cu atoms and 4p orbitals of Se atoms.
It is noted that the energy difference between the lowest two conduction bands (i.e., ECB1−ECBM) of LaCuOSe at Gamma point is 0.1 eV, which is smaller than that of 0.19 eV for BiCuOSe at Z point (see Fig. 2c, d). As shown in Fig. 1, smaller energy difference between the nearest two bands around the Fermi level results in higher band degeneracy, leading to higher effective DOS for LaCuOSe than BiCuOSe in the n-type doing regime. In contrast, the energy difference between the two valence band valleys (one is at the Gamma point, and the other is on the M-G line) of BiCuOSe is almost 0 eV (i.e., EVBM−EVB1), which is much smaller than that of 0.15 eV for LaCuOSe, suggesting higher effective DOS for BiCuOSe than LaCuOSe in the p-type doing regime. The strategy of improving effective DOS by band degeneracy have also been reported in other TE materials with multi-band and/or multi-band valleys10,36,37.
Relaxation time and electronic transport property
Based on the optimized lattice structures of LaCuOSe and BiCuOSe, their electrical conductivities σ and relaxation time τ are studied by the Boltzmann transport equation with the BoltzTraP2 code. According to the deformation potential (DP) theory, the energy-dependent relaxation time is defined as38
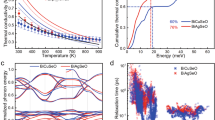
where r is related to specific scatting mechanism. Since the couplings of carriers and acoustic phonons for LaCuOSe and BiCuOSe are the predominant scattering, the r is set as −1/210. The h, Cii, kB, m* and E1 are the Planck constant, elastic constant, Boltzmann constant, effective mass and DP constant, respectively. The calculated Cii, m* and E1 are listed in Table 2. Inserting these coefficients to Eq. (2), we obtain the relaxation times of BiCuOSe and LaCuOSe as a function of cattier concentration, as shown in Fig. 3a, b. The results show that, firstly, the relaxation time of BiCuOSe is always larger than that of LaCuOSe at given carrier type, carrier concentration, and temperature because of the smaller average effective mass. Secondly, the relaxation times of the two crystals are dependent on carrier types, i.e., the hole relaxation times are always smaller than the electron relaxation times at given temperature and carrier concentration due to the larger hole effective masses. Thirdly, the relaxation times for BiCuOSe and LaCuOSe are dependent on the temperature regardless of carrier types, i.e., the relaxation times decrease as temperature rises due to the more frequent scattering of carriers at the higher temperature, as is the case with layered GeAs210 and GeSe39. For example, the relaxation times for n-type BiCuOSe and LaCuOSe vary over large range from 8.2 to 2.8 fs and 7.3 to 2.4 fs at the temperature of 300–900 K, respectively. The calculated hole relaxation time of BiCuOSe is close to the value reported by Yang et al. (1.26 fs at 780 K)17. However, there is no reliable report for relaxation time of LaCuOSe.
Inserting the relaxation time to σ/τ, the electrical conductivities for BiCuOSe and LaCuOSe are obtained, as shown in Fig. 3c, d. Generally, in all cases, the σ of both materials increase with the increase of carrier concentration. On one hand, the electrical conductivities of n-type BiCuOSe and LaCuOSe are always higher than those of p-type BiCuOSe and LaCuOSe because of lower scattering caused by longer electron relaxation times. We further plot the band decomposed charge densities around the CBM and VBM for both materials in Fig. 2g–j to explain the different transport behaviors of electrons and holes. Here, the isosurface level is set at 0.0005. For n-type BiCuOSe and LaCuOSe, all of the atoms are connected by charge densities, which can provide many conduction paths of electrons and effectively improve the electronic transport properties. For p-type BiCuOSe and LaCuOSe, there is no conduction channel can be found between atoms due to the strong localization of charge densities, which leads to weak charge transfer between atoms and thus reduces the electrical conductivities. Therefore, for BiCuOSe and LaCuOSe, the σ of n-type systems are most likely larger than those of p-type systems. On the other hand, regardless of carrier types, the electrical conductivity of BiCuOSe is higher than that of LaCuOSe at same temperature and carrier concentration due to the lower scattering caused by longer relaxation time. We note, however, experimental room temperature conductivity of BiCuOSe (112 S m−1)13 is smaller than that of LaCuOSe (2560 S m−1)33, due to the lower intrinsic carrier concentration of BiCuOSe (~1 × 1018 cm−3) than that of LaCuOSe (~2 × 1019 cm−3). This can be understood from electronic structure point of view. Hole carrier concentrations of both materials can be calculated based on the Fermi distribution theory, i.e.,
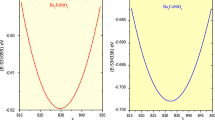
in which, NV, f (E), ħ, EV and EF are the effective DOS of holes, Fermi distribution function, reduced Planck constant, energies of VBM and Fermi level, respectively. The values of EV − EF for BiCuOSe (−0.44 eV) is more negative than that of LaCuOSe (−0.26 eV), leading to smaller intrinsic carrier concentration for BiCuOSe compared with LaCuOSe.
Seebeck coefficient and power factor
The calculated Seebeck coefficients S are given in Fig. 4a, b. For a specific temperature, the absolute value of S for p-type (n-type) BiCuOSe is always larger (smaller) than LaCuOSe at the same carrier concentration, apart from the case of the S for p-type BiCuOSe at 900 K with the concentration below 1 × 1019 cm−3. For example, the Seebeck coefficients of p-type (n-type) LaCuOSe and BiCuOSe are 563 and 621 μV K−1 (−582 and −495 μV K−1) at 300 K with the carrier concentration of 1 × 1018 cm−3, respectively. In order to explain the difference in the Seebeck coefficients between LaCuOSe and BiCuOSe, the internal relationship between S and electronic structure is explored7, i.e.,
in which, the N, n, r, e, and kB are the effective DOS near Fermi level, carrier concentration, scattering mechanism parameter, electron charge and Boltzmann constant, respectively. According to the above equations, we can find that at given carrier concentration, the S is determined by N, which is affect by band degeneracy, as discussed in Fig. 1. This is also consistent with the charge density and DOS analysis. For example, Fig. 2e, f show that the slope of DOS around the CBM (VBM) for LaCuOSe is larger (smaller) than that of BiCuOSe, thus the absolute of S for n-type (p-type) LaCuOSe is larger (smaller) than that of BiCuOSe. Here, the large slope of DOS and Seebeck coefficient for p-type BiCuOSe are attributed to the band valley degeneracy around the CBM, and the band degeneracy around the VBM contributes to the large Seebeck coefficient of n-type LaCuOSe.
On the other band, the abnormal S-coefficient (greed dashed lines) for p-type BiCuOSe at 900 K with the carrier concentration form 1 × 1018 cm−3 to 1 × 1019 cm−3 can be attributed to bipolar conduction effect. The clear signature of bipolar conduction effect is that at high temperatures, the absolute value of Seebeck coefficient for narrow gap semiconductor increases first and then decreases40,41. At the bipolar conduction regime (carrier concentration form 1 × 1018 to 1 × 1019 cm−3 for BiCuOSe), although holes is still the majority carrier, yet the contribution from minority carriers, i.e. electrons, cannot be ignored for thermal excitation of extra carriers at very high temperatures. As a result, the net contribution of the minority carrier leads to deviation of the ideal S ∝ n−2/3 relationship with a smaller Seebeck coefficient at low p-type doping regime. With further increase of hole doping level, Seebeck coefficient is again determined by majority carriers of hole and follows the S ∝ n−2/3 relationship. Similar minority carrier modified Seebeck coefficient has also been reported in the previous literatures6,42. Here we note that this bipolar conduction modified Seebeck coefficient behavior only becomes significant at very high temperature in low band gap semiconductors. Since the band gap of LaCuOSe (2.59 eV) is much larger than BiCuOSe (0.87 eV), thus the bipolar conduction effect on the Seebeck coefficient of LaCuOSe is suppressed, as reflected in Fig. 4a.
Power factor PF is an important parameter to measure the electronic transport property, which determines the coupling effects between S and σ, i.e., the σ increases as the carrier concentration rises, while the S is inversely proportional to carrier concentration. Hence, one can fit a balanced value of carrier concentration between S and σ to obtain the optimal power factor PF. The calculated power factors of LaCuOSe and BiCuOSe are plotted Fig. 4c, d. For both BiCuOSe and LaCuOSe, the optimal PF values for n-type systems are always higher than those for p-type systems due to the larger electrical conductivities. Regardless of carrier types, the optimal PF value decreases as the temperature rises because of the inverse correlation between electrical conductivity and temperature. More important is that the highest PF value of n-type LaCuOSe is 2.58 mW m−1 K−2 at 300 K, which is 1.5 times larger than that of 1.71 mW m−1 K−2 for n-type BiCuOSe. This value is also found larger than the optimal PF values of many layered TE materials at room temperature, such as Bi2O2Se (~0.4 mW m−1 K−2)43 and Bi2O2Te (~0.55 mW m−1 K−2)43. Higher power factor of n-type LaCuOSe is mainly because the larger Seebeck coefficient caused by conduction band degeneracy and higher optimal carrier concentration (which corresponds to a higher electrical conductivity). For p-type systems, BiCuOSe shows higher optimal PF value than LaCuOSe under each considered temperature, which can be attribute to its larger Seebeck coefficient and higher electrical conductivity.
Thermal transport property
The electronic thermal conductivities κe and lattice thermal conductivities κ1 of LaCuOSe and BiCuOSe are further investigated. In this study, the electronic thermal conductivities for the two compounds are obtained by44,45,46
in which, κ0 is the electronic thermal conductivity calculated under closed circuit condition, and L is Lorenz constant. The calculated results are given in Fig. 5a, b. It shows that the electronic thermal conductivities of n-type systems are always larger than p-type systems for both BiCuOSe and LaCuOSe. Besides, regardless of carrier types, the κe of BiCuOSe is higher than that of LaCuOSe at same temperature and carrier concentration. The thermal transport behavior of carriers can be explained by that the κe is linearly related to σ, and thus the variation of κe follows the same trend of σ with the carrier concentration and temperature (see Fig. 3c, d).
Based on second and third-order interatomic force constants (IFCs), the lattice thermal conductivities of LaCuOSe and BiCuOSe are obtained, as shown in Fig. 5c, d. Obviously, the average lattice thermal conductivity of LaCuOSe is larger than that of BiCuOSe under each considered temperature. For example, the average lattice thermal conductivities of LaCuOSe and BiCuOSe are 1.73 W m−1 K−1 and 1.00 W m−1 K−1 at 300 K, respectively, which are close to the experiment values of 2.1 W m−1 K−1 for LaCuOSe26 and 0.88 W m−1 K−1 for BiCuOSe12. Such low lattice thermal conductivities for LaCuOSe and BiCuOSe are comparable to those of many well-known TE materials, like PbTe and Bi2O2Se, for which the lattice thermal conductivities have been reported to be ~2.1 W m−1 K−1 47 and ~1.1 W m−1 K−1 43, respectively. Simultaneously, the lattice thermal conductivities of the two crystals are of anisotropic character. At room temperature, the lattice thermal conductivities along the in-plane and out-of-plane directions (κ1a and κ1c) are 2.51 W m−1 K−1 and 0.18 W m−1 K−1 for LaCuOSe, 1.36 W m−1 K−1 and 0.32 W m−1 K−1 for BiCuOSe, respectively. The ratios κ1a/κ1c of LaCuOSe and BiCuOSe are 13.64 and 4.24 at 300 K, respectively, which are larger than those of 6.55 for GeAs210 and 3.44 for phosphorene48.
The phonon spectra of LaCuOSe and BiCuOSe are plotted in Fig. 6a, b. It shows that the frequency gaps between the high and low frequency optical branches of LaCuOSe and BiCuOSe are 2.01 and 1.92 THz, respectively. The high frequency optical modes of LaCuOSe (BiCuOSe) are governed by O atoms, and the low frequency optical branches and acoustic branches are mainly dominated by La (Bi), Se and Cu atoms. Since the vibrational frequencies of Bi atoms are lower than those of La atoms, all of phonon modes of BiCuOSe move toward lower frequencies compared to LaCuOSe, implying that the phonon branches of BiCuOSe are more localized than LaCuOSe. According to the phonon spectra, the larger difference in the lattice thermal conductivities between LaCuOSe and BiCuOSe can be understand by the definition of lattice thermal conductivity49:
in which, the CV, Vg and l are the lattice heat capacity, phonon group velocity, and phonon mean-free path (PMFP), respectively.
Within the harmonic approximation, the heat capacity can be given by50
where, the \(C_{{\mathrm{ph}}}[\omega _\lambda ({\mathbf{q}})]\) is the contribution of phonon modes for q points in the first Brillouin zone to the heat capacity. The λ is the index of the phonon modes. The calculated temperature-dependent heat capacities of LaCuOSe and BiCuOSe are given in Fig. 6c. It shows that the heat capacities of the two compounds show almost identical trends and values with temperature. Besides, their heat capacities exhibit the expected T3 law at the low temperatures, and reach the Dulong-Petit classical limit at high temperatures (99.1 J mol−1 K−1 for BiCuOSe and 98.9 J mol−1 K−1 for LaCuOSe). Therefore, the larger difference in the lattice thermal conductivities between LaCuOSe and BiCuOSe is independent to the heat capacities of the two compounds. Our calculated result of the heat capacity for BiCuOSe is in good agreement with the result reported by Liu et al.50
The phonon group velocities of acoustic phonon modes for LaCuOSe and BiCuOSe are given in Table 3. It can be seen that BiCuOSe exhibits lower acoustic phonon group velocity Vg at given branch and orientation as compared with LaCuOSe. This is because the acoustic phonon group velocity is proportional to the slope of phonon modes at Gamma point, and the phonon branches of BiCuOSe are more localized than LaCuOSe. On the other hand, the cumulative lattice thermal conductivities as a function of PMFPs for the two crystals are plotted in Fig. 6d. It shows that the κ1 increases rapidly with the increase of PMFP and then keeps stable when reach the upper limit of PMFP. The upper limit of PMFP for BiCuOSe (~80 nm) is lower than that of LaCuOSe (~150 nm) at room temperature. As compared with LaCuOSe, the lower Vg and PMFP of BiCuOSe indicates more frequent scattering of phonons and lower heat transport property, which gives a reasonable explanation for the lower κ1 of BiCuOSe than LaCuOSe. In contrast, the upper limits of PMFP are ~300 nm for PbTe47 and ~20 nm for Bi2O2Te43, corresponding to the lattice thermal conductivities of ~2.1 W m−1 K−1 and ~0.57 W m−1 K−1, respectively. We also note that the lattice thermal conductivities of LaCuOSe and BiCuOSe at 300 K will decrease 50% when the size of nanostructures below 4.1 nm and 2.0 nm, respectively. Hence, the low-dimensional LaCuOSe and BiCuOSe may exhibit better TE performance than bulk phase49,51.
The anisotropic lattice thermal conductivities for LaCuOSe and BiCuOSe are further explained. Generally, the thermal transport properties of layered crystals often are of anisotropic character due to the strong in-plane bonding and weak out-of-plane bonding, which can be reflected in the phonon group velocity Vg and Debye temperature ΘD, i.e., κ1 is positively correlated with ΘD and Vg for a specific direction10. Table 3 shows large difference of ΘD and Vg for BiCuOSe and LaCuOSe along the different directions, implying that lattice thermal conductivities of the two crystals exhibit strong anisotropy. Similar phenomena have been observed in other layered materials10,43.
Dimensionless figure of merit
According to the calculated electronic and thermal transport coefficients, the ZT values of the two crystals are obtained, as shown in Fig. 7. Firstly, for both BiCuOSe and LaCuOSe, the optimal ZT values of n-type systems are always higher than those of p-type systems at a given temperature because of the higher electrical conductivities. As compared with the p-type doping approach, the maximum ZT values at 900 K could be improved 60% and 450% by using n-type doping for BiCuOSe and LaCuOSe, respectively. Secondly, for p-type systems, BiCuOSe exhibits higher optimal ZT value than LaCuOSe regardless of temperatures due to the larger Seebeck coefficient, higher electrical conductivity and lower lattice thermal conductivity. For instance, the optimal ZT value of 0.75 for BiCuOSe is 2.3 times than that of 0.32 for LaCuOSe at the temperature of 900 K. Thirdly, for n-type systems, the optimal ZT value of LaCuOSe is always larger than that of BiCuOSe at same temperature because of the larger Seebeck coefficient and higher optimal carrier concentration. For example, the optimal ZT value of LaCuOSe is 1.46 with the carrier concentration of ~2.5 × 1020 cm−3 at 900 K, which is about 22% larger than that of 1.2 with the carrier concentration of ~1 × 1020 cm−3 for BiCuOSe. The highest ZT value of LaCuOSe is also superior to that of many typical TE materials such as Bi2O2Se52 and LaOBiSSe53, for which the ZT values have been reported to be ~0.95 at 800 K and ~0.54 at 900 K, respectively. Therefore, the TE performance of LaCuOSe is better than that of BiCuOSe, and n-type doping can improve the ZT values of BiCuOSe and LaCuOSe remarkably.
We reiterate that for practical thermoelectric applications, both n-type and p-type components are very important for realization of complete thermoelectric modules toward large area, portable, high power and energy efficient applications. However, stable n-type doping for layered oxyselenides, such as LaCuOSe and BiCuOSe, are known to be difficulty due to the high volatility of more than one cations (Bi and Cu) under high-temperature materials synthesis. Therefore, previous literatures are primarily focused on hole doping because p-type BiCuOSe is commonly believed to show best thermoelectric performance among these materials. However, our work demonstrates that the n-type version of oxyselenides, although not easy to be synthesized, show unexpectedly high performance than the p-type, thus highlight the significances of n-type oxyselenides. We note that n-type doping of Cu-based oxyselenides have been recently experimentally synthesized by cation and anion codoping strategy54, thus providing illumination for n-type LaCuOSe. Additionally, from energy efficiency and cost-effective perspectives, the ZT values of materials should exceed 1.5 for practical application55. Thus, to fully realize the potential of LaCuOSe for thermoelectric energy harvesting, the working temperature is suggested to be on the order of 900 K.
Finally, we discuss the validity of models and approximations used in this calculation. (1) The DP theory considers the scattering between longitudinal acoustic phonons and carriers, which is proven as predominant scattering mechanism in BiCuOSe and LaCuOSe33,56, thus DP theory can provide relatively good approximation for their relaxation times and electrical conductivities. However, the phonon anharmonicity, i.e., the scattering among various phonons, is not taken into consideration in DP theory, which will become stronger as temperature increases. Thus, the relaxation times and ZT values of BiCuOSe and LaCuOSe may be underestimated at high temperatures, due to the weakening of phonon-carrier scattering caused by strong phonon-phonon interactions57. Unfortunately, there is no reliable theory to explicitly evaluate the effect of anharmonicity on carrier scattering (the difficulty of many-body interactions)58,59, thus DP theory is generally widely adopted to approximately evaluate the relaxation times of TE materials (including BiCuOSe-type materials) at high temperatures10,60,61. Meanwhile, we also note that the contribution of phonon anharmonicity of LaCuOSe and BiCuOSe are comparable because of similar Grüneisen parameters, which are 1.93 and 1.84 for BiCuOSe and LaCuOSe, respectively27. Hence, the neglection of phonon anharmonicity effect is not expected to significantly change the comparison of the thermoelectric performance of LaCuOSe and BiCuOSe. (2) The carrier concentration can also impact scattering mechanism. We analyze carrier transport based on single parabolic band (SPB) model, in which the m* is calculated straightforwardly by band curvatures at CBM/VBM. While the effects of inter-pocket scattering are generally neglected, because of their relatively weak contributions at normal carrier concentration levels. Under this approximation, DP theory with SPB model is shown to yield a good prediction for relaxation time and thermoelectric properties in such conditions55,62 and it is thus also widely used for materials with multi-band and/or multi-band valleys10,63. Strictly speaking, for materials with multi-band and/or multi-band valley behaviors such as LaCuOSe and BiCuOSe, electrons (holes) will first occupy the energy pocket right at the band edge, e.g. VBM or CBM. Then for the case of higher carrier concentrations, the extra carriers will continue to fill the orbitals next to the level of VBM/CBM. The m* of carriers in different energy pockets is different, and carriers transition between different energy pockets will cause inter-picket scattering, thus the average m* and carrier mobility of carriers will be changed at high doping level28. Therefore, SPB model may overestimate the ZT values of LaCuOSe and BiCuOSe at high carrier concentrations. However, in our work, the discussed carrier concentration is not so high, therefore, it is still valid to use SPB model to compare the thermoelectric properties of LaCuOSe and BiCuOSe. (3) The maximum ZT value of p-type BiCuOSe in this work is less than the experimentally reported value of 1.5 at 873 K64. The difference between our calculated results and experimental values comes from the following two aspects: on one hand, electrical conductivity is calculated by the semi-classical Boltzmann transport theory, which only considers doped carriers with associated scattering and neglects the effects of remaining ions in the host lattice (ionization scattering) on the crystal and electronic structures. On the other hand, element doping induced phonon anharmonicity can lead to extra phonon scattering, thus screening lattice thermal conductivity. While this can be easily measured experimentally, it is computationally prohibitive to calculate by current transport theory under Boltzmann framework. Thus, theoretical simulations based on ideal crystal with carrier doping tends to overestimate κ165. Our obtained results are comparable to other theoretical reported ZT value17,52.
In conclusion, we systematically investigate and compare the intrinsic TE performance of LaCuOSe and BiCuOSe by utilizing first-principles calculations in this paper. The calculated results show that because of the different A-site cations between BiCuOSe and LaCuOSe, their electronic structures show significant difference. In addition to the wider band gap of LaCuOSe than BiCuOSe, the most important thing is that band valley degeneracy of BiCuOSe is found around the VBM, while LaCuOSe shows band degeneracy behavior around the CBM. Band degeneracy can significant enhance the Seebeck coefficient, which leads to that the S-coefficient of p-type (n-type) BiCuOSe is larger (smaller) than that of LaCuOSe at same temperature and carrier concentration. Due to the longer electron relaxation times, the electrical conductivities of both BiCuOSe and LaCuOSe for n-type systems are higher than those for p-type systems. A large power factor of 2.58 mW m−1 K−2 for n-type LaCuOSe can be achieved at 900 K because of the larger Seebeck coefficient and higher optimal carrier concentration, which is 1.5 times larger than that of 1.71 mW m−1 K−2 for n-type BiCuOSe. Besides, the average lattice thermal conductivity of BiOCuSe (1.00 W m−1 K−1 at 300 K) is lower than that of LaCuOSe (1.73 W m−1 K−1 at 300 K) due to lower phonon group velocity and phonon mean-free path. Under the co-effect of those transport coefficients, the optimal ZT value of 1.46 for LaCuOSe is obtained with the carrier concentration of ~2.5 × 1020 cm−3 at 900 K, which is about 22% larger than that of 1.2 for BiCuOSe with the carrier concentration of ~1 × 1020 cm−3. The present study thus demonstrates the critical role of La element in promoting TE performance of layered oxyselenides, which will provide beneficial information for further related studies.
Methods
First principle calculations
Our calculations are performed within DFT by using the Vienna Ab Initio Simulation Package (VASP)66,67,68. The generalized gradient approximations (GGA)69 with the Perdew-Burke-Ernzerhof (PBE) parameterization is applied as the exchange-correlation potential. The Heyd-Scuseria-Ernzerhof (HSE06) hybrid density functional70 is also employed to obtain accurate band structures and transport properties. The Brillouin zones of the primitive cells are sampled with Monkhorst-Pack k-meshes of 12 × 12 × 6 for relaxation and self-consistent calculation. The energy and the force convergence criterion are chosen to be 10−4 eV and 10−5 eV Å−1, respectively. The cutoff energy of the plane-wave is set at 400 eV. The electronic transport properties are implemented in the BoltzTraP2 code71 by utilizing Boltzmann transport theory and relaxation time approximation (RTA). The phonon structure is obtained by utilizing the Phonopy package72. The lattice thermal conductivity is calculated by solving the Boltzmann transport equation as implemented in ShengBTE code65. The second and third-order interatomic force constants (IFCs) are obtained using 4 × 4 × 1 and 3 × 3 × 1 supercells as inputs of Phonopy and thirdorder.py script65. The 10th nearest neighbors are chosen as the interaction cutoff for the third-order IFCs. The effects of SOC are considered for all calculations.
Van der Waals interactions test
For van der Waals (vdW) systems, the semi-empirical schemes like DFT-D3 method have been widely used to consider vdW interaction73,74,75. Besides the semi-empirical schemes, the vdW treatments with the exchange-correlation functional correction like optB86b-vdW are also effective methods76,77,78. To investigate the influences of vdW interaction on the calculated results, we compare the lattice parameters, band structure, and phonon spectra for LaCuOSe and BiCuOSe obtained by standard DFT, DFT-D3, and optB86b-vdW methods in Table 1 and Figs. 8, 9. For LaCuOSe, it is shown that the lattice parameters obtained by DFT method with and without vdW correction are all in reasonable agreement with experimental values29, as shown in Table 1. Particularly, the band structure (and phonon spectra) show similar character to each other for standard DFT, DFT-D3 and optB86b-vdW calculations (see Figs. 8, 9). In the case of BiCuOSe, we also find that consideration of vdW correction has small influences on the band structure and phonon spectra. The vdW correction, thus, is not taken into account in the subsequent calculations.
Data availability
The data that support the findings of this study are available from corresponding author upon reasonable request.
References
He, J. & Tritt, T. M. Advances in thermoelectric materials research: Looking back and moving forward. Science 357, 1369–1369 (2017).
Snyder, G. J. & Toberer, E. S. Complex thermoelectric materials. Nat. Mater. 7, 105–114 (2008).
Kanishka, B. et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 489, 414–418 (2012).
Jaworski, C. M. et al. Combining alloy scattering of phonons and resonant electronic levels to reach a high thermoelectric figure of merit in PbTeSe and PbTeS alloys. Energy Environ. Sci. 4, 4155–4162 (2011).
Ren, G. K. et al. Layered oxygen-containing thermoelectric materials: mechanisms, strategies, and beyond. Mater. Today 29, 68–85 (2019).
Zhao, L. D. et al. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373–377 (2014).
Guo, D. et al. Strain effects to optimize thermoelectric properties of doped Bi2O2Se via tran-blaha Modified Becke-Johnson density functional theory. J. Phys. Chem. C. 117, 21597–21602 (2013).
Orabi, R. A. R. A. et al. Band degeneracy, low thermal conductivity, and high thermoelectric figure of merit in SnTe-CaTe alloys. Chem. Mater. 28, 376–384 (2016).
Ming, H. et al. Improved figure of merit of Cu2SnSe3 via band structure modifification and energy-dependent carrier scattering. Acs Appl. Mater. Inter. 12, 19693–19700 (2020).
Wang, F. Q. et al. Exceptional thermoelectric properties of layered GeAs2. Chem. Mater. 29, 9300–9307 (2017).
Hiramatsu, H. et al. Crystal structures, optoelectronic properties, and electronic structures of layered oxychalcogenides MCuOCh (M = Bi, La, Ch = S, Se, Te): Effects of electronic configurations of M3+ ions. Cheminform 39, 326–334 (2008).
Bleijs, D. A., Figdor, C. G. & Kooyk, Y. V. Bi1−xSrxCuSeO oxyselenides as promising thermoelectric materials. Appl. Phys. Lett. 97, 092118 (2010).
Zhao, L. D. et al. BiCuSeO oxyselenides: New promising thermoelectric materials. Energy Environ. Sci. 7, 2900–2924 (2014).
Lin, P. et al. Influence of Pb doping on the electrical transport properties of BiCuSeO. Appl. Phys. Lett. 102, 703 (2013).
Jing, L. I. et al. Thermoelectric properties of Mg doped p-type BiCuSeO oxyselenides. J. Alloy. Compd. 551, 649–653 (2013).
Lan, J. L. et al. Enhanced thermoelectric properties of Pb-doped BiCuSeO ceramics. Adv. Mater. 96, 2710–2713 (2013).
Yang, J. et al. Low effective mass leading to an improved zt value by 32% for n-type BiCuSeO: A first-principles study. J. Mater. Chem. A 2, 13923–13931 (2014).
Sallis, S. et al. Role of lone pair electrons in determining the optoelectronic properties of BiCuSeO. Phys. Rev. B 85, 085207 (2012).
Lacheisserie É. D. T. D., Gignoux D. & Schlenker M. Magnetism (Springer, New York, 2005).
Riseborough, P. S. Heavy fermion semiconductors. Adv. Phys. 49, 257–320 (2000).
Morenzin, J. et al. Localization and bandwidth of the 3d-orbitals in magnetic Ni and Co clusters. Pure Appl. Chem. 72, 2149–2157 (2000).
Hiramatsu, H. et al. Excitonic blue luminescence from p-LaCuSeO/n-InGaZn5O8 light-emitting diode at room temperature. Appl. Phys. Lett. 87, L604 (2005).
Yanagi, H. et al. Magnetic and carrier transport properties of Mn-doped p-type semiconductor LaCuSeO: An investigation of the origin of ferromagnetism. J. Appl. Phys. 100, 33710–33717 (2006).
Hidenori, H. et al. Origins of hole doping and relevant optoelectronic properties of wide gap p-type semiconductor, LaCuSeO. J. Am. Chem. Soc. 132, 15060–15067 (2010).
Scanlon, D. O. et al. Understanding doping anomalies in degenerate p-type semiconductor LaCuOSe. J. Mater. Chem. C. 2, 3429–3438 (2014).
Yasukawa, M., Ueda, K. & Hosono, H. Thermoelectric properties of layered oxyselenides La1–xSrxCuOSe (x = 0 to 0.2). J. Appl. Phys. 95, 3594–3597 (2004).
Saha, S. K. & Dutta, G. Elastic and thermal properties of the layered thermoelectrics BiOCuSe and LaCuSeO. Phys. Rev. B 94, 125209 (2016).
Hidenori, H. et al. Origin of high-density hole doping and anisotropic hole transport in a wide gap layered semiconductor LaCuOSe studied by first-principles calculations. Phys. Status Solidi A 207, 1636–1641 (2010).
Ohki, Y. et al. Temperature dependence of the band edge emission of the wide gap semiconductor (LaO)CuCh (Ch = S, Se, Te). Angew. Chem. Int. Ed. 850, 1309 (2006).
Su, X. L. et al. High thermoelectric performance in the wide band-gap AgGa1-xTe2 compounds: directional negative thermal expansion and intrinsically low thermal conductivity. Adv. Funct. Mater. 29, 1806534 (2019).
Xiao, C. et al. Magnetic ions in wide band gap semiconductor nanocrystals for optimized thermoelectric properties. Mater. Horiz. 1, 81–86 (2014).
Sang, D. K. et al. Monolayer beta-tellurene: A promising p-type thermoelectric material via first-principles calculations. Nanoscale 11, 18116–18123 (2019).
Hiramatsu, H. et al. Wide gap p-type degenerate semiconductor: Mg-doped LaCuSeO. Thin Solid Films 445, 304–308 (2003).
Saha, S. K. Exploring the origin of ultralow thermal conductivity in layered BiCuSeO. Phys. Rev. B 92, 041202 (2015).
Kusainova, A. M. et al. New layered compounds with the general composition (MO) (CuSe), where M = Bi, Nd, Gd, Dy, and BiOCuS: syntheses and crystal structure. J. Solid State Chem. 112, 189–191 (1994).
Zhao, L. D. et al. Snse: A remarkable new thermoelectric material. Energy Environ. Sci. 9, 3044–3060 (2016).
Zhao, L. D. et al. Ultrahigh power factor and thermoelectric performance in hole-doped single-crystal SnSe. Science 351, 141–144 (2016).
Bardeen, J. & Shockley, W. S. Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 80, 72–80 (1950).
Hao, S. Q. et al. Computational prediction of high thermoelectric performance in hole doped layered GeSe. Chem. Mater. 28, 3218–3226 (2016).
Parker, D. & Singh, D. J. Thermoelectric properties of AgGaTe2 and related chalcopyrite structure materials. Phys. Rev. B 85, 125209 (2012).
Li, G. P., Ding, G. Q. & Gao, G. Y. Thermoelectric properties of SnSe2 monolayer. J. Phys.-Condens. Mat. 29, 105001 (2017).
Shahi, P. et al. Bipolar conduction is the origin of the electronic transition in pentatellurides: metallic vs. semiconducting behavior. Phys. Rev. X 8, 021055 (2018).
Wang, C. et al. Electron and phonon transport properties of layered Bi2O2Se and Bi2O2Te from first-principles calculations. N. J. Phys. 20, 123014 (2018).
Jonson, M. & Mahan, G. D. Mott’s formula for the thermopower and the Wiedemann-Franz Law. Phys. Rev. B Condens. Mat. 21, 4223–4229 (1980).
Stojanovic, N. et al. Thermal conductivity in metallic nanostructures at high temperature: electrons, phonons and the Wiedemann-Franz Law. Phys. Rev. B 82, 2283 (2010).
Madsen, G. K. H. & Singh, D. J. Boltztrap. A code for calculating band-structure dependent quantities ☆. Comput. Phys. Commun. 175, 67–71 (2006).
Tian, Z. et al. Phonon conduction in PbSe, PbTe and PbTe1-xSex from first-principles calculations. Phys. Rev. B 85, 45–51 (2012).
Zhu, L., Zhang, G. & Li, B. Coexistence of size-dependent and size-independent thermal conductivities in phosphorene. Phys. Rev. B 90, 214302 (2014).
Sun, Z. H. et al. Pressure tuning of the thermal conductivity of gallium ArSeNiDe from first-principles calculations. Phys. Chem. Chem. Phys. 20, 30331–30339 (2018).
Liu, G. et al. Thermal properties of layered oxychalcogenides BiCuOCh (Ch = S, Se, and Te): A first-principles calculation. J. Appl. Phys. 119, 185109 (2016).
Sun, Z. H. et al. Disparate strain response of the thermal transport properties of bilayer penta-graphene as compared to that of monolayer penta-graphene. Phys. Chem. Chem. Phys. 21, 15647–15655 (2019).
Zou, D. et al. Electronic structures and thermoelectric properties of layered BiCuOCh oxychalcogenides (Ch = S, Se and Te): first-principles calculations. J. Mater. Chem. A 1, 8888–8896 (2013).
Wang, G. et al. First-principles study of the electronic structure and thermoelectric properties of LaOBiCh2 (Ch=S, Se). Mod. Phys. Lett. B 31, 1750265 (2017).
Zhang, X. et al. Attempting to realize n-type BiCuSeO. J. Solid State Chem. 258, 510–516 (2018).
Pei, Y. Z. et al. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 473, 66–69 (2011).
Ren, G. K. et al. Enhancing thermoelectric performance in hierarchically structured BiCuSeO by increasing bond covalency and weakening carrier-phonon coupling. Energy Environ. Sci. 10, 1590–1599 (2017).
Zhou, J. J., Hellman, O. & Bernardi, M. Electron-phonon scattering in the presence of soft modes and electron mobility in SrTiO3 perovskite from first principles. Phys. Rev. Lett. 121, 226603 (2018).
Whalley, L. D. et al. Phonon anharmonicity, lifetimes and thermal transport in CH3NH3PbI3 from many-body perturbation theory. Phys. Rev. B 94, 220301 (2016).
Zhou, J., Cheng, J. L. & Wu, M. W. Spin relaxation in n-type GaAs quantum wells from a fully microscopic approach. Phys. Rev. B 75, 045305 (2007).
Fan, D. D. et al. Understanding the electronic and phonon transport properties of thermoelectric material BiCuSeO: A first-principles study. Phys. Chem. Chem. Phys. 19, 12913–12920 (2016).
Zhao, T. Q. et al. GeAs2: A IV-V group 2D semiconductor with ultralow thermal conductivity and high thermoelectric efficiency. Chem. Mater. 29, 6261–6268 (2017).
Pei, Y. Z. et al. Optimum carrier concentration in n-type PbTe thermoelectrics. Adv. Energy Mater. 4, 9201–9210 (2014).
Bilc, D. I. et al. Low-dimensional transport and large thermoelectric power factors in bulk semiconductors by band engineering of highly directional electronic states. Phys. Rev. Lett. 114, 136601 (2015).
Liu, Y. et al. Synergistically optimizing electrical and thermal transport properties of BiCuSeO via a dual-doping approach. Adv. Energy Mater. 6, 1502423 (2016).
Wu, L. et al. Shengbte: A solver of the boltzmann transport equation for phonons ☆. Comput. Phys. Commun. 185, 1747–1758 (2014).
Kresse, G. & Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Hafner, J. Ab initio molecular-dynamics for liquid-metals. Phys. Rev. B 47, 558–561 (1993).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Madsen, G. K. H., Carrete, J. & Verstraete, M. J. Boltztrap2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 231, 140–145 (2018).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Grimme, S. et al. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Yang, X. Y., Luo, W. & Ahuja, R. Fluoride ion batteries: Designing flexible M2CH2 (M = Ti or V) MXenes as high-capacity cathode materials. Nano Energy 74, 104911 (2020).
Wu, Y. X. et al. Promising thermoelectric performance in van der Waals layered SnSe2. Mater. Today Phys. 3, 127–136 (2017).
Klimeš, J. et al. Fast track communication: Chemical accuracy for the van der Waals density functional. J. Phy. Condens. Mat. 22, 22201 (2010).
Xin, L., Sullivan, M. B. & Su, Y. Q. First-principles investigations of the atomic, electronic, and thermoelectric properties of equilibrium and strained Bi2Se3 and Bi2Te3 including van der Waals interactions. Phys. Rev. B 86, 184111 (2012).
Ding, X. et al. NbS2: A promising p-type ohmic contact for two-dimensional materials. Phys. Rev. Appl. 12, 064061 (2019).
Acknowledgements
Haiyan Xiao was supported by the NSAF Joint Foundation of China (Grant No.U1930120). Liang Qiao was supported by National Natural Science Foundation of China (Grant No. 11774044, 52072059). Zhibin Gao acknowledges the financial support from MOE tier 1 funding of NUS Faculty of Science, Singapore (Grant No. R-144-000-402-114). The theoretical calculations are performed using the supercomputer resources at TianHe-1 located at National Supercomputer Center in Tianjin.
Author information
Authors and Affiliations
Contributions
H.Y.X. and L.Q. conceived the idea. N.W. and M.L.L. conducted the simulation and analysis. Z.B.G., Z.J.L., and S.L. provided advices on this work. All authors participated in the writing and correction of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, N., Li, M., Xiao, H. et al. Band degeneracy enhanced thermoelectric performance in layered oxyselenides by first-principles calculations. npj Comput Mater 7, 18 (2021). https://doi.org/10.1038/s41524-020-00476-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00476-3
This article is cited by
-
Investigating the novel thermoelectric properties of magnesium, calcium, and barium divanadate oxides (XV2O6 where X = Mg, Ca, and Ba) for waste heat recovery applications in energy harvesting devices
Applied Physics A (2024)
-
Local symmetry distortion induced anomalous thermal conduction in thermoelectric layered oxyselenides
npj Computational Materials (2023)
-
Remarkable thermoelectric performance of carbon-based schwarzites
Advanced Composites and Hybrid Materials (2023)
-
High Thermoelectric Properties of Janus WSeS Bilayer Membranes with Different Stacking Modes
Journal of Electronic Materials (2022)
-
Electrical performance enhancement by resonant states in PbSe single-crystal growth via Bi-flux method
Journal of Materials Science: Materials in Electronics (2021)