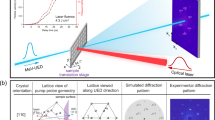
Abstract
Time-resolved mapping of lattice dynamics in real- and momentum-space is essential to better understand several ubiquitous phenomena such as heat transport, displacive phase transition, thermal conductivity, and many more. In this regard, time-resolved diffraction and microscopy methods are employed to image the induced lattice dynamics within a pump–probe configuration. In this work, we demonstrate that inelastic scattering methods, with the aid of theoretical simulation, are competent to provide similar information as one could obtain from the time-resolved diffraction and imaging measurements. To illustrate the robustness of the proposed method, our simulated result of lattice dynamics in germanium is in excellent agreement with the time-resolved x-ray diffuse scattering measurement performed using x-ray free-electron laser. For a given inelastic scattering data in energy and momentum space, the proposed method is useful to image in-situ lattice dynamics under different environmental conditions of temperature, pressure, and magnetic field. Moreover, the technique will profoundly impact where time-resolved diffraction within the pump–probe setup is not feasible, for instance, in inelastic neutron scattering.
Similar content being viewed by others
Introduction
Inelastic scattering of matter allows us to probe quasi-particles (QPs) such as phonons (quantized lattice vibrations), magnons (quantized spin excitations), and polarons1,2,3,4. These QPs have finite energy and lifetime that carries information about the intra- and inter-QPs interactions and their coupling strength, necessary to understand the materials’ response to external stimuli. Thermal conductivity5,6, heat capacity7,8,9, and phase transitions7,10,11 are among many of the material properties that are often described by directly invoking various QPs. Optical, x-ray, neutron, and electron scattering methods – for example, Raman scattering, inelastic x-ray scattering (IXS), inelastic neutron scattering (INS), and electron energy loss spectroscopy (EELS) – have been routinely employed to measure these QPs1,3,4. Typically these measurements are performed in the momentum and energy domains (k–ω), and lack information on temporal dynamics, i.e., k–t and x–t imaging – time evolution of momentum or real space coordinates which ranges from femto- to several nano-seconds12,13.
To image k–t and x–t dynamics, a pump–probe setup having two ultrashort pulses, where the duration of the probe pulse must be shorter than the characteristic timescale of motion that is under probe, are required. Thanks to tremendous technological advancement, it has become possible to generate ultrashort x-ray and electron pulses14,15,16, and image the lattice dynamics in k–t and x–t domains. For example, the time-resolved x-ray and electron diffraction within a pump–probe configuration are used to image the lattice dynamics in the k–t domain17,18,19,20,21,22,23,24, and the ultrafast electron microscopy has recently been demonstrated for the imaging in the x–t domain at an unprecedented spatiotemporal resolution25,26,27. However, similar advances have not been taken for neutron sources to produce an ultrashort neutron pulse for imaging the lattice dynamics28. At this juncture, it is not straightforward whether one can employ neutron sources within a pump–probe setup with sufficient atomic-scale spatiotemporal resolution to image lattice or spin dynamics28.
In this work, we theoretically demonstrate that methods based on inelastic scattering are suitable to extract similar information as one could get from the time-resolved imaging of lattice dynamics in k–t or x–t domains. Our approach is general and equally applicable to IXS, INS, and EELS. In general, all these inelastic scattering based methods probe dynamical structure factor S(k, ω), apart from pre-factors, in experiments. The inelastic scattering methods provide k–ω resolved measurement of QPs and comprise a powerful way to investigate the correlated motion of atoms and electrons1,3,4. We should mention that in ideal conditions, irrespective of whether measurements are in k–ω, k–t, or x–t domains, they provide similar information after coordinate transformation(s). However, in practice, one measurement domain may have an advantage over the other. For example, under static environmental conditions of temperature, pressure, or magnetic field, the four-dimensional (4D) k–ω mapping of QPs is preferred because of its superior energy and momentum resolutions ( ~ 0.1 meV and ~ 0.5 nm−1)2,29,30,31, from which one can readily extract the QP energy, group velocity, and linewidth. On the other hand, the k–t domain is useful for tracking the temporal evolution of atomic motions upon photoexcitation-induced structural phase transitions32 or the measurement of long-wavelength phonon lifetime (of the order of tens of picoseconds, which is not easily accessible in the k–ω domain). Moreover, mapping the acoustic phonon wavefronts or the nucleation of waves from defects and interfaces in nanostructures is better suited for the x–t domain26,33.
In the following, we show that S(k, ω) (obtained from experimental measurements or simulations) encodes all the essential information to image the lattice dynamics in the k–t and x–t domains after coordinate transformation without the causality violation. In particular, as we illustrate, our approach is well-suited to image the first-order states (i.e., emission or absorption of a single phonon at q ≃ 0 from inelastically scattering photons or disorder-activated continuum34) and second-order ‘squeezed’ states17 in the k–t domain (squeezed states are generated in the entire reciprocal lattice immediately after pumping the sample with a visible or near-infrared pump pulse)17,35. The temporal evolution and decay of the measured intensity from the change in phonon occupation at a given k point due to electron–electron, electron–phonon, and phonon–phonon scattering channels17,36,37 are not explicitly included within the current framework. However, we consider the finite lifetime of first- or second-order states by including the phonon linewidths. Moreover, our methodology allows for x–t imaging of the coherent phonon dynamics from a point-like nucleation site or an extended defect. Our approach of imaging dynamics in the x–t domain can be directly compared with the electron microscopy data, as we demonstrate later by an example.
Results and discussion
Computational approach
Silicon is used in the present work to demonstrate the proposed concept. The S(k, ω) is simulated in the (H, H, L) reciprocal plane following the same procedure as in our previous studies38,39. The range of energy transfer lies from 0 to 80 meV with a step size of 0.25 meV (i.e., energy resolution), whereas the momentum transfer range varies from (0, 0, 0) to (4, 4, 7) reciprocal lattice units (r.l.u.) with the step size of 0.025 r.l.u. (see Supplementary Fig. S3). Here, a = 0.543 nm is used as the lattice parameter of silicon. After calculating S(k, ω) and using fluctuation-dissipation theorem, the imaginary part of the response function χ(k, ω) is obtained as, \({\rm{Im}}[\chi ({\bf{k}},\omega )]=-\pi [S({\bf{k}},\omega )-S({\bf{k}},-\omega )]\). S(k, ω) and S(k, − ω) are related to each other by \(S({\bf{k}},-\omega )=\exp (-\beta \hslash \omega )\,S({\bf{k}},\omega )\) with \(\beta ={({k}_{{\rm{B}}}T)}^{-1}\), where kB is the Boltzmann’s constant3. In the following all results are shown at T = 300 K. It is known that the real part of the response function is related to its imaginary part by the Kramers–Kronig relation40.
Here, \({\mathcal{P}}\) represents the principal value of the integral. Fourier transform is performed to obtain χ(k, t) from χ(k, ω), which is complex in nature (see Supplementary Material for derivation). Equation (1) ensures that χ(k, t) = 0 for t < 0 and enforces the causality. It should be emphasized that direct Fourier transform of S(k, ω) to I(k, t), i.e., \(I({\bf{k}},t)=\hslash \int S({\bf{k}},\omega )\exp ({\rm{i}}\omega t)\ d\omega\),1 is not the time evolution measured in time-resolved experiments, as I(k, t) violates causality. Note that, there is always a limitation in the energy resolution while measuring S(k, ω) in an experiment. The discrete nature of the binned ω during experiment causes periodic nature of χ(k, t). The time resolution of χ(k, t) is estimated by Fourier law as Δt = 2π \(\hslash\)/(80 meV) = 51.5 fs and the time duration of the lattice dynamics is related to the range of the sampled values of ω. Here, the time duration of the lattice dynamics in silicon is 8.2 ps. We note that the Δt and time duration are proportional to the energy transfer and energy binning (or resolution) and will vary from one experimental setup to another. For example, Abbamonte and co-workers have imaged density disturbances in water with attosecond time resolution (Δt = 41.3 attoseconds) with incident x-ray energy and resolution of 100 eV and 0.3 eV, respectively41.
Response function in momentum domain
Figure 1 represents snapshots of the real and imaginary parts of the normalized χ(k, t) in the top and bottom rows, respectively. The dynamics can be seen as induced by the point-like source in x,42 akin to the nucleation site in electron microscopy imaging. From this point-like source term, silicon absorbs the energy at t = 0, and phonon modes are generated in the entire reciprocal space (localized source in x is delocalized in k). The snapshots are shown in the (H, H, L) reciprocal plane for different time instances. We note that a (weak) optical pump pulse will also lead to the same χ(k, t) snapshots, as the pump pulse will generate first- and second-order states in the entire reciprocal space. The first-order disorder-activated continuum is generated in the absence of perfect crystalline order34. In contrast, the second-order squeezed states are generated by the coupling of a photon (momentum q ≃ 0) with the two phonon modes of near-equal and opposite momenta (i.e., at k and −k due to the conservation of momentum)35. Thus in the present study, the simulated snapshots can be considered to arise from either a point-like source in x or generation of first- and second-order states. As evident from Fig. 1, these generated phonons propagate through the system and decay at different times for different k points according to their lifetime. It is possible to extract the lifetime of these phonon modes at different k values from the real and imaginary parts of the normalized χ(k, t) as we discuss below.
The real and imaginary parts of χ(k, ω) at a particular k = (0.75, 0.75, 0.75) r.l.u. is presented in Fig. 2a. Because of the phonon polarization factor1, at this particular k value, two phonon modes have finite intensity at energy values ω1 = 28 meV (longitudinal acoustic) and ω2 = 60 meV (longitudinal optic). The full width at half maximum (FWHM) at these two energy values are Γ1 = 0.1 meV and Γ2 = 0.4 meV (obtained from first-principles simulation of Silicon43), which are known as decay widths of these modes. To extract the lifetime of these modes, χ(k, t) is calculated from χ(k, ω). The imaginary and real parts of χ(k, t) are shown in Fig. 2b, c, respectively. The lifetime (τ) of both the active modes is obtained by fitting the exponentially decaying sinusoidal oscillation at the given k value, and are τ1 = 13.7 and τ2 = 3.0 ps. The fitted τ values are consistent with the values expected form its inverse relationship with Γ, i.e., Γ = 1/(π τ), confirming the accuracy of our implementation. Also, the interferences visible in Fig. 2b, c are due to the presence of two active modes.
a Real and imaginary parts of χ(k, ω) at particular k = (0.75, 0.75, 0.75) r.l.u. The decay widths corresponding to two active modes are Γ1 = 0.1 meV and Γ2 = 0.4 meV. b Imaginary part of χ(k, t), which provides the lifetimes of the active phonon modes as τ1 = 13.7 ps and τ2 = 3.0 ps. c Real part of χ(k, t), which gives the same values of the lifetimes of the active phonon modes. All the quantities plotted in sub-plots are normalized.
Till now, we have discussed dynamics induced by the point-like disturbance in x, or first- and second-order states that lead to the excitation of all phonon modes in the reciprocal space. Let us analyze how χ(k, t) manifests when the extended source in x induces the dynamics, which excites the phonon modes active at a single k value. A general time-dependent extended external source next(x, t) can be treated as a Gaussian envelop in the k–ω domain with standard deviation σ controlling the spatial extent of the source. The induced dynamics nind can subsequently be modeled as
where k0 is the mean k value at which phonons are excited. The real and imaginary parts of χ(k, ω) at k0 = (1.75, 1.75, 2.50) r.l.u. showing finite intensity for the three phonon modes are shown in Fig. 3a. Since momentum transfer k and phonon wavevector q at k0 are not entirely parallel or perpendicular to each other, the three modes have mixed transverse and longitudinal character. We emphasize that for an infinitely extended source as considered here, dynamics at all other k points are zero. As one can observe from Fig. 3b, c, finite linewidths of the phonon modes allow them to decay in few picoseconds. Note that we do not explicitly include the phonon scattering channels in our approach. When included, these scattering channels will increase the phonon population with time at other k points that satisfy the momentum and energy conservation17,36,37.
Response function and time-resolved diffuse x-ray scattering
To know how well-grounded the discussed method of extracting χ(k, t) from S(k, ω) (obtained from inelastic scattering measurements or simulations) is, we will compare our simulated results with the measured χ(k, t). Trigo et al. have performed time-resolved diffuse x-ray scattering on germanium17. In that experiment, an optical pump pulse of 800 nm with a nominal width of 50 fs was used to generate correlated pairs of phonons with equal and opposite momenta at k and −k, i.e., the squeezed states having 〈u(t)〉 = 0. Here u is the atomic displacement, and t denotes the pump–probe delay time. A 50 fs x-ray pulse having 10 keV photon energy from Linac Coherent Light Source (LCLS) was used to probe diffuse scattering from the squeezed states at various pump–probe delay times. The temporal evolution of the equal-time correlation function was probed17. Due to the time-resolved nature of the experiment, the time evolution of the squeezed states and the anharmonic decay of phonons is seen in the k–t domain. Note that for the squeezed states, the diffuse scattering intensity oscillates at twice the phonon frequency17.
Figure 4 presents the comparison of the experimental data from ref. 17 with our simulated result of χ(k, t) for germanium. To demonstrate the merit of our work, we have chosen the data at k = (− 0.10, 0.00, − 0.08) r.l.u. only. Since χ(k, t) is dependent on the phonon mode polarization, the calculated intensity at k is due to the oscillations at 2ω ~ 5.5 meV. In the experiment, the normalized difference intensity was shown, which provides the time-resolved value of the equal-time correlation function at k and −k17. As reflected from the figure, the present simulated result is an excellent agreement with the experimental data for τ ~ 3.7 ps. Such a large value of τ for dispersive phonon modes, which is straightforward to obtain from k–t domain measurements, is not so easy to extract from INS or IXS measurements owing to the finite instrument resolution in k and ω29,30,31.
Normalized difference intensity of the time-resolved diffuse scattering at k = ( − 0.10, 0.00, − 0.08) r.l.u. is from the experiment presented in ref. 17 (black color), and our simulated χ(t) is shown by blue color.
In spite of the excellent agreement, an important question arises: how the two different methods – time-resolved diffuse x-ray scattering and inelastic x-ray scattering, yield the same information. In ref. 17, it is mentioned that time-resolved diffuse x-ray scattering probes equal-time density–density correlation function: \(\langle \hat{n}({\bf{-k}},t)\,\hat{n}({\bf{k}},t)\rangle\) with \(\hat{n}\) as a density operator44,45. On the other hand, it is well-established that inelastic x-ray scattering probes density–density correlation function at different time: \(\langle \hat{n}({\bf{-k}},t)\,\hat{n}({\bf{k}},0)\rangle\), which is related to the Van Hove correlation function3,42,46. However, there is no contradiction as the experiment was performed without energy resolution and the presented data were energy integrated17. The density–density correlation function at different time, probed by inelastic x-ray scattering, reduces to equal-time density–density correlation function in the case where energy resolution is lacking. Therefore, without energy resolution, time-resolved diffuse x-ray scattering and inelastic scattering yield identical information: \(\langle \hat{n}({\bf{-k}},t)\,\hat{n}({\bf{k}},t)\rangle\), apart from a pre-factor (see Supplementary Material for derivation).
Response function in real space
Not only time-resolved scattering methods in a pump–probe configuration provide the temporal evolution of correlation function, but also help us to visualize atomic motion (lattice dynamics) in the x–t domain12,13, for example, as in the time-resolved electron microscopy experiments25,26,33. In the following, we demonstrate that momentum and energy-resolved inelastic scattering signal also provides the snapshots of the lattice dynamics in the x–t domain. For this purpose, we need to perform one more Fourier transform from momentum space to real space to obtain χ(x, t) from χ(k, t). Following Fourier relation, the spatial resolution along the [H, H, 0] direction is estimated as Δx = 2π/(6.5 Å−1) = 0.96 Å , whereas along the [0, 0, L] direction is Δx = 2π/(8.1 Å−1) = 0.78 Å. The spatial extent of the dynamics ranges from (0, 0) to (153, 108) Å. Similar to the time resolution and duration, the spatial resolution and extent are governed by momentum transfer and momentum resolution of the measurements/simulations.
The snapshot of χ(x, t) indicates how and where the disturbance, imparted at t = 0, has traveled in real space. χ(x, t) at t = 400 fs in the (H, H, L) plane is shown in Fig. 5. In this case, the dynamics is induced by a point source at x = (0, 0, 0) in silicon. As silicon crystal is anisotropic, therefore the phonon propagation is not spherical as generally assumed for the scattering of light waves from a point-like source. Instead, the anisotropic phonon group velocity governs the 3D extent of energy re-distribution after time t. The extent of disturbance along a particular direction at any given time can be estimated from the maximum velocity given by the dispersion of longitudinal acoustic mode at the zone-center. In the present case, the maximum velocity along the [H, H, 0] direction is 8958 ms−1, whereas it is 8381 ms−1 along the [0, 0, L] direction.
Figure 6 presents the entire dynamics along [1, 1, 0] and [0, 0, 1] directions in upper and lower panels, respectively. Before the disturbance at t < 0, the system is in equilibrium. At t = 0, the system is struck with a negative disturbance. As a result of this disturbance, a positive recoil at the origin is generated, surrounded by a minimal positive build-up. As visible from the figure, the density-induced disturbance is propagating through the entire system as time evolves. At large time instances, the disturbance is still into the system, but the order is minimal due to the spread of energy into the system (no dissipation of energy from the system). Such time-resolved images can be captured nowadays using real-space femtosecond electron imaging, as recently demonstrated for the phonon nucleation and launch at a crystal step-edge in the WSe2 flake26. At this point, it is important to mention that Abbamonte and co-workers have employed a similar reconstruction method of χ(x, t) from inelastic x-ray scattering data to visualize electron dynamics in various systems41,47,48.
Practical challenges
Despite the applicability of our approach to inelastic scattering methods, we should keep experimental and data analysis limitations in mind. For example, 4D momentum-, crystallographic direction-, and energy-resolved datasets of lattice dynamics are presently feasible with high-resolution ( ~ 1 meV, or better) INS and IXS29,30,31. In EELS, the energy resolution may always not be suitable for low-energy phonons ( < 30 meV), as intense zero-loss peak masks the spectrum49,50. Even in INS and IXS measurements, the scattering intensity varies among elements. Since x-ray scattering cross-section increases with the atomic number Z, phonon intensity of low Z elements is considerably weak. Moreover, acquiring a complete 4D dataset using IXS with an array of monochromators will require a long measurement time (several days, as measurements at a few momentum transfers generally take 15–120 min). Similarly, in INS, several elements have small coherent scattering cross-section (i.e., H, V, Co) or high absorption coefficient (i.e., B, Cd); thus, phonon dispersion measurements remain challenging in materials with these elements. INS measurements also have kinematic constraints (all momentum and energy transfer are not accessible), and energy resolution, instead of being a constant number, depends on the phonon energy1,2. Deconvolution of energy resolution from the measured 4D dataset to extract the intrinsic details, for example, τ, is not always straightforward51. Recent advances in experimental techniques and data analysis are overcoming many of the limitations. Together with simulations, they can provide full or complementary information, as demonstrated in this study.
In summary, we have established that inelastic scattering methods have potential to image lattice dynamics with atomic-scale spatiotemporal resolution. Few tens of femtoseconds temporal and ~ 1 Å spatial resolutions can be achieved during the reconstruction of lattice dynamics by utilizing the superior energy and momentum resolutions of inelastic scattering measurements. Our proposed theoretical method allows for direct imaging of lattice dynamics and enables us to extract the lifetime of selective phonon modes. Moreover, there is a flexibility to decide whether a single phonon mode or several phonon modes participate in the dynamics by choosing the disturbance source’s spatial extent in the real space. The excellent agreement between the present simulated result and the measured lattice dynamics in germanium provides confidence and robustness of the proposed method. We believe that the current approach will be an alternative to time-resolved diffraction methods to image lattice dynamics and beneficial to the situations where time-resolved diffraction is not easy to perform, such as neutron scattering and in-situ measurement conditions.
Methods
Dynamical structure factor calculation
The dynamical structure factor S(k, ω) was calculated using the following expression:
where fd(k) is the form factor for atom d (can be replaced by the neutron scattering length \(\overline{{b}_{d}}\) for inelastic neutron scattering), \({\bf{k}}={\bf{k}}^{\prime} -{\bf{k}}^{\prime\prime}\) is the wavevector or momentum transfer, and k″ and \({\bf{k}}^{\prime}\) are the final and incident wavevector of the scattered particle, respectively; q is the phonon wavevector, ωs is the eigenvalue, and eds is the eigenvector of the phonon corresponding to the branch index s, d is the atom index in the unit cell, τ is the reciprocal lattice vector, \(\exp (-2{W}_{d})\) is corresponding to the Debye–Waller factor, and \({n}_{s}={\left[\exp \left(\frac{\hslash {\omega }_{s}}{{k}_{{\rm{B}}}T}\right)-1\right]}^{-1}\) is the Bose–Einstein occupation factor. The + and − sign in Eq. (3) correspond to phonon creation and phonon annihilation, respectively. The phonon eigenvalues and eigenvectors (simulation details are same as presented in refs. 38 and 39) in Eq. (3) were obtained by solving dynamical matrix using Phonopy52. Phonon dispersion curves, S(k, ω) and constant energy slices of S(k, ω) of silicon and germanium are given in Supplementary Information.
Data availability
Data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
Code availability
Code that support the findings of this study are available from the corresponding authors on reasonable request.
References
Squires, G. Introduction to the Theory of Thermal Neutron Scattering (Cambridge Univ. Press, 1978).
Willis, B. & Carlile, C. Experimental Neutron Scattering. (Oxford Univ. Press, Oxford, 2009).
Schülke, W. Electron Dynamics by Inelastic X-ray Scattering (Oxford Univ. Press, 2007).
Egerton, R. F. Electron Energy-loss Spectroscopy in the Electron Microscope (Springer Science & Business Media, 2011).
Niedziela, J. et al. Selective breakdown of phonon quasiparticles across superionic transition in CuCrSe2. Nat. Phys. 15, 73–78 (2019).
Lindsay, L. & Polanco, C. A. Handbook of Materials Modeling: Applications: Current and Emerging Materials 735–765 (Springer International Publishing, 2020).
Dove, M. Introduction to Lattice Dynamics. (Cambridge Univ. Press, Cambridge, 1993).
Fultz, B. Vibrational thermodynamics of materials. Prog. Mater. Sci. 55, 247–352 (2010).
Bansal, D. et al. Phonon anharmonicity and negative thermal expansion in SnSe. Phys. Rev. B 94, 054307 (2016).
Bansal, D. et al. Momentum-resolved observations of the phonon instability driving geometric improper ferroelectricity in yttrium manganite. Nat. Commun. 9, 15 (2018).
Bansal, D. et al. Magnetically driven phonon instability enables the metal–insulator transition in h-FeS. Nat. Phys. 16, 669–675 (2020).
Gaffney, K. J. & Chapman, H. N. Imaging atomic structure and dynamics with ultrafast x-ray scattering. Science 316, 1444–1448 (2007).
Sciaini, G. & Miller, R. J. D. Femtosecond electron diffraction: heralding the era of atomically resolved dynamics. Rep. Prog. Phys. 74, 096101 (2011).
Hartmann, N. et al. Attosecond time–energy structure of x-ray free-electron laser pulses. Nat. Photonics 12, 215 (2018).
Emma, P. et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 4, 641–647 (2010).
Morimoto, Y. & Baum, P. Diffraction and microscopy with attosecond electron pulse trains. Nat. Phys. 14, 252–256 (2018).
Trigo, M. et al. Fourier-transform inelastic x-ray scattering from time-and momentum-dependent phonon–phonon correlations. Nat. Phys. 9, 790–794 (2013).
Clark, J. et al. Ultrafast three-dimensional imaging of lattice dynamics in individual gold nanocrystals. Science 341, 56–59 (2013).
Elsaesser, T. & Woerner, M. Perspective: structural dynamics in condensed matter mapped by femtosecond x-ray diffraction. J. Chem. Phys. 140, 020901 (2014).
Bredtmann, T., Ivanov, M. & Dixit, G. X-ray imaging of chemically active valence electrons during a pericyclic reaction. Nat. Commun. 5, 1–7 (2014).
Fritz, D. M. et al. Ultrafast bond softening in bismuth: mapping a solid’s interatomic potential with x-rays. Science 315, 633–636 (2007).
Siwick, B. J., Dwyer, J. R., Jordan, R. E. & Miller, R. J. D. An atomic-level view of melting using femtosecond electron diffraction. Science 302, 1382–1385 (2003).
Wall, S. et al. Atomistic picture of charge density wave formation at surfaces. Phys. Rev. Lett. 109, 186101 (2012).
Brown, S. B. et al. Direct imaging of ultrafast lattice dynamics. Sci. Adv. 5, eaau8044 (2019).
Flannigan, D. J. & Zewail, A. H. 4D electron microscopy: principles and applications. Acc. Chem. Res. 45, 1828–1839 (2012).
Cremons, D. R., Plemmons, D. A. & Flannigan, D. J. Femtosecond electron imaging of defect-modulated phonon dynamics. Nat. Commun. 7, 1–8 (2016).
Fu, X., Chen, B., Tang, J., Hassan, M. T. & Zewail, A. H. Imaging rotational dynamics of nanoparticles in liquid by 4d electron microscopy. Science 355, 494–498 (2017).
Pomerantz, I. et al. Ultrashort pulsed neutron source. Phys. Rev. Lett. 113, 184801 (2014).
Ehlers, G., Podlesnyak, A., Niedziela, J., Iverson, E. & Sokol, P. The new cold neutron chopper spectrometer at the spallation neutron source: design and performance. Rev. Sci. Instrum. 82, 085108 (2011).
Stone, M. et al. A comparison of four direct geometry time-of-flight spectrometers at the spallation neutron source. Rev. Sci. Instrum. 85, 045113 (2014).
Said, A. H. et al. High-energy-resolution inelastic X-ray scattering spectrometer at beamline 30-ID of the advanced photon source. J. Synchrotron Radiat. 27, 827–835 (2020).
Wall, S. et al. Ultrafast disordering of vanadium dimers in photoexcited VO2. Science 362, 572–576 (2018).
Cremons, D. R., Plemmons, D. A. & Flannigan, D. J. Defect-mediated phonon dynamics in TaS2 and WSe2. Struct. Dyn. 4, 044019 (2017).
Carles, R., Zwick, A., Renucci, M. & Renucci, J. A new experimental method for the determination of the one phonon density of states in GaAs. Solid State Commun. 41, 557–560 (1982).
Henighan, T. et al. Control of two-phonon correlations and the mechanism of high-wavevector phonon generation by ultrafast light pulses. Phys. Rev. B 94, 020302 (2016).
Stern, M. J. et al. Mapping momentum-dependent electron-phonon coupling and nonequilibrium phonon dynamics with ultrafast electron diffuse scattering. Phys. Rev. B 97, 165416 (2018).
Murphy-Armando, F. et al. Evolution of non-thermal phonon and electron populations in photo-excited germanium on picosecond timescales. Preprint at https://arxiv.org/abs/1911.12145 (2019).
Bao, F., Archibald, R., Bansal, D. & Delaire, O. Hierarchical optimization for neutron scattering problems. J. Comput. Phy. 315, 39–51 (2016).
Bao, F., Archibald, R., Niedziela, J., Bansal, D. & Delaire, O. Complex optimization for big computational and experimental neutron datasets. Nanotechnology 27, 484002 (2016).
Jackson, J. D. Classical Electrodynamics (John Wiley & Sons, 2007).
Abbamonte, P., Finkelstein, K. D., Collins, M. D. & Gruner, S. M. Imaging density disturbances in water with a 41.3-attosecond time resolution. Phys. Rev. Lett. 92, 237401 (2004).
Abbamonte, P. et al. Ultrafast imaging and the phase problem for inelastic x-ray scattering. Adv. Mater. 22, 1141–1147 (2010).
Carrete, J. et al. almabte: a solver of the space–time dependent Boltzmann transport equation for phonons in structured materials. Comp. Phys. Commun. 220, 351–362 (2017).
Dixit, G., Slowik, J. M. & Santra, R. Theory of time-resolved nonresonant x-ray scattering for imaging ultrafast coherent electron motion. Phys. Rev. A 89, 043409 (2014).
Dixit, G., Vendrell, O. & Santra, R. Imaging electronic quantum motion with light. Proc. Natl Acad. Sci. 109, 11636–11640 (2012).
Van Hove, L. Correlations in space and time and born approximation scattering in systems of interacting particles. Phys. Rev. 95, 249–262 (1954).
Abbamonte, P. et al. Dynamical reconstruction of the exciton in lif with inelastic x-ray scattering. Proc. Natl Acad. Sci. 105, 12159–12163 (2008).
Abbamonte, P., Reed, J. P., Joe, Y., Gan, Y. & Casa, D. Implicit spatial averaging in inversion of inelastic x-ray scattering data. Phys. Rev. B 80, 054302 (2009).
Krivanek, O. L. et al. Vibrational spectroscopy in the electron microscope. Nature 514, 209–212 (2014).
Venkatraman, K., Levin, B. D., March, K., Rez, P. & Crozier, P. A. Vibrational spectroscopy at atomic resolution with electron impact scattering. Nat. Phys. 15, 1237–1241 (2019).
Lin, J. Y. et al. MCViNE–an object oriented monte carlo neutron ray tracing simulation package. Nucl. Instrum. Methods Phys. Res. Sect. A 810, 86–99 (2016).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Acknowledgements
G.D. acknowledges fruitful discussion with Sucharita Giri. A.P.R. acknowledges the financial support from IRCC-IITB. D.B. thanks the financial support from MHRD-STARS under project no.: STARS/APR2019/PS/345/FS, and BRNS – DAE under project no.: 58/14/30/2019-BRNS/11117. G. D. acknowledges support from Science and Engineering Research Board (SERB) India (Project No. ECR/2017/001460) and the Ramanujan fellowship (SB/S2/ RJN-152/2015).
Author information
Authors and Affiliations
Contributions
D.B. and G.D. conceived the idea, designed the research, and supervised the work. N.R. and A.P.R. performed simulations. All authors discussed the results and contributed to the final manuscript. D.B. and G.D. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rana, N., Roy, A.P., Bansal, D. et al. Four-dimensional imaging of lattice dynamics using ab-initio simulation. npj Comput Mater 7, 7 (2021). https://doi.org/10.1038/s41524-020-00475-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00475-4