Introduction

Recent years have seen tremendous development in topological quantum materials (TQMs), including topological insulators (TIs) and semimetals with nontrivial band topology. However, there remain a few challenges to practical applications of TQMs. For example, the challenge in the development of TIs1,2,3,4,5, one of the most widely studied classes of topological materials, is to protect their key features against disorders or defects that may destroy their quantized conductance6,7. On the other hand, the discovery of Chern insulators8,9,10,11 with broken time-reversal symmetry is a challenge because of the incompatibility between ferromagnetism and electronic insulation. Topological semimetals (TSMs), defined using a local topological invariant, have become a hot spot in the family of topological materials because of their rich physical properties. One of the most important TSMs is the Weyl semimetal (WSM), whose band dispersion near the Weyl point can be described by the “Weyl equation.”12 Although nonmagnetic WSMs have been thoroughly studied in recent years13,14,15,16,17,18, magnetic WSMs (MWSMs) are still rare, despite their great potential as building blocks for next-generation ultra-fast topological spintronics.

MWSMs exhibit many exotic physical properties, such as quantized anomalous Hall effects19, large anomalous Hall conductivity (AHC)20,21,22, and domain wall physics23. Since the theoretical discovery of pyrochlore Y2Ir2O724, the first MWSM, several other potential MWSMs have been reported. They include HgCr2Se419, Heusler compounds25,26,27,28,29, Fe3Sn230, Sn2Nb2O731, spinel compounds32, and rare earth materials33. Recent experiments confirmed the predicted shandite structure of Co3Sn2S2 as an MWSM by directly observing its Fermi-arc and linear dispersion bulk bands34,35. Simultaneously, the magnetic Weyl fermion line was confirmed by directly observing the drumhead surface states in the room-temperature magnet Co2MnGa36. However, our understanding of their structural stabilities, microscopic physical mechanism of Weyl points, topological phase transition, and emergent properties of cobalt (Co)-based shandites and their alloys is still lacking.

In this article, we investigate the topological properties of Co3MM’X2 (M/M’ = Ge, Sn, Pb and X = S, Se, Te, denoted as Co-MM’-X for simplicity) compounds with high thermodynamic stabilities. Using a global structure search approach based on a particle swarm optimization (PSO) algorithm, we discovered that their structural stabilities as a shandite phase are well described by a structural tolerance factor—defined by the ratio between the atomic radii of the metal and the chalcogen atoms constituting a compound—below which the shandite structure becomes unstable. Shandite becomes a ground state for Co-Sn-S, Co-SnPb-S, Co-Pb-S, and Co-Pb-Se, metastable for Co-Sn-Se and Co-Ge-S, and unstable for Co-Ge-Se and Te-based systems. We determined that Co-SnPb-S alloys can be three-dimensional (3D) quantum anomalous Hall metals (QAHMs) or MWSMs, depending on the relative positions of the Sn and Pb atoms. The MWSM phase had an AHC of 1290 Ω−1 cm−1 near the Fermi level, even higher than that of Co3Sn2S2. We established a tight-binding (TB) model that reproduced the number and types of Weyl points for a Co-M-X system, analyzed by first-principles calculations. Our TB model explains that the formation of nodal lines originates from the interlayer coupling between Co atoms in different Kagome layers, and the number and types of Weyl points are mainly governed by the interaction between interlayer M’ and Co atoms.

Results

Crystal structures and magnetic ground states for Co-MM’-X

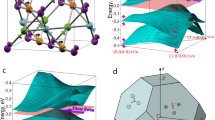
Figure 1a depicts the crystal structure of a shandite compound, Co-MM’-X, in which the cobalt atoms form a Kagome lattice. Figure 1b depicts the atomic configurations projected on the Kagome lattice. Metal atoms occupy both the in-plane sites of the Kagome lattice and the sites in between the Kagome lattice layers; metals on each site are labeled as M and M’. Figure 2a summarizes the stable and metastable crystal phases of Co-MM’-X (M/M’ = Ge, Sn, Pb and X = S, Se, Te) found by PSO37,38 based on first-principles density functional theory (DFT) calculations (see “Methods” section). The crystal structures are color coded and arranged by the energy hierarchy for a given composition, i.e., the one listed first is the most stable configuration. Here the frequency indicates the number of times the given crystal was identified, thus it relates the probability of discovering each structure. The energy differences (ΔE) between the shandites and the ground-state structures for the given compounds are listed in Fig. S1. The compounds Co-Sn-S, Co-Pb-S, Co-Pb-Se, and Co-SnPb-S have the shandite structure (the space group 166, red bar in Fig. 2a) as their most stable structure, whereas the shandite structure becomes unstable for Co-Ge-Se and Co-M-Te. For Co-Sn-Se, Co-Ge-S, Co-GeSn-S, and Co-GePb-S, other structures are the most stable ones, with energy differences of less than ~60 meV per formula compared with that of the shandite, showing that the shandite is metastable for those compounds. Note that moderately metastable materials, with energies above the ground state commensurate with the found metastability range (~70 meV/atom, varying by chemistry and composition), are also reasonable candidates for synthesis39.

Fig. 1: The crystal structure of Co-MM’-X and tight-binding parameters.
figure 1

a The crystal structure of shandite Co-MM’-X (the pink arrows represent the orientation of spin). b The Kagome plane embedded in the shandite structure (highlighted by the dotted gray line in a); t1 and t2 represent the NN and NNN hopping parameters between Co orbitals in the Kagome plane, respectively; and t3, t4, and t5 are the NN hopping parameters between the interlayer orbitals of Co atoms, between the orbitals of Co and M’, and between the orbitals of Co and X, respectively (see the main text for details). c The BZ for the shandite structure, where the dotted lines indicate the kb = kc mirror plane (M010 in real space) as well as the equivalent mirror planes owing to the C3z symmetry.

Full size image
Fig. 2: Stable configurations of Co-based compounds.
figure 2

a The low-energy structures for Co-based materials (Co-M-X or Co-MM’-X), where the crystal structures are color coded and arranged by the energy hierarchy for a given composition, i.e., the one listed first is the most stable configuration. The red bars represent the shandite structure (No. 166). The vertical axis represents the emergent frequency of different structures from the PSO simulation. We introduced a structure tolerance factor (s), s = r(M)/r(X) as a structure descriptor for shandite, where r(M) and r(X) indicate the radius of a metal and a chalcogen, respectively, and the average atomic radius of two metal atoms is taken as r(M) for metal alloys. The s values of each compound are listed. b The energy differences (ΔE) between the shandites and the ground-state structures and the energy difference between FM and nonmagnetic states (EFM − ENM) for the given compounds are plotted in terms of s in black and blue lines, respectively. If the shandite structure is the ground-state structure, ΔE and EFM − ENM calculate the energy difference to the second stable structure.

Full size image

We discovered that the ratio between the sizes of the metal atoms and the sizes of the chalcogens is related to the structural stability of a shandite; and we introduced a structure tolerance factor (s), s = r(M)/r(X) as a structure descriptor for shandite, where r(M) and r(X) indicate the radius of a metal and a chalcogen, respectively, and the average atomic radius of two metal atoms is taken as r(M) for metal alloys. As demonstrated in Fig. 2a, only the compounds with large s values (≥1.5) adopt shandite as a ground-state structure. The relationship between the tolerance factor s and the stability of the shandite structure is presented in Fig. 2b. We further analyzed the magnetic stabilities categorized in the ferromagnetic (FM), A-type anti-ferromagnetic (AFM), C-type AFM, and nonmagnetic states (see Fig. S2 of SI), and concluded that all the shandite structures maintain an FM ground state with the spin oriented along the z direction (the energy differences between different magnetic states are summarized in Table S1). Given the structural and magnetic stabilities, we propose Co-Pb-S and Co-SnPb-S as magnetic shandite compounds that may be synthesized by experiments. Interestingly, recently, the alloy system Co3Sn2-xInxS2 has been synthesized40,41 by the Bridgeman technique42 and was identified to maintain a large AHC (1500 ± 300 Ω−1 cm−1 at x = 0.15). Our calculations also confirmed the stability of Co-Sn-S, as it has already been synthesized and identified as an FM WSM43. In the following discussion, we mainly focus on the Co-MM’-S systems.

Weyl points in Co-M-S (M = Ge, Sn, Pb) systems

The shandite Co-Sn-S has nodal lines located at the kb = kc (kb and ka range from \(- \frac{\pi }{2}\) to \(\frac{\pi }{2}\)) mirror plane (M010 in real space) in the Brillouin zone (BZ)20,22,44 (see the planes highlighted in Fig. 1c; those three mirror planes are equivalent owing to the C3z rotation symmetry along the z direction). We first investigated the band structures of compounds Co-M-S (M = Ge, Sn, Pb) that have FM ground states with the easy axis perpendicular to the Kagome plane (z direction). The band structures without spin–orbit coupling (SOC) included confirmed that they are all nodal-line semimetals (see Fig. S3), with nodal lines (for spin-up subspace) formed in the kb = kc mirror plane (centered at the L point); and they split into Weyl points as SOC is introduced. Figure 3a, b show two-dimensional (2D) band structures with SOC in kb = kc mirror plane, where the Weyl points—crossing points between valence bands and conduction bands—are highlighted by the red dots. By plotting the inverses of energy gaps between the conduction and valence bands, we can clearly identify the existence of the Weyl points (Fig. 3c). On the kb = kc mirror plane, Co-Ge-S and Co-Sn-S each have a pair of Weyl points, while Co-Pb-S has three pairs. Note that the Weyl points in each pair are symmetric with respect to the inversion center (L point) in the BZ, thus they maintain opposite chirality. Figure 3d presents one-dimensional (1D) band structures, tangential to the nodal lines at Weyl points, that identify type-II Weyl points14 for Co-Ge-S and Co-Pb-S and type-I Weyl points for Co-Sn-S. Given the C3z symmetry of the system, there are three type pairs of type-II Weyl points in the BZ (another two pairs of Weyl points are located at the ka = kb and ka = kc mirror planes) for Co-Ge-S, nine type-II pairs for Co-Pb-S, and three type-I pairs for Co-Sn-S. Our results for Co-Sn-S are consistent with theory20,22,44 and experiments34,35 in the literature. The compound Co-Pb-S had two pairs of Weyl points so close that they almost formed short nodal lines; resolving those Weyl points might be an experimental challenge. We further explored the whole BZ in search of Weyl points located at general points and found additional Weyl points for Co-Pb-S. They were two nonequivalent type-I Weyl points, one located close to the Fermi level (~5 meV higher) and the other one at ~88 meV above the Fermi level. Considering C3z and mirror symmetries, there were 12 pairs of Weyl points located at general points in the BZ. The type, energy level, position, chirality (characterized by Berry curvature around each Weyl points, see Fig. S4), and the number of Weyl points for Co-M-S systems are summarized in Table S2.

Fig. 3: Energy bands and energy gaps for Co-M-S compounds.
figure 3

a 2D plots of conduction and valence bands in kb = kc mirror plane for Co-M-S systems. b Enlarged data points of the region highlighted by the yellow lines in a. c 2D maps of the inverse energy band gaps (1/gap) in the kb = kc mirror plane. If the gap is large, the value of 1/gap is small (white color). Nodal lines open up small bandgaps with SOC, resulting in the high-intensity blue lines in the 1/gap curve. The red points highlight the Weyl points (W) with “+” and “−” signs indicating their chiralities. d Energy plots along the lines tangential to the Weyl points highlighted in c, identifying the types of Weyl points. The top, middle, and bottom panels are data for Co-Ge-S, Co-Sn-S, and Co-Pb-S, respectively.

Full size image

3D quantum anomalous Hall phase and large AHC in Co-based alloy systems

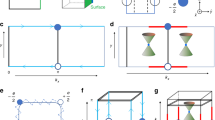
The shandite Co-MM’-S (M/M’ = Sn and Pb) has two distinctive configurations, depending on the occupation of Sn and Pb atoms at either at in-plane (M) or interlayer (M’) sites of the Kagome plane (see Fig. 1a). Both structures have shandite FM ground states (see Table S1 of SI), and the formation enthalpy of the Co-SnPb-S is lower than that of Co-PbSn-S by ~45 meV per formula unit. Interestingly, these two configurations display very distinctive topological properties: Co-SnPb-S belongs to the 3D quantum anomalous Hall phase45,46, whereas Co-PbSn-S is an MWSM with AHC (~1290 Ω−1 cm−1) higher than that of Co-Sn-S, as explained below in detail.

Figure 4a compares the band structures of Co-SnPb-S and Co-PbSn-S in the kb = kc mirror plane. Both systems are nodal-line semimetals if the SOC effects are not considered (see Fig. S3). In the case of Co-SnPb-S, the SOC induces gaps in the nodal line without creating any Weyl points, as indicated in the inverse-gap plot of the kb = kc mirror plane of Fig. 4b. The compound Co-SnPb-S with a finite local band gap becomes more stable than the metallic compound Co-PbSn-S. We further confirmed that no Weyl points existed at other general points by performing dense k-points calculations (401 × 401 × 401) employing the Wannier interpolation method (see “Methods” section).

Fig. 4: 2D band structures, inverse gaps, and anomalous Hall conductivity (AHC) of compounds Co-SnPb-S and Co-PbSn-S.
figure 4

a 2D plots for conduction and valence bands in kb = kc mirror plane for systems. Red dots highlight the Weyl points of Co-PbSn-S; there are no Weyl points for Co-SnPb-S. b The 3D plot for the inverse of the band gaps in the kb = kc mirror plane. Unlike the case of Co-PbSn-S showing Weyl points (W1 and W2), Co-SnPb-S presents energy gaps along the nodal line without leaving any Weyl points in the mirror plane. c AHC.

Full size image

In a stark contrast to the Co-SnPb-S with no Weyl points, Co-PbSn-S contained type-II Weyl points with SOC. There was a pair of type-II Weyl points (Fig. 4b, \(W_1^ -\) and \(W_1^ +\); see Fig. S5a for their types and energy levels) in the kb = kc mirror plane and another pair (\(W_2^ -\) and \(W_2^ +\)) located at the ka = kb = kc axis (i.e., the z axis in real space) in the BZ with opposite chirality (the specific coordinate of this pair of Weyl points can be seen in Table S2). Note that, near this pair of Weyl points, we found that a strict flat band pierces two bands (these conduction and valance bands cross each other, leading to the type-II Weyl point in the ka = kb = kc axis [Fig. 4b, \(W_2^ -\) and \(W_2^ +\)]) and formed another four critical-tilt Weyl points in the ka = kb = kc axis (Fig. S5b). The physical mechanism underlying the Weyl points formed from 3D flat band has been demonstrated before31. This kind of critical-tilt Weyl point may be a good candidate for investigating the strongly correlated Weyl physics. The calculated AHC for Co-PbSn-S was as high as 1290 Ω−1 cm−1, higher than that of Co-Sn-S. See the AHC of the Co-based systems in Fig. S6. A recent paper36 reports Co2MnGa that has a giant AHC (~1530 Ω−1 cm−1) at the energy ~50 meV below the Fermi level. The compound Co-PbSn-S had a peak in AHC closer to the Fermi level (~15 meV above the Fermi level) (Fig. 4c), which makes it a promising candidate for topological spin-transport devices.

On the other hand, Co-SnPb-S has another distinctive topological property—a 3D QAHM; its band structure can adiabatically evolve into a 3D quantum anomalous Hall insulator45 without any band crossing47,48. To confirm its nontrivial band topology, we followed the criteria proposed by Jin et al.45: (1) the first Chern number of a 2D cut with four time-reverse invariant momenta (TRIM) points is a non-zero integer, and (2) the product over the inversion eigenvalues of all occupied bands at eight TRIM points must be 1. We calculated the first Chern number for Co-SnPb-S in a time reversal invariant plane (ka = 0 plane with kb and kc ranging from \(- \frac{\pi }{2}\) to \(\frac{\pi }{2}\)) as 1 (\(C|_{k_a = 0} = 1\)); i.e., it is a 2D Chern insulator. Then we evaluated the parities for all the occupied bands at eight TRIM points (see Table S3), which also satisfied the second condition. Thus we conclude that Co-SnPb-S is a QAHM with an AHC of ~530 Ω−1 cm−1, much lower than that of Co-PbSn-S, perhaps because of the lack of Weyl points (Fig. 4b).

Discussion

TB model for the Co-based shandite structure

We analyzed the contribution of each atomic species to the emergence of nodal lines through band inversion between the conduction and valence bands. For all the compounds—Co-Sn-S, Co-SnPb-S, and Co-PbSn-S—the dxy and \(d_{z^2}\) orbitals of Co atoms were the main contributors to the formation of the nodal lines (small contribution from \(d_{yz},d_{xz},d_{x^2 - y^2}\)), with some contributions from the pz orbitals of metals located at the interlayer sites (See Fig. S7), negligible contributions from any metals located at the intralayer sites, and the S atoms for the band inversion. We tried to use dxy and \(d_{z^2}\) orbitals for each Co atom to construct the TB model. However, we find that it cannot reproduce the nodal line in the kb = kc mirror plane. We noted that the crystal field that surrounds the Co atom maintains a low symmetry. Thus the five d orbitals of a Co atom will split and each of them belongs to 1D irreducible representation, with orbital moments quenched (Leff = 0)49. When the onsite SOC is “turned on,” the total angular momentum equals to 1/2 (Jeff = 1/2). Hence, we try to use a pseudospin Jeff = 1/2 (J1/2) orbital50,51 on each Co atom to construct our TB model.

Our TB Hamiltonian included interactions between J1/2 orbitals on each Co atom, pz orbitals of interlayer metal atoms, and pz orbitals of S atom. For simplicity, we assumed an infinitely large exchange field and limited our discussion in the spin-majority subspace, which reduced to six orbitals in total in the unit cell. Our TB Hamiltonian reads

$${H} = {H}_{\mathrm {Co}}+{H}_{\mathrm {soc}}+{H}_{\mathrm {Rashba}}+{{H}_{\mathrm {Co-M}}+{H}_{\mathrm {Co-S}}+{H}_{\mathrm {onsite}}}.$$
(1)

The first term, HCo, describes the hopping interactions between the J1/2 orbitals of Co atoms:

$$H_{{\rm{Co}}} = \sum \limits_{ < ij > \alpha } t_1c_{i\alpha }^\dagger c_{j\alpha } + \sum \limits_{ \ll ij \gg \alpha } t_2c_{i\alpha }^\dagger c_{j\alpha } + \sum \limits_{ < ij > \alpha } t_3c_{i\alpha }^\dagger c_{j\alpha }{\mathrm{,}}$$
(2)

where \(c_{i\alpha }^\dagger\) and cjα represent creation and annihilation of an electron on the α (J1/2) orbital at i site and j site, respectively, t1 and t2 are the nearest neighbor (NN) and next nearest neighbor (NNN) hopping parameters between the orbitals in the Kagome plane (see Fig. 1), respectively, t3 is the NN hopping parameter between the interlayer orbitals (see Fig. 1), and <ij> and <<ij>> represent the NN and NNN sites for each, respectively. The effective SOC interaction between the Co atoms is incorporated in the second term, HSOC, as the interaction between J1/2 orbitals in the Kagome plane:

$$H_{{\rm{soc}}} = it_{{\rm{so}}}\sum\limits_{ < ij > \alpha } {v_{ij}} c_{i\alpha }^\dagger c_{j\alpha },$$
(3)

where tso is the effective SOC hopping strength between the NN J1/2 orbitals and the sign (vij = ±1) depends on the position of an intralayer M atom relative to the Co-Co bond52 (note that the NNN SOC interaction is negligible). In stark contrast to the hexagonal systems, such as silicene52, in which the effective NN SOC interaction vanishes and the next nonzero interaction term is from the NNN interactions, the effective NN SOC of the Co-based system interaction was preserved by the intralayer M atoms that formed a triangle sublattice embedded in the Kagome lattice of Co atoms.

The third term, HRashba, is the NN Rashba SOC term expressed as

$$H_{{\rm{Rashba}}} = it_{\rm{R}}\sum \limits_{ < ij > } {u_{ij}} c_{i\alpha }^\dagger (\vec \sigma \times \overrightarrow {d_{ij}^0} )^zc_{j\alpha },$$
(4)

where tR is an effective Rashba hopping strength between the NN J1/2 orbitals of Co atoms, \((\vec \sigma \times \overrightarrow {d_{ij}^0} )^z\) represents the z component of a vector product between the Pauli matrix and unit vector of Co-Co bond, \(d_{ij}^0\), and the sign of the term (uij = ±1) depends on the position of the interlayer M atom relative to the NN Co atoms. HCo–M is the interaction between the nearest Co and interlayer M atom orbitals, i.e., J1/2 and pz orbitals, respectively:

$${H}_{{\rm{Co-M}}} = \sum \limits_{ < ij > \alpha\beta} {t_{4}} c_{i\alpha }^\dagger c_{j\beta },$$
(5)

where a and β represent the J1/2 orbital of Co and the pz orbital of the M atom at the interlayer site, respectively, and t4 represents the hopping parameter between the nearest orbitals. The term, HCo–S, describes the interaction between Co and S atoms:

$${H}_{{\rm{Co-S}}} = \sum \limits_{ < ij > \alpha\gamma} {t_{5}} c_{i\alpha }^\dagger c_{j\gamma},$$
(6)

where γ is the pz orbital of the S atom and t5 represents the hopping parameter between the nearest orbitals. The term Honsite represents the onsite energies of pz orbitals of M and S atoms:

$$H_{{\rm{onsite}}} = \varepsilon _{\rm{M}}\sum\limits_i {c_{i\beta }^\dagger } c_{i\beta } + \varepsilon _{\rm{S}}\sum\limits_i {c_{i\gamma }^\dagger } c_{i\gamma },$$

where εM and εS are the onsite energies of the pz of M and pz of S atoms, respectively. Here we set the onsite energies of J1/2 of Co to be zero.

Next, we investigated the role of each term of the Hamiltonian in the emergence of nodal lines, as well as the formation of Weyl points. The first two terms of HCo in Eq. (2) describe the interactions between Co atoms in the Kagome lattice plane. We failed to capture nodal lines with those terms solely (see Fig. S8a), but with the addition of the interlayer interaction (the third term in Eq. (2)]), we were able to monitor the emergence of the nodal lines centered at the L point of BZ (Fig. S8), even without considering any additional terms from metal atoms. Interestingly, we found that the emergence of the nodal line is decided by the competition between t2 and t3 (t1 = −1.0 is fixed, see Fig. S9). Upon application of the NN SOC interaction between the Co atoms in the Kagome plane (Eq. (3)), the nodal line split into two pairs of Weyl points in the kb = kc mirror plane. Those Weyl points were robust against further application of the Rashba SOC (Eq. (4)). We found it interesting that the interaction between metals and Co atoms (Eq. (5)) resulted in the correct number of Weyl points, as well as their types, as identified by DFT (Fig. 5a, b): one pair for Co-Ge-S and Co-Sn-S, three pairs for Co-Pb-S, and their types (type-I and type-II). Finally, the last term in the Hamiltonian (Eq. (6)), the interaction between S and Co, slightly modified the shape of the nodal lines and the types of Weyl points in the mirror plane. In summary, the nearest interlayer coupling between J1/2 effective orbitals of Co atoms resulted in the emergence of the nodal lines, whereas the number of Weyl points and their types were mainly determined by the interaction between pz orbitals of M and J1/2 of Co. Additionally, the number of Weyl points and their types were sensitive to the onsite energy of pz orbitals (εM) of the M atoms. Figure 5c presents the phase diagram of a Co-based shandite structure in the parameter space of t4 and εM, where the number and type of Weyl points are those located on the ka = kb mirror plane. At the boundary between W-I and W-II regions, there is a phase transition from type-I to type-II, in which the band crossing is close to a critical tilt. Our DFT results revealed that Co-Sn-Se holds this kind of critical tilt band dispersion at this boundary (see Fig. S5c). These results indicate that our TB captured the essential physical mechanisms that governs the emergence of nodal lines as well as Weyl points in CoMS (M = Ge, Sn, Pb) systems. It is noted that, although our TB model does consider the role of intralayer metal site, we can describe the QAHM state which the alloy system Co-SnPb-S maintains. However, for Co-PbSn-S alloy, based on our TB model, with changing the parameters (t4 and εM), we did not find the pair of Weyl points that are located at the z axis (\(W_2^-\) and \(W_2^ +\), see Fig. 4b). We guess this may be attributed to two reasons. One is that Weyl points emerge occasionally with fine-tuned parameters. Hence, it is challengeable to find them if the allowed parameter space is small. The phase diagram (Fig. 5c) is calculated with fixing some parameters (t1 = −1, t2 = −0.4, t3 = 1.3, tso = −0.1, tRashba = −0.1, t5 = −1.0, and εS = −4.0), and only t4 and εM are allowed to change. These fix parameters may also limit the finding of the pair of Weyl point at the z axis. Another reason may be from the TB model itself. The Co-based WSMs have complex band structure whose bands are highly hybridized with each other. Nevertheless, our TB model is a simplified model without considering the role of intralayer metal site. For the alloy system Co-PbSn-S, the Pb and Sn atoms locate at the intralayer and interlayer site, respectively. Our model does not consider the interaction between Pb (intralayer) and other atoms. This simplification may also limit the finding of the pair of Weyl points (\(W_2^ -\) and \(W_2^ +\) in Fig. 4b) for Co-PbSn-S system.

Fig. 5: Weyl points and phase diagram.
figure 5

a A pair of Weyl points in the kb = kc mirror plane with parameters t1 = −1, t2 = −0.4, t3 = 1.3, tso = −0.1, tRashba = −0.1, t4 = −1.3, t5 = −0.85, and εM = −2.4. b Three pairs of Weyl points in the mirror plane with parameter t1 = −1, t2 = −0.4, t3 = 1.3, tso = −0.1, tRashba = −0.1, t4 = −1.8, t5 = −1.0, and εM = −1.0 (all units in eV). c The phase diagram in the t4 and εM parameter space with t1 = −1, t2 = −0.4, t3 = 1.3, tso = −0.1, tRashba = −0.1, t5 = −1.0, and εS = −4.0, where QAHM, W-I, and W-II stand for compounds with quantum anomalous Hall metal and type-I and type-II Weyl semimetals, respectively; and the numbers in parentheses indicate the number of Weyl points in the kb = kc mirror plane. Here all the units of the parameters are in eV.

Full size image

In summary, we systematically investigated the stability and electronic properties of shandite Co-based materials. For structural stability, we found a good “descriptor” (i.e., r[M]/r]X]) that can identify not only the stability of the shandite crystal structure but also the stability of the magnetic states. For electronic properties, we found that the behavior of Weyl points was strongly dependent on chemical composition. In particular, the WSM Co-PbSn-S exhibited a large AHC very close to the Fermi level and is a good candidate as a spintronic transport device. Finally, with an effective TB model, we revealed that the band inversion nodal line in the Co-based Kagome lattice was derived from the interlayer coupling between Co atoms and that the behavior of Weyl points was mainly determined by the interaction between Co atoms and the interlayer M atoms. Our work gives a clear physical picture of the origination of the Weyl fermion in the Co-based Kagome lattice and provides guidance for synthesizing the predicted stable TQMs.

Methods

DFT calculations

Electronic structures were determined by DFT calculations as implemented in the Vienna ab initio simulation package53. The projector augmented wave54,55 was used to treat the ion–electron interactions, and a generalized gradient approximation of the Perdew–Burke–Ernzerhof56 functional was applied to consider the exchange–correlation potential. The cutoff energy and k-mesh were 500 eV and 8 × 8 × 8, respectively. All the structures were optimized using a conjugate gradient approach with the atomic forces <0.01 eV/Å.

PSO simulations

Crystal structure predictions for each chemical composition were carried out by employing the PSO algorithm implemented in the software Crystal Structure Analysis by Particle Swarm Optimization38. For a single prediction, each generation consisted of 30 structures, and structural evolution proceeded to at least the tenth generation. For each generation, 60% of the structures were constructed through the PSO algorithm, and the remaining 40% were randomly produced to prevent premature convergence of structural prediction. During the structure search process, structural relaxations and total energy calculations were performed using first-principles calculations.

Anomalous Hall conductivity

First, for T3MM’X2, we use 3d orbitals of T, 5p orbitals of M(M’), and 3p orbitals of X to construct the TB Hamiltonian as implemented in the Wannier90 package57. Then, based on this TB Hamiltonian, we used the WannierTools58 to calculate the AHC for the T3MM’X2 system. The AHC can be obtained as the sum of Berry curvatures for the occupied bands59:

$$\sigma _{xy} = - \frac{{2\pi e^2}}{h}\int_{{\rm {BZ}}} {\frac{{d^3({\boldsymbol{k}})}}{{(2\pi )^3}}} \sum\limits_n {f_n} \left( {\boldsymbol{k}} \right){\Omega}_n^z\left( {\boldsymbol{k}} \right).$$
(7)

Here Ω is the Berry curvatures, n is the index of the occupied bands, and f is the Fermi–Dirac distribution function. We used a 150 × 150 × 150 k-points grid to calculate the value of AHC.

Effective TB model

The numerical TB model was implemented in the Pythtb60 package, which uses the orthogonal TB approach. The Bloch-like basis function can be constructed as follows:

$$\left| {\chi _i^{\boldsymbol{k}}} \right\rangle = \sum \limits _{\boldsymbol{R}} e^{i{\boldsymbol{k}} \cdot \left( {{\boldsymbol{R}} + {\boldsymbol{t}}_i} \right)}\left| {\phi _{{\boldsymbol{R}}i}} \right\rangle .$$
(8)

R and i are the site and orbital index, respectively, ti is the position of orbital i in the home unit cell, and ϕRi is the TB basis orbital in cell R and should satisfy the following condition:

$$\left\langle {\phi _{{\boldsymbol{Ri}}}{\mathrm{|}}\phi _{{\boldsymbol{Rj}}}} \right\rangle = \delta _{{\boldsymbol{RR}}\prime }\delta _{ij},$$
(9)

which is the so-called orthogonal TB approach. The eigenstates can be expanded as

$$\left| {\psi _{n{\boldsymbol{k}}}} \right\rangle = \sum \limits_i C_i^{n{\boldsymbol{k}}}\left| {\chi _i^{\boldsymbol{k}}} \right\rangle .$$
(10)

Then the Hamiltonian at k point can be written as

$$H_{ij}^{\boldsymbol{k}} = \left\langle {\chi _i^{\boldsymbol{k}}} |H| {\chi _j^{\boldsymbol{k}}} \right\rangle = \sum \limits_{\boldsymbol{R}} {e^{i{\boldsymbol{k}} \cdot \left( {{\boldsymbol{R}} + {\boldsymbol{t}}_j - {\boldsymbol{t}}_i} \right)}} H_{ij}({\boldsymbol{R}}).$$
(11)

Here the phase factor \(e^{i{\boldsymbol{k}} \cdot \left( {{\boldsymbol{R}} + {\boldsymbol{t}}_j - {\boldsymbol{t}}_i} \right)}\) is included, which is called convention I60. By solving the matrix equation

$$H_{k \cdot }C_{n{\boldsymbol{k}}} = E_{n{\boldsymbol{k}}}C_{n{\boldsymbol{k}}},$$
(12)

we can get the eigenvalue and eigenstate at each k point and thus get the whole bands in the BZ.