Abstract
Rechargeable batteries have a profound impact on our daily life so that it is urgent to capture the physical and chemical fundamentals affecting the operation and lifetime. The phase-field method is a powerful computational approach to describe and predict the evolution of mesoscale microstructures, which can help to understand the dynamic behavior of the material systems. In this review, we briefly introduce the theoretical framework of the phase-field model and its application in electrochemical systems, summarize the existing phase-field simulations in rechargeable batteries, and provide improvement, development, and problems to be considered of the future phase-field simulation in rechargeable batteries.
Similar content being viewed by others
Introduction
Due to the rapid consumption of non-renewable fossil fuels and aggravation of environment problems1, energy storage becomes a fundamental issue for the integration of renewable sources into electric power systems2,3. Therefore, energy storage plays an essential role in future energy sustainable development3,4. Breakthroughs in energy storage technology can make energy distribution and adjustment across time and space, which has revolutionary significance to the production and consumption of energy. During the past decades, the research of electrochemical energy storage has developed rapidly, especially in rechargeable batteries (RBs), has been carried out. Currently, RBs still have many problems, such as high cost and thermal safety problems; hence, it is necessary to improve the energy efficiency, life span, safety, and cost performance, which requires a combination of theory, experiment, and computation to accelerate the research and development of key materials.
To discover, develop, manufacture, and deploy advanced materials at least twice as fast as is possible today, at a fraction of the cost, the US Government announced the Materials Genome Initiative in June 20115. This initiative calls for significant advances in three research areas: computation platform (i.e., multiscale computational materials science), database platform (i.e., open-source cyber infrastructure for data management), and experiment platform (i.e., an integrated approach combining computation and experiments)6, aiming to develop more accurate and powerful Integrated Computational Materials Engineering tools to replace expensive and time-consuming experimental procedures. In general, there are three methods in materials science—theoretical, experimental, and computational researches. Computational research is neither as difficult as theoretical research nor as time-consuming and laborious as experimental research. Rapid progress of computer technology makes computational research become a significant means for investigating microstructure evolution of material systems. The phase-field model is a computational research model, which describes microstructure evolution of material systems based on thermodynamics. In this review, we mainly focus on application of the phase-field model in RBs, including both the existing simulation results and future development trend.
Theoretical framework of the phase-field model is discussed in ‘Basics of phase-field model’ section. Existing phase-field simulations and further development and problems for phase-field simulations of RBs are summarized and discussed in ‘Existing phase-field simulation results for RBs’ section. Concluding remarks and perspectives are given in ‘Concluding remarks and perspectives’ section.
Basics of phase-field model
In thermodynamics, a phase is defined as a spatial region with relatively uniform and stable structure, and a field is a function of space and time. Literally, the phase-field model is a computational model which describes microstructure evolution of material systems as a function of space and time. One feature of the phase-field model is the diffuse interface. Slovenian physicist Stefan proposed the sharp interface method around 1890 to deal with phase-boundary problems. The connective conditions between phases are essential for solving the sharp interface model, which further needs tracking of phase boundaries. However, morphology and motion of phase boundaries for practical problems may be rather complex, which brings tremendous difficulty for solving the sharp interface model. The diffuse interface model, i.e., phase-field model, introduces the phase-field variable to indicate the phase state of the system, which varies continuously across a phase boundary. Evolution of the phase-field variable directly reflects the phase transition process, and no phase-boundary tracking is needed, which reduces complexity of the problem enormously. The other feature of the phase-field method is convenience for dealing with applied fields. If the system involves the concentration, temperature, and applied electromagnetic field except phase transition, more phase-field variables are needed to describe these factors of the system. All the field variables introduced form a complete variable set for describing the system, whereby the free energy functional of the system can be constructed. Evolution equations of field variables are derived according to principles of local equilibrium7 and free energy minimization8, which are usually nonlinear partial differential equations. An applied field can be considered as a part contribution to the free energy functional and its effect on evolution of the system can be reflected through its effect on the free energy functional. Microstructure evolution of material systems can be extracted after solving the evolution equations numerically. It can be seen that the description way of phase-field for material systems is consistent with that of Maxwell’s theory for electromagnetic fields. In essence, the phase-field model is an application of thought of classical field theory in materials science.
Theoretical framework of phase-field model
In the phase-field model, the most basic field variables are phase-field variables \(\phi _\alpha\) \((\alpha = 1, \ldots ,n)\), which describe phase states of the system. Phase-field variables may have the different meanings in different phase-field models, but they are always regarded as non-conserved variables since phases can be produced or disappear. Their evolution obeys the Allen–Cahn equation9
In general, there is not only one component in the system; so concentration variables \(c_i\) \((i = 1, \ldots ,m)\) should be introduced to describe the system. If there is no chemical reaction, concentration variables are regarded as conserved variables. Their evolution obeys the Cahn–Hilliard equation10
In Eqs. (1) and (2), \(L_{\alpha \beta }\) is the interface mobility between phases \(\alpha\) and \(\beta\), \(M_{ij}\) is the atomic mobility between components \(i\) and \(j\), \(f\) is the free energy density, and \(\frac{{\delta f}}{{\delta \phi _\beta }} = \frac{{\partial f}}{{\partial \phi _\beta }} - \nabla \cdot \frac{{\partial f}}{{\partial \nabla \phi _\beta }}\) and \(\frac{{\delta f}}{{\delta c_j}} = \frac{{\partial f}}{{\partial c_j}} - \nabla \cdot \frac{{\partial f}}{{\partial \nabla c_j}}\) are the variational derivatives. Compared with common derivatives, variational derivatives include the contribution of field variable gradients.
For solving Eqs. (1) and (2), the total free energy of the system (including the chemical free energy, elastic energy, electric energy, etc.) should be expressed as a functional of the introduced field variables:
\(f^{\mathrm {elec}}\) and \(f^{\mathrm {elas}}\) can be calculated according to electrodynamics and elasticity theory, respectively. The chemical free energy density of a single phase \(f_\alpha ^{\mathrm {chem}}\) can be obtained from computational thermodynamics. However, \(f^{\mathrm {chem}}\) cannot be obtained directly from computational thermodynamics at present and it can be constructed reasonably through \(f_\alpha ^{\mathrm {chem}}\) as follows:
where \(W_{\alpha \beta }\) is the potential barrier, \(\varepsilon _\alpha\) and \(\kappa _i\) are the coefficients of additional energy from phase-field and concentration gradients, and \(h\left( {\phi _\alpha } \right) = \phi _\alpha ^3(6\phi _\alpha ^2 - 15\phi _\alpha + 10)\) is the weight function of phase \(\alpha\). The phenomenological parameters \(W_{\alpha \beta }\), \(\varepsilon _\alpha\), and \(L_{\alpha \beta }\) can be evaluated from the relations between them and some physical parameters. It should be pointed that \(M_{ij}\) and \(\kappa _i\) are not phenomenological parameters of the phase-field model, and they can be determined by thermodynamic and diffusion kinetic databases. Equation (4) has very explicit physical meaning: the chemical free energy density includes the homogeneous part (the former two terms, which are only relevant to field variables) and inhomogeneous part (the latter two terms, which are relevant to field variable gradients). The homogeneous part includes the weighted average of all individual phases (first term of right side) and interface potential barrier (second term of right side), and the inhomogeneous part includes the contributions from phase-field gradients (third term of right side) and concentration gradients (fourth term of right side).
Electrochemical phase-field model
Application of the phase-field model in electrochemical systems involves electric field and sometimes involves elasticity. The electric potential \(\Phi\) and stain tensor ε are (possibly) introduced to describe the electrochemical system. \(f^{\mathrm {elec}}\) and \(f^{\mathrm {elas}}\) can be expressed as follows:
where \(\rho ^{\mathrm {elec}}\) is the charge density, \(F_0\) is the Faraday constant, \(z_i\) is the valence of components \(i\), \(V_{{\mathrm{mol}}}\) is the molar volume of the system, εα and \({\boldsymbol{\varepsilon }}_\alpha ^0\) are the total and eigen stain tensors of phase \(\alpha\), and \({\boldsymbol{C}}_\alpha\) is the stiffness tensor of phase \(\alpha\). Strictly speaking, elasticity in electrochemistry is usually a kinetic problem. The relaxation process is very quick compared with diffusion and phase transition, so for simplicity, elasticity is treated as an equilibrium problem and it is generally assumed that the stresses or strains of two phases are equal in the interface. The former, known as Reuss limit11,12, is applicable to the case that at least one solid phase is soft; the latter, known as Voigt limit12,13, is applicable to the case that two solid phases are both hard.
The equations of electric potential and stain are as follows:
where \(\sigma ^{\mathrm {elec}}\) is the conductivity of the electrochemical system. Equations (1) and (2) must be modified for the electrochemical system because of existence of chemical reactions, i.e., the source term \(n_{i,\alpha }\) (produced moles of component \(i\) in phase \(\alpha\) per unit volume and time) should be taken into account. The modified phase-field and concentration equations can be expressed as
The source term \(n_{i,\alpha }\) may be taken as different expressions in different papers, but it is generally a function of the current density, phase-field, and concentration. The current density is given by the famous Butler–Volmer equation
where \(j_0\) is the exchange current density in equilibrium, \(R\) is the gas constant, \(a\) is the coefficient of activation energy in oxidation reaction, and \(\eta = \frac{1}{{zF_0V_{{\mathrm{mol}}}}}\mathop {\sum }\limits_i \frac{{\delta f}}{{\delta c_i}}\) is the overpotential. Equations (7)–(10) constitute basic kinetic equations, which describes microstructure evolution of electrochemical systems.
Existing phase-field simulation results for RBs
Ionic diffusion
Experiments and calculations showed that the diffusion of Li in FePO4 crystal has strong anisotropic and LixFePO4 has a strong tendency to separate the solid phase of Li-rich and Li-poor14,15,16. However, in 2011, Bai et al.17 challenged the idea. Their work demonstrated that phase separation is dynamically inhibited when the battery is operating at larger current, because the reaction limitation in nanoparticles eliminate the thermodynamic driving force. Bazant and colleagues18 further investigated the coherent non-equilibrium subsurface phase morphologies in LixFePO4 nanoparticles in 2018 and the results showed that the anisotropy of the interface plays an important role in determining the morphology of the subsurface phase. Recently, Fleck et al.19 developed a continuum phase-field model considering anisotropic (orthorhombic) and inhomogeneous elastic effects to simulate the diffusion-limited phase transformation during Li intercalation in LiFePO4 nanoparticles. Hong et al.20 proposed a hybrid mode of phase transformation to explain the phase-growth morphology and kinetics. The results showed that the surface reaction and Li diffusion in different crystallographic directions control the phase-boundary migration20. In addition, many researchers have further studied the relationship between Li diffusion and phase transition in LiFePO416,21,22, phase stability in LiFePO4 nanoparticles23,24,25, and response performance of the LiFePO4 cathode26. For example, Chueh et al.27 explored the influence of surface diffusion on LixFePO4 phase transition. Their results showed that the LixFePO4 is a three-dimensional Li-ions conductor with three plane migration paths: bulk diffusion, surface diffusion and electrolyte diffusion28.
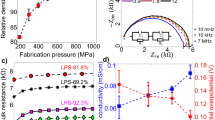
Solid-state batteries are promising candidates increase the safety and long-term circulation capacity29. In 2017, Chen et al30. developed a multiscale model which integrates the DFT calculation and phase-field simulation. The effective ion conductivity of β-Li3PS4 electrolyte was predicted via the phase-field simulation (Fig. 1). In 2019, Gamon et al.31 studied Li-Al-O-S series compounds via the combining the experiment and phase-field simulation. They discovered a sulfide Li3AlS3, which expands the possibility for exploring new interesting structures via phase-field simulations31. In 2020, combining the DFT calculation and phase-field simulation, Shen et al.32 revealed the role of grain boundary in ionic conduction of solid electrolyte.
a Process of predicting effective ion conductivity, b atom displacements of the optimized surface structure, c distribution of the phase variable on the solid electrolyte surface, d effective ion conductivity of β-Li3PS4, reproduced with permission from ref. 30. Copyright American Chemical Society, 2017.
Stress evolution and fracture
Previous stress-studying phase-field models in the anode usually treated the lithiation stress as a diffusion-induced stress, i.e., Li diffusion in electrodes makes the composition deviates from its stoichiometric state33,34,35,36,37,38. If Li distribution is non-uniform, deviation from stoichiometry usually results in a volume change and generates stress39,40,41. Prussin42 dealt with diffusion-induced stress by analogy with thermal stress. In 2005, Garcia et al.43 first studied the stress due to Li-ion intercalation and they split the total strain into elastic strain and inelastic strain. At the same time, Christensen and Newman44,45 considered the mechanical stress and fracture during Li-ion intercalation.
Si is a promising next-generation anode material for Li-ion batteries because of the low cost and high theoretical capacity. Lithiation and delithiation in the Si anode result in elastic and plastic deformation46. Chen et al.37 proposed a phase-field model coupled with large elastic-plastic deformation to investigate the phase evolution, morphology, and stress mitigation inside the crystalline Si electrode during Li intercalation. Zhao et al.35,47 and Bower et al.33 formulated computational frameworks to model diffusion-induced plastic deformation. Walk et al.48 combined the Cahn–Hilliard equation with small and large deformations, respectively, to analyze the stress evolution. Gao and Hong49 further developed a phase-field model, which considered both volumetric and deviatoric inelastic deformation as direct results of the lithiation at the reaction front. Harris et al.50 studied Li ion transport and Li elastoplasticity at electrode-electrolyte interfaces, and the results showed that contact elastic-plasticity depends on the ratio of Li yield strength to composite roughness50,51,52. To reduce the volume change of the Si anode during charging–discharging process, nano-silicon anode materials are mostly used in experiments. In 2014, Yang et al.53 proposed a chemo-mechanical model to study the deformation of Si nanowire (NW) during lithiation. In 2015, Xie et al.54 developed a phase-field model to study the structure deformation and stress evolution of Si NW during lithiation. There are large local stresses and stress gradients at the initial lithiation process, indicating that NW structure may generate damage and fracture54. Moreover, several models and studies have been reported on the electrochemical and mechanical responses of the amorphous Si electrode during the Li-intercalation process55,56,57,58.
Stress generated by diffusion via expansion and shrinkage in intercalation and deintercalation of metal cations causes micro-cracks, which leads to fracture with large deformation39,59. The mechanism of the crack propagation in electrode during charging–discharging process is critical to understand structure stability of the battery electrode59. In 2009, Hakim and Karma60 developed a phase-field model to capture initiation of crack and instability of fast cracks, etc.61. Bhandakkar et al.62,63 established a cohesion model of crack nucleation to explore the critical characteristic dimension for the crack propagation. Woodford et al.64, Zhu et al.65, Gao and Zhou66, and Klinsmann et al.67 studied the effects of diffusion-induced stress, lithiation-induced softening, realistic electrochemical loading conditions, and inertia on the Li fracture with improved phase-field models, respectively. Zhao et al.47,68 and Zuo and Zhao59 developed phase-field models to investigate the initial conditions of cracks in Si particles and crack propagation process. Huttin et al.69 and Liang and Chen70 studied the stress generation and crack evolution of LixMn2O4 and LiFePO4 particles, respectively. Recently, Miehe et al.71 and Stein et al.72 conducted a comprehensive study on the effect of chemical reaction on fracture surfaces (Fig. 2). The state of charge is the ratio of amounts of Li ions inside the particle at current state and those at full lithiation state72.
a Initial state, b phase segregation, c phase interface and crack tip movement, d crack tip begins to branch, e phase interface moves towards center, f final state, reproduced with permission from ref. 72. Copyright Elsevier, 2016.
Electrodeposition and dendrite growth
In Li-ion batteries, the formation of Li dendrite during charging processes is one of the main obstacles in their widespread application, which will result in decrease of reversible capacity and an internal short circuit28,73. Upon Li deposition, the surface of the electrode particles usually cracks due to volumetric expansion, and new Li is exposed for further reactions74,75. Li dissolution in discharging processes creates pits and crevices with low impedance, and Li-ion flow at the defects leads to rapid growth of metal filaments and dendrites76,77. Therefore, understanding the physical mechanisms of this complex non-equilibrium process is essential to improve performance of Li-ion batteries. In 2003, Monroe and Newman78 first established an electrochemical model for dendrite growth, which is aimed at evolution of dendrite tip height and growth velocity in Li-polymer batteries. The next year, Guyer et al.79,80 developed a 1D phase-field model to investigate the charge separation on the interface and kinetic behavior of electrodeposition process. Later, Shibuta et al.81 coupled the Cahn–Hilliard equation with the Butler–Volmer equation to simulate the 2D electrodeposition. Ely et al.82,83 developed a phase-field model to describe growth kinetics of Li deposits. However, all these models assume a linear kinetics, which are not applicable for systems far from equilibrium. Liang and Chen70,84 presented a nonlinear phase-field model, which takes the Butler–Volmer reaction kinetics into account, which can simulate and predict the Li deposit growth during charging processes without considering the SEI layer effect. Enrique et al.85 generalized DeWitt’s model to study the morphological evolution of Li-metal electrode during electrodeposition86. In 2015, Chen et al.87 established a consistent thermodynamic phase-field model to investigate the dendritic patterns, as shown in Fig. 3.
Evolution of a order parameter, b Li+ concentration, c electric potential, reproduced with permission from ref. 87. Copyright Elsevier, 2015.
A plenty of works have been done to research the influence factors of Li dendrite growth. Jana et al.83 presented a phase-field model to assess the effect of current density on lithium dendrite growth. Yurkiv et al.88,89 studied the influence of the stress and the SEI on Li electrodeposition, and reproduced filament structure of Li observed in experiments. Harris et al.90 studied the effect of external pressure on the dendrite growth in lithium metal batteries. Their results showed that if there is sufficient local stress, Li avoids plating at the tips of growing Li dendrite. Hong et al.91 developed a grand potential-based phase-field model, which reveals the fundamental physical insights related to the intimate, dynamic competition between dendrite growth, ion transport, and electrochemical reactions. Liu et al.92 discovered that the shape of SEI can limit the dendrite morphology, e.g., denser SEI lead to slower dendrite growth. Recently, Zhang et al.93 described the Li dendrites growth with various conductive structures by using phase-field model. Xu et al.94 first studied the adhesion effect of lithium dendrites between the interface layer and lithium metal and they found that enhanced adhesion energy can help inhibit the growth of Li dendrite. Chen et al.95 investigated the thermal effect on the Li dendrites growth. Hong et al.96 further revealed that the temperature-dependent performance of batteries is related to the reaction barrier and ionic diffusion barrier.
Besides, Zn is regarded as a promising anode material due to high theoretical capacity, non-toxicity, and abundant sources. The main problems are corrosion and dendrite growth. Cogswell97 developed a phase-field model based on Marcus kinetics for concentrated solutions to simulate dendritic growth of Zn. In 2015, Wang et al.98 studied the influence of overpotential, surface energy anisotropy, electric field and ion concentration on the dendrite growth and morphology. In 2019, Wang et al.99 studied the influence of overpotential, interface energy anisotropy, ion diffusion rate, electrolyte concentration, and electrolyte conductivity on the morphology of Zn electrodeposition. Very recently, Yurkiv et al.100 investigated ion concentration, electrostatic potential, stress strain, and dendritic morphology of zinc electrodeposition. Hong et al.101 studied the electrodeposition of Zn and designed a hybrid aqueous ZnSO4/solid polymer composite electrolyte to delay the dendrite growth.
Further development and problems to be considered
Improvement and development
To our understanding, there are two kinds of electrochemical simulation. One is describing a kinetic phenomenon in electrochemistry, which needs a reasonable free energy functional. The other is a kinetic process of a practical electrochemical system, which needs the realistic thermodynamic database to provide free energy functional of the system. Most existing phase-field simulations of batteries materials belong to the former where their electrolyte solutions are treated as ideal solution. Obviously, such simulations cannot reflect individuality of the investigated systems. Therefore, for phase-field simulations of RBs, future improvement should focus on coupling thermodynamic databases of the electrode and electrolyte to investigate individuality of the systems and its difference with a similar battery system. In thermodynamics, the free energy of single phases is constructed by molar fractions. For multiphase systems, the forgoing molar fractions mean phase molar fractions, which are referred to phase concentrations. However, the diffusion kinetics only provides the evolution equation of total concentrations. Consequently, there are two ways to connect thermodynamic databases and phase-field simulations: (1) using total concentrations to describe evolution of components and decomposing them into phase concentrations by a certain rule, and (2) constructing the evolution equation of phase concentrations. The former is represented by KKS model102, wherein the principle of equal chemical potential is used to decompose total concentrations. However, this principle is only applicable for equilibrium and weak non-equilibrium states, but not applicable for strong non-equilibrium states. A system may undergo a strong non-equilibrium initially and a weak non-equilibrium finally. It is quite difficult to find a universally valid way to decompose total concentrations, so constructing phase-concentration equations are more advisable to connect thermodynamic databases and phase-field simulations. In 2012, Steinbach et al.103,104 proposed a phase-field model which directly gives the phase-concentration equations, but their equations cannot degenerate into Fick’s diffusion equation from the interface to the bulk. More rigorous phase-concentration equations are needed in the phase-field model for its universal applicability and convenient linkage with realistic thermodynamic databases.
The deposition reaction in charging process generally involves two phases (electrode and electrolyte). However, the intercalation reaction in discharging process may produce several new phases, i.e., three or more phases may be involved in the intercalation reaction. Presently, most phase-field models are rather successful in dealing with two-phase systems, but may be problematic when extended to multiphase systems (three phases and above). Nonrigorous mathematical treatment will be needed or nonphysical simulation results will appear; therefore, for phase-field simulations of RBs, further development is needed to build a highly rigorous and self-consistent phase-field model for multicomponent multiphase systems to describe, compare, analyze, predict, improve, and control properties of battery materials in the intercalation reaction. The expected phase-field model for multicomponent multiphase systems should have following properties: (1) all evolution equations are continuous in space and time, and the phase-concentration equations should naturally degenerates into Fick’s diffusion equations from the interface to the bulk; (2) the evolution equations of field variables directly reflect their constraint conditions and the same simulation result must be provided for different choice of independent variables; (3) the evolution equations of field variables can guarantee them in the proper range automatically, and truncation can be avoided in numerical simulations, except for the numerical errors; (4) field variables should be calculated strictly according to the evolution equation and free energy functional and non-logical mathematical skills must be removed from numerical simulations; and (5) it can be built into a sustainable open-source phase-field simulation community.
Problems to be considered
Intercalation of Li into the electrode leads to plastic deformation, which is related to the intercalation rate and viscoelastic behavior of the electrode, which is obviously different from the plastic deformation under external force. Subsequent phase-field simulations need to consider the quantitative relation between the above two factors and plastic deformation. The elasticity tensor is relevant to Li-ion concentration. At present, the function of elasticity tensor with respect to Li-ion concentration is assumed to be linear. However, this assumption is comparatively rough and a reasonable model is needed to reflect their actual relation in subsequent simulations involving stress. The plastic deformation resulting from cracks in the electrode will expose new surface of the electrode, where the electrochemical reaction and Li nucleation occur. Accordingly, the effect of plastic deformation on Li nucleation should be included in further simulations involving stress. The battery electrode is generally made of many grains mixed by adhesive. The shape of grains affects the Li-ion transport and stress distribution in the electrode105,106. This resulting stress sequentially affects the chemical potential, intercalation potential, deposition potential, and battery capacity. The grain-shape effect of the electrode should be considered in future simulations involving stress.
With the recent developments in solid-state electrolyte, the conductivity of the solid-state electrolyte at room temperature can be comparable or even larger than that of the liquid electrolyte. However, only few studies have been carried out to analyze the Li dendrite growth within solid electrolyte and liquid crystalline electrolyte. The nucleation and dendrite growth mechanism for solid and liquid crystalline electrolytes should be further studied. Based on the experimental studies about aqueous hybrid electrolyte battery in recent years, it has been found that hybrid ions can inhibit the dendrite growth107,108. However, the inhibition mechanism of dendrite growth in hybrid electrolyte is still unknown and needs deep investigations. Compared with ionic deposition in liquid electrolyte batteries, that in solid electrolyte batteries109 depends on not only the current density, temperature, and electrolyte but also elasticity tensor of solid electrolyte, viscoplastic behavior of the electrode, and coating stress. These factors need to be considered in subsequent simulations110.
Concluding remarks and perspectives
To our understanding, phase-field simulations can be classified into three levels. The first level describes microstructure evolution of materials, and compares microstructure evolution of similar materials to ascertain a material with better properties, which is a mixture of qualitative, semi-quantitative, and quantitative investigations. The second level analyzes the link between microstructure and performance, and predicts performance evolution of the system according to its simulation results, which is a mixture of semi-quantitative and quantitative investigations. The third level improves performance of the system based on its influence factors and controls its better service performance by adjusting its physical environment, which is a quantitative investigation. At present, phase-field simulations in RBs belong to the first two levels; specifically, most simulations are still in the first level. Progress of phase-field simulations for RBs toward quantification needs accurate thermodynamic and kinetic databases of the system. However, an RB is such a complicated system that many mechanical, chemical, thermal, and electric changes are involved in its charging or discharging processes. Therefore, the further phase-field model needs to combine DFT and MD to be developed into a multiscale model, whereby adjustable parameters can be eliminated and all parameters in the simulations can be obtained in terms of theoretical calculations or experimental measurements. After all, validity and rationality of the phase-field method, to a large extent, relies on physical, chemical, and mechanical parameters, and accurate thermodynamic and kinetic databases of the system.
References
Desilvestro, J. & Haas, O. Metal oxide cathode materials for electrochemical energy storage: a review. J. Electrochem. Soc. 137, 5C–22C (1990).
Gogotsi, Y. & Simon, P. True performance metrics in electrochemical energy storage. Science 334, 917–918 (2011).
Pires, V. F., Romero-Cadaval, E., Vinnikov, D., Roasto, I. & Martins, J. F. Energy storage therefore has a fundamental role to play in integrating future sustainable energy supplies with technical services and products. Energy Convers. Manag. 86, 453–475 (2014).
Pires, V. F., Romero-Cadaval, E., Vinnikov, D., Roasto, I. & Martins, J. F. Power converter interfaces for electrochemical energy storage systems–a review. Energy Convers. Manag. 86, 453–475 (2014).
National Science and Technology Council (US). Materials Genome Initiative for Global Competitiveness (National Science and Technology Council, 2011).
Chen, L.-Q. Phase-field method and Materials Genome Initiative (MGI). Chin. Sci. Bull. 59, 1641–1645 (2014).
De Groot, S. R. & Mazur, P. Non-equilibrium Thermodynamics (Courier Corporation, 2013).
Steinbach, I. et al. A phase field concept for multiphase systems. Phys. D 94, 135–147 (1996).
Cahn, J. W. On spinodal decomposition. Acta Metall. 9, 795–801 (1961).
Allen, S. M. & Cahn, J. W. Ground state structures in ordered binary alloys with second neighbor interactions. Acta Metall. 20, 423–433 (1972).
Reuss, A. Berechnung der Fliessgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z‐J. Appl. Math. Mech. 9, 49–58 (1929).
Hill, R. Elastic properties of reinforced solids: some theoretical principles. J. Mech. Phys. Solids 11, 357–372 (1963).
Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. 274, 573–587 (1889).
Cogswell, D. A. & Bazant, M. Z. Coherency strain and the kinetics of phase separation in LiFePO4 nanoparticles. ACS Nano 6, 2215–2225 (2012).
Singh, G. K., Ceder, G. & Bazant, M. Z. Intercalation dynamics in rechargeable battery materials: general theory and phase-transformation waves in LiFePO4. Electrochim. Acta 53, 7599–7613 (2008).
Bazant, M. Z. Theory of Chemical Kinetics and Charge Transfer based on Nonequilibrium Thermodynamics. Acc. Chem. Res. 46, 1144–1160 (2013).
Bai, P., Cogswell, D. A. & Bazant, M. Z. Suppression of phase separation in LiFePO4 nanoparticles during battery discharge. Nano Lett. 11, 4890–4896 (2011).
Nadkarni, N. et al. Interplay of phase boundary anisotropy and electro-auto-catalytic surface reactions on the lithium intercalation dynamics in LixFePO4 plateletlike nanoparticles. Phys. Rev. Mater. 2, 085406 (2018).
Fleck, M., Federmann, H. & Pogorelov, E. Phase-field modeling of Li-insertion kinetics in single LiFePO4-nano-particles for rechargeable Li-ion battery application. Comput. Mater. Sci. 153, 288–296 (2018).
Hong, L. et al. Two-dimensional lithium diffusion behavior and probable hybrid phase transformation kinetics in olivine lithium iron phosphate. Nat. Commun. 8, 1194 (2017).
Balakrishna, A. R., Chiang, Y.-M. & Carter, W. C. Li-diffusion accelerates grain growth in intercalation electrodes a phase-field study-annotated. Preprint at arXiv:1806.06890 (2018).
Heo, T. W., Chen, L.-Q. & Wood, B. C. Phase-field modeling of diffusional phase behaviors of solid surfaces: a case study of phase-separating LixFePO4 electrode particles. Comput. Mater. Sci. 108, 323–332 (2015).
Burch, D. & Bazant, M. Z. Size-dependent spinodal and miscibility gaps for intercalation in nanoparticles. Nano Lett. 9, 3795–3800 (2009).
Tang, M. et al. Model for the particle size, overpotential, and strain dependence of phase transition pathways in storage electrodes: application to nanoscale olivines. Chem. Mater. 21, 1557–1571 (2009).
Cogswell, D. A. & Bazant, M. Z. Size-dependent phase morphologies in LiFePO4 battery particles. Electrochem. Commun. 95, 33–37 (2018).
Majdabadi, M. M., Farhad, S., Farkhonde, M., Fraser, R. A. & Fowler, M. Simplified electrochemical multi-particle model for LiFePO4 cathodes in lithium-ion batteries. J. Power Sources 275, 633–643 (2015).
Li, Y. et al. Fluid-enhanced surface diffusion controls intraparticle phase transformations. Nat. Mater. 17, 915–922 (2018).
Li, Y., Hu, S., Sun, X. & Stan, M. A review: applications of the phase field method in predicting microstructure and property evolution of irradiated nuclear materials. npj Comput. Mater. 3, 16 (2017).
Leube, B. T. et al. Lithium transport in Li4.4M0.4M'0.6S4 (M = Al3+, Ga3+, and M′ = Ge4+, Sn4+): combined crystallographic, conductivity, solid state NMR, and computational studies. Chem. Mater. 30, 7183–7200 (2018).
Hu, J.-M. et al. Phase-field based multiscale modeling of heterogeneous solid electrolytes: applications to nanoporous Li3PS4. ACS Appl. Mater. Inter. 9, 33341–33350 (2017).
Gamon, J. et al. Computationally guided discovery of the sulfide Li3AlS3 in the Li-Al-S phase field: structure and lithium conductivity. Chem. Mater. 31, 9699–9714 (2019).
Shen, K. et al. Revealing the effect of grain boundary segregation on Li ion transport in polycrystalline anti-perovskite Li3ClO: a phase field study. Phys. Chem. Chem. Phys. 22, 3030–3036 (2020).
Bower, A. F., Guduru, P. R. & Sethuraman, V. A. A finite strain model of stress, diffsion, plastic flow and electrochemical reactions in a lithium-ion half-cell. J. Mech. Phys. Solids 59, 804–828 (2011).
Haftbaradaran, H., Song, J., Curtin, W. A. & Gao, H. Continuum and atomistic models of strongly coupled diffusion, stress, and solute concentration. J. Power Sources 196, 361–370 (2011).
Zhao, K., Pharr, M., Vlassak, J. J. & Suo, Z. Inelastic hosts as electrodes for high- capacity lithium-ion batteries. J. Appl. Phys. 109, 016110 (2011).
Yao, Y. et al. Interconnected silicon hollow nanospheres for lithium-ion battery anodes with long cycle life. Nano Lett. 11, 2949–2954 (2011).
Chen, L. et al. A phase-field model coupled with large elasto-plastic deformation: application to lithiated Silicon electrodes. J. Electrochem. Soc. 161, F3164–F3172 (2014).
Wang, X. et al. A phase-field model integrating reaction-diffusion kinetics and elasto-plastic deformation with application to lithiated selenium-doped germanium electrodes. Int. J. Mech. Sci. 144, 158–171 (2018).
Zhang, X.-y, Hao, F., Chen, H.-s & Fang, D.-n Diffusion-induced stress and delamination of layered electrode plates with composition-gradient. Mech. Mater. 91, 351–362 (2015).
Lim, C., Yan, B., Yin, L. & Zhu, L. Simulation of diffusion-induced stress using reconstructed electrodes particle structures generated by micro/nano-CT. Electrochim. Acta 75, 279–287 (2012).
Zhuang, Y. et al. Understanding the Li diffusion mechanism and positive effect of current collector volume expansion in anode free batteries. Chin. Phys. B 29, 068202 (2020).
Prussin, S. Generation and distribution of dislocations by solute diffusion. J. Appl. Phys. 32, 1876 (1961).
Garcı́a, R. E., Chiang, Y.-M., Carter, W. C., Limthongkul, P. & Bishop, C. M. Microstructural modeling and design of rechargeable lithium-ion batteries. J. Electrochem. Soc. 152, A255 (2005).
Christensen, J. & Newman, J. Stress generation and fracture in lithium insertion materials. J. Solid State Electrochem. 10, 293–319 (2006).
Christensen, J. & Newman, J. A mathematical model of stress generation and fracture in lithium manganese oxide. J. Electrochem. Soc. 153, A1019–A1030 (2006).
Anand, L. A Cahn–Hilliard-type theory for species diffusion coupled with large elastic–plastic deformations. J. Mech. Phys. Solids 60, 1983–2002 (2012).
Zhao, K., Pharr, M., Cai, S., Vlassak, J. J. & Suo, Z. Large plastic deformation in high-capacity Lithium-ion batteries caused by charge and discharge. J. Am. Ceram. Soc. 94, S226–S235 (2011).
Walk, A.-C., Huttin, M. & Kamlah, M. Comparison of a phase-field model for intercalation induced stresses in electrode particles of lithium ion batteries for small and finite deformation theory. Eur. J. Mech. A Solids 48, 74–82 (2014).
Gao, F. & Hong, W. Phase-field model for the two-phase lithiation of silicon. J. Mech. Phys. Solids 94, 18–32 (2016).
Harris, S. J. & Lu, P. Effects of inhomogeneities-nanoscale to mesoscale-on the durability of Li-ion batteries. J. Phys. Chem. C 117, 6481–6492 (2013).
Zhang, X., Wang, Q. J., Harrison, K. L., Roberts, S. A. & Harris, S. J. Pressure-driven interface evolution in solid-state lithium metal batteries. Cell Rep. Phys. Sci. 1, 100012 (2020).
Forster, J. D., Harris, S. J. & Urban, J. J. Mapping Li+ concentration and transport via in situ confocal Raman microscopy. J. Phys. Chem. Lett. 5, 2007–2011 (2014).
Yang, H. et al. A chemo-mechanical model of lithiation in silicon. J. Mech. Phys. Solids 70, 349–361 (2014).
Xie, Y., Qiu, M., Gao, X., Guan, D. & Yuan, C. Phase field modeling of silicon nanowire based lithium ion battery composite electrode. Electrochim. Acta 186, 542–551 (2015).
Bucci, G., Nadimpalli, S. P. V., Sethuraman, V. A., Bower, A. F. & Guduru, P. R. Measurement and modeling of the mechanical and electrochemical response of amorphous Si thin film electrodes during cyclic lithiation. J. Mech. Phys. Solids 62, 276–294 (2014).
Pal, S. et al. Modeling the delamination of amorphous-silicon thin film anode for lithium-ion battery. J. Power Sources 246, 149–159 (2014).
De, S., Gordon, J. & Sikha, G. Mathematical model for silicon electrode–Part II. Simulations on different electrode nanostructures. J. Power Sources 262, 524–533 (2014).
Sikha, G., De, S. & Gordon, J. Mathematical model for silicon electrode–Part I. 2-d model. J. Power Sources 262, 514–523 (2014).
Zuo, P. & Zhao, Y.-P. A phase field model coupling lithium diffusion and stress evolution with crack propagation and application in lithium ion batteries. Phys. Chem. Chem. Phys. 17, 287–297 (2015).
Hakim, V. & Karma, A. Laws of crack motion and phase-field models of fracture. J. Mech. Phys. Solids 57, 342–368 (2009).
Aranson, I. S., Kalatsky, V. A. & Vinokur, V. M. Continuum field description of crack propagation. Phys. Rev. Lett. 85, 118 (2000).
Bhandakkar, T. K. & Gao, H. Cohesive modeling of crack nucleation under diffusion induced stresses in a thin strip: implications on the critical size for flaw tolerant battery electrodes. Int. J. Solids Struct. 47, 1424–1434 (2010).
Bhandakkar, T. K. & Gao, H. Cohesive modeling of crack nucleation in a cylindrical electrode under axisymmetric diffusion induced stresses. Int. J. Solids Struct. 48, 2304–2309 (2011).
Woodford, W. H., Chiang, Y.-M. & Carter, W. C. “Electrochemical shock” of intercalation electrodes: a fracture mechanics analysis. J. Electrochem. Soc. 157, A1052 (2010).
Zhu, M., Park, J. & Sastry, A. M. Fracture analysis of the cathode in Li-ion batteries: a simulation study. J. Electrochem. Soc. 159, A492–A498 (2012).
Gao, Y. F. & Zhou, M. Coupled mechano-diffusional driving forces for fracture in electrode materials. J. Power Sources 230, 176–193 (2013).
Klinsmann, M., Rosato, D., Kamlah, M. & McMeeking, R. M. Modeling crack growth during Li insertion in storage particles using a fracture phase field approach. J. Mech. Phys. Solids 92, 313–344 (2016).
Zhao, K., Pharr, M., Vlassak, J. J. & Suo, Z. Fracture of electrodes in lithium-ion batteries caused by fast charging. J. Appl. Phys. 108, 073517 (2010).
Huttin, M. & Kamlah, M. Phase-field modeling of stress generation in electrode particles of lithium ion batteries. J. Appl. Phys. 101, 133902 (2012).
Liang, L. & Chen, L.-Q. Nonlinear phase field model for electrodeposition in electrochemical systems. Appl. Phys. Lett. 105, 263903 (2014).
Miehe, C., Dal, H., Schänzel, L. M. & Raina, A. A phase-field model for chemo-mechanical induced fracture in lithium-ion battery electrode particles. Int. J. Numer. Meth. Eng. 106, 683–711 (2016).
Zhao, Y., Xu, B.-X., Stein, P. & Gross, D. Phase-field study of electrochemical reactions at exterior and interior interfaces in Li-ion battery electrode particles. Comp. Methods Appl. Mech. Engrg. 312, 428–446 (2016).
Guan, P. & Liu, L. Phase-field simulation of lithium-ion diffusion in solid electrolyte interphase. ECS Trans. 66, 81–91 (2015).
Cheng, X.-B., Zhang, R., Zhao, C.-Z. & Zhang, Q. Toward safe lithium metal anode in rechargeable batteries: a review. Chem. Rev. 117, 10403–10473 (2017).
Yang, H. et al. Recent progress and perspective on lithium metal anode protection. Energy Storage Mater. 14, 199–221 (2018).
Zheng, G. et al. Interconnected hollow carbon nanospheres for stable lithium metal anodes. Nat. nanotechnol. 9, 618–623 (2014).
Liu, W., Lin, D., Pei, A. & Cui, Y. Stabilizing lithium metal anodes by uniform Li-ion flux distribution in nanochannel confinement. J. Am. Chem. Soc. 138, 15443–15450 (2016).
Monroe, C. & Newman, J. Dendrite growth in lithium/polymer systems. J. Electrochem. Soc. 150, A1377–A1384 (2003).
Guyer, J. E., Boettinger, W. J., Warren, J. A. & McFadden, G. B. Phase field modeling of electrochemistry. I. Equilibrium. Phys. Rev. E 69, 021603 (2004).
Guyer, J. E., Boettinger, W. J., Warren, J. A. & McFadden, G. B. Phase field modeling of electrochemistry II: kinetics. Phys. Rev. E 69, 021604 (2004).
Shibuta, Y., Okajima, Y. & Suzuki, T. Phase-field modeling for electrodeposition process. Sci. Tech. Adv. Mater. 8, 511–518 (2007).
Ely, D. R., Jana, A. & García, R. E. Phase field kinetics of lithium electrodeposits. J. Power Sources 272, 581–594 (2014).
Jana, A., Ely, D. R. & García, R. E. Dendrite-separator interactions in lithium-based batteries. J. Power Sources 275, 912–921 (2015).
Liang, L. et al. Nonlinear phase-field model for electrode-electrolyte interface evolution. Phys. Rev. E 86, 051609 (2012).
DeWitt, S., Hahn, N., Zavadil, K. & Thornton, K. Computational examination of orientation-dependent morphological evolution during the electrodeposition and electrodissolution of magnesium. J. Electrochem. Soc. 163, A513–A521 (2016).
Enrique, R. A., DeWitt, S. & Thornton, K. Morphological stability during electrodeposition. MRS Commun. 7, 658–663 (2017).
Chen, L. et al. Modulation of dendritic patterns during electrodeposition: A nonlinear phase-field model. J. Power Sources 300, 376–385 (2015).
Yurkiv, V., Foroozan, T., Ramasubramanian, A., Shahbazian-Yassar, R. & Mashayek, F. Phase-field modeling of solid electrolyte interface (SEI) influence on Li dendritic behavior. Electrochim. Acta 265, 609–619 (2018).
Yurkiv, V., Foroozan, T., Ramasubramanian, A., Shahbazian-Yassar, R. & Mashayek, F. The influence of stress field on Li electrodeposition in Li-metal battery. MRS Commun. 8, 1285–1291 (2018).
Zhang, X. et al. Rethinking how external pressure can suppress dendrites in lithium metal batteries. J. Electrochem. Soc. 166, A3639–A3652 (2019).
Hong, Z. & Viswanathan, V. Phase-field simulations of lithium dendrite growth with open-source software. ACS Energy Lett. 3, 1737–1743 (2018).
Mu, W., Liu, X., Wen, Z. & Liu, L. Numerical simulation of the factors affecting the growth of lithium dendrites. J. Energy Storage 26, 100921 (2019).
Zhang, R., Shen, X., Cheng, X.-B. & Zhang, Q. The dendrite growth in 3D structured lithium metal anodes: electron or ion transfer limitation? Energy Storage Mater. 23, 556–565 (2019).
Xu, B. et al. Engineering interfacial adhesion for high-performance lithium metal anode. Nano Energy 67, 104242 (2020).
Yan, H. H., Bie, Y. H., Cui, X. Y., Xiong, G. P. & Chen, L. A computational investigation of thermal effect on lithium dendrite growth. Energy Convers. Manage. 161, 193–204 (2018).
Hong, Z. & Viswanathan, V. Prospect of thermal shock induced healing of lithium dendrite. ACS Energy Lett. 4, 1012–1019 (2019).
Cogswell, D. A. Quantitative phase-field modeling of dendritic electrodeposition. Phys. Rev. E 92, 011301 (2015).
Wang, K. et al. Dendrite growth in the recharging process of zinc–air battery. J. Mater. Chem. A 3, 22648–22655 (2015).
Wang, K., Xiao, Y., Pei, P., Liu, X. & Yichun, Wang A phase-field model of dendrite growth of electrodeposited zinc. J. Electrochem. Soc. 166, D389–D394 (2019).
Yurkiv, V. et al. Understanding Zn electrodeposits morphology in secondary batteries using phase-field model. J. Electrochem. Soc. 167, 060503 (2020).
Hong, Z., Ahmad, Z. & Viswanathan, V. Design principles for dendrite suppression with porous polymeraqueous solution hybrid electrolyte for Zn metal anodes. ACS Energy Lett. 5, 2466–2474 (2020).
Kim, S. G., Kim, W. T. & Suzuki, T. Phase-field model for binary alloys. Phys. Rev. E 60, 7186 (1999).
Zhang, L. & Steinbach, I. Phase-field model with finite interface dissipation: Extension to multi-component multi-phase alloys. Acta Mater. 60, 2702–2710 (2012).
Steinbach, I., Zhang, L. & Plapp, M. Phase-field model with finite interface dissipation. Acta Mater. 60, 2689–2701 (2012).
Shi, S. et al. Multi-scale computation methods: their applications in lithium-ion battery research and development. Chin. Phys. B 25, 018212 (2016).
Zou, Z. et al. Mobile ions in composite solids. Chem. Rev. 120, 4169–4221 (2020).
Shu, Q., Chen, L., Xia, Y., Gong, X. & Gu, X. Proton-induced dysfunction mechanism of cathodes in an aqueous lithium ion battery. J. Phys. Chem. C 117, 6929–6932 (2013).
Liu, Y. et al. Nanostructured alkali cation incorporated δ-MnO2 cathode materials for aqueous sodium-ion batteries. J. Mater. Chem. A 3, 7780–7785 (2015).
Wang, A., Kadam, S., Li, H., Shi, S. & Qi, Y. Review on modeling of the anode solid electrolyte interphase (SEI) for lithium-ion batteries. npj Comput. Mater. 4, 15 (2018).
Hong, Z. et al. Open-sourcing phase-field simulations for accelerating energy materials design and optimization. ACS Energy Lett. 5, 3254–3259 (2020).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (numbers U2030206, 51802187, and 11874254), Shanghai Pujiang Program (number 2019PJD016), and Shanghai Sailing Program (number 18YF1408700).
Author information
Authors and Affiliations
Contributions
All authors contributed to collecting the references and outlining the review paper. Q.W., Y.L., and G.Z. drafted the review. S.S. led the writing of the review. All authors participated in revising the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Q., Zhang, G., Li, Y. et al. Application of phase-field method in rechargeable batteries. npj Comput Mater 6, 176 (2020). https://doi.org/10.1038/s41524-020-00445-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00445-w
This article is cited by
-
Thermodynamics of multi-sublattice battery active materials: from an extended regular solution theory to a phase-field model of LiMnyFe1-yPO4
npj Computational Materials (2023)
-
Understanding and design of metallic alloys guided by phase-field simulations
npj Computational Materials (2023)
-
A Second-order Time-Accurate Unconditionally Stable Method for a Gradient Flow for the Modica–Mortola Functional
Journal of Scientific Computing (2023)
-
Chemo-mechanical coupling phase-field modeling of lithium dendrite growth within solid electrolyte
Journal of Solid State Electrochemistry (2023)
-
Recent Computational Approaches for Accelerating Dendrite Growth Prediction: A Short Review
Multiscale Science and Engineering (2023)